Natural Vegetation Area Design in an Arid Region Based on Water Resource Carrying Capacity—Taking Minqin County as an Example
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Data Processing
2.3.1. Water Supply Design for NVDA Solutions
2.3.2. Development Model Design for NVDA Solution
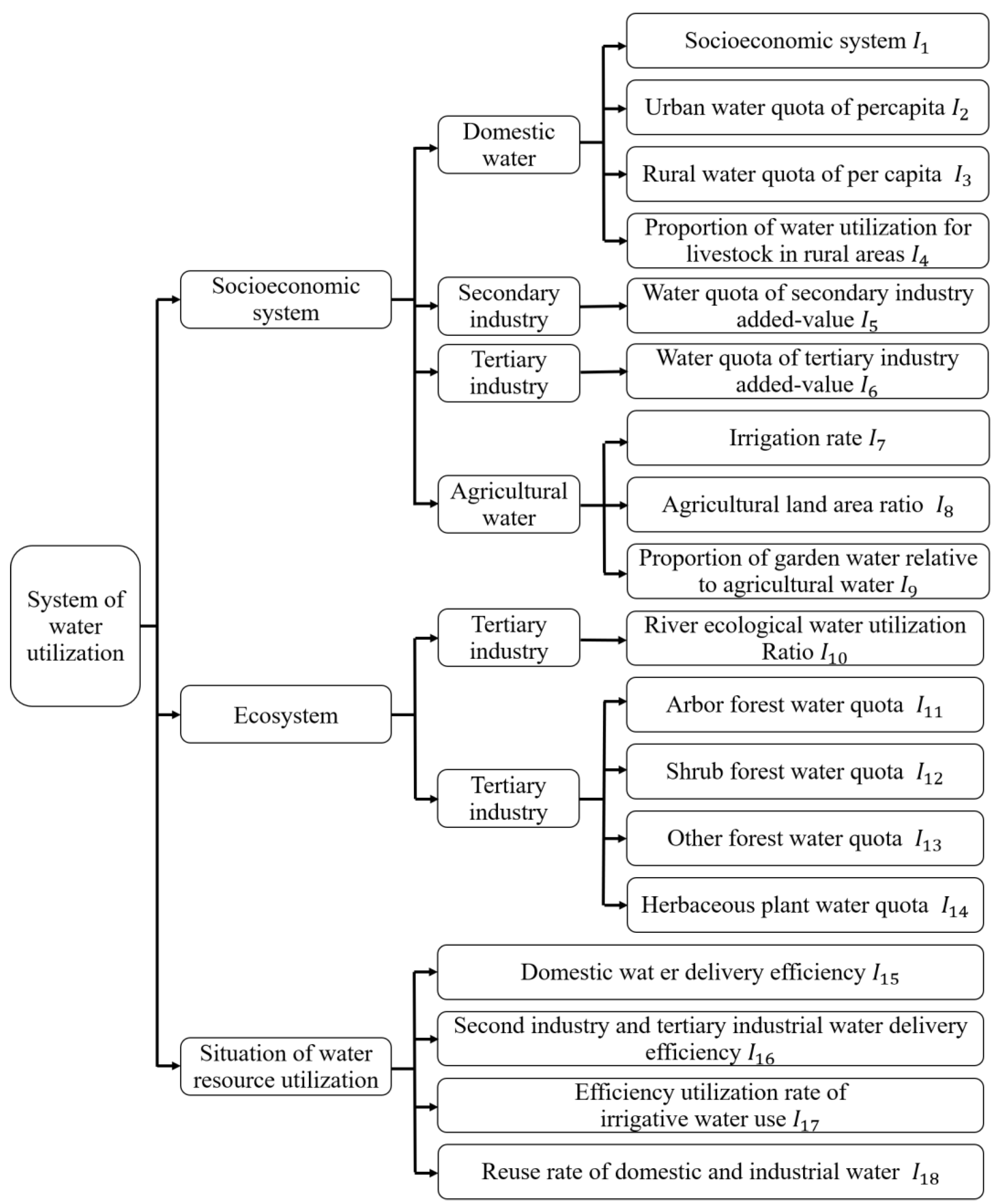
2.3.3. Evaluation Indicators in Development Model Evaluation
2.3.4. Vegetation Water Demand Quota Calculation
2.3.5. Groundwater Evaporation Intensity Calculation
2.3.6. Vegetation coefficient calculation
2.3.7. NVDA Calculation
2.3.8. NVDA Evaluation
3. Results and Analysis
3.1. Preferred Method for Calculating Groundwater Evaporation Intensity
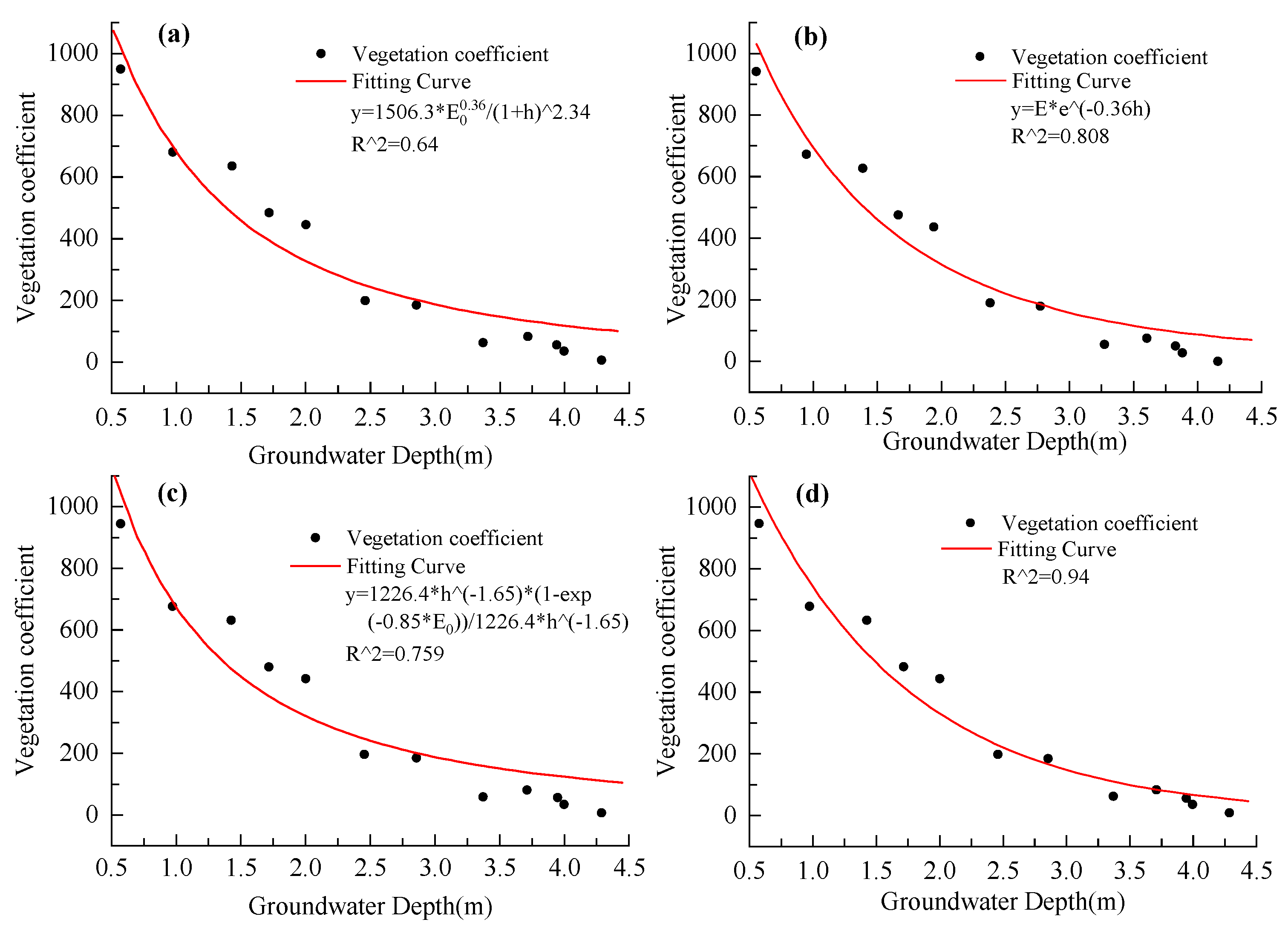
3.2. Trend of Vegetation Coefficient with Depth of Groundwater Burial
3.3. NVDA under Different Developmental Models
3.4. Water Ecological Status of Natural Vegetation under Different Developmental Patterns
4. Discussion
4.1. Feasibility of Predicting Natural Vegetation Design in Arid Areas Based on NVDA
4.2. Strategies for Meeting the Sustainable Supply of Regional Water Resource Carrying Capacity
4.3. Reliability of the Results of Natural Vegetation Area Calculation Based on NDVI
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.N.; Li, Z.Q.; Xu, J.H.; Shen, Y.J.; Xing, X.X.; Xie, T.; Li, Z.; Yang, L.S.; Xi, H.Y.; Zhu, C.G.; et al. Changes and protection suggestions in water resources and ecological environment in arid region of Northwest China. Bull. Chin. Acad. Sci. 2023, 38, 385–393. [Google Scholar] [CrossRef]
- Yin, J.; Slater, L.; Gu, L.; Liao, Z.; Guo, S.; Gentine, P. Global Increases in Lethal Compound Heat Stress: Hydrological Drought Hazards Under Climate Change. Geophys. Res. Lett. 2022, 49, e2022GL100880. [Google Scholar] [CrossRef]
- Lv, B.; Liu, C.; Li, T.; Meng, F.; Fu, Q.; Ji, Y.; Hou, R. Evaluation of the Water Resource Carrying Capacity in Heilongjiang, Eastern China, Based on the Improved TOPSIS Model. Ecol. Indic. 2023, 150, 110208. [Google Scholar] [CrossRef]
- Song, X.; Kong, F.; Zhan, C. Assessment of Water Resources Carrying Capacity in Tianjin City of China. Water Resour. Manag. 2011, 25, 857–873. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S.; Zhang, H.; Wang, Z.; Zhou, C.; Chen, X. Determination of Ecological Flow Thresholds for Rainfall-Recharging Rivers Based on Multiple Hydrological Methods. Front. Environ. Sci. 2023, 11, 1116633. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, Y.; Niu, J.; Gui, D.; Hu, B.X. Prediction of the Irrigation Area Carrying Capacity in the Tarim River Basin under Climate Change. Agriculture 2022, 12, 657. [Google Scholar] [CrossRef]
- Xie, M.; Zhang, C.; Zhang, J.; Wang, G.; Jin, J.; Liu, C.; He, R.; Bao, Z. Projection of Future Water Resources Carrying Capacity in the Huang-Huai-Hai River Basin under the Impacts of Climate Change and Human Activities. Water 2022, 14, 2006. [Google Scholar] [CrossRef]
- Ren, L.; Gao, J.; Song, S.; Li, Z.; Ni, J. Evaluation of Water Resources Carrying Capacity in Guiyang City. Water 2021, 13, 2155. [Google Scholar] [CrossRef]
- Li, J.; Zhong, Y.D.; Wang, Z.L.; Sun, X. Research progress in environmental carrying capacity of eco-tourism in China. Chin. J. Ecol. 2006, 25, 1141–1146. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Lei, K.; Meng, W.; Khu, S.-T. Industrial Structural Upgrading and Spatial Optimization Based on Water Environment Carrying Capacity. J. Clean Prod. 2017, 165, 1462–1472. [Google Scholar] [CrossRef]
- Wang, P.; Wei, Y.; Zhong, F.; Song, X.; Wang, B.; Wang, Q. Evaluation of Agricultural Water Resources Carrying Capacity and Its Influencing Factors: A Case Study of Townships in the Arid Region of Northwest China. Agriculture 2022, 12, 700. [Google Scholar] [CrossRef]
- Chi, M.; Zhang, D.; Zhao, Q.; Yu, W.; Liang, S. Determining the Scale of Coal Mining in an Ecologically Fragile Mining Area under the Constraint of Water Resources Carrying Capacity. J. Environ. Manag. 2021, 279, 111621. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Xiao, C.; Qi, Z.; Meng, F.; Liang, X. Development Tendency Analysis for the Water Resource Carrying Capacity Based on System Dynamics Model and the Improved Fuzzy Comprehensive Evaluation Method in the Changchun City, China. Ecol. Indic. 2021, 122, 107232. [Google Scholar] [CrossRef]
- Dai, D.; Sun, M.; Lv, X.; Lei, K. Evaluating Water Resource Sustainability from the Perspective of Water Resource Carrying Capacity, a Case Study of the Yongding River Watershed in Beijing-Tianjin-Hebei Region, China. Environ. Sci. Pollut. R 2020, 27, 21590–21603. [Google Scholar] [CrossRef] [PubMed]
- Ren, B.; Sun, B.; Shi, X.; Zhao, S.; Wang, X. Analysis of the Cooperative Carrying Capacity of Ulan Suhai Lake Based on the Coupled Water Resources–Water Environment–Water Ecology System. Water 2022, 14, 3102. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Q.; Cai, J. Research on the Urban Water Resources Carrying Capacity by Using System Dynamics Simulation. Hydrol. Res. 2023, 54, 418–434. [Google Scholar] [CrossRef]
- Meng, C.; Wang, X.; Li, Y. An Optimization Model for Water Management Based on Water Resources and Environmental Carrying Capacities: A Case Study of the Yinma River Basin, Northeast China. Water 2018, 10, 565. [Google Scholar] [CrossRef]
- Qin, G.; Li, H.; Wang, X.; Ding, J. Research on Water Resources Design Carrying Capacity. Water-Sui 2016, 8, 157. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, S.; Guo, X.; Cheng, L.; Guo, Y.; Ding, A. Interannual Variation in Riparian Vegetation Cover and Its Relationship with River Flow under a High Level of Human Intervention: An Example from the Yongding River Basin. Environ. Monit. Assess. 2021, 193, 406. [Google Scholar] [CrossRef]
- Xue, Y.; Lu, H.; Guan, Y.; Tian, P.; Yao, T. Impact of Thermal Condition on Vegetation Feedback under Greening Trend of China. Sci. Total Environ. 2021, 785, 147380. [Google Scholar] [CrossRef]
- Duan, Y.; Tang, J.; Li, Z.; Yang, Y.; Dai, C.; Qu, Y.; Lv, H. Optimal Planning and Management of Land Use in River Source Region: A Case Study of Songhua River Basin, China. IJERPH 2022, 19, 6610. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Shi, M.; Liu, C.; Wang, B.; Kang, H.; Hu, X. Changes of Ecosystem Services and Landscape Patterns in Mountainous Areas: A Case Study in the Mentougou District in Beijing. Sustainability 2018, 10, 3689. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.; Wang, X.; Jin, Z.; Chen, F. Multi-Level Fuzzy Comprehensive Evaluation for Water Resources Carrying Capacity in Xuzhou City, China. Sustainability 2023, 15, 11369. [Google Scholar] [CrossRef]
- Aarnoudse, E.; Bluemling, B.; Qu, W.; Herzfeld, T. Groundwater Regulation in Case of Overdraft: National Groundwater Policy Implementation in North-West China. Int. J. Water Resour. D 2019, 35, 264–282. [Google Scholar] [CrossRef]
- Hao, Y.; Xie, Y.; Ma, J.; Zhang, W. The Critical Role of Local Policy Effects in Arid Watershed Groundwater Resources Sustainability: A Case Study in the Minqin Oasis, China. Sci. Total Environ. 2017, 601–602, 1084–1096. [Google Scholar] [CrossRef]
- Duan, C.Q.; Liu, C.M.; Chen, X.N.; Liu, W.H.; Zheng, H.X. Preliminary Research on Regional Water Resources Carrying Capacity Conception and Method. Acta Geogr. Sin. 2010, 65, 82–90. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, Y.; Li, W. Ecological Water Demand of Natural Vegetation in the Lower Tarim River. J. Geogr. Sci. 2010, 20, 261–272. [Google Scholar] [CrossRef]
- Gupta, P.; Sarma, K. Variations in Groundwater Quality under Different Vegetation Types in Delhi, India. IJPE 2016, 2, 69–72. [Google Scholar] [CrossRef]
- Ye, S.T.; Shi, X.F.; Miao, X.F. Analysis of water supply problem using the empirical formula of diving evaporation. Hydrogeol. Eng. Geol. 1982, 4, 49–52+10. [Google Scholar] [CrossRef]
- Shen, L.C. Discussion on the experience formula of diving evaporation. J. Hydraul. Eng. 1985, 7, 36–42. [Google Scholar] [CrossRef]
- Lei, Z.D.; Yang, S.X.; Xie, S.C. Analysis and empirical formula for stable evaporation of diving. J. Hydraul. Eng. 1984, 8, 62–66. [Google Scholar] [CrossRef]
- Tang, H.X.; Su, Y.S.; Zhang, H.P. Experimental study on evaporation of phreatic water and improvement of its empirical formula. J. Hydraul. Eng. 1989, 10, 37–44. [Google Scholar] [CrossRef]
- Poon, S.H.; Rockinger, M.; Tawn, J. Extreme Value Dependence in Financial Markets: Diagnostics, Models, and Financial Implications. Rev. Financ. Stud. 2004, 17, 581–610. [Google Scholar] [CrossRef]
- Neri, F.; Tirronen, V. Scale Factor Local Search in Differential Evolution. Memetic. Comp. 2009, 1, 153–171. [Google Scholar] [CrossRef]
- Jiang, T.L.; Zhang, H.J.; Ma, G.J.; Shi, Y.Y.; Wang, Y.Y. Study on indirect calculation method parameters for ecological water requirement of vegetation in arid area. J. Water Resour. Water Eng. 2019, 30, 254–260. [Google Scholar]
- Yang, X.Y.; Zhang, X.; Cai, H.J. Study on Ecological Water Demand of Minqin County in the Lower Reaches of Shiyang River Basin. Agric. Res. Arid. Reg. 2006, 24, 169–173. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, Q.; Liao, S. Spatio-Temporal Characteristics of Water Ecological Footprint and Countermeasures for Water Sustainability in Japan. Int. J. Env. Res. Pub. Health 2022, 19, 10380. [Google Scholar] [CrossRef]
- Guo, Y.; Shao, J.; Zhang, Q.; Cui, Y. Relationship between Water Surface Area of Qingtu Lake and Ecological Water Delivery: A Case Study in Northwest China. Sustainability 2021, 13, 4684. [Google Scholar] [CrossRef]
- Hao, B.; Su, X.L.; Ma, X.Y. Study on ecological water requirement for natural vegetation in Minqin County of Gansu Province. J. Northwest. AF Univ. Nat. Sci. Ed. 2010, 38, 158–164. [Google Scholar]
- Yue, C.; Wang, Q.; Li, Y. Evaluating Water Resources Allocation in Arid Areas of Northwest China Using a Projection Pursuit Dynamic Cluster Model. Water Supply 2019, 19, 762–770. [Google Scholar] [CrossRef]
- Li, J.; Lei, X.; Fu, Q.; Li, T.; Qiao, Y.; Chen, L.; Liao, W. Multi-Scale Research of Time and Space Differences about Ecological Footprint and Ecological Carrying Capacity of the Water Resources. Appl. Water Sci. 2018, 8, 22. [Google Scholar] [CrossRef]
- Li, B.; Wang, X.; Wei, T.; Zeng, Y.; Zhang, B. Analysis of Sustainable Utilization of Water Resources in Karst Region Based on the Ecological Footprint Model—Liupanshui City Case. J. Water Supply Res. Technol. Aqua. 2018, 67, 566–575. [Google Scholar] [CrossRef]
- Gao, P.; Niu, X.; Wang, B.; Zheng, Y. Land Use Changes and Its Driving Forces in Hilly Ecological Restoration Area Based on Gis and Rs of Northern China. Sci. Rep. 2015, 5, 11038. [Google Scholar] [CrossRef]
- Shen, G.; Yang, X.; Jin, Y.; Luo, S.; Xu, B.; Zhou, Q. Land Use Changes in the Zoige Plateau Based on the Object-Oriented Method and Their Effects on Landscape Patterns. Remote Sens. 2019, 12, 14. [Google Scholar] [CrossRef]
- Xue, X.; Liao, J.; Hsing, Y.; Huang, C.; Liu, F. Policies, Land Use, and Water Resource Management in an Arid Oasis Ecosystem. Environ. Manag. 2015, 55, 1036–1051. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, Y.; Li, W. Ecological Water Rights and Water-Resource Exploitation in the Three Headwaters of the Tarim River. Quatern Int. 2014, 336, 20–25. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Ma, W.; Zhou, Q. Assessment of the Carrying Capacity and Suitability of Spatial Resources and the Environment and Diagnosis of Obstacle Factors in the Yellow River Basin. IJERPH 2023, 20, 3496. [Google Scholar] [CrossRef]
- Shao, M.; Wang, Y.; Xia, Y.; Jia, X. Soil Drought and Water Carrying Capacity for Vegetation in the Critical Zone of the Loess Plateau: A Review. Vadose Zone J. 2018, 17, 1–8. [Google Scholar] [CrossRef]
- Bartholomeus, R.P.; Stagge, J.H.; Tallaksen, L.M.; Witte, J.P.M. Sensitivity of Potential Evaporation Estimates to 100 Years of Climate Variability. Hydrol. Earth Syst. Sci. 2015, 19, 997–1014. [Google Scholar] [CrossRef]


| Region Type | Small-Scale Region | Mid-Scale Region | Large-Scale Region |
|---|---|---|---|
| Water-rich area | 85% | 90% | 95% |
| Water-scarce area | 80% | 85% | 90% |
| Formula Number | Formula Name | Formula Form | References |
|---|---|---|---|
| 1 | Shen | [30] | |
| 2 | Ye | [29] | |
| 3 | Lei | [31] | |
| 4 | Mao | [35] | |
| 5 | Zhang | ||
| 6 | Anti-log | ||
| 7 | Shu | ||
| 8 | Averyanov |
| Groundwater depth (m) | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
| Vegetation coefficient | 1.98 | 1.63 | 1.56 | 1.45 | 1.38 | 1.29 | 1.00 |
| Type | Subtype | WREPI |
|---|---|---|
| Ecological safety | I | <0.25 |
| II | 0.25–0.50 | |
| III | 0.50–0.75 | |
| Ecological alarm | I | 0.75–1.00 |
| II | 1.00–1.25 | |
| Ecological insecurity | I | 1.25–1.50 |
| II | 1.50–1.75 | |
| III | >1.75 |
| Equation | Phreatic Water Evaporation at Different Depths (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.25 | ||||
| Shen’s equation | 1042.89 | 617.84 | 325.75 | 264.10 | 153.24 | 115.88 | 87.66 | 85.38 | 0.92 | 0.71 | 0.91 |
| Ye’s equation | 1056.18 | 669.79 | 345.80 | 268.16 | 125.05 | 79.13 | 47.58 | 45.23 | 0.92 | 0.71 | 0.90 |
| Le’s equation | 1056.88 | 624.00 | 319.03 | 258.77 | 120.76 | 104.08 | 92.76 | 83.25 | 0.91 | 0.71 | 0.91 |
| Optimization results | 1051.11 | 652.30 | 338.14 | 266.61 | 142.48 | 101.84 | 72.35 | 70.04 | 0.93 | 0.71 | 0.93 |
| Zhang’s results | 993.10 | 706.86 | 360.60 | 274.55 | 163.59 | 150.27 | 94.34 | 83.13 | 1.00 | 0.71 | 1.00 |
| Arbor | Shrubs | Herbals | Other Forests | |
|---|---|---|---|---|
| Groundwater depth (m) | 2.0–4.5 | 3.0–4.0 | 3.0–4.5 | 3.5–4.5 |
| Calculation depth (m) | 3.3 | 3.5 | 3.7 | 4.0 |
| Vegetation coefficient () | 1.324 | 1.253 | 1.167 | 1.016 |
| Phreatic water evaporation () (mm) | 153.06 | 134.38 | 118.53 | 99.01 |
| Vegetation water requirement quota () (mm) | 202.65 | 168.38 | 138.33 | 100.59 |
| Indicators | Development Model in 2017 | Development Model in 2025 | ||||
|---|---|---|---|---|---|---|
| Stability | Recovery | Optimization | Stability | Recovery | Optimization | |
| 34.33% | 39.33% | 44.33% | 53.60% | 58.60% | 63.60% | |
| 0.095 | 0.105 | 0.115 | 0.095 | 0.105 | 0.115 | |
| 0.040 | 0.050 | 0.060 | 0.040 | 0.050 | 0.060 | |
| 14% | 15% | 16% | 15% | 16% | 17% | |
| 62 | 57 | 52 | 59 | 54 | 49 | |
| 6 | 5 | 4 | 5 | 4 | 3 | |
| 4000 | 3800 | 3600 | 3800 | 3600 | 3400 | |
| 7.47% | 6.47% | 5.47% | 6.47% | 5.47% | 4.47% | |
| 3% | 5% | 7% | 5% | 7% | 9% | |
| 70% | 68% | 66% | 70% | 68% | 66% | |
| 3300 | 3300 | 3300 | 3300 | 3300 | 3300 | |
| 2850 | 2850 | 2850 | 2850 | 2850 | 2850 | |
| 2100 | 2100 | 2100 | 2100 | 2100 | 2100 | |
| 1950 | 1950 | 1950 | 1950 | 1950 | 1950 | |
| 0.9 | 0.91 | 0.92 | 0.91 | 0.92 | 0.93 | |
| 0.91 | 0.92 | 0.93 | 0.92 | 0.93 | 0.94 | |
| 0.43 | 0.44 | 0.45 | 0.64 | 0.65 | 0.66 | |
| 40% | 42% | 44% | 66% | 68% | 70% | |
| Stability | Recovery | Optimization | |
|---|---|---|---|
| Arbor forest area () | 6204.22 | 7064.08 | 7976.10 |
| Shrub forest area () | 391,451.98 | 445,703.98 | 503,247.95 |
| Herbaceous area () | 240,138.00 | 273,419.13 | 308,719.74 |
| Other forest area () | 24,134.20 | 27,479.00 | 31,026.76 |
| Stability | Recovery | Optimization | |
|---|---|---|---|
| Arbor forest area () | 7026.50 | 7869.03 | 8717.09 |
| Shrub forest area () | 443,333.45 | 496,492.24 | 549,999.91 |
| Herbaceous area () | 271,964.92 | 304,575.42 | 337,399.95 |
| Other forest area () | 27,332.85 | 30,610.25 | 33,909.16 |
| Vegetation Type | Development Mode | WRCC | WEF | Water Ecological Deficit (Surplus) | WREPI |
|---|---|---|---|---|---|
| Arbor area | Stability | 0.44 | 0.36 | 0.08 | 0.81 |
| Recovery | 0.66 | 0.30 | 0.55 | ||
| Optimization | 0.90 | 0.54 | 0.40 | ||
| Shrub area | Stability | 0.37 | 0.31 | 0.06 | 0.84 |
| Recovery | 0.55 | 0.24 | 0.57 | ||
| Optimization | 0.74 | 0.43 | 0.42 | ||
| Herbage area | Stability | 0.30 | 0.21 | 0.09 | 0.70 |
| Recovery | 0.45 | 0.24 | 0.47 | ||
| Optimization | 0.61 | 0.40 | 0.34 | ||
| The other forest area | Stability | 0.22 | 0.23 | −0.01 | 1.05 |
| Recovery | 0.33 | 0.10 | 0.70 | ||
| Optimization | 0.44 | 0.21 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yu, J.; Jiang, T.; Yu, S.; Zhou, C.; Li, F.; Chen, X. Natural Vegetation Area Design in an Arid Region Based on Water Resource Carrying Capacity—Taking Minqin County as an Example. Water 2023, 15, 3238. https://doi.org/10.3390/w15183238
Zhang H, Yu J, Jiang T, Yu S, Zhou C, Li F, Chen X. Natural Vegetation Area Design in an Arid Region Based on Water Resource Carrying Capacity—Taking Minqin County as an Example. Water. 2023; 15(18):3238. https://doi.org/10.3390/w15183238
Chicago/Turabian StyleZhang, Hengjia, Jiandong Yu, Tianliang Jiang, Shouchao Yu, Chenli Zhou, Fuqiang Li, and Xietian Chen. 2023. "Natural Vegetation Area Design in an Arid Region Based on Water Resource Carrying Capacity—Taking Minqin County as an Example" Water 15, no. 18: 3238. https://doi.org/10.3390/w15183238
APA StyleZhang, H., Yu, J., Jiang, T., Yu, S., Zhou, C., Li, F., & Chen, X. (2023). Natural Vegetation Area Design in an Arid Region Based on Water Resource Carrying Capacity—Taking Minqin County as an Example. Water, 15(18), 3238. https://doi.org/10.3390/w15183238





