Significant Increases in Water Vapor Pressure Correspond with Climate Warming Globally
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. GLDAS NOAH Data
2.1.2. NOAA GML Data
2.1.3. AVHRR NDVI Data
2.2. Methods
2.2.1. Linear Regression Model
2.2.2. Pearson Correlation Analysis
2.2.3. Partial Correlation Analysis
2.2.4. Mann–Kendall Nonparametric Test
2.2.5. Calculation of Vapor Pressure Deficit
3. Results
3.1. Spatiotemporal Characteristics of Global Warming
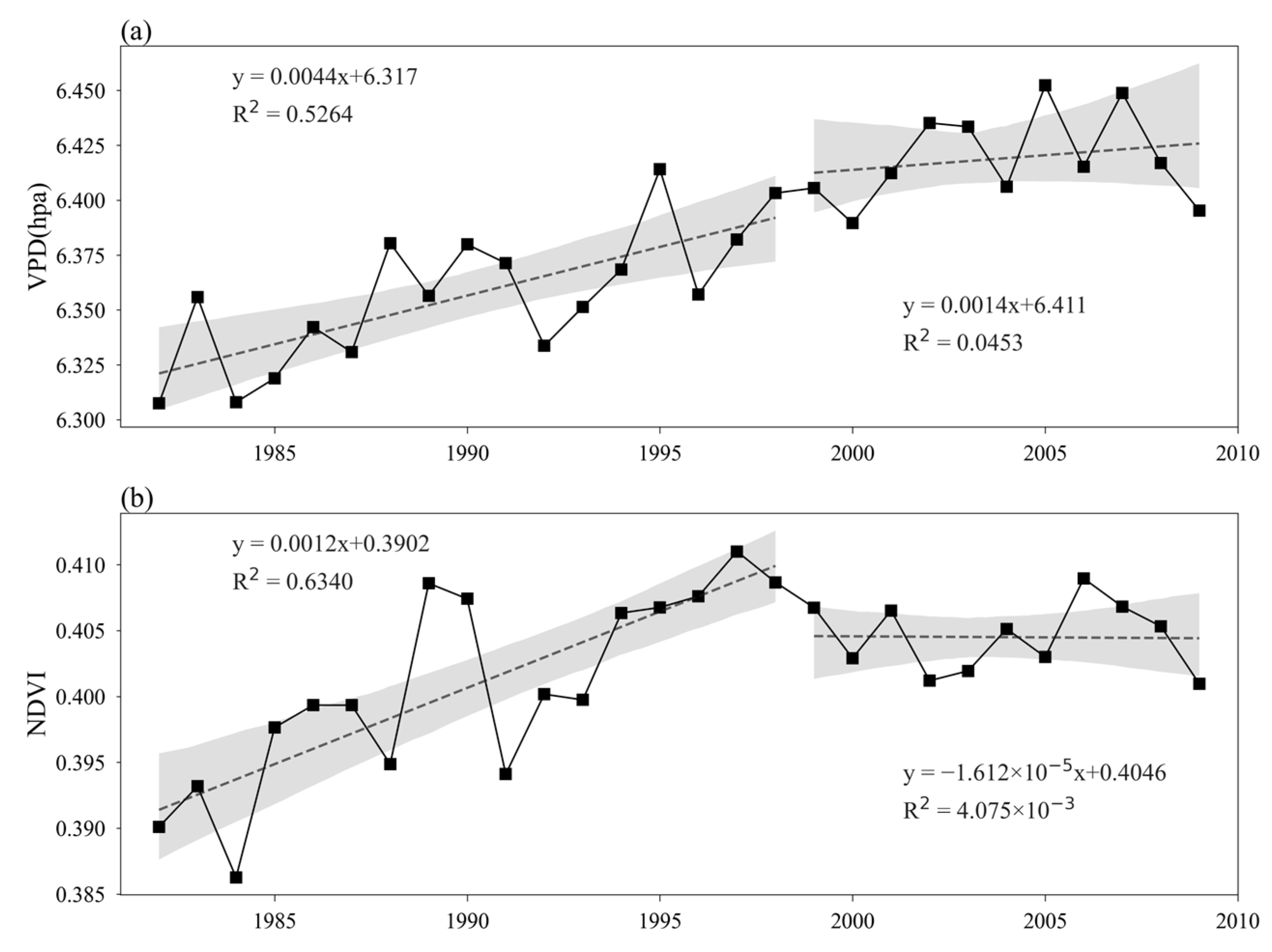
3.2. Variations in Climate Factors Characterizing Water Vapor
3.3. Increased VPD Determines Global Warming
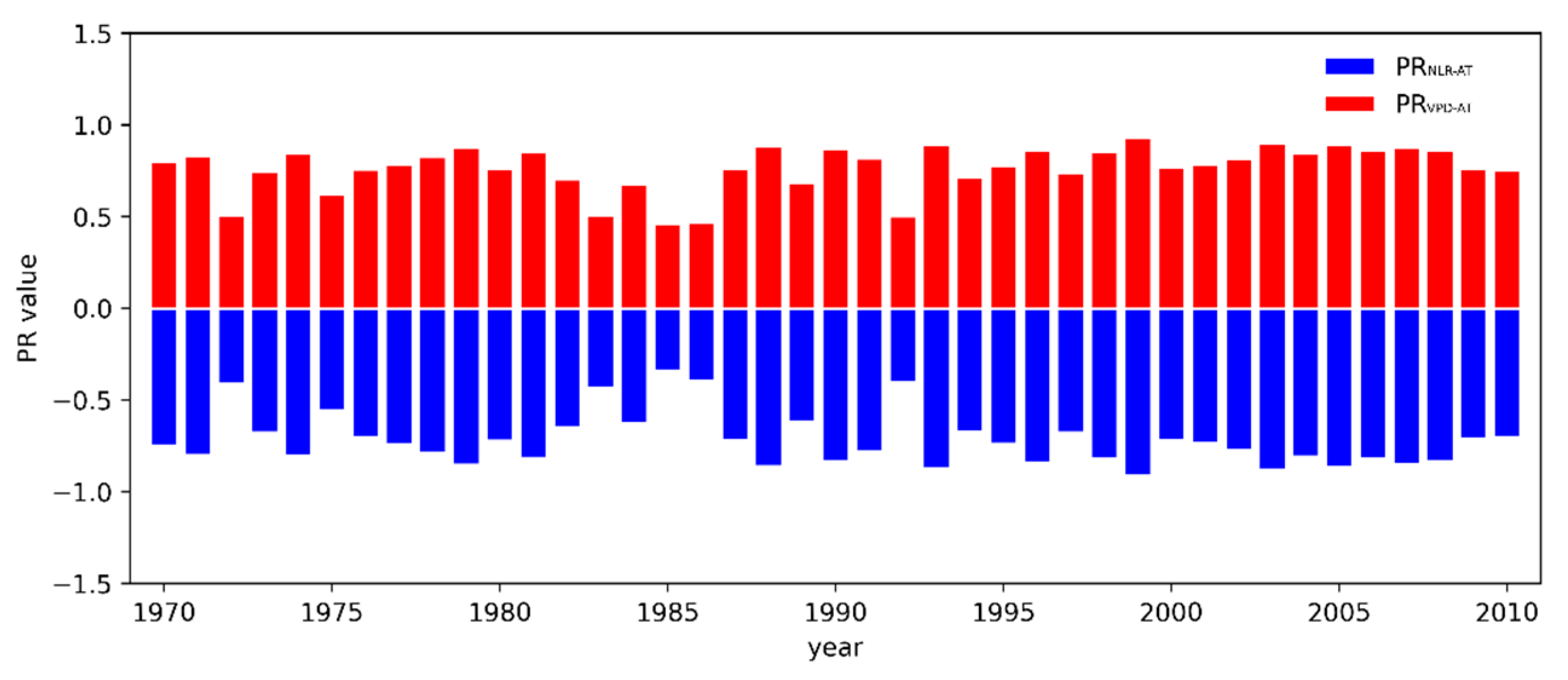
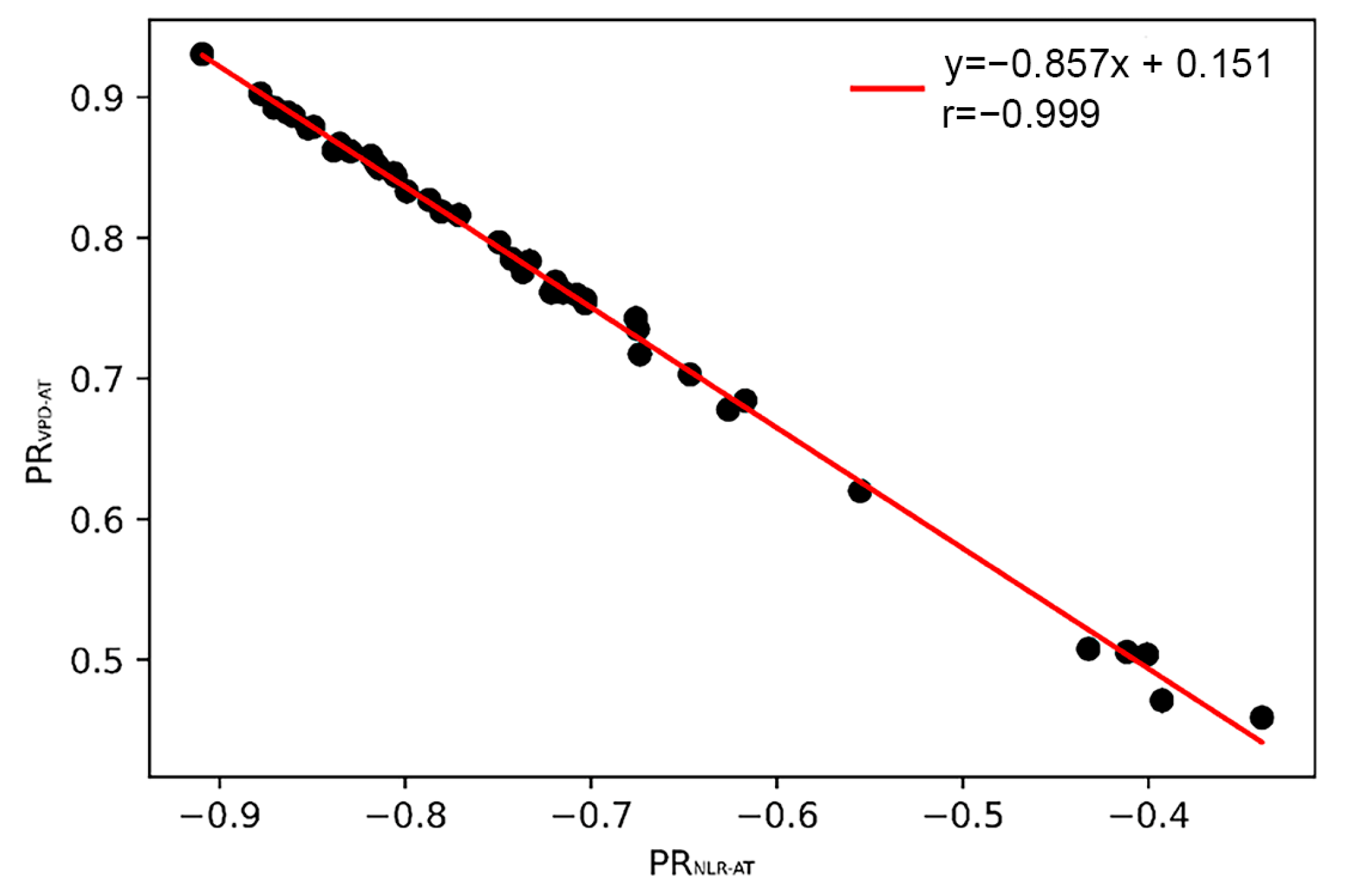
3.4. Mutual Effect between Global Warming and Water Vapor
3.4.1. Proposed Framework of Global Warming and Water Vapor Feedback
3.4.2. Quantitative Analysis on Mutual Effect between Global Warming and Water Vapor
3.5. Implications from the Response of Vegetation to VPD
4. Discussion
4.1. Enlightening of VPD and CO2 Effect on Global Warming
4.2. Uncertainty and Expectations for Future Studies
5. Conclusions
- (1)
- From 1970 to 2010, global air temperature, VPD, and specific humidity showed an increasing trend, with a significantly positive correlation. When both the actual water vapor content and the saturated water vapor increased, the rise in the actual water vapor was lower than that of the saturated water vapor pressure.
- (2)
- Compared with the increasing concentration of CO2, the increased VPD plays a more important role in global warming.
- (3)
- There was a strong complementary relationship between the contribution of net longwave radiation and water vapor to global warming, and the increase in saturated water vapor dominated the decrease in net longwave radiation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Name |
| VPD | Vapor pressure deficit |
| GLDAS | Global Land Data Assimilation System |
| NOAA | National Oceanic and Atmospheric Administration |
| GML | Global Monitoring Laboratory |
| NLR | Net longwave radiation |
| ENSO | El Niño-Southern Oscillation |
| DLR | Downward longwave radiation |
| RATPAC-A | Radiosonde Atmospheric Temperature Products for Assessing Climate dataset A |
| SWV | Stratospheric water vapor |
| GSFC | Goddard Space Flight Center |
| NCEP | National Center for Environmental Prediction |
| LSM | Land surface model |
| NDVI | Normalized difference vegetation index |
| ET | Evapotranspiration |
| AT | Air temperature |
| SH | Specific humidity |
| PRCO2–AT | Partial correlation coefficient between CO2 and air temperature |
| PRVPD–AT | Partial correlation coefficient between VPD and air temperature |
| PRNLR–AT | Partial correlation coefficient between NLR and air temperature |
References
- Hu, A.G. Global Climate Change and China’s Green Development. Chin. J. Popul. Resour. Environ. 2011, 9, 9–15. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Lang, P.A.; Gregory, K.B. Economic Impact of Energy Consumption Change Caused by Global Warming. Energies 2019, 12, 3575. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Burke, M. Global warming has increased global economic inequality. Proc. Natl. Acad. Sci. USA 2019, 116, 9808–9813. [Google Scholar] [CrossRef] [PubMed]
- Albouy, C.; Delattre, V.; Donati, G.; Frolicher, T.L.; Albouy-Boyer, S.; Rufino, M.; Pellissier, L.; Mouillot, D.; Leprieur, F. Global vulnerability of marine mammals to global warming. Sci. Rep. 2020, 10, 548. [Google Scholar] [CrossRef]
- Cai, W.; Ng, B.; Geng, T.; Wu, L.; Santoso, A.; McPhaden, M.J. Butterfly effect and a self-modulating El Nino response to global warming. Nature 2020, 585, 68. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, C.; Mueller, C.; Wang, C.; Ciais, P.; Janssens, I.; Penuelas, J.; Asseng, S.; Li, T.; Elliott, J.; et al. Emergent constraint on crop yield response to warmer temperature from field experiments. Nat. Sustain. 2020, 3, 908–916. [Google Scholar] [CrossRef]
- Zhao, T.; Tu, K.; Yan, Z. Advances of Atmospheric Water Vapor Change and Its Feedback Effect. Progress. Inquisitiones Mutat. Clim. 2013, 9, 79–88. [Google Scholar]
- Houghton, J.T. Climate Change 2001: The Scientific Basis: Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Al-Ghussain, L. Global warming: Review on driving forces and mitigation. Environ. Prog. Sustain. 2019, 38, 13–21. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Balmaseda, M.A. Earth’s Energy Imbalance. J. Clim. 2014, 27, 3129–3144. [Google Scholar] [CrossRef]
- Lesins, G.; Duck, T.J.; Drummond, J.R. Surface Energy Balance Framework for Arctic Amplification of Climate Change. J. Clim. 2012, 25, 8277–8288. [Google Scholar] [CrossRef]
- Zeppetello, L.R.V.; Donohoe, A.; Battisti, D.S. Does Surface Temperature Respond to or Determine Downwelling Longwave Radiation? Geophys. Res. Lett. 2019, 46, 2781–2789. [Google Scholar] [CrossRef]
- Wild, M. Decadal changes in radiative fluxes at land and ocean surfaces and their relevance for global warming. Wires Clim. Chang. 2016, 7, 91–107. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhou, S.X. The study on the enhanced greenhouse effect of water vapor. Energy Conserv. 2012, 7, 11–13+39. [Google Scholar]
- Landman, W. Climate change 2007: The physical science basis. S. A. Geogr. J. 2010, 92, 86–87. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Miao, Q. Regional Characteristics of Summer Precipitation and Water Vapor Amount in Northwest China. Clim. Environ. Res. 2003, 8, 35–42. [Google Scholar]
- Liu, L.; Niu, Q.; Heng, J.; Li, H.; Xu, Z. Characteristics of dry and wet conversion and dynamic vegetation response in Yarlung Zangbo River basin. Trans. Chin. Soc. Agric. Eng. 2020, 36, 175–184. [Google Scholar]
- Gao, F.; Cui, G.; Tao, L.; Huang, X.; Hua, Z. Analysis of Tropospheric Water Vapor Influence on Greenhouse Effect. J. Eng. Thermophys. 2014, 35, 722–725. [Google Scholar]
- Wu, F.; Li, W.; Li, W. Causes of Arctic Amplification: A Review. Adv. Earth Sci. 2019, 34, 232–242. [Google Scholar] [CrossRef]
- Gao, F.; Hua, Z.; Cui, G.; Tao, L. Impacts of Water-vapor Concentration Variation on Greenhouse Effect: Quantitative Analysis. Environ. Sci. Technol. 2013, 36, 182–186. [Google Scholar]
- Solomon, S.; Rosenlof, K.H.; Portmann, R.W.; Daniel, J.S.; Davis, S.M.; Sanford, T.J.; Plattner, G. Contributions of Stratospheric Water Vapor to Decadal Changes in the Rate of Global Warming. Science 2010, 327, 1219–1223. [Google Scholar] [CrossRef]
- Mao, K.; Chen, J.; Li, Z.; Ma, Y.; Song, Y.; Tan, X.; Yang, K. Global water vapor content decreases from 2003 to 2012: An analysis based on MODIS data. Chin. Geogr. Sci. 2017, 27, 1–7. [Google Scholar] [CrossRef]
- Dessler, A.E.; Schoeberl, M.R.; Wang, T.; Davis, S.M.; Rosenlof, K.H. Stratospheric water vapor feedback. Proc. Natl. Acad. Sci. USA 2013, 110, 18087–18091. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Huang, H. Stratospheric Water Vapor Feedback Disclosed by a Locking Experiment. Geophys. Res. Lett. 2020, 47, e2020GL087987. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y. The Surface Warming Attributable to Stratospheric Water Vapor in CO2-Caused Global Warming. J. Geophys. Res. Atmos. 2020, 125, e2020JD032752. [Google Scholar] [CrossRef]
- Li, F.; Xiao, J.; Chen, J.; Ballantyne, A.; Jin, K.; Li, B.; Abraha, M.; John, R. Global Water Use Efficiency Saturation Due to Increased Vapor Pressure Deficit. Science 2023, 381, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Park Williams, A.; Berg, A.M.; Cook, B.I.; Zhang, Y.; Hagemann, S.; Lorenz, R.; Seneviratne, S.I.; Gentine, P. Land-atmosphere feedbacks exacerbate concurrent soil drought and atmospheric aridity. Proc. Natl. Acad. Sci. USA 2019, 116, 18848–18853. [Google Scholar] [CrossRef]
- De Carcer, P.S.; Vitasse, Y.; Penuelas, J.; Jassey, V.E.J.; Buttler, A.; Signarbieux, C. Vapor-pressure deficit and extreme climatic variables limit tree growth. Glob. Chang. Biol. 2018, 24, 1108–1122. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Cheng, W.; Zhao, Z.; Guo, J.; Ding, H.; Wang, N. Interannual and Seasonal Vegetation Changes and Influencing Factors in the Extra-High Mountainous Areas of Southern Tibet. Remote Sens. 2019, 11, 1392. [Google Scholar] [CrossRef]
- Grossiord, C.; Buckley, T.N.; Cernusak, L.A.; Novick, K.A.; Poulter, B.; Siegwolf, R.T.W.; Sperry, J.S.; McDowell, N.G. Plant responses to rising vapor pressure deficit. New Phytol. 2020, 226, 1550–1566. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, P. Comparision of GLDAS Noah Model Hydrological Outputs with Ground Observations and Satellite Observations in China. Water Resour. Power 2017, 35, 1–6. [Google Scholar]
- Zhang, H.; Zhang, L.L.; Li, J.; An, R.D.; Deng, Y. Climate and Hydrological Change Characteristics and Applicability of GLDAS Data in the Yarlung Zangbo River Basin, China. Water 2018, 10, 254. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, X.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 Forcing Data and Noah Model Simulations over China at the Monthly Scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Lu, M.; Sun, Y.; Yang, W.; Zhao, J. Soil quality assessment of alpine grassland in permafrost regions of Tibetan Plateau based on principal component analysis. J. Glaciol. Geocryol. 2018, 40, 469–479. [Google Scholar]
- Liu, J.; You, Q.; Zhou, Y.; Ma, Q.; Cai, M. Spatiotemporal Distribution and Trend of Cloud Water Content in China Based on ERA-Interim Reanalysis. Plateau Meteorol. 2018, 37, 1590–1604. [Google Scholar]
- Sun, R.; Chen, S.; Su, H. Spatiotemporal variations of NDVI of different land cover types on the Loess Plateau from 2000 to 2016. Prog. Geogr. 2019, 38, 1248–1258. [Google Scholar] [CrossRef]
- Li, H.; Liu, L.; Liu, X.; Li, X.; Xu, Z. Greening Implication Inferred from Vegetation Dynamics Interacted with Climate Change and Human Activities over the Southeast Qinghai-Tibet Plateau. Remote Sens. 2019, 11, 2421. [Google Scholar] [CrossRef]
- Hu, S.; Zhan, C.; Zhao, R.; Liu, L. Detecting Changes and Causes of Vegetation Greenness in the Hengduan Mountains Region, China. Mt. Res. 2019, 37, 669–680. [Google Scholar]
- Yang, W.; Long, D.; Bai, P. Impacts of future land cover and climate changes on runoff in the mostly afforested river basin in North China. J. Hydrol. 2019, 570, 201–219. [Google Scholar] [CrossRef]
- Gu, F.; Gou, X.; Deng, Y.; Su, J.; Lin, W.; Yu, A. Analysis of temperature variations over the Yunnan-Guizhou Plateau from 1960 to 2014. J. Lanzhou Univ. Nat. Sci. 2018, 54, 721–730. [Google Scholar]
- Zhang, H.; Wu, B.; Yan, N. Remote Sensing Estimates of Vapor Pressure Deficit: An Overview. Adv. Earth Sci. 2014, 29, 559–568. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 1998. [Google Scholar]
- Gray, V. Climate Change 2007: The Physical Science Basis Summary for Policymakers. Energy Envion. 2007, 18, 433–440. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ju, W.; Chen, J.M.; Ciais, P.; Cescatti, A.; Sardans, J.; Janssens, I.A.; Wu, M.; Berry, J.A.; et al. Recent Global Decline of CO2 Fertilization Effects on Vegetation Photosynthesis. Science 2020, 370, 1295–1300. [Google Scholar] [CrossRef]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z.; et al. Increased Atmospheric Vapor Pressure Deficit Reduces Global Vegetation Growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef]
- Su, J.; Wen, M.; Ding, Y.; Gao, Y.; Song, Y. Hiatus of Global Warming: A Review. Chin. J. Atmos. Sci. 2016, 40, 1143–1153. [Google Scholar]
- Xu, Y.; Li, J.; Wang, Q.; Lin, X. Review of the Research Progress in Global Warming Hiatus. Adv. Earth Sci. 2019, 34, 175–190. [Google Scholar]
- Karl, T.R.; Arguez, A.; Huang, B.; Lawrimore, J.H.; McMahon, J.R.; Menne, M.J.; Peterson, T.C.; Vose, R.S.; Zhang, H. Possible artifacts of data biases in the recent global surface warming hiatus. Science 2015, 348, 1469–1472. [Google Scholar] [CrossRef]
- Wang, S.; Luo, Y.; Zhao, Z.; Wen, X.; Huang, J. How Long will the Pause of Global Warming Stay Again? Progress. Inquisitiones Mutat. Clim. 2014, 10, 465–468. [Google Scholar]
- Liu, Y.; Li, T. The global warming trend accelerates sharply. Ecol. Econ. 2019, 35, 1–4. [Google Scholar]
- Ma, Y.; Ren, Z.; Wang, Y. Analysis on the Trend of the Long-term Changes of Global Gas Temperature in the Past 100 Years. J. Shandong Meteorol. 2014, 34, 5. [Google Scholar]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Shuang, L.; Liuni, Y.; Jingjing, L. Statistical characteristics analysis of global specific humidity vertical profile. Proc. SPIE 2020, 11439, 1143911–1143919. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Massmann, A.; Gentine, P.; Lin, C. When Does Vapor Pressure Deficit Drive or Reduce Evapotranspiration? J. Adv. Model. Earth Syst. 2019, 11, 3305–3320. [Google Scholar] [CrossRef] [PubMed]
- Ruckstuhl, C.; Philipona, R.; Morland, J.; Ohmura, A. Observed relationship between surface specific humidity, integrated water vapor, and longwave downward radiation at different altitudes. J. Geophys. Res. 2007, 112, D3. [Google Scholar] [CrossRef]
- Gordon, N.D.; Jonko, A.K.; Forster, P.M.; Shell, K.M. An observationally based constraint on the water-vapor feedback. J. Geophys. Res. 2013, 118, 12435–12443. [Google Scholar] [CrossRef]
- Ingram, W. Some implications of a new approach to the water vapour feedback. Clim. Dyn. 2013, 40, 925–933. [Google Scholar] [CrossRef]
- Stephens, G.L.; Li, J.; Wild, M.; Clayson, C.A.; Loeb, N.; Kato, S.; L’Ecuyer, T.; Stackhouse, P.W., Jr.; Lebsock, M.; Andrews, T. An update on Earth’s energy balance in light of the latest global observations. Nat. Geosci. 2012, 5, 691–696. [Google Scholar] [CrossRef]
- Zapadka, T.; Niak, S.A.B.W.; Niak, B.W. A simple formula for the net long-wave radiation flux in the southern Baltic Sea. Oceanologia 2001, 43, 265–277. [Google Scholar]
- Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; et al. Characteristics, drivers and feedbacks of global greening. Nat. Rev. Earth Environ. 2020, 1, 14–27. [Google Scholar] [CrossRef]
- Ishii, Y.; Harigae, S.; Tanimoto, S.; Yabe, T.; Yoshida, T.; Taki, K.; Komatsu, N.; Watanabe, K.; Negishi, M.; Tatsumoto, H. Spatial variation of phosphorus fractions in bottom sediments and the potential contributions to eutrophication in shallow lakes. Limnology 2010, 11, 5–16. [Google Scholar] [CrossRef]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [CrossRef]
- Zeng, Z.; Piao, S.; Li, L.Z.X.; Zhou, L.; Ciais, P.; Wang, T.; Li, Y.; Lian, X.; Wood, E.F.; Friedlingstein, P.; et al. Climate Mitigation from Vegetation Biophysical Feedbacks during the Past Three Decades. Nat. Clim. Chang. 2017, 7, 432–436. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Williams, A.P.; Gentine, P. Projected Increases in Intensity, Frequency, and Terrestrial Carbon Costs of Compound Drought and Aridity Events. Sci. Adv. 2019, 5, eaau5740. [Google Scholar] [CrossRef]
- Berg, A.; McColl, K.A. No Projected Global Drylands Expansion under Greenhouse Warming. Nat. Clim. Chang. 2021, 11, 331–337. [Google Scholar] [CrossRef]
- He, B.; Chen, C.; Lin, S.; Yuan, W.; Chen, H.W.; Chen, D.; Zhang, Y.; Guo, L.; Zhao, X.; Liu, X.; et al. Worldwide Impacts of At-mospheric Vapor Pressure Deficit on the Interannual Variability of Terrestrial Carbon Sinks. Natl. Sci. Rev. 2022, 9, nwab150. [Google Scholar] [CrossRef] [PubMed]
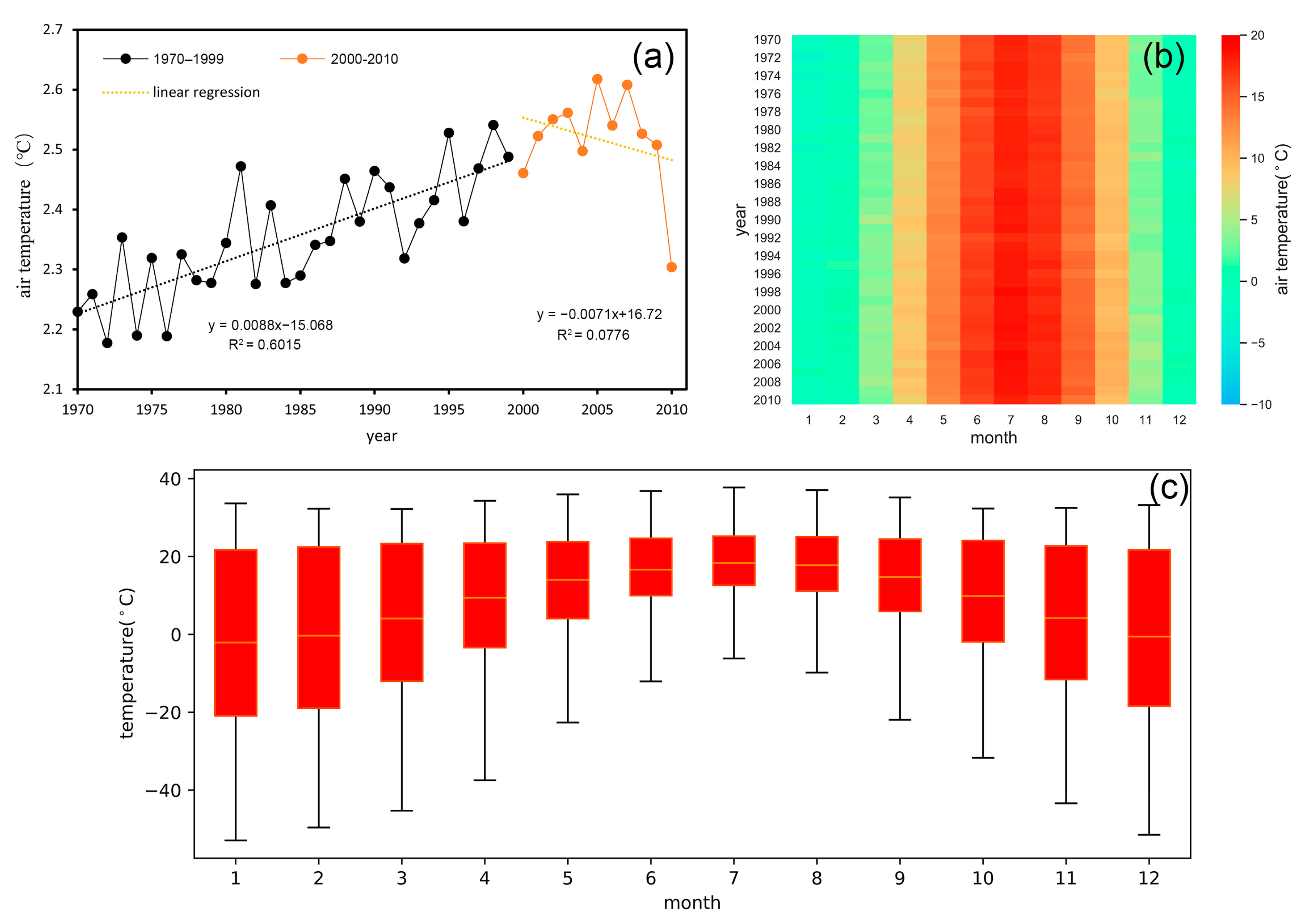
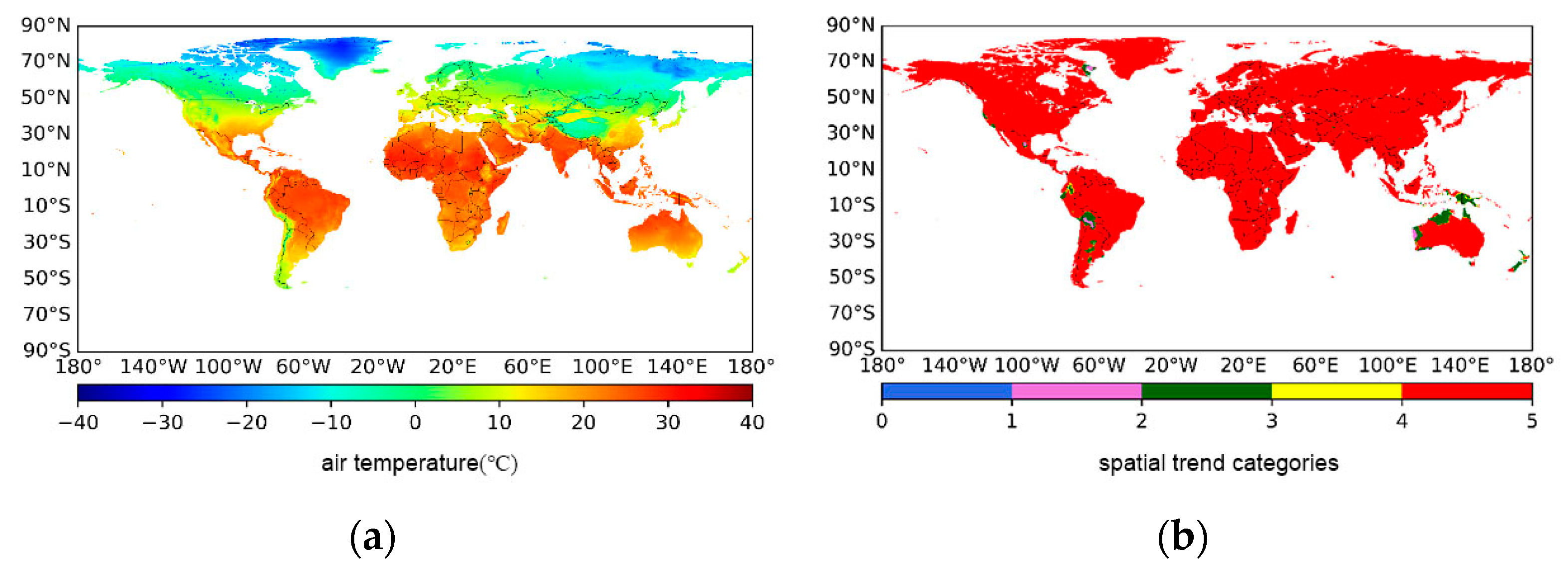
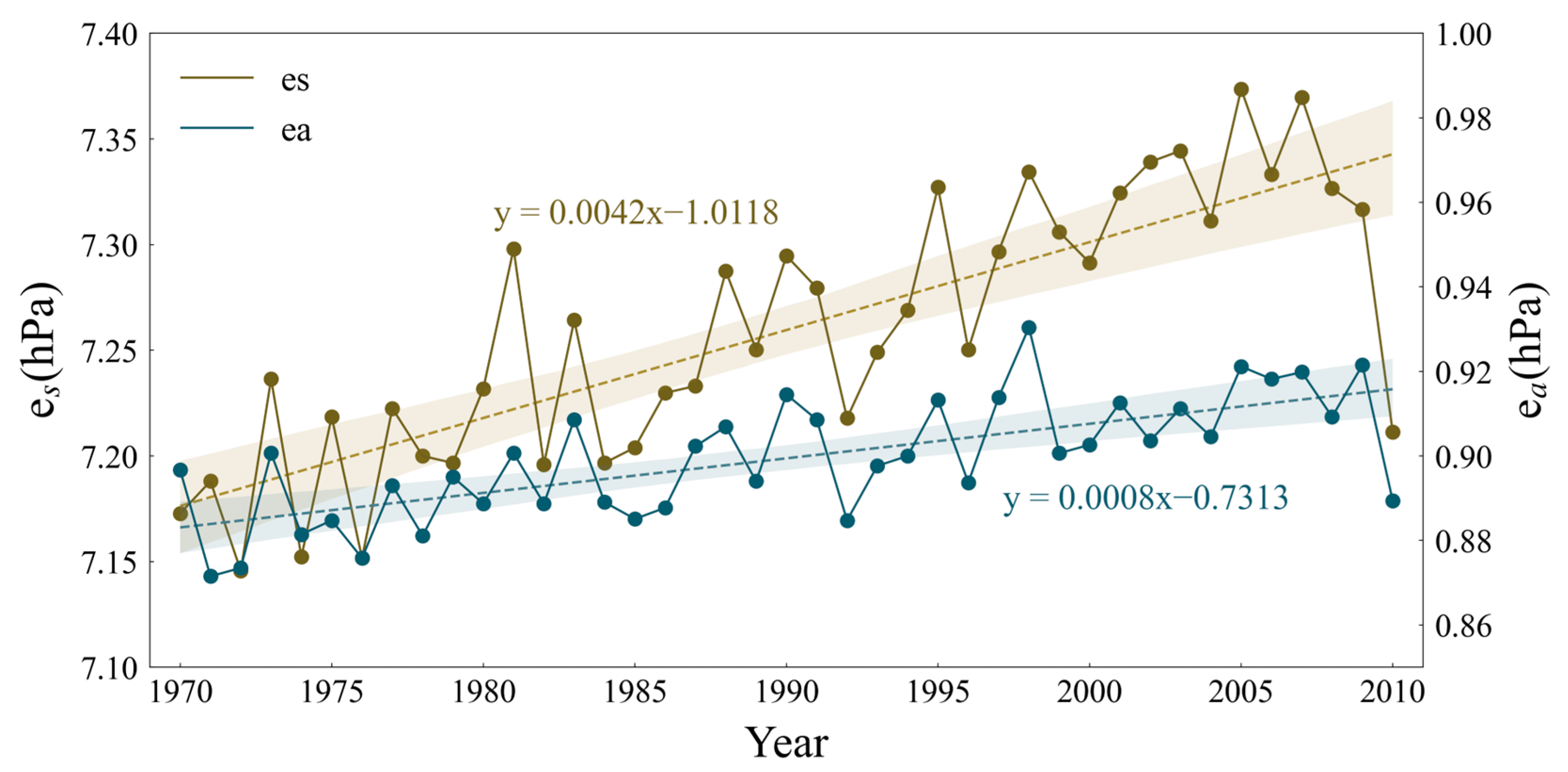


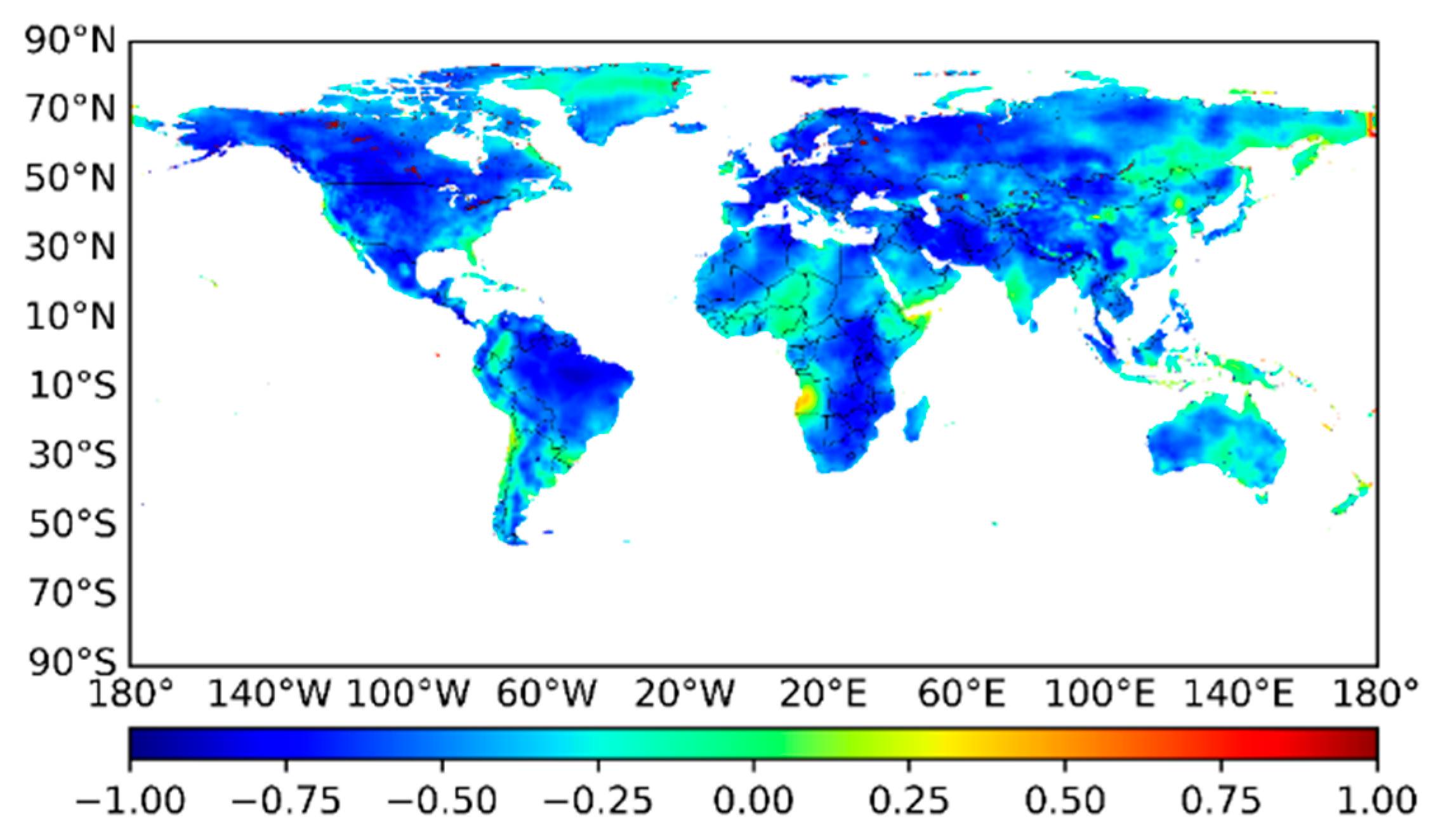

| Sen’s Slope | Z Value | Trend | Percentage (%) | Number |
|---|---|---|---|---|
| ≥0.0003 | ≤−1.64 | Significant warming | 88.089 | 4–5 |
| ≥0.0003 | −1.64–1.64 | Slight warming | 9.602 | 3–4 |
| −0.0003–0.0003 | −1.64–1.64 | Relatively stable | 0.252 | 2–3 |
| ≤−0.0003 | −1.64–1.64 | Slight cooling | 1.818 | 1–2 |
| ≤−0.0003 | ≥1.64 | Significant cooling | 0.239 | 0–1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Cheng, Y.; Liu, L.; Huang, Y.; Sun, H. Significant Increases in Water Vapor Pressure Correspond with Climate Warming Globally. Water 2023, 15, 3219. https://doi.org/10.3390/w15183219
Zhou X, Cheng Y, Liu L, Huang Y, Sun H. Significant Increases in Water Vapor Pressure Correspond with Climate Warming Globally. Water. 2023; 15(18):3219. https://doi.org/10.3390/w15183219
Chicago/Turabian StyleZhou, Xueting, Yongming Cheng, Liu Liu, Yuqi Huang, and Hanshi Sun. 2023. "Significant Increases in Water Vapor Pressure Correspond with Climate Warming Globally" Water 15, no. 18: 3219. https://doi.org/10.3390/w15183219
APA StyleZhou, X., Cheng, Y., Liu, L., Huang, Y., & Sun, H. (2023). Significant Increases in Water Vapor Pressure Correspond with Climate Warming Globally. Water, 15(18), 3219. https://doi.org/10.3390/w15183219







