1. Introduction
Slope stability evaluation is one of the important and popular research topics in geotechnical engineering. Due to the existence of complex loads and geological conditions, as well as the inherent variability of soil physical and mechanical parameters, slope failure is actually uncertain [
1]. The influence of these uncertain factors on slope stability cannot be considered by a single safety factor [
2]. Slope reliability analysis is a useful supplement to the deterministic method of slope stability [
3].
In the past few decades, the research on slope reliability analysis methods has developed rapidly and achieved many meaningful results. However, most researchers simplified the slope stability analysis problems into two-dimensional plane strain problems, ignoring the three-dimensional effects of actual slopes, which will overestimate or underestimate their stabilities [
4,
5,
6]. Especially for slopes with obvious longitudinal changes in soil properties along the slope surface, concentrated loads acting on the surface, irregular potential failure surfaces, or short slopes with non-negligible boundary conditions, their 3D effects are particularly significant, and 3D reliability analysis must be carried out [
7].
Three-dimensional slope reliability analysis requires higher computational costs than two-dimensional simulation, and sometimes the calculation time is even more than one month [
8]. This is one of the reasons why 3D slope reliability analysis cannot be widely used in practical engineering. However, in the preliminary design of highway engineering, it is often necessary to quickly evaluate the stability of slopes of hundreds of sections [
9]. In the study of 3D slope reinforcement measures, it is also necessary to quickly judge the effects of different reinforcement measures [
10,
11]. In these cases, there is an urgent need for a method that can quickly perform 3D slope reliability analysis without significant loss of accuracy.
In recent years, the research on 3D slope reliability analysis methods has gradually increased with the improvement of computer performance. The existing 3D slope reliability analysis methods mainly include the analytical method [
12,
13], stochastic finite element method (SFEM) [
1,
14], stochastic limit equilibrium method (SLEM) [
15], and stochastic limit analysis method (SLAM) [
16]. The research of these methods is carried out under the framework of combining the deterministic method of 3D slope stability and the reliability calculation method. The limit state performance function generally adopts the expression form of the difference between safety factor
and one. The obvious differences in accuracy and computational efficiency of various methods are mainly derived from the efficiency of the solution method of safety factor and the reliability algorithm. The analytical method has a small amount of calculation, but it is difficult to apply in engineering practice because the sliding surface must be a special combination shape with a cylindrical surface in the middle and a vertical plane or an ellipsoid surface at both ends. Based on the finite element method and strength reduction technology, the stochastic finite element method has the advantage of automatically obtaining the critical sliding surface. However, when the probability of slope failure is very small, its computational cost is very high [
17]. The stochastic limit analysis method constructs the static allowable stress field or the maneuvering allowable velocity field according to the large-scale geotechnical parameter samples, based on the lower bound theorem or the upper bound theorem. The safety factor of the slope is solved by means of mathematical programming. If the number of soil parameter samples is large, the calculation efficiency is low. Therefore, the stochastic limit equilibrium method with a clear concept and high computational efficiency is still the most widely used method in engineering practice.
The conventional 3D slope limit equilibrium methods are obtained by extending the 2D slice methods. According to the different assumptions of the inter-column force, they can be divided into the 3D simplified Bishop method [
18,
19], 3D simplified Janbu method [
18,
19], 3D Morgenstern–Price method [
20,
21], and so on. Safety factor expressions are usually complex nonlinear implicit expressions, which require multiple numerical iterations to solve, and sometimes encounter non-convergence problems. Some scholars used the stochastic response surface method (SRSM) [
22], intelligent response surface method (IRSM) [
23], genetic algorithm (GA) [
8], support vector machine (SVM) [
4], and other surrogate models to simplify complex nonlinear implicit performance functions into approximate equivalent explicit expressions, which effectively solves the difficult problem of 3D slope reliability calculation. However, these methods require a large amount of data to generate enough samples to obtain surrogate models. For highly nonlinear and small failure probability problems, it is difficult to fit the surrogate models.
Sarma [
24] proposed a good idea to replace the safety factor with a critical horizontal acceleration coefficient
for slope stability analysis. In the process of solving
, no numerical iteration occurs, and no non-convergence problem will be encountered. However, the formula of the Sarma method is cumbersome and the solving process is not very convenient. Zhu [
25] proposed an explicit solution for the 3D slope safety factor by correcting the normal stresses on the slip surface. His method does not need to assume the inter-column force, so it does not belong to the “column method”. The calculation principle of the method is simple without iteration and non-convergence problems, and the calculation results are reliable. In this paper, a new method for calculating the reliability of the 3D slope was proposed by using the critical horizontal acceleration coefficient as the criterion of slope stability under the mode of the 3D limit equilibrium method with normal stress correction of the sliding surface.
Among the reliability algorithms, the Monte Carlo simulation (MCS) method is the most widely used because of its simple concept. As long as there are enough samples, the approximate accurate reliability calculation results can be obtained. However, in the case of slopes with small failure probability, the calculation is very time-consuming. The subset simulation method (SS) reduces the sample requirements and is an efficient method for solving the reliability analysis of slopes with small failure probability [
26]. In this paper, the subset simulation method is used to calculate the reliability of the 3D slope.
In the author’s previous work [
27], it has been proved that the limit state performance function using the critical horizontal acceleration coefficient expression can indeed significantly improve the computational efficiency probability of 2D slope reliability. In this paper, we extend the previous work to the 3D slope and comprehensively study the accuracy and efficiency of the obtained algorithm.
The research framework of this paper is as follows. Firstly, based on the 3D limit equilibrium method with normal stress correction on the sliding surface, four main equilibrium equations including the critical horizontal acceleration coefficient and three correction parameters were established. Secondly, according to the definition of the critical horizontal acceleration coefficient, its explicit expression was derived. Thirdly, a simplified method for calculating the reliability of the three-dimensional slope is proposed by using the difference expression between the critical horizontal acceleration coefficient and the critical value and combining it with the reliability algorithm. Finally, the effectiveness and reliability of the proposed method are verified by two slope examples.
2. Three-Dimensional Limit Equilibrium Method Based on the Modification of Normal Stresses over Slip Surface
2.1. Fundamental Assumptions
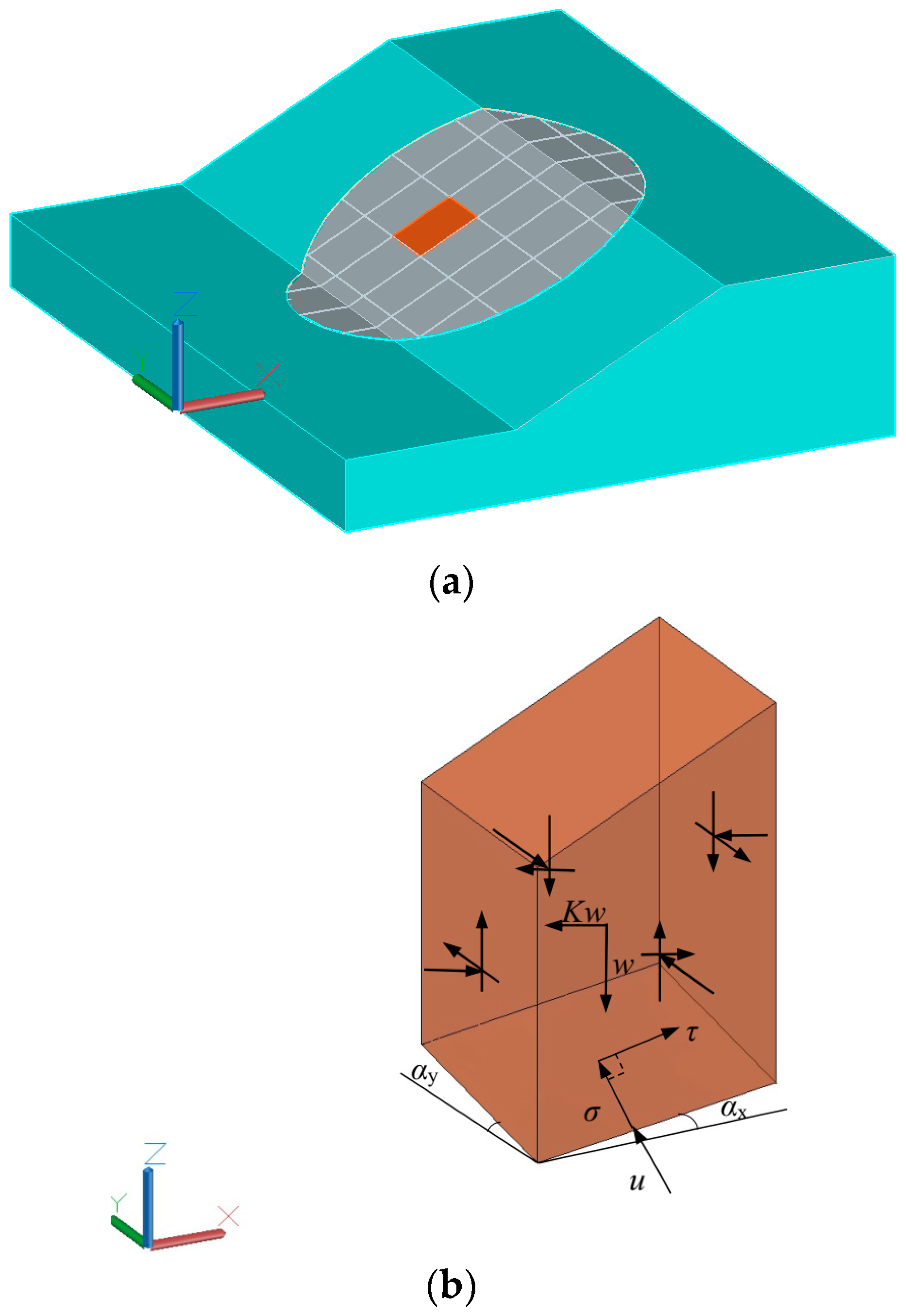
A 3D slope with a general shape sliding surface and a coordinate system are shown in
Figure 1a. It is assumed that the horizontal projections of the sliding direction of each point on the sliding surface are parallel to each other and opposite to the positive direction of the
x-axis. The slope surface is represented by
, and the sliding surface is represented by
. The slope is divided into many soil columns. As shown in
Figure 1b, one of the soil columns has a width of
and a length of
. The horizontal projection area of the soil column is
, and the angles with the
and
axes are
and
, respectively. The angle between the outer normal direction and the
z-axis is
.
According to the geometric relation,
can be calculated by Equation (1).
where
Assuming that the soil column weight is and the horizontal acceleration coefficient is , then the horizontal seismic force is , and the position of the action point is .
There are normal stress and shear stress at the bottom of the column, which are expressed by and , respectively. The pore water pressure is expressed by . The cohesion and effective internal friction angle of the soil at the sliding surface are and , respectively.
The direction cosines of the normal force and shear force at the bottom of the column are
and
, respectively. As the sliding direction is parallel to the
-axis,
. From the geometrical relation, it follows that
where
In order to simplify the calculation, the initial normal stress distribution
on the sliding surface adopts the 3D extended form of the Fellenius method [
28].
The initial normal stresses over the slip surface need to be corrected to make the 3D sliding body meet the required equilibrium conditions. Let the correction function be
, then
2.2. Three-Dimensional Limit Equilibrium Equations
For 3D slopes, only the reliability calculation results that rigorously meet the force balance in three directions and the moment balance conditions around three axes are accurate. The research shows that the quasi-rigorous solution is very close to the rigorous solution, and the difference can be ignored. The former is more suitable for practical engineering [
25]. Therefore, in order to solve the problem of rapid analysis of 3D slope reliability, a quasi-rigorous simplified method of 3D slope reliability based on four main equilibrium equations of the sliding body is proposed.
When the 3D sliding body reaches the limit equilibrium state under the action of the force in three directions and the torque around the
y-axis, the following equations can be listed (in order to simplify, “
” in all formulas are omitted.):
Substituting Equations (7) and (8) into Equation (10a–d) leads to
It is assumed that safety factor values of the entire sliding surface are equal, and the relationship between normal stress and shear stress obeys the Mohr–Coulomb failure criterion.
Equation (11a–d) is rearranged as
In order to make Equation (14a–d) statically determinate and solvable, the correction function must contain three undetermined parameters and its general form can be taken as
Substituting Equations (12) and (15) into Equation (14a–d), we can obtain
where
| |
| |
| |
| |
| |
| |
| |
| |
| |
Assuming that safety factor is a known parameter and the initial normal stress distribution is determined, then , , , , , , , , and , these parameters can be solved by a definite integral. Substituting the 31 parameters into Equation (16a–d), we can obtain the statically determinate solvable limit equilibrium equations with four unknowns , , and .
Equation (16a–d) can be rewritten in a matrix form
According to Cramer’s rule,
,
,
and
can be solved.
where
4. Numerical Examples
By analyzing the calculation results of the 3D slope reliability of two classical examples, the feasibility of the proposed method is verified. The limit state performance function adopts the proposed
expression (denoted as
method) and
expression (denoted as
method, the specific calculation method is shown in Zhu [
25]). The FOSM approximate analytical method, MCS, and SS methods were used to calculate the reliability. By coupling two limit state performance functions and three reliability algorithms, six methods are obtained, which are called the
+ MCS method,
+ SS method,
+ MCS method,
+ SS method,
+ FOSM method, and
+ FOSM method, respectively. The reliability index, failure probability, and calculation time of the six methods were compared. The calculation time is the CPU occupancy time of the program running on the same computer.
4.1. Example 1
Example 1 is derived from the homogeneous slope in Arai [
32]. The geometric dimensions of the slope section are shown in
Figure 3, and the soil parameters are listed in
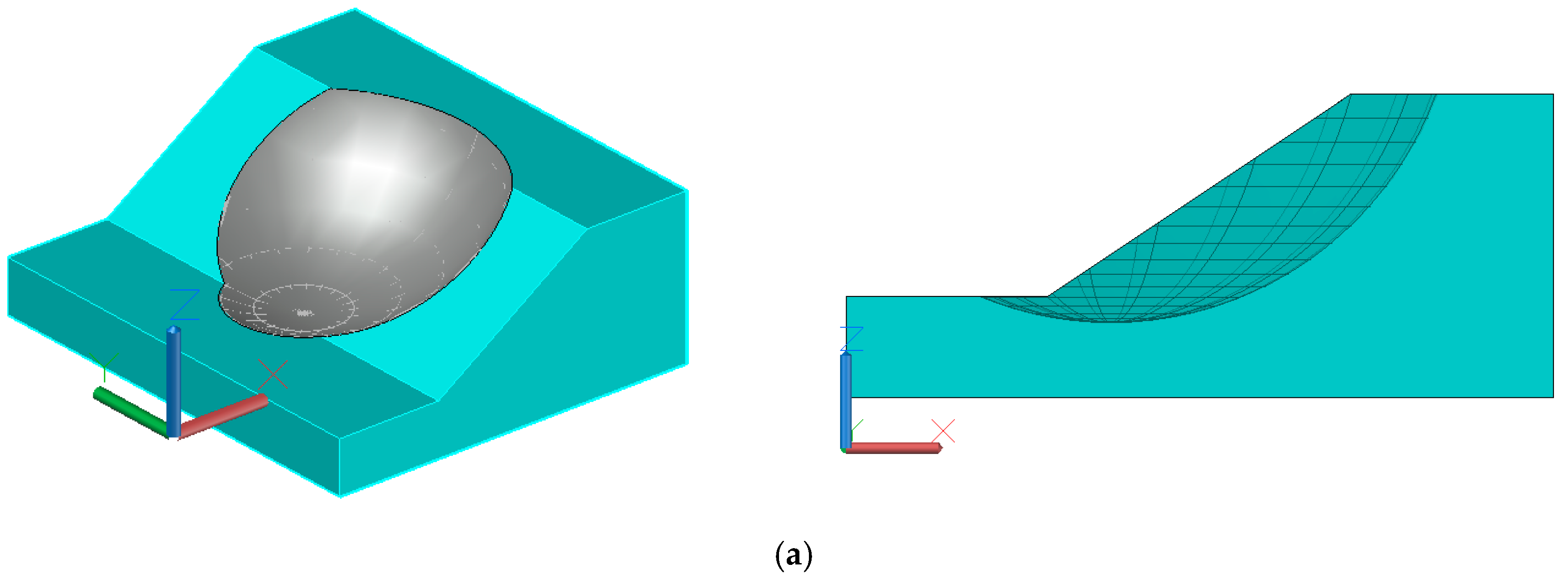
Table 1. The cohesion and internal friction angle of the soil are independent of each other and obey the normal distribution. Considering the two cases with and without seismic force on the slope,
is 0 and 0.1, respectively. Both sliding surfaces are spherical, and the position and range are shown in
Figure 4. The equations are
(denoted by sliding surface 1, abbreviated as S1) and
(denoted by sliding surface 2, abbreviated as S2). The results of the six methods are shown in
Table 2.
In the case of no seismic load on the slope (i.e.,
= 0.1) and the sliding surface is S1, the calculation results in Tun [
8] are taken as the reference values. Among the six methods, the relative errors of the reliability index and failure probability of
+ MCS method are the smallest, while that of the
+ FOSM method is the largest. The relative error of the
+ SS method is the second smallest. Except that the relative error of the failure probability of the
+ FOSM method reaches 22.22%, those of other results are less than 20%. However, the computational efficiency of the six methods is very different. The calculation time of the
+ MCS method is the longest, but it is much less than that in Tun [
8]. Both the
+ FOSM and
+ FOSM methods have very short CPU time, even less than 0.5 s. The calculation time of the
+ SS method is slightly less than that of the
+ SS method, which is about half of the
+ MCS method and one-fourth of the
+ MCS method.
When there is a seismic load on the slope (i.e., = 0.1) and the slip surface is S2, the failure probability of the 3D slope increases and the reliability index decreases. The results of + MCS, + SS, and + FOSM are very close. The maximum relative errors of the reliability index and failure probability are 3.80% and 7.37%, respectively. In Example 1, the reliability indexes of the 3D slope are slightly higher than that of the 2D slope.
From the above, it can be concluded that the performance function can improve the efficiency of the 3D slope reliability analysis without an obvious loss of precision. The method coupled with the SS method can further reduce the amount of calculation.
4.2. Example 2
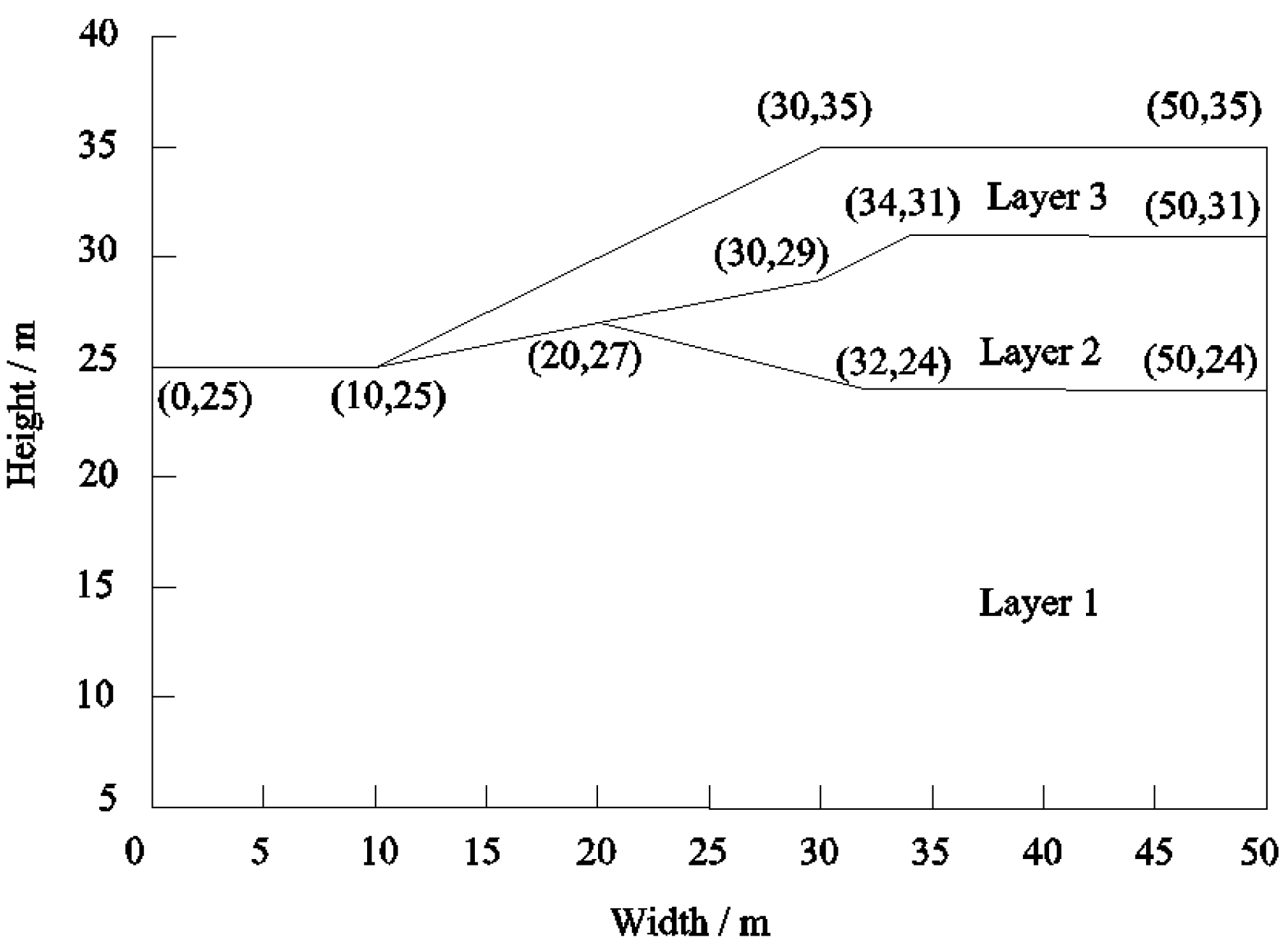
The second example is a slope with three soil layers, which is adapted from a slope stability test question of the Australian Computer Aided Design Association (ASCD) [
33]. The distribution of the soil layer in the slope section is shown in
Figure 5. The material parameter variables are normally distributed and are listed in
Table 3.
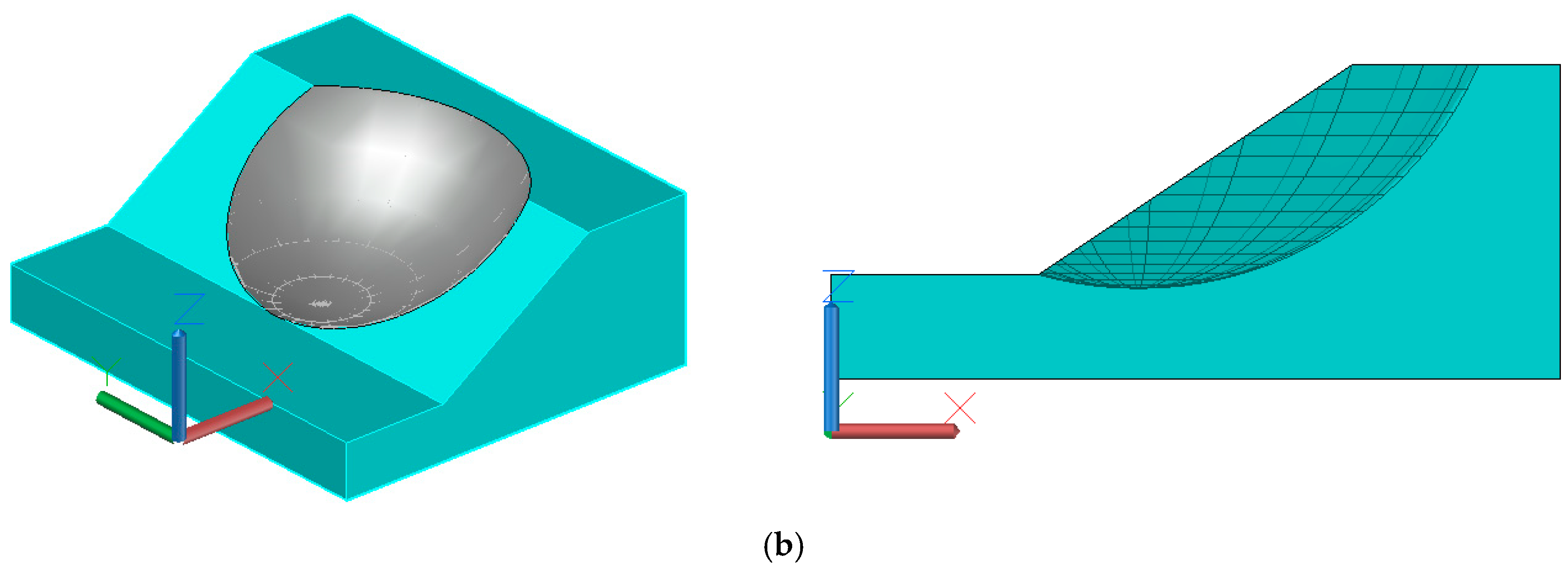
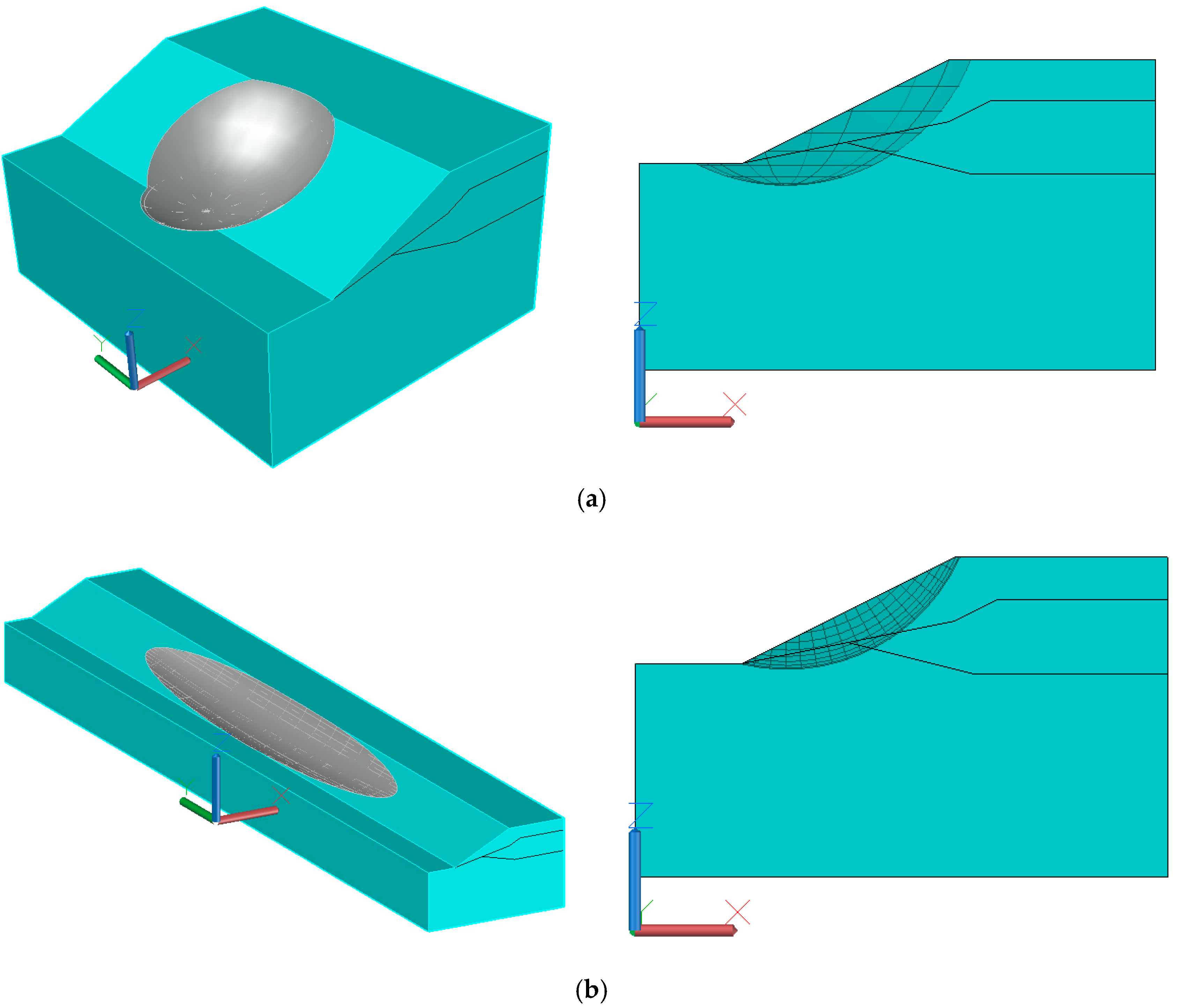
In order to compare with the 2D results, several 3D slope reliability analyses with different lengths are carried out. Firstly, a 3D slope with a spherical sliding surface of 40 m long is designed. Then, keeping the shape of the cross-section of the slope unchanged, the length of the slope is expanded by an integer multiple (the slope length expansion multiple is denoted by
). The sliding surfaces of long slopes are all ellipsoids, and their longitudinal axis length increases with the slope length. The positions and ranges of two kinds of sliding surfaces are shown in
Figure 6.
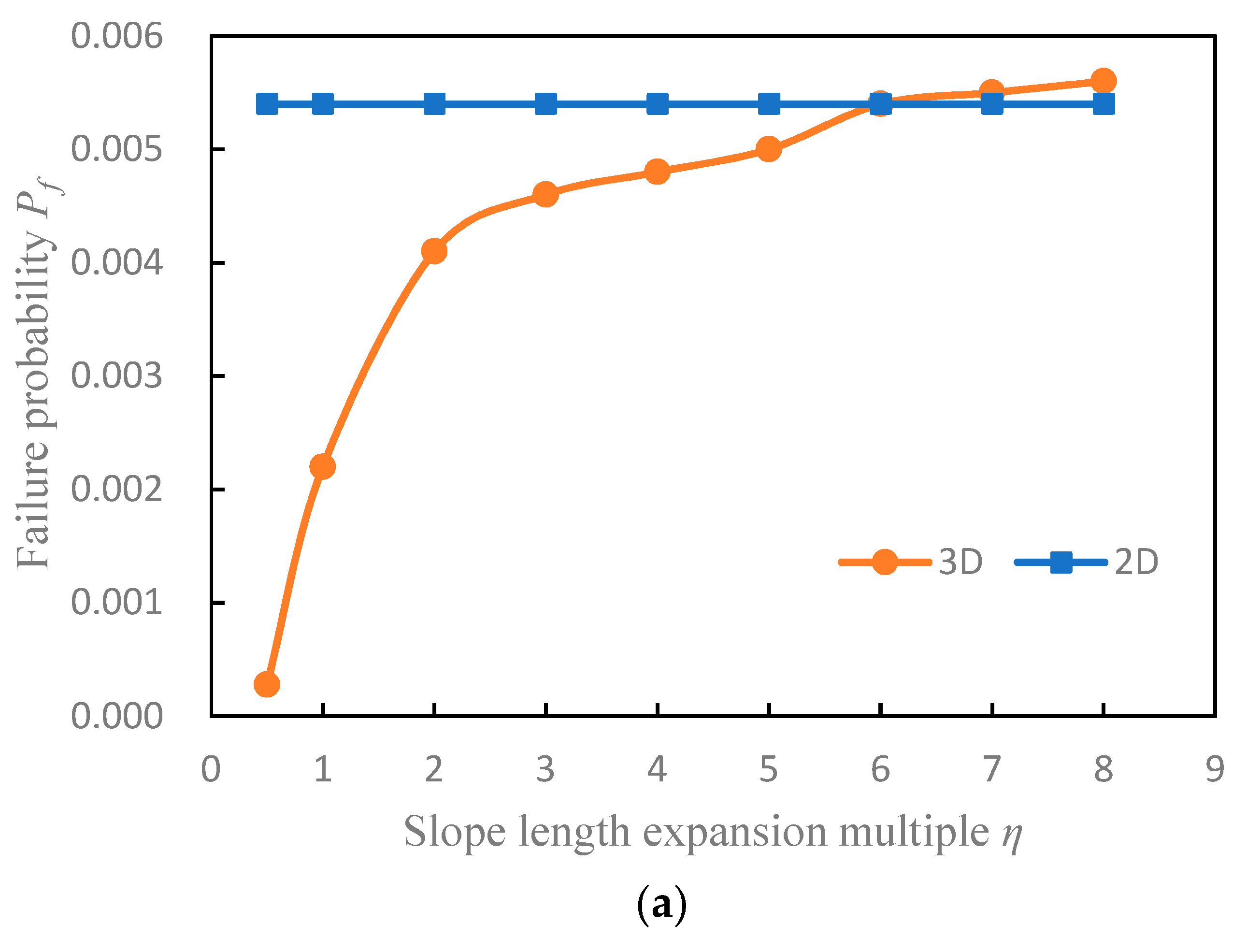
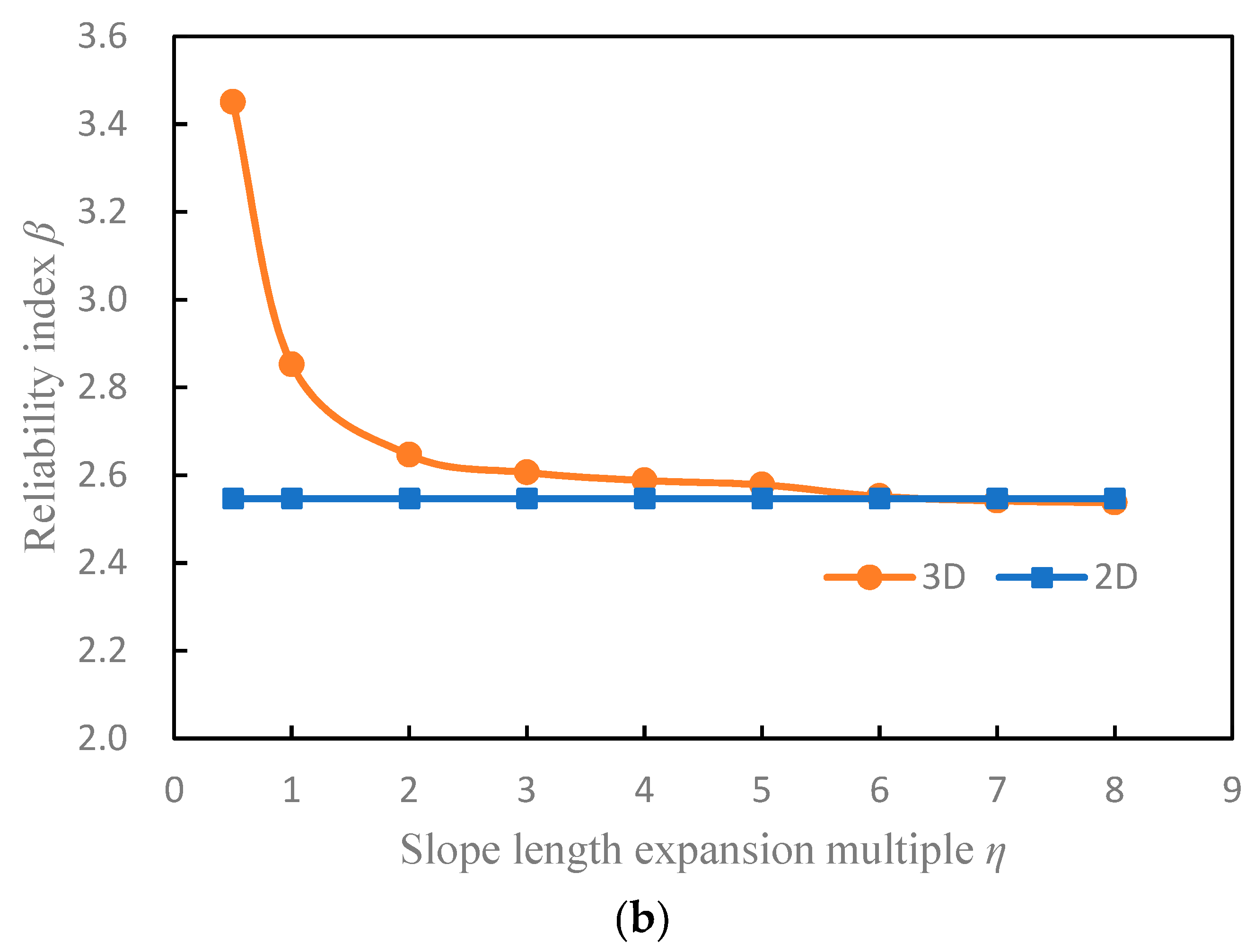
Table 4 lists the results of the 3D slope reliability calculation with different methods under the condition of two kinds of sliding surfaces. The curves of the reliability index and failure probability with slope length are shown in
Figure 7.
It can be seen from
Table 4 that the failure probability of
+ MCS,
+ MCS,
+ SS, and
+ SS is basically the same as that of Tun [
8] in the case of the 3D spherical slip surface, with the maximum relative error of reliability index at less than 5%. The calculated results of
+ FOSM and
+ FOSM are quite different from those of Tun [
8], with the maximum relative error of failure probability at more than 50%. In terms of calculation efficiency, the calculation time of the six methods is still very different, but they are far less than that of Tun [
8]. Among these methods, the
+ SS method is the one with good calculation accuracy and efficiency.
When the slope length is increased by seven times ( = 7), the failure probabilities of the + MCS and + SS methods are very close and slightly larger than those of the 2D results. It can be seen that the results of the 2D slope reliability analysis are not always conservative.
Figure 7 shows the trend of increasing failure probability and decreasing reliability index with increasing slope length. When
= 6, the reliability results of the 3D slope are roughly equal to those of the 2D slope. If
is greater than 6, the failure probability of the 3D slope will exceed that of the 2D slope. For the case of long slopes, only the 2D reliability analysis does not necessarily provide a conservative result. It is consistent with the conclusions of Xiao [
1] and Qi [
34]. It is very necessary to analyze the 3D reliability of the actual long slope.
5. Conclusions
The traditional 3D slope reliability analysis method has low computational efficiency. The reason is that the limit state function is generally expressed by the safety factor, which needs to be solved iteratively. Under the framework of the limit equilibrium method of the 3D slip surface normal stress correction, the critical horizontal acceleration coefficient is used as an alternative to the safety factor to measure the stability of the slope. Coupled with the reliability algorithm, a simplified method for calculating the reliability of the 3D slope is proposed.
By studying two 3D slope examples, the following conclusions can be drawn:
- (1)
This method has the advantages of simple calculation, no iterative convergence problem, and high calculation efficiency. Combined with the SS method, it can fully reflect the advantages of high accuracy and efficiency.
- (2)
By changing to a value greater than zero, this method can conveniently calculate 3D slope reliability under seismic loads without large-scale modification of the calculation program.
- (3)
In the case of a long slope, the results of 2D reliability calculation do not necessarily underestimate the stability of the slope, so it is necessary to carry out 3D slope reliability analysis.
This method only considers the force balance in three directions and moment balance in the y-axis direction and does not belong to the rigorous 3D limit equilibrium method. However, the quasi-rigorous solution is very close to the rigorous solution, and the difference can be ignored. At present, the spatial variability of soil parameters and the influence of groundwater on the reliability of 3D slopes are not considered in this method. Especially, the variability of soil parameters in the direction of slope length will make the results of 3D slope reliability analysis significantly different from those of the 2D slope. That will be the focus of the next research work on this method. In addition, on the basis of this method and a large number of practical 3D slope reliability studies, the design charts can be made for designers to use conveniently, which can improve the practical application value of this method.