Improvements and Evaluation of the FLake Model in Dagze Co, Central Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. GloboLakes Surface Water Temperature
2.2.2. Dagze Co Water Temperature Monitoring Data
2.2.3. In situ Water Clarity Dataset
2.2.4. China Meteorological Forcing Dataset (CMFD)
2.3. Model Description and Experimental Design
2.3.1. FLake Description and Configuration
2.3.2. Experimental Design
2.4. Methodology
3. Results
3.1. Validation of Default FLake Simulations
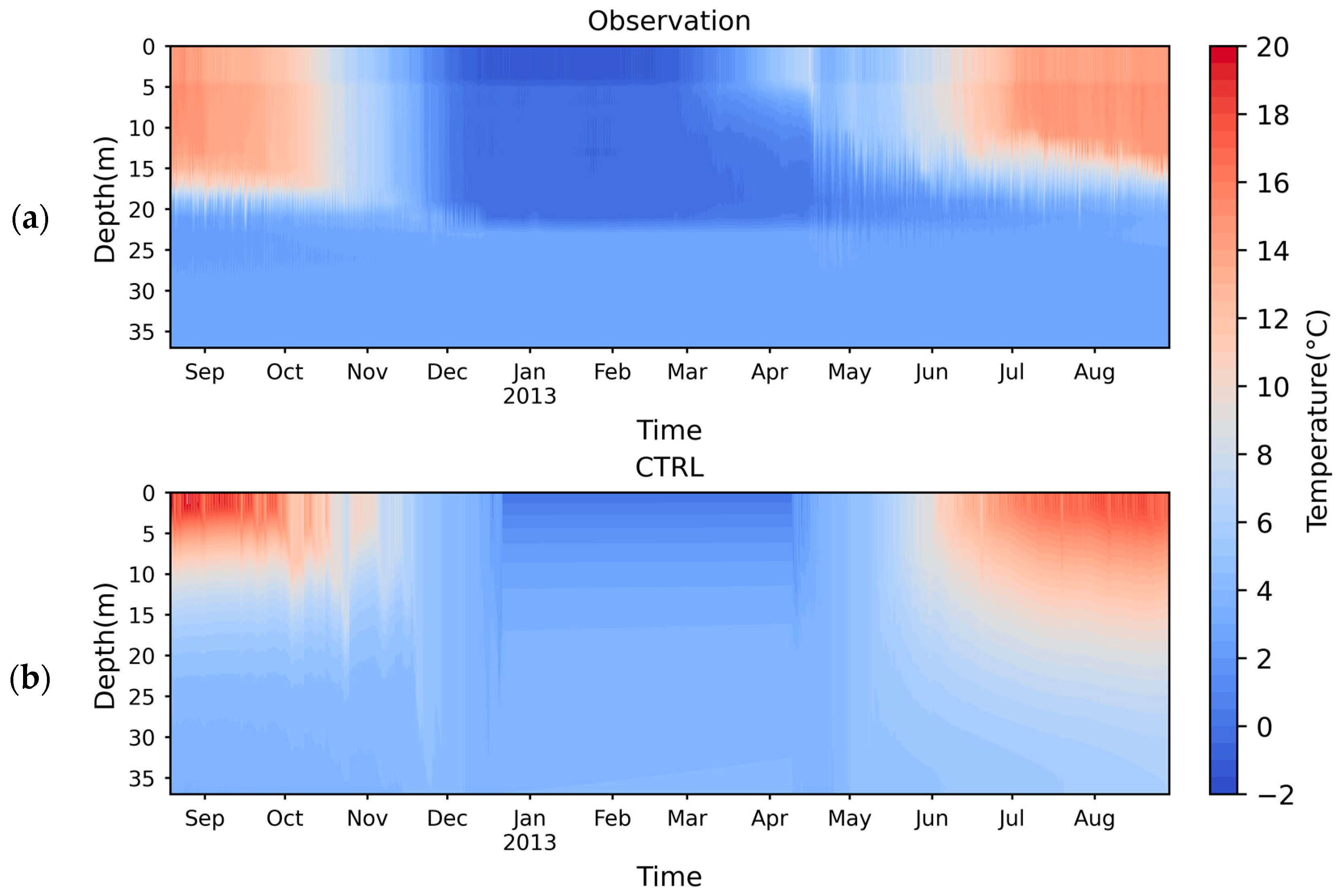
3.1.1. Lake Surface Water Temperature
3.1.2. Vertical Temperature Profile
3.2. Parameter Sensitivity Experiment
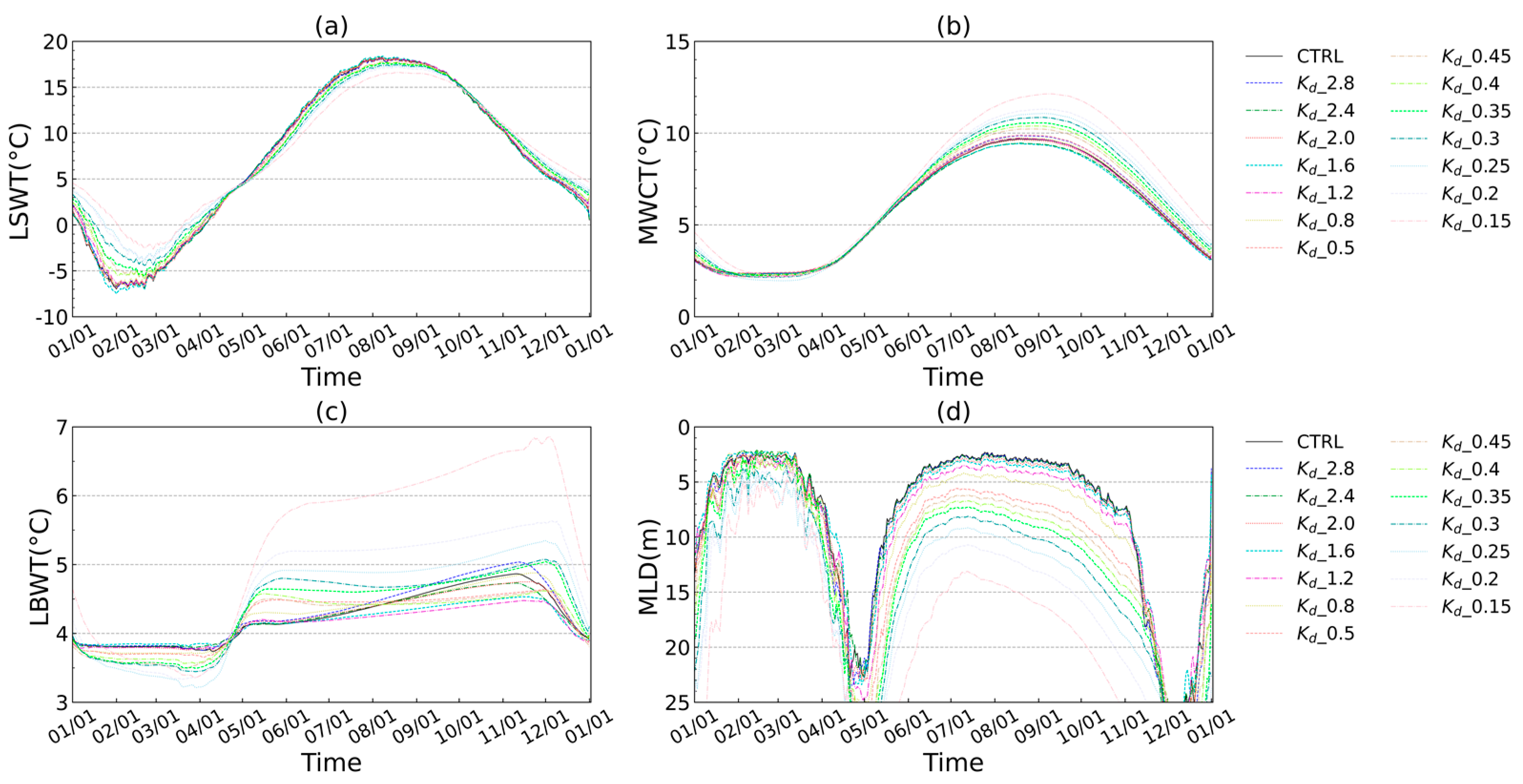
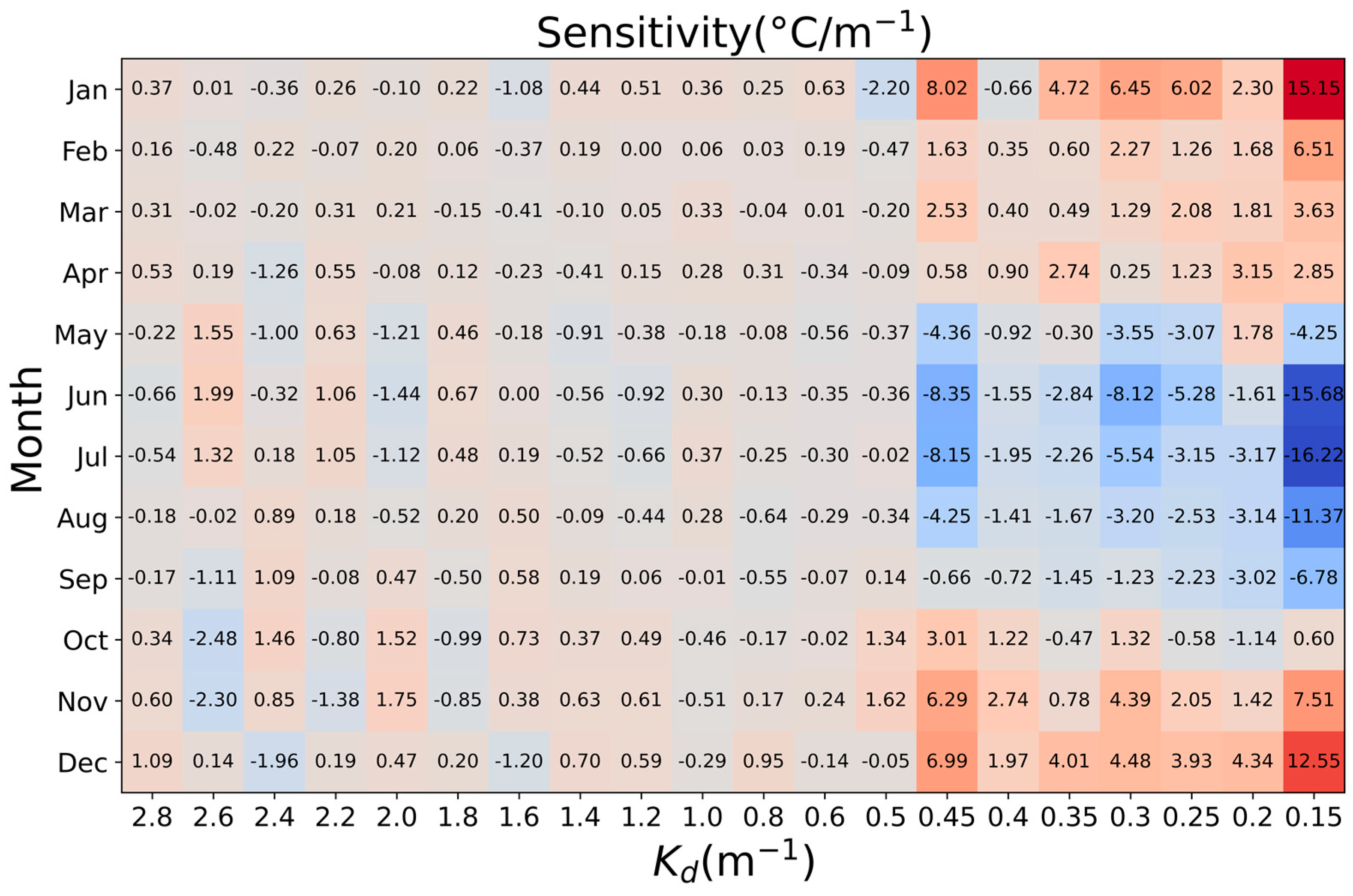
3.2.1. Extinction Coefficient
3.2.2. Friction Velocity
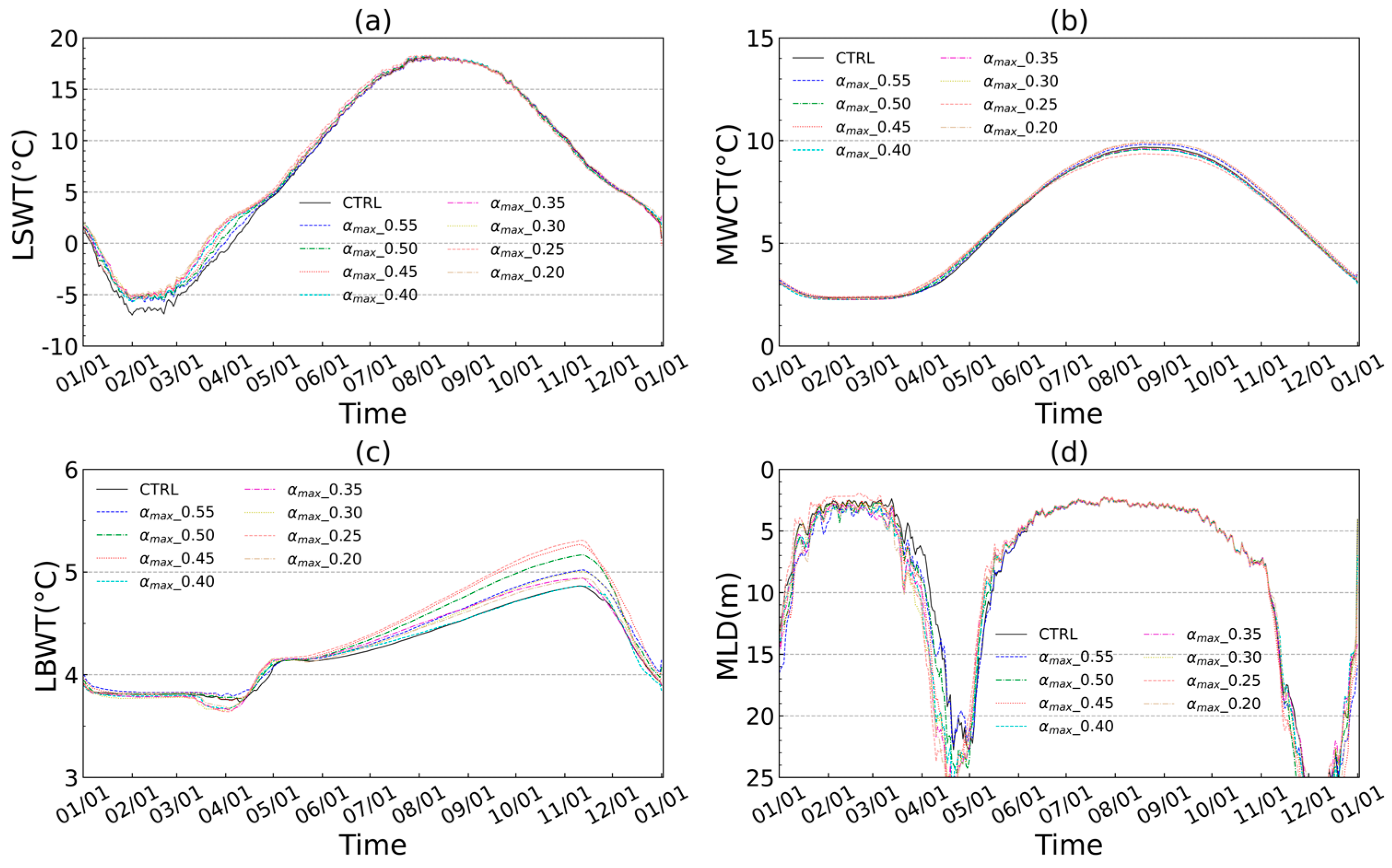
3.2.3. Ice Albedo
3.3. Improvements in FLake Performance
3.3.1. Optimization of Key Parameters
3.3.2. Salinity Parameterization
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, G.Q.; Luo, W.; Chen, W.F.; Zheng, G.X. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef]
- Ma, R.H.; Yang, G.S.; Duan, H.T.; Jiang, J.H.; Wang, S.M.; Feng, X.Z.; Li, A.N.; Kong, F.X.; Xue, B.; Wu, J.L.; et al. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2010, 54, 283–289. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Donk, E.V. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar]
- Sun, L.; Wang, B.; Ma, Y.; Shi, X.; Wang, Y. Analysis of ice phenology of middle and large lakes on the Tibetan Plateau. Sensors 2023, 23, 1661. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Huang, A.; Ma, W.; Wen, L.; Zhu, L.; Yang, X.; Wu, Y.; Gu, C. Drivers of warming in lake Nam Co on Tibetan Plateau over the past 40 years. J. Geophys. Res. Atmos. 2022, 127, e2021JD036320. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H. Future warming accelerates lake variations in the Tibetan Plateau. Int. J. Climatol. 2022, 42, 8687–8700. [Google Scholar] [CrossRef]
- Gilarranz, L.J.; Narwani, A.; Odermatt, D.; Siber, R.; Dakos, V. Regime shifts, trends, and variability of lake productivity at a global scale. Proc. Natl. Acad. Sci. USA 2022, 119, e2116413119. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Wang, Y.; Lazhu; Wang, L.; Ma, W.; Su, B. Analysis of lake stratification and mixing and its influencing factors over high elevation large and small lakes on the Tibetan Plateau. Water 2023, 15, 2094. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Shi, K.; Zhang, Y.L.; Moreno-Madrinan, M.J.; Xu, X.; Zhou, Y.Q.; Qin, B.Q.; Zhu, G.W.; Jeppesen, E. Water clarity response to climate warming and wetting of the Inner Mongolia-Xinjiang Plateau: A remote sensing approach. Sci. Total Environ. 2021, 796, 148916. [Google Scholar] [CrossRef]
- Brown, L.C.; Duguay, C.R. The response and role of ice cover in lake-climate interactions. Prog. Phys. Geogr. Earth Environ. 2010, 34, 671–704. [Google Scholar] [CrossRef]
- Woolway, R.I.; Sharma, S.; Weyhenmeyer, G.A.; Debolskiy, A.; Golub, M.; Mercado-Bettin, D.; Perroud, M.; Stepanenko, V.; Tan, Z.; Grant, L.; et al. Phenological shifts in lake stratification under climate change. Nat. Commun. 2021, 12, 2318. [Google Scholar] [CrossRef]
- Maberly, S.C.; O’Donnell, R.A.; Woolway, R.I.; Cutler, M.E.J.; Gong, M.; Jones, I.D.; Merchant, C.J.; Miller, C.A.; Politi, E.; Scott, E.M.; et al. Global lake thermal regions shift under climate change. Nat. Commun. 2020, 11, 1232. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Cao, X.; Li, G.; Huang, W.; Leppäranta, M.; Arvola, L.; Huotari, J.; Li, Z. Mass and heat balance of a lake ice cover in the central Asian arid climate zone. Water 2020, 12, 2888. [Google Scholar] [CrossRef]
- Zhao, Z.; Huang, A.; Ma, W.; Wu, Y.; Wen, L.; Lazhu; Gu, C. Effects of lake Nam Co and surrounding terrain on extreme precipitation over Nam Co basin, Tibetan Plateau: A case study. J. Geophys. Res. Atmos. 2022, 127, e2021JD036190. [Google Scholar] [CrossRef]
- Su, D.S.; Wen, L.J.; Gao, X.Q.; Lepparanta, M.; Song, X.Y.; Shi, Q.Q.; Kirillin, G. Effects of the largest lake of the Tibetan Plateau on the regional climate. J. Geophys. Res.-Atmos. 2020, 125, e2020JD033396. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, A.N.; Yang, B.; Dong, G.T.; Wen, L.J.; Lazhu; Zhang, Z.Q.; Fu, Z.P.; Zhu, X.Y.; Zhang, X.D.; et al. Numerical study on the climatic effect of the lake clusters over Tibetan Plateau in summer. Clim. Dyn. 2019, 53, 5215–5236. [Google Scholar] [CrossRef]
- Kirillin, G.; Wen, L.; Shatwell, T. Seasonal thermal regime and climatic trends in lakes of the Tibetan highlands. Hydrol. Earth Syst. Sci. 2017, 21, 1895–1909. [Google Scholar] [CrossRef]
- Lazhu; Yang, K.; Wang, J.B.; Lei, Y.B.; Chen, Y.Y.; Zhu, L.P.; Ding, B.H.; Qin, J. Quantifying evaporation and its decadal change for Lake Nam Co, central Tibetan Plateau. J. Geophys. Res.-Atmos. 2016, 121, 7578–7591. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Kokhanovsky, A.A. Solar heating of ice-covered lake and ice melting. J. Quant. Spectrosc. Radiat. Transf. 2023, 294, 108391. [Google Scholar] [CrossRef]
- Boehrer, B.; Schultze, M. Stratification of lakes. Rev. Geophys. 2008, 46, e2006rg000210. [Google Scholar] [CrossRef]
- Wilson, H.L.; Ayala, A.I.; Jones, I.D.; Rolston, A.; Pierson, D.; de Eyto, E.; Grossart, H.-P.; Perga, M.-E.; Woolway, R.I.; Jennings, E. Variability in epilimnion depth estimations in lakes. Hydrol. Earth Syst. Sci. 2020, 24, 5559–5577. [Google Scholar] [CrossRef]
- Notaro, M.; Holman, K.; Zarrin, A.; Fluck, E.; Vavrus, S.; Bennington, V. Influence of the Laurentian Great Lakes on regional climate. J. Clim. 2013, 26, 789–804. [Google Scholar] [CrossRef]
- Mallard, M.S.; Nolte, C.G.; Bullock, O.R.; Spero, T.L.; Gula, J. Using a coupled lake model with WRF for dynamical downscaling. J. Geophys. Res.-Atmos. 2014, 119, 7193–7208. [Google Scholar] [CrossRef]
- Zhou, X.; Lazhu; Yao, X.; Wang, B. Understanding two key processes associated with alpine lake ice phenology using a coupled atmosphere-lake model. J. Hydrol. Reg. Stud. 2023, 46, 101334. [Google Scholar] [CrossRef]
- Le Moigne, P.; Colin, J.; Decharme, B. Impact of lake surface temperatures simulated by the FLake scheme in the CNRM-CM5 climate model. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 31274. [Google Scholar] [CrossRef]
- Xiao, C.L.; Lofgren, B.M.; Wang, J.; Chu, P.Y. Improving the lake scheme within a coupled WRF-lake model in the Laurentian Great Lakes. J. Adv. Model. Earth Syst. 2016, 8, 1969–1985. [Google Scholar] [CrossRef]
- Subin, Z.M.; Riley, W.J.; Mironov, D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Syst. 2012, 4, e2011ms000072. [Google Scholar] [CrossRef]
- Mironov, D.; Heise, E.; Kourzeneva, E.; Ritter, B.; Schneider, N.; Terzhevik, A. Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO. Boreal Environ. Res. 2010, 15, 218–230. [Google Scholar]
- Xue, P.; Ye, X.; Pal, J.S.; Chu, P.Y.; Kayastha, M.B.; Huang, C. Climate projections over the Great Lakes Region: Using two-way coupling of a regional climate model with a 3-D lake model. Geosci. Model Dev. 2022, 15, 4425–4446. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Machul’skaya, E.E.; Glagolev, M.V.; Lykossov, V.N. Numerical modeling of methane emissions from lakes in the permafrost zone. Izv. Atmos. Ocean. Phys. 2011, 47, 252–264. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, A.; Lu, Y.; Lazhu; Yang, X.; Qiu, B.; Zhang, Z.; Zhang, X. Numerical study of the thermal structure and circulation in a large and deep dimictic lake over Tibetan Plateau. J. Geophys. Res. Ocean. 2021, 126, e2021jc017517. [Google Scholar] [CrossRef]
- Aijaz, S.; Ghantous, M.; Babanin, A.V.; Ginis, I.; Thomas, B.; Wake, G. Nonbreaking wave-induced mixing in upper ocean during tropical cyclones using coupled hurricane-ocean-wave modeling. J. Geophys. Res. Ocean. 2017, 122, 3939–3963. [Google Scholar] [CrossRef]
- Gu, H.P.; Jin, J.M.; Wu, Y.H.; Ek, M.B.; Subin, Z.M. Calibration and validation of lake surface temperature simulations with the coupled WRF-lake model. Clim. Chang. 2015, 129, 471–483. [Google Scholar] [CrossRef]
- Xu, L.J.; Liu, H.Z.; Du, Q.; Wang, L. Evaluation of the WRF-lake model over a highland freshwater lake in southwest China. J. Geophys. Res.-Atmos. 2016, 121, 13989–14005. [Google Scholar] [CrossRef]
- Hostetler, S.W.; Bates, G.T.; Giorgi, F. Interactive coupling of a lake thermal-model with a regional climate model. J. Geophys. Res.-Atmos. 1993, 98, 5045–5057. [Google Scholar] [CrossRef]
- Perroud, M.; Goyette, S.; Martynov, A.; Beniston, M.; Anneville, O. Simulation of multiannual thermal profiles in deep Lake Geneva: A comparison of one-dimensional lake models. Limnol. Oceanogr. 2009, 54, 1574–1594. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Goyette, S.; Martynov, A.; Perroud, M.; Fang, X.; Mironov, D. First steps of a lake model intercomparison project: LakeMIP. Boreal Environ. Res. 2010, 15, 191–202. [Google Scholar]
- Stepanenko, V.M.; Martynov, A.; Jöhnk, K.D.; Subin, Z.M.; Perroud, M.; Fang, X.; Beyrich, F.; Mironov, D.; Goyette, S. A one-dimensional model intercomparison study of thermal regime of a shallow, turbid midlatitude lake. Geosci. Model Dev. 2013, 6, 1337–1352. [Google Scholar] [CrossRef]
- Huang, A.; Lazhu; Wang, J.; Dai, Y.; Yang, K.; Wei, N.; Wen, L.; Wu, Y.; Zhu, X.; Zhang, X.; et al. Evaluating and improving the performance of three 1-D lake models in a large deep lake of the central Tibetan Plateau. J. Geophys. Res.-Atmos. 2019, 124, 3143–3167. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, A.N.; Lazhu; Yang, X.Y.; Qiu, B.; Wen, L.J.; Zhang, Z.Q.; Fu, Z.P.; Zhu, X.Y.; Zhang, X.D.; et al. Improvements of the coupled WRF-Lake model over Lake Nam Co, Central Tibetan Plateau. Clim. Dyn. 2020, 55, 2703–2724. [Google Scholar] [CrossRef]
- Guo, S.; Zhu, D.; Chen, Y. Improvement and evaluation of the latest version of WRF-Lake at a deep riverine reservoir. Adv. Atmos. Sci. 2023, 40, 682–696. [Google Scholar] [CrossRef]
- Usman, M.; Ndehedehe, C.E.; Farah, H.; Ahmad, B.; Wong, Y.; Adeyeri, O.E. Application of a conceptual hydrological model for streamflow prediction using multi-source precipitation products in a semi-arid river basin. Water 2022, 14, 1260. [Google Scholar] [CrossRef]
- Thiery, W.; Martynov, A.; Darchambeau, F.; Descy, J.P.; Plisnier, P.D.; Sushama, L.; van Lipzig, N.P.M. Understanding the performance of the FLake model over two African Great Lakes. Geosci. Model Dev. 2014, 7, 317–337. [Google Scholar] [CrossRef]
- Rooney, G.G.; Bornemann, F.J. The performance of FLake in the Met Office Unified Model. Tellus A Dyn. Meteorol. Oceanogr. 2013, 65, 21363. [Google Scholar] [CrossRef]
- Kirillin, G.; Hochschild, J.; Mironov, D.; Terzhevik, A.; Golosov, S.; Nützmann, G. FLake-Global: Online lake model with worldwide coverage. Environ. Model. Softw. 2011, 26, 683–684. [Google Scholar] [CrossRef]
- Layden, A.; MacCallum, S.N.; Merchant, C.J. Determining lake surface water temperatures worldwide using a tuned one-dimensional lake model (FLake, v1). Geosci. Model Dev. 2016, 9, 2167–2189. [Google Scholar] [CrossRef]
- Huang, L.; Wang, X.H.; Sang, Y.X.; Tang, S.C.; Jin, L.; Yang, H.; Ottle, C.; Bernus, A.; Wang, S.L.; Wang, C.Z.; et al. Optimizing lake surface water temperature simulations over large lakes in China with FLake model. Earth Space Sci. 2021, 8, e2021ea001737. [Google Scholar] [CrossRef]
- Wang, B.B.; Ma, Y.M.; Chen, X.L.; Ma, W.Q.; Su, Z.B.; Menenti, M. Observation and simulation of lake-air heat and water transfer processes in a high-altitude shallow lake on the Tibetan Plateau. J. Geophys. Res.-Atmos. 2015, 120, 12327–12344. [Google Scholar] [CrossRef]
- Wen, L.J.; Lyu, S.H.; Kirillin, G.; Li, Z.G.; Zhao, L. Air-lake boundary layer and performance of a simple lake parameterization scheme over the Tibetan highlands. Tellus Ser. A-Dyn. Meteorol. Oceanogr. 2016, 68, 31091. [Google Scholar] [CrossRef]
- Su, D.S.; Hu, X.Q.; Wen, L.J.; Lyu, S.H.; Gao, X.Q.; Zhao, L.; Li, Z.G.; Du, J.; Kirillin, G. Numerical study on the response of the largest lake in China to climate change. Hydrol. Earth Syst. Sci. 2019, 23, 2093–2109. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Ma, W.; Su, B.; Dong, X. Evaluation of ten methods for estimating evaporation in a small high-elevation lake on the Tibetan Plateau. Theor. Appl. Climatol. 2018, 136, 1033–1045. [Google Scholar] [CrossRef]
- Wen, L.; Wang, C.; Li, Z.; Zhao, L.; Lyu, S.; Leppäranta, M.; Kirillin, G.; Chen, S. Thermal responses of the largest freshwater lake in the Tibetan Plateau and its nearby saline lake to climate change. Remote Sens. 2022, 14, 1774. [Google Scholar] [CrossRef]
- Su, R.; Xie, Z.; Ma, W.; Ma, Y.; Wang, B.; Hu, W.; Su, Z. Summer lake destratification phenomenon: A peculiar deep lake on the Tibetan Plateau. Front. Earth Sci. 2022, 10, 839151. [Google Scholar] [CrossRef]
- Wang, M.; Hou, J.; Lei, Y. Classification of Tibetan lakes based on variations in seasonal lake water temperature. Chin. Sci. Bull. 2014, 59, 4847–4855. [Google Scholar] [CrossRef]
- Wang, M.D.; Hou, J.Z.; Lazhu; Li, X.M.; Liang, J.; Xie, S.Y.; Tang, W.J. Changes in the lake thermal and mixing dynamics on the Tibetan Plateau. Hydrol. Sci. J.-J. Des Sci. Hydrol. 2021, 66, 838–850. [Google Scholar] [CrossRef]
- Politi, E.; Maccallum, S.; Cutler, M.E.J.; Merchant, C.J.; Rowan, J.S.; Dawson, T.P. Selection of a network of large lakes and reservoirs suitable for global environmental change analysis using Earth Observation. Int. J. Remote Sens. 2016, 37, 3042–3060. [Google Scholar] [CrossRef]
- Zhang, R.; Chan, S.; Bindlish, R.; Lakshmi, V. Evaluation of global surface water temperature data sets for use in passive remote sensing of soil moisture. Remote Sens. 2021, 13, 1872. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, L.P.; Wang, J.B.; Ju, J.T.; Ma, Q.F.; Qiao, B.J.; Wang, Y.; Xu, T.; Chen, H.; Kou, Q.Q.; et al. In-situ water quality investigation of the lakes on the Tibetan Plateau. Sci. Bull. 2021, 66, 1727–1730. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Mironov, D.V. Parameterization of Lakes in Numerical Weather Prediction: Description of a Lake Model; COSMO Technical Report, Nol 11; Deutscher Wetterdienst: Offenbach am Main, Germany, 2008; p. 41. [Google Scholar]
- Salgado, R.; Le Moigne, P. Coupling of the FLake model to the Surfex externalized surface model. Boreal Environ. Res. 2010, 15, 231–244. [Google Scholar]
- Baijnath-Rodino, J.A.; Duguay, C.R. Assessment of coupled CRCM5–FLake on the reproduction of wintertime lake-induced precipitation in the Great Lakes Basin. Theor. Appl. Climatol. 2019, 138, 77–96. [Google Scholar] [CrossRef]
- Martynov, A.; Laprise, R.; Sushama, L.; Winger, K.; Separovic, L.; Dugas, B. Reanalysis-driven climate simulation over CORDEX North America domain using the Canadian Regional Climate Model, version 5: Model performance evaluation. Clim. Dyn. 2013, 41, 2973–3005. [Google Scholar] [CrossRef]
- Song, X.Y.; Wen, L.J.; Li, M.S.; Du, J.; Su, D.S.; Yin, S.C.; Lv, Z. Comparative study on applicability of different lake models to typical lakes in Qinghai-Tibetan Plateau. Plateau Meteorol. 2020, 39, 213–225. [Google Scholar] [CrossRef]
- Lang, J.H.; Ma, Y.M.; Li, Z.G.; Su, D.S. The impact of climate warming on lake surface heat exchange and ice phenology of different types of lakes on the Tibetan Plateau. Water 2021, 13, 634. [Google Scholar] [CrossRef]
- Li, Z.G.; Ao, Y.H.; Lyu, S.; Lang, J.H.; Wen, L.J.; Stepanenko, V.; Meng, X.H.; Zhao, L. Investigation of the ice surface albedo in the Tibetan Plateau lakes based on the field observation and MODIS products. J. Glaciol. 2018, 64, 506–516. [Google Scholar] [CrossRef]
- Zolfaghari, K.; Duguay, C.R.; Pour, H.K. Satellite-derived light extinction coefficient and its impact on thermal structure simulations in a 1-D lake model. Hydrol. Earth Syst. Sci. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Caldwell, D.R. Maximum density points of pure and saline water. Deep-Sea Res. 1978, 25, 175–181. [Google Scholar] [CrossRef]
- Lang, J.; Lyu, S.; Li, Z.; Ma, Y.; Su, D. An investigation of ice surface albedo and its influence on the high-altitude lakes of the Tibetan Plateau. Remote Sens. 2018, 10, 218. [Google Scholar] [CrossRef]
- Rinke, K.; Yeates, P.; Rothhaupt, K.O. A simulation study of the feedback of phytoplankton on thermal structure via light extinction. Freshw. Biol. 2010, 55, 1674–1693. [Google Scholar] [CrossRef]
- Heiskanen, J.J.; Mammarella, I.; Ojala, A.; Stepanenko, V.; Erkkila, K.M.; Miettinen, H.; Sandstrom, H.; Eugster, W.; Lepparanta, M.; Jarvinen, H.; et al. Effects of water clarity on lake stratification and lake-atmosphere heat exchange. J. Geophys. Res.-Atmos. 2015, 120, 7412–7428. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Remote sensing estimation of water clarity for various lakes in China. Water Res. 2021, 192, 116844. [Google Scholar] [CrossRef] [PubMed]




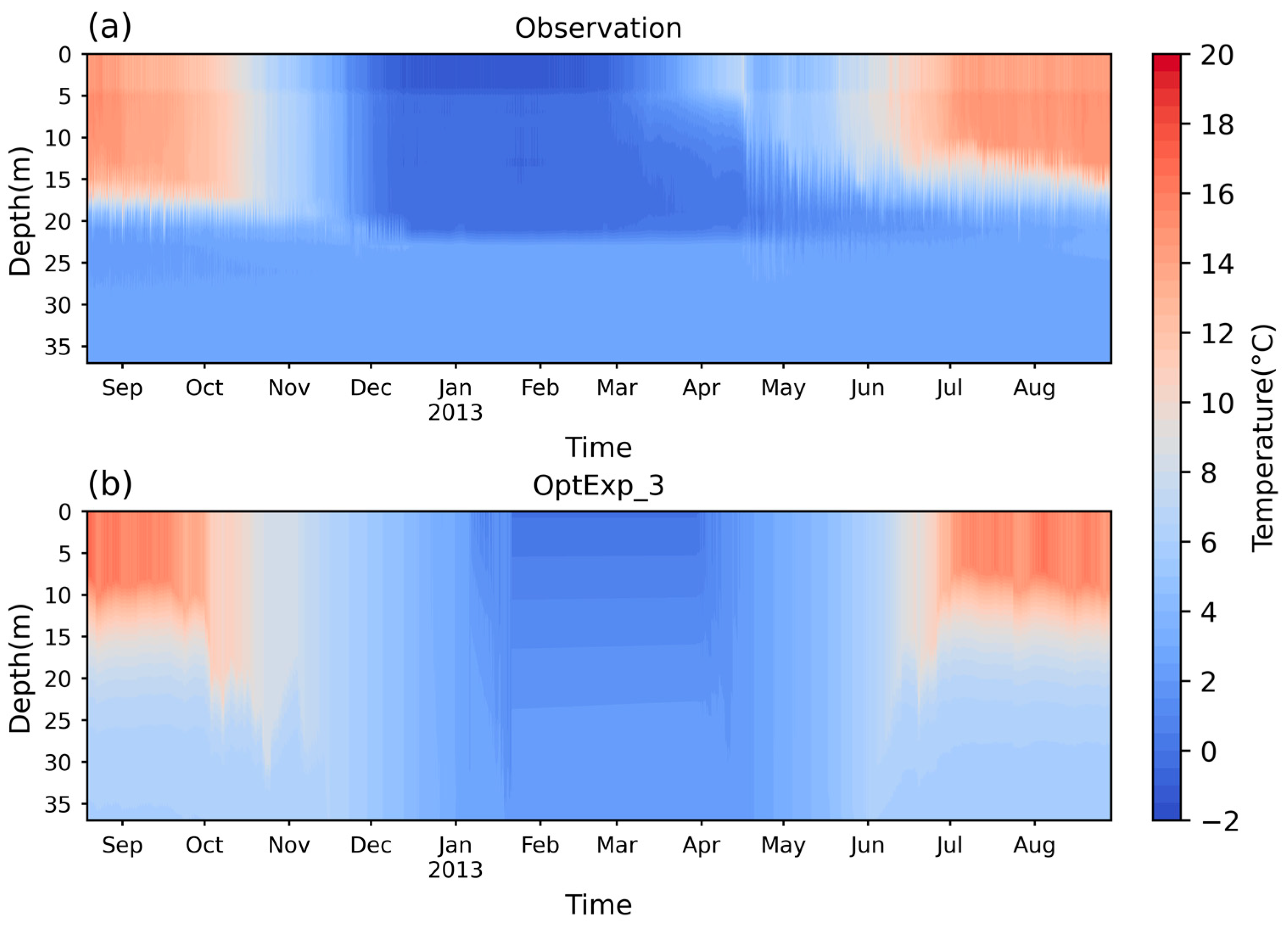
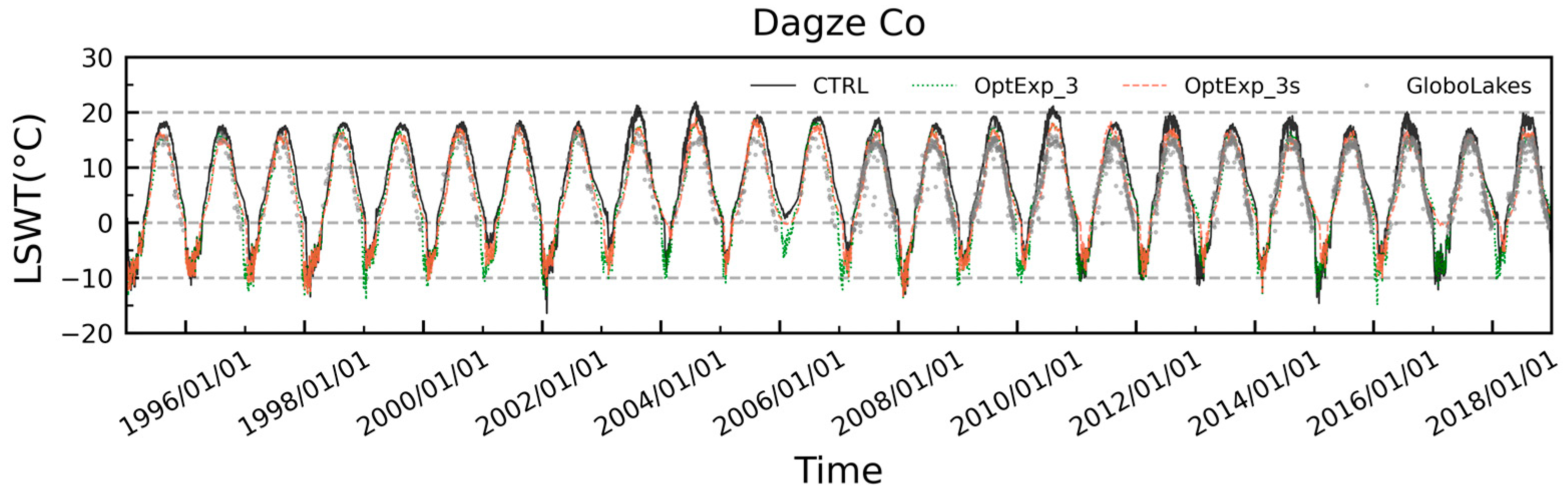
| Experiments | Kd (m−1) | Friction Velocity (m−1) | White Ice Albedo | Salinity (g L−1) |
|---|---|---|---|---|
| CTRL | 3.0 | u* | 0.6 | 0 |
| SenExp_Kd | 0.15–0.5, 0.05 1 0.6–2.8, 0.2 1 | u* | 0.6 | 0 |
| SenExp_u* | 3.0 | u* × (1.2–2.0, 0.2) 1 | 0.6 | 0 |
| SenExp_ | 3.0 | u* | 0.20–0.55, 0.05 1 | 0 |
| OptExp_1 | Equation (7) (SDD~7 m) | u* | 0.6 | 0 |
| OptExp_2 | Equation (7) (SDD~7 m) | u* × f_opt(2.0) | 0.6 | 0 |
| OptExp_3 | Equation (7) (SDD~7 m) | u* × f_opt(2.0) | alb_opt (0.25) | 0 |
| OptExp_3s | Equation (7) (SDD~7 m) | u* × f_opt(2.0) | alb_opt (0.25) | 14.7 |
| Experiments | Bias (°C) | RMSE (°C) | R |
|---|---|---|---|
| CTRL | 3.08 | 3.62 | 0.91 |
| OptExp_1 | 3.14 | 3.66 | 0.90 |
| OptExp_2 | 2.20 | 2.72 | 0.86 |
| OptExp_3 | 2.00 | 2.48 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, B.; Liu, M.; Su, D.; Wen, L.; Li, M.; Lin, Z.; Lang, J.; Song, X. Improvements and Evaluation of the FLake Model in Dagze Co, Central Tibetan Plateau. Water 2023, 15, 3135. https://doi.org/10.3390/w15173135
Cao B, Liu M, Su D, Wen L, Li M, Lin Z, Lang J, Song X. Improvements and Evaluation of the FLake Model in Dagze Co, Central Tibetan Plateau. Water. 2023; 15(17):3135. https://doi.org/10.3390/w15173135
Chicago/Turabian StyleCao, Bilin, Minghua Liu, Dongsheng Su, Lijuan Wen, Maoshan Li, Zhiqiang Lin, Jiahe Lang, and Xingyu Song. 2023. "Improvements and Evaluation of the FLake Model in Dagze Co, Central Tibetan Plateau" Water 15, no. 17: 3135. https://doi.org/10.3390/w15173135
APA StyleCao, B., Liu, M., Su, D., Wen, L., Li, M., Lin, Z., Lang, J., & Song, X. (2023). Improvements and Evaluation of the FLake Model in Dagze Co, Central Tibetan Plateau. Water, 15(17), 3135. https://doi.org/10.3390/w15173135









