Utilizing Entropy-Based Method for Rainfall Network Design in Huaihe River Basin, China
Abstract
:1. Introduction
2. Study Area and Dataset
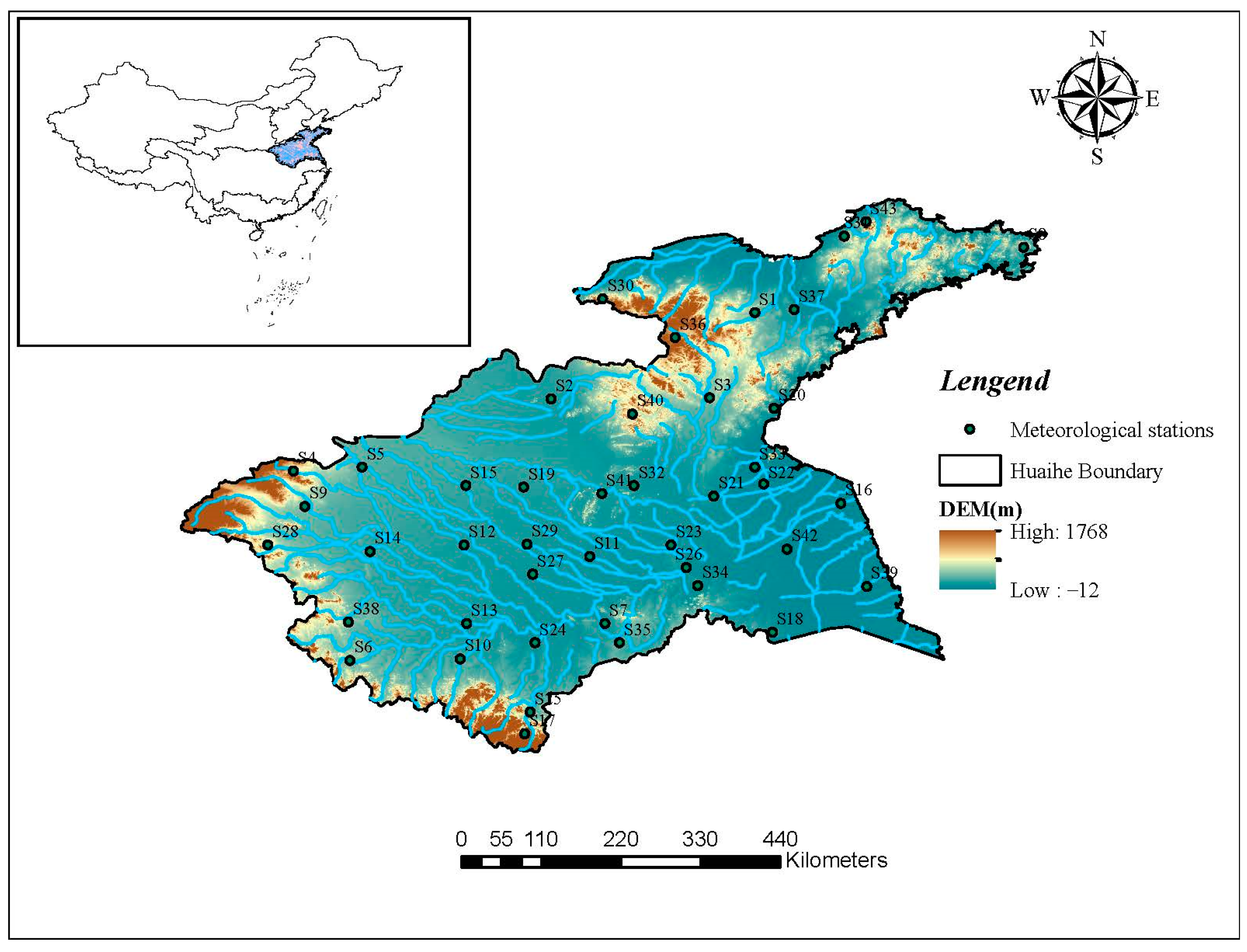
2.1. Study Area
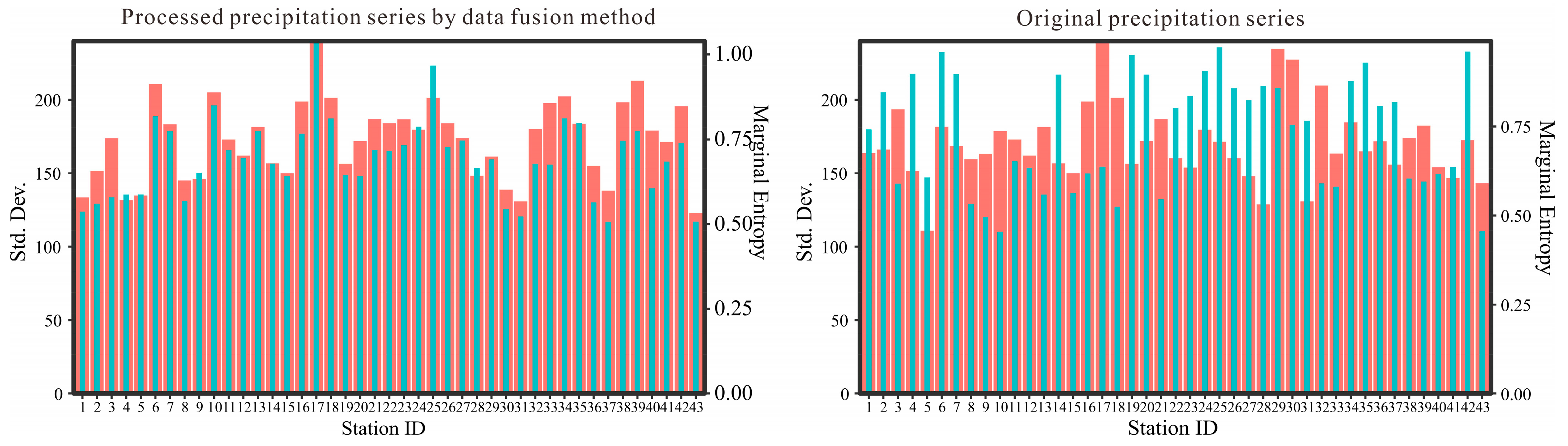
2.2. Data Processing
- (i)
- Firstly, regional rainy days were selected as at least one station having precipitation records (). In contrast, regional non-rainy days were defined as all stations in the basin having no precipitation records.
- (ii)
- Secondly, adjacent regional rainy days would be separated by non-rainy days. Thus, effective interval days () were defined, which was used to accumulate precipitation records from adjacent rainy days.
- (iii)
- Thirdly, autocorrelation tests were implemented to ensure the processed series obeyed the “independent and identically distributed” assumption.
3. Methods
3.1. Entropy-Based Indexes for Station Network Optimization
- (1)
- Marginal entropy (ME):
- (2)
- Joint entropy (JE):
- (3)
- Total correlation (TC):
- (1)
- For example, choosing 2 sites from 43 sites would result in 903 () possible combinations. In the same way, choosing 6 sites from 43 sites would result in 6,096,454 ( 6,096,454) possible combinations. Therefore, it was not necessary to exhaustively search all possible combinations of the given number of gauges. Instead, we commenced by generating a multitude of potential gauge combinations, specifically 90,000 in this study.
- (2)
- The joint entropy and total correlation for each combination of gauges can be calculated using the processed precipitation data. However, it is important to note that these two information indexes, namely joint entropy and total correlation, need to be computed using an appropriate discretization method, which is investigated in Section 3.2.
- (3)
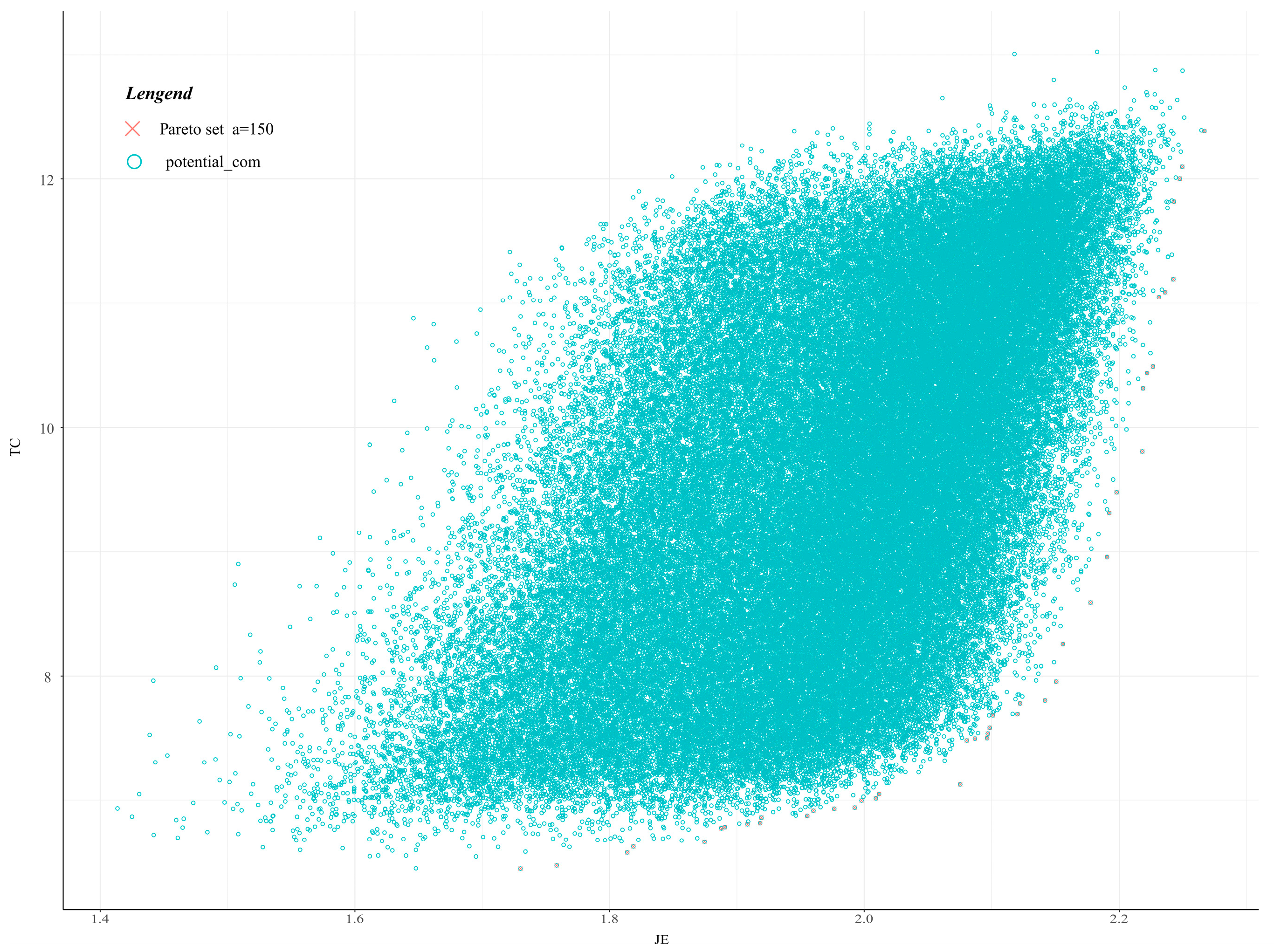
- Based on these two objective functions, ( and ), a certain number of Pareto solutions () can be derived as approximations to the optimal function. This is because it is impossible to satisfy both objective functions simultaneously.
- (4)
- The frequency of station selection is calculated by examining the occurrence of the label (in this case, represents the label for a specific station) in the Pareto solutions. Since different stations have different frequencies of label occurrence, the selected frequency can be determined using the following calculation:
3.2. Three Kinds of Quantization Methods for Entropy Calculation
4. Results
4.1. Analysis of Processed Data in the HRB
4.2. Selection of Data Discretization Method
4.3. The Impact of Time Variability in Precipitation on the Optimization Results of Gauge Networks in the Huaihe River Basin
5. Discussion
6. Conclusions
- (1)
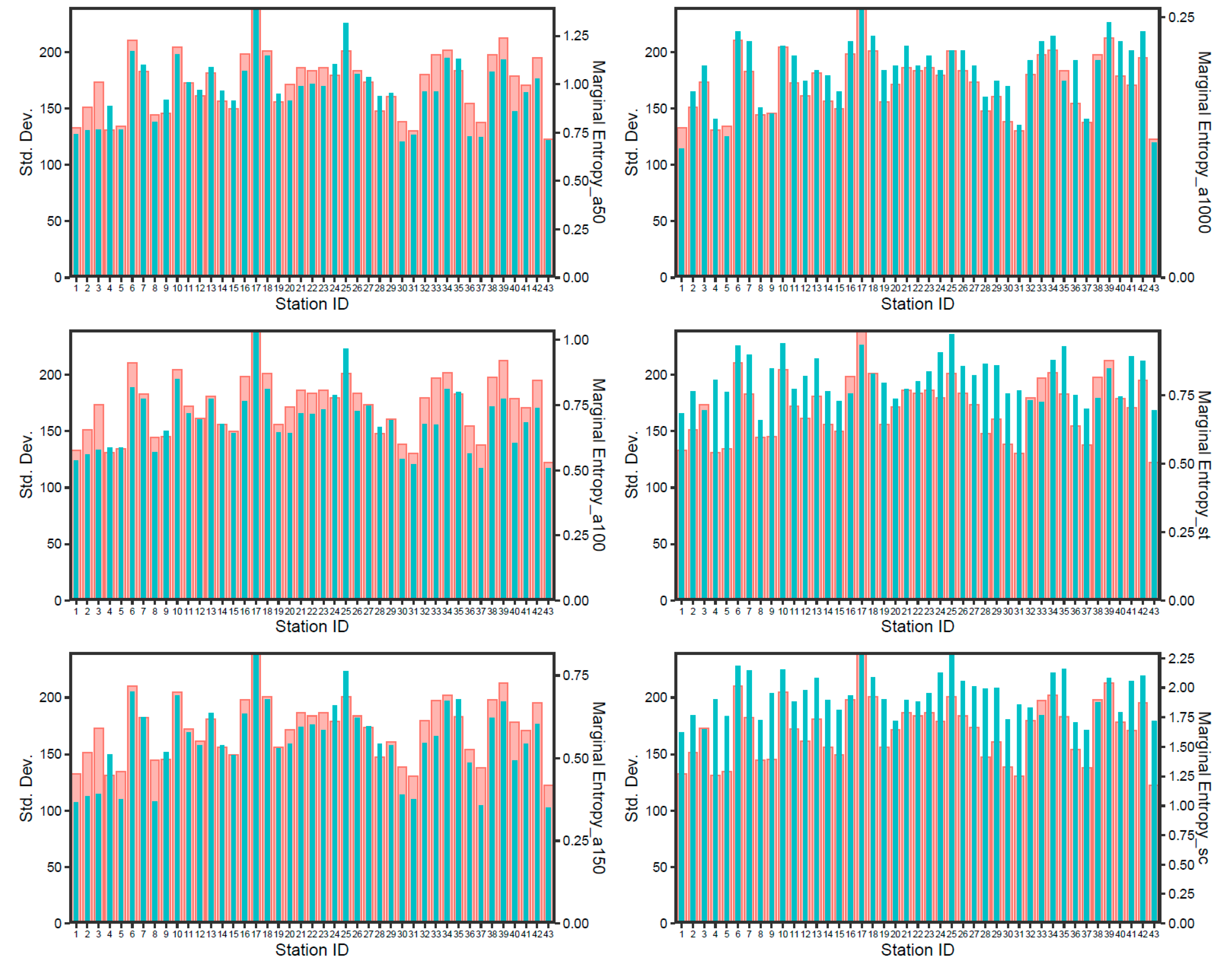
- Careful selection of discretization technology is the basis for station network optimization. This study compared the network optimization results derived from three kinds of discretization methods, including the floor function-based approach, Scott’s equal bin width histogram (EWH-Sc) approach, and Sturges’s equal bin width histogram (EWH-St) approach (Figure 5). The floor function-based approach with a = 100 was selected as the most suitable discretization method for this study by optimizing the matching degree of the variance and edge entropy sequence of the measured values at each station.
- (2)
- The criterion of maximizing the joint entropy and minimizing the total correlation (maxJE-minTC) was able to generate potential Pareto solution sets for the optimal network. The frequency of selecting sites in the Pareto solution set proposed in this study provides a new approach for characterizing the results of station network optimization.
- (3)
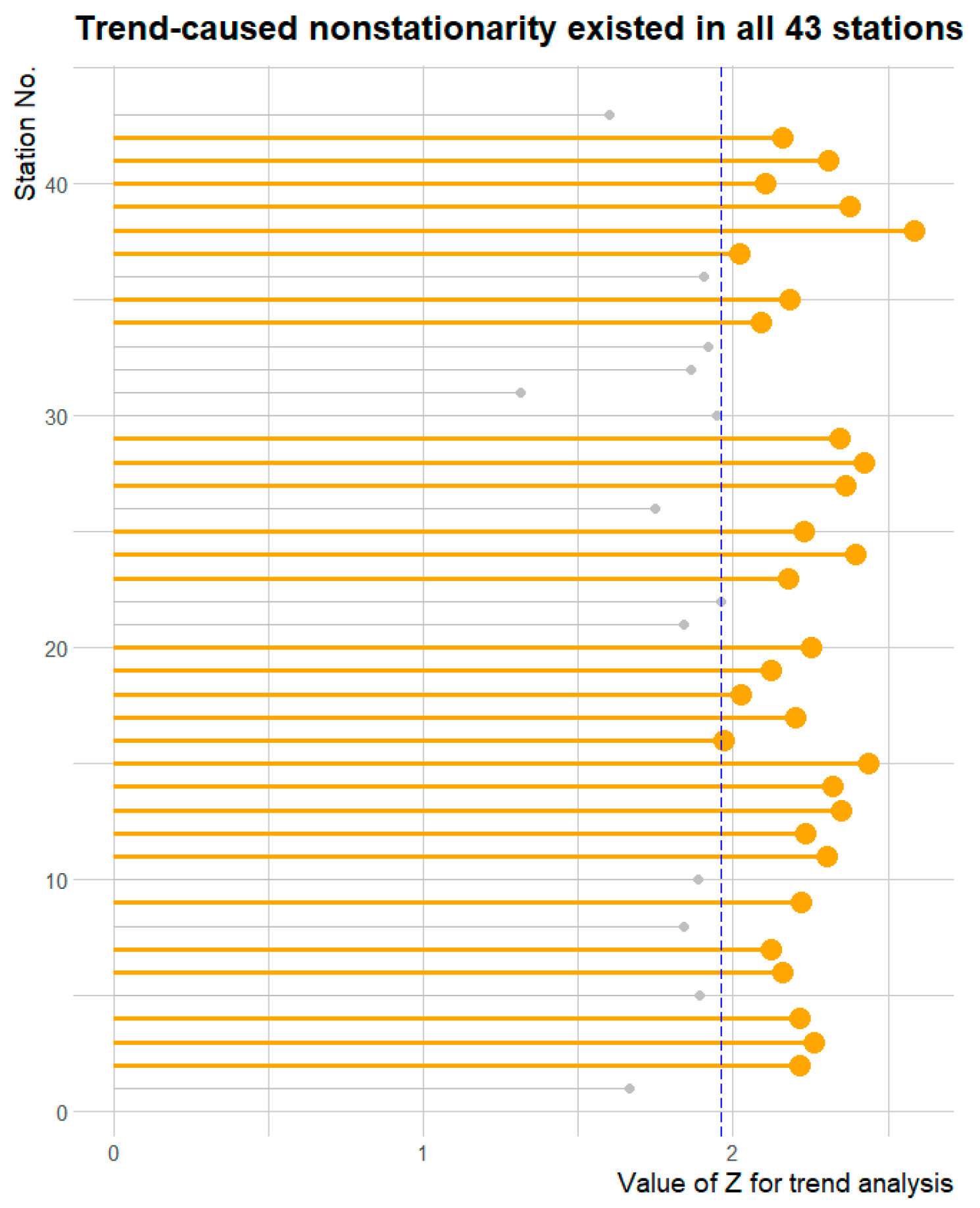
- Due to the trend-caused nonstationarity in almost 75% of all stations in the HRB, taking the impact of temporal variability in the precipitation series on the final rain gauge network optimization results into consideration is of great significance. The analysis results indicated that the degree of nonstationarity in the processed precipitation series is directly proportional to the frequency of station selection.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, A.K.; Coulibaly, P. Developments in hydrometric network design: A review. Rev. Geophys. 2009, 47, 2415–2440. [Google Scholar] [CrossRef]
- Chaconhurtado, J.C.; Alfonso, L.; Solomatine, D.P. Rainfall and streamflow sensor network design: A review of applications, classification, and a proposed framework. Hydrol. Earth Syst. Sci. 2017, 21, 3071–3091. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L.; Zou, X.; Chen, X.; Liu, J.; Zou, Y.; et al. A kriging and entropy-based approach to raingauge network design. Environ. Res. 2018, 161, 61–75. [Google Scholar] [CrossRef] [PubMed]
- Joseph, R.; Mujumdar, P.P.; Bhowmik, R.D. Reconstruction of urban rainfall measurements estimate the spatiotemporal variability of extreme rainfall. Water 2022, 14, 3900. [Google Scholar] [CrossRef]
- Muhamad Ali, M.Z.; Othman, F. Raingauge network optimization in a tropical urban area by coupling cross-validation with the geostatistical technique. Hydrol. Sci. J. 2018, 63, 474–491. [Google Scholar]
- Adhikary, S.K.; Yilmaz, A.G.; Muttil, N. Optimal design of rain gauge network in the Middle Yarra River catchment, Australia. Hydrol. Process. 2015, 29, 2582–2599. [Google Scholar] [CrossRef]
- Aalto, J.; Pirinen, P.; Jylhä, K. New gridded daily climatology of Finland: Permutation-based uncertainty estimates and temporal trends in climate. J. Geophys. Res. Atmos. 2016, 121, 3807–3823. [Google Scholar] [CrossRef]
- Shafiei, M.; Ghahraman, B.; Saghafian, B.; Pande, S.; Gharari, S.; Davary, K. Assessment of rain-gauge networks using a probabilistic GIS based approach. Hydrol. Res. 2014, 45, 551–562. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula based multisite model for daily precipitation simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef]
- Singh, V.P. The use of entropy in hydrology and water resources. Hydrol. Process. 1997, 11, 587–626. [Google Scholar] [CrossRef]
- Su, H.T.; You, G.J.Y. Developing an entropy-based model of spatial information estimation and its application in the design of precipitation gauge networks. J. Hydrol. 2014, 519, 3316–3327. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Information theory-based approach for location of monitoring water level gauges in polders. Water Resour. Res. 2010, 46, W03528. [Google Scholar] [CrossRef]
- Fuentes, M.; Chaudhuri, A.; Holland, D.M. Bayesian entropy for spatial sampling design of environmental data. Environ. Ecol. Stat. 2007, 14, 323–340. [Google Scholar] [CrossRef]
- Li, H.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wu, J. Developing an entropy and copula-based approach for precipitation monitoring network expansion. J. Hydrol. 2021, 598, 126366. [Google Scholar] [CrossRef]
- Gu, X.H.; Zhang, Q.; Singh, V.P.; Shi, P.J. Nonstationarity in timing of extreme precipitation across China and impact of tropical cyclones. Glob. Planet. Chang. 2017, 149, 153–165. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Z.M.; Wang, D.; Liu, T.; Yang, J. Impact of climate change on hydrologic extremes in the upper basin of the Yellow River Basin of China. Adv. Meteorol. 2016, 2016, 1404290. [Google Scholar] [CrossRef]
- Ganguli, P.; Coulibaly, P. Does nonstationarity in rainfall requires nonstationary intensity-duration-frequency curves? Hydrol. Earth Syst. Sci. 2017, 21, 6461–6483. [Google Scholar] [CrossRef]
- Agilan, V.; Umamahesh, N.V. What are the best covariates for developing nonstationary rainfall intensity-duration-frequency relationship? Adv. Water Resour. 2017, 101, 11–22. [Google Scholar] [CrossRef]
- Call, B.C.; Belmont, P.; Schmidt, J.C.; Wilcock, P.R. Changes in floodplain inundation under nonstationary hydrology for an adjustable, alluvial river channel. Water Resour. Res. 2017, 53, 3811–3834. [Google Scholar] [CrossRef]
- Ghanbari, M.; Arabi, M.; Obeysekera, J.; Sweet, W. A coherent statistical model for coastal flood frequency analysis under nonstationary sea level conditions. Earth’s Future 2019, 7, 162–177. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L. A two-phase copula entropy-based multiobjective optimization approach to hydrometeorological gauge network design. J. Hydrol. 2017, 555, 228–241. [Google Scholar] [CrossRef]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Cao, Q.; Qi, Y. The variability of vertical structure of precipitation in Huaihe River Basin of China: Implications from long-term spaceborne observations with TRMM precipitation radar. Water Resour. Res. 2014, 50, 3690–3705. [Google Scholar] [CrossRef]
- Chen, G.; Sha, W.; Iwasaki, T. Diurnal variation of precipitation over southeastern China: Spatial distribution and its seasonality. J. Geophys. Res. Atmos. 2009, 114, D13103. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, H.; Zhang, R.; Qian, W.; Luo, Z. Comparison of rainfall characteristics and convective properties of monsoon precipitation systems over South China and the Yangtze and Huai River Basin. J. Clim. 2013, 26, 110–132. [Google Scholar] [CrossRef]
- He, H.; Zhang, F. Diurnal variations of warm-season precipitation over Northern China. Mon. Weather Rev. 2010, 138, 1017–1025. [Google Scholar] [CrossRef]
- Zhou, T.; Yu, R.; Chen, H.; Dai, A.; Pan, U. Summer precipitation frequency, intensity, and diurnal cycle over China: A comparison of satellite data with rain gauge observations. J. Clim. 2008, 21, 3997–4010. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Y.; Gao, F.; Xiao, X. Diurnal variations in convective storm activity over contiguous North China during the warm season based on radar mosaic climatology. J. Geophys. Res. Atmos. 2012, 117, D20115. [Google Scholar] [CrossRef]
- Liu, C. Rainfall contributions from precipitation systems with different sizes, convective intensities, and durations over the Tropics and Subtropics. J. Hydrometeorol. 2011, 12, 394–412. [Google Scholar] [CrossRef]
- Xu, W. Precipitation and convective characteristics of summer deep convection over East Asia observed by TRMM. Mon. Weather Rev. 2013, 141, 1577–1592. [Google Scholar] [CrossRef]
- Guo, Z.; Fang, J.; Sun, X.; Yang, Y.; Tang, J. Sensitivity of summer precipitation simulation to microphysics parameterization over eastern China: Convection-permitting regional climate simulation. J. Geophys. Res. Atmos. 2019, 124, 9183–9204. [Google Scholar] [CrossRef]
- Milly, P.; Betancourt, J.; Falkenmark, M.; Hirsch, R.; Kundzewicz, Z.; Lettenmaier, D.; Stouffer, R. Climate change—Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Wang, D.; Singh, V.P.; Lu, H.; Wang, Y.; Wu, J.; Wang, L.; Liu, J.; Zhang, J. Multivariate hazard assessment for nonstationary seasonal flood extremes considering climate change. J. Geophys. Res. Atmos. 2020, 125, e2020JD032780. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.; Singh, V.P.; Lu, H.; Wang, Y.; Wu, J.; Wang, L.; Liu, J.; Zhang, J. Copula-based seasonal rainfall simulation considering nonstationarity. J. Hydrol. 2020, 590, 125439. [Google Scholar] [CrossRef]





| Station No. | Original Data | Processed Data | ||
|---|---|---|---|---|
| Maximum (mm) | SD a (mm) | Maximum | SD | |
| S1 | 188.8 | 6.9 | 945.7 | 132.9 |
| S2 | 191.3 | 8.4 | 868.6 | 151.2 |
| S3 | 288.6 | 8.9 | 1183.7 | 173.3 |
| S4 | 189.4 | 7.4 | 818.4 | 131.1 |
| S5 | 217.8 | 7.7 | 913.7 | 134.4 |
| S6 | 276.2 | 10.9 | 1279.3 | 210.3 |
| S7 | 216.7 | 9.7 | 1086.3 | 182.8 |
| S8 | 257.7 | 8.6 | 1073.9 | 144.5 |
| S9 | 177.2 | 7.9 | 896.9 | 145.4 |
| S10 | 206.9 | 10.5 | 1313.7 | 104.4 |
| S11 | 232.6 | 9.3 | 1193.9 | 172.4 |
| S12 | 285.3 | 9.1 | 1013.3 | 161.3 |
| S13 | 226.1 | 9.8 | 1186.8 | 181.1 |
| S14 | 225.4 | 8.8 | 1109.7 | 156.2 |
| S15 | 363.6 | 8.6 | 1062.9 | 149.6 |
| S16 | 263.2 | 9.9 | 1456.0 | 198.3 |
| Discretization Approaches | Number |
|---|---|
| Floor function-based with a = 50 | 27 |
| Floor function-based with a = 100 | 29 |
| Floor function-based with a = 150 | 48 |
| Floor function-based with a = 1000 | 100 |
| EWH-Sc | 17 |
| EWH-St | 37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, Y.; Wang, Y.; Xu, P. Utilizing Entropy-Based Method for Rainfall Network Design in Huaihe River Basin, China. Water 2023, 15, 3115. https://doi.org/10.3390/w15173115
Liu J, Li Y, Wang Y, Xu P. Utilizing Entropy-Based Method for Rainfall Network Design in Huaihe River Basin, China. Water. 2023; 15(17):3115. https://doi.org/10.3390/w15173115
Chicago/Turabian StyleLiu, Jian, Yanyan Li, Yuankun Wang, and Pengcheng Xu. 2023. "Utilizing Entropy-Based Method for Rainfall Network Design in Huaihe River Basin, China" Water 15, no. 17: 3115. https://doi.org/10.3390/w15173115






