An Efficient Dynamic Coupling Calculation Method for Dam–Reservoir Systems Based on FEM-SBFEM
Abstract
:1. Introduction
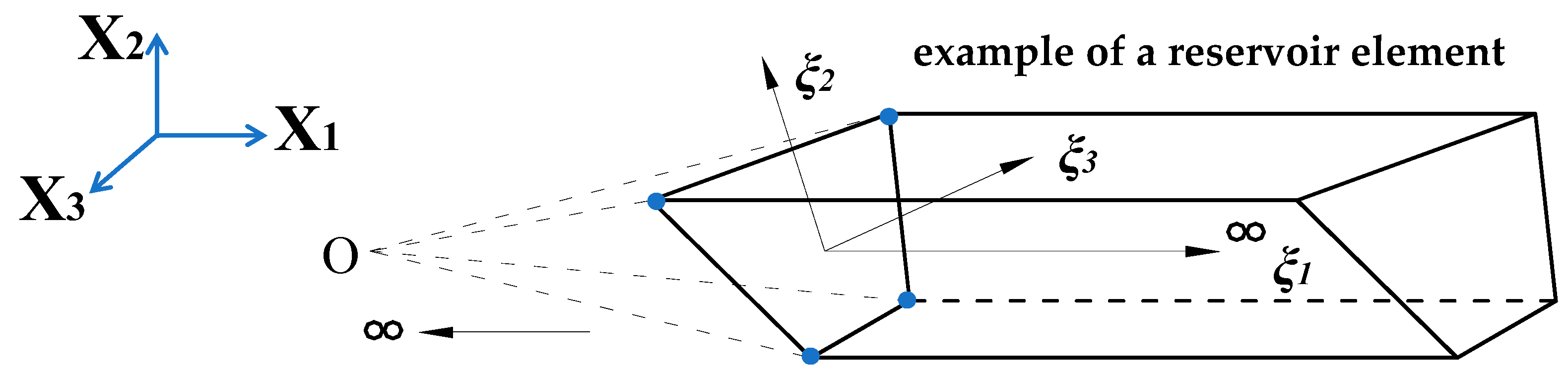
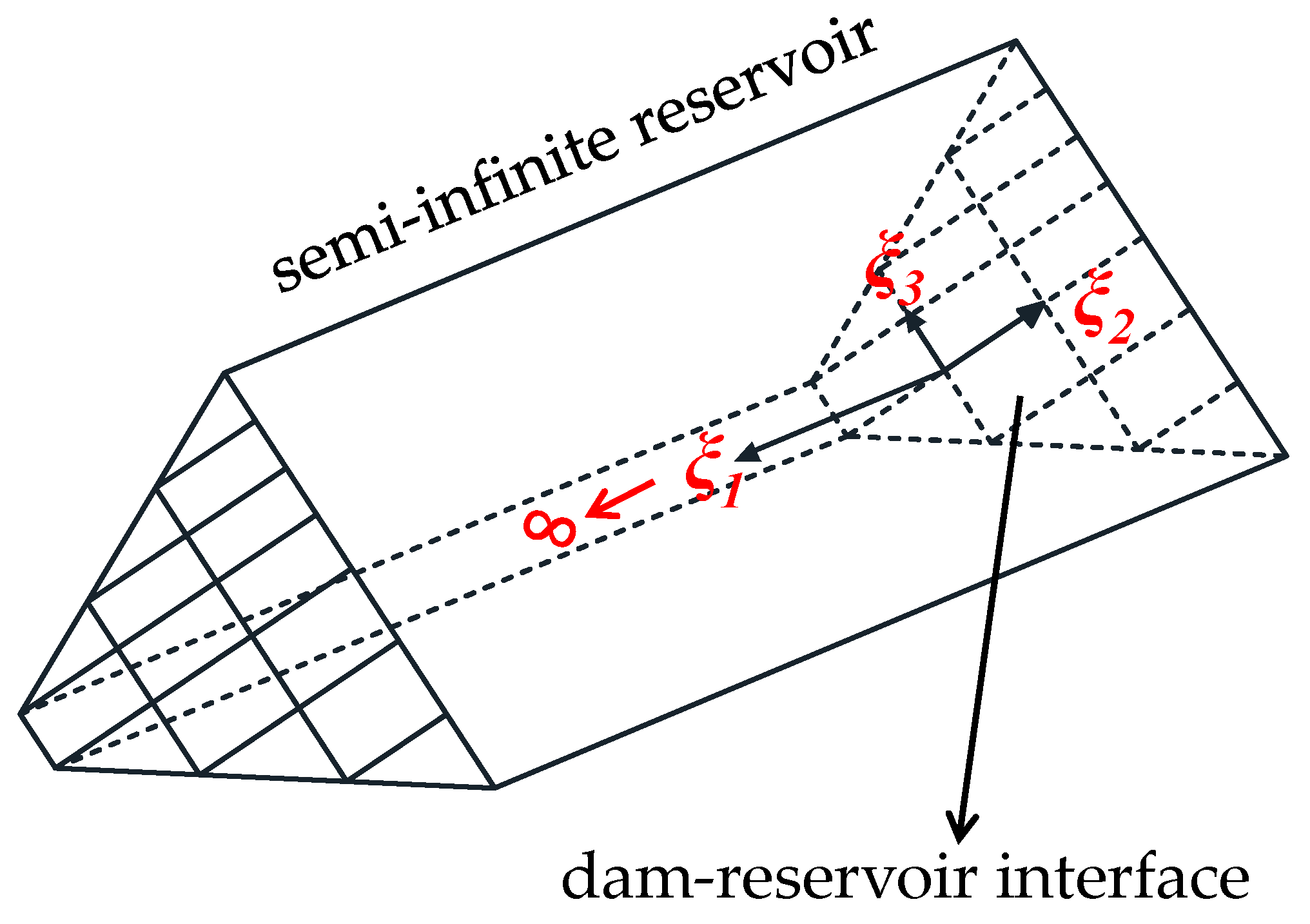
2. A Calculating Method for Hydrodynamic Pressure of Reservoir Based on SBFEM
2.1. The Basic Equation and Boundary Conditions
2.2. Solution for Hydrodynamic Pressure Based on SBFEM
3. An Efficient Dynamic Coupling Calculation Method for Dam–Reservoir Systems
3.1. Conventional Dynamic Coupling Analysis Method for Dam–Reservoir Systems
3.2. Simplification of Hydrodynamic Pressure Additional Mass Matrix
3.2.1. Physical Meaning and Distribution Characteristics of Matrix
3.2.2. Theoretical Analysis and Simplified Processing Method
3.3. Efficient Dynamic Coupling Calculation Method Based on FEM-SBFEM
4. Dynamic Coupling Analysis of Arch Dam and Reservoir Systems
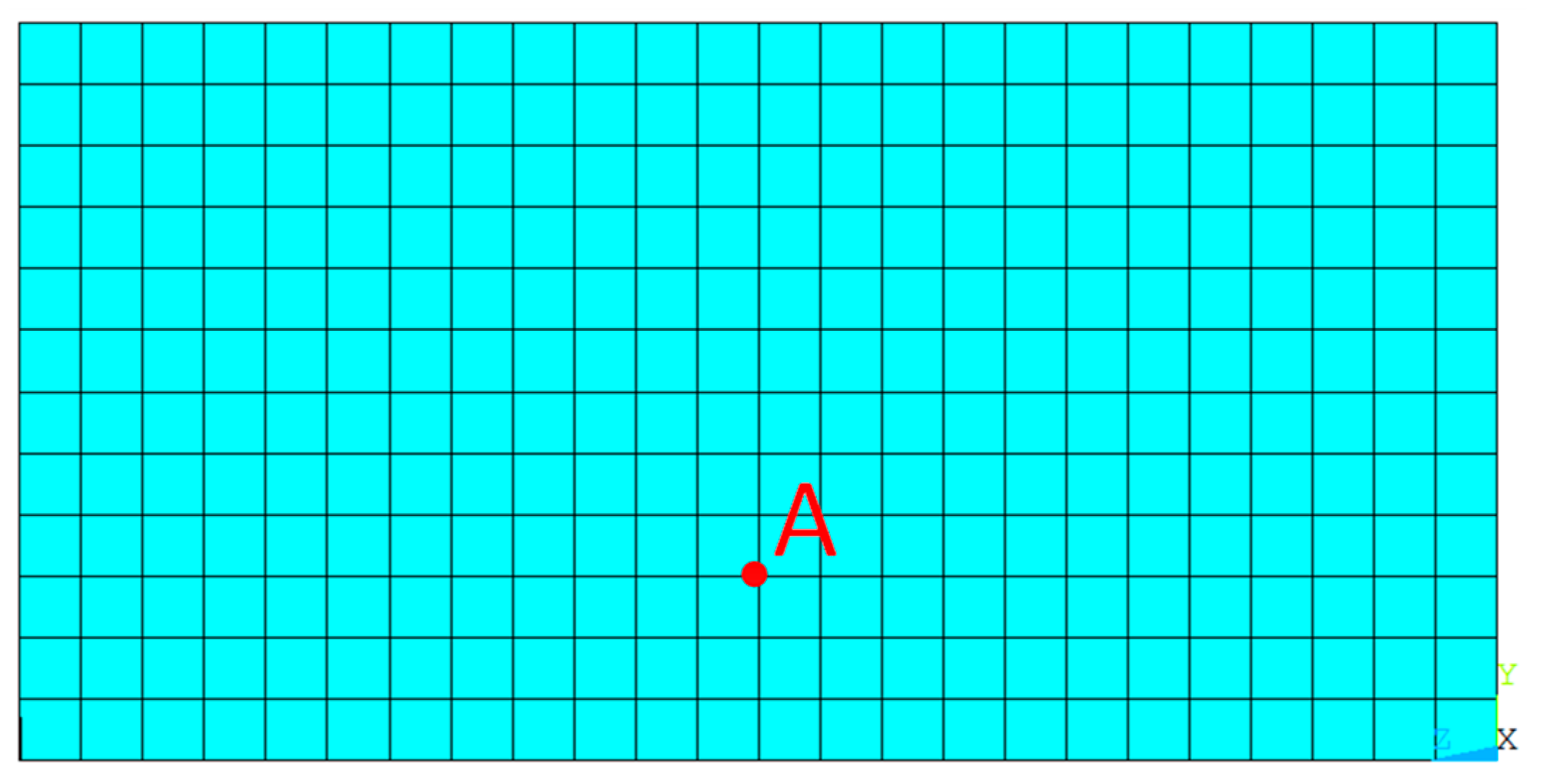
4.1. Calculation Model
4.1.1. Dam and Reservoir Model
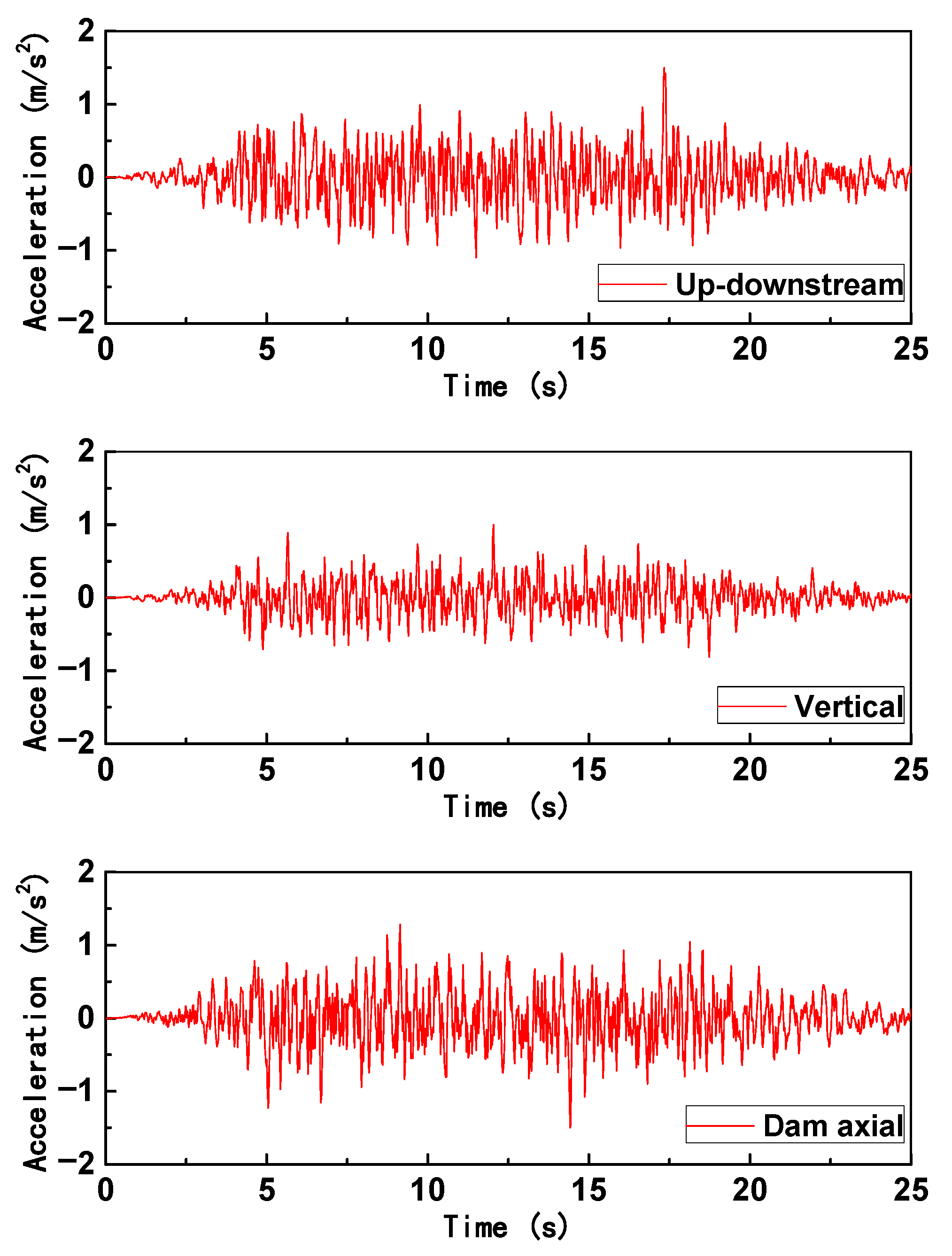
4.1.2. Material Parameters, Input Seismic Load, and Damping Methods
4.2. Effect of Additional Mass Matrix Simplification
4.3. Results and Discussion
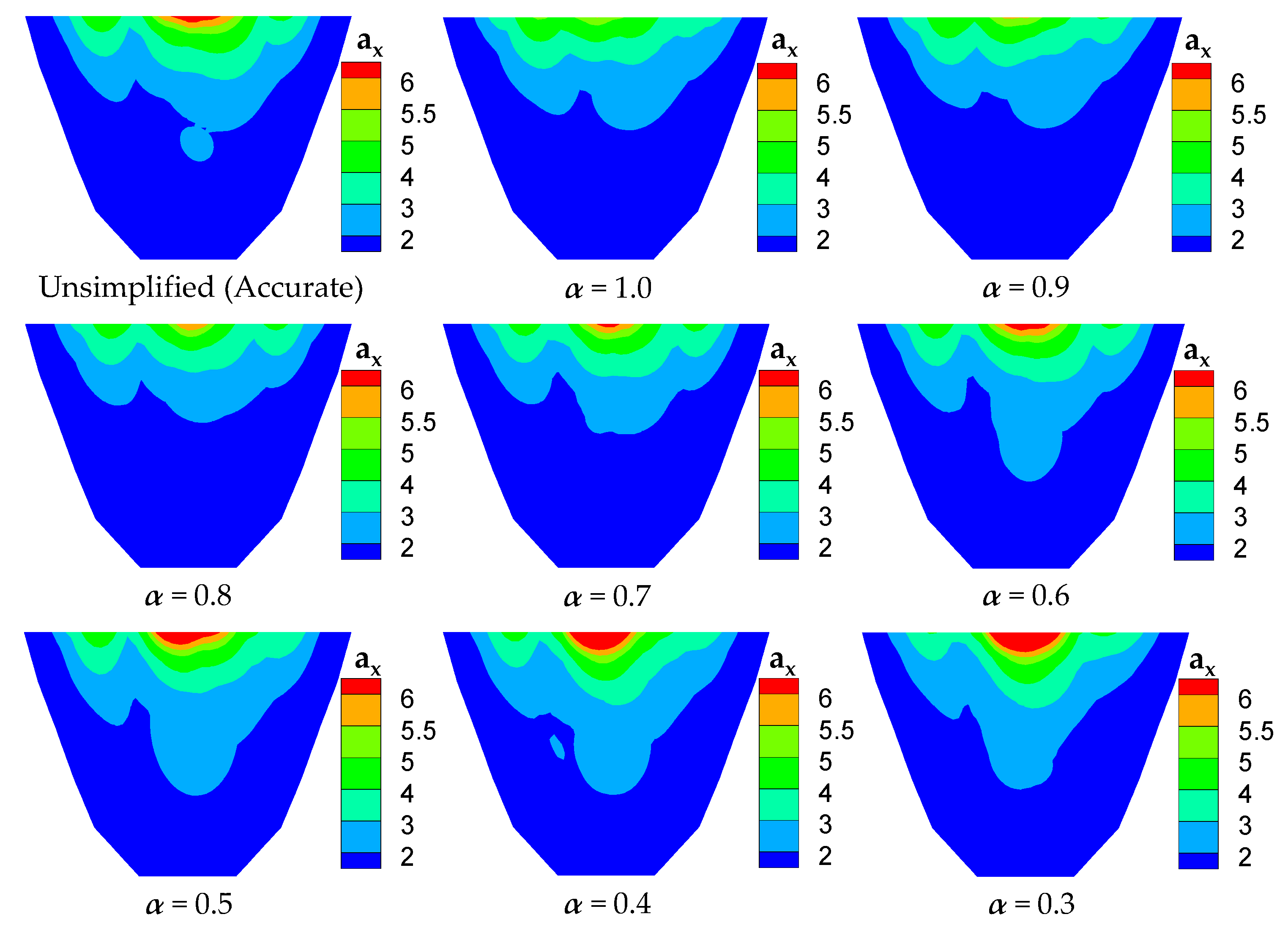
4.3.1. Acceleration of Arch Dam
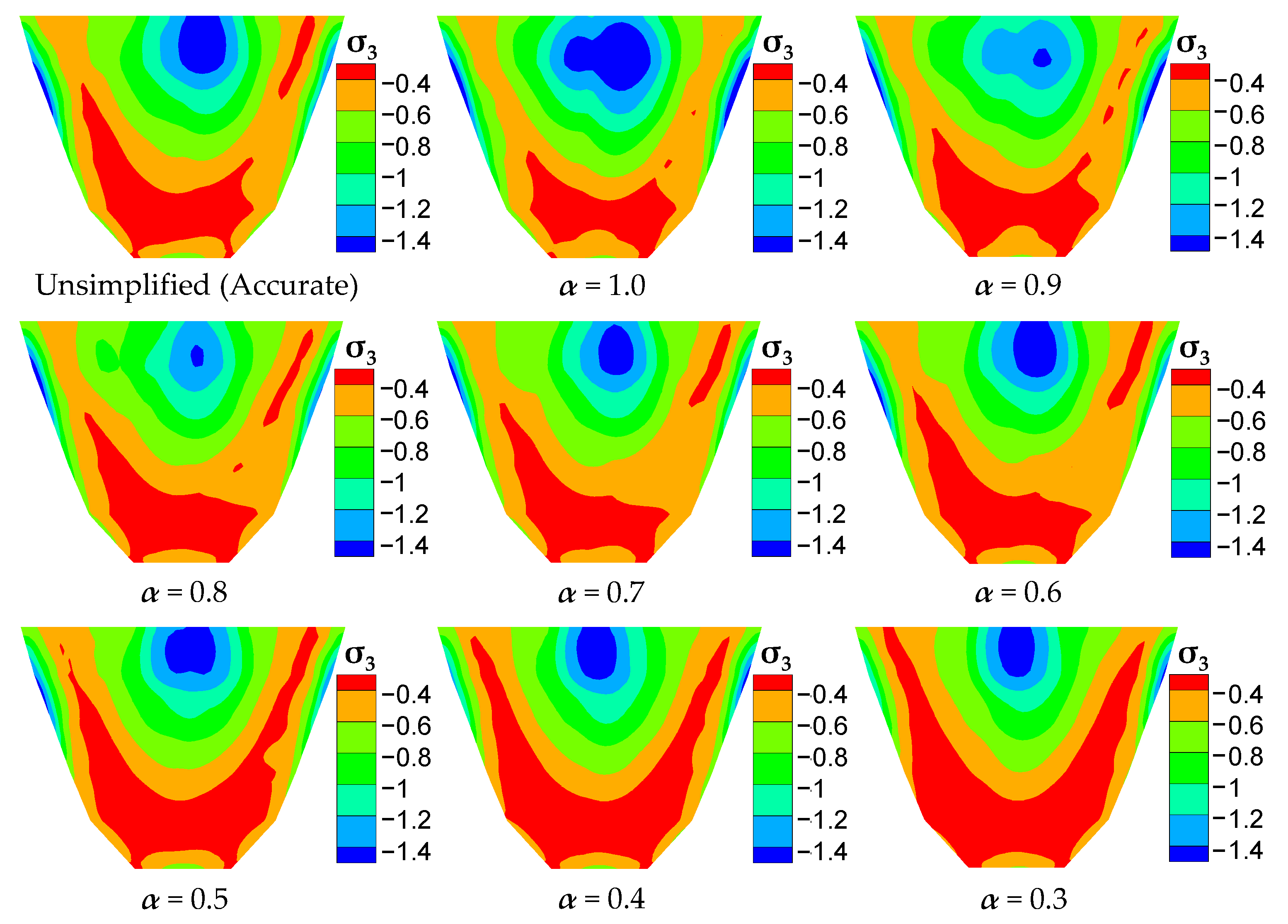
4.3.2. Stress of Arch Dam
4.3.3. Computational Efficiency
4.3.4. Suggested Value of Reduction Coefficient α
5. Conclusions
- An efficient 3D dynamic fluid–solid coupling calculation method for dam–reservoir systems based on the FEM-SBFEM is proposed by simplifying the hydrodynamic pressure additional mass matrix according to the physical meaning and distribution characteristics of the additional matrix. The proposed method not only ensures the high accuracy of the numerical calculation results but also greatly reduces the consumption time of the dynamic coupling calculation.
- The hydrodynamic pressure added mass matrix has a great influence on the computational efficiency of dynamic coupling analysis. The proposed method, which is simple and easy to implement, only needs to determine a reduction coefficient α (0 < α ≤ 1.0) to simplify the hydrodynamic pressure added mass matrix to a great extent and save a lot of memory occupied by the added mass matrix.
- The suggested value of the reduction coefficient α for the added mass matrix of the hydrodynamic pressure is selected to be 0.6 so as to ensure that the distribution law of the dynamic response of the dam is consistent with the accurate solution, which means the unsimplified additional mass matrix condition. The error of the maximum value of the dynamic response of the dam is limited to within 5%, which is acceptable, and the elapsed time of calculation can be reduced to one twentieth of the accurate solution, which is a great jump in calculation efficiency.
- The proposed method provides an accurate and efficient approach for dynamic fluid–solid coupling analysis and seismic safety evaluation of dam and reservoir systems and makes the application of dam–reservoir systems and a fluid–solid coupling analysis method in fine analysis with large-scale DOFs technically feasible.
- The proposed dynamic coupling calculation method can also be further applied to the nonlinear numerical analysis of CFRD and the fine damage analysis of concrete dams under earthquake conditions. Furthermore, the additional mass matrix simplification method in the dynamic coupling analysis of dam and reservoir systems provided in this study is also applicable to the additional mass of hydrodynamic pressure calculated by other numerical methods (FEM, BEM, PSBFEM, etc.).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, C.; Wolf, J.P. The scaled boundary finite-element method—Alias consistent infinitesimal finite-element cell method—For elastodynamics. Comput. Methods Appl. Mech. Eng. 1997, 147, 329–355. [Google Scholar] [CrossRef]
- Xu, J.; Xu, H.; Yan, D.; Chen, K.; Zou, D. A Novel Calculation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM and Its Application in Nonlinear Cross-Scale CFRD-Reservoir Systems. Water 2022, 14, 867. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, M.; Zhang, J.; Du, X. Scaled Boundary Perfectly Matched Layer (SBPML): A novel 3D time-domain artificial boundary method for wave problem in general-shaped and heterogeneous infinite domain. Comput. Methods Appl. Mech. Eng. 2023, 403, 115738. [Google Scholar] [CrossRef]
- Zhang, P.; Du, C.; Zhao, W.; Zhang, D. Hydraulic fracture simulation of concrete using the SBFEM-FVM model. Struct. Eng. Mech. 2021, 80, 553–562. [Google Scholar]
- Li, J.; Shi, Z.; Liu, L.; Song, C. An efficient scaled boundary finite element method for transient vibro-acoustic analysis of plates and shells. Comput. Struct. 2020, 231, 106211. [Google Scholar] [CrossRef]
- Fouladi, M.Q.; Badiei, P.; Vahdani, S. A study on full interaction of water waves with moored rectangular floating breakwater by applying 2DV scaled boundary finite element method. Ocean Eng. 2021, 220, 108450. [Google Scholar] [CrossRef]
- Wang, P.; Lu, R.; Yan, Q.; Bao, X.; Zhang, J.; Liu, L. The internal substructure method for shock wave input in 2D fluid-structure interaction analysis with unbounded domain using doubly-asymptotic ABC. Mech. Adv. Mater. Struct. 2023, 30, 3111–3124. [Google Scholar] [CrossRef]
- Pfeil, S.; Gravenkamp, H.; Duvigneau, F.; Woschke, E. Scaled boundary finite element method for hydrodynamic bearings in rotordynamic simulations. Int. J. Mech. Sci. 2021, 199, 106427. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, X.; Wang, P.; Du, X.; Liu, J. Seismic water-structure interaction analysis using a modified SBFEM and FEM coupling in a frequency domain. Ocean Eng. 2019, 189, 106374. [Google Scholar] [CrossRef]
- Deeks, A.J.; Cheng, L. Potential flow around obstacles using the scaled boundary finite-element method. Int. J. Numer. Methods Fluids 2003, 41, 721–741. [Google Scholar] [CrossRef]
- Li, B.; Cheng, L.; Deeks, A.J.; Teng, B. A modified scaled boundary finite-element method for problems with parallel side-faces. Part II. Application and evaluation. Appl. Ocean Res. 2005, 27, 224–234. [Google Scholar] [CrossRef]
- Li, B.; Cheng, L.; Deeks, A.J.; Zhao, M. A semi-analytical solution method for two-dimensional Helmholtz equation. Appl. Ocean Res. 2006, 28, 193–207. [Google Scholar] [CrossRef]
- Teng, B.; Zhao, M.; He, G.H. Scaled boundary finite element analysis of the water sloshing in 2D containers. Int. J. Numer. Methods Fluids 2006, 52, 659–678. [Google Scholar] [CrossRef]
- Cao, F.S.; Teng, B. Scaled boundary finite element analysis of wave passing a submerged breakwater. China Ocean Eng. 2008, 22, 241–251. [Google Scholar]
- Song, H.; Tao, L. Hydroelastic response of a circular plate in waves using scaled boundary FEM. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar]
- Song, H.; Tao, L. Semi-analytical solution of Poisson’s equation in bounded domain. ANZIAM J. 2009, 51, C169–C185. [Google Scholar] [CrossRef]
- Song, H.; Tao, L. An efficient scaled boundary FEM model for wave interaction with a nonuniform porous cylinder. Int. J. Numer. Methods Fluids 2010, 63, 96–118. [Google Scholar] [CrossRef]
- Liu, J.; Lin, G.; Li, J. Short-crested waves interaction with a concentric cylindrical structure with double-layered perforated walls. Ocean Eng. 2012, 40, 76–90. [Google Scholar] [CrossRef]
- Lin, G.; Du, J.; Hu, Z. Dynamic dam-reservoir interaction analysis including effect of reservoir boundary absorption. Sci. China Ser. E Technol. Sci. 2007, 50, 1–10. [Google Scholar] [CrossRef]
- Lin, G.; Wang, Y.; Hu, Z. An efficient approach for frequency-domain and time-domain hydrodynamic analysis of dam-reservoir systems. Earthq. Eng. Struct. Dyn. 2012, 41, 1725–1749. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Hu, Z. Study on the effects of hydrodynamic pressure on the dynamic stresses in slabs of high CFRD based on the scaled boundary finite-element method. Soil Dyn. Earthq. Eng. 2016, 88, 223–236. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Su, X. Error study of Westergaard’s approximation in seismic analysis of high concrete-faced rockfill dams based on SBFEM. Soil Dyn. Earthq. Eng. 2017, 94, 88–91. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Hu, Z.; Su, X. A nonlinear analysis of dynamic interactions of CFRD-compressible reservoir system based on FEM-SBFEM. Soil Dyn. Earthq. Eng. 2018, 112, 24–34. [Google Scholar] [CrossRef]
- Wang, X.; Jin, F.; Prempramote, S.; Song, C. Time-domain analysis of gravity dam–reservoir interaction using high-order doubly asymptotic open boundary. Comput. Struct. 2011, 89, 668–680. [Google Scholar] [CrossRef]
- Gao, Y.; Jin, F.; Wang, X.; Wang, J. Finite Element Analysis of Dam–Reservoir Interaction Using High-Order Doubly Asymptotic Open Boundary. In Seismic Safety Evaluation of Concrete Dams; Butterworth-Heinemann: Oxford, UK, 2013; pp. 173–198. [Google Scholar]
- Das, S.K.; Mandal, K.K.; Niyogi, A.G. Finite element-based direct coupling approach for dynamic analysis of dam–reservoir system. Innov. Infrastruct. Solut. 2023, 8, 44. [Google Scholar] [CrossRef]
- Gorai, S.; Maity, D. Seismic Performance Evaluation of Concrete Gravity Dams in Finite-Element Framework. Pract. Period. Struct. Des. Constr. 2022, 27, 04021072. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Zhang, Y.; Guo, L.; Wang, Y.; Thira Htun, T.T. Influences on the seismic response of a gravity dam with different foundation and reservoir modeling assumptions. Water 2021, 13, 3072. [Google Scholar] [CrossRef]
- Pelecanos, L.; Kontoe, S.; Zdravković, L. The effects of dam–reservoir interaction on the nonlinear seismic response of earth dams. J. Earthq. Eng. 2020, 24, 1034–1056. [Google Scholar] [CrossRef]
- Sharma, V.; Fujisawa, K.; Murakami, A. Space–time FEM with block-iterative algorithm for nonlinear dynamic fracture analysis of concrete gravity dam. Soil Dyn. Earthq. Eng. 2020, 131, 105995. [Google Scholar] [CrossRef]
- Karabulut, M.; Kartal, M.E. Seismic analysis of Roller Compacted Concrete (RCC) dams considering effect of viscous boundary conditions. Comput. Concr. Int. J. 2019, 27, 255–266. [Google Scholar]
- Wang, J.T.; Lv, D.D.; Jin, F.; Zhang, C.H. Earthquake damage analysis of arch dams considering dam–water–foundation interaction. Soil Dyn. Earthq. Eng. 2013, 49, 64–74. [Google Scholar] [CrossRef]
- Bayraktar, A.; Kartal, M.E. Linear and nonlinear response of concrete slab on CFR dam during earthquake. Soil Dyn. Earthq. Eng. 2010, 30, 990–1003. [Google Scholar] [CrossRef]
- Wang, J.T.; Chopra, A.K. Linear analysis of concrete arch dams including dam-water-foundation rock interaction considering spatially varying ground motions. Earthq. Eng. Struct. Dyn. 2010, 39, 731–750. [Google Scholar] [CrossRef]
- Bayraktar, A.; Dumanoǧlu, A.A.; Calayir, Y. Asynchronous dynamic analysis of dam-reservoir-foundation systems by the Lagrangian approach. Comput. Struct. 1996, 58, 925–935. [Google Scholar] [CrossRef]
- Fok, K.L.; Chopra, A.K. Earthquake analysis of arch dams including dam–water interaction, reservoir boundary absorption and foundation flexibility. Earthq. Eng. Struct. Dyn. 1986, 14, 155–184. [Google Scholar] [CrossRef]
- Fenves, G.; Chopra, A.K. Earthquake analysis of concrete gravity dams including reservoir bottom absorption and dam-water-foundation rock interaction. Earthq. Eng. Struct. Dyn. 1984, 12, 663–680. [Google Scholar] [CrossRef]
- Bouaanani, N.; Miquel, B. An error estimator for transmitting boundary conditions in fluid-structure interaction problems. WIT Trans. Built Environ. 2011, 115, 169–178. [Google Scholar]
- Küçükarslan, S.; Coşkun, S.B. Transient dynamic analysis of dam-reservoir interaction by coupling DRBEM and FEM. Eng. Comput. 2004, 21, 692–707. [Google Scholar] [CrossRef]
- Fahjan, Y.M.; Börekçi, O.S.; Erdik, M. Earthquake-induced hydrodynamic pressures on a 3D rigid dam–reservoir system using DRBEM and a radiation matrix. Int. J. Numer. Methods Eng. 2003, 56, 1511–1532. [Google Scholar] [CrossRef]
- Tsai, C.S.; Lee, G.C.; Yeh, C.S. Time-domain analyses of three-dimensional dam-reservoir interactions by BEM and semi-analytical method. Eng. Anal. Bound. Elem. 1992, 10, 107–118. [Google Scholar] [CrossRef]
- Tsai, C.S. Analyses of three-dimensional dam—Reservoir interactions based on bem with particular integrals and semi-analytical solution. Comput. Struct. 1992, 43, 863–872. [Google Scholar] [CrossRef]
- Tsai, C.S.; Lee, G.C. Arch dam–fluid interactions: By FEM–BEM and substructure concept. Int. J. Numer. Methods Eng. 1987, 24, 2367–2388. [Google Scholar] [CrossRef]
- Degao, Z.; Xianjing, K.; Bin, X. User Manual for Geotechnical Dynamic Nonlinear Analysis; Institute of Earthquake Engineering, Dalian University of Technology: Dalian, China, 2005. [Google Scholar]
- Dassault Systemes Simulia Corp. ABAQUS Analysis User’s Guide. 2016. Available online: http://130.149.89.49:2080/v2016/books/usb/default.htm?startat=pt04ch18s01aus106.html (accessed on 24 August 2023).
- Chen, K.; Zou, D.; Tang, H.; Liu, J.; Zhuo, Y. Scaled boundary polygon formula for Cosserat continuum and its verification. Eng. Anal. Bound. Elem. 2021, 126, 136–150. [Google Scholar] [CrossRef]
- Qu, Y.; Zou, D.; Kong, X.; Yu, X.; Chen, K. Seismic cracking evolution for anti-seepage face slabs in concrete faced rockfill dams based on cohesive zone model in explicit SBFEM-FEM frame. Soil Dyn. Earthq. Eng. 2020, 133, 106106. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Zou, D.; Xu, B.; Kong, X.; Liu, H.; Zhou, Y. Numerical simulation of the seismic response of the Zipingpu concrete face rockfill dam during the Wenchuan earthquake based on a generalized plasticity model. Comput. Geotech. 2013, 49, 111–122. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Liu, J.; Zhuo, Y. A high-precision formula for mixed-order polygon elements based on SBFEM. Comput. Geotech. 2023, 155, 105209. [Google Scholar] [CrossRef]
- Nie, X.; Chen, K.; Zou, D.; Kong, X.; Liu, J.; Qu, Y. Slope stability analysis based on SBFEM and multistage polytree-based refinement algorithms. Comput. Geotech. 2022, 149, 104861. [Google Scholar] [CrossRef]


| Added Mass Matrix | Unsimplified (Accurate) | α = 1.0 | α = 0.9 | α = 0.8 | α = 0.7 | α = 0.6 | α = 0.5 | α = 0.4 | α = 0.3 |
|---|---|---|---|---|---|---|---|---|---|
| ax (m/s2) | 6.583 | 5.518 | 5.596 | 5.989 | 6.280 | 6.554 | 7.209 | 7.926 | 8.075 |
| ay (m/s2) | 2.285 | 2.287 | 2.339 | 2.364 | 2.327 | 2.282 | 2.339 | 2.376 | 2.419 |
| Added Mass Matrix | α = 1.0 | α = 0.9 | α = 0.8 | α = 0.7 | α = 0.6 | α = 0.5 | α = 0.4 | α = 0.3 |
|---|---|---|---|---|---|---|---|---|
| Error of ax | 16.2% | 15.0% | 9.0% | 4.6% | 0.4% | 9.5% | 20.4% | 22.7% |
| Error of ay | 0.1% | 2.4% | 3.5% | 1.8% | 0.1% | 2.3% | 4.0% | 5.9% |
| Added Mass Matrix | Unsimplified (Accurate) | α = 1.0 | α = 0.9 | α = 0.8 | α = 0.7 | α = 0.6 | α = 0.5 | α = 0.4 | α = 0.3 |
|---|---|---|---|---|---|---|---|---|---|
| σ1 (MPa) | 1.567 | 1.643 | 1.520 | 1.588 | 1.615 | 1.564 | 1.471 | 1.497 | 1.458 |
| σ3 (MPa) | −1.604 | −1.783 | −1.685 | −1.617 | −1.551 | −1.568 | −1.508 | −1.555 | −1.521 |
| Added Mass Matrix | α = 1.0 | α = 0.9 | α = 0.8 | α = 0.7 | α = 0.6 | α = 0.5 | α = 0.4 | α = 0.3 |
|---|---|---|---|---|---|---|---|---|
| Error of σ1 | 4.9% | 3.0% | 1.3% | 3.1% | 0.2% | 6.1% | 4.5% | 7.0% |
| Error of σ3 | 11.2% | 5.0% | 0.8% | 3.3% | 2.2% | 6.0% | 3.1% | 5.2% |
| Added Mass Matrix | Unsimplified (Accurate) | α = 1.0 | α = 0.9 | α = 0.8 | α = 0.7 | α = 0.6 | α = 0.5 | α = 0.4 | α = 0.3 |
|---|---|---|---|---|---|---|---|---|---|
| consumption time (hours) | 117.799 | 5.804 | 5.810 | 5.861 | 5.897 | 5.835 | 5.801 | 5.822 | 5.856 |
| time-consuming ratio | 100.0% | 4.9% | 4.9% | 5.0% | 4.9% | 5.0% | 4.9% | 4.9% | 5.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Xu, J.; Yan, D.; Chen, K.; Zou, D. An Efficient Dynamic Coupling Calculation Method for Dam–Reservoir Systems Based on FEM-SBFEM. Water 2023, 15, 3095. https://doi.org/10.3390/w15173095
Xu H, Xu J, Yan D, Chen K, Zou D. An Efficient Dynamic Coupling Calculation Method for Dam–Reservoir Systems Based on FEM-SBFEM. Water. 2023; 15(17):3095. https://doi.org/10.3390/w15173095
Chicago/Turabian StyleXu, He, Jianjun Xu, Dongming Yan, Kai Chen, and Degao Zou. 2023. "An Efficient Dynamic Coupling Calculation Method for Dam–Reservoir Systems Based on FEM-SBFEM" Water 15, no. 17: 3095. https://doi.org/10.3390/w15173095






