Two-Leak Isolation in Water Distribution Networks Based on k-NN and Linear Discriminant Classifiers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sensor Placement
2.2. Leak Isolation Strategy
2.2.1. Dataset Generation
2.2.2. Leak Classification
2.2.3. k-NN Classifier
- 1.
- The training of the k-NN classifier is an offline process. In this process, a set of residual samples corresponding to leaks of available classes given by (21) is stored and each residual is assigned to its class label. The dataset used to train the classifier is obtained by performing all possible leak scenarios according to the procedure described in Section 2.2.1.
- 2.
- Leak class prediction is an online process. Here, a continuous comparison of the most recent residual is performed with the labeled residuals from the training dataset (21). If the leak class is denoted by according to (13), and is the probability that the leak location corresponds to the class given the residual , the k-NN classifier assumes thatwhere is the number of residuals in the i-th class among the k nearest neighbors to the residual . The class with the highest probability is chosen as the output of the classifier:
2.2.4. Discriminant Analysis Classifier
- 1.
- The training of the DA classifier is an offline process where a set of residual samples corresponding to all possible leakage scenarios are assigned to the corresponding class by means of (21), this stage being when the discriminant functions are generated. In the same way, the dataset to train this classifier is obtained by simulating the leakage scenarios according to the procedure described in Section 2.2.1.
- 2.
- Leak class prediction is an online process. In this process, predictions are made using the actual residual and the predictive model obtained in the training stage. If the leak class is denoted by according to (13), then is the probability that the leak corresponds to the class given the residual , and the DA classifier computeswhere is the prior probability that the residual corresponds to the i-th class, is the unconditional probability of and is the per se probability computed as probability density function of in class considering that every density within each class is a Gaussian distribution computed as follows:where d is the Mahalanobis distance from the residual r to the class centroid, and is the covariance matrix of the class.The class with the highest probability is chosen as the output of the classifier:
3. Results
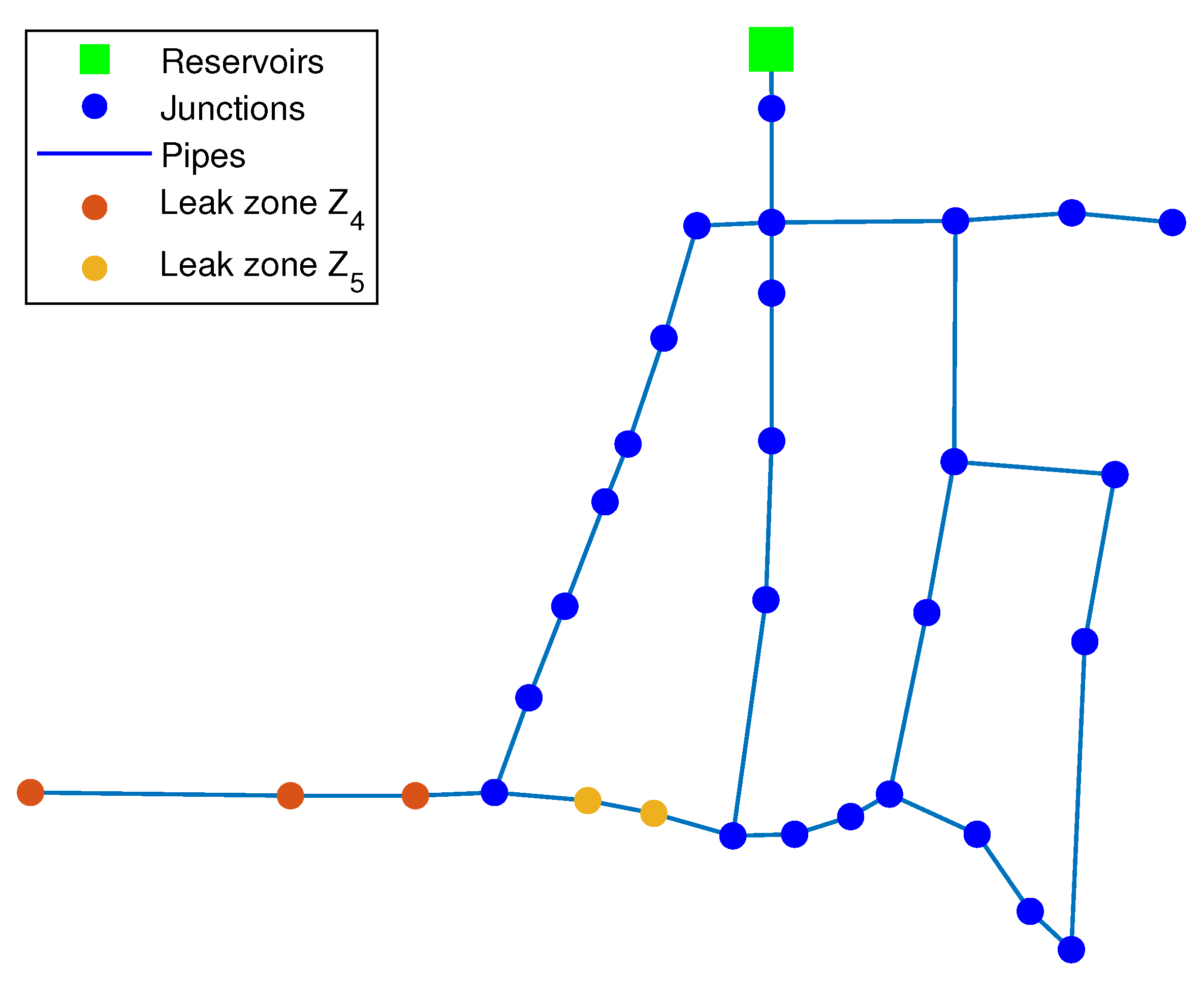
3.1. Hanoi WDN Case Study
3.1.1. Leak Scenario
3.1.2. Leak Scenario
3.1.3. Leak Scenario
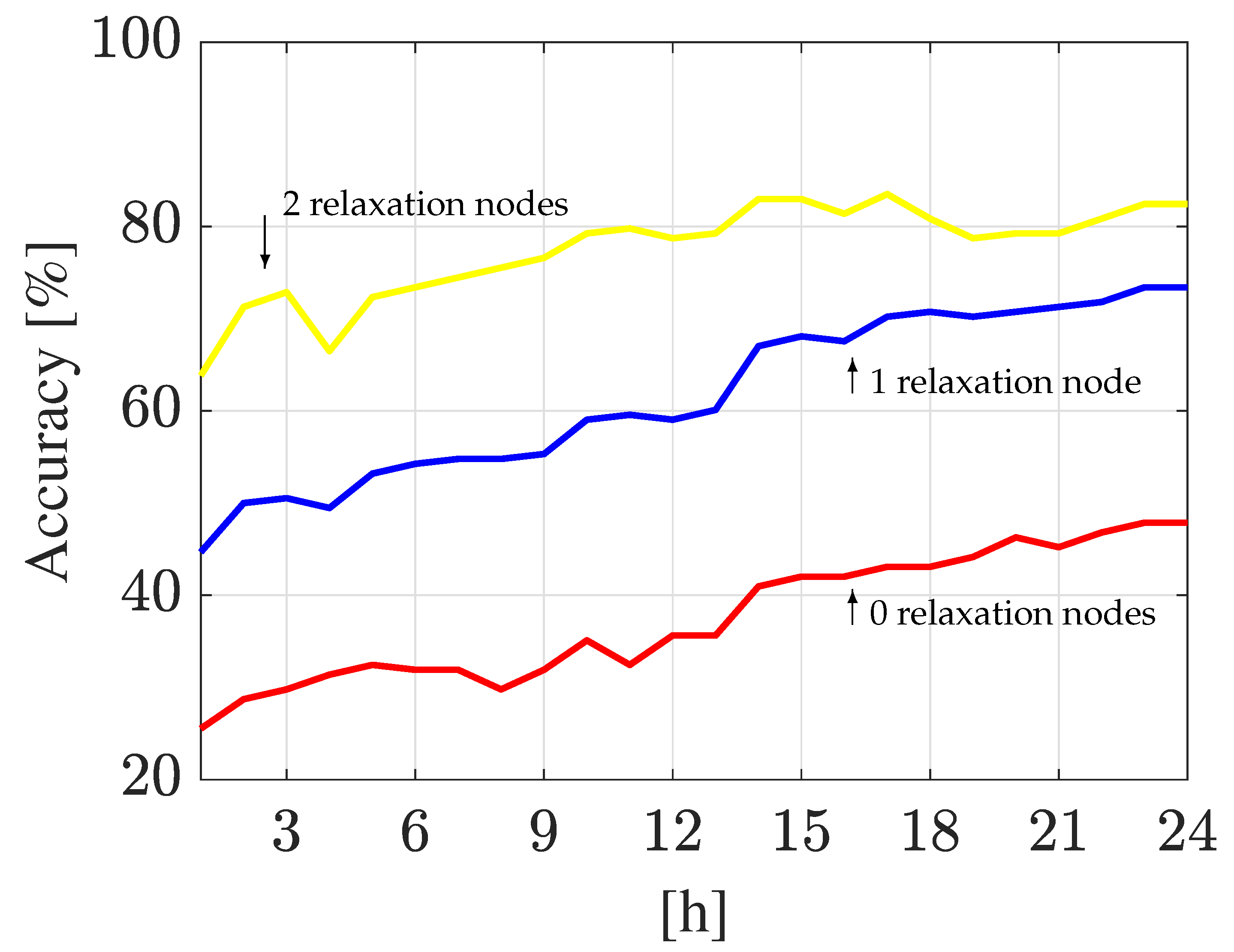
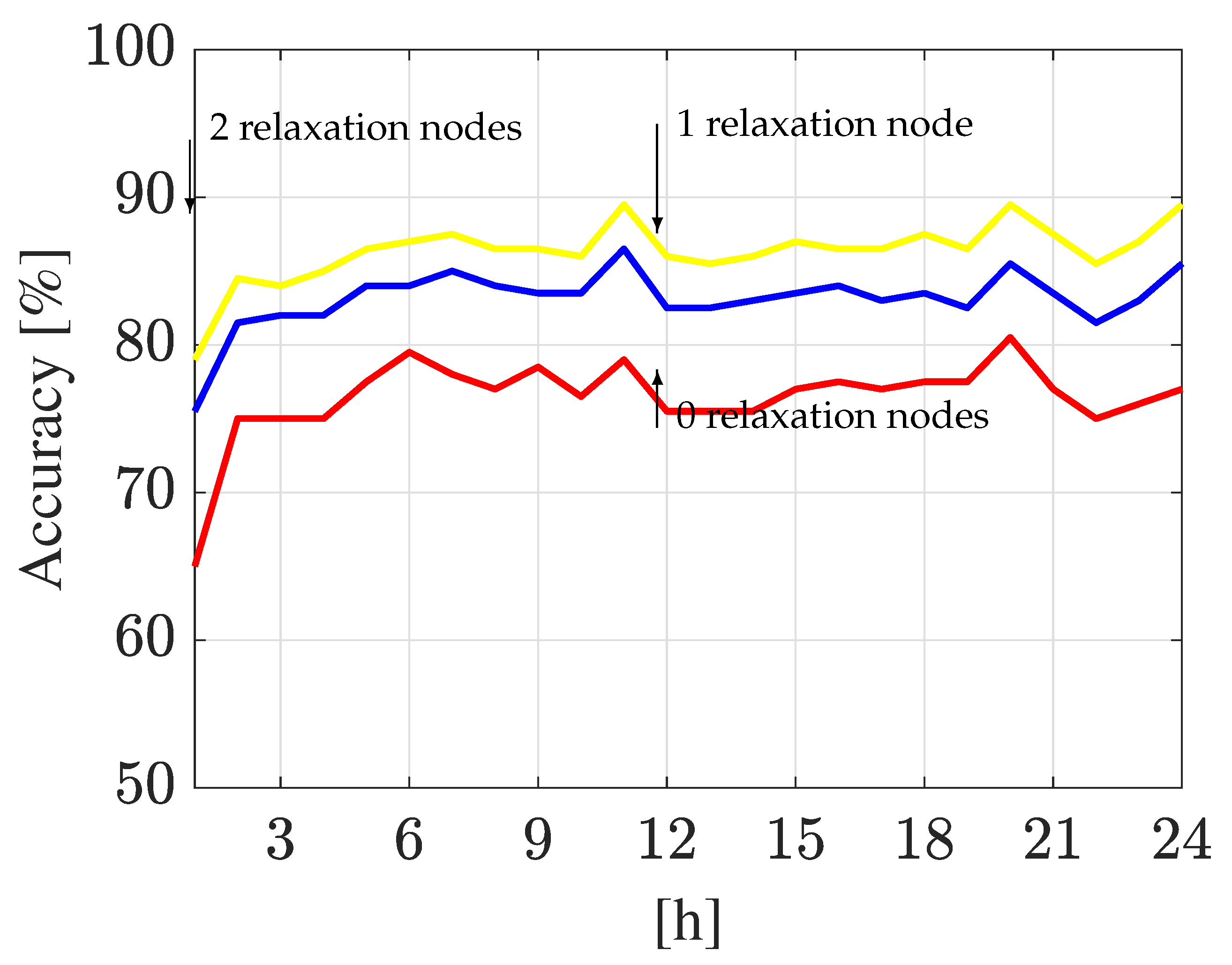
3.1.4. Relaxation Node Analysis
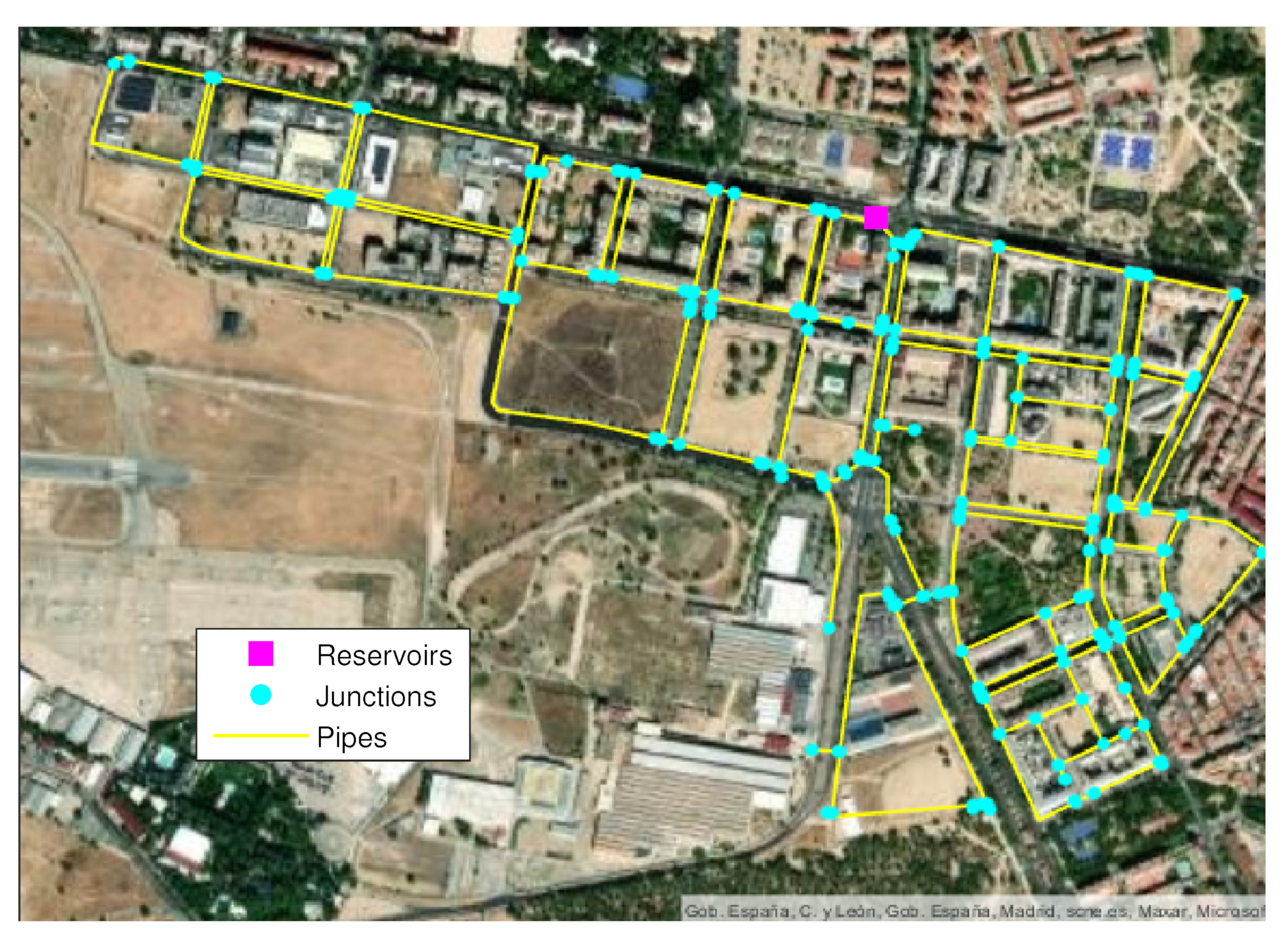
3.2. Madrid’s DMA Case Study
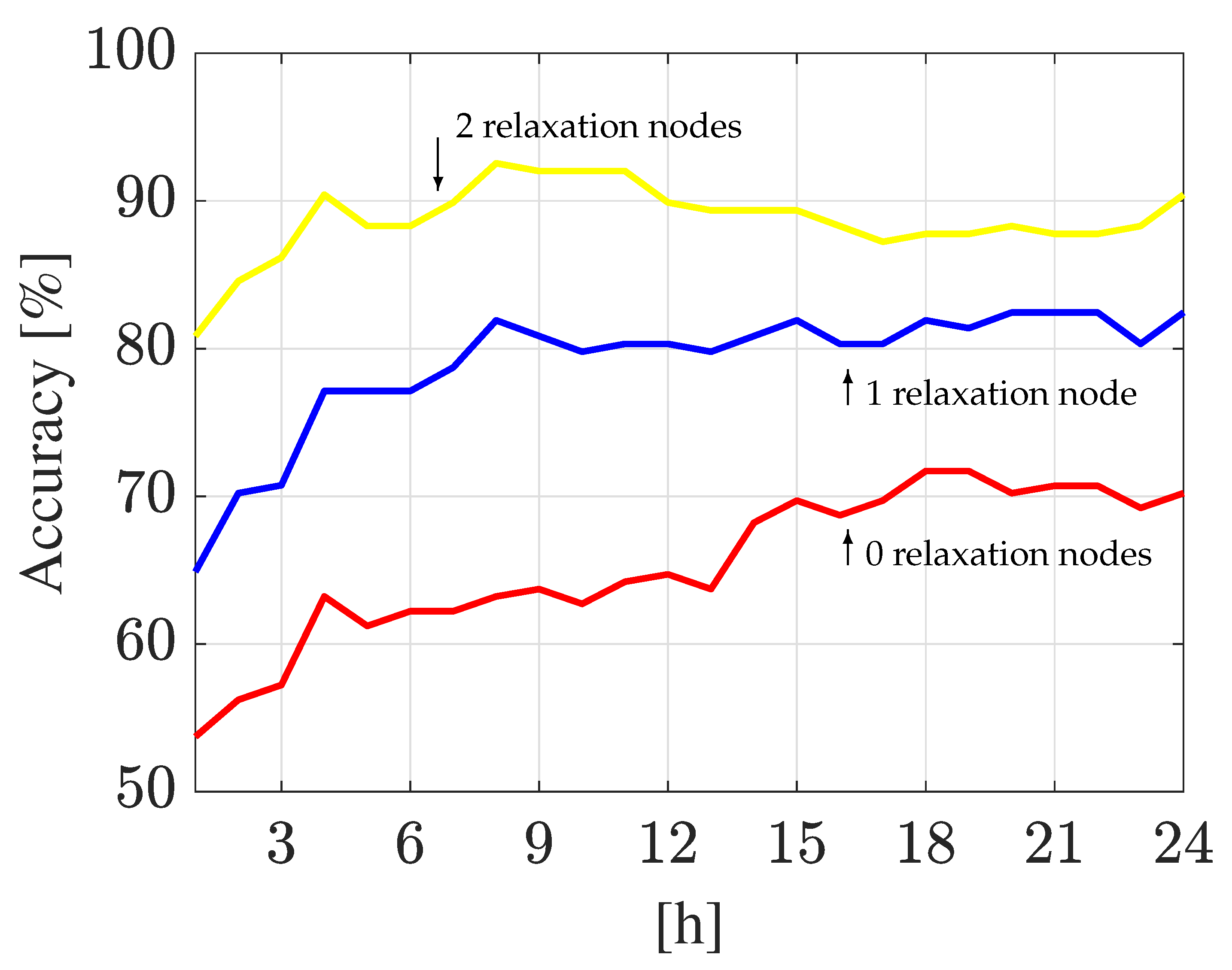
Relaxation Node Analysis
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| WDN | Water Distribution Network |
| OECD | Organization for Economic Cooperation and Development |
| FIR | Finite Impulse Response |
| RBF | Radial Base Function |
| DA | Discriminant Analysis |
| k-NN | k Nearest Neighbors |
| h | Hour |
| L/s | Liters per second |
| Leak flow rate used for estimation of residuals | |
| Leak flow rate used for estimation of sensitivities | |
| Set of real numbers | |
| diag | Diagonal matrix |
| max | Maximum Value |
| arg max | Maximum argument |
Appendix A. Sensor-Placement-Methodology-Based Algorithm
| Algorithm A1: Sensor-placement-methodology-based algorithm. |
|
Appendix B. Dataset-Generation-Methodology-Based Algorithm
| Algorithm A2: Dataset-generation-methodology-based algorithm |
|
Appendix C. Leak-Localization-Strategy-Based Algorithm
| Algorithm A3: Leak-localization-strategy-based algorithm |
|
References
- OECD. Water Governance in Cities; OECD: Paris, France, 2016; p. 140. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Kim, H.; Shin, E.; Chung, W. Energy demand and supply, energy policies, and energy security in the Republic of Korea. Energy Policy 2011, 39, 6882–6897. [Google Scholar] [CrossRef]
- Qi, S.; Gao, J.; Wu, W.; Qiao, Y.; Tu, M.; Wang, J. Research on an Optimized Leakage Locating Model in Water Distribution System. Procedia Eng. 2014, 89, 1569–1576. [Google Scholar] [CrossRef]
- Delgado-Aguiñaga, J.A.; Begovich, O. Water Leak Diagnosis in Pressurized Pipelines: A Real Case Study; Springer International Publishing: Cham, Switzerland, 2017; pp. 235–262. [Google Scholar] [CrossRef]
- Santos-Ruíz, I.; Bermúdez, J.; López-Estrada, F.; Puig, V.; Torres, L.; Delgado-Aguiñaga, J. Online leak diagnosis in pipelines using an EKF-based and steady-state mixed approach. Control. Eng. Pract. 2018, 81, 55–64. [Google Scholar] [CrossRef]
- Navarro-Díaz, A.; Delgado-Aguiñaga, J.A.; Begovich, O.; Besançon, G. Two Simultaneous Leak Diagnosis in Pipelines Based on Input-Output Numerical Differentiation. Sensors 2021, 21, 8035. [Google Scholar] [CrossRef] [PubMed]
- Torres, L.; Verde, C.; Molina, L. Leak diagnosis for pipelines with multiple branches based on model similarity. J. Process. Control. 2021, 99, 41–53. [Google Scholar] [CrossRef]
- Delgado-Aguiñaga, J.; Santos-Ruiz, I.; Besançon, G.; López-Estrada, F.; Puig, V. EKF-based observers for multi-leak diagnosis in branched pipeline systems. Mech. Syst. Signal Process. 2022, 178, 109198. [Google Scholar] [CrossRef]
- Fuentes-Mariles, O.; Palma-Nava, A.; Rodriguez-Vazquez, K. Estimation and location of leaks in a drinking water pipeline network using genetic algorithms. Ing. Investig. Tecnol. 2011, 12, 235–242. [Google Scholar] [CrossRef]
- Puig, V.; Ocampo-Martínez, C.; Pérez, R.; Cembrano, G.; Quevedo, J.; Escobet, T. Real-Time Monitoring and Operational Control of Drinking-Water Systems; Springer: Cham, Switzerland, 2017; p. 428. [Google Scholar] [CrossRef]
- Choi, J.; Jeong, G.; Kang, D. Multiple Leak Detection in Water Distribution Networks Following Seismic Damage. Sustainability 2021, 13, 8306. [Google Scholar] [CrossRef]
- Alves, D.; Blesa, J.; Duviella, E.; Rajaoarisoa, L. Multi-leak detection and isolation in water distribution networks. In Proceedings of the 2nd International Joint Conference on Water Distribution Systems Analysis & Computing and Control in the Water Industry, Valencia, Spain, 18–22 July 2022. [Google Scholar]
- Vanijjirattikhan, R.; Khomsay, S.; Kitbutrawat, N.; Khomsay, K.; Supakchukul, U.; Udomsuk, S.; Suwatthikul, J.; Oumtrakul, N.; Anusart, K. AI-based acoustic leak detection in water distribution systems. Results Eng. 2022, 15, 100557. [Google Scholar] [CrossRef]
- Yang, J.; Wen, Y.; Li, P. Leak acoustic detection in water distribution pipelines. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 3057–3061. [Google Scholar] [CrossRef]
- Iwanaga, M.; Brennan, M.; Almeida, F.; Scussel, O.; Cezar, S. A laboratory-based leak noise simulator for buried water pipes. Appl. Acoust. 2022, 185, 108346. [Google Scholar] [CrossRef]
- Fan, H.; Tariq, S.; Zayed, T. Acoustic leak detection approaches for water pipelines. Autom. Constr. 2022, 138, 104226. [Google Scholar] [CrossRef]
- Pérez, R.; Puig, V.; Pascual, J.; Quevedo, J.; Landeros, E.; Peralta, A. Methodology for leakage isolation using pressure sensitivity analysis in water distribution networks. Control. Eng. Pract. 2011, 19, 1157–1167. [Google Scholar] [CrossRef]
- Pérez, R.; Quevedo, J.; Puig, V.; Nejjari, F.; Cugueró, M.; Sanz, G.; Mirats, J. Leakage isolation in water distribution networks: A comparative study of two methodologies on a real case study. In Proceedings of the 2011 19th Mediterranean Conference on Control & Automation (MED), Corfu Island, Greece, 21–23 June 2011; pp. 138–143. [Google Scholar] [CrossRef]
- Ponce, M.V.C.; Castañón, L.E.G.; Cayuela, V.P. Model-based leak detection and location in water distribution networks considering an extended-horizon analysis of pressure sensitivities. Hydroinformatics 2014, 16, 649–670. [Google Scholar] [CrossRef]
- Soldevila, V.; Tornil-Sin, S.; Blesa, J.; Fernandez-Canti., R.; Puig, V. Modeling and Monitoring of Pipelines and Networks Advanced Tools for Automatic Monitoring and Supervision of Pipelines; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Carreño-Alvarado, E.; Reynoso-Meza, G.; Montalvo, I.; Izquierdo, J. A comparison of machine learning classifiers for leak detection and isolation in urban networks. In Proceedings of the Congress on Numerical Methods in Engineering CMN 2017, Valencia, Spain, 3–5 July 2017. [Google Scholar]
- Romero-Tapia, G.; Fuente, M.; Puig, V. Leak Localization in Water Distribution Networks using Fisher Discriminant Analysis. In Proceedings of the 10th IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes SAFEPROCESS, Warsaw, Poland, 29–31 August 2018. [Google Scholar] [CrossRef]
- Sun, C.; Parellada, B.; Puig, V.; Cembrano, G. Leak Localization in Water Distribution Networks Using Pressure and Data-Driven Classifier Approach. Water 2020, 12, 54. [Google Scholar] [CrossRef]
- Ferrandez-Gamot, L.; Busson, P.; Blesa, J.; Tornil-Sin, S.; Puig, V.; Duviella, E.; Soldevila, A. Leak Localization in Water Distribution Networks using Pressure Residuals and Classifiers. IFAC-PapersOnLine 2015, 48, 220–225. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; Blesa, J.; Puig, V.; López-Estrada, F. Leak localization in water distribution networks using classifiers with cosenoidal features. IFAC-PapersOnLine 2020, 53, 16697–16702. [Google Scholar] [CrossRef]
- Cordoba, G.C.; Tuhovčák, L.; Tauš, M. Using Artificial Neural Network Models to Assess Water Quality in Water Distribution Networks. Procedia Eng. 2014, 70, 399–408. [Google Scholar] [CrossRef]
- Przystałka, P. Performance optimization of a leak detection scheme for water distribution networks. IFAC-PapersOnLine 2018, 51, 914–921. [Google Scholar] [CrossRef]
- Basnet, L.; Brill, D.; Ranjithan, R.; Mahinthakumar, K. Supervised Machine Learning Approaches for Leak Localization in Water Distribution Systems: Impact of Complexities of Leak Characteristics. J. Water Resour. Plan. Manag. 2023, 149, 04023032. [Google Scholar] [CrossRef]
- Sourabh, N.; Timbadiya, P.; Patel, P.L. Leak detection in water distribution network using machine learning techniques. ISH J. Hydraul. Eng. 2023, 7, 1–19. [Google Scholar] [CrossRef]
- Javadiha, M.; Blesa, J.; Soldevila, A.; Puig, V. Leak Localization in Water Distribution Networks Using Deep Learning. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1426–1431. [Google Scholar] [CrossRef]
- Örn Garðarsson, G.; Boem, F.; Toni, L. Graph-Based Learning for Leak Detection and Localisation in Water Distribution Networks. IFAC-PapersOnLine 2022, 55, 661–666. [Google Scholar] [CrossRef]
- Hu, Z.; Shen, D.; Chen, W. Deep learning-based burst location with domain adaptation across different sensors in water distribution networks. Comput. Chem. Eng. 2023, 176, 108313. [Google Scholar] [CrossRef]
- Arbesser-Rastburg, G.; Fuchs-Hanusch, D. Serious Sensor Placement—Optimal Sensor Placement as a Serious Game. Water 2020, 12, 2876. [Google Scholar] [CrossRef]
- Ferreira, B.; Carriço, N.; Covas, D. Optimal Number of Pressure Sensors for Real-Time Monitoring of Distribution Networks by Using the Hypervolume Indicator. Water 2021, 13, 2235. [Google Scholar] [CrossRef]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN Model-Based Approach in Classification. In Proceedings of the on the Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE, Catania, Italy, 3–7 November 2003; Meersman, R., Tari, Z., Schmidt, D.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 986–996. [Google Scholar]
- Asadi Majd, A.; Samet, H.; Ghanbari, T. k-NN based fault detection and classification methods for power transmission systems. Control Mod. Power Syst. 2017, 32, 41601. [Google Scholar] [CrossRef]
- Alkarkhi, A.F.; Alqaraghuli, W.A. (Eds.) Chapter 10—Discriminant Analysis and Classification. In Easy Statistics for Food Science with R; Academic Press: Cambridge, MA, USA, 2019; pp. 161–175. [Google Scholar] [CrossRef]
- Viimeksi, P. Discriminant Analysis—IBM Documentation. 2021. Available online: https://www.ibm.com/docs/en/spss-statistics/beta?topic=features-discriminant-analysis (accessed on 1 June 2023).
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S.; Polycarpou, M.M. EPANET-MATLAB Toolkit: An Open-Source Software for Interfacing EPANET with MATLAB. In Proceedings of the Critical Information Infrastructures Security. Computing & Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016. [Google Scholar] [CrossRef]
- Casillas, M.V.; Garza-Castañón, L.E.; Puig, V. Optimal Sensor Placement for Leak Location in Water Distribution Networks using Evolutionary Algorithms. Water 2015, 7, 6496–6515. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V.; Valencia-Palomo, G.; Hernández, H.R. Pressure Sensor Placement for Leak Localization in Water Distribution Networks Using Information Theory. Sensors 2022, 22, 443. [Google Scholar] [CrossRef]


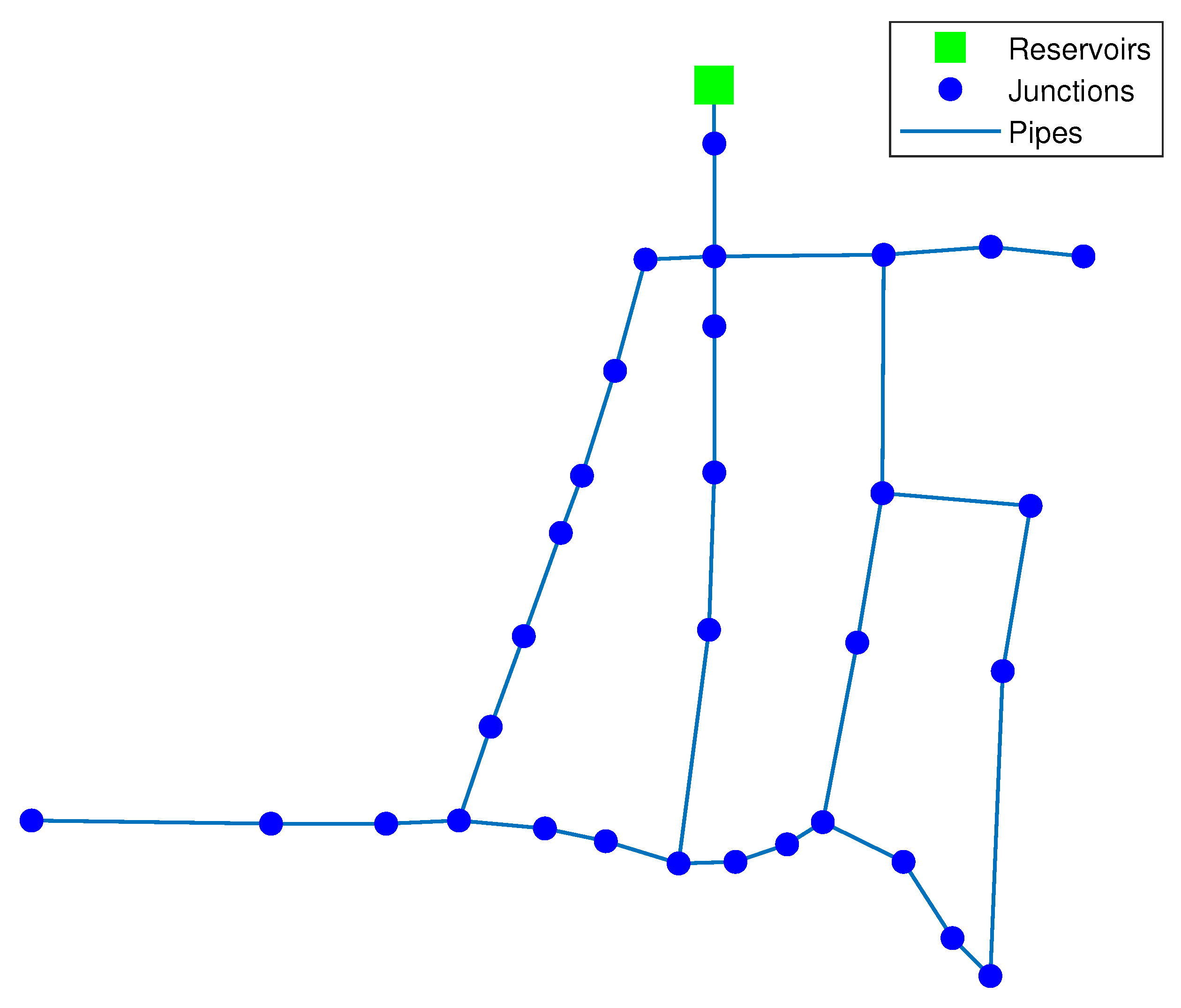
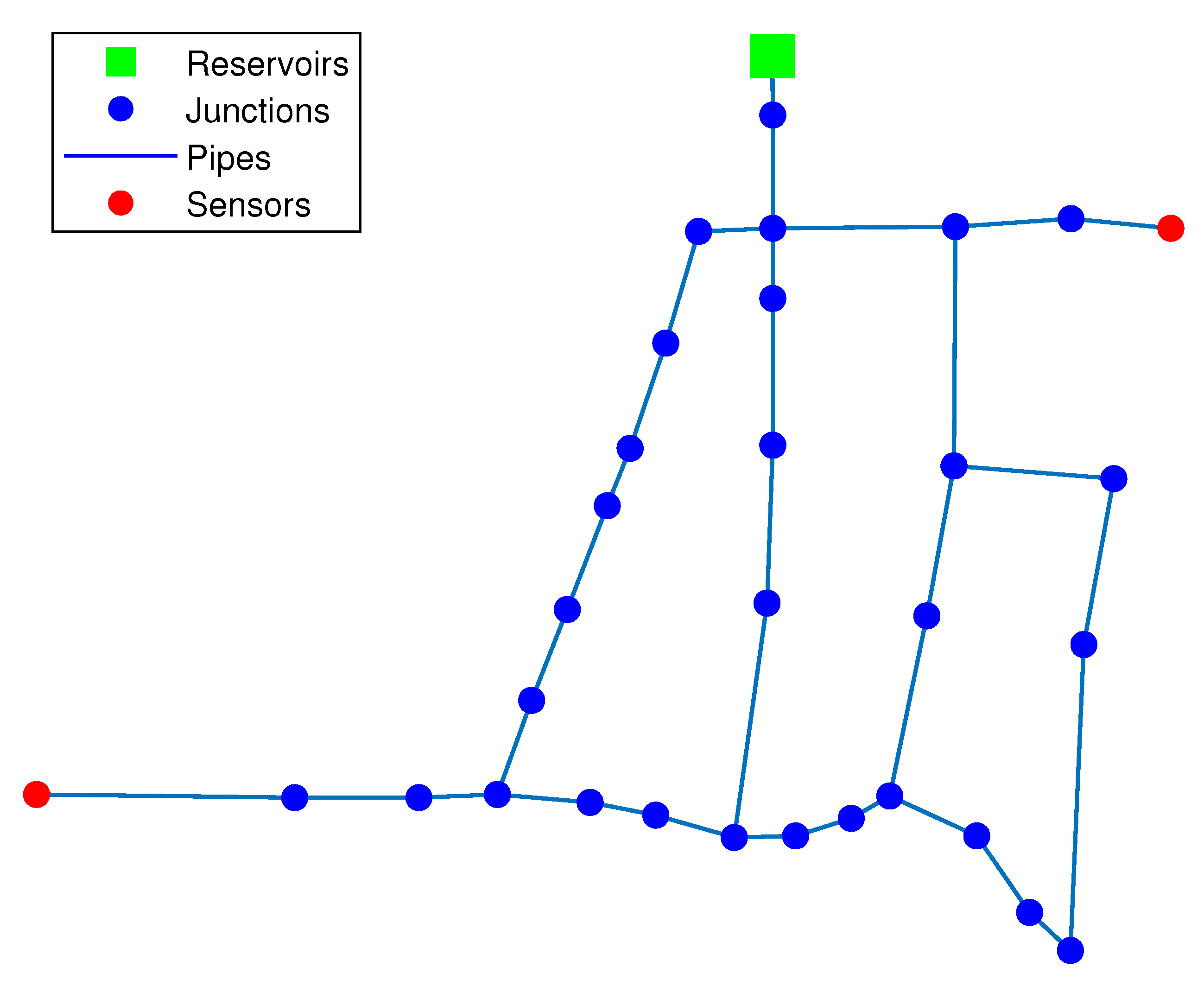
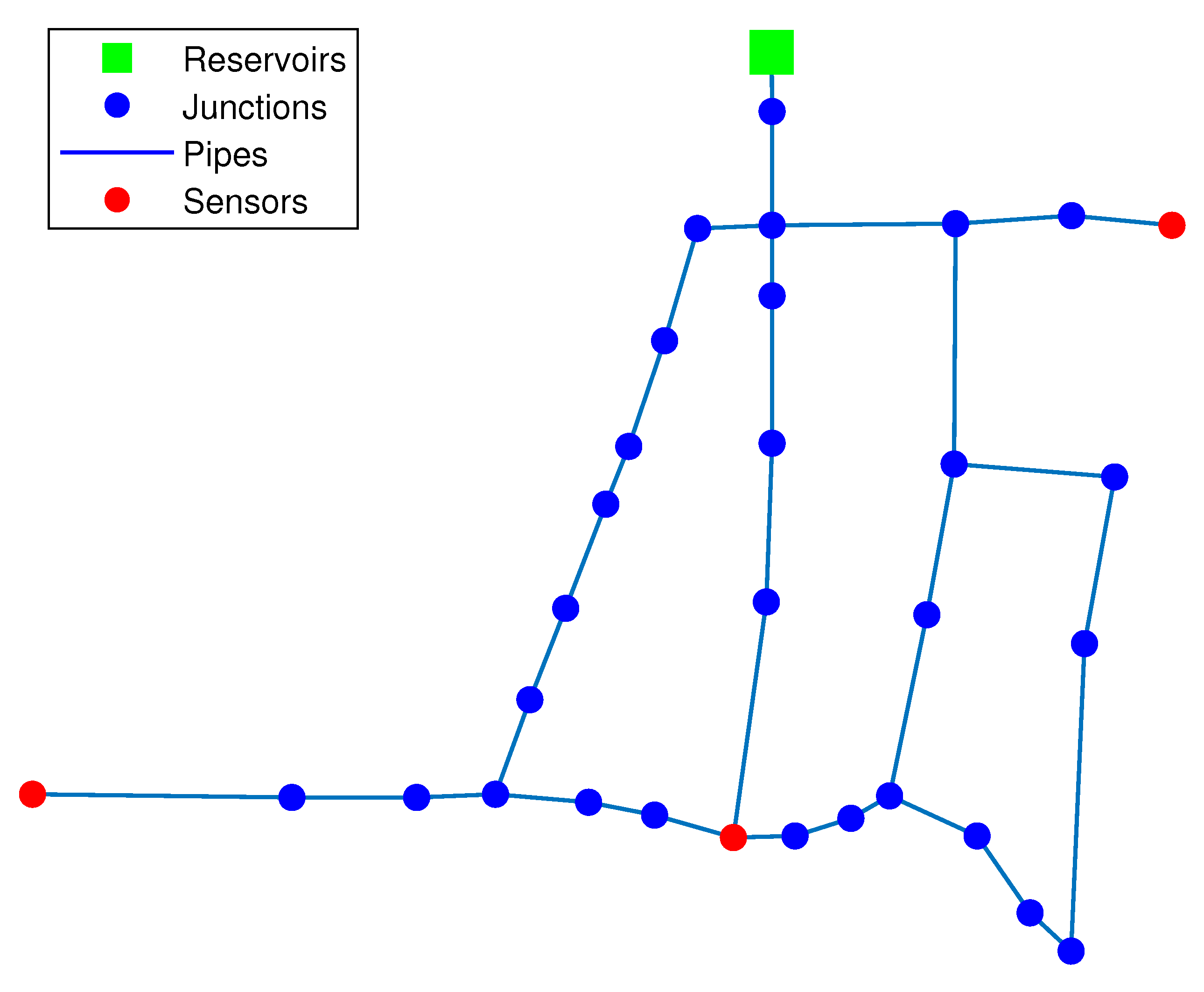



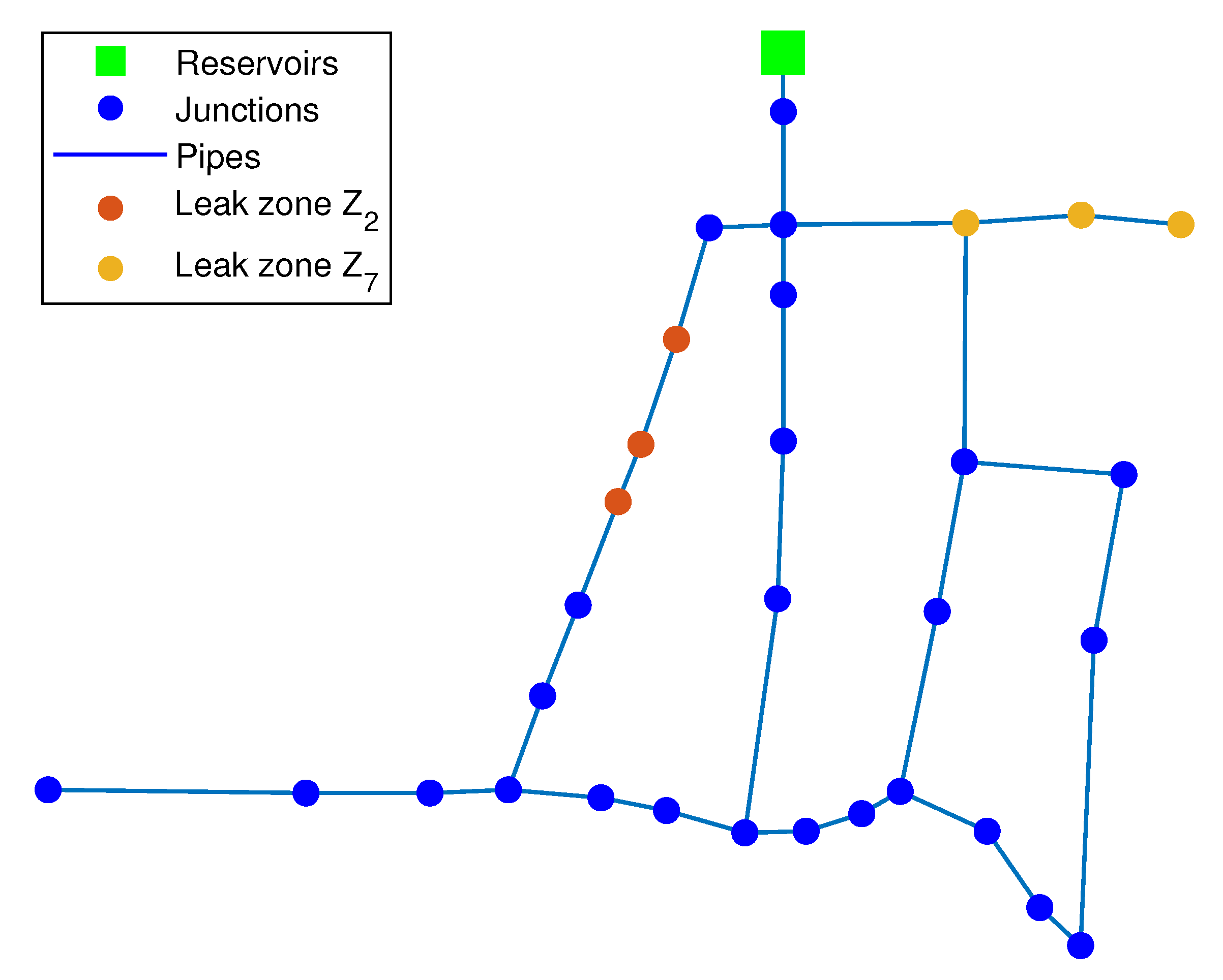
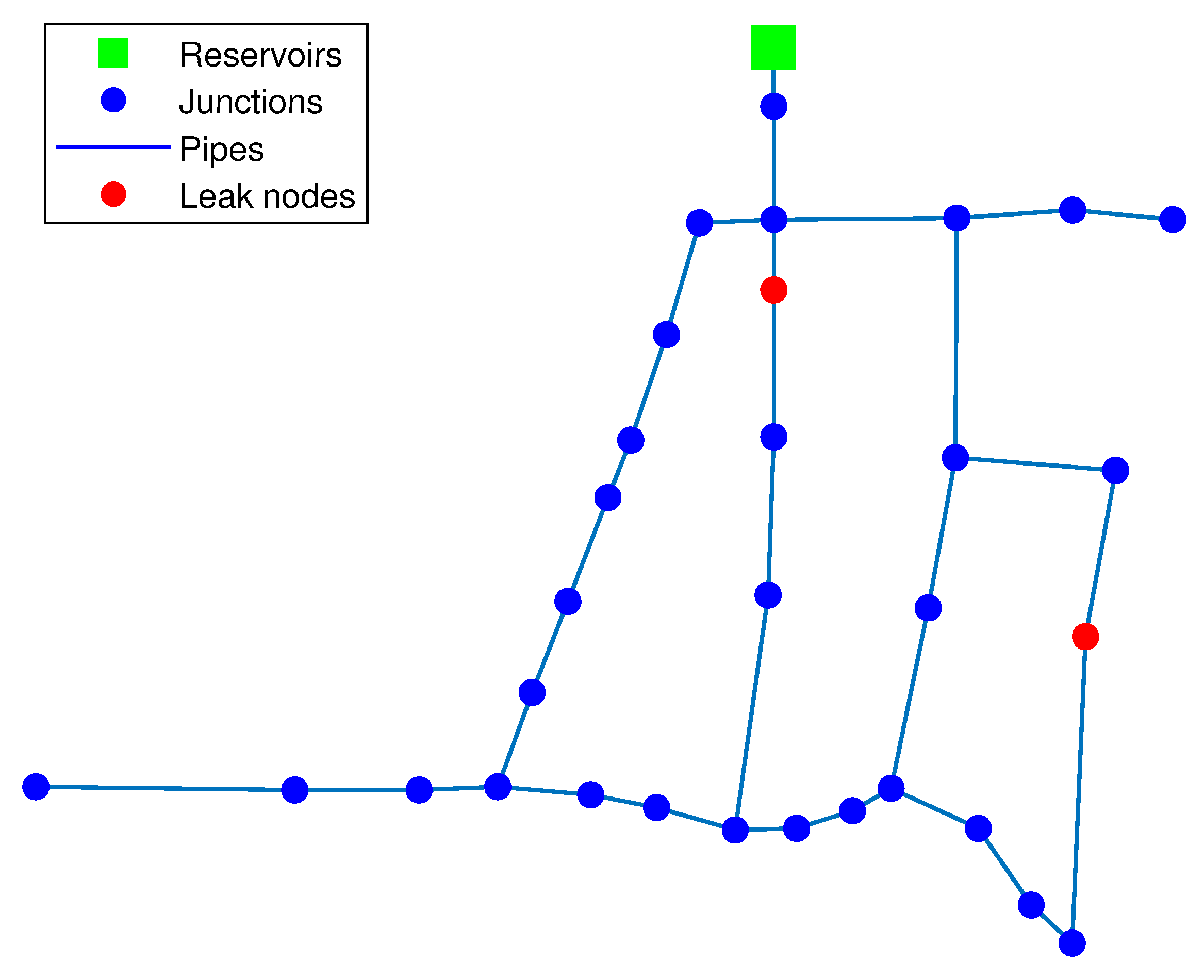
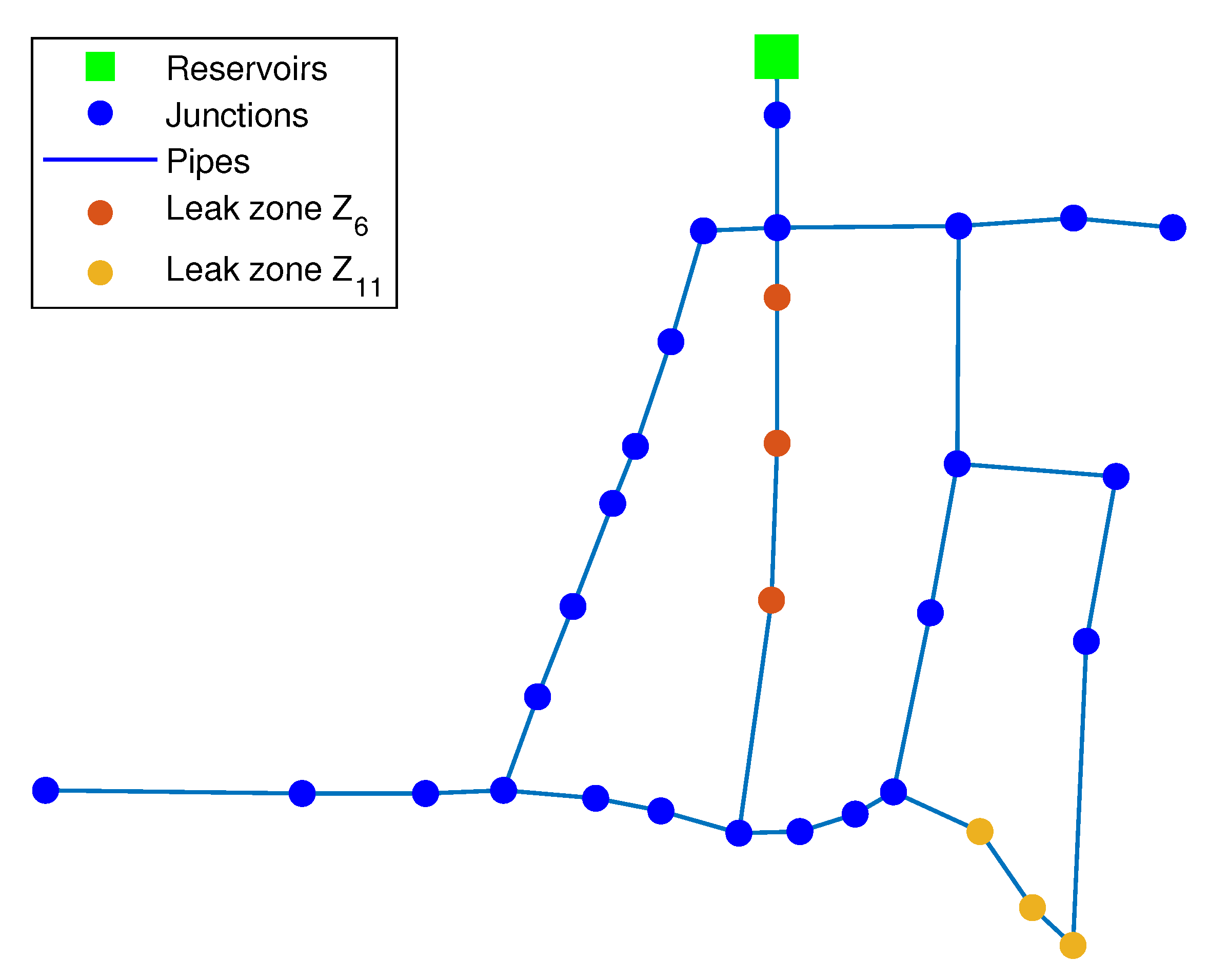
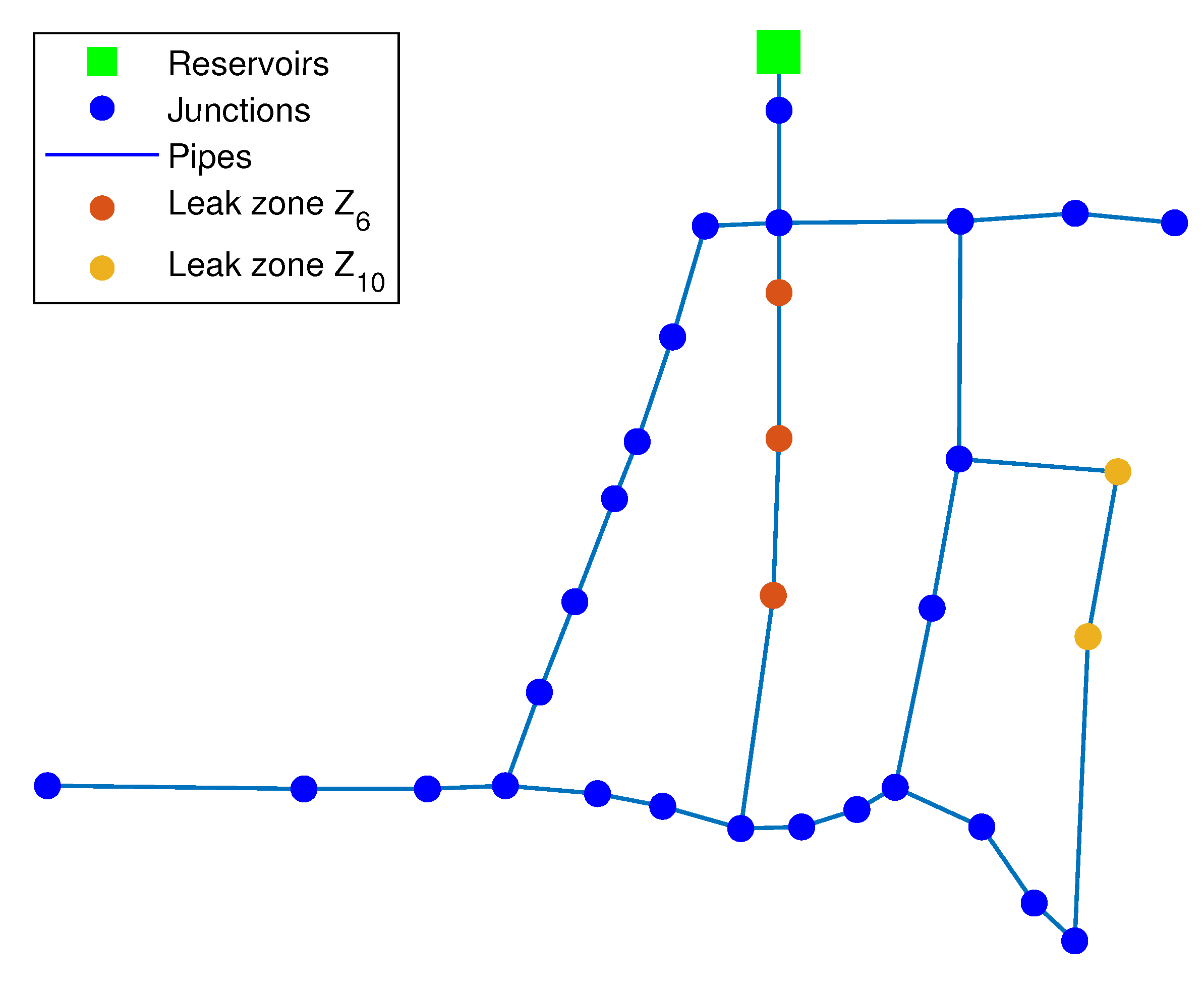
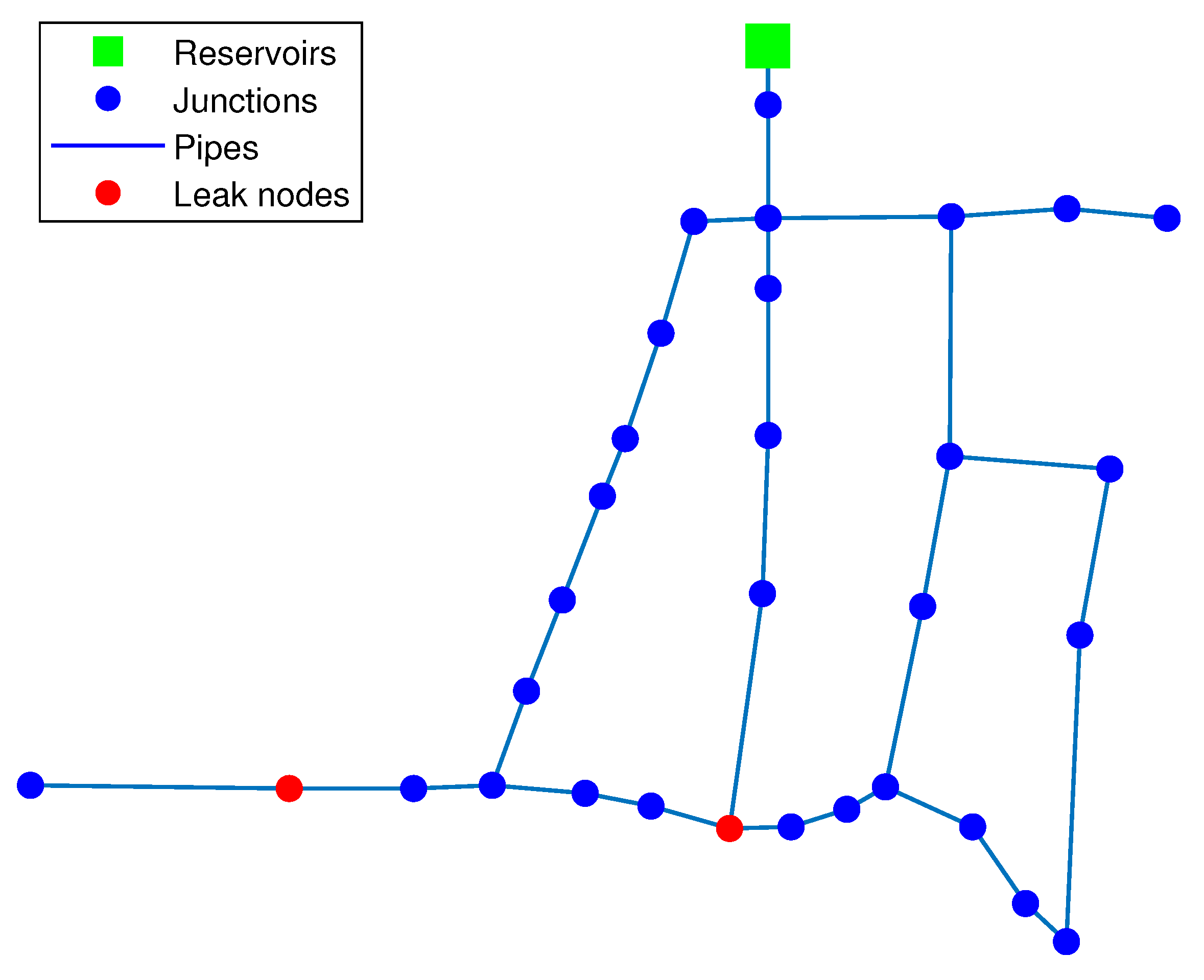


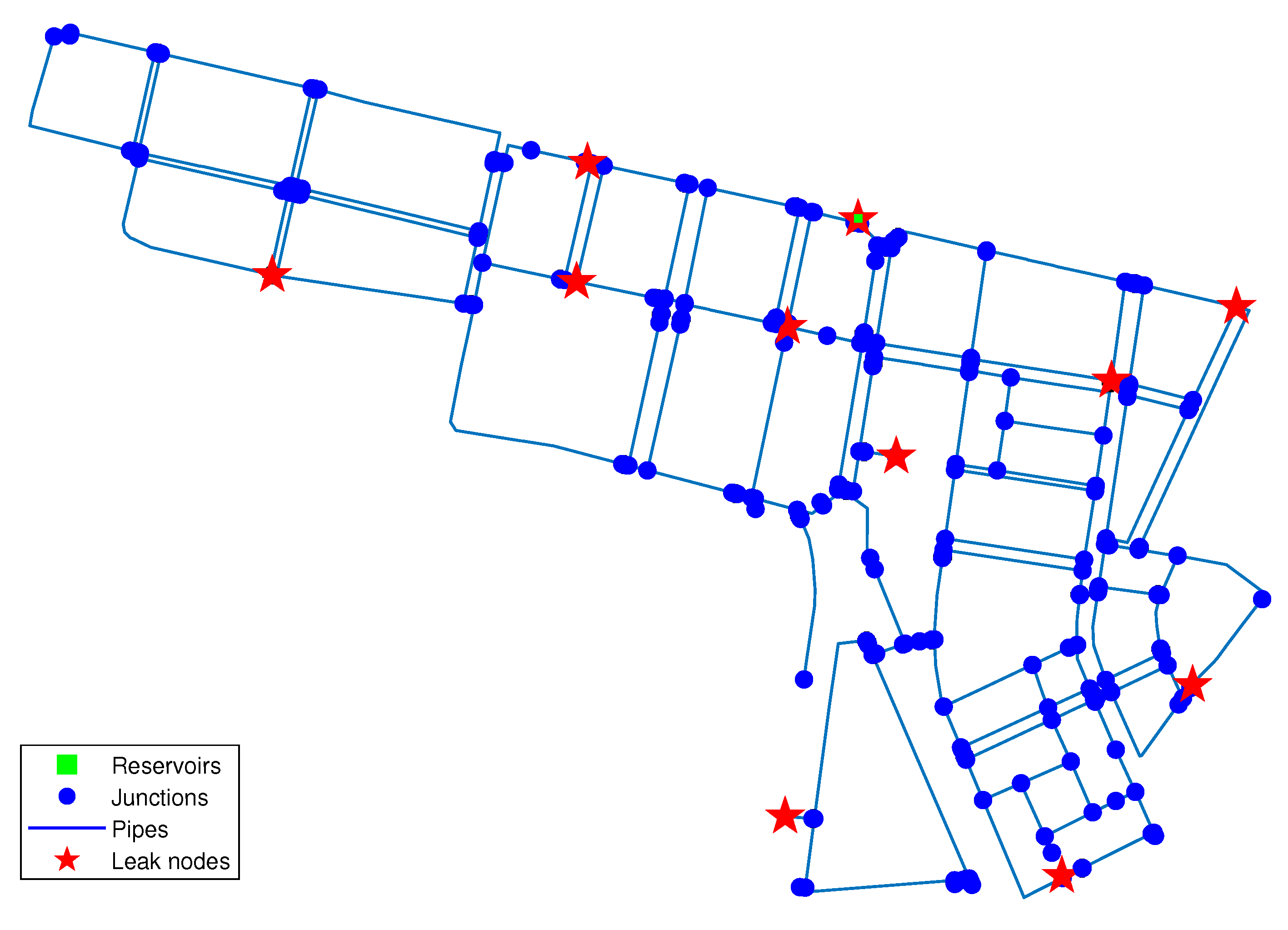
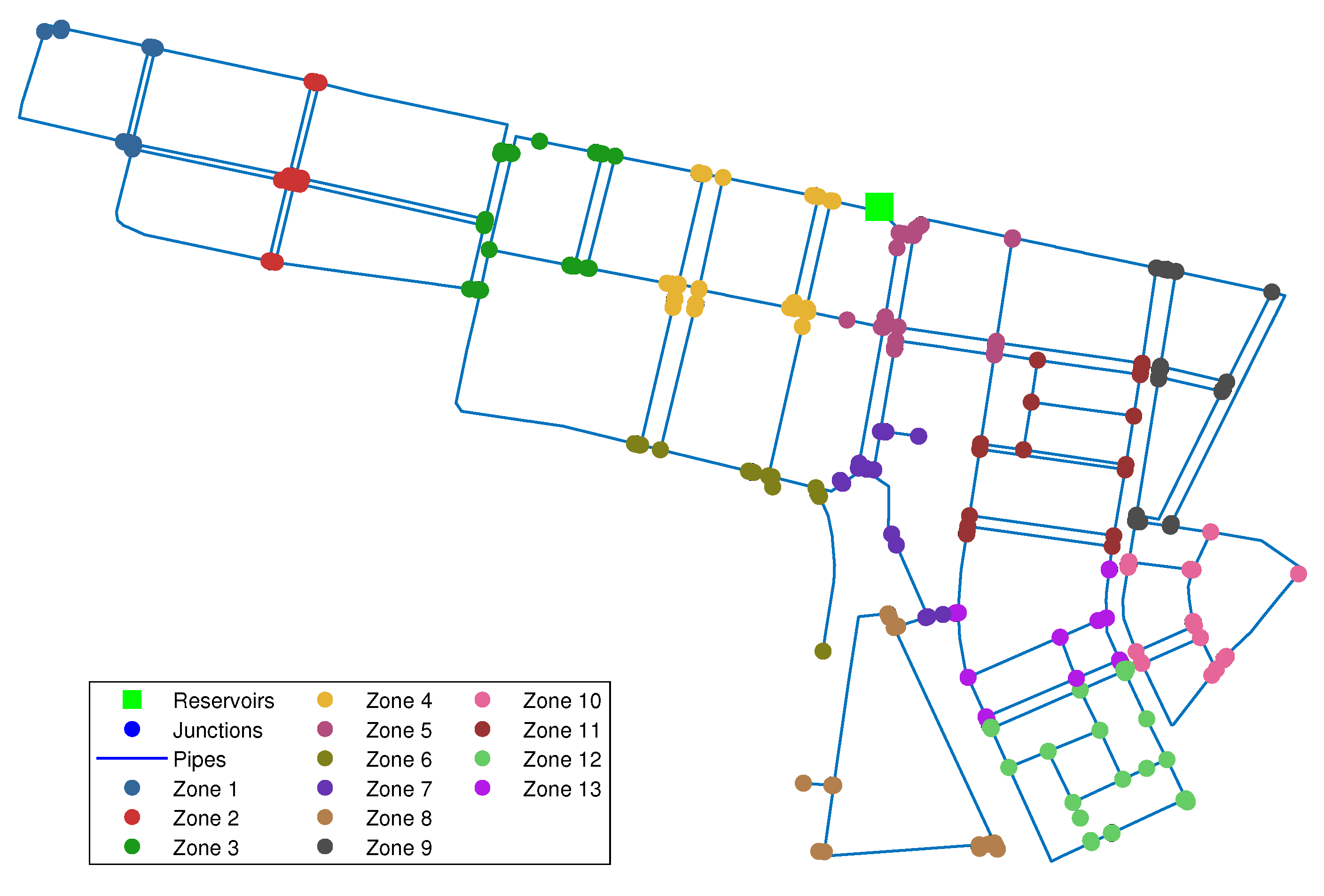

| Sensor’s Number | Optimal Placement |
|---|---|
| 2 sensors | 12, 21 |
| 3 sensors | 12, 15, 21 |
| Zone | Node Set |
|---|---|
| 1, 2, 3 | |
| 4, 5, 6 | |
| 7, 8, 9 | |
| 10, 11, 12 | |
| 13, 14 | |
| 16, 17, 18 | |
| 19, 20, 21 | |
| 22, 23, 24 | |
| 15, 25, 26 | |
| 27, 28 | |
| 29, 30, 31 |
| Relaxation Nodes | Hanoi WDN | Madrid DMA | ||||||
|---|---|---|---|---|---|---|---|---|
| k-NN | DA | k-NN | DA | |||||
| = 1 | = 24 | = 1 | = 24 | = 1 | = 24 | = 1 | = 24 | |
| 0 | 25.5% | 48.0% | 53.5% | 70.0% | 23.5% | 36.0% | 65.0% | 77.0% |
| 1 | 40.5% | 73.5% | 65.0% | 82.5% | 29.0% | 46.0% | 75.5% | 85.5% |
| 2 | 64.0% | 82.5% | 81.0% | 90.5% | 35.0% | 53.5% | 79.0% | 89.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Argote, C.A.; Begovich-Mendoza, O.; Navarro-Díaz, A.; Santos-Ruiz, I.; Puig, V.; Delgado-Aguiñaga, J.A. Two-Leak Isolation in Water Distribution Networks Based on k-NN and Linear Discriminant Classifiers. Water 2023, 15, 3090. https://doi.org/10.3390/w15173090
Rodríguez-Argote CA, Begovich-Mendoza O, Navarro-Díaz A, Santos-Ruiz I, Puig V, Delgado-Aguiñaga JA. Two-Leak Isolation in Water Distribution Networks Based on k-NN and Linear Discriminant Classifiers. Water. 2023; 15(17):3090. https://doi.org/10.3390/w15173090
Chicago/Turabian StyleRodríguez-Argote, Carlos Andrés, Ofelia Begovich-Mendoza, Adrián Navarro-Díaz, Ildeberto Santos-Ruiz, Vicenç Puig, and Jorge Alejandro Delgado-Aguiñaga. 2023. "Two-Leak Isolation in Water Distribution Networks Based on k-NN and Linear Discriminant Classifiers" Water 15, no. 17: 3090. https://doi.org/10.3390/w15173090
APA StyleRodríguez-Argote, C. A., Begovich-Mendoza, O., Navarro-Díaz, A., Santos-Ruiz, I., Puig, V., & Delgado-Aguiñaga, J. A. (2023). Two-Leak Isolation in Water Distribution Networks Based on k-NN and Linear Discriminant Classifiers. Water, 15(17), 3090. https://doi.org/10.3390/w15173090







