The Transient Characteristics of the Cavitation Evolution of the Shroud of High-Speed Pump-Jet Propellers under Different Operating Conditions
Abstract
:1. Introduction
2. Calculation Model
Establishment of the Calculation Model
3. Numerical Simulation and Boundary Conditions
3.1. Turbulence Model
3.2. Cavitation Model
3.3. Boundary Conditions
3.4. Grid Division and Grid Independence Test
4. Experimental System and Experimental Method
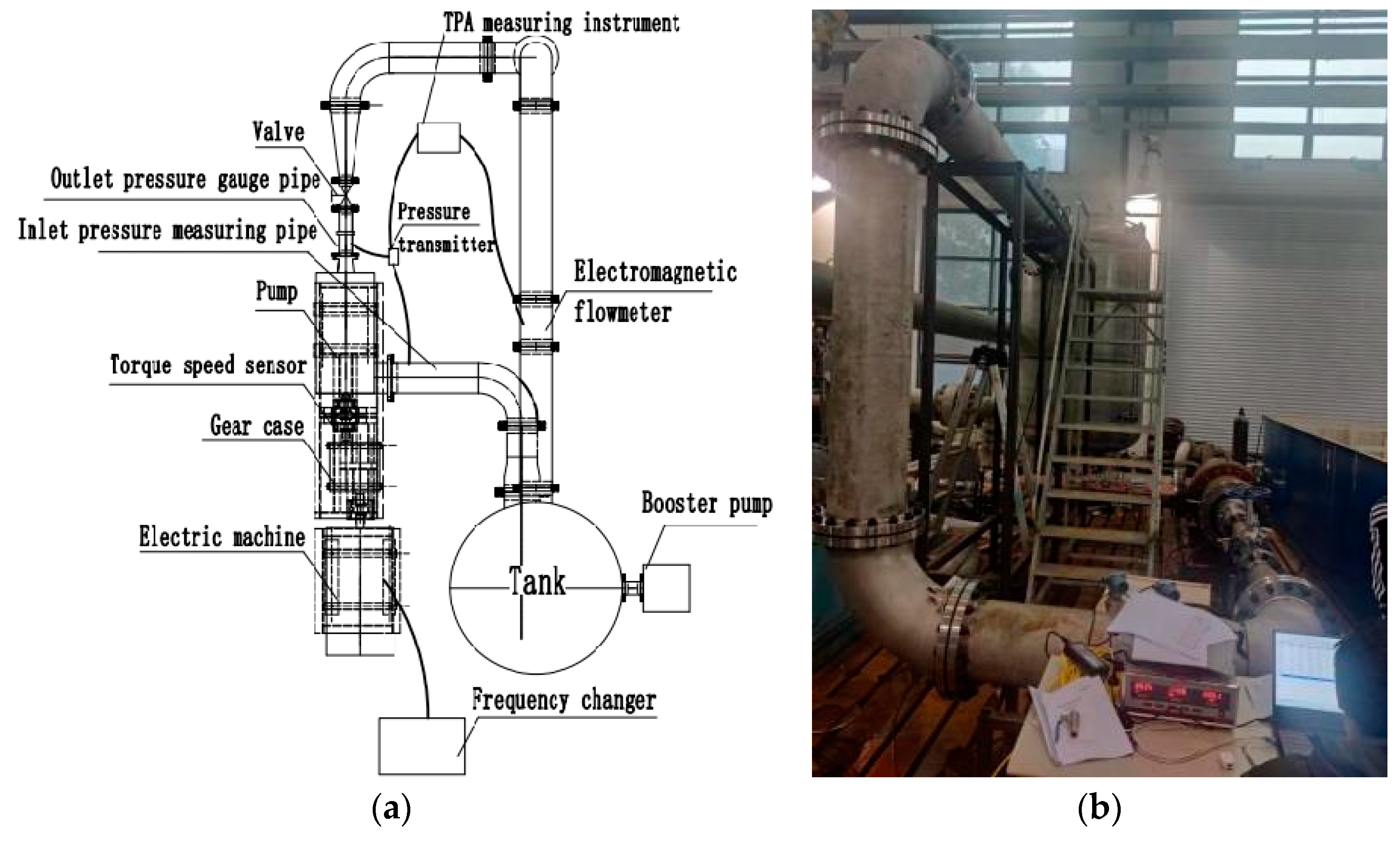
4.1. Experimental System
4.2. Experimental Methods and Results
5. Calculation Results and Analysis
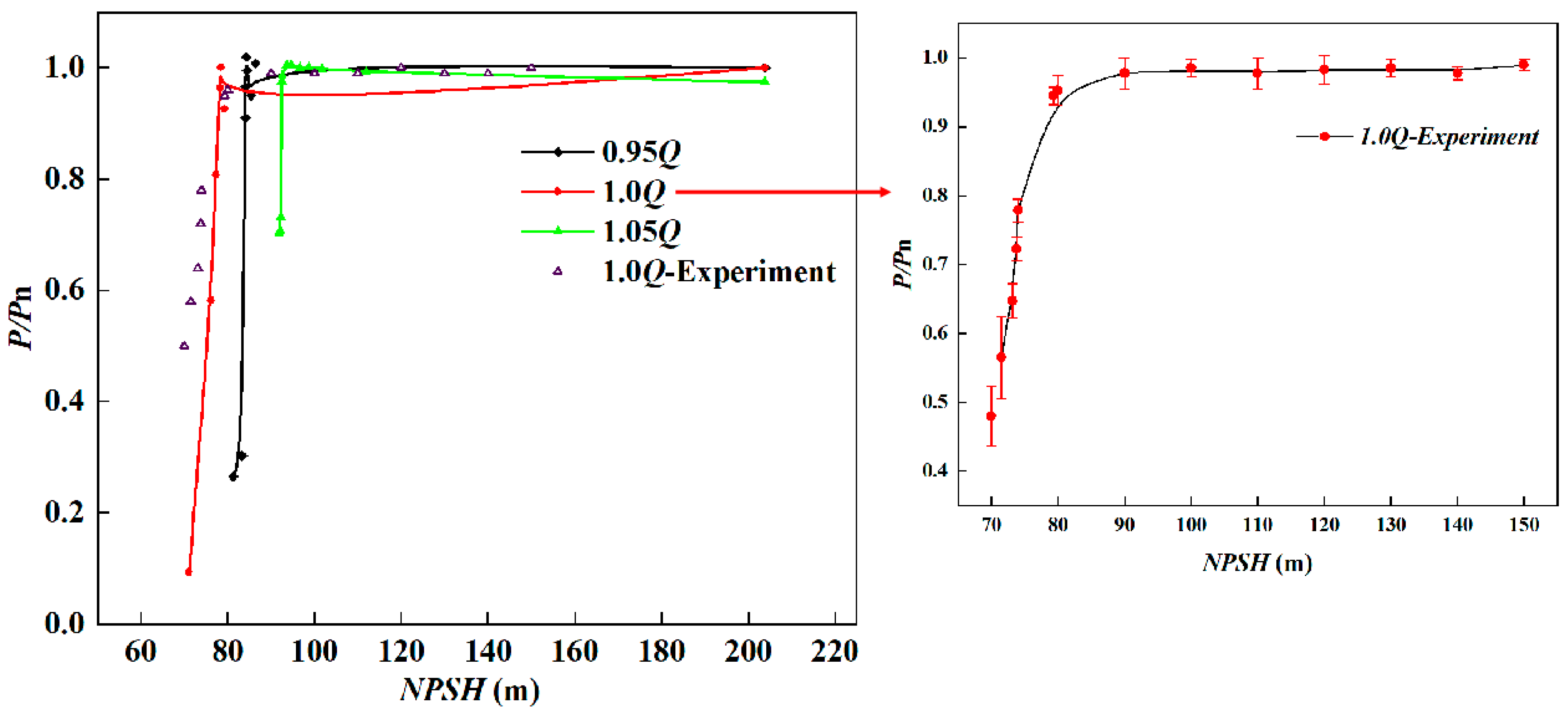
5.1. Cavitation Experiment and Analysis
5.2. Cavity Change Characteristic Analysis
5.2.1. Change in the Impeller Cavity Volume Fraction
5.2.2. Cavitation Distribution of Impeller Blades
5.2.3. Characteristics of Cavitation Changes in Impeller Blades
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sbragio, R.; Moura, A.J.d.S.; da Silva, R.C. Design and Cfd Self-Propulsion Analysis of A Ducted Propeller for A Darpa Suboff Hull Autonomous Underwater Vehicle. In Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering, Online, 3–7 August 2020. [Google Scholar]
- Xia, C.Z.; Cheng, L.; Shang, Y.N.; Zhou, J.R.; Yang, F.; Jin, Y. Numerical simulation on the cavitation of waterjet propulsion pump. Iop Conf. 2016, 129, 012011. [Google Scholar] [CrossRef]
- Rakibuzzaman; Kim, K.; Suh, S.-H. Numerical and experimental investigation of cavitation flows in a multistage centrifugal pump. J. Mech. Sci. Technol. 2018, 32, 1071–1078. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, Y.; Zhang, J.; Zhu, J. Experimental studies of unsteady cavitation at the tongue of a pump-turbine in pump mode—ScienceDirect. Renew. Energy 2021, 177, 1265–1281. [Google Scholar] [CrossRef]
- Hu, F.; Chen, T.; Wu, D.; Wang, L. Experiment study of cavitation induced vibration and noise of guide vane mixed flow pump. J. Drain. Irrig. Mach. Eng. 2013, 31, 1021–1024. [Google Scholar]
- Al-Obaidi, A.R.; Mishra, R. Experimental investigation of the effect of air injection on performance and detection of cavitation in the centrifugal pump based on vibration technique. Arab. J. Sci. Eng. 2020, 45, 5657–5671. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Experimental comparative investigations to evaluate cavitation conditions within a centrifugal pump based on vibration and acoustic analyses techniques. Arch. Acoust. 2020, 45, 541–556. [Google Scholar]
- Al-Obaidi, A.R. Experimental investigation of cavitation characteristics within a centrifugal pump based on acoustic analysis technique. Int. J. Fluid Mech. Res. 2020, 47, 501–515. [Google Scholar] [CrossRef]
- Al-Obaidi, A. Experimental and Numerical Investigations on the Cavitation Phenomenon in a Centrifugal Pump. Ph.D. Dissertation, University of Huddersfield, Huddersfield, UK, 2018. [Google Scholar]
- Lu, Y.; Tan, L.; Han, Y.; Liu, M. Cavitation-vibration correlation of a mixed flow pump under steady state and fast start-up conditions by experiment. Ocean Eng. 2022, 251, 111158. [Google Scholar] [CrossRef]
- Thamsen, P.U.; Bubelach, T.; Pensler, T.; Springer, P. Cavitation in Single-Vane Sewage Pumps. Int. J. Rotating Mach. 2008, 2008, 354020. [Google Scholar] [CrossRef]
- Chai, L.; Li, S.; Hu, H.; Ye, H. Analysis of impeller geometric parameters affecting the centrifugal pump cavitation performance based on CFD simulations. In Proceedings of the 6th International Symposium on Fluid Machinery and Fluid Engineering, Wuhan, China, 22–25 October 2014. [Google Scholar]
- Qiu, C.; Huang, Q.; Pan, G.; Shi, Y.; Dong, X. Numerical simulation of hydrodynamic and cavitation performance of pumpjet propulsor with different tip clearances in oblique flow. Ocean Eng. 2020, 209, 107285. [Google Scholar] [CrossRef]
- Wang, B.-L.; Liu, Z.-H.; Li, H.-Y.; Wang, Y.-Y.; Liu, D.-C.; Zhang, L.-X.; Peng, X.-X. On the numerical simulations of vortical cavitating flows around various hydrofoils. J. Hydrodyn. Ser B 2017, 29, 926–938. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, Y.; Shi, W.; Cao, W.; Shi, Y. Cavitating Flow in the Volute of a Centrifugal Pump at Flow Rates Above the Optimal Condition. J. Mar. Sci. Eng. 2021, 9, 446. [Google Scholar]
- Ji, B.; Luo, X.; Wang, X.; Peng, X.; Wu, Y.; Xu, H. Unsteady numerical simulation of cavitating turbulent flow in centrifugal pumps. J. Lanzhou Univ. Technol. 2008, 133, 011102. [Google Scholar]
- Kan, K.; Zheng, Y.; Chen, Y.; Xie, Z.; Yang, G.; Yang, C. Numerical study on the internal flow characteristics of an axial-flow pump under stall conditions. J. Mech. Sci. Technol. 2018, 32, 4683–4695. [Google Scholar] [CrossRef]
- Medvitz, R.B.; Kunz, R.F.; Boger, D.A.; Lindau, J.W.; Yocum, A.M.; Pauley, L.L. Performance Analysis of Cavitating Flow in Centrifugal Pumps Using Multiphase CFD. J. Fluids Eng. 2002, 124, 377–383. [Google Scholar] [CrossRef]
- Altosole, M.; Benvenuto, G.; Figari, M.; Campora, U. Dimensionless Numerical Approaches for the Performance Prediction of Marine Waterjet Propulsion Units. Int. J. Rotating Mach. 2012, 2012, 321306. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, L.; Shi, W.; Zhao, R.; Wang, H.; Van Esch, B.B. Numerical analysis of unsteady tip leakage vortex cavitation cloud and unstable suction-side-perpendicular cavitating vortices in an axial flow pump. Int. J. Multiph. Flow 2015, 77, 244–259. [Google Scholar] [CrossRef]
- Shen, X.; Zhao, X.; Xu, B.; Zhang, D.; Yang, G.; Shi, W.; van Esch, B.B. Unsteady characteristics of tip leakage vortex structure and dynamics in an axial flow pump. Ocean Eng. 2022, 266, 112850. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Analysis of the effect of various impeller blade angles on characteristic of the axial pump with pressure fluctuations based on time-and frequency-domain investigations. Iran. J. Sci. Technol. Trans. Mech. Eng. 2021, 45, 441–459. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Influence of guide vanes on the flow fields and performance of axial pump under unsteady flow conditions: Numerical study. J. Mech. Eng. Sci. 2020, 14, 6570–6593. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Mohammed, A.A. Numerical Investigations of Transient Flow Characteristic in Axial Flow Pump and Pressure Fluctuation Analysis Based on the CFD Technique. J. Eng. Sci. Technol. Rev. 2019, 12, 70–79. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Numerical investigation of flow field behaviour and pressure fluctuations within an axial flow pump under transient flow pattern based on CFD analysis method. J. Phys. Conf. Ser. 2019, 1279, 012069. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Effect of Different Guide Vane Configurations on Flow Field Investigation and Performances of an Axial Pump Based on CFD Analysis and Vibration Investigation. Exp. Tech. 2023, 1–20. [Google Scholar] [CrossRef]
- Milani, M.; Montorsi, L.; Muzzioli, G.; Lucchi, A. A Cfd Approach for The Simulation of An Entire Swash-Plate Axial Piston Pump Under Dynamic Operating Conditions. In International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar]
- Zhang, Y.; Song, P.; Xu, C.; Tian, Y.; Zhang, J. Experimental and Numerical Investigations of Cavitation in a Centrifugal Pump with Pre-whirl Regulation. Trans. Chin. Soc. Agric. Mach. 2014, 45, 131–137. [Google Scholar]
- Han, W.; Zhang, T.; Su, Y.L.; Chen, R.; Qiang, Y.; Han, Y. Transient Characteristics of Water-Jet Propulsion with a Screw Mixed Pump during the Startup Process. Math. Probl. Eng. 2020, 2020, 5691632. [Google Scholar] [CrossRef]
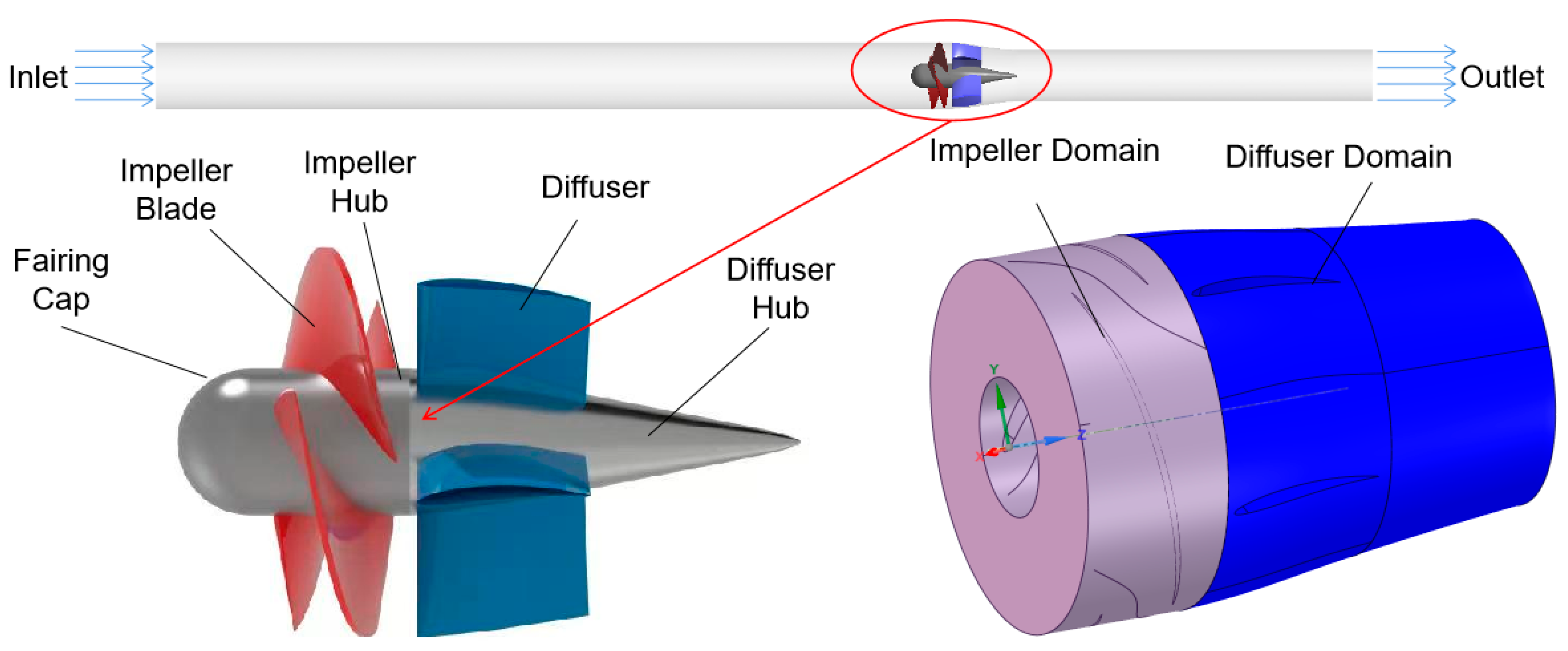






| Scheme | Impeller Domain | Diffuser Domain | Internal Domain | Efficiency/% |
|---|---|---|---|---|
| 1 | 659259 | 989440 | 476177 | 85.74 |
| 2 | 1091644 | 1836496 | 644494 | 86.32 |
| 3 | 2173485 | 2047547 | 909270 | 87.47 |
| 4 | 3077421 | 2951054 | 143765 | 88.15 |
| 5 | 5397257 | 3523181 | 3697778 | 88.17 |
| NPSH (m) | Volume Fraction of Cavitation | ||
|---|---|---|---|
| 0.95 Q | 1.0 Q | 1.05 Q | |
| 50 | 0.402632 | 0.402582 | 0.402554 |
| 60 | 0.335245 | 0.335237 | 0.335237 |
| 70 | 0.274699 | 0.27458 | 0.274566 |
| 80 | 0.013541 | 0.117368 | 0.203432 |
| 85 | 0 | 0.0185164 | 0.159795 |
| 90 | 0 | 0 | 0.11025 |
| 95 | 0 | 0 | 0.0379525 |
| 100 | 0 | 0 | 0 |
| 150 | 0 | 0 | 0 |
| 200 | 0 | 0 | 0 |
| t | 1/6 T | 1/3 T | 1/2 T | 2/3 T | 5/6 T | T | |
|---|---|---|---|---|---|---|---|
| 0.95 Q |  |  | |||||
| 1.0 Q |  |  | |||||
| 1.1 Q | 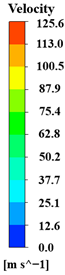 |  | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, G.; Shi, W.; Yi, J.; Fu, Q.; Zhu, R.; Duan, Y. The Transient Characteristics of the Cavitation Evolution of the Shroud of High-Speed Pump-Jet Propellers under Different Operating Conditions. Water 2023, 15, 3073. https://doi.org/10.3390/w15173073
Gan G, Shi W, Yi J, Fu Q, Zhu R, Duan Y. The Transient Characteristics of the Cavitation Evolution of the Shroud of High-Speed Pump-Jet Propellers under Different Operating Conditions. Water. 2023; 15(17):3073. https://doi.org/10.3390/w15173073
Chicago/Turabian StyleGan, Gongchang, Wenhao Shi, Jinbao Yi, Qiang Fu, Rongsheng Zhu, and Yuchen Duan. 2023. "The Transient Characteristics of the Cavitation Evolution of the Shroud of High-Speed Pump-Jet Propellers under Different Operating Conditions" Water 15, no. 17: 3073. https://doi.org/10.3390/w15173073




