A Dimension-Reduced Line Element Method for 3D Transient Free Surface Flow in Porous Media
Abstract
:1. Introduction
2. Governing Equations
- (1)
- The initial condition [11]
- (2)
- The potential head boundary S1 [11]where the overline represents prescribed value, and S1 denotes the flow boundaries below the upstream and downstream water levels and are valued by the given water heads and , respectively.
- (3)
- (4)
- The Signorini-type seepage boundary S3
- (5)
- The transient free surface boundary
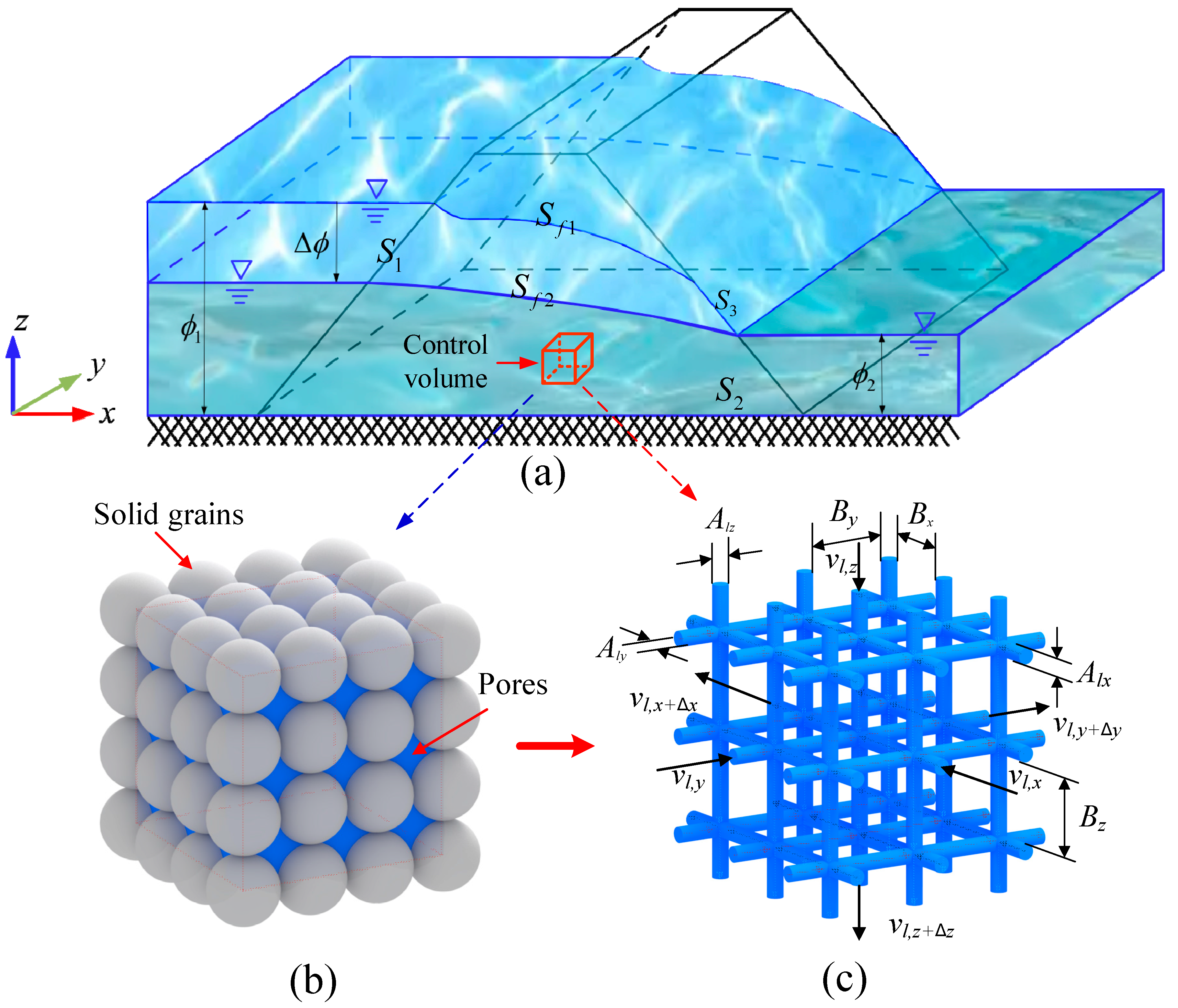
3. The Line Element Method
3.1. Equivalent Flow Velocity and Hydraulic Conductivity
3.2. Equivalent Continuity Equations
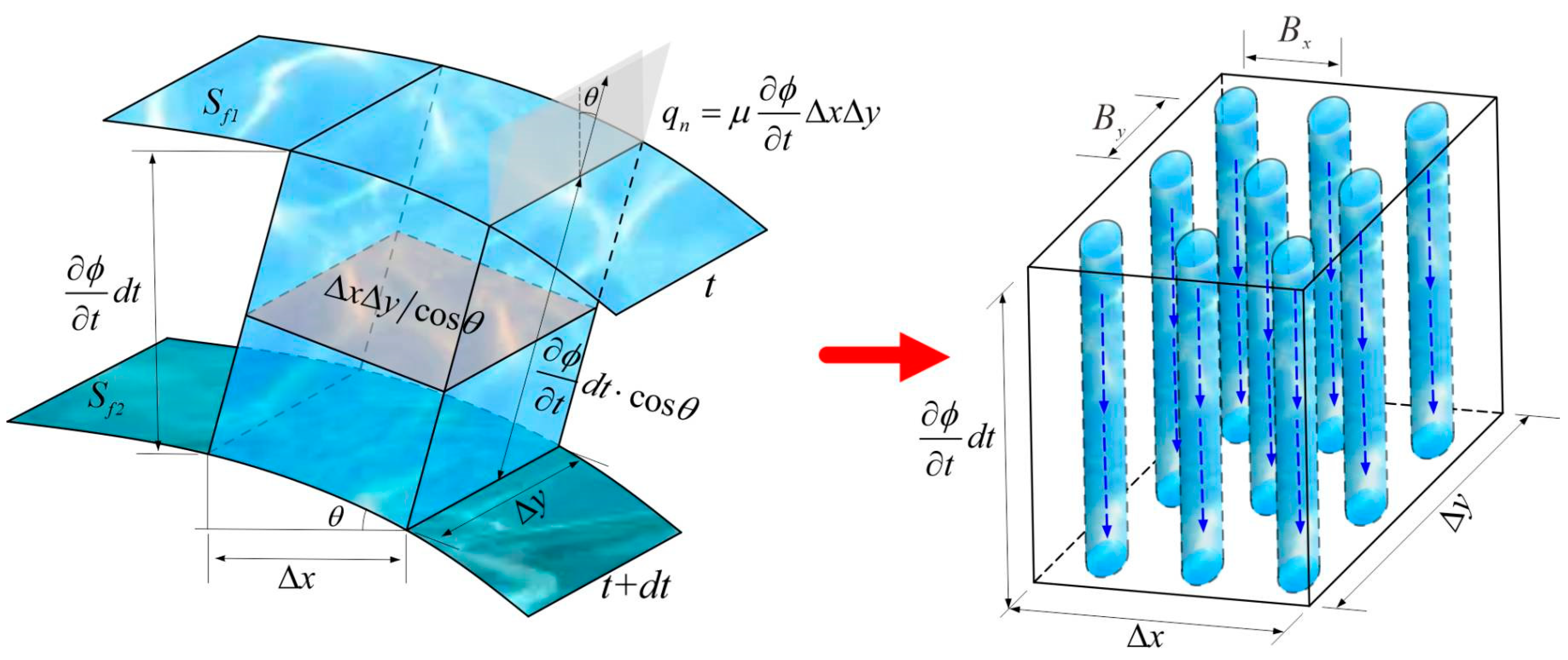
3.3. Equivalent Transient Free Surface Boundary
3.4. Unified Formulations and Numerical Procedure
4. Validations
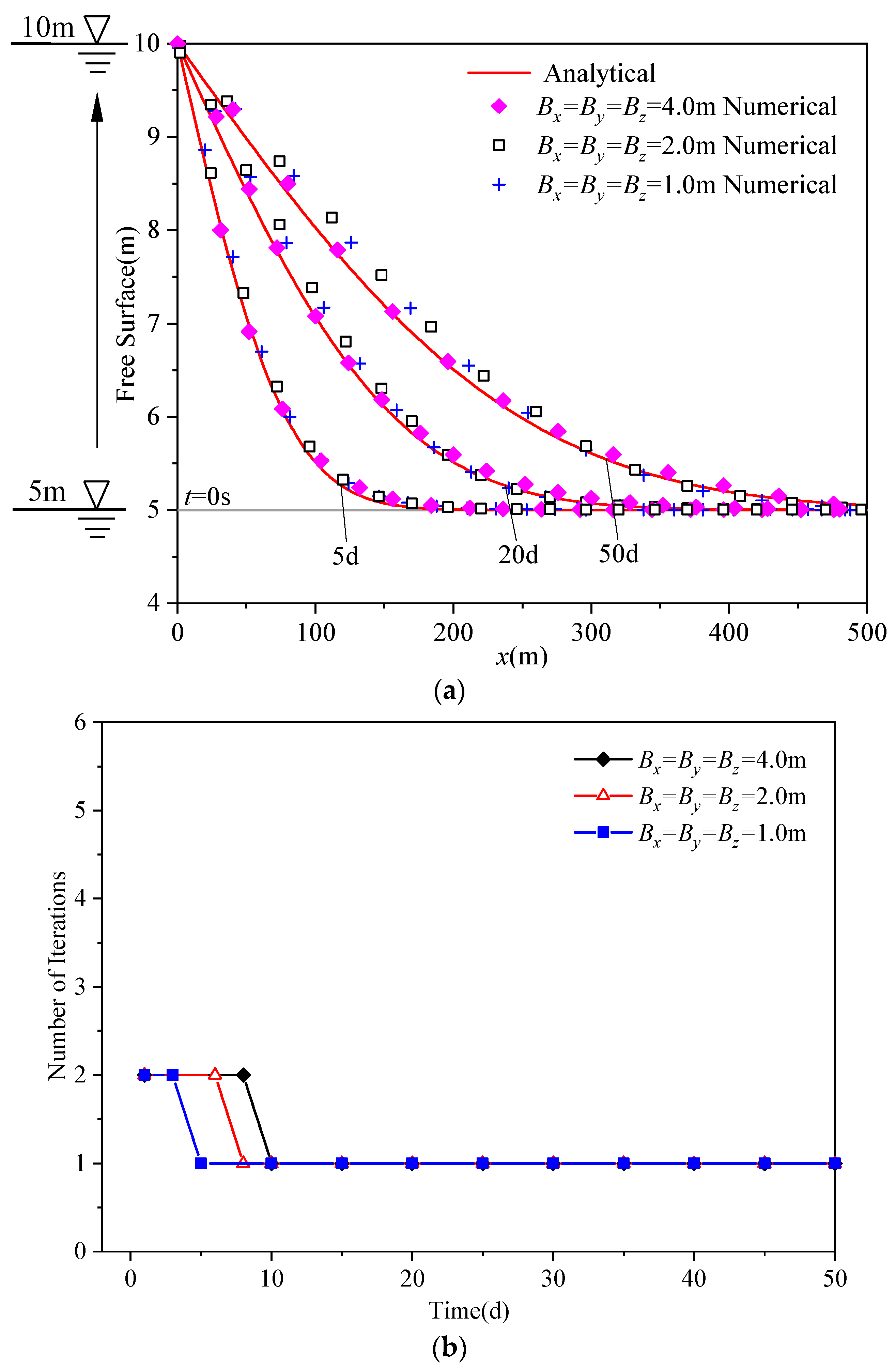
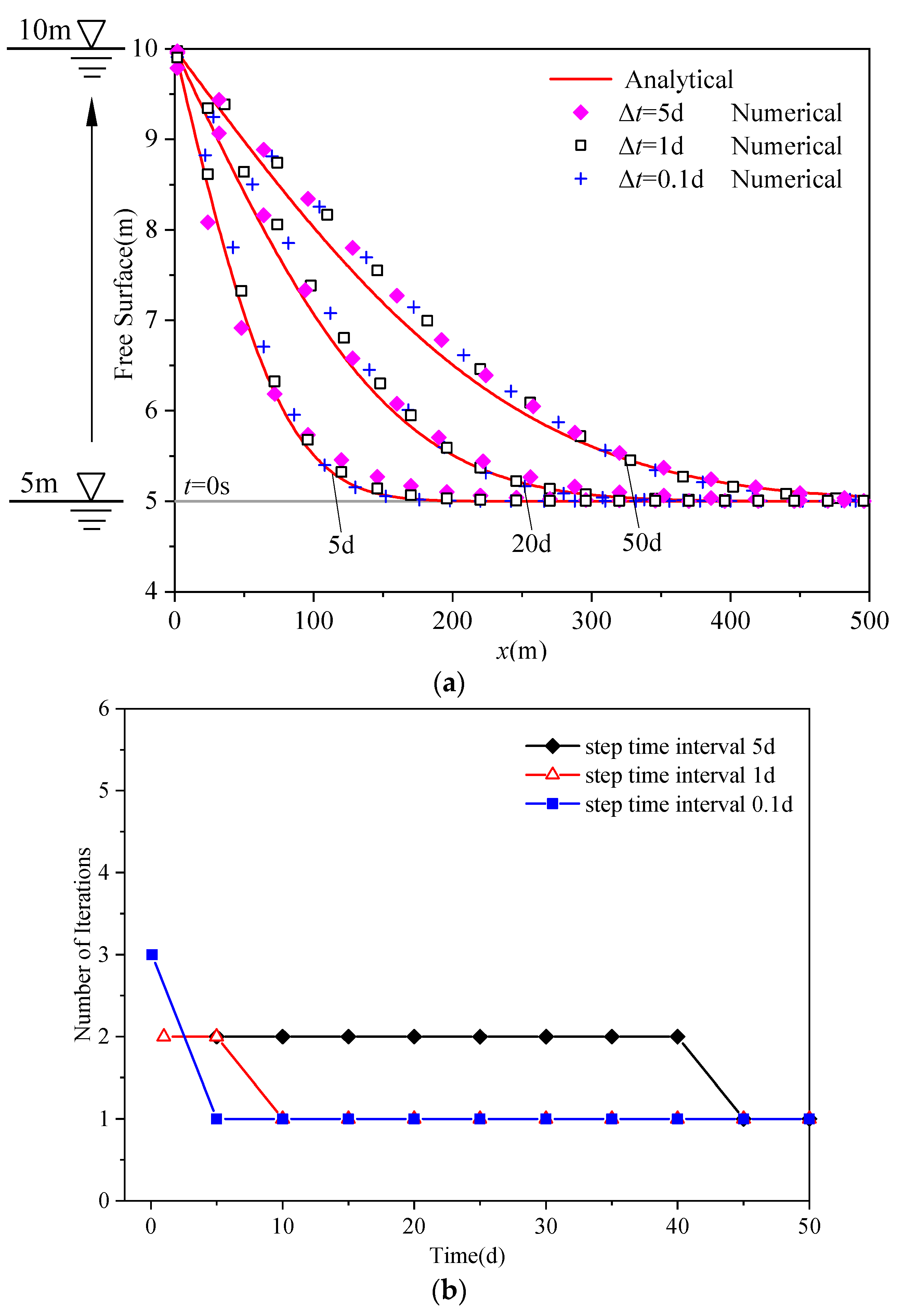
4.1. An Unconfined Aquifer
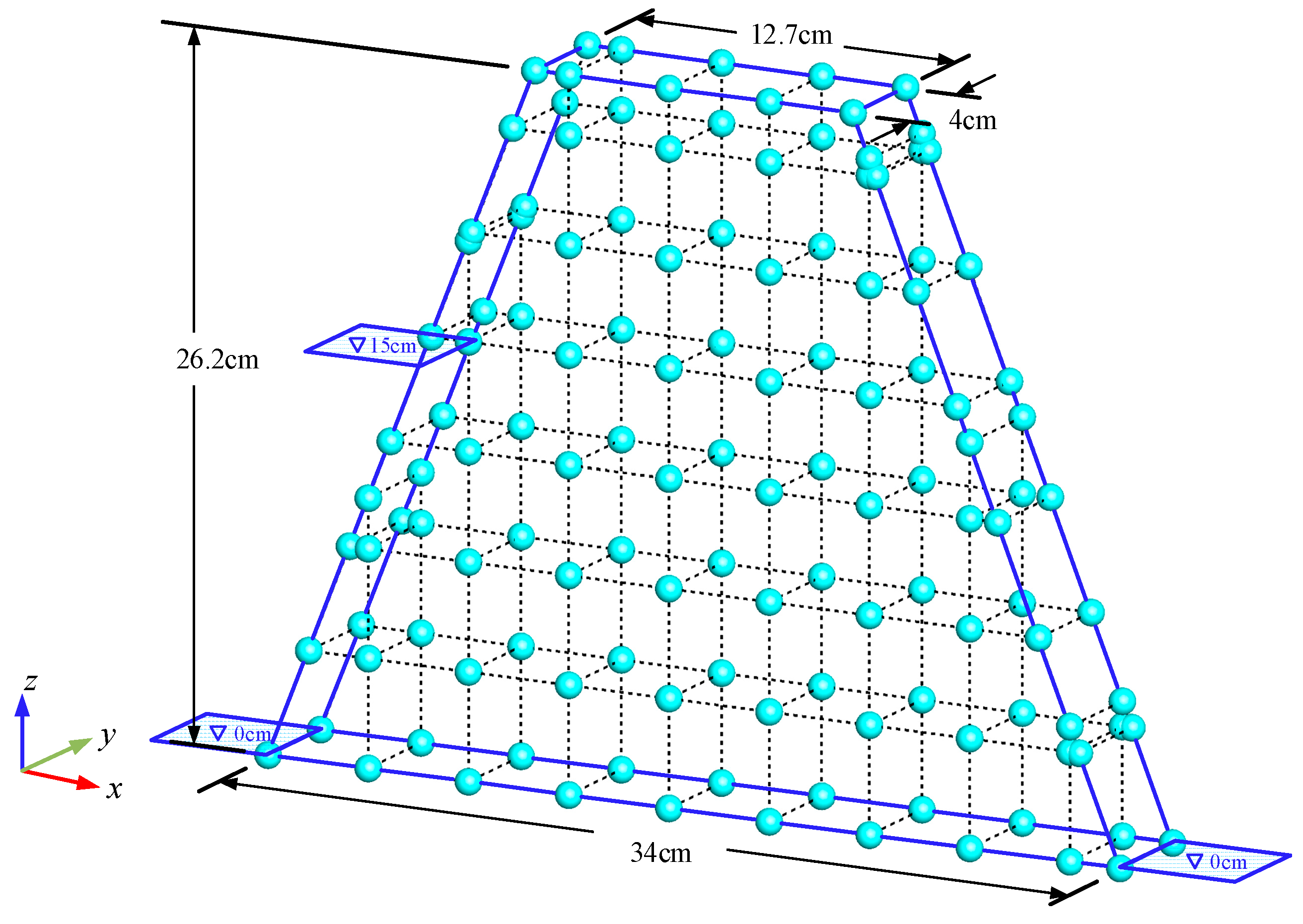
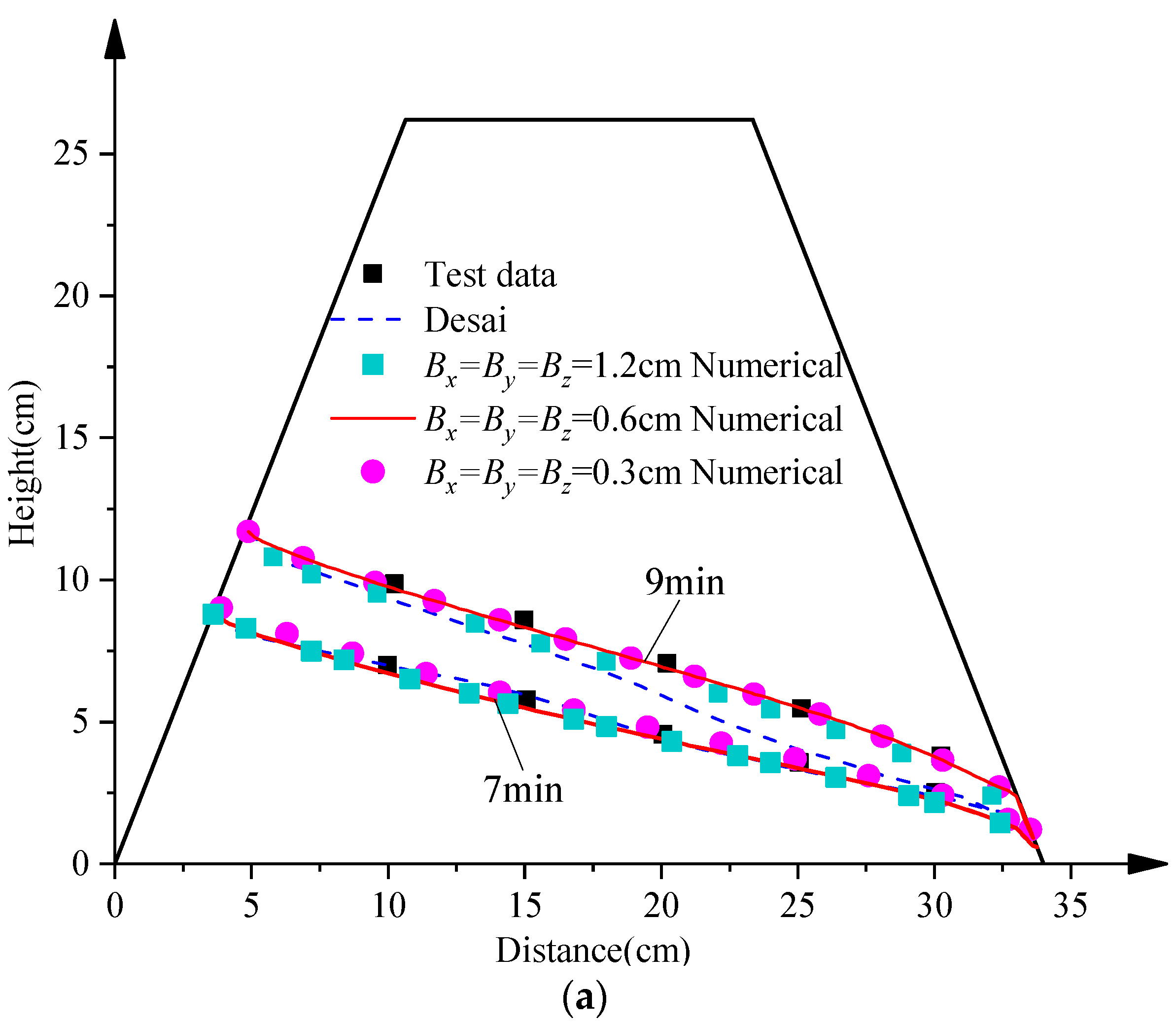
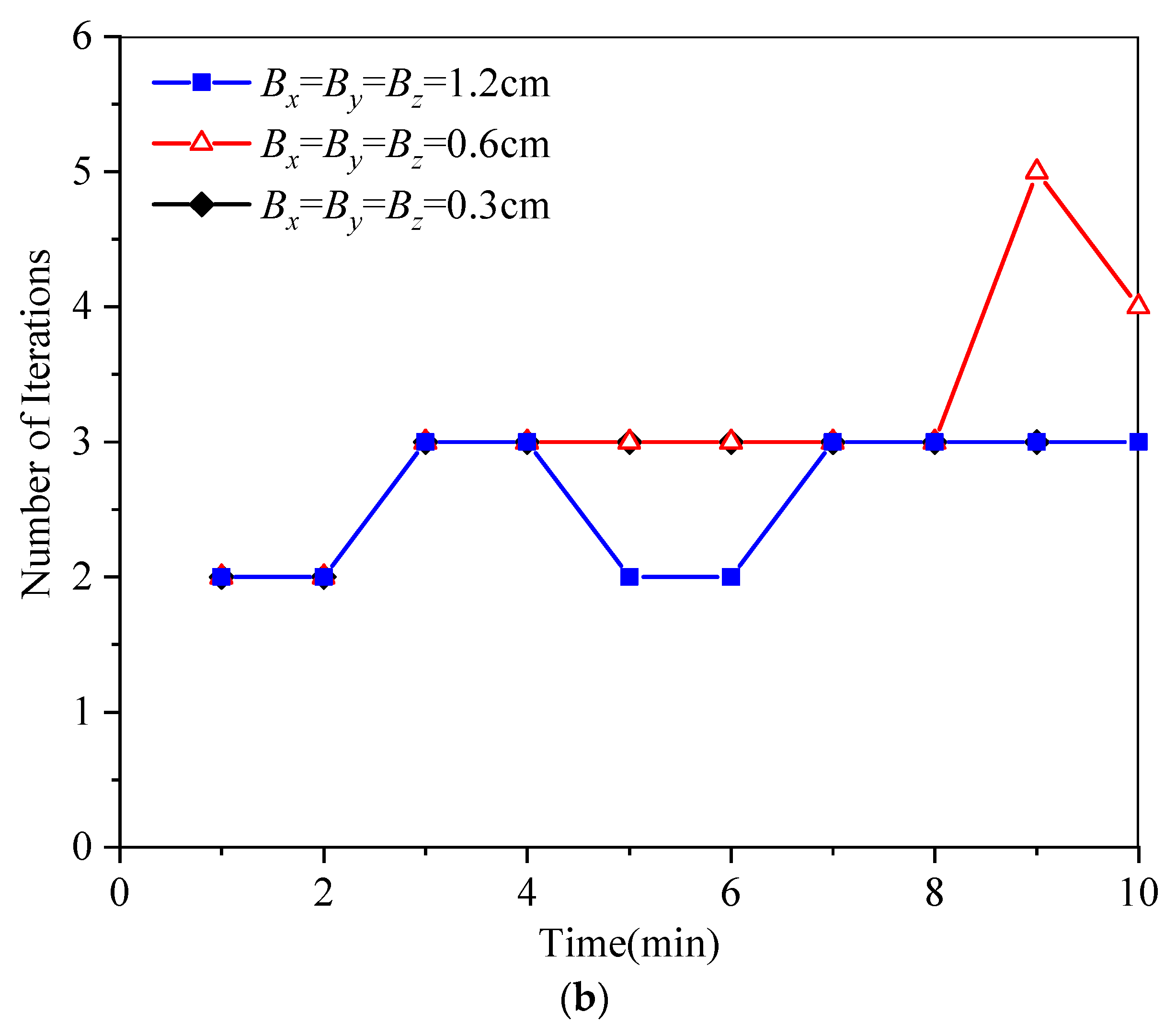
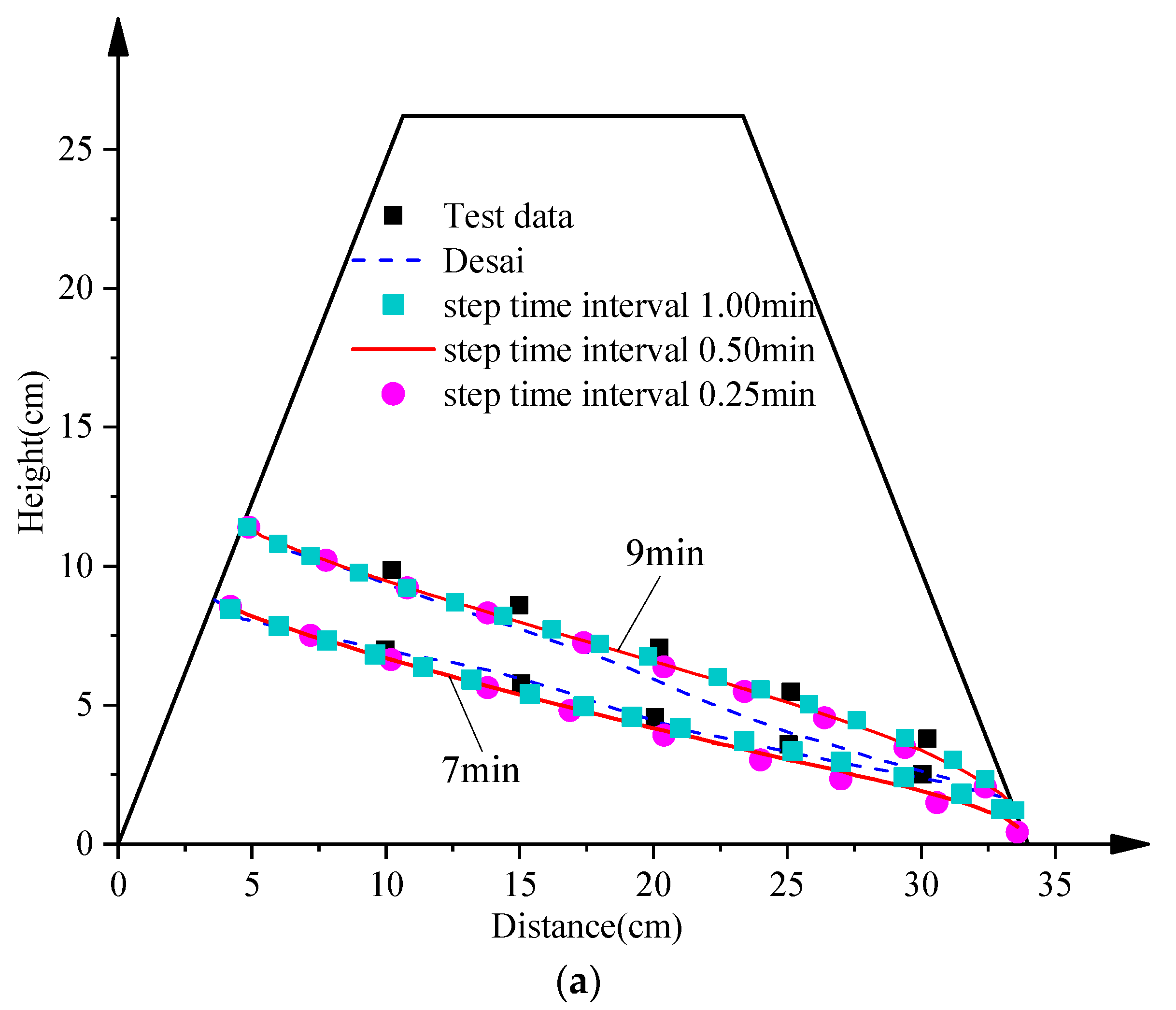
4.2. A Trapezoidal Dam
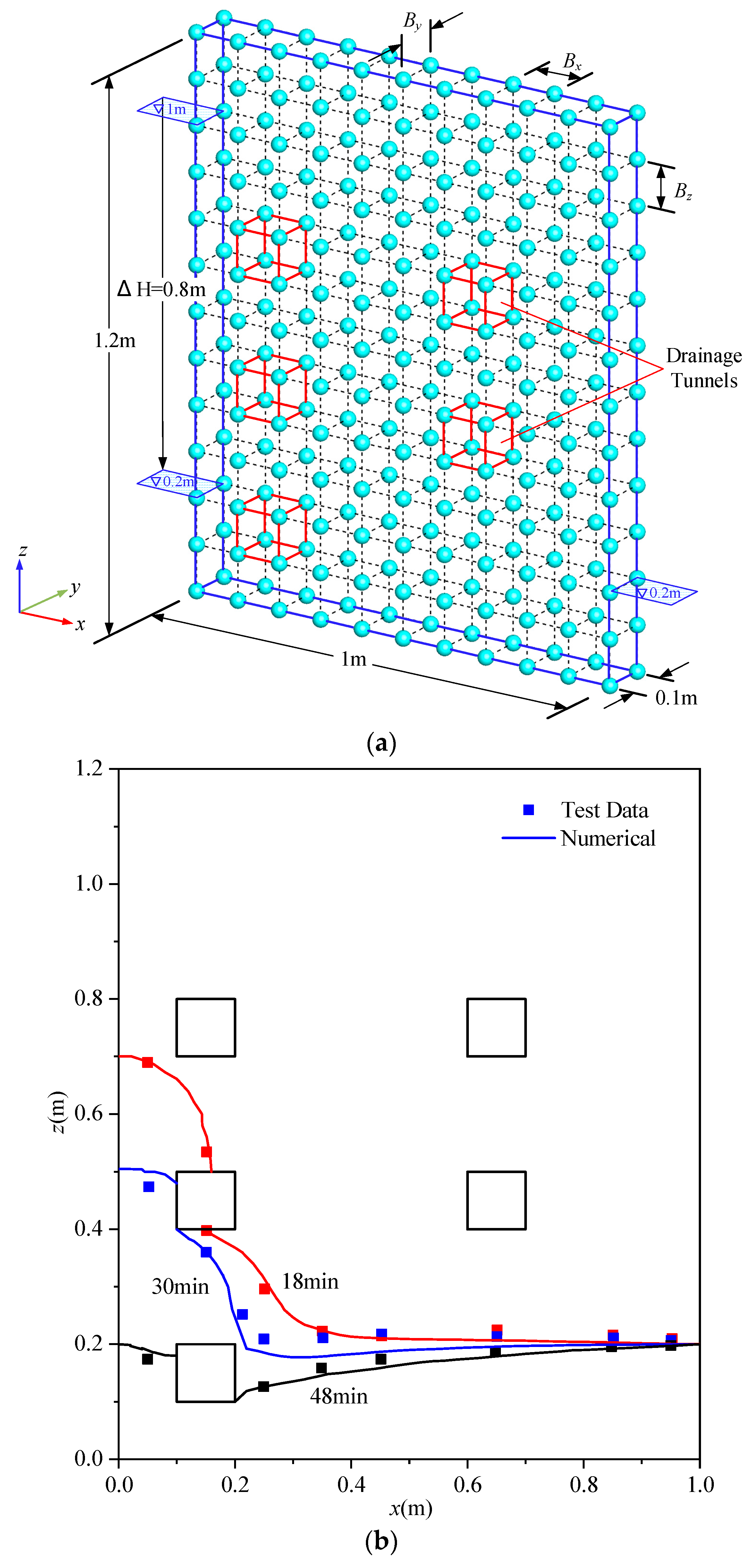
4.3. A Sand Flume
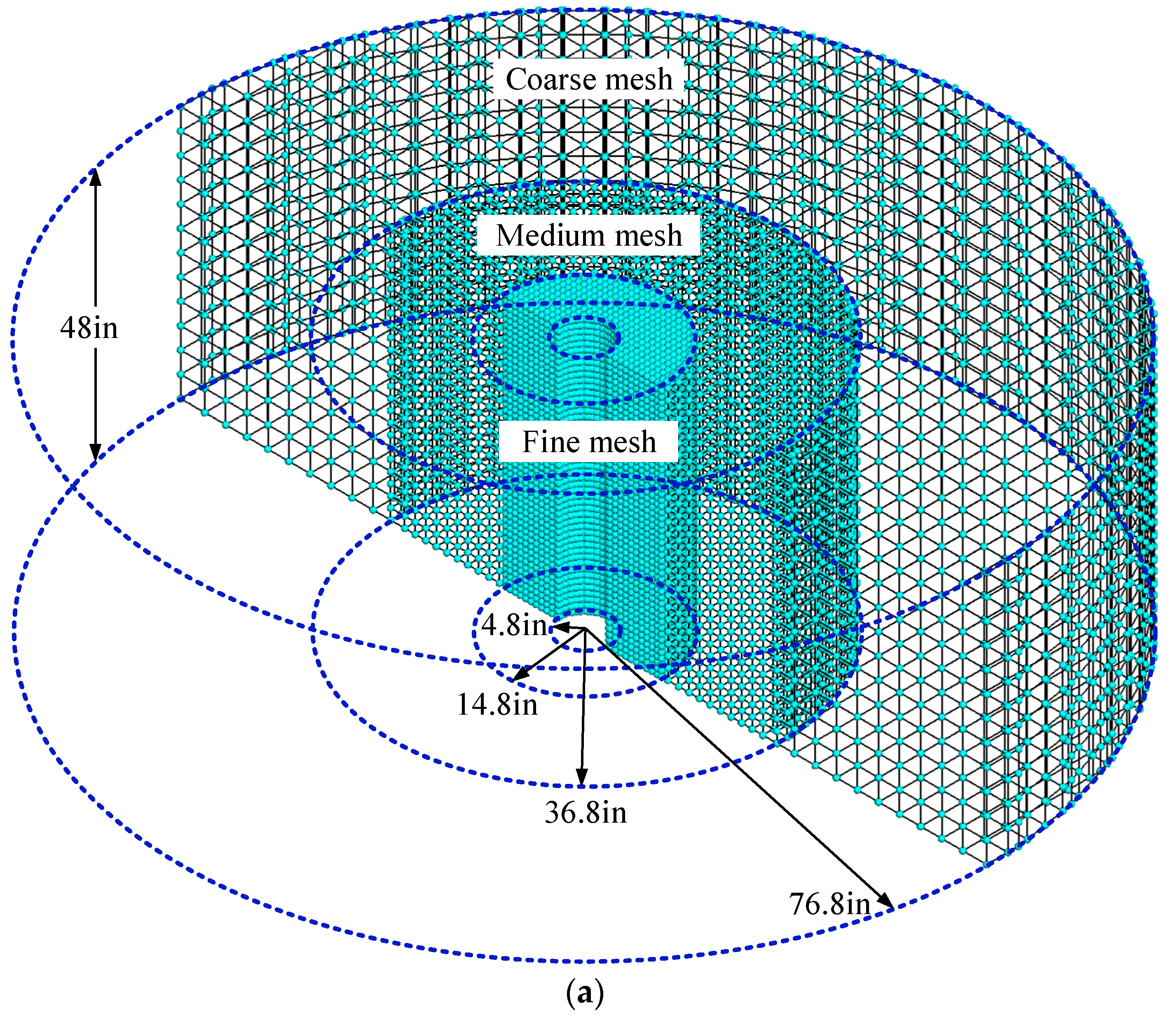
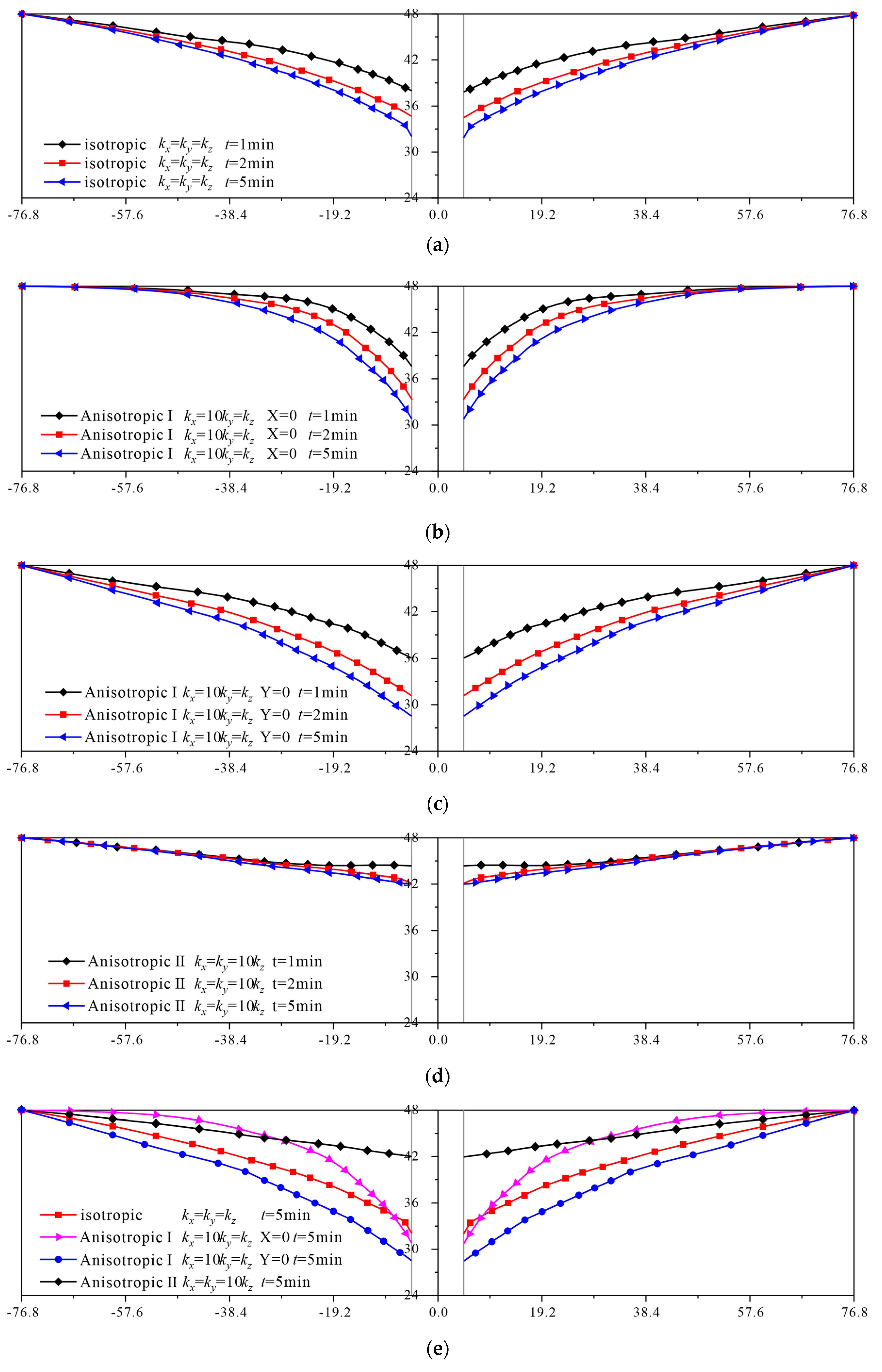
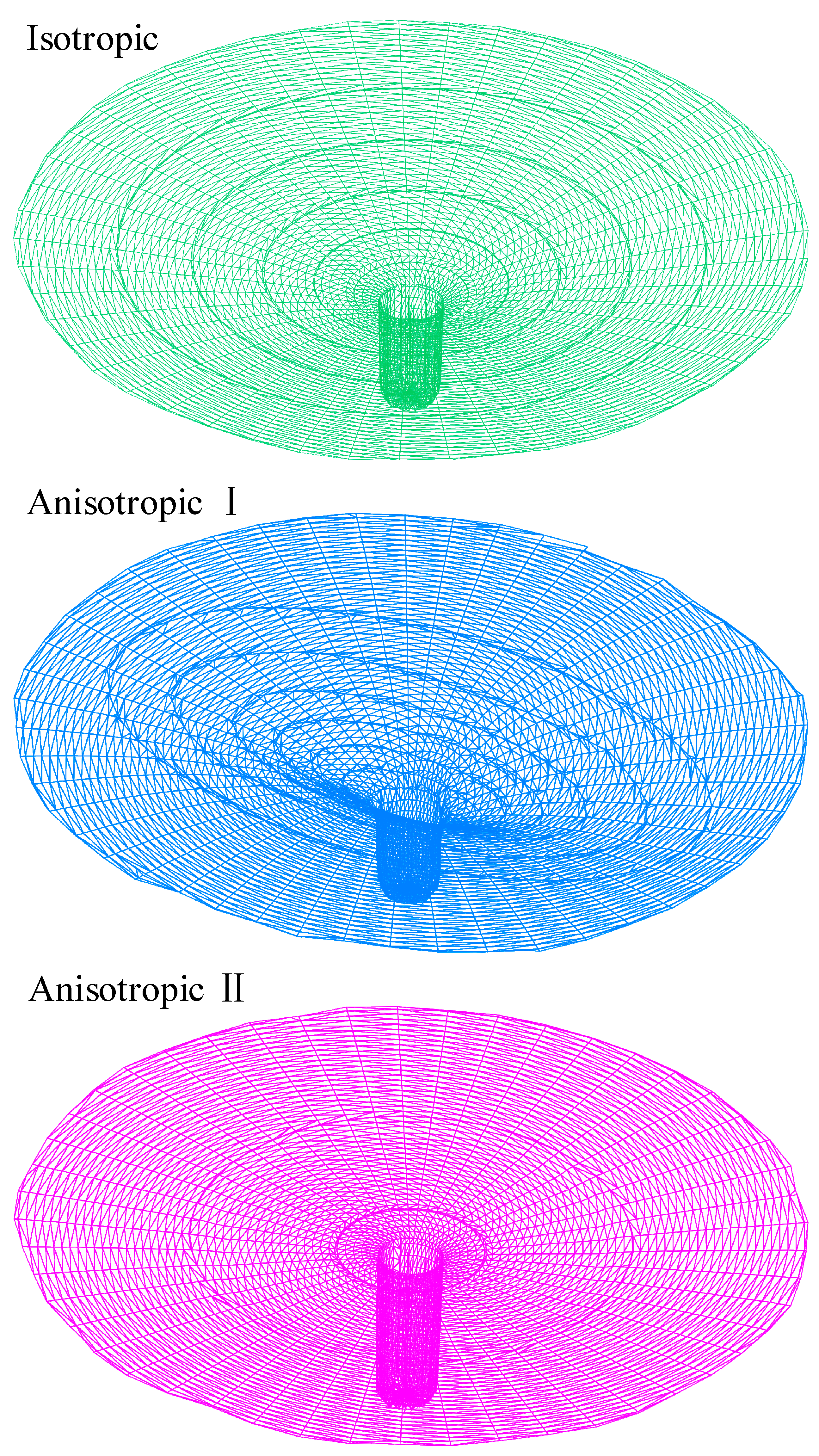
4.4. A 3D Well
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, C.; Chen, Y.; Jiang, Q.; Lu, W. A generalized multi-field coupling approach and its application to stability and deformation control of a high slope. J. Rock Mech. Geotech. Eng. 2011, 3, 193–206. [Google Scholar] [CrossRef]
- Jiang, Q.; Qi, Z.; Wei, W.; Zhou, C. Stability assessment of a high rock slope by strength reduction finite element method. Bull. Eng. Geol. Environ. 2015, 74, 1153–1162. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Xue, S.; Wang, R.; Xiao, M. Stability analysis of a typical landslide mass in the Three Gorges Reservoir under varying reservoir water levels. Environ. Earth Sci. 2020, 79, 42. [Google Scholar] [CrossRef]
- Ye, Z.; Fan, X.; Zhang, J.; Sheng, J.; Chen, Y.; Fan, Q.; Qin, H. Evaluation of connectivity characteristics on the permeability of two-dimensional fracture networks using geological entropy. Water Resour. Res. 2021, 57, e2020WR029289. [Google Scholar] [CrossRef]
- Ye, Z.; Yang, J.; Xiong, F.; Huang, S.; Cheng, A. Analytical relationships between normal stress and fluid flow for single fractures based on the two-part Hooke’s model. J. Hydrol. 2022, 608, 127633. [Google Scholar] [CrossRef]
- Asghar, Z.; Ali, N.; Waqas, M.; Nazeer, M.; Khan, W.A. Locomotion of an efficient biomechanical sperm through viscoelastic medium. Biomech. Model Mechanobiol. 2020, 19, 2271–2284. [Google Scholar] [CrossRef]
- Asghar, Z.; Ali, N.; Javid, K.; Waqas, M.; Dogonchi, A.S.; Khan, W.A. Bio-inspired propulsion of micro-swimmers within a passive cervix filled with couple stress mucus. Comput. Methods Programs Biomed. 2020, 189, 105313. [Google Scholar] [CrossRef]
- Javid, K.; Waqas, M.; Asghar, Z.; Ghaffari, A. A theoretical analysis of Biorheological fluid flowing through a complex wavy convergent channel under porosity and electro-magneto-hydrodynamics Effects. Comput. Methods Programs Biomed. 2020, 191, 105413. [Google Scholar] [CrossRef]
- Neuman, S.; Witherspoon, P. Analysis of nonsteady flow with a free surface using the finite element method. Water Resour. Res. 1971, 7, 611–623. [Google Scholar] [CrossRef]
- Desai, C.S.; Lightner, J.G.; Somasundaram, S. A numerical procedure for 3D transient free surface seepage. Adv. Water Resour. 1983, 6, 175–181. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, R.; Zhou, C.; Li, D.; Rong, G. A new parabolic variational inequality formulation of Signorini’s condition for non-steady seepage problems with complex seepage control systems. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1034–1058. [Google Scholar] [CrossRef]
- Rafiezadeh, K.; Ataie-Ashtiani, B. Transient free-surface seepage in 3D general anisotropic media by BEM. Eng. Anal. Bound. Elem. 2014, 46, 51–66. [Google Scholar] [CrossRef]
- Akhtar, S.; Hussain, Z.; Nadeem, S.; Najjar, I.R.; Sadoun, A.M. CFD analysis on blood flow inside a symmetric stenosed artery: Physiology of a coronary artery disease. Sci. Prog. 2023, 106, 00368504231180092. [Google Scholar] [CrossRef] [PubMed]
- Akhtar, S.; Hussain, Z.; Khan, Z.A.; Nadeem, S.; Alzabut, J. Endoscopic balloon dilation of a stenosed artery stenting via CFD tool open-foam: Physiology of angioplasty and stent placement. Chin. J. Phys. 2023, 85, 143–167. [Google Scholar] [CrossRef]
- Lin, S.; Cao, X.; Zheng, H.; Li, Y.; Li, W. An improved meshless numerical manifold method for simulating complex boundary seepage problems. Comput. Geotech. 2023, 155, 105211. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Xu, Z.H.; Ma, G.W.; Li, S.C. A graph-theoretic pipe network method for water flow simulation in a porous medium: GPNM. Int. J. Heat Fluid Flow 2014, 45, 81–97. [Google Scholar] [CrossRef]
- Afzali, S.H.; Monadjemi, P. Simulation of flow in porous media: An experimental and modeling study. J. Porous Media 2014, 17, 469–481. [Google Scholar] [CrossRef]
- Abareshi, M.; Hosseini, S.M.; Sani, A.A. Equivalent pipe network model for a coarse porous media and its application to two-dimensional analysis of flow through rockfill structures. J. Porous Media 2017, 20, 303–324. [Google Scholar] [CrossRef]
- Moosavian, N. Pipe network modelling for analysis of flow in porous media. Can. J. Civ. Eng. 2019, 46, 1151–1159. [Google Scholar] [CrossRef]
- Ye, Z.; Qin, H.; Chen, Y.; Fan, Q. An equivalent pipe network model for free surface flow in porous media. Appl. Math. Model. 2020, 87, 389–403. [Google Scholar] [CrossRef]
- Ye, Z.; Fan, Q.; Huang, S.; Cheng, A. A 1D line element model for transient free surface flow in porous media. Appl. Math. Comput. 2021, 392, 125747. [Google Scholar]
- Ren, F.; Ma, G.; Wang, Y.; Fan, L. Pipe network model for unconfined seepage analysis in fractured rock masses. Int. J. Rock Mech. Min. Sci. 2016, 88, 183–196. [Google Scholar] [CrossRef]
- Wei, W.; Jiang, Q.; Ye, Z.; Xiong, F.; Qin, H. Equivalent fracture network model for steady seepage problems with free surfaces. J. Hydrol. 2021, 603, 127156. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, C.; Zheng, H. A numerical solution to seepage problems with complex drainage systems. Comput. Geotech. 2008, 35, 383–393. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1937, 15, S32–S48. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Y.; Li, B.; Yu, L. Estimating permeability of porous media based on modified Hagen-Poiseuille flow in tortuous capillaries with variable lengths. Microfluid. Nanofluid. 2016, 20, 120. [Google Scholar] [CrossRef]
- Sheng, J.; Huang, T.; Ye, Z.; Hu, B.; Liu, Y.; Fan, Q. Evaluation of van Genuchten-Mualem model on the relative permeability for unsaturated flow in aperture-based fractures. J. Hydrol. 2019, 9, 315–324. [Google Scholar] [CrossRef]
- Oden, J.T.; Kikuchi, N. Theory of variational inequalities with applications to problems of flow through porous media. Int. J. Eng. Sci. 1980, 18, 1173–1284. [Google Scholar] [CrossRef]
- Zhang, W. Calculation of Unsteady Flow of Groundwater and Evaluation of Groundwater Resources; Science Press: Beijing, China, 1983. [Google Scholar]
- Hu, R.; Chen, Y.F.; Zhou, C.B.; Liu, H.H. A numerical formulation with unified unilateral boundary condition for unsaturated flow problems in porous media. Acta Geotech. 2017, 12, 277–291. [Google Scholar] [CrossRef]
- Hall, H. An investigation of steady flow toward a gravity well. Houille Blanche 1955, 10, 8–35. [Google Scholar] [CrossRef]
- Cooley, R. Some new procedures for numerical solution of variably saturated flow problems. Water Resour. Res. 1983, 19, 1271–1285. [Google Scholar] [CrossRef]
- Clement, T.; Wise, W.; Molz, F. A physically based, two-dimensional, finitedifference algorithm for modeling variably saturated flow. J. Hydrol. 1994, 161, 71–90. [Google Scholar] [CrossRef]
- Ward, A.L.; Zhang, Z.F. Effective Hydraulic Properties Determined from Transient Unsaturated Flow in Anisotropic Soils. Vadose Zone J. 2007, 6, 913–924. [Google Scholar] [CrossRef]
- Zhang, Z.F. Relationship between Anisotropy in Soil Hydraulic Conductivity and Saturation. Vadose Zone J. 2014, 13, 1–8. [Google Scholar] [CrossRef]
- Yuan, Q.; Yin, D.; Chen, Y. A simple line-element model for three-dimensional analysis of steady free surface flow through porous media. Water 2023, 15, 1030. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yuan, Q.; Ye, Z.; Peng, Z. A Dimension-Reduced Line Element Method for 3D Transient Free Surface Flow in Porous Media. Water 2023, 15, 3072. https://doi.org/10.3390/w15173072
Chen Y, Yuan Q, Ye Z, Peng Z. A Dimension-Reduced Line Element Method for 3D Transient Free Surface Flow in Porous Media. Water. 2023; 15(17):3072. https://doi.org/10.3390/w15173072
Chicago/Turabian StyleChen, Yuting, Qianfeng Yuan, Zuyang Ye, and Zonghuan Peng. 2023. "A Dimension-Reduced Line Element Method for 3D Transient Free Surface Flow in Porous Media" Water 15, no. 17: 3072. https://doi.org/10.3390/w15173072




