Impact of Hydraulic Variable Conditions in the Solution of Pumping Station Design through Sensitivity Analysis
Abstract
:1. Introduction
2. Methodology
2.1. Required Data
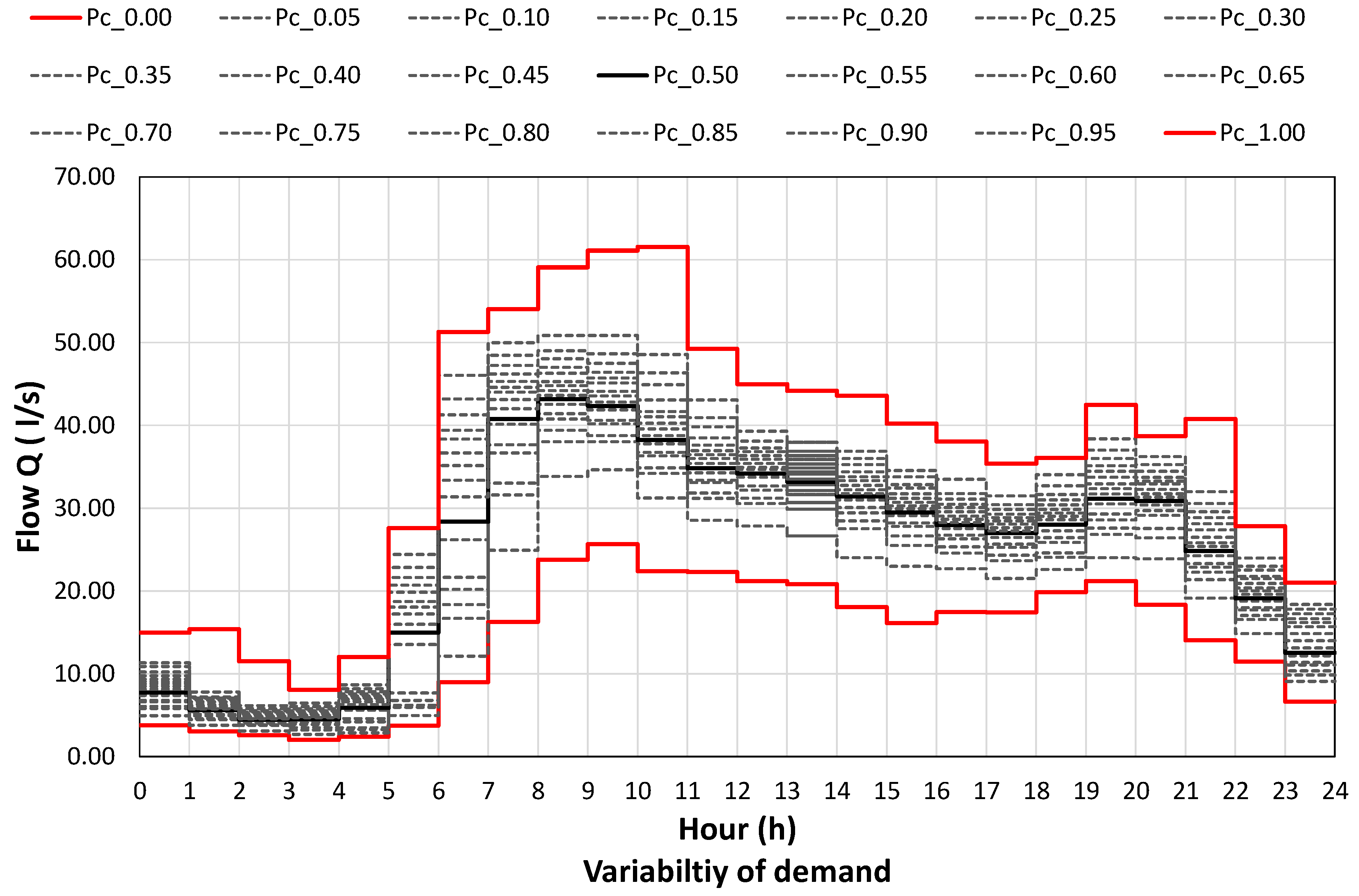
2.1.1. Demand Pattern
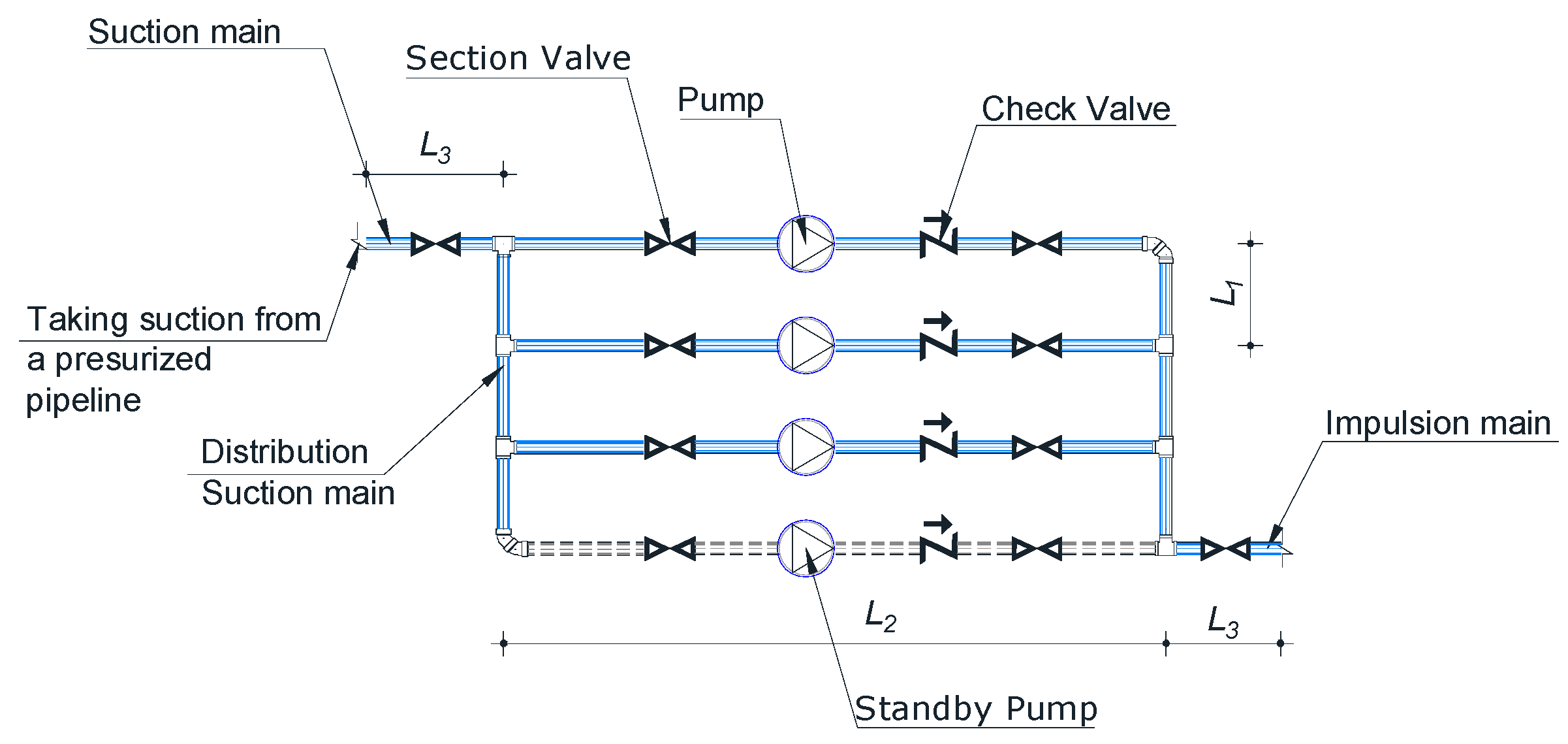
2.1.2. PS Layout
2.1.3. Setpoint Curve
2.1.4. Pump Model
2.2. Approches of PS Design
2.2.1. Classical Approach
2.2.2. Approach Based on the AHP
- Size: The size of the PS is a function of the number of pumps installed and the length of the pipelines in the station (see Figure 1). A higher score is assigned to this sub-criterion if the installation area is small. In this way, the highest size is assigned a score of 0 and the smallest size is assigned a score of 1. Equations (8) and (9) are used to evaluate the size of the PS.
- 2.
- Flexibility: The flexibility of the PS is associated with the number of pumps installed, i.e., the higher the number of pumps installed, the larger the flexibility. A higher score is assigned if the number of pumps installed is large. The potential solution with the highest number of pumps (b) is assigned a score of 1 and the solution with the smallest number of pumps is assigned a score of 0.
- 3.
- Complexity of control: This sub-criterion is related to the complexity of operation of the control system. The smaller the number of control elements in the system, the less complex the control system is considered to be. The complexity of operation is evaluated with a numeric score from 0 to 1 (see Table 2), corresponding to the highest and lowest levels of complexity, respectively, for the control systems. The scores are obtained from pairwise comparisons of the different control system strategies based on the AHP.
- 4.
- Investment cost: This includes the costs of the pumps, pipes, fittings, and control elements, as well as their installation. The investment costs are annualized considering the life cycle of the elements and the annual interest rate, and they are represented by Equation (10). A higher score is assigned to this sub-criterion if the investment cost is small. In this way, the solution with the lowest investment cost is assigned a score of 1 while 0 goes to the solution with the highest investment cost.
- 5.
- Operational cost: This sub-criterion is related to the yearly cost (EUR) of energy consumed for operation of the PS, and it is calculated using Equation (12).
- 6.
- Maintenance cost: This signifies the expenses associated with performing maintenance tasks within the PS in order to uphold its optimal state. The regularity and expenses of maintenance tasks for the PS components are derived from a database, which is used to calculate the yearly maintenance expenditures. This cost is represented by Equation (13). This sub-criterion receives a higher rating when the maintenance cost is low. In this way, the solution with the lowest maintenance cost has a score of 1, while the solution with the highest maintenance cost has a score of 0.
- 7.
- MEI: The minimum efficiency index (MEI) is a metric used to evaluate the energy efficiency of a pump. It is a standardized way to assess the efficiency of different pump models. A higher MEI value signifies better overall efficiency and suggests that the pump operates more efficiently across a range of flow rates. This index is established by EU regulation 547/2012 [28]. This regulation established an MEI of 0.7 as excellent, and an MEI below 0.4 as not acceptable. This sub-criterion is evaluated using a numeric scale from 0 to 1 with pairwise comparison of different MEI values based on the AHP. The obtained scores are detailed in Table 3:
- 8.
- CO2 emission: This signifies the volume of CO2 generated by the PS during its functioning. It is calculated by multiplying the energy utilized by the PS with the emission factor EF determined by El Ministerio de la Transformación Ecológica y el Reto Demográfico [29]. This sub-criterion is evaluated in terms of Kg of CO2 in a year.
- 9.
- Performance of regulation: This performance (ηRS) relates the required energy at the demand node of the network to the energy delivered by the PS and is defined as the ratio of the required head of the network (Hc) to the head pumping (H) (see Equation (15)). This sub-criterion receives a high score if the regulation’s performance is good. Consequently, a score of 1 is given to the solution exhibiting the best regulatory performance, whereas a score of 0 is attributed to the solution with the worst regulatory performance.
2.3. Sensitibity Analysis
3. Case Study
3.1. Results
3.2. Discussion
4. Conclusions
- The tolerance range for the variation in amortization interest rate was undefined because the amortization rate did not affect the selection of the ultimate solution in either PS design approach (see Table 8).
- Variations in the amortization interest rate impacted both pumping station design approaches in the same way. These mainly affected the investment costs and, consequently, the LCC in the final solutions of both approaches. However, the pump model of the ultimate solutions in both approaches remained unchanged.
- Variations in the mean flow (Qm) within the tolerance range (Qmin < Qm < Qmax) had an impact on operational costs, GHG emissions, and LCC, while maintaining the ultimate solution of the original case study in both approaches.
- Fluctuations in the average flow rate outside the tolerance range generated significant effects on the selection of the final solution in both design approaches. In the first approach, with the flow variation outside the tolerance range, the final solution was changed mainly in the pump model and its flow capacity, while in the second approach, the final solution was changed in the pump model and its flow capacity, the number of pumps, and the control strategy.
- Fluctuations in static head (ΔH) and losses (R) had a greater impact on the first design approach compared to the second approach.
- Variations in static head (ΔH) and losses (R) within the tolerance range in the setpoint curve primarily impacted operational costs, greenhouse gas (GHG) emissions, and the LCC of the ultimate solutions in both design approaches. However, the first approach, which considered only LCC, was more susceptible to changes in losses, while the second approach, incorporating multi-criteria analysis including technical, economic, and environmental factors, was more robust facing variations in the variables of static head (ΔH) and losses (R).
- On the other hand, when the variations of the static head (ΔH) and losses (R) were outside the tolerance range, the main impact on the selected solutions in both approaches was a change in the pump model, with different flow and pumping head capacity, from that of the ultimate solution in the original case study.
- The sensitivity analysis revealed important differences between the two design approaches regarding the electric tariff (TE), as can be observed in Table 13. The tolerance range of the electric tariff (TE) of the first approach had a defined width, whereas the tolerance range (TE) in the second approach was undefined because variation in this variable did not affect its ultimate solution.
- The solution obtained in the first approach was affected by significant variations in the electric tariff, as they were considered in the present work. In contrast, the solution obtained in the second approach remained unaffected by changes in the electric tariff, even when the electric tariff (TE) had extreme variations.
- Changes in the electric tariff primarily impacted operational costs, but they had a significant impact only on the ultimate solution of the first approach, which relied solely on LCC. The second approach, considering technical, economic, and environmental aspects, based on the AHP, resulted in a more robust solution that remained unchanged despite variations in the annual electricity tariff (TE).
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Leiby, V.M.; Burke, M.E. Energy Efficiency Best Practices for North American Drinking Water Utilities; WRF: Albany, NY, USA, 2011. [Google Scholar]
- Luna, T.; Ribau, J.; Figueiredo, D.; Alves, R. Improving energy efficiency in water supply systems with pump scheduling optimization. J. Clean. Prod. 2019, 213, 342–356. [Google Scholar] [CrossRef]
- Makaremi, Y.; Haghighi, A.; Ghafouri, H.R. Optimization of Pump Scheduling Program in Water Supply Systems Using a Self-Adaptive NSGA-II; a Review of Theory to Real Application. Water Resour. Manag. 2017, 31, 1283–1304. [Google Scholar] [CrossRef]
- Carpitella, S.; Brentan, B.; Montalvo, I.; Izquierdo, J.; Certa, A. Multi-criteria analysis applied to multi-objective optimal pump scheduling in water systems. Water Sci. Technol. Water Supply 2019, 19, 2338–2346. [Google Scholar] [CrossRef]
- Martin-Candilejo, A.; Martin-Carrasco, F.J.; Santillán, D. How to select the number of active pumps during the operation of a pumping station: The convex hyperbola charts. Water 2021, 13, 1474. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R. Accounting for Greenhouse Gas Emissions in Multiobjective Genetic Algorithm Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 146–155. [Google Scholar] [CrossRef]
- Torregrossa, D.; Capitanescu, F. Optimization models to save energy and enlarge the operational life of water pumping systems. J. Clean. Prod. 2019, 213, 89–98. [Google Scholar] [CrossRef]
- Alandi, P.P.; Pérez, P.C.; Álvarez, J.F.O.; Hidalgo, M.M.; Martín-Benito, J.M.T. Pumping Selection and Regulation for Water-Distribution Networks. J. Irrig. Drain. Eng. 2005, 131, 273–281. [Google Scholar] [CrossRef]
- Lamaddalena, N.; Khila, S. Efficiency-driven pumping station regulation in on-demand irrigation systems. Irrig. Sci. 2013, 31, 395–410. [Google Scholar] [CrossRef]
- Karpenko, M.; Stosiak, M.; Šukevičius, Š.; Skačkauskas, P.; Urbanowicz, K.; Deptuła, A. Hydrodynamic Processes in Angular Fitting Connections of a Transport Machine’s Hydraulic Drive. Machines 2023, 11, 355. [Google Scholar] [CrossRef]
- Olszewski, P. Genetic optimization and experimental verification of complex parallel pumping station with centrifugal pumps. Appl. Energy 2016, 178, 527–539. [Google Scholar] [CrossRef]
- Cimorelli, L.; Covelli, C.; Molino, B.; Pianese, D. Optimal regulation of pumping station in water distribution networks using constant and variable speed pumps: A technical and economical comparison. Energies 2020, 13, 2530. [Google Scholar] [CrossRef]
- Briceño-León, C.X.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Mora-Melia, D.; Fuertes-Miquel, V.S. Use of fixed and variable speed pumps in water distribution networks with different control strategies. Water 2021, 13, 479. [Google Scholar] [CrossRef]
- Deptuła, A.; Augustynowicz, A.; Stosiak, M.; Towarnicki, K.; Karpenko, M. The Concept of Using an Expert System and Multi-Valued Logic Trees to Assess the Energy Consumption of an Electric Car in Selected Driving Cycles. Energies 2022, 15, 4631. [Google Scholar] [CrossRef]
- Saaty, T.L. Analytic Hierarchy Process; McGraw Hil: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Aşchilean, I.; Badea, G.; Giurca, I.; Naghiu, G.S.; Iloaie, F.G. Choosing the optimal technology to rehabilitate the pipes in water distribution systems using the AHP method. Energy Procedia 2017, 112, 19–26. [Google Scholar] [CrossRef]
- Kurbatova, A.; Abu-Qdais, H.A. Using multi-criteria decision analysis to select waste to energy technology for a mega city: The case of Moscow. Sustainability 2020, 12, 9828. [Google Scholar] [CrossRef]
- Briceño-León, C.X.; Sanchez-Ferrer, D.S.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Mora-Melia, D. Methodology for pumping station design based on analytic hierarchy process (AHP). Water 2021, 13, 2886. [Google Scholar] [CrossRef]
- Briceño-León, C.X.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Creaco, E. Integrating Demand Variability and Technical, Environmental, and Economic Criteria in Design of Pumping Stations Serving Closed Distribution Networks. J. Water Resour. Plan. Manag. 2023, 149, 04023002. [Google Scholar] [CrossRef]
- Lee, C.; Tien, I. Sensitivity analysis of interdependency parameters using probabilistic system models. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering, Brussels, Belgium, 26–30 May 2019; pp. 1–13. [Google Scholar]
- Morosini, A.F.; Haghshenas, S.S.; Haghshenas, S.S.; Choi, D.Y.; Geem, Z.W. Sensitivity analysis for performance evaluation of a real water distribution system by a pressure driven analysis approach and artificial intelligence method. Water 2021, 13, 1116. [Google Scholar] [CrossRef]
- Jensen, H.; Jerez, D. A Stochastic Framework for Reliability and Sensitivity Analysis of Large Scale Water Distribution Networks. Reliab. Eng. Syst. Saf. 2018, 176, 80–92. [Google Scholar] [CrossRef]
- Walski, T.; Creaco, E. Selection of pumping configuration for closed water distribution systems. J. Water Resour. Plan. Manag. 2016, 142, 04016009. [Google Scholar] [CrossRef]
- Sanks, R.L. Pumping Station Design, 2nd ed.; Butterworth-Heinemann: Woburn, MA, USA, 1998. [Google Scholar]
- Coelho, B.; Andrade-Campos, A.G. A new approach for the prediction of speed-adjusted pump efficiency curves. J. Hydraul. Res. 2016, 54, 586–593. [Google Scholar] [CrossRef]
- Hydraulic Institute. Pump Life Cycle Costs: A Guide to LCC Analysis for Pumping Systems, 2nd ed.; Office of Energy Efficiency and Renewable Energy (EERE), Energy Efficiency Office, Advanced Manufacturing Office: Washington, DC, USA, 2001.
- The European Union Comission. Commission Regulation (EU) N0 547/2012. Off. J. Eur. Union 2012, 4, 178–183. [Google Scholar]
- Oficina Española del Cambio Climático (OECC). Factores de Emisión Registro de Huella de Carbono, Compensacion y Proyectos de Absorción de Dióxido de Carbono; Ministerio para la Transición Ecológica y el Reto Demográfico España: Madrid, Spain, 2022.



| Saaty’s Scale | Proposed Scale | ||||
|---|---|---|---|---|---|
| NS | Ci | Cj | Ci | Cj | NS |
| 1 | 50.00% | 50.00% | 50.00% | 50.00% | 1.00 |
| 2 | 67.67% | 33.33% | 55.00% | 45.00% | 1.22 |
| 3 | 75.00% | 25.00% | 60.00% | 40.00% | 1.50 |
| 4 | 80.00% | 20.00% | 65.00% | 35.00% | 1.86 |
| 5 | 83.33% | 16.67% | 70.00% | 30.00% | 2.33 |
| 6 | 85.71% | 14.29% | 75.00% | 25.00% | 3.00 |
| 7 | 87.50% | 12.50% | 80.00% | 20.00% | 4.00 |
| 8 | 88.89% | 11.11% | 85.00% | 15.00% | 5.67 |
| 9 | 90.00% | 10.00% | 90.00% | 10.00% | 9.00 |
| Control System Configuration | Complexity Level | Numeric Score |
|---|---|---|
| 1 | 1.00 |
| 2 | 0.57 |
| 3 | 0.32 |
| 4 | 0.15 |
| 5 | 0.07 |
| MEI Index | Numeric Score |
|---|---|
| 0.1 | 0.05 |
| 0.2 | 0.07 |
| 0.3 | 0.12 |
| 0.4 | 0.27 |
| 0.5 | 0.40 |
| 0.6 | 0.61 |
| 0.7 | 1.00 |
| Data | Qm (L/s) | ΔH (m) | R | c |
| 25.00 | 29.50 | 0.0109 | 1.95 | |
| Approaches | First Approach | Second Approach | |
|---|---|---|---|
| Pump Characteristics | Pump Model | 32 | 64 |
| Q0 (L/s) | 22.71 | 16.97 | |
| H0 (m) | 61.06 | 61.52 | |
| ηmax (%) | 61% | 83% | |
| Tec. Aspects | C1 (m2) | 151.20 | 140.80 |
| C2 | 0 FSP–3 VSP | 1 FSP–3 VSP | |
| C3 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 5355.78 | 12,778.24 |
| C5 (EUR/year) | 13,079.49 | 9460.92 | |
| C6 (EUR/year) | 1193.21 | 1462.31 | |
| Env. Aspects | C7 | 0.10 | 0.70 |
| C8 Kg CO2 | 57,041.02 | 41,208.60 | |
| C9 (%) | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 19,628.48 | 23,701.47 | |
| Approaches | Ti + 50% = 4.5% | Ti − 50% = 1.5% | Ti + 50% = 4.5% | Ti − 50% = 1.5% | |
|---|---|---|---|---|---|
| Approach 1 | Approach 1 | Approach 2 | Approach 2 | ||
| Pump Characteristics | PumpModel | 32 | 32 | 64 | 64 |
| Q0 (L/s) | 22.71 | 22.71 | 16.97 | 16.97 | |
| H0 (m) | 61.06 | 61.06 | 61.52 | 61.52 | |
| ηmax (%) | 61% | 61% | 83% | 83% | |
| Tec. Aspects | C1 (m2) | 151.20 | 151.20 | 140.80 | 140.80 |
| C2 | 0 FSP–3 VSP | 0 FSP–3 VSP | 1 FSP–3 VSP | 1 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 5876.52 | 4866.67 | 13,928.41 | 11,688.22 |
| C5 (EUR/year) | 13,079.49 | 13,079.49 | 9460.92 | 9460.92 | |
| C6 (EUR/year) | 1193.21 | 1137.46 | 1462.31 | 1462.31 | |
| Env. Aspects | C7 | 0.10 | 0.10 | 0.70 | 0.70 |
| C8 Kg CO2 | 57,041.02 | 57,041.02 | 41,208.60 | 41,208.60 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 20,197.24 | 19,187.39 | 24,851.63 | 22,611.45 | |
| Approaches | Qm_max = Qm + 1% (25.25 L/s) | Qm + 2% (25.5 L/s) | Qm_max = Qm − 3% (24.25 L/s) | Qm − 4% (24.0 L/s) | |
|---|---|---|---|---|---|
| Approach 1 | Approach 1 | Approach 1 | Approach 1 | ||
| Pump Characteristics | Pump Model | 32 | 33 | 32 | 31 |
| Q0 (L/s) | 22.71 | 24.32 | 22.71 | 19.50 | |
| H0 (m) | 61.06 | 78.73 | 61.06 | 50.43 | |
| ηmax (%) | 61% | 61% | 61% | 70% | |
| Tec. Aspects | C1 (m2) | 151.20 | 151.20 | 151.20 | 158.40 |
| C2 | 0 FSP–3 VSP | 0 FSP–3 VSP | 1 FSP–2 VSP | 2 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 5355.78 | 6604.70 | 5152.23 | 6328.61 |
| C5 (EUR/year) | 13,258.22 | 13,320.51 | 12,552.96 | 10,594.24 | |
| C6 (EUR/year) | 1193.21 | 1193.21 | 1170.78 | 1739.98 | |
| Env. Aspects | C7 | 0.10 | 0.11 | 0.10 | 0.10 |
| C8 Kg CO2 | 57,814.90 | 58,075.52 | 54,760.90 | 46,194.04 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 19,807.21 | 21,118.41 | 18,875.97 | 18,662.84 | |
| Approaches | Qm_max = Qm + 2% (25.50 L/s) | Qm + 3% (25.75 L/s) | Qm_min = Qm − 2% (24.50 L/s) | Qm − 3% (24.25 L/s) | |
|---|---|---|---|---|---|
| Approach 2 | Approach 2 | Approach 2 | Approach 2 | ||
| Pump Characteristics | Pump Model | 64 | 33 | 64 | 44 |
| Q0 (L/s) | 16.97 | 24.32 | 16.97 | 19.50 | |
| H0 (m) | 61.52 | 78.73 | 61.52 | 50.43 | |
| ηmax (%) | 83% | 61% | 83% | 70% | |
| Tec. Aspects | C1 (m2) | 140.80 | 140.80 | 140.80 | 144.00 |
| C2 | 1 FSP–3 VSP | 0 FSP–3 VSP | 1 FSP–3 VSP | 6 FSP–0 VSP | |
| C3 | 5 | 5 | 5 | 3 | |
| Eco. Aspects | C4 (EUR/year) | 12,778.24 | 8376.14 | 12,778.24 | 9542.55 |
| C5 (EUR/year) | 9732.85 | 13,501.42 | 9193.33 | 14,782.81 | |
| C6 (EUR/year) | 1462.31 | 1210.36 | 1462.31 | 1918.87 | |
| Env. Aspects | C7 | 0.70 | 0.12 | 0.70 | 0.70 |
| C8 Kg CO2 | 42,387.25 | 58,858.99 | 40,048.68 | 64,669.36 | |
| C9 (%) | 100% | 100% | 100% | 71% | |
| Life Cycle Cost (EUR/year) | 23,973.41 | 23,087.92 | 23,433.88 | 26,244.24 | |
| Approaches | ΔHmax = ΔH + 5% (30.98 m) | ΔH + 6% (31.27 m) | ΔHmin = ΔH − 8% (27.14 m) | ΔH − 9% (26.85 m) | |
|---|---|---|---|---|---|
| Approach 1 | Approach 1 | Approach 1 | Approach 1 | ||
| Pump Characteristics | Pump Model | 32 | 33 | 32 | 31 |
| Q0 (L/s) | 22.71 | 24.32 | 22.71 | 19.50 | |
| H0 (m) | 61.06 | 78.73 | 61.06 | 50.43 | |
| ηmax (%) | 61% | 61% | 61% | 70% | |
| Tec. Aspects | C1 (m2) | 151.20 | 151.20 | 151.20 | 158.40 |
| C2 | 0 FSP–3 VSP | 0 FSP–3 VSP | 1 FSP–2 VSP | 2 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 5355.78 | 6604.70 | 5355.78 | 6328.61 |
| C5 (EUR/year) | 13,549.89 | 13,494.90 | 12,334.95 | 10,471.42 | |
| C6 (EUR/year) | 1193.21 | 1193.21 | 1193.21 | 1739.98 | |
| Env. Aspects | C7 | 0.10 | 0.11 | 0.10 | 0.10 |
| C8 Kg CO2 | 59,104.26 | 58,860.22 | 53,775.66 | 45,625.47 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 20,098.88 | 21,292.80 | 18,883.94 | 18,540.02 | |
| Approaches | ΔHmax = ΔH + 7% (31.57 m) | ΔH + 8% (31.27 m) | ΔHmin = ΔH − 21% (23.31 m) | ΔH − 22% (23.01 m) | |
|---|---|---|---|---|---|
| Approach 2 | Approach 2 | Approach 2 | Approach 2 | ||
| Pump Characteristics | Pump Model | 64 | 32 | 64 | 31 |
| Q0 (L/s) | 16.97 | 22.71 | 16.97 | 19.35 | |
| H0 (m) | 61.52 | 61.06 | 61.52 | 50.43 | |
| ηmax (%) | 83% | 61% | 83% | 70% | |
| Tec. Aspects | C1 (m2) | 140.80 | 140.80 | 140.80 | 140.80 |
| C2 | 1 FSP–3 VSP | 1 FSP–3 VSP | 1 FSP–3 VSP | 1 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 12,778.24 | 6261.77 | 12,778.24 | 5447.80 |
| C5 (EUR/year) | 9922.35 | 13,839.98 | 8092.24 | 9421.28 | |
| C6 (EUR/year) | 1462.31 | 1462.31 | 1462.31 | 1462.31 | |
| Env. Aspects | C7 | 0.70 | 0.10 | 0.70 | 0.19 |
| C8 Kg CO2 | 43,226.87 | 60,376.79 | 35,223.68 | 41,029.30 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 24,162.90 | 21,564.06 | 22,814.32 | 16,331.39 | |
| Approaches | Rmax = R + 5% (0.0114) | R + 6% (0.0116) | Rmin = R − 7% (0.0101) | R − 8% (0.0100) | |
|---|---|---|---|---|---|
| Approach 1 | Approach 1 | Approach 1 | Approach 1 | ||
| Pump Characteristics | Pump Model | 32 | 33 | 32 | 31 |
| Q0 (L/s) | 22.71 | 24.32 | 22.71 | 19.35 | |
| H0 (m) | 61.06 | 78.73 | 61.06 | 50.43 | |
| ηmax (%) | 61% | 61% | 61% | 70% | |
| Tec. Aspects | C1 (m2) | 151.20 | 151.20 | 151.20 | 158.40 |
| C2 | 0 FSP–3 VSP | 0 FSP–3 VSP | 1 FSP–2 VSP | 2 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 5355.78 | 6604.70 | 5355.78 | 6328.61 |
| C5 (EUR/year) | 13,233.72 | 13,139.54 | 12,864.50 | 10,990.73 | |
| C6 (EUR/year) | 1193.21 | 1193.21 | 1193.21 | 1739.98 | |
| Env. Aspects | C7 | 0.10 | 0.11 | 0.10 | 0.10 |
| C8 Kg CO2 | 57,707.91 | 57,290.64 | 56,111.42 | 47,912.66 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 19,782.71 | 20,937.44 | 19,413.48 | 19,059.32 | |
| Approaches | Rmax = R + 6% (0.0116) | R + 7% (0.0117) | Rmin = R − 19% (0.0088) | R − 20% (0.0087) | |
|---|---|---|---|---|---|
| Approach 2 | Approach 2 | Approach 2 | Approach 2 | ||
| Pump Characteristics | Pump Model | 64 | 32 | 64 | 31 |
| Q0 (L/s) | 16.97 | 22.71 | 16.97 | 19.35 | |
| H0 (m) | 61.52 | 61.06 | 61.52 | 50.43 | |
| ηmax (%) | 83% | 61% | 83% | 70% | |
| Tec. Aspects | C1 (m2) | 140.80 | 140.80 | 140.80 | 140.80 |
| C2 | 1 FSP–3 VSP | 1 FSP–3 VSP | 1 FSP–3 VSP | 1 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 12,778.24 | 6261.77 | 12,778.24 | 5447.80 |
| C5 (EUR/year) | 9595.57 | 13,301.39 | 9035.25 | 10,640.50 | |
| C6 (EUR/year) | 1462.31 | 1462.31 | 1462.31 | 1462.31 | |
| Env. Aspects | C7 | 0.70 | 0.10 | 0.70 | 0.19 |
| C8 Kg CO2 | 41,790.42 | 58,000.73 | 39,369.32 | 46,400.27 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 23,836.13 | 21,025.46 | 23,757.32 | 17,550.61 | |
| Approaches | TEmax = EUR 0.17 | TEmin = EUR 0.034 | TEmax = EUR 0.17 | TEmin = EUR 0.034 | |
|---|---|---|---|---|---|
| Approach 1 | Approach 1 | Approach 2 | Approach 2 | ||
| Pump Characteristics | Pump Model | 31 | 32 | 64 | 64 |
| Q0 (L/s) | 19.35 | 22.71 | 16.97 | 16.97 | |
| H0 (m) | 50.43 | 61.06 | 61.52 | 61.52 | |
| ηmax (%) | 70% | 61% | 83% | 83% | |
| Tec. Aspects | C1 (m2) | 140.80 | 151.20 | 140.80 | 140.80 |
| C2 | 1 FSP–3 VSP | 0 FSP–3 VSP | 1 FSP–3 VSP | 1 FSP–3 VSP | |
| C3 | 5 | 5 | 5 | 5 | |
| Eco. Aspects | C4 (EUR/year) | 12,778.24 | 5355.78 | 12,778.24 | 12,778.24 |
| C5 (EUR/year) | 3875.56 | 5357.86 | 19,377.78 | 9460.92 | |
| C6 (EUR/year) | 1462.31 | 1193.21 | 1462.31 | 1397.98 | |
| Env. Aspects | C7 | 0.70 | 0.10 | 0.70 | 0.70 |
| C8 Kg CO2 | 41,208.60 | 57,041.02 | 41,208.60 | 41,208.60 | |
| C9 (%) | 100% | 100% | 100% | 100% | |
| Life Cycle Cost (EUR/year) | 11,906.85 | 33,233.21 | 33,618.33 | 18,116.11 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Briceño-León, C.X.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Creaco, E. Impact of Hydraulic Variable Conditions in the Solution of Pumping Station Design through Sensitivity Analysis. Water 2023, 15, 3067. https://doi.org/10.3390/w15173067
Briceño-León CX, Iglesias-Rey PL, Martinez-Solano FJ, Creaco E. Impact of Hydraulic Variable Conditions in the Solution of Pumping Station Design through Sensitivity Analysis. Water. 2023; 15(17):3067. https://doi.org/10.3390/w15173067
Chicago/Turabian StyleBriceño-León, Christian X., Pedro L. Iglesias-Rey, F. Javier Martinez-Solano, and Enrico Creaco. 2023. "Impact of Hydraulic Variable Conditions in the Solution of Pumping Station Design through Sensitivity Analysis" Water 15, no. 17: 3067. https://doi.org/10.3390/w15173067







