Estimating Typhoon-Induced Maximum Flood for Spillway Safety Assessment—Case Studies in Taiwan
Abstract
:1. Introduction
2. Storm Transposition Method for PMP Estimation
2.1. Structure of Storm Transposition Method
2.2. Procedure for PMP Estimation Using Storm Transposition Method
- (1)
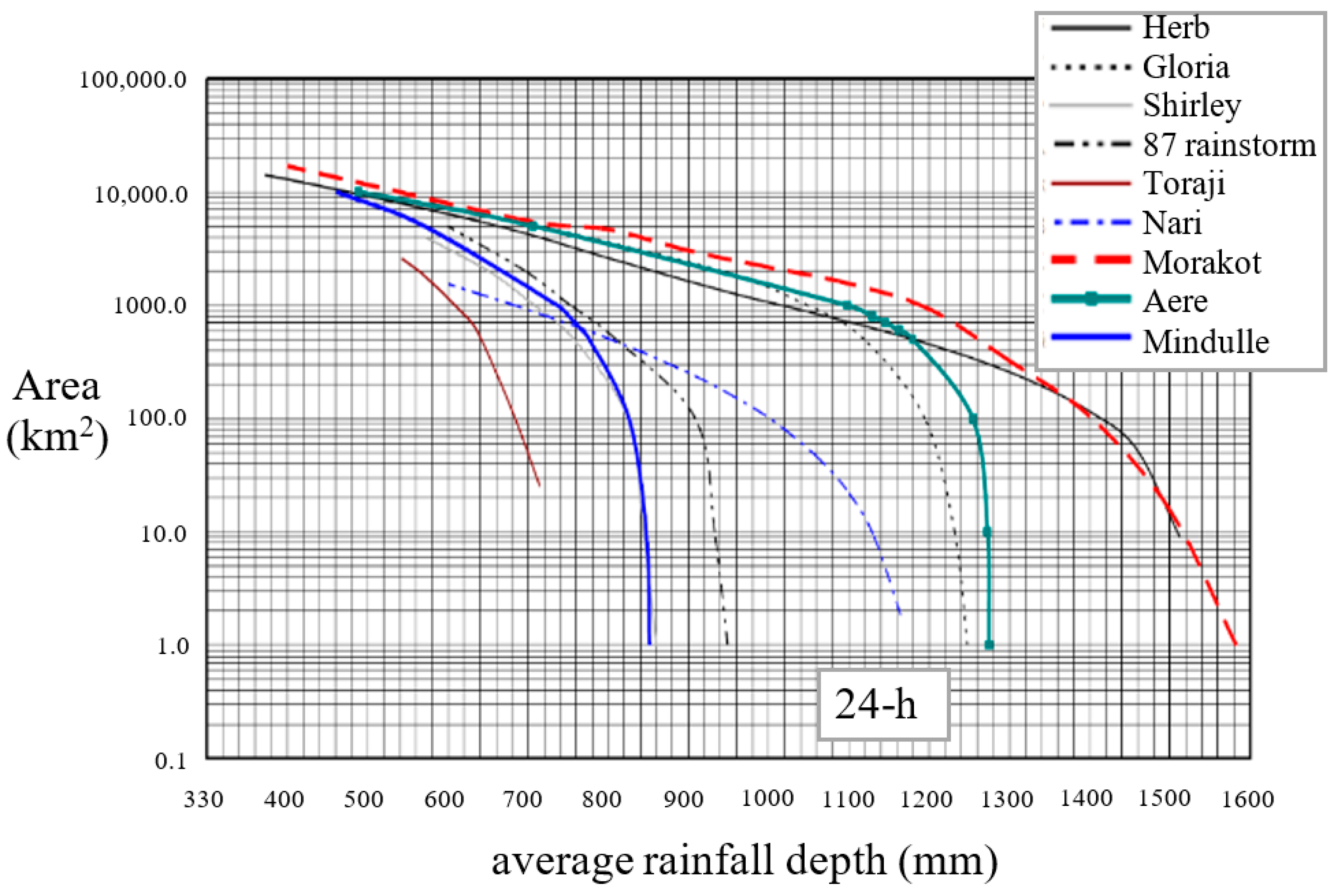
- Collect historical severe typhoon rainstorm records to develop rainfall depth-area-duration (DAD) curves for each typhoon event (as the examples shown in Figure 3);
- (2)
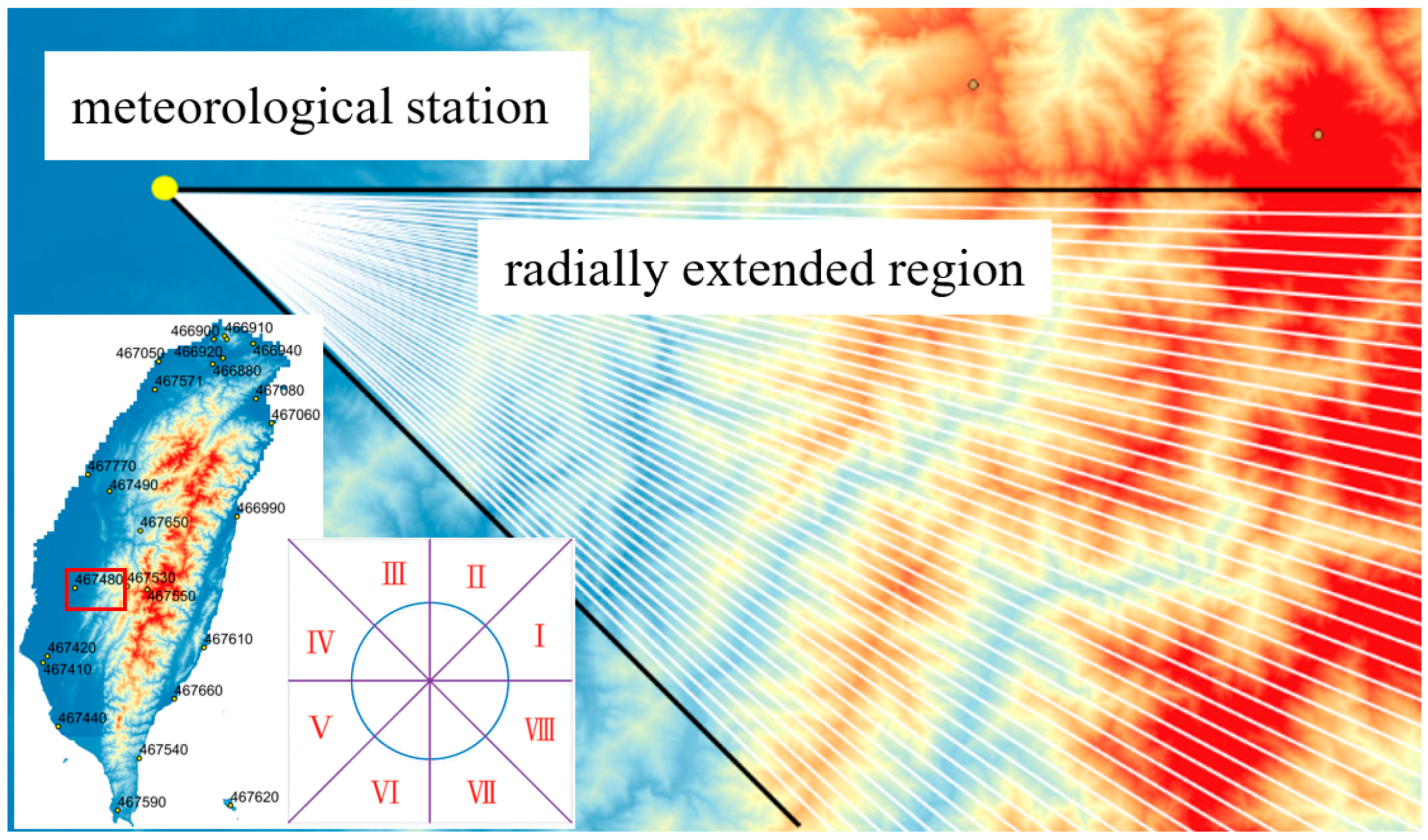
- Determine the inflow barrier height (Z2) according to the topography of the target watershed. The inflow barrier height can be assigned as the elevation of the watershed outlet (as shown in Figure 1).
- (3)
- Choose a meteorological station near the target site and find the 24-h highest dewpoint temperature (TH2) in the historical records. Using TH2 and the elevation of the meteorological station (H2) to determine the sea-level dewpoint temperature (T2).
- (4)
- According to the sea-level dewpoint temperature (T2) to estimate the precipitable water, W2A, in the atmosphere column between 1000 mb and 200 mb, and the precipitable water, W2B, between 1000 mb and the elevation at the watershed outlet (Z2). Then the precipitable water in the target watershed can be estimated by W2 = W2A − W2B;
- (5)
- Select a meteorological station near the ith typhoon rainstorm center. Determine the inflow barrier height (Z1)i of the event according to the typhoon track and the surrounding topography of the meteorological station;
- (6)
- Check the 24-h highest dewpoint temperature (TH1)i in the ith typhoon event. Using (TH1)i and the elevation of the meteorological station (H1) to determine the sea-level dewpoint temperature (T1)i.
- (7)
- According to the sea-level dewpoint temperature (T1)i, calculate the precipitable water (W1A)i in the atmosphere column between 1000 mb and 200 mb and calculate the precipitable water of the atmosphere column from 1000 mb to the barrier height (Z1)i in the ith typhoon event. Then the precipitable water at the meteorological station is ;
- (8)
- The moisture adjustment ratio of the ith typhoon event is ;
- (9)
- Determine the T-hr rainfall depth from the DAD curve in the ith typhoon event corresponding to the area of the target watershed, and then the T-hr precipitable water at the target site can be estimated by ;
- (10)
- Repeat Steps (5) to (9) to calculate the precipitable water of different durations in the ith typhoon event;
- (11)
- Repeat Steps (5) to (10) to calculate the precipitable water for all the typhoon events;
- (12)
- Plot the precipitable water of different durations for all the selected severe typhoon events and develop an envelope curve at the target site (as the examples shown in Figure 4).
- (13)
- According to the envelope curve, the increment of the cumulated rainfall depth at each hour can be calculated. A design hyetograph can be developed by applying the alternative block method [19] using the calculated increments.
- (14)
- The PMP rainstorm hyetograph can be substituted into a rainfall-runoff model for runoff routing for the PMF estimation at the target watershed.
3. Typhoon Rainstorm Model for PMP Estimation
3.1. Circulation Rainfall
3.2. Orographic Rainfall
3.3. Design Typhoon Rainstorm
3.4. Procedure for PMP Estimation Using Typhoon Rainstorm Method
- (1)
- Select historical typhoon events which had significant rainfall and caused large inflow in the target reservoir watershed;
- (2)
- Collect typhoon records from the nearby meteorological station, including typhoon track, wind direction, maximum force seven wind direction and speed, atmospheric pressure, temperature, rainfall depth, and radius of the typhoon circulation;
- (3)
- Analyze the effective slope for the target site according to the approach angle of the ith typhoon;
- (4)
- Estimate the total rainfall depth of the ith typhoon event by summing the circulation rainfall depth (Equation (3)) and the orographic rainfall depth (Equation (4));
- (5)
- Define a ratio to describe the deviation between the observed rainfall (Pobs) and the estimated rainfall in the ith typhoon event as ;
- (6)
- Repeat steps (3) to (5) to obtain the ratio for each typhoon event and to obtain an average adjustment ratio as ;
- (7)
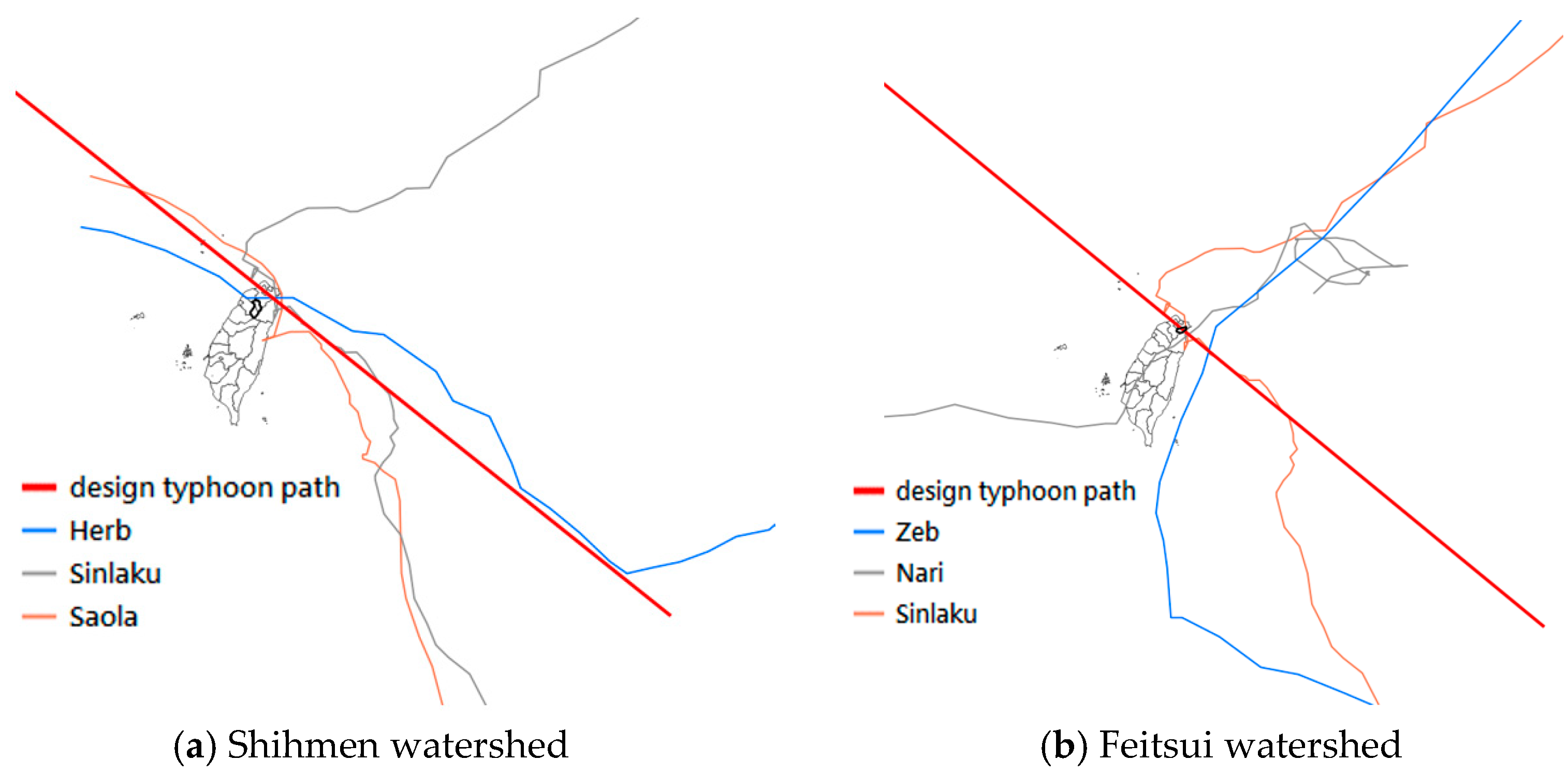
- Determine the design typhoon path based on the selected historical severe typhoon tracks (the bold red line, as shown in Figure 5);
- (8)
- Determine the parameters of the design typhoon and then calculate the circulation rainfall depth (Pc) and orographic rainfall depth (Po) along the design typhoon path at each time step;
- (9)
- When the design typhoon circle covers the target watershed, use the average adjustment ratio () to adjust the estimated rainfall depth at each time step;
- (10)
- The adjusted-rainfall depth in the progress of the design typhoon is regarded as the PMP of the target watershed.
4. Probable Maximum Flood Analysis
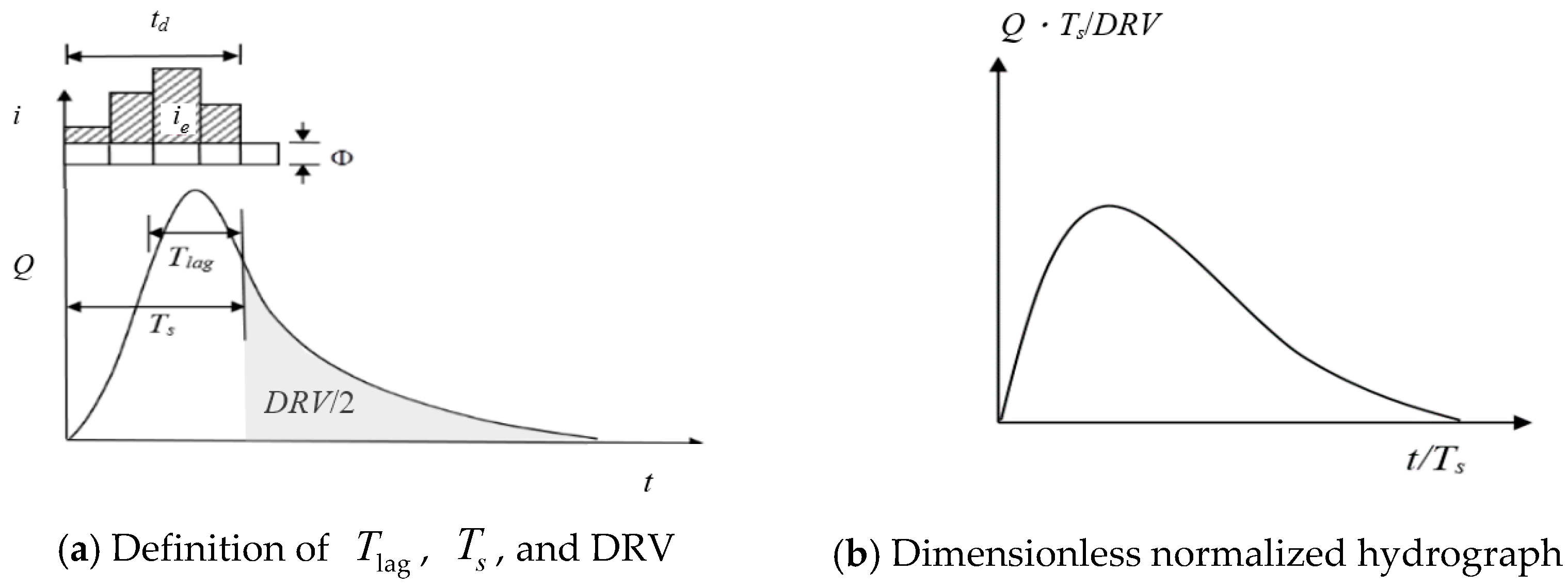
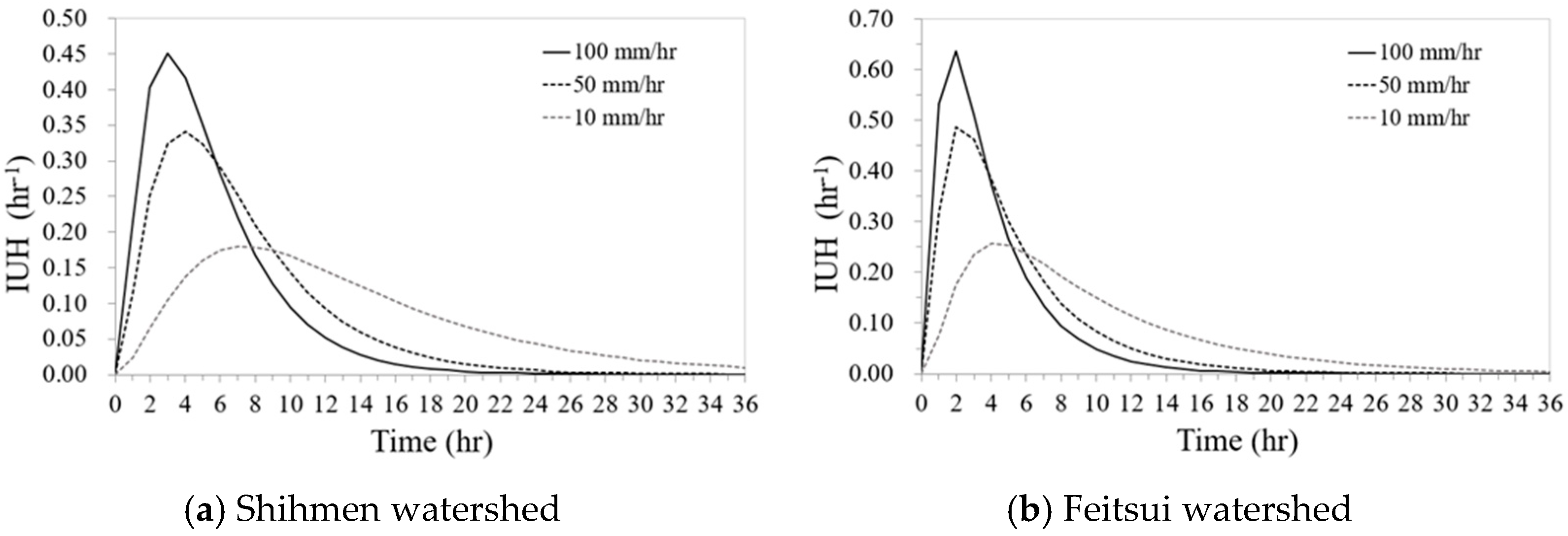
4.1. Dimensionless Unit Hydrograph Model
4.2. Kinematic-Wave-Based Geomorphologic IUH Model
5. Case Studies of Shihmen and Feitsui Reservoir Watersheds
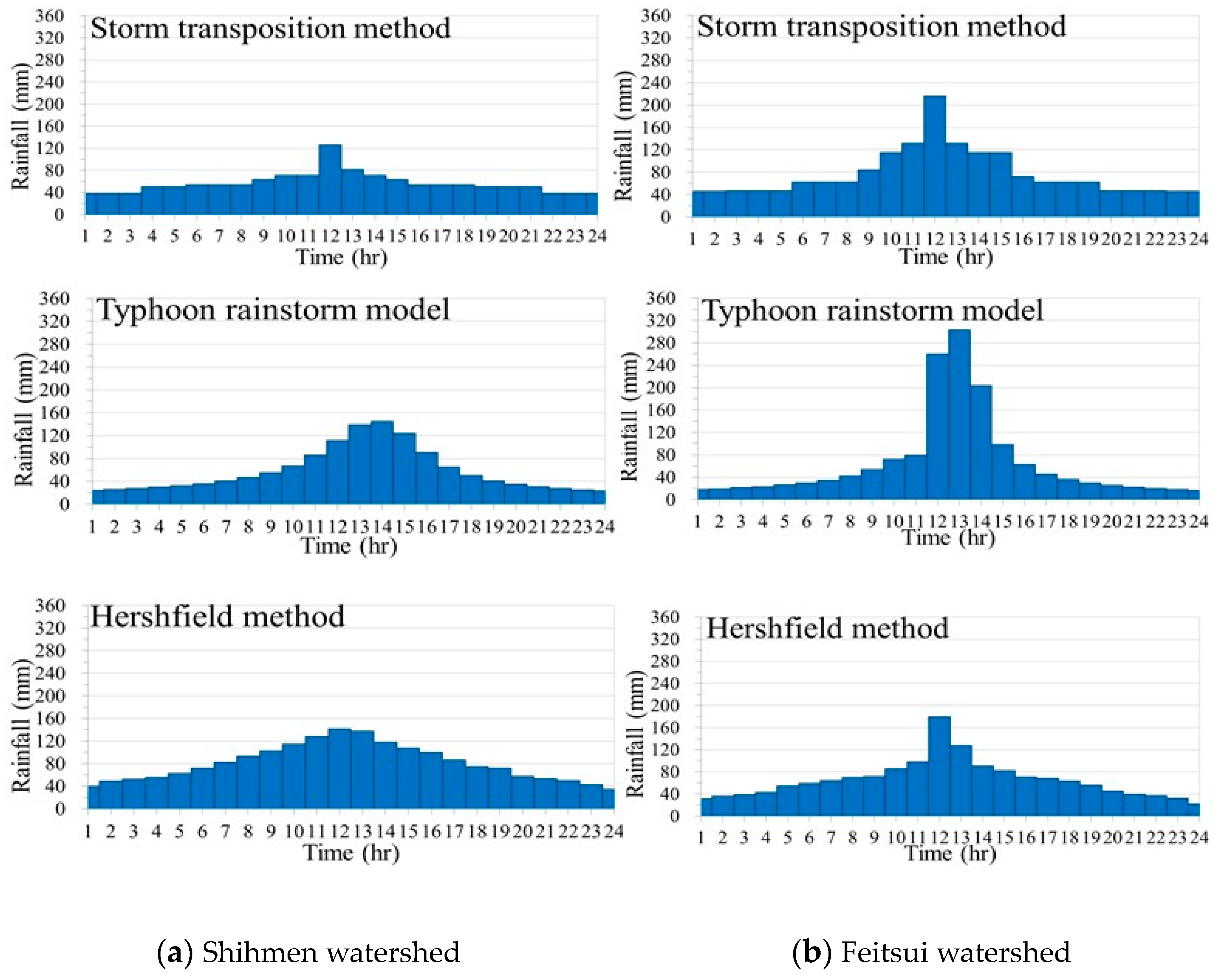
5.1. Probable Maximum Precipitation Analysis
5.2. Spillway Safety Assessment Based on Probable Maximum Flood Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Federal Energy Regulatory Commission. Engineering Guidelines, Chapter VIII. Determination of the Probable Maximum Flood; Federal Energy Regulatory Commission: Washington, DC, USA, 2001.
- World Meteorological Organization. Manual on Estimation of Probable Maximum Precipitation (PMP); WMO-No. 1045; World Meteorological Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Hershfield, D.M. Rainfall Frequency Atlas of the United States; Technical Paper No. 40; Weather Bureau, United States Department of Commerce: Washington, DC, USA, 1961.
- Hershfield, D.M. Estimating the probable maximum precipitation. J. Hydraul. Div. 1961, 87, 99–116. [Google Scholar] [CrossRef]
- Hershfield, D.M. Method for Estimating Probable Maximum Precipitation. J. Am. Waterworks Assoc. 1965, 57, 965–972. [Google Scholar] [CrossRef]
- Thompson, C.S.; Tomlinson, A.I. Probable maximum precipitation in New Zealand for small areas and short durations. J. Hydrol. 1993, 31, 78–90. [Google Scholar]
- Collier, C.G.; Hardaker, P.J. Estimating probable maximum precipitation using a storm model approach. J. Hydrol. 1996, 183, 277–306. [Google Scholar] [CrossRef]
- Svensson, C.; Rakhecha, P.R. Estimation of probable maximum precipitation for dams in the Hongru River catchment, China. Theor. Appl. Climatol. 1998, 59, 79–91. [Google Scholar] [CrossRef]
- Al-Mamun, A.; Hashim, A. Generalized long duration probable maximum precipitation (PMP): Isohyetal map for Peninsular Malaysia. J. Spat. Hydrol. 2004, 4, 20–35. [Google Scholar]
- Fernando, W.C.D.K.; Wickramasuriya, S.S. The hydrometeorological estimation of probable maximum precipitation under varying scenarios in Sri Lanka. Int. J. Climatol. 2011, 31, 668–676. [Google Scholar] [CrossRef]
- Lee, J.; Choi, J.; Lee, O.; Yoon, J.; Kim, S. Estimation of probable maximum 1080 precipitation in Korea using a regional climate model. Water 2017, 9, 240. [Google Scholar] [CrossRef]
- Afzali-Gorouh, Z.; Bakhtiari, B.; Qaderi, K. Probable maximum precipitation estimation in a humid climate. Nat. Hazards Earth Syst. Sci. 2018, 18, 3109–3119. [Google Scholar] [CrossRef]
- Liao, Y.; Lin, B.; Chen, X.; Ding, H. A new look at storm separation technique in estimation of probable maximum precipitation in mountainous areas. Water 2020, 12, 1177. [Google Scholar] [CrossRef]
- Wang, S.D.; Liu, G.Y.; Qu, K.G.; Lin, Z.M.; Huang, Z.C.; Xie, W.Q. Research on the Maximum Possible Rainstorm at the Feicui Valley Dam Site; Air Force Meteorological Center Research Report No. 13; Air Force Meteorological Center: Taipei, Taiwan, 1977. [Google Scholar]
- Wang, S.D. Research on probable maximum precipitation (PMP) of major reservoirs in Taiwan. In Proceedings of the Second Symposium on Water Conservancy Engineering, Taipei, Taiwan, 4–7 September 1984; pp. 333–347. [Google Scholar]
- Liu, C.-C.; Yang, T.-C.; Kuo, C.-M.; Chen, J.-M.; Yu, P.-S. Estimating probable maximum precipitation by considering combined effect of typhoon and southwesterly air flow. Terr. Atmos. Ocean. Sci. 2016, 27, 991–1003. [Google Scholar] [CrossRef]
- Hart, T.L. Survey of Probable Maximum Precipitation Studies Using the Synoptic Method of Storm Transposition and Maximization. In Proceedings of the Workshop on Spillway Design, Melbourne, Australia, 7–9 October 1981; Conference Series No. 6, Australian Water Resources Council, Australian Department of National Development and Energy. Australian Government Publishing Service: Canberra, Australia, 1982. [Google Scholar]
- Schreiner, L.C.; Riedel, J.T. Probable Maximum Precipitation Estimates, United States East of the 105th Meridian; Hydrometeorological Rep. 51; U.S. Department of Commerce, National Oceanic and Atmospheric Administration: Washington, DC, USA, 1978.
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Lee, C.S.; Huang, L.R.; Shen, H.S.; Wang, S.T. A climatology model for forecasting typhoon rainfall in Taiwan. Nat. Hazards 2006, 37, 87–105. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Xie, X.L.; Qiao, F.L.; Chen, Z.G.; Huang, Q.F. Analysis of precipitation characteristics in Zengwen Reservoir catchment area and research on precipitation forecast of typhoon. Atmos. Sci. 1981, 8, 1–18. [Google Scholar]
- Lee, K.T.; Yen, B.C. Geomorphology and kinematic-wave-based hydrograph deviation. J. Hydraul. Eng. 1997, 123, 73–80. [Google Scholar] [CrossRef]
- Taiwan Provincial Water Conservancy Bureau. Research on the Application of Taiwan Hydrological Data Computer Files—Dimensionless Unit Hydrograph Calculation of Major River Basins in Taiwan; Taiwan Provincial Water Conservancy Bureau: Taichung, Taiwan, 2002.
- Yen, B.C.; Lee, K.T. Unit hydrograph derivation for ungaged watersheds by stream order laws. J. Hydrol. Eng. 1997, 2, 1–9. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Valdes, J.B. The geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef]
- Henderson, F.M.; Wooding, R.A. Overland flow and groundwater flow from a steady rainfall of finite duration. J. Geophys. Res. 1964, 69, 1531–1540. [Google Scholar] [CrossRef]
- Chang, X. Exploring the Possible Maximum Flood Volume of Shihmen Reservoir with the Concept of Area Reduction Factor. Master’s Thesis, Department of Civil Engineering, National Central University, Taoyuan City, Taiwan, 2013. [Google Scholar]
- Northern Region Water Resources Office. Reservoir Safety Assessment Report; Northern Region Water Resources Office: Taipei, Taiwan, 2015. [Google Scholar]
- Northern Region Water Resources Office. Reservoir Safety Assessment Report; Northern Region Water Resources Office: Taipei, Taiwan, 2020. [Google Scholar]
- World Meteorological Organization. Manual for Estimation of Probable Maximum Precipitation; Operational Hydrology Report No. 1; World Meteorological Organization: Geneva, Switzerland, 1986.
- Water Resource Agency. Hydrological Design Application Manual; Water Resource Agency: Taipei, Taiwan, 2001.


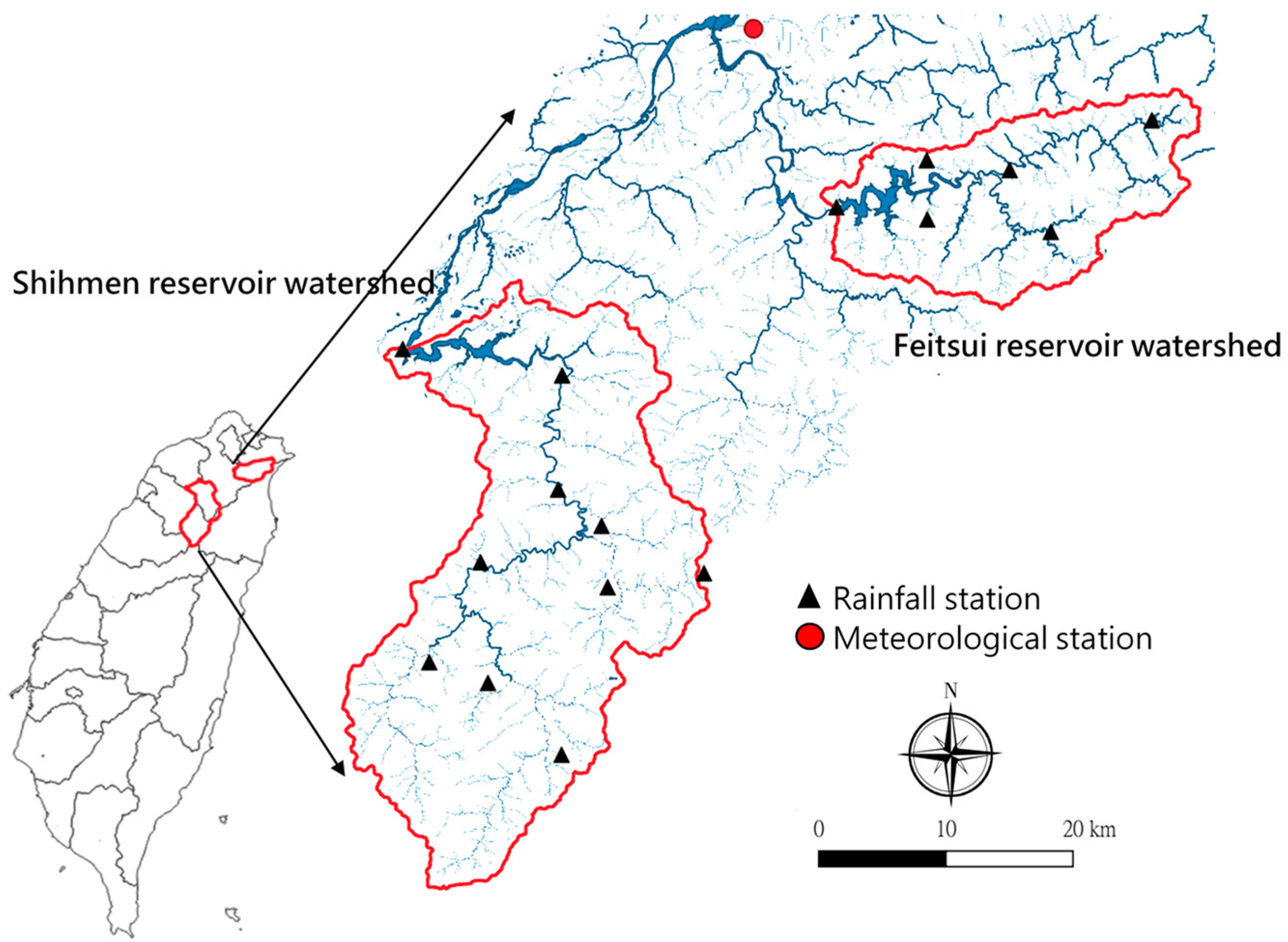

| Watershed | Shihmen | Feitsui |
|---|---|---|
| Watershed area (km2) | 758.9 | 302.38 |
| Mainstream length (km) | 101.61 | 53.29 |
| Mainstream slope (m/m) | 0.02689 | 0.00969 |
| Watershed mean slope (m/m) | 0.4161 | 0.3022 |
| Watershed mean elevation (m) | 1408.1 | 477.5 |
| Watershed outlet elevation (m) | 224.2 | 69.9 |
| Dam height (m) | 133.1 | 122.5 |
| Reservoir storage (106 m3) | 2.02 | 3.35 |
| Design flood discharge (m3/s) | 13,800 | 9870 |
| Typhoon Rainstorm | Observation Stations | Target Basin | |||
|---|---|---|---|---|---|
| Station | Elevation (m) | Dewpoint (°C) | Sea-Level Dewpoint (°C) | Barrier Height/ Wind Azimuth | |
| 1959/08 T.D. | Tainan | 40.8 | 24.7 | 24.9 | 20.4 m (NNW) |
| 1960/07 Shirley | Taichung | 84.0 | 24.1 | 24.4 | 223.3 m (NNW) |
| 1963/09 Gloria | Taipei | 6.3 | 25.2 | 25.2 | 396.7 m (ENE) |
| 1996/07 Herb | Alishan | 2413.4 | 15.6 | 25.2 | 1206.7 m (NNW) |
| 2001/09 Nari | Chiayi | 26.9 | 24.1 | 24.2 | 1335.4 m (NNE) |
| 2004/06 Mindulle | Taichung | 84.0 | 23.5 | 23.8 | 499.3 m (SSW) |
| 2004/08 Aere | Hsinchu | 26.9 | 23.6 | 23.7 | 29.4 m (WNW) |
| 2008/09 Sinlaku | Taichung | 84.0 | 25.0 | 25.3 | 817.7 m (NNE) |
| 2009/08 Morakot | Alishan | 2413.4 | 16.5 | 26.1 | 1206.7 m (NNW) |
| Watershed | (mm) | PMP (mm) | |||
|---|---|---|---|---|---|
| 100-yr | 1000-yr | Storm Transposition Method | Typhoon Rainstorm Model | Hershfield’s Method | |
| Shihmen | 1140 | 1592 | 1359 | 1386 | 1934 |
| Feitsui | 772 | 1036 | 1823 | 1526 | 1576 |
| Watershed | QT (m3/s) | PMF (m3/s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Storm Transposition Method | Typhoon Rainstorm Model | Hershfield’s Method | ||||||
| 100-yr | 1000-yr | KW-GIUH | DUH | KW-GIUH | DUH | KW-GIUH | DUH | |
| Shihmen | 8678 | 11,988 | 17,107 | 16,582 | 25,023 | 23,235 | 26,962 | 24,163 |
| Feitsui | 5586 | 7667 | 14,168 | 10,950 | 15,949 | 14,630 | 11,435 | 9350 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.T.; Hsu, Y.-H.; Yang, J.Z. Estimating Typhoon-Induced Maximum Flood for Spillway Safety Assessment—Case Studies in Taiwan. Water 2023, 15, 3040. https://doi.org/10.3390/w15173040
Lee KT, Hsu Y-H, Yang JZ. Estimating Typhoon-Induced Maximum Flood for Spillway Safety Assessment—Case Studies in Taiwan. Water. 2023; 15(17):3040. https://doi.org/10.3390/w15173040
Chicago/Turabian StyleLee, Kwan Tun, Yu-Han Hsu, and Jing Zong Yang. 2023. "Estimating Typhoon-Induced Maximum Flood for Spillway Safety Assessment—Case Studies in Taiwan" Water 15, no. 17: 3040. https://doi.org/10.3390/w15173040
APA StyleLee, K. T., Hsu, Y.-H., & Yang, J. Z. (2023). Estimating Typhoon-Induced Maximum Flood for Spillway Safety Assessment—Case Studies in Taiwan. Water, 15(17), 3040. https://doi.org/10.3390/w15173040






