Assessment of River Regime of Chenab River in Post-Chiniot Dam Project Scenario

Abstract

Dams and reservoirs trap most sediments, and clear water can cause downstream riverbed degradation or aggradation. As a result, the river adjusts its dynamics and channel geometry to regain equilibrium between sediment supply and transport capacity. This study aimed to assess the river regime of the Chenab River in the post-Chiniot Dam Project scenario using a one-dimensional numerical model. After calibration and validation using historic flows and river surveys, simulations were carried out for 5, 10, and 30 years. The sediment model was validated with Brune’s curve, which showed a Nash–Sutcliffe efficiency value of 0.734. The results showed that the river experienced continuous degradation of sediments for the first 16 years and showed a maximum erosion of 8 m at 680 m downstream of the dam. The reach experienced aggradation at 15 km downstream of the dam for the first 10 years and then became stable and showed a maximum deposition of 0.9 m. The ratio of sediments passed through the dam to sediments transported out of reach varied from 0.833 to 0.921, showing that the river reach would continue to attain equilibrium even after 30 years of reservoir operation. The study would be helpful for the prediction of possible future changes in the Chenab River.

1. Introduction

The development and operation of dams/reservoirs can have many benefits for the area and communities, such as water supply, flood control, irrigation, fisheries, hydropower development, and recreational purposes [1]. However, their side effects may also appear. With the operation of dams/reservoirs, most of the sediments in the river become entrapped in the reservoir, which may form a delta in the river and can appear in a long upstream range. Sedimentation in the reservoirs can reduce the usability and capacity of the reservoir and, thus, its benefits [2]. Sediment-free water released from the reservoir can also cause downstream riverbed degradation. If no remedial measures are incorporated in the design and construction, a dam/reservoir may lose its essential functions and may pose a threat to the area at both upstream and downstream sides [3]. Downstream river reach losses require sediment load to maintain a riparian ecosystem and also cause threats to the structures constructed on the downstream side [4].

The development of reservoirs and dams significantly impacts the discharge and sediment transport phenomenon and causes changes both upstream and downstream of dams. The effects of dams and reservoirs on the sediment phenomenon are greatly influenced by the fluctuations in sediment transport of the river reach, its regime, and the morphology of the river [5]. Morphological alterations in alluvial rivers can have substantial effects on flood risk infrastructure and pose various complications for sustainable engineering, watershed planning and management, and river restoration [6]. The characteristics of an alluvial river can be described with the help of the regime of that river [7]. Water and sediment transportation and characteristics are critical for the functioning of riverine ecosystems [8]. All factors, including variability of the discharge, temperature, evapotranspiration, and relationships between discharge, depth, width, and the slope of the river, have different responses towards the drainage basin, river discharges, and their shape at different times of the year, which helps to determine the changes in river morphology around the world [9].

A long-term balance between erosional and depositional forces in the river corresponding to attaining almost a permanent geometric shape of a channel is termed dynamic equilibrium. When a system delivers and removes sediments in a balanced way, then the system is said to be in an equilibrium state [10]. If, for any reason, external forces on the system vary, the system will be in a transient phase until it moves to a new dynamic equilibrium [11]. A river system changes its geometry and dynamics due to adjustments made by natural or synthetic processes. To regain its stability and equilibrium of incoming sediment load and capacity of sediment transport in the control volume by adjusting its geometrical characteristics [12]. As a result, the river adjusts its dynamics and channel geometry in order to regain an equilibrium between sediment supply and transport capacity [13]. The movement of water and sediment coincides in natural rivers, floodplains, and coastal areas. This simultaneous movement greatly impacts the river morphology and its entire hydrodynamics [14]. The addition of environmental effects and natural events like floods and landslides rapidly alters its morphology [15].

The knowledge and experience of the complete sedimentation processes like detachment, entrainment, transportation, deposition, and consolidation of the load are essential factors to be kept in mind for analyzing the sedimentation processes in the catchment. Artificial structures like irrigation networks, hydropower projects, domestic and industrial supply of water, and urbanization of riverine landscapes alter the natural phenomena and ecosystem, which causes accelerated sedimentation processes and ultimately results in the change of river regime [16].

Studying river training is one of the objectives of river engineering, which involves rivers’ behavior and phenomena. Shape and other river characteristics, sediment accumulation, and riverbed erosion are among the most problematic and important topics in hydraulics and river engineering [17]. Technological innovations in this field have enabled experts to solve complex equations of hydraulics and sediment transport issues through numerical modeling and simulations [18].

Kim [19] studied the riverbed from the Daechung regulation dam to the Geum estuary in Korea (L = 130 km) to assess riverbed change for 20 years of dam operation using the HEC-RAS one-dimensional numerical model. Daily runoff data were obtained, analyzed, and matched with the Precipitation Runoff Modeling System value. Four sediment transport equations were used in the model to study the riverbed change for 20 years.

Morphological changes in the Nile River and the impact of the Merowe Dam were studied with the help of a 1D numerical model Mike11. It predicted high degradation in the first hundred kilometers in the downstream reach of Merowe Dam, thus, showing that this reach was sensitive to high flows. After 50 years of dam construction, the pattern for riverbed changes was comparable with the bed after 15 years of dam operation. However, after 15 years of operation, the middle portion of the study shows aggradation [20].

A study was conducted in Romania to analyze the morphological changes and sediment load in the Oltenita, Calarasi Danube River reach [21]. A one-dimensional numerical model was used. The Digital Terrain Model (DTM) was used to extract the river schematic network, and the HEC-GeoRAS tool was used for topographical–bathymetric data. Unsteady flow analysis was used for calibrating and validating the numerical model in HEC-RAS. Sediment and hydrologic data from two upstream and two downstream gauging stations from 2008 to 2011 was used.

Mathematical modeling of the operations dealing with water and sediment load in a complex situation is a handy and well-applicable method to examine the impacts on different levels [22]. Advancements in the field of computer technology and the use of software have brought considerable development in the field of numerical modeling [23]. In contrast, physical modeling has been a difficult job to do with massive effort and cost. Analysis of different scenarios is also quite tricky in physical modeling, but numerical modeling has changed this phenomenon to a remarkable extent. Numerical modeling has also helped engineers and scientists to optimize physical modeling [24].

Numerical models can be 1D, 2D, or 3D models. The scale of the domain often guides the choice of the model dimension. The 1D models may perform reliably and appropriately if the field data are limited for developing 2D or 3D models [25]. All numerical or physical models for hydrological studies have simplified versions of the real world [26]. Many advanced numerical models generate reasonable solutions of simple conservation equations (conservation of energy, mass, and momentum) [27]. As per the hydro informatics perspective, a model is an assembly of signs that performs as a sign, so a hydrological model is the assembly of characters that serve as a demonstration of the natural system or a part of the system [26]. Numerical models are now used by water resource engineers for assessment and river morphology. Numerical models are generally cost-effective tools for predicting sediment transport in rivers for longer periods [28]. A numerical model is a very influential tool if appropriately utilized by an experienced person. The assessment of limitations and their impact on the model is a complex task and needs special attention [29].

Sediment models are complex and very sensitive to the hydraulics parameters used in the model [30]. Sediment models based on the data of hydrologic or hydraulic models need extra validation to reach an acceptable result [31]. For instance, the roughness coefficient of the river and its floodplain in a 1D model may generate results that are different from the prototype; then, the sediment model may calculate inaccurate scour or deposition in the river. Therefore, an adjustment in the roughness coefficient may be required between the river and its floodplain to become an acceptable range of results [32]. Generally, all fluids move in three dimensions; however, certain equations are derived to represent the movement into one and two-dimensional forms. If forces acting on the water body are more dominant in one direction, i.e., along the river, and negligible in other directions, then, the one-dimensional form of the equation is derived [33]. A one-dimensional model functions on the principle of conservation of mass, i.e., continuity equation [34]. The one-dimensional sediment-transport numerical model has evolved tremendously over the last many years and has been used for sediment transport studies and erosion or deposition of rivers [35].

Numerical modeling of steady and unsteady conditions for longer rivers or reaches and for longer duration like years are generally analyzed using a one-dimensional model. De Saint–Venant equations are used as flow equations for averaging the shallow water equations over the cross-sectional area [36]. One-dimensional numerical simulation has been an efficient tool for modeling river systems and their behaviors. In longer river reaches, these one-dimensional steady or quasi-steady flow models have been utilized and provided reliable results in applied hydraulics [35].

$$\left(1-{\mathsf{\lambda }}_{\mathrm{p}}\right)\mathrm{B}\left(\frac{𝜕{\mathrm{Z}}_0}{𝜕\mathrm{t}}\right)=-\frac{𝜕{\mathrm{Q}}_{\mathrm{s}}}{𝜕\mathrm{x}}$$

(1)

where B is channel width, Z₀ is bed elevation, λ_p is the porosity of the active layer, t is time, x is length, and Q_s is sediment discharge.

There are certain benefits of using the one-dimensional sediment model compared to the two-dimensional or three-dimensional ones. One-dimensional numerical models are simpler, easy to use, and require less topographic data as river survey data are used to develop river cross-sections [37]. Calibration is quite simpler in these models, for instance, changing the roughness coefficient along the cross-sections may calibrate the model. These models are best suitable for usage where input data are limited. The hydraulics of structures are not so complex in a one-dimensional model, and less data would serve the required purpose. One-dimensional models compute the results in much less time than other complex models, which consumes much time and energy [32]. There are also certain disadvantages when comparing the 1D numerical models with 2D or 3D models. To calculate the actual flow area, cross-sections in 1D should be placed perpendicular to the direction of flow, which is always an issue for longer reaches. Assumptions exist in these 1D models that the water’s surface would change in one direction among consecutive cross-sections, which is not necessarily the case in reality [32].

In order to select an appropriate model for the sediment transport analysis, the objectives of the study, its extent, duration, and availability of data need to be defined before the start of the study. In Pakistan, the HEC-RAS by the Hydrologic Engineering Centre of USACE is commonly used due to its free-of-cost availability and validity on Pakistani rivers. This tool has been used on mega projects in the country like Dasu and Bunji HPPs, which supports the utility of this model. The HEC-RAS calculates sediment transport capacity and then predicts the changes in the riverbed by the Exner equation.

Although Pakistan has water rights to the Chenab River as per the Indus Water Treaty (IWT), flow regulation of the Chenab River could not be planned as no natural storage site is available on the Chenab River [38]. The irrigation supplies depend on available river flows, which are abundant in Kharif and low in Rabi. At Marala, the flows during the Rabi season are insufficient to meet the irrigation requirement [39]. Water shortage in the Chenab River is met through storage at Mangla and Tarbela. Khanki Barrage on the Chenab River is fed through Upper Jhelum Canal (UJC), while Qadirabad Barrage is fed through the Rasul Qadirabad (RQ) link canal. The UJC and RQ link canal use Jhelum River flows regulated through the Mangla reservoir. During the Rabi period, deficient flows of Trimmu Barrage on Chenab River are met through the CJ Link canal from the Tarbela and Chashma reservoir on Indus River.

Considering the irrigation requirement of the Rabi period [40], regulation of the Chenab River is essential by creating some storage sites to provide additional flows in the Rabi season. Chenab River, with plain topography, can have a low-height dam reservoir in the flood plain surrounded by dykes on either bank. To meet the objective, storage sites between Marala and Trimmu Barrage have been identified by the Water and Power Development Authority (WAPDA). One of those sites is the Chiniot Dam (0.9 MAF). At this site, river flows in two narrow gorges and embankments anchored to these hills would create an excellent topographic situation favorable for developing a low-level reservoir. The preliminary study confirms that a barrage in two parts, one on each gorge of Chiniot hills and the upstream boundary of the reservoir with dykes raised at a conservation level of 190 m, can develop a storage capacity of 1110 Mm³ (0.9 MAF) [41]. The objectives of the Chiniot Dam project are water storage of 1110 Mm³ (0.9 MAF), flood mitigation, power generation (80 MW/275 GWh), water supply to the nearby community, and groundwater recharge.

Floods in the Chenab River bring sand and silt deposits. The sediment supply increases as the flow increases during the monsoon season, as the sediment rate is directly proportional to the flood discharge [42]. The Chenab River Basin is a unique and complex river basin that encounters extreme hydrological conditions and complicated features of its mountains in the basin [43]. The slope of the river is quite steep in its u/s reaches and then gradually reduces when it reaches downward areas. The river, generally, has a gradient of 10 m/km in the upper reaches and then reduces to 3 m/km in the lower reaches [44]. Because of its higher altitude in the upper and middle portions of the basin, it has snow-dominant regions. The Chenab River catchment revealed that there are very high erosion rates. The mean annual rainfall in the basin ranges from 279 to 2215 mm [45]. As compared to the Main Indus River and adjoining tributaries in the Upper Indus Basin, the Chenab River Basin contains a smaller portion in the Karakoram, which is the main reason for the smaller fraction of sediment than the tributaries in the Upper Indus Basin [46].

There are no dam or mega hydropower projects on the main Chenab River, so no study has been conducted on the Chenab River as far as its regime and sedimentation are concerned. So, conducting a research study on River Chenab was necessary to assess the effects and changes on river regimes with the construction of the proposed Chiniot Dam Project. Storage reservoirs alter a river’s natural flow and sediment supply, and this change subsequently affects channel hydrodynamics. Flow patterns and sediment supply vary spatially throughout the river system. Dams may also affect the downstream ecosystems through the effects of altered flow and sediment regimes [47]. The impacts of sediment transport due to the construction of a dam or reservoir relate the sediment load with the river regime and, ultimately, river morphology. In case rivers receive less discharge with respect to sediment, they would lack the flushing capability of sediment from that river and accumulate sediments and alter the slope of the riverbed, putting the river in a quasi-equilibrium state [48]. Dams interrupt the entry of sediments into the reservoirs and cause their accumulation, ultimately decreasing reservoir storage and disturbing reservoir operation [49]. Sediment inflow in the rivers from the catchment area can also cause the blockage of intakes in the dams and severely damage the turbine runners and water tunnels [50].

Since the reasons for the alteration of river regimes are not obvious, a broader understanding of this phenomenon is needed to classify the fluvial dynamics depending on different river types for improved water resource management in the future. The focus of this study was to analyze the long-term changes in the Chenab River Regime due to the construction of the Chiniot Dam Project. The study would be helpful for the prediction of possible future changes in the Chenab River profile downstream of the Chiniot Dam Project.

2. Materials and Methods

A one-dimensional HEC-RAS numerical model was used for this research study. The HEC-RAS uses a standard step method for steady, gradually varied flow to calculate the water level and profile. The quasi-unsteady flow approach uses a series of steady flow computations for hydrodynamic modeling. In quasi-unsteady modeling, the model does not conserve the flow, but it provides a stable solution using the sequence of steady flow computations [51].

Three types of input files are required to develop the HEC-RAS sediment model [52], which include a geometry file, a flow file (quasi-unsteady or unsteady), a sediment data file, and a sediment analysis plan file.

2.1. Input Data and Data Collection

In order to prepare the numerical model, mainly three types of input data are required:

i.

Geometric data, i.e., river cross sections;

ii.

Flow data;

iii.

Sediment data;

2.1.1. Geometric Data

River cross-sections were obtained from physical surveys conducted by the Survey Division of the Punjab Irrigation Department. Survey data from three different years were collected from the Punjab Irrigation Department. Basic geometry was developed using the river survey data of the year 1999. Another two-year survey (2005–2006 and 2013–2014) was used to calibrate and validate the model. The survey data collected consists of river stations and elevations at each station for each cross-section.

Further, cross-sections were interpolated to reduce the spacing between cross-sections where the river changes its direction or section. Geometric data in the model consisted of a series of cross-sections collected through river surveys to establish the Chenab River study reach. The length of the study area was 130 km consisting of 76 cross-sections, including 11 interpolated cross-sections where the river changed its direction and width (near the Chiniot Dam site and Rivaz Bridge). Maximum spacing between two consecutive cross-sections was about 3 km, whereas minimum spacing between the two cross-sections was 365 m. Cross-sections near the Chiniot Dam site were also compared with those obtained from the feasibility study of the project. On the upstream side of the project, 17 cross-sections were added to the model to represent the reservoir area of about 35 km. At the most upstream, cross-section sediment data were used as an upstream boundary condition. The geometric model of the study area plotted in the software is shown in Figure 1.

Interpolated cross-sections were required to stabilize the numerical model as rapid change in flow or sediment from one cross-section to another cross-section causes model instability [53]. Therefore, the Hydrologic Engineering Centre recommends interpolating the cross-sections for consistent flow and sediment delivery within cross-sections. Interpolation of cross-sections was carried out using the interpolation tool in the HEC-RAS. Despite all the information provided in the model, some assumptions and simplifications in the geometry of the study reach have been made to obtain appropriate geometry for the model. Manning’s coefficient “n” was taken considering the land use, soil type, and project area. Manning’s “n” value of 0.04 was used for the left and right overbanks, whereas the value of 0.026 was used for the main channel. Manning’s “n” value was finalized after the hydraulic calibration and validation of the model.

2.1.2. Quasi-Unsteady Flow Data

The Quasi-unsteady flow approach was used in the numerical model, which requires flow data as an upstream boundary condition, normal depth, stage series, or a rating curve as a downstream boundary condition. In this study, a rating curve has been adopted for downstream boundary conditions.

Quasi-unsteady flow hydraulics are essential for sediment transport modeling. Flow data were collected and shifted to the Excel sheet to develop the graphs and set data to the HEC-RAS model. The HEC-RAS can incorporate some boundary conditions to be inserted in the quasi-unsteady flow file: flow series, lateral flow series, uniform lateral flow, normal depth, stage series, rating curve, time series gate openings, and internal stage boundary condition. Flow series data were the only option that could be used at the upstream cross-section as an upstream boundary condition in a quasi-unsteady flow file.

Discharge data were collected from the Punjab Irrigation Department (PID) and the Hydro Planning Organization (HPO) of WAPDA. The nearest discharge gauge installed was at Qadirabad; no flow was entering or leaving the reach from Qadirabad to the project site, i.e., Chiniot Dam. Therefore, the same data were utilized for the study reach as gains and losses are considered the same. Historic flow data, i.e., 1999–2015, were taken from the HPO, while recent data, i.e., 2016–2020, were taken from the PID. In the Chenab River, a major flood occurred in 2014, showing a flood value of 26,307 m³/s, as shown in the graph below. Daily flow series data were used for the model input, as shown in Figure 2.

Computation increments were also used for dividing the flow duration, i.e., daily, based on the flow intensity. The flow at a given period would remain constant, and thus, the model calculated the hydrodynamics and geometry based on the provided flow. The computation interval (CI) forces the model to divide the flow duration into parts from which the model could compute hydrodynamics and geometry for each duration, i.e., computation interval. Division of the flow intervals based on the flow intensity would provide stability to the numerical model as sudden changes in flow and, thus, computations could generate instability in the model, and the model could crash without completing the computations.

An internal stage boundary condition was used to replicate the model’s reservoir levels condition in a quasi-unsteady flow. Reservoir levels were obtained from the reservoir operation study; these levels were inserted as an internal boundary just before the inline structure representing the dam for the whole duration of the study. In this way, the internal stage boundary condition helped the simulation of reservoir operation without routing the flows.

Maximum, average, and minimum reservoir levels for each month have been plotted and presented in Figure 3, showing that the maximum reservoir level was 190 m.a.s.l. and the minimum reservoir level was 182 m.a.s.l. A stage hydrograph was inserted to represent the levels in the model.

As a downstream boundary condition, a rating curve was prepared using the downstream cross-section, as shown in Figure 4. The rating curve describes the discharge against the stage in the river section, as every river has its own function of stage and discharge relationship.

2.1.3. Sediments Data

Sediment data were obtained from the Hydro Planning WAPDA. The WAPDA used the historic sediment data for the feasibility study of the Chiniot Dam Project. Sediment data were used to prepare the sediment rating curve, which was necessary for the upstream boundary condition in the sediment data file. Different parameters needed to be selected and inserted into the model, considering the suitability to the study reach.

Ackers and White was used in the study as it was the most suitable transport function for the study reach and has widely been used in previous studies in the Indus River Basin System [54]. This function was best suited for gradations ranging from sand to fine gravel [55]. This function was also vetted for the study reach during sediment calibration and validation. Fall velocity was computed using the Ruby approach in the model, which is based on Stoke’s law for finer sediments and an impact relation for larger sediments and is best suitable for silt, sand, and fine grains [56]. The Copeland method was used for sorting as this method is designed for sand-bed rivers [57].

Bed gradation data of the study reach were collected from the WAPDA. Bed gradation testing was carried out at the Central Material Testing Laboratory (CMTL) WAPDA during the feasibility study of the Chiniot Dam Project. Bed material near the proposed project site varies from the course silt to coarse sand material used for the complete study reach. Bed gradation data were inserted in the model’s initial conditions and transport parameters of the sediment data file. The grain size distribution of the bed sample near the dam site at a depth of 1 m is presented in Figure 5.

A sediment boundary condition was required at the upstream cross-section where it was assumed that sediment load enters the reach. There are many options for the selection of boundary conditions in the sediment file of the model, including rating curve, sediment load series, equilibrium load, and clear water (no sediment).

As the sediment data were available for the study, the reach and rating curve was developed and used to create the sediment rating curve boundary condition in the model. A sediment rating curve calculates how much sediment load is entering at a specific time concerning its flow. The model then computes the sediment load going out of reach at the downstream cross-section. Then bed change was determined using sediment calculations based on its transport function, river geometry, properties of the sediment entering, and hydraulic parameters. The sediment rating curve was developed with the help of available sediment and river flow data. This data set was then imported into the HEC-RAS model as a boundary condition. Sediment gradations were also assigned to each grain class as coarser gradation would settle in the upper reaches of the reservoir, and finer sediments would pass through the dam. These gradations were modified a few times to achieve the model’s sediment calibration. The sediment rating curve and data input in the model are shown in Figure 6 and Figure 7, respectively.

2.2. Development of the Numerical Model

Flow series data were inserted into the quasi-unsteady flow file as an upstream boundary condition. Flow intervals were further subdivided into three computational increments ranging from 6 h to 24 h based on the flow magnitude for that particular period. An internal stage boundary condition was used to replicate the model’s reservoir levels condition in quasi-unsteady flow. The rating curve was used as a downstream boundary condition for the model; the rating curve was developed with the help of a cross-section at the downstream end of the study reach just upstream of Trimmu Barrage. Historic water levels against the corresponding flows were checked for the rating curve’s reliability. Finally, a plan file was prepared with all the input files prepared earlier, i.e., geometric data file, quasi-unsteady data file, and sediment data file. Starting and ending dates were given for which the simulations needed to be run, i.e., 5 years, 10 years, and 30 years. Output level 5 was selected in sediment output options in the options menu.

2.3. Assumptions and Limitations

During the study, certain assumptions were made due to the non-availability of complete data. Therefore, some assumptions were made where deemed necessary. These assumptions included that no lateral inflow or sediment entered the reach and no flow was entering or leaving the reach from the Qadirabad Barrage to the proposed Chiniot Dam Project site. It was also assumed that the bed gradation of the study reach was consistent throughout the study period. Very few samples of the bed gradation were taken and used in the study reach. Throughout the study reach, a consistent Manning’s n value was used separately for the main channel and the overbanks. To calculate the actual flow area, cross-sections in the 1D model should be placed perpendicular to the direction of flow, which is always an issue for longer reaches. Assumptions in these 1D models include that the surface of the water would change in one direction among consecutive cross-sections, which is not necessarily the case in reality.

In general, there are always some limitations of a numerical model as the 1D model is based on a 1D algorithm, so it simulates the sediment transport along the length of the river. It does not cater to the change in velocity along the depth or width of the river.

3. Results and Discussion

The simulation results were compared for 5, 10, and 30 years of dam operation. Invert elevations, invert change, and sediment mass in cumulative graphs were plotted, and the results for the changes in the river regime were compared due to the proposed project.

3.1. Hydraulic Calibration and Validation of Model

Sediment models are very sensitive to hydraulic modeling; therefore, the model geometry and hydraulic parameters should be calibrated before sediment modeling. The numerical model was hydraulically calibrated by changing Manning’s n value in the reach. Observed water levels with corresponding flows at the downstream end of the study reach were used to calibrate the model. Both subcritical and mixed regime flows were checked in the steady flow analysis for calibration and validation.

Different but consistent values of Manning’s n were kept in the main channel and overbanks throughout the reach. Channel roughness in the main channel was 0.026, and at overbanks, it was kept at 0.040. Flows and water levels used for the calibration are tabulated below in

Table 1. Hydraulic calibration and validation of model.

Location	Date	Discharge (m3/s)	Observed Water Depths (m)	Modelled Water Depths (m)	MAPE (%)	MSE	R2	NSE
Hydraulic Calibration
Chiniot Bridge (dam site)	25 July 2001	2266	4.34	4.45	2.53	0.012	0.984	0.938
	25 July 2000	4169	4.53	4.61	1.76	0.006
	9 August 1999	2555	5.01	5.28	5.39	0.073
	30 August 1997	15,480	5.96	6.04	1.34	0.006
Hydraulic Validation
Rivaz Bridge (85 km d/s of dam site)	26 July 2001	3257	4.98	4.83	3.01	0.022	0.978	0.962
	25 July 2000	5280	4.86	4.78	1.65	0.006
	10 August 1999	2747	5.53	5.72	3.43	0.036
	31 August 1997	16,624	6.54	6.59	0.76	0.002

.

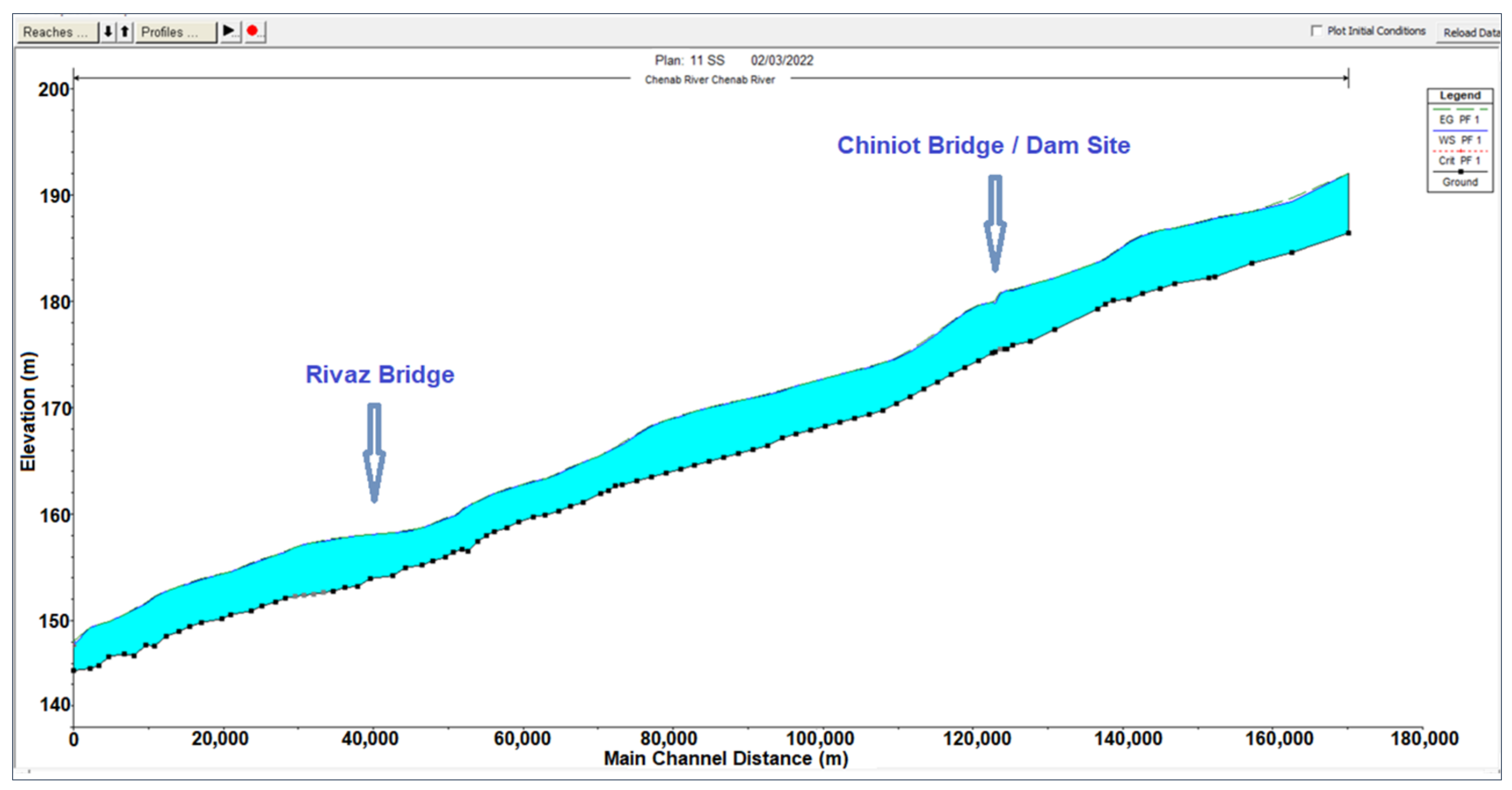
Values of R² and NSE indicate the strong correlation between the observed and computed water depths. The mean absolute percent error (MAPE) and mean square error (MSE) have also been calculated, showing an acceptable margin of error in the modeled values. Hence, the model is successfully calibrated and validated. Water surface profiles were generated for the whole reach against flood values and levels from 1997 to 2001. The water surface profile for the 2001 flood value is shown in Figure 8, where the locations of the Chiniot Dam site and Rivaz Bridge site were marked for the purpose of comparing observed water depths and computed water depths.

3.2. Sediment Calibration and Validation of Model

Sediment calibration for a river reach involves various steps to determine the reasonable parameters suitable for desirable sediment simulation. It may require numerous changes in specific parameters until the model reaches acceptable validity. The HEC-RAS was quite reasonable, using the available transport equation and fall velocity to simulate the discharge with sediment load. Different parameters were checked with varying combinations to achieve the level of acceptability. These results were compared with the observed values, and the parameters that provided closer values to the measured ones were selected.

Sediment calibration and validation of the simulated results with the actual observations was the most critical aspect of this study. It required many plans to reach a suitable outcome. Many parameters were changed throughout the calibration process.

Different parameters that were checked for suitability are as follows:

• Sediment transport function;
• Fall velocity;
• Sorting method;
• Different sets of bed gradations;
• Sediment rating curve;
• Sediment gradations.

Sediment aggradation or degradation in the reach with and without the downstream of the proposed Chiniot Dam was depicted with the changes in the channel invert elevation over the study period. Total change in sediment volume may differ from section to section; therefore, channel invert elevation criteria throughout the reach were adopted for the sediment model.

The sediment model was quite sensitive to sediment load and bed gradation. If higher sediment gradation were incorporated in the model, a considerable sediment load would deposit at the start of the reach, ultimately causing the model instability. Being a silty and sandy river, the model behaved more stable when finer sediment was used in the load. The sensitive parameters observed in the calibration of sediment transport were the transport function and bed gradation concerning this regime change study, whereas sediment load gradation was the most uncertain and sensitive parameter, which could change the river profile in the whole reach and affect the regime in the river. At the start, the adopted set of load gradation and bed gradation could not produce the desired results with the observed bed profile; however, after many hits and trials, a suitable combination was attained that could provide the approximate similarity. Similarly, different transport functions were checked, keeping in view the suitability of the function with the observed river bed and area; therefore, the most suitable transport function was selected in combination with other selected parameters.

The sediment calibration of the modeled river profile was carried out with the observed river survey of 2005–2006 for the reach from the Chiniot Dam site to 45 km downstream of the proposed dam site. River surveys were carried out by the Irrigation Department of the Government of Punjab, and the department does not conduct the complete river survey in a single year; instead, they carry out river surveys for different reaches in different years. For the study reach, limited river survey data were available, which were utilized for the modeling purpose. The values of the coefficient of determination (R²) and Nash coefficient (NSE) are 0.984 and 0.983, respectively, which indicates that the model is successfully calibrated.

After obtaining the desired calibration of the sediment transport, the validation was carried out of the fine-tuned parameters selected during sediment calibration. The sediment model was validated with the same parameters for different sections and periods. For the validation, an 80 km reach was used. The value of the coefficient of determination (R²) during the validation process was obtained as 0.989, and the value of the Nash coefficient was 0.986. The results for calibration and validation are tabulated in

Table 2. Sediment calibration and validation of the model.

Sr. No.	Description	Location	R2	NSE
1	Sediment calibration with a 2005–2006 river survey.	Chiniot Dam site and 45 km downstream reach.	0.984	0.983
2	Sediment validation with a 2013–2014 river survey.	Just upstream of Trimmu Barrage to upstream 80 km reach.	0.989	0.986

.

The values indicated a good correlation between the observed and computed bed profiles. A comparison of modeled riverbed profiles with the observed riverbed profiles obtained in both calibration (2005–2006) and validation (2013–2014) was plotted below in Figure 9a,b, respectively.

When the hydraulic and sediment parameters were finalized after calibration and validation, the HEC-RAS model was assigned to the proposed dam at its location for scenario modeling and analysis.

3.3. Validation of the Sediment Model for Trap Efficiency

To validate the simulated results of the sediment model with the assigned dam for trap efficiency, Brune’s curve was used. Brune’s curve is commonly used to determine the trap efficiency and is a function of the reservoir capacity inflow ratio. As per the calculations from Brune’s curve, the useful life of the Chiniot reservoir is estimated to be approximately 50 years, as shown in

Table 3. Life of Reservoir using Brune’s curve.

Capacity		Inflow	Cap./Inflow Ratio	Trap Efficiency		Annual Sediments		Loss of Capacity (MAF)	No. of Years in
(% Age)	(MAF)	(MAF)		From Brune Curve	Average Increment	Transport (MAF /Year)	Trapped (MAF /Year)		Which Capacity is Lost
									(Years)
II	III	IV	III/IV	VI	VII	VIII	VII × VIII	X	X/IX
100%	1.04	12.25	0.085	84.48%		0.027			0
					83.88%		0.023	0.104
90%	0.936	12.25	0.076	83.28%		0.027			4.6
					82.43%		0.022	0.104
80%	0.832	12.25	0.068	81.58%		0.027			4.7
					80.71%		0.022	0.104
70%	0.728	12.25	0.059	79.83%		0.027			4.8
					78.56%		0.021	0.104
60%	0.624	12.25	0.051	77.28%		0.027			4.9
					76.01%		0.021	0.104
50%	0.52	12.25	0.042	74.73%		0.027			5.1
					72.56%		0.020	0.104
40%	0.416	12.25	0.034	70.38%		0.027			5.3
					67.38%		0.018	0.104
30%	0.312	12.25	0.025	64.38%		0.027			5.7
					59.77%		0.016	0.104
20%	0.208	12.25	0.017	55.17%		0.027			6.4
					46.58%		0.013	0.104
10%	0.104	12.25	0.008	38.00%		0.027			8.3
								Total	50 years

below.

Brune’s curve calculations were compared with the modeled results, and a summary is depicted in

Table 4. Sediment validation using Brune’s curve results.

Number of Years of Operation	Trap Efficiency from Brune’s Curve (%)	Sediment Entered (Million Tons)	Sediment Trapped (Million Tons)	Trap Efficiency from Model (%)	NSE
5	83.28	68.275	57.364	84.02	0.734
10	81.58	172.545	136.471	79.09
20	77.28	391.401	300.542	76.79
30	70.38	583.790	436.572	74.78

below.

It showed the number of years of reservoir operation, i.e., 5, 10, 20, and 30 years and then estimated the trap efficiency from Brune’s curve in percentage. Sediment entered and sediment trapped were taken from the modeled results, and then sediment trap efficiency was calculated against different periods in percentage. The results showed satisfactory validation of the sediment modeling in the post-Chiniot Dam Project scenario. A Nash coefficient of 0.734 showed a good correlation between trap efficiency computed from Brune’s curve and the model.

3.4. Scenario Modeling

After successfully calibrating and validating the model, it was operated for the following scenarios to assess the river regime of the Chenab River.

3.4.1. River Regime after 5 Years of Chiniot Dam Operation

The results for the Chenab River reach regime change with the proposed Chiniot Dam Project were deduced from the numerical model and presented in graphical forms. Invert levels, change in invert levels, and cumulative sediment mass inflow were plotted by the model and are shown in Figure 10, Figure 11 and Figure 12, respectively.

Invert-level charts plotted the graph between main channel distance (m) and invert elevations (m.a.s.l). The results showed that initially, erosion was observed just below the proposed dam due to the dam’s operation and passage of clear water from the reservoir. In invert change charts, graphs were plotted between the main channel distance (m) and invert change (m), which shows the changes in the river bed of the post-Chiniot Dam and the original riverbed. The plots in Figure 10 and Figure 11 also show the transition stage between the erosion and deposition of sediments at 12 km downstream of the dam. Afterward, the river profile showed variations between deposition and erosion till the end of the reach. In cumulative mass inflow charts, graphs were plotted with the main channel distance (m) and cumulative sediment mass inflow (tons) with the location of the proposed dam. The amount of sediment mass inflow at the proposed dam location is also depicted on each graph. The maximum amount of sediment inflow of 18 million tons was observed at two sites, i.e., 15 km and 75 km downstream of the dam, after 5 years of reservoir operation.

After 5 years of dam operation, 68.275 million tons of sediment mass (13.655 million tons per year) entered the reach, out of which 57.364 million tons (11.473 million tons per year) became trapped in the Chiniot Dam. A total of 10.911 million tons of sediment mass (2.182 million tons per year) was transported downstream of the dam, and 13.083 million tons (2.617 million tons per year) were transported out of reach.

The results showed deposition in the reservoir and mostly erosion in the downstream reach of the dam. At just 680 m downstream of the dam, an erosion of 4.8 m was observed.

The maximum negative invert change of 4.8 m occurred at 680 m downstream of the proposed dam, and the maximum positive invert change of 0.8 m occurred 15 km downstream of the proposed dam.

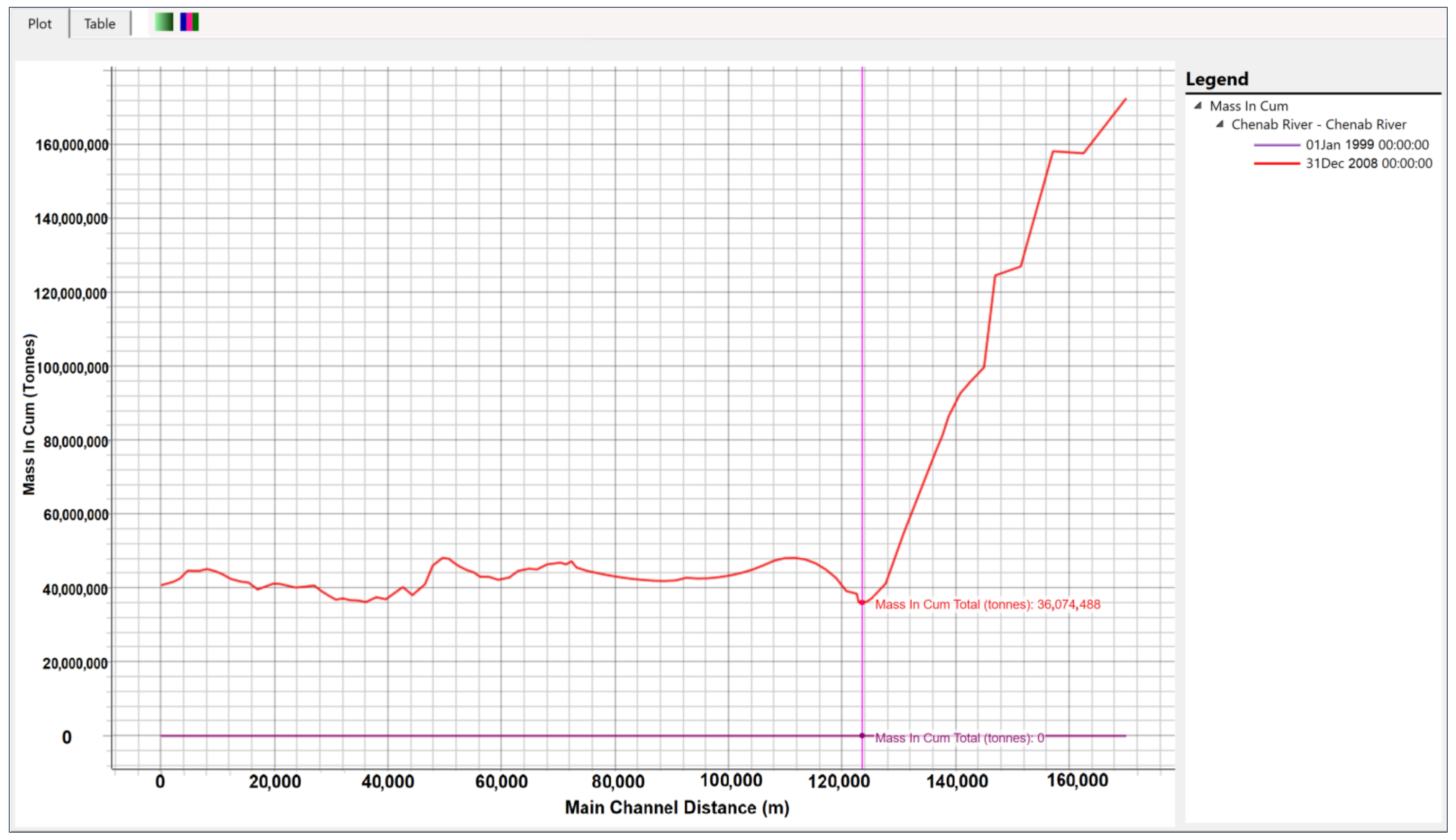
3.4.2. River Regime after 10 Years of Chiniot Dam Operation

The invert levels, change in invert levels, and cumulative sediment mass inflow plotted by the model are shown in Figure 13, Figure 14 and Figure 15, respectively. In the inverted elevation graph, upstream of the proposed dam showed an accumulation of sediment in the reservoir, which is more than the 5-year dam operation scenario. Similarly, the invert level change graph showed higher values, particularly on the dam’s upstream side.

After 10 years of dam operation, 172.545 million tons of sediment mass (17.254 million tons per year) entered the reach, out of which 136.471 million tons (13.647 million tons per year) became trapped in the Chiniot Dam. A total of 36.074 million tons of sediment mass (3.607 million tons per year) were transported downstream of the dam, and 40.707 million tons (4.071 million tons per year) were transported out of reach.

The results showed deposition in the reservoir and mostly erosion in the downstream reach of the dam. At 680 m downstream of the dam, an erosion of 6.1 m was observed. A maximum negative invert change of 6.1 m occurred 680 m downstream of the proposed dam, and a maximum positive invert change of 0.9 m occurred 15 km downstream of the proposed dam. As it is evident from Figure 15, the maximum amount of sediment inflow of 48 million tons was observed at two locations, i.e., 15 km and 75 km downstream of the dam, after 10 years of reservoir operation.

3.4.3. River Regime after 30 Years of Chiniot Dam Operation

Results in Figure 16, Figure 17 and Figure 18 show the invert elevations, changes in invert levels, and sediment inflow, respectively, after 30 years of dam operation. The plotted values show higher invert elevations and changes in invert levels than the previously discussed dam operation scenarios, which showed that sediment is continuously accumulating with the passage of time upstream of the proposed dam.

After 30 years of dam operation, 583.790 million tons of sediment mass (19.459 million tons per year) entered the reach, out of which 436.572 million tons (14.552 million tons per year) became trapped in the Chiniot Dam. A total of 147.219 million tons of sediment mass (4.907 million tons per year) was transported downstream of the dam, and 159.788 million tons (5.326 million tons per year) were transported out of reach.

The results showed deposition in the reservoir and mostly erosion in the downstream reach of the dam. At 680 m downstream of the dam, erosion of 8.0 m was observed. The maximum negative invert change of 8.0 m occurred at 680 m downstream of the proposed dam, and the maximum positive invert change of 0.9 m occurred at 75 km downstream of the proposed dam. Figure 18 shows that the maximum amount of sediment inflow of 175 million tons was observed at three locations, i.e., 15 km, 55 km, and 75 km downstream of the dam after 30 years of reservoir operation.

3.5. Summary of Scenario Modeling

Results obtained from scenario modeling are tabulated and compared with each other. Modeling results related to sediment load entered per year (million tons), sediment load trapped in reservoir per year (million tons), sediment load transported out of river reach per year (million tons), maximum deposition in the reach (m), and maximum erosion in the reach (m) are shown in

Table 5. Comparison of river regimes after 5, 10, and 30 years of operation.

Sr. No.	Description	Regime after 5 Years	Regime after 10 Years	Regime after 30 Years
1	Sediment load entered per year (million tons)	13.655	17.254	19.459
2	Sediment load trapped in dam per year (million tons)	11.473	13.647	14.552
3	Sediment load transported out of river reach per year (million tons)	2.617	4.071	5.326
4	Maximum deposition (in meters)	0.8	0.9	0.9
5	Maximum erosion (in meters)	4.8	6.1	8.0

.

After 5 years of dam operation, 13.655 million tons of sediment load were entered per year on average, and after 10 years of dam operation, 17.254 million tons of sediment load were entered per year on average, whereas, after 30 years, 19.459 million tons of sediment load per year on average were entered into the reach. The trend of increasing sediment load per year was mainly due to the increasing trend of volume of water during these years. Sediment transport is directly proportional to the water inflow; therefore, more sediment passes through with more water flowing in the river. The maximum velocity observed just downstream of the dam at the start of operation was 1.3 m/s, which gradually reduced with time and remained within the range of 0.4 to 0.5 m/s.

Similarly, trends of sediment load trapped and sediment load transported out of the river reach increased with the passage of time. Sediment load trapped in the reservoir per year on average, after 5 years of its operation, was 11.473 million tons per year, and after 10 years, it was 13.647 million tons per year, whereas, after 30 years, it was 14.552 million tons per year.

A maximum deposition of 0.8 m was observed during the first five years of operation, which remained almost consistent, and a slight change was observed during 10 and 30 years of operation. A maximum deposition of 0.9 m was computed by the model. A maximum erosion of 4.8 m was noted during the first five years of operation, which showed a significant change in erosion with the passage of time and was observed as 6.1 m and 8.0 m after 10 and 30 years of reservoir operation, respectively.

The time series data of river invert change during the study period at different sections, i.e., 680 m, 10 km, 15 km, 50 km, and 100 km downstream of the dam, are presented the Figure 19. These plots show that invert change just downstream of the dam shows continuous degradation of sediments for the first 16 years and then experiences mild variations with time. It is also witnessed from the plotted values that the study reached experienced aggradation of sediments at 15 km downstream of the dam for the first 10 years and then became stable for the remaining period. Variations in the invert change of the river bed at 10 km, 50 km, and 100 km downstream of the dam show very mild degradation in reach throughout the study period.

4. Conclusions

This study tested the HEC-RAS 1D model using the quasi-unsteady approach for assessing morpho dynamics in the post-Chiniot Dam Project scenario. The focus of this study was to analyze the long-term changes in the Chenab River Regime due to the construction of the Chiniot Dam Project. The sediment model was calibrated and validated using river surveys conducted in 2005–2006 and 2013–2014. The sediment model was further validated for trap efficiency using Brune’s curve. The results showed satisfactory validation and a Nash coefficient of 0.734 showed a good correlation between trap efficiency computed from Brune’s curve and the numerical model. The model has simulated the river regime for 5, 10, and 30 years of dam operation. The results indicated that the river continues to attain equilibrium even after 30 years of the proposed dam operation.

It was concluded from the research work that after the first 5 years of dam operation, the ratio of sediment that passed through the dam to the sediment transported out of reach was 0.833. After 10 years of dam operation, the ratio was 0.886, and after 30 years of operation, it was 0.921, which shows that river reach would continue to attain its equilibrium even after 30 years of dam operation. Also, relatively less sediment was carried in the river from the reservoir, but it delivered more sediment downstream of the reach, which showed more erosion than deposition. Moreover, the study reach showed maximum erosion of 8 m just downstream of the proposed Chiniot Dam and a maximum deposition of 0.9 m at 15 km downstream.

It was also concluded that the river showed continuous degradation of sediments for the first 16 years just downstream of the dam and then experienced mild variations with time but could not attain its equilibrium state. It was further evident that the study reaches experienced aggradation of sediments only at 15 km downstream of the dam for the first 10 years and then became stable for the remaining period. Other sections of the study reach experienced mild degradation of river beds throughout 30 years of dam operation.

Furthermore, fluvial dynamics depend on many factors and influxes from the upstream catchment. Therefore, to classify certain patterns of river morphology, more studies in different regions on the impact of reservoirs on downstream reaches should be conducted to predict the impact depending on the river type for better water resource management.

As future recommendations and further assessment of this study area, the same reach should be carried out with a combination of 1D and 2D models to analyze variations in the bed change along the river’s width. Analyze the same river reach using an unsteady flow modeling approach with fresh river survey and data to assess under which conditions the model performs well.