Evaluation of Methods for Estimating Long-Term Flow Fluctuations Using Frequency Characteristics from Wavelet Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. FFI
2.3. Wavelet Transform
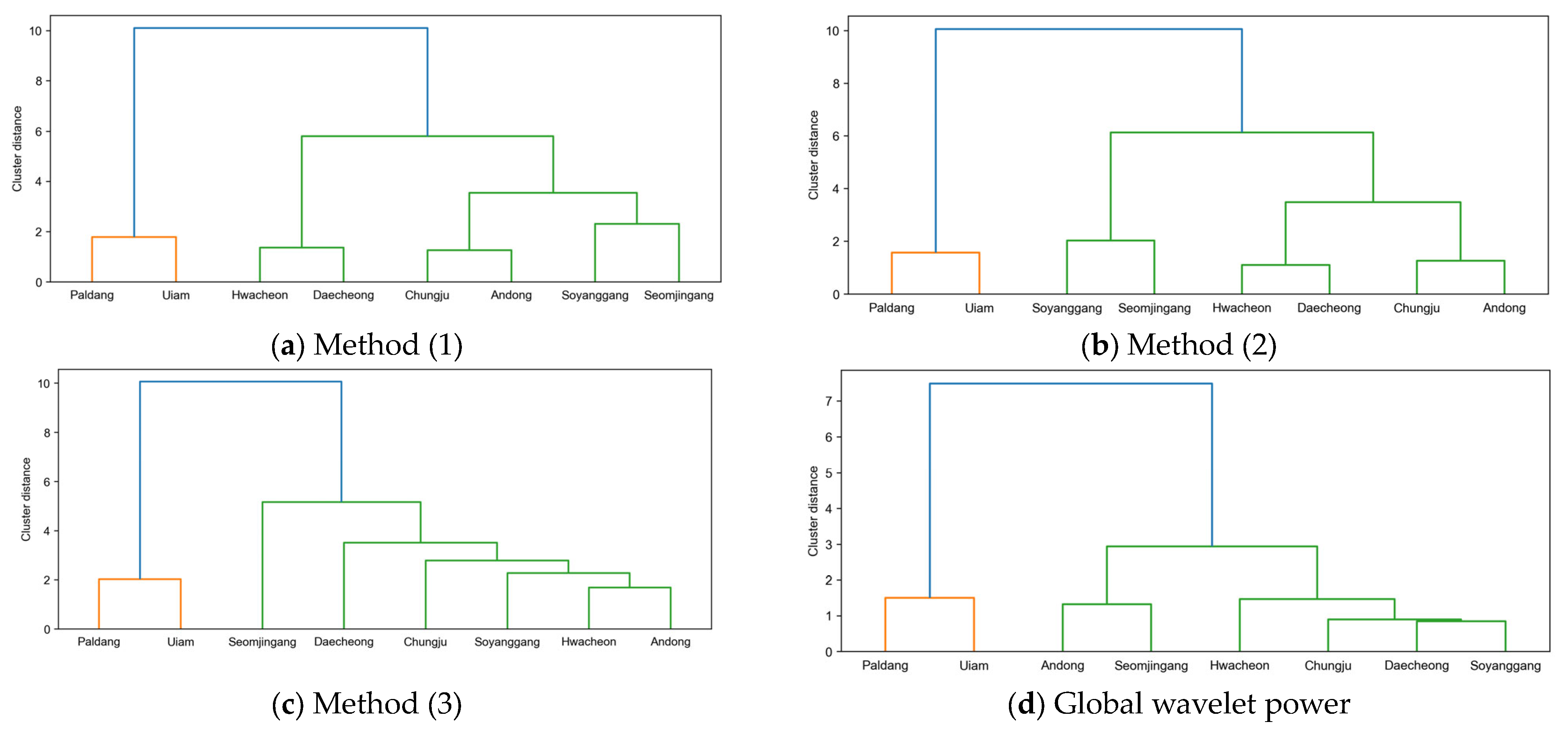
2.4. Regionalization of Basins
3. Results
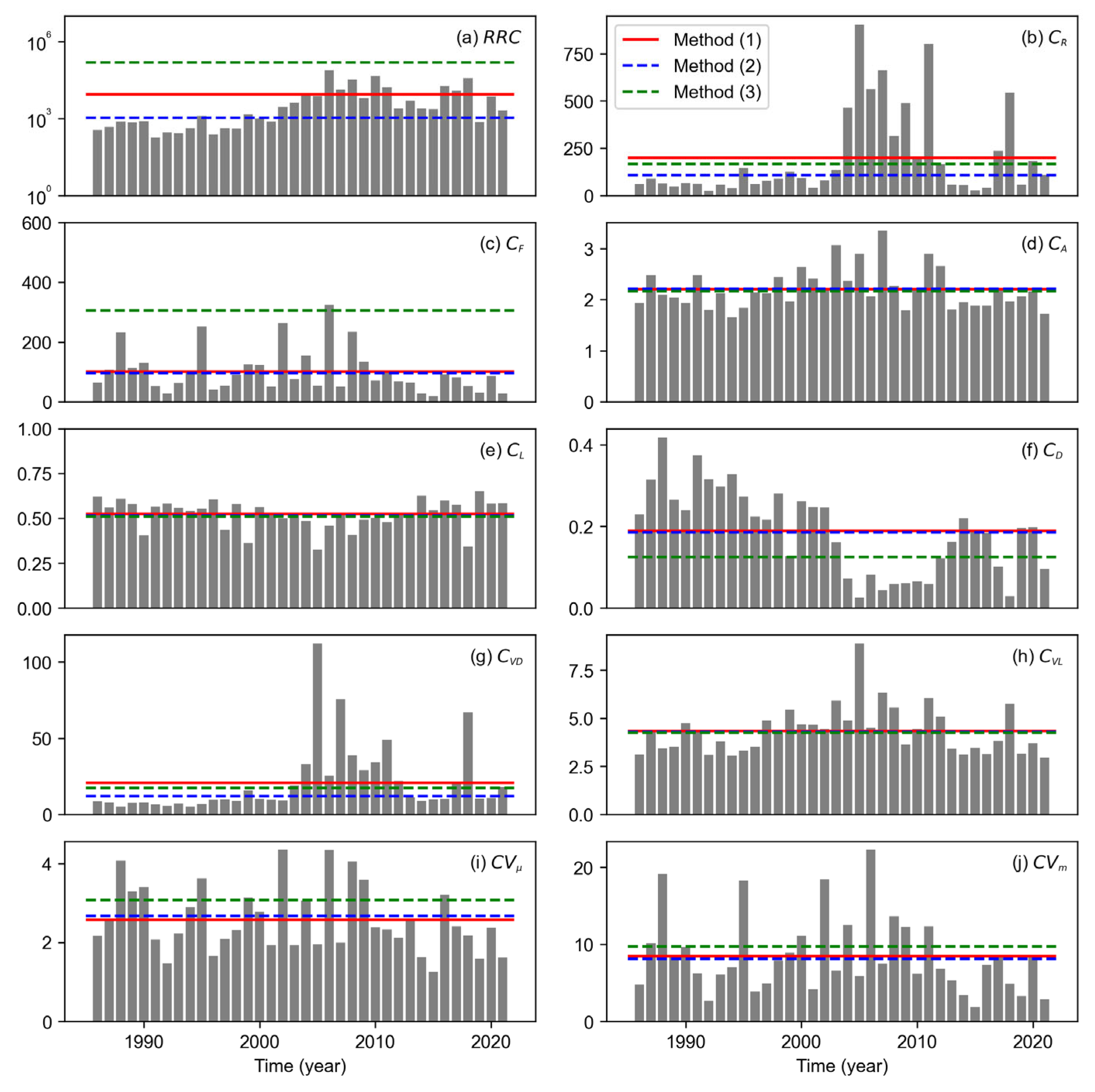
3.1. Pre-Analysis and Estimation of FFI and L-FFI
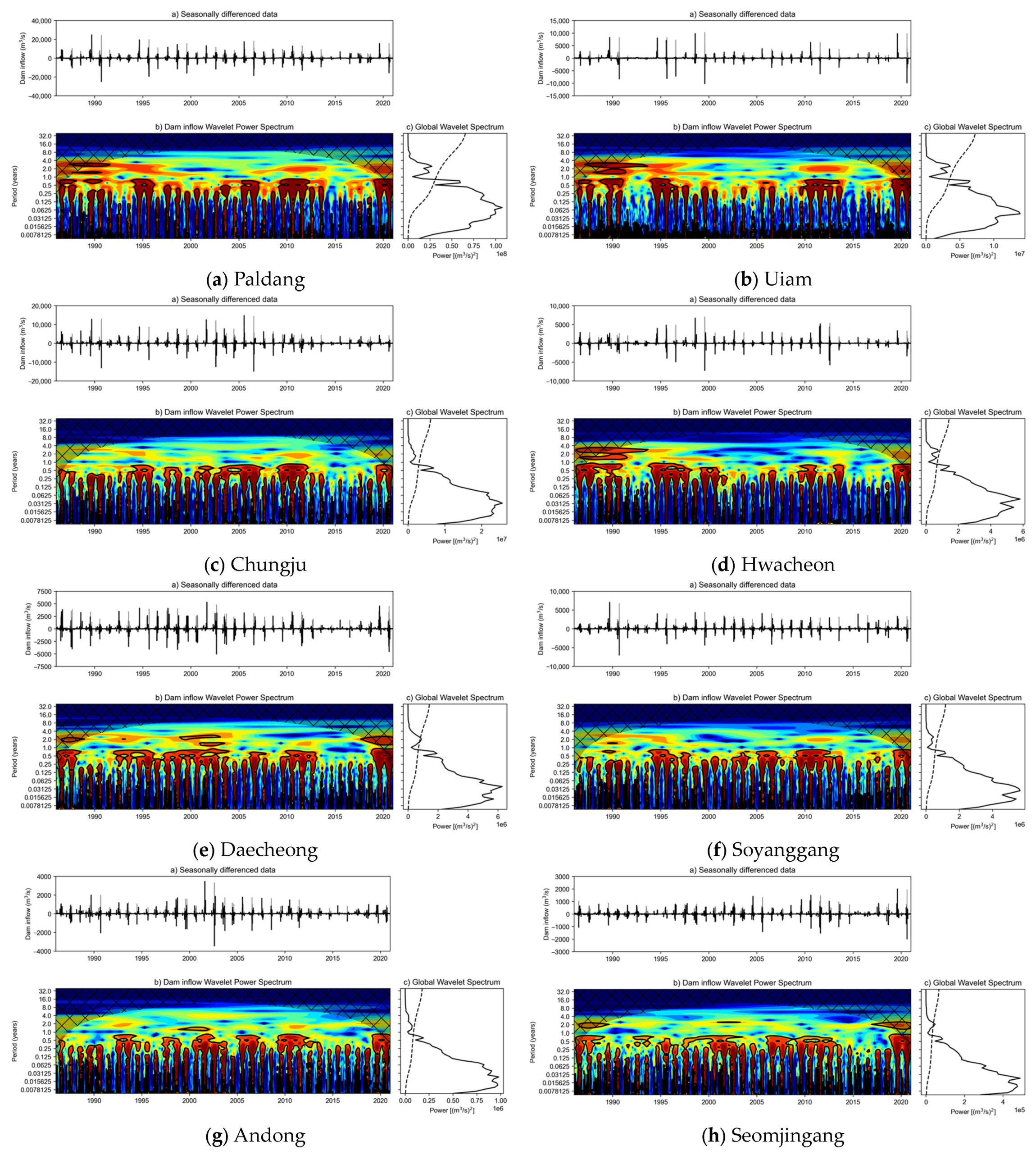
3.2. Wavelet Analysis
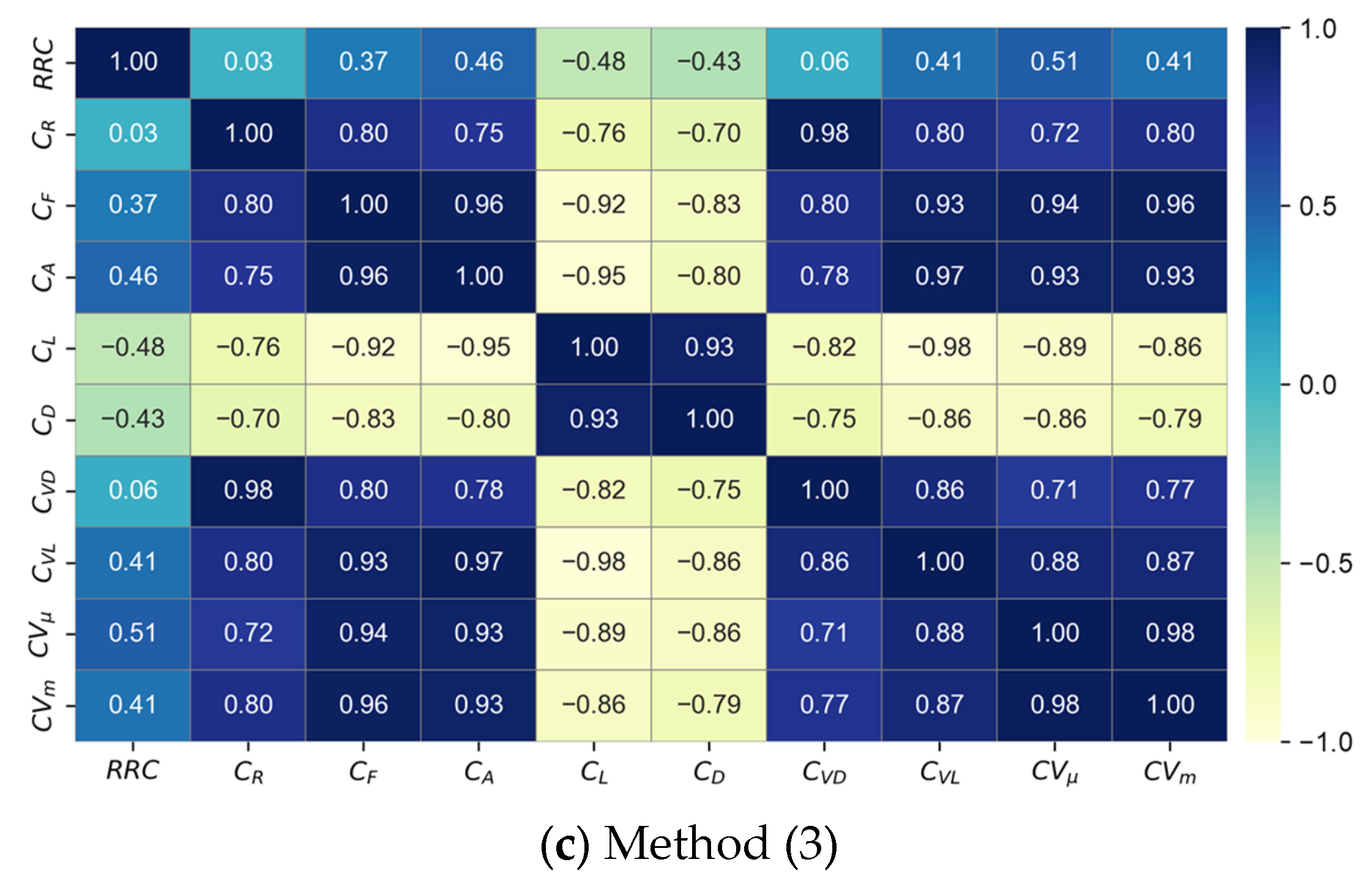
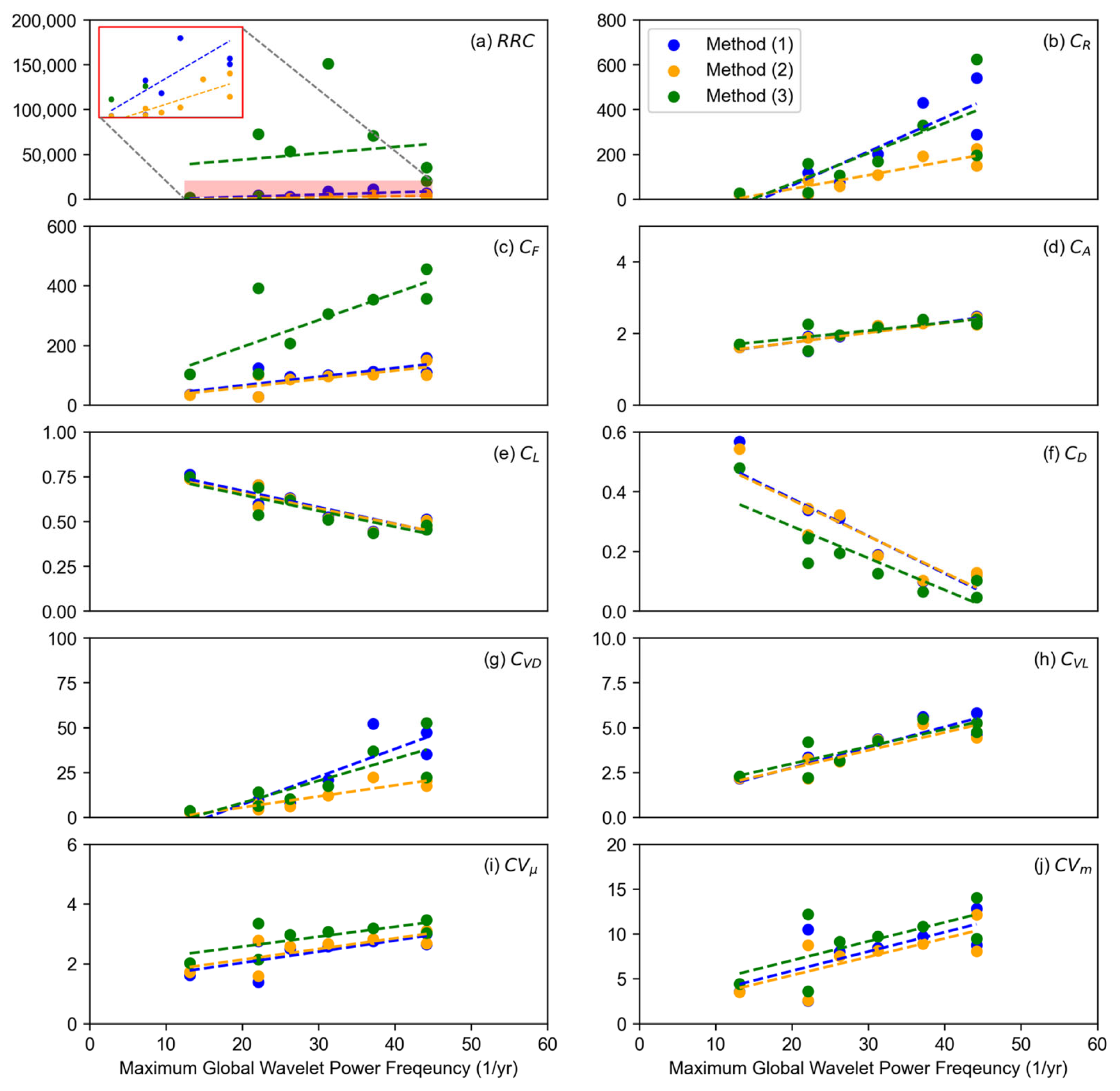
3.3. Evaluation of Methods for L-FFI Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Curry, R.A.; Gehrels, J.; Noakes, D.L.G.; Swainson, R. Effects of River Flow Fluctuations on Groundwater Discharge through Brook Trout, Salvelinus Fontinalis, Spawning and Incubation Habitats. Hydrobiologia 1994, 277, 121–134. [Google Scholar] [CrossRef]
- Huang, Y.; Schmitt, F.G.; Lu, Z.; Liu, Y. Analysis of Daily River Flow Fluctuations Using Empirical Mode Decomposition and Arbitrary Order Hilbert Spectral Analysis. J. Hydrol. 2009, 373, 103–111. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Over, T.M. River Flow Fluctuation Analysis: Effect of Watershed Area. Water Resour. Res. 2010, 46, W12529. [Google Scholar] [CrossRef]
- Vesipa, R.; Camporeale, C.; Ridolfi, L. Effect of River Flow Fluctuations on Riparian Vegetation Dynamics: Processes and Models. Adv. Water Resour. 2017, 110, 29–50. [Google Scholar] [CrossRef]
- Chalise, D.R.; Sankarasubramanian, A.; Ruhi, A. Dams and Climate Interact to Alter River Flow Regimes across the United States. Earth Future 2021, 9, e2020EF001816. [Google Scholar] [CrossRef]
- Won, T.S. Discussing the Special Characteristics of Korean Rivers. KSCE J. Civ. Environ. Eng. Res. 1962, 10, 63–72. [Google Scholar]
- Park, S.W. A Hydrological Study on the Flow Characteristic of the Keum River. J. Korean Soc. Agric. Eng. 1974, 16, 3438–3453. [Google Scholar]
- Lee, J.W.; Woo, H.S. Analysis of River Regime of the Major Rivers in Korea. In Proceedings of the Korea Water Resources Association Conference, Daejeon, Republic of Korea, 10 July 1992; pp. 177–186. [Google Scholar]
- Lee, J.W.; Kim, H.S.; Woo, H.S. An Analysis of the Effect of Damming on Flow Duration Characteristics of Five Major Rivers in Korea. KSCE J. Civ. Environ. Eng. Res. 1993, 13, 79–91. [Google Scholar]
- Lee, E.H. A Study on the Change of the River-Regime Coefficient in the Han River and Nakdong River. Geogr. J. Korean 2008, 42, 211–222. [Google Scholar]
- Handayani, Y.L.; Sujatmoko, B.; Oktavia, G. Stream’s Regime Coefficient in Upstream Rokan Watershed of Riau Province. In MATEC Web of Conference, Proceedings of the International Conference on Advances in Civil and Environmental Engineering, Bali, Indonesia, 24–25 October 2018; EDP Sciences: Les Ulis, France, 2019; Volume 276, p. 04013. [Google Scholar]
- Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.O.; Jenouvrier, S.; Stenseth, N.C. Wavelet Analysis of Ecological Time Series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef] [PubMed]
- Nakken, M. Wavelet Analysis of Rainfall–Runoff Variability Isolating Climatic from Anthropogenic Patterns. Environ. Modell. Softw. 1999, 14, 283–295. [Google Scholar] [CrossRef]
- Kailas, S.V.; Narasimha, R. Quasi-Cycles in Monsoon Rainfall by Wavelet Analysis. Curr. Sci. 2000, 78, 592–595. Available online: https://www.jstor.org/stable/24104088 (accessed on 1 May 2023).
- Souza Echer, M.P.; Echer, E.; Nordemann, D.J.; Rigozo, N.R.; Prestes, A. Wavelet Analysis of a Centennial (1895–1994) Southern Brazil Rainfall Series (Pelotas, 31 46′ 19″ S 52 20′ 33″ W). Clim. Chang. 2008, 87, 489–497. [Google Scholar] [CrossRef]
- Campozano, L.; Mendoza, D.; Mosquera, G.; Palacio-Baus, K.; Célleri, R.; Crespo, P. Wavelet Analyses of Neural Networks Based River Discharge Decomposition. Hydrol. Process. 2020, 34, 2302–2312. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, P.; Kumar, A.; Elbeltagi, A.; Kuriqi, A. Modeling Stage–Discharge–Sediment Using Support Vector Machine and Artificial Neural Network Coupled with Wavelet Transform. Appl. Water Sci. 2022, 12, 87. [Google Scholar] [CrossRef]
- Budu, K. Comparison of Wavelet-Based ANN and Regression Models for Reservoir Inflow Forecasting. J. Hydrol. Eng. 2014, 19, 1385–1400. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, M.K.; Chatterjee, C.; Mishra, A. Reservoir Inflow Forecasting Using Ensemble Models Based on Neural Networks, Wavelet Analysis and Bootstrap Method. Water Resour. Manag. 2015, 29, 4863–4883. [Google Scholar] [CrossRef]
- Tran, T.D.; Tran, V.N.; Kim, J. Improving the Accuracy of Dam Inflow Predictions Using a Long Short-Term Memory Network Coupled with Wavelet Transform and Predictor Selection. Mathematics 2021, 9, 551. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Seman, L.O.; Aquino, L.S.; Coelho, L. dos S. Wavelet-Seq2Seq-LSTM with Attention for Time Series Forecasting of Level of Dams in Hydroelectric Power Plants. Energy 2023, 274, 127350. [Google Scholar] [CrossRef]
- Labat, D. Wavelet Analysis of the Annual Discharge Records of the World’s Largest Rivers. Adv. Water Resour. 2008, 31, 109–117. [Google Scholar] [CrossRef]
- Ashraf, F.B.; Haghighi, A.T.; Riml, J.; Mathias Kondolf, G.; Kløve, B.; Marttila, H. A Method for Assessment of Sub-Daily Flow Alterations Using Wavelet Analysis for Regulated Rivers. Water Resour. Res. 2022, 58, e2021WR030421. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Zheng, W. Wavelet Analysis of Dam Injection and Discharge in Three Gorges Dam and Reservoir with Precipitation and River Discharge. Water 2022, 14, 567. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B.M.J. Non-Linear Canonical Correlation Analysis in Regional Frequency Analysis. Stoch. Environ. Res. Risk Assess. 2016, 30, 449–462. [Google Scholar] [CrossRef]
- Ahani, A.; Mousavi Nadoushani, S.S.; Moridi, A. A Hybrid Regionalization Method Based on Canonical Correlation Analysis and Cluster Analysis: A Case Study in Northern Iran. Hydrol. Res. 2019, 50, 1076–1095. [Google Scholar] [CrossRef]
- Ahani, A.; Mousavi Nadoushani, S.S.; Moridi, A. Regionalization of Watersheds Based on the Concept of Rough Set. Nat. Hazards 2020, 104, 883–899. [Google Scholar] [CrossRef]
- Ahani, A.; Mousavi Nadoushani, S.S.; Moridi, A. Regionalization of Watersheds by Finite Mixture Models. J. Hydrol. 2020, 583, 124620. [Google Scholar] [CrossRef]
- Kanishka, G.; Eldho, T.I. Streamflow Estimation in Ungauged Basins Using Watershed Classification and Regionalization Techniques. J. Earth Syst. Sci. 2020, 129, 186. [Google Scholar] [CrossRef]
- Ferreira, R.G.; da Silva, D.D.; Elesbon, A.A.A.; dos Santos, G.R.; Veloso, G.V.; Fraga, M.d.S.; Fernandes-Filho, E.I. Geostatistical Modeling and Traditional Approaches for Streamflow Regionalization in a Brazilian Southeast Watershed. J. South Am. Earth Sci. 2021, 108, 103355. [Google Scholar] [CrossRef]
- Ahani, A.; Mousavi Nadoushani, S.S.; Moridi, A. A Ranking Method for Regionalization of Watersheds. J. Hydrol. 2022, 609, 127740. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology, 1st ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Park, S.D. Development and Management of Water Resources in South and North Gangwon-Do. In Understanding the Divided Gangwon-do: Situation and Prospects; Hanul Academy: Seoul, Republic of Korea, 1999; p. 605. [Google Scholar]
- Park, S.-D. Dimensionless Flow Duration Curve in Natural River. J. Korean Water Resour. Assoc. 2003, 36, 33–44. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Autocorrelation Function and Spectrum of Stationary Processes and Analysis of Seasonal Time Series. In Time Series Analysis: Forecasting and Control, 2nd ed.; Holden-Day: San Francisco, CA, USA, 1976; pp. 21–43. [Google Scholar]
- Gardner, E.S., Jr. Exponential Smoothing: The State of the Art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Rabiner, L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and Reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Huang, N.E.; Long, S.R.; Shen, Z. The Mechanism for Frequency Downshift in Nonlinear Wave Evolution. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1996; Volume 32, pp. 59–117C. [Google Scholar]
- Rehman, N.; Mandic, D.P. Multivariate Empirical Mode Decomposition. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 466, 1291–1302. [Google Scholar] [CrossRef]
- Duan, J.-S.; Rach, R. A New Modification of the Adomian Decomposition Method for Solving Boundary Value Problems for Higher Order Nonlinear Differential Equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Accelerating the Convergence of Adomian Decomposition Method (ADM). J. Comput. Sci. 2019, 31, 54–59. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis. In Prentice Hall Signal Processing, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995; Volume 778. [Google Scholar]
- Hlawatsch, F.; Auger, F. Time-Frequency Analysis: Concepts and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wigner, E.P. On the Quantum Correction for Thermodynamic Equilibrium. In Part I: Physical Chemistry. Part II: Solid State Physics; Springer: Heidelberg, Germany, 1997; pp. 110–120. [Google Scholar]
- Smith, L.C.; Turcotte, D.L.; Isacks, B.L. Stream Flow Characterization and Feature Detection Using a Discrete Wavelet Transform. Hydrol. Process. 1998, 12, 233–249. [Google Scholar] [CrossRef]
- Gabor, D. Theory of Communication. Part 1: The Analysis of Information. J. Inst. Electr. Eng. Part III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.-M. Wavelets and Their Applications, 1st ed.; ISTE: London, UK, 2007; ISBN 978-1-905209-31-6. [Google Scholar]
- Ngui, W.K.; Leong, M.S.; Hee, L.M.; Abdelrhman, A.M. Wavelet Analysis: Mother Wavelet Selection Methods. Appl. Mech. Mater. 2013, 393, 953–958. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Azevedo, N.; Soares, M.J. Using Wavelets to Decompose the Time–Frequency Effects of Monetary Policy. Physica A 2008, 387, 2863–2878. [Google Scholar] [CrossRef]
- Rua, A. Measuring Comovement in the Time–Frequency Space. J. Macroecon. 2010, 32, 685–691. [Google Scholar] [CrossRef]
- Lee, J.; Lee, H.; Yoo, C. Selection of mother wavelet for bivariate wavelet analysis. J. Korean Water Resour. Assoc. 2019, 52, 905–916. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Amer. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Srinivas, V.V. Regionalization of Watersheds Using Soft Computing Techniques. ISH J. Hydraul. Eng. 2009, 15, 170–193. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.; Hao, Z.-C.; Chen, X.; Zhang, Z.; Xu, C.-Y.; Sun, L. Regional Frequency Analysis and Spatio-Temporal Pattern Characterization of Rainfall Extremes in the Pearl River Basin, China. J. Hydrol. 2010, 380, 386–405. [Google Scholar] [CrossRef]
- Hassan, B.G.; Ping, F. Formation of Homogenous Regions for Luanhe Basin-by Using L-Moments and Cluster Techniques. Int. J. Environ. Sci. Dev. 2012, 3, 205. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Soleimani, S.; Sadikoglu, F. Application of Different Clustering Approaches to Hydroclimatological Catchment Regionalization in Mountainous Regions, a Case Study in Utah State. J. Mt. Sci. 2018, 15, 461–484. [Google Scholar] [CrossRef]
- Ramachandra Rao, A.; Srinivas, V.V. Regionalization of Watersheds by Hybrid-Cluster Analysis. J. Hydrol. 2006, 318, 37–56. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
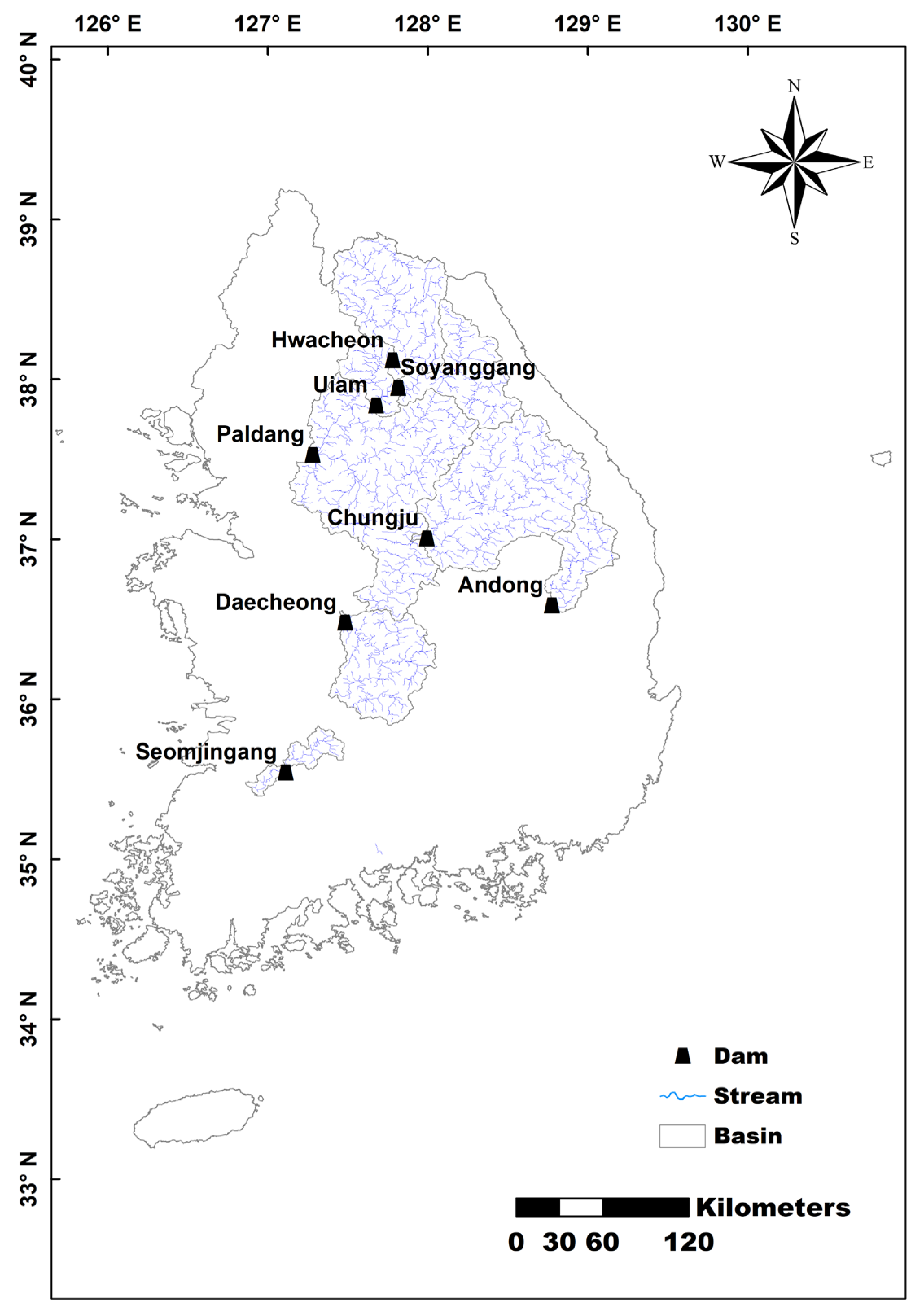
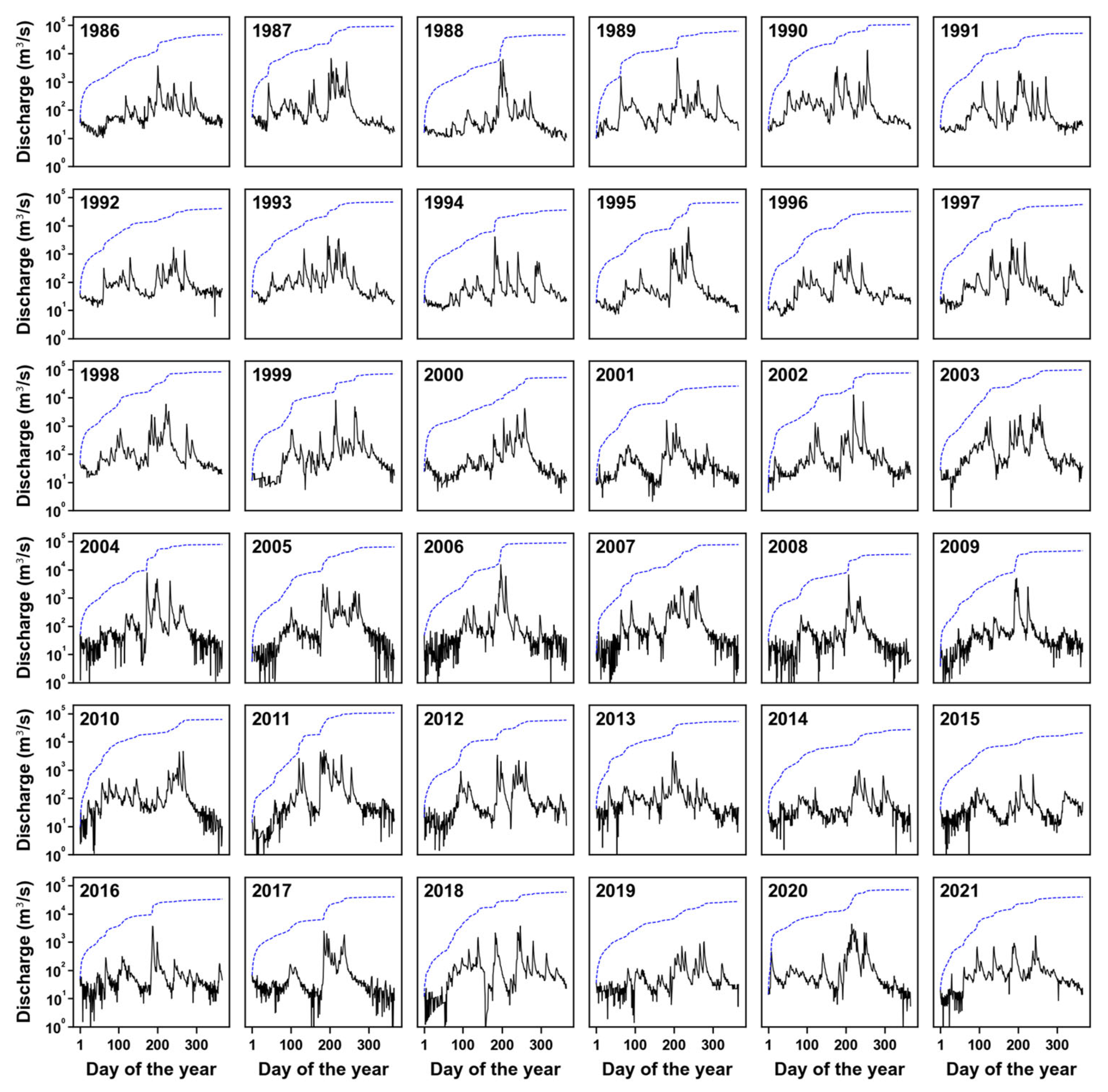

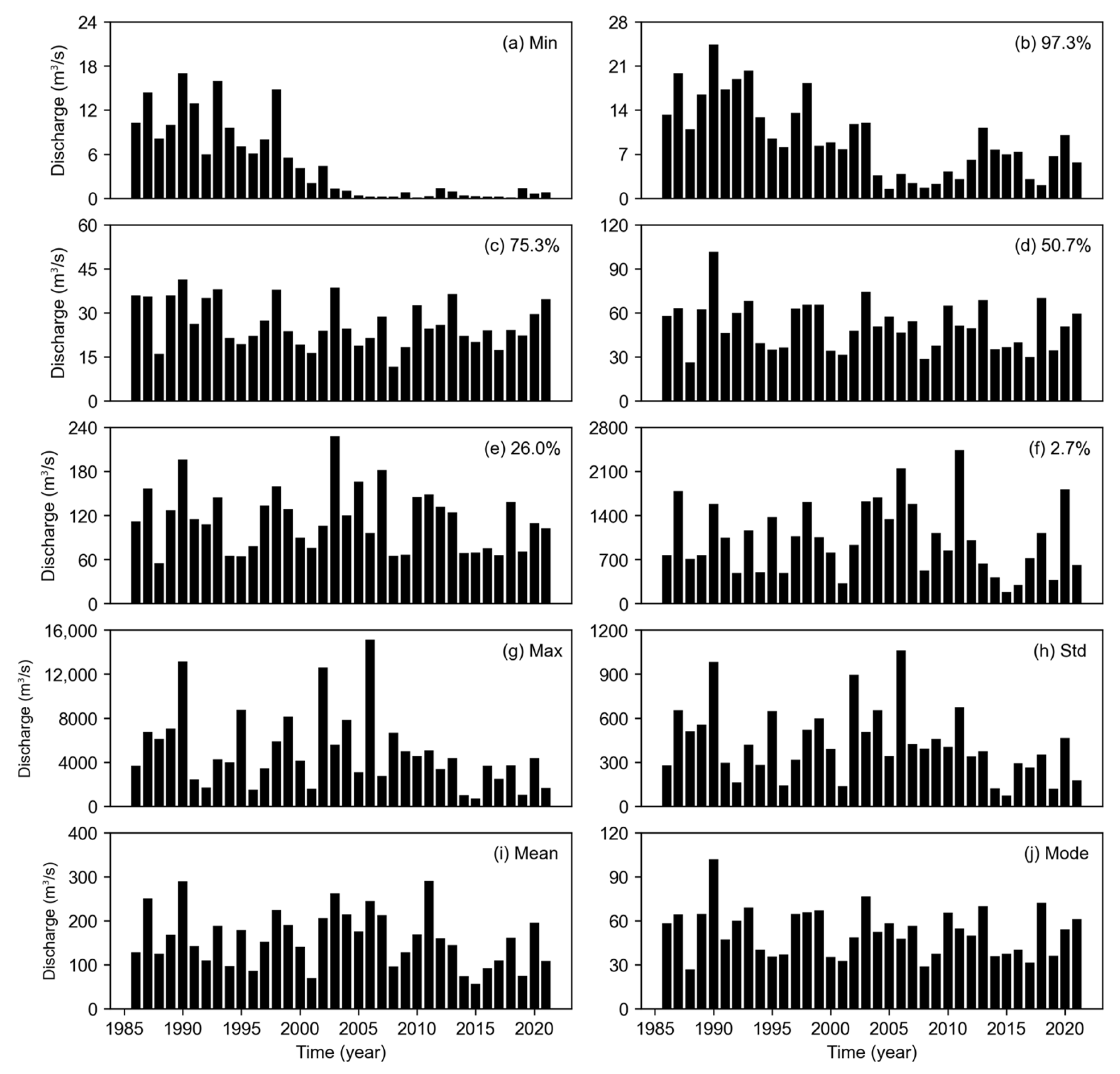
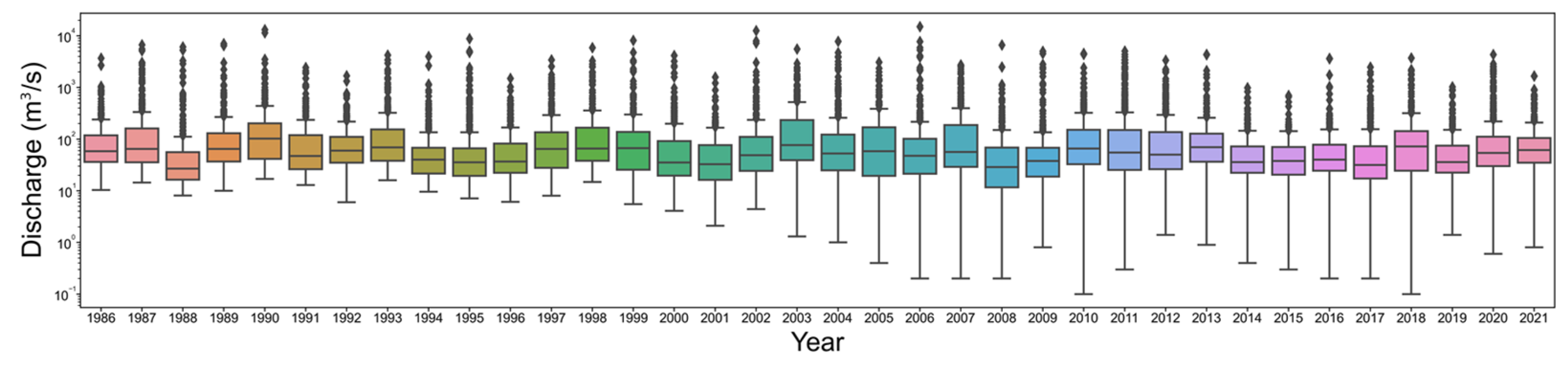
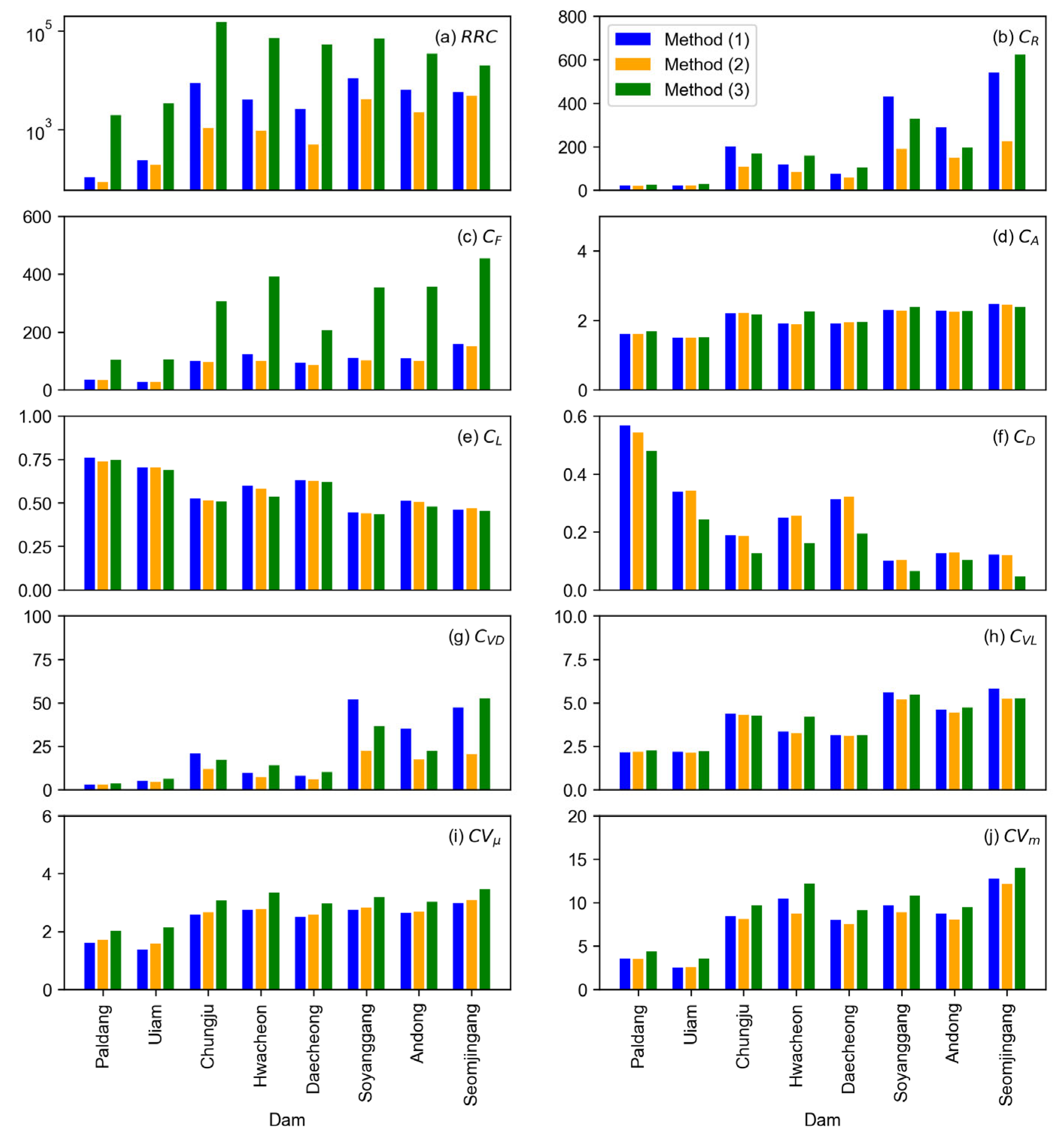



| Dam Name | Basin Area (km2) | Channel Length (km) | Total Storage (106 m3) |
|---|---|---|---|
| Paldang | 23,800 | 377.6 | 244 |
| Uiam | 7709 | 230.9 | 80 |
| Chungju | 6648 | 270.6 | 2750 |
| Hwacheon | 3901 | 178.1 | 1018 |
| Daecheong | 3204 | 208.1 | 1490 |
| Soyanggang | 2703 | 136.0 | 2900 |
| Andong | 1584 | 142.4 | 1248 |
| Seomjingang | 763 | 74.2 | 466 |
| Symbol | Equation | Index | Description |
|---|---|---|---|
| River regime coefficient | The ratio of the maximum flow to the minimum flow | ||
| Flow regime coefficient | The ratio of the high flow to the low flow excepting for the extreme flows | ||
| Flood coefficient | The ratio of the maximum flow to the approximate mode flow | ||
| Abundance coefficient | The ratio of the approximate third quartile flow to the approximate median flow | ||
| Low coefficient | The ratio of the approximate first quartile flow to the approximate median flow | ||
| Drought coefficient | The ratio of the high flow to the approximate median flow | ||
| Variance of the drought coefficient | The ratio of the approximate third quartile flow to the low flow | ||
| Variance of the low coefficient | The ratio of the approximate third quartile flow to the approximate first quartile flow | ||
| Coefficient of variance based on mean | The variation of the flows to the mean flow | ||
| Coefficient of variance based on median | The variation of the flows to the median flow |
| Year | Min | Max | RRC | Year | Min | Max | RRC |
|---|---|---|---|---|---|---|---|
| 1986 | 10.3 | 3683.9 | 357.7 | 2004 | 4.1 | 4154.6 | 1013.3 |
| 1987 | 14.4 | 6731.8 | 467.5 | 2005 | 2.1 | 1586.5 | 755.5 |
| 1988 | 8.1 | 6121.9 | 755.8 | 2006 | 4.4 | 12,599.5 | 2863.5 |
| 1989 | 10.0 | 7043.6 | 704.4 | 2007 | 1.3 | 5575.2 | 4288.6 |
| 1990 | 17.0 | 13,142.1 | 773.1 | 2008 | 1.0 | 7808.1 | 7808.1 |
| 1991 | 12.9 | 2427.0 | 188.1 | 2009 | 0.4 | 3084.2 | 7710.5 |
| 1992 | 6.0 | 1692.0 | 282.0 | 2010 | 0.2 | 15,126.4 | 75,632.0 |
| 1993 | 16.0 | 4250.0 | 265.6 | 2011 | 0.2 | 2735.2 | 13,676.0 |
| 1994 | 9.6 | 4003.4 | 417.0 | 2012 | 0.2 | 6662.3 | 33,311.5 |
| 1995 | 7.1 | 8776.2 | 1236.1 | 2013 | 0.8 | 5012.7 | 6265.9 |
| 1996 | 6.1 | 1496.3 | 245.3 | 2014 | 0.1 | 4586.1 | 45,861.0 |
| 1997 | 8.0 | 3428.5 | 428.6 | 2015 | 0.3 | 5059.9 | 16,866.3 |
| 1998 | 14.8 | 5897.2 | 398.5 | 2016 | 1.4 | 3373.7 | 2409.8 |
| 1999 | 5.5 | 8156.7 | 1483.0 | 2017 | 0.9 | 4379.9 | 4866.6 |
| 2000 | 4.1 | 4154.6 | 1013.3 | 2018 | 0.4 | 989.1 | 2472.8 |
| 2001 | 2.1 | 1586.5 | 755.5 | 2019 | 0.3 | 700.4 | 2334.7 |
| 2002 | 4.4 | 12,599.5 | 2863.5 | 2020 | 0.2 | 3663.7 | 18,318.5 |
| 2003 | 1.3 | 5575.2 | 4288.6 | 2021 | 0.2 | 2467.1 | 12,335.5 |
| Index | Method (1) | Method (2) | Method (3) |
| 8723.5 | 1059.8 | 151,264.0 | |
| 200.4 | 108.1 | 167.7 | |
| 100.9 | 96.2 | 305.6 | |
| 2.2 | 2.2 | 2.2 | |
| 0.5 | 0.5 | 0.5 | |
| 0.2 | 0.2 | 0.1 | |
| 20.7 | 12.0 | 17.3 | |
| 4.3 | 4.3 | 4.3 | |
| 2.6 | 2.7 | 3.1 | |
| 8.4 | 8.1 | 9.7 |
| Dam | M-GWP [(m3/s)2] | Period (year) | Frequency (1/y) |
|---|---|---|---|
| Paldang | 107,505,864 | 0.076 | 13.1 |
| Uiam | 13,904,177 | 0.045 | 22.1 |
| Chungju | 25,609,269 | 0.032 | 31.2 |
| Hwacheon | 5,821,673 | 0.045 | 22.1 |
| Daecheong | 6,286,009 | 0.038 | 26.3 |
| Soyanggang | 5,658,015 | 0.027 | 37.1 |
| Andong | 979,627 | 0.023 | 44.2 |
| Seomjingang | 488,983 | 0.023 | 44.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Moon, G.; Lee, J.; Jun, C.; Choi, J. Evaluation of Methods for Estimating Long-Term Flow Fluctuations Using Frequency Characteristics from Wavelet Analysis. Water 2023, 15, 2968. https://doi.org/10.3390/w15162968
Lee J, Moon G, Lee J, Jun C, Choi J. Evaluation of Methods for Estimating Long-Term Flow Fluctuations Using Frequency Characteristics from Wavelet Analysis. Water. 2023; 15(16):2968. https://doi.org/10.3390/w15162968
Chicago/Turabian StyleLee, Jinwook, Geonsoo Moon, Jiho Lee, Changhyun Jun, and Jaeyong Choi. 2023. "Evaluation of Methods for Estimating Long-Term Flow Fluctuations Using Frequency Characteristics from Wavelet Analysis" Water 15, no. 16: 2968. https://doi.org/10.3390/w15162968
APA StyleLee, J., Moon, G., Lee, J., Jun, C., & Choi, J. (2023). Evaluation of Methods for Estimating Long-Term Flow Fluctuations Using Frequency Characteristics from Wavelet Analysis. Water, 15(16), 2968. https://doi.org/10.3390/w15162968








