Scour Development Around an Oblong Bridge Pier: A Numerical and Experimental Study
Abstract
1. Introduction
2. The Hydrodynamic Model
2.1. Framework
2.2. Flow Computation
2.3. Sediment Transport Equations
3. Local Scouring Experimental Data
4. Numerical Model Setup
4.1. Mesh Geometrical Dimensions
4.2. Boundary Conditions and Input Parameters
5. Results and Discussion
5.1. General Considerations
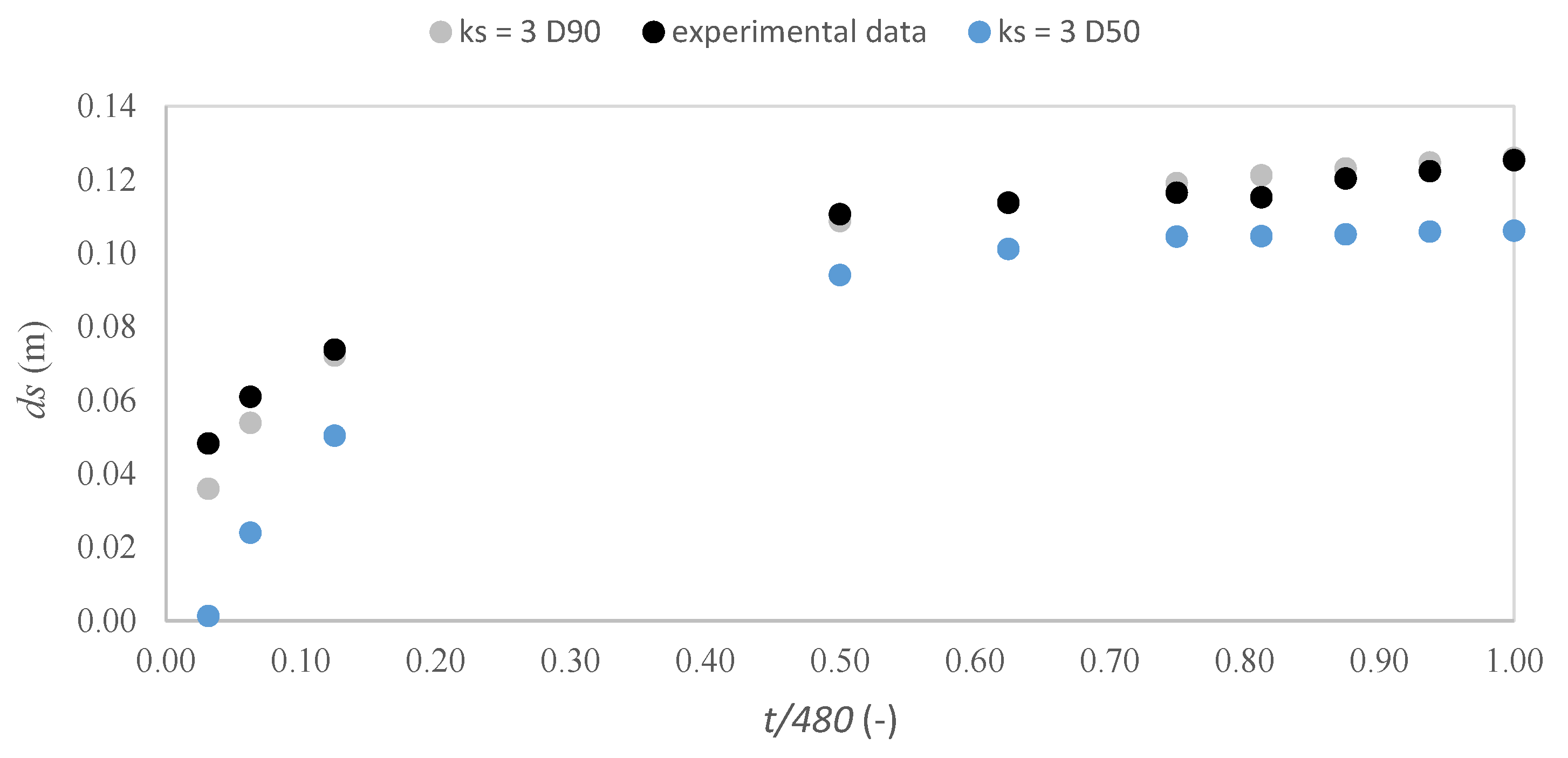
5.2. Scour Depth Estimates
5.3. Bed Morphology
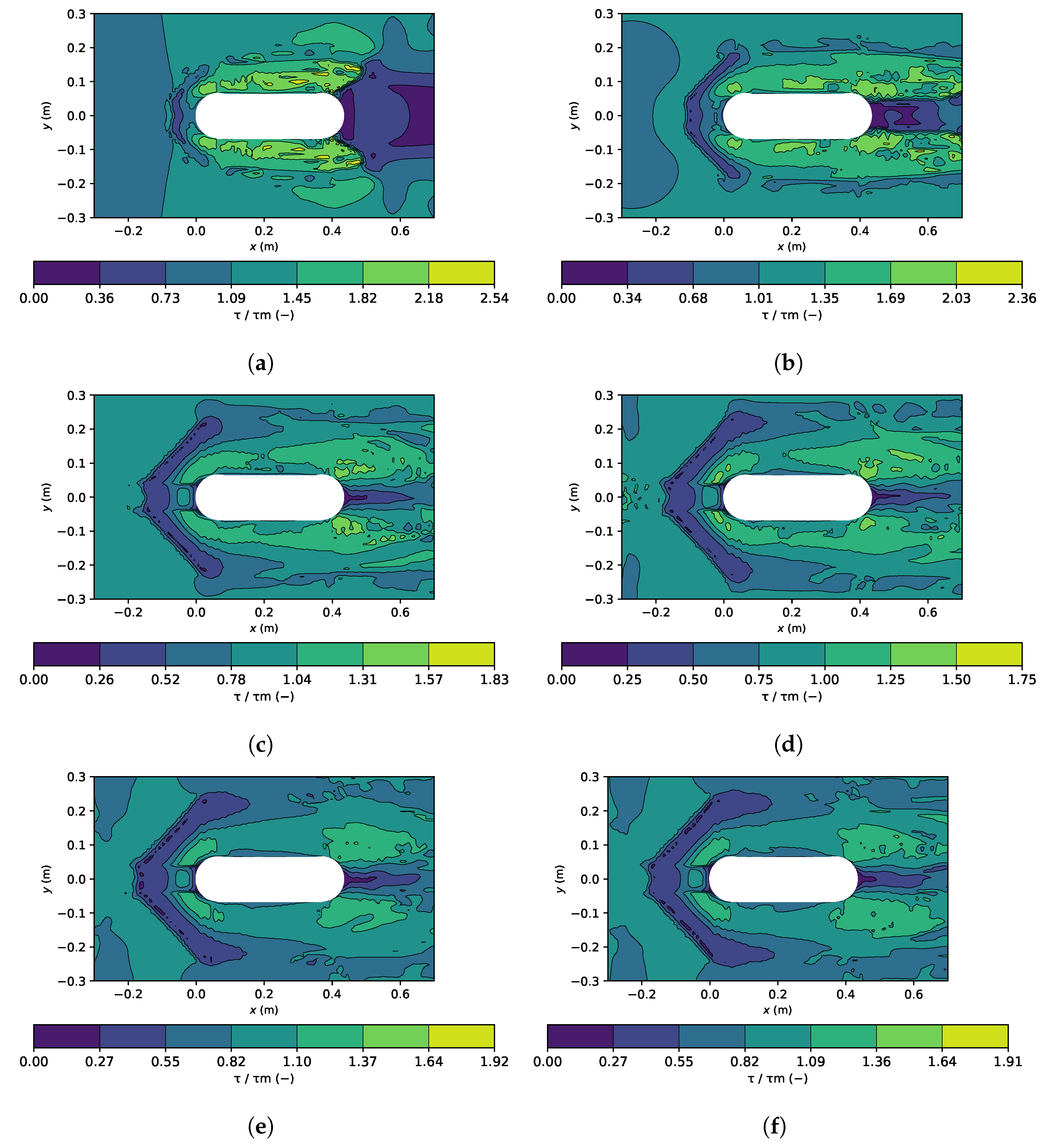
5.4. Bed Shear Stress
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cook, W.; Barr, P.J.; Halling, M.W. Bridge Failure Rate. J. Perform. Constr. Facil. 2015, 29, 04014080. [Google Scholar] [CrossRef]
- Flint, M.M.; Fringer, O.; Billington, S.L.; Freyberg, D.; Diffenbaugh, N.S. Historical Analysis of Hydraulic Bridge Collapses in the Continental United States. J. Infrastruct. Syst. 2017, 23, 04017005. [Google Scholar] [CrossRef]
- Proske, D. Bridge Collapse Frequencies Versus Failure Probabilities; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Rocha, J.S.; do Carmo, J.S.A.; Lemos, L.J.L.; da Silva, V.D.; da Silva Rebelo, C.A. Pontes construídas sobre fundos aluvionares: O colapso da ponte Hintze Ribeiro. Recur. Hidricos 2008, 29, 41–57. [Google Scholar]
- Chiew, Y.M.; Lai, J.S.; Link, O. Experimental, Numerical and Field Approaches to Scour Research. Water 2020, 12, 1749. [Google Scholar] [CrossRef]
- Dargahi, B. The turbulent flow field around a circular cylinder. Exp. Fluids 1989, 8, 1–12. [Google Scholar] [CrossRef]
- Hoffmans, G.; Verheij, H. Scour Manual; A.A. Balkema/CRC Press: Rotterdam, The Netherlands, 1997; Volume 96. [Google Scholar]
- Melville, B.W.; Raudkivi, A.J. Flow characteristics in local scour at bridge piers. J. Hydraul. Res. 1977, 15, 373–380. [Google Scholar] [CrossRef]
- Graf, W.; Istiarto, I. Flow pattern in the scour hole around a cylinder. J. Hydraul. Res. 2002, 40, 13–20. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2006, 42, 1–19. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, S.G.; Ettema, R. Coherent Structures in the Flow Field around a Circular Cylinder with Scour Hole. J. Hydraul. Eng. 2008, 134, 572–587. [Google Scholar] [CrossRef]
- Diab, R.M.A.E.A. Experimental Investigation on Scouring Around Piers of Different Shape and Alignment in Gravel. Ph.D. Thesis, TU Darmstadt, Darmstadt, Germany, 2011. [Google Scholar]
- Bento, A.M.; Viseu, T.; Pêgo, J.P.; Couto, L. Experimental Characterization of the Flow Field around Oblong Bridge Piers. Fluids 2021, 6, 370. [Google Scholar] [CrossRef]
- Escauriaza, C.; Paola, C.; Voller, V.R. Computational Models of Flow, Sediment Transport and Morphodynamics in Rivers. In Gravel-Bed Rivers; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 1–31. [Google Scholar] [CrossRef]
- Briley, W.R.; McDonald, H. Computation of three-dimensional horseshoe vortex flow using the Navier-Stokes equations. In Proceedings of the Seventh International Conference on Numerical Methods in Fluid Dynamics, Stanford, CA, USA, 23–27 June 1980; Springer: Berlin/Heidelberg, Germany, 1981; pp. 91–98. [Google Scholar] [CrossRef]
- Kwak, D.; Rogers, S.E.; Kaul, U.K.; Chang, J.L.C. A numerical study of incompressible juncture flows. In Proceedings of the Tenth International Conference on Numerical Methods in Fluid Dynamics, Beijing, China, 23–27 June 1986; Springer: Berlin/Heidelberg, Germany, 1986; pp. 398–402. [Google Scholar] [CrossRef]
- Deng, G.B.; Piquet, J. Navier-Stokes computations of horseshoe vortex flows. Int. J. Numer. Methods Fluids 1992, 15, 99–124. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X.L.; Wang, J.H. Numerical investigation of local scour around three adjacent piles with different arrangements under current. Ocean Eng. 2017, 142, 625–638. [Google Scholar] [CrossRef]
- Olsen, N.R.B.; Melaaen, M.C. Three-Dimensional Calculation of Scour Around Cylinders. J. Hydraul. Eng. 1993, 119, 1048–1054. [Google Scholar] [CrossRef]
- Olsen, N.R.B.; Kjellesvig, H.M. Three-dimensional numerical flow modeling for estimation of maximum local scour depth. J. Hydraul. Res. 1998, 36, 579–590. [Google Scholar] [CrossRef]
- Richardson, J.E.; Panchang, V.G. Three-Dimensional Simulation of Scour-Inducing Flow at Bridge Piers. J. Hydraul. Eng. 1998, 124, 530–540. [Google Scholar] [CrossRef]
- Wang, S.; Jia, Y. Computational simulations of local scour at bridge crossings-Capabilities and limitations. In Proceedings of the Proceedings ASCE International Water Resources Engineering Conference: Past Accomplishments and New Challenges” ASCE, Seattle, WA, USA, 8–12 August 1999. [Google Scholar]
- Chang, W.Y.; Lai, J.S.; Yen, C.L. Simulation of scour depth evolution at pier nose. In Proceedings of the 1999 International Water Resources Engineering Conference, Seattle, WA, USA, 8–12 August 1999; Session BS–05. Water Resources Publications LLC: Highlands Ranch, CO, USA, 1999. [Google Scholar]
- Tseng, M.H.; Yen, C.L.; Song, C.C.S. Computation of three-dimensional flow around square and circular piers. Int. J. Numer. Methods Fluids 2000, 34, 207–227. [Google Scholar] [CrossRef]
- Chen, H. Numerical simulation of scour around complex piers in cohesive soil. In Proceedings of the First International Conference on Scour of Foundations International Society of Soil Mech and Foundations, College Station, TX, USA, 17–20 November 2002. [Google Scholar]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Baranya, S.; Olsen, N.R.B.; Stoesser, T.; Sturm, T. Three-Dimensional RANS Modeling of Flow Around Circular Piers using Nested Grids. Eng. Appl. Comput. Fluid Mech. 2012, 6, 648–662. [Google Scholar] [CrossRef]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredsøe, J. Numerical investigation of flow and scour around a vertical circular cylinder. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140104. [Google Scholar] [CrossRef]
- Sumer, B. A review of recent advances in numerical modelling of local scour problems. In Proceedings of the Fifth International Conference on Scour and Erosion, San Francisco, CA, USA, 7–10 November 2010; CRC Press: Boca Raton, FL, USA, 2015; pp. 61–70. [Google Scholar] [CrossRef]
- Jia, Y.; Altinakar, M.; Guney, M.S. Three-dimensional numerical simulations of local scouring around bridge piers. J. Hydraul. Res. 2017, 56, 351–366. [Google Scholar] [CrossRef]
- Olsen, N. A Three-Dimensional Numerical Model for Simulation of Sediment Movements in Water Intakes with Moving Option—User’s Manual; The Norwegian University of Science and Technology: Trondheim, Norway, 2018. [Google Scholar]
- Bento, A.M.; Couto, L.; Viseu, T.; Pêgo, J.P. Image-Based Techniques for the Advanced Characterization of Scour around Bridge Piers in Laboratory. J. Hydraul. Eng. 2022, 148, 06022004. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD; DCW Industries, Inc.: La Cãnada, CA, USA, 2006. [Google Scholar]
- Patankar, S.; Spalding, D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Hines, Jonathan. A Comparative Study of the SIMPLE and Fractional Step Time Integration Methods for Transient Incompressible Flows. Master’s Thesis, University of Waterloo, Waterloo, ON, USA, 2008.
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Hemisphere Pub. Corp. McGraw-Hill: New York, NY, USA, 1980; p. 197. [Google Scholar]
- Olsen, N. A Three-Dimensional Numerical Model for Simulation of Sediment Movements in Water Intakes. Ph.D. Thesis, Norwegian Institute of Technology, University of Trondhein, Trondheim, Norway, 1991. [Google Scholar]
- Melaaen, M.C. Calculation of fluid flows with staggered and nonstaggered curvilinear nonorthogonal grids-the theory. Numer. Heat Transf. Part B Fundam. 1992, 21, 1–19. [Google Scholar] [CrossRef]
- Versteeg, H.K. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education Ltd.: Harlow, UK; New York, NY, USA, 2007. [Google Scholar]
- Exner, F. Zur physik der dunen. Akad. Wiss. Wien Math. Naturwiss. Kl. 1920, 129, 929–952. (In German) [Google Scholar]
- Exner, F.M. Uber die wechselwirkung zwischen wasser und geschiebe in flussen. Akad. Wiss. Wien Math. Naturwiss. Kl. 1925, 134, 165–204. [Google Scholar]
- Rijn, L.C.V. Sediment Transport, Part III: Bed forms and Alluvial Roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Shields, A. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; Caltech Library: Pasadena, CA, USA, 1936. [Google Scholar]
- Brooks, N.H. Discussion on “Boundary shear stresses in curved trapezoidal channels”. J. Hydraul. Div. ASCE 1963, 89, 327–333. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Demir, H.; Melville, B.W. Scour at Wide Piers and Long Skewed Piers; Transportation Research Board: Washington, DC, USA, 2011; Volume 682. [Google Scholar] [CrossRef]
- Bento, A.M. Risk-Based Analysis of Bridge Scour Prediction. Ph.D. Thesis, Faculty of Engineeing of the University of Porto, Porto, Portugal, 2021. [Google Scholar]
- Thompson, J.F. Elliptic grid generation. Appl. Math. Comput. 1982, 10–11, 79–105. [Google Scholar] [CrossRef]
- Alemi, M.; Maia, R. Numerical Simulation of the Flow and Local Scour Process around Single and Complex Bridge Piers. Int. J. Civ. Eng. 2016, 16, 475–487. [Google Scholar] [CrossRef]
- Olsen, N.R.B. Numerical Modelling and Hydraulics; Technical Report; Norwegian University of Science and Technology: Trondheim, Norway, 2012. [Google Scholar]
- Keefer, T.N. The Relation of Turbulence to Diffusion in Open-Channel Flows; US Department of the Interior, Geological Survey, Water Resources Division: Reston, VA, USA, 1971.
- Naas, S.L. Flow Behavior in Alluvial Channel Bends. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1977. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Rodi, W. Turbulence Models and Their Application in Hydraulics: A State-of-the Art Review; A.A. Balkema: Rotterdam, The Netherlands; Broofield, VT, USA, 1993. [Google Scholar]
- Guo, J. Hunter Rouse and Shields diagram. In Advances in Hydraulics and Water Engineering; World Scientific Publishing Company: Singapore, 2002. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries, and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993; Volume 1006. [Google Scholar]
- Matos Fernandes, M. Mecânica dos Solos—Conceitos e Princípios Fundamentais; Oficina de Textos: São Paulo, Brazil, 2016; Volume 1. [Google Scholar]




| Q | h | V | |||||
|---|---|---|---|---|---|---|---|
| Experiment | 0.0923 | 0.1440 | 0.3205 | 1.0295 | 0.2696 | 46,150 | 35,253.47 |
| t (min) | (m) | (m) | (%) |
|---|---|---|---|
| 15 | 0.048 | 0.036 | 25.4 |
| 30 | 0.061 | 0.054 | 11.8 |
| 60 | 0.074 | 0.072 | 2.2 |
| 240 | 0.111 | 0.109 | 1.7 |
| 300 | 0.114 | 0.114 | −0.2 |
| 360 | 0.117 | 0.119 | −2.3 |
| 390 | 0.115 | 0.121 | −5.2 |
| 420 | 0.120 | 0.123 | −2.4 |
| 450 | 0.122 | 0.125 | −2.0 |
| 480 | 0.125 | 0.126 | −0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bento, A.M.; Pêgo, J.P.; Viseu, T.; Couto, L. Scour Development Around an Oblong Bridge Pier: A Numerical and Experimental Study. Water 2023, 15, 2867. https://doi.org/10.3390/w15162867
Bento AM, Pêgo JP, Viseu T, Couto L. Scour Development Around an Oblong Bridge Pier: A Numerical and Experimental Study. Water. 2023; 15(16):2867. https://doi.org/10.3390/w15162867
Chicago/Turabian StyleBento, Ana Margarida, João Pedro Pêgo, Teresa Viseu, and Lúcia Couto. 2023. "Scour Development Around an Oblong Bridge Pier: A Numerical and Experimental Study" Water 15, no. 16: 2867. https://doi.org/10.3390/w15162867
APA StyleBento, A. M., Pêgo, J. P., Viseu, T., & Couto, L. (2023). Scour Development Around an Oblong Bridge Pier: A Numerical and Experimental Study. Water, 15(16), 2867. https://doi.org/10.3390/w15162867







