A Geological Site Selection Method of a Coal Mine Underground Reservoir and Its Application

Abstract

The selection of a suitable location is a crucial prerequisite for the construction of an underground reservoir in water-scarce coal-mining regions, while there are few reports related. In this research, the geological influencing factors of water storage capacity of an underground reservoir were investigated. Caved sandstone provides effective storage space for mine water and mudstone in the floor prevents the mine water in the goaf from leaking downward. The water storage capacity of coal mine underground reservoir is positively correlated with the coal thickness, sandstone ratio of the roof, water storage coefficient, and effective safety thickness, and is negatively correlated with the elevation of the main coal floor and sandstone ratio of the floor. A mathematical model of water storage coefficient was established and a geological site selection method of a coal mine underground reservoir was proposed based on an entropy weight method. With a HJT coal mine in the Shendong coal mining area of China as a case study, the implementation of this method was elaborated. For an existing underground reservoir, located in the goaf of No. 12301 fully mechanized long wall mining face of No. 1⁻² coal seam in the HJT mine field, the water storage coefficient (Q) and the site selection suitability index (SI) were 0.2194 (Q) and 0.544 (SI, at a good level). The estimated values were consistent with the actual situation, which may verify the accuracy and reliability of this method to some extent. SI was estimated for No. 2⁻² coal seams and the suitable locations for the construction of underground reservoirs were predicted in this mine field.

1. Introduction

The Shendong mining area is situated in the arid and semi-arid region of Northwestern China, where water resources are relatively scarce and ecological conditions are fragile. The annual output of the Shendong coal mining area is greater than 200 million tons of coal and the high intensity coal mining activities exert adverse effects on local water resources and ecology [1,2]. Therefore, how to address the “coal–water–ecology” conflict is a key technical issue in the mining area [3,4,5]. To safeguard the underground water resources in the mining area, the Shendong Coal Company took measures to seal off water-conducting fractures and intercept the migration of groundwater, which achieved certain positive results [6,7]. Based on a large amount of engineering practice, Gu proposed a novel method of establishing coal mine distributed underground water reservoirs with “guide, store, and utilize” as the core concept [8] (Figure 1). This method redirects mine water to the goaf for purification, storage, and utilization, and can effectively reduce evaporation loss and achieve efficient utilization of mine water resources. [9,10]. In recent years, researchers made considerable efforts in the construction technology of reservoir dams [11,12,13], layout of pipeline networks and tunnels, reservoir capacity design [14], and safety facility management of coal mine underground reservoirs [3,15,16,17,18].

The major influencing factors of the performance of an underground reservoir include the self-flowing replenishment of mine water, water-proofing of the floor, size of water storage space and water storage coefficient, and the safe distance from underlying minable coal seams. Li et al. proposed a calculation method of aquifer recharge of underground reservoir based on pumping data, and injecting data and the total storage space volume [19]. Ju et al. proposed that the water storage volume of the underground reservoir is equal to the sum of the void volume in the caving zone and the roof bed separation void volume in terms of physical simulation and on-site measurement results and established a calculation formula of storage volume based on the water level within the caving zone [20]. Pang et al. estimated the effective water storage volume of underground reservoir in different zones of overlying strata based on the vertical displacement trajectory equation of each stratum in the overburden [21,22]. Song et al. analyzed various influencing factors of the storage coefficient of underground reservoir, such as elastic modulus, Poisson’s ratio, overlying strata stress, and density, combining fluid–solid coupling seepage mechanism, established an underground water reservoir storage coefficient model that considered effective stress, and proposed an analytical solution to the model [23]. Li et al. investigated the suitability of constructing underground reservoirs for multi-seam coal mining and established a mathematical model between the water storage coefficient and the fragmentation dilatancy coefficient of the broken rock mass in the goaf area with consideration of the height of water-conducting fractured zone [24]. Guo et al. investigated the influence of mine water quality on the site selection of underground reservoir in the Shendong coal mining area and proposed that the goafs with poor mine water quality and adverse water–rock interactions are not suitable for the construction of underground reservoirs [25]. Rodrigo Álvarez et al. evaluated the recharge of water resources in some flooded and interconnected coal mines by considering the infiltration of effective rainfall into the goaf, the contribution of groundwater, and the loss of surface water flow and found that fluctuations in water level can cause a decrease in mine water quality in Northwestern Spain [26].

The selection of a suitable location is a crucial prerequisite for the construction of an underground reservoir, while there are few studies on the site selection of underground reservoir. In this research, a mathematical model of water storage coefficient was established and a quantitatively geological site selection method of a coal mine underground reservoir was proposed. With a HJT well field in the Shendong coal-mining area as a case study, the implementation of this method is elaborated. The research outcomes may benefit the construction of coal mine underground reservoirs.

2. Site Selection Model of Coal Mine Underground Reservoir

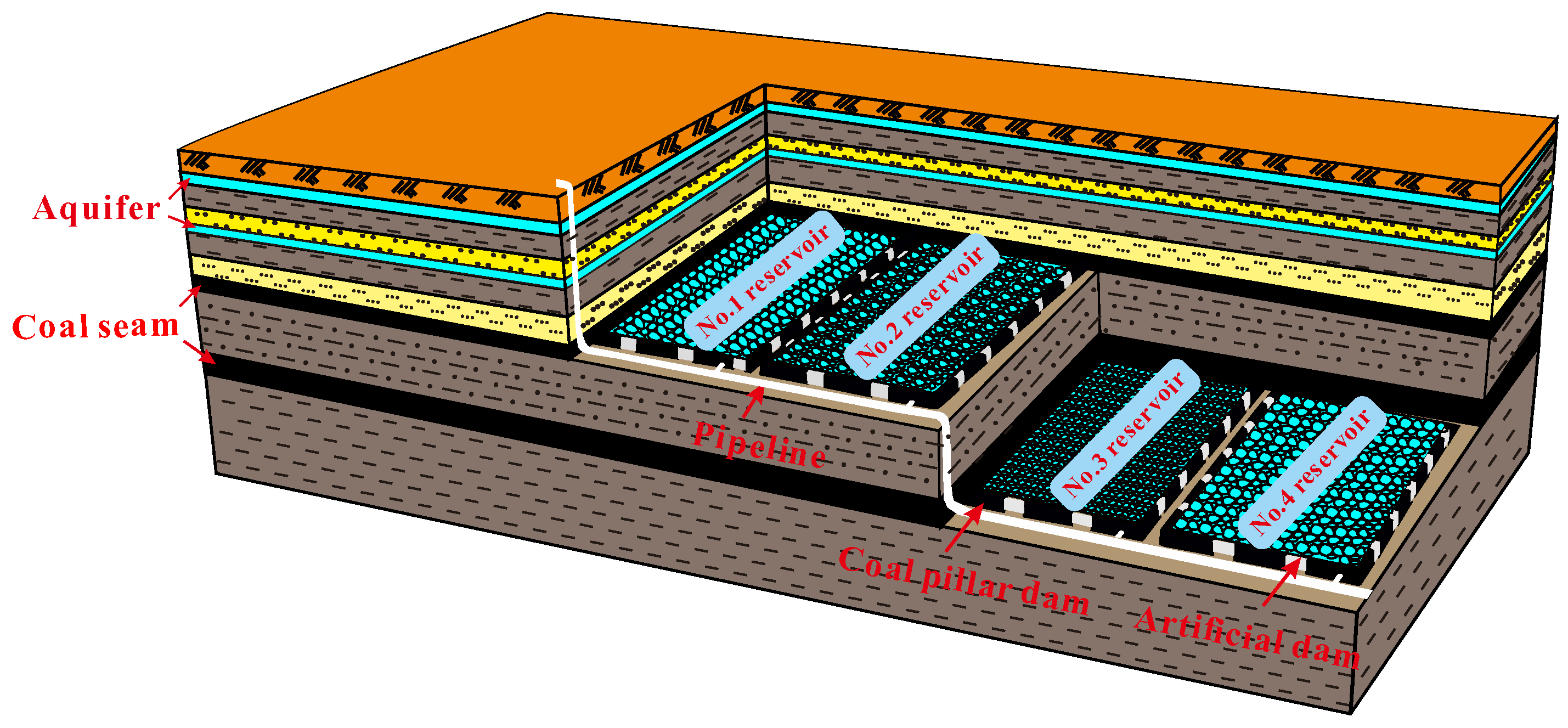
2.1. Geological Influences of Water Storage Capacity of an Underground Reservoir

It should be noted first that the distributed coal mine underground reservoirs are only applicable to coal mining areas with simple geological structures. Geological structures, such as faults and karst collapse columns, have a significant impact on the distribution of mining stress, hydraulic fractures, and permeability, which may cause the leakage or even failure of an underground reservoir. The construction of underground reservoirs needs to avoid the areas where these geological structures are well developed.

The water storage capacity of underground reservoir is closely related to the geological conditions, such as the coal seam thickness, floor elevation, roof and floor lithology, and so on. The water storage space volume is positively related to the thickness of the coal seam in the reservoir area. The area with a lower elevation of floor is conducive to the self-flow of mine water. The shale and mudstone usually contain a lot of clay minerals and these minerals have a small particle size and a small average pore radius and a high porosity. Although the shale and mudstone have a high porosity, the permeability and gravity water supply are low, which is not conducive to the effective storage and supply of mine water in the underground reservoir. The average radius of mineral particles and pores is larger in sandstone than in mudstone and shale rocks. Therefore, the sandstone usually has a big effective storage space, a high permeability, and a high gravitational specific yield, which are beneficial to the water storage and water supply of underground reservoirs. Therefore, the main geological influences of coal mine underground reservoir include: the thickness of coal seam (M), the elevation of coal seam floor (Z), the sand ratio of roof (R), and the sand ratio of floor (F). Herein, R refers to the proportion of sandstone in a certain thickness range of roof and F refers to the ratio of sandstone thickness to fracture zone depth in the range of floor mining fractures.

According to the geological report and drilling data of the study area, the elevation of the main coal seam floor and the thickness of the coal seam can be directly obtained. The height of caving zone should be determined first when calculating R. It can be estimated according to Equation (1) [27,28]. According to the thickness of coal seam, the rock bulking coefficient and the dip angle of coal seam, the thickness of sandstone in the height range of caving zone is counted, and the roof sand ratio R can be obtained. The greater the R value, the better the permeability of the roof strata, which is conducive to the construction of the underground reservoir.

$$h_1=\frac{M}{(k-1)\mathit{cos}\alpha }$$

(1)

where h₁ is the height of the caving zone, m; M is the thickness of coal seam, m; k is the rock bulking coefficient, which is negatively correlated with the overlying load of caving rock, dimensionless; the larger the overlying load is, the smaller the bulking coefficient is; generally, it is 1.1–1.5; α is the dip angle of coal seam, °.

Similarly, to calculate of the floor sand ratio F, the depth of the floor fracture zone should be first determined. According to a Chinese coal industry standard [29] “Specification for coal pillar retention of building, water body, railway and main roadway and coal mining under pressure” issued by the State Administration of Coal Industry of China on 26 May 2000, the failure depth of the working face floor can be estimated by Equation (2). It is worth noting that this equation is only applicable to shallow coal seams extracted using a long wall fully mechanized mining method. By statistically measuring the thickness of sandstone in the depth range of the floor fracture zone, the floor sand ratio F can be obtained. The larger the F value, the worse the water resistance of the floor. A high F value indicates that the risk of leakage of mine water is relatively high in the reservoir, which is unfavorable for the construction of underground reservoirs.

$$h_2=0.0085H+0.1665\alpha +0.1079L-4.3579$$

(2)

where h₂ is the depth of the floor fracture zone, m; H is the buried depth of coal seam, m; L is the width of the mining face, m.

2.2. Development of a Model of Water Storage Coefficient

The water storage coefficient is an important factor affecting the water storage capacity of underground reservoirs [23]. In this research, it was used as one of the main indicators for the site suitability evaluation of the underground reservoirs in coal mines.

The rocks in the goaf can be regarded as porous media. The Terzaghi effective stress of porous media can be expressed as follows.

$${\sigma }_{ij}^{\prime }={\sigma }_{ij}-\varnothing p{\delta }_{ij}$$

(3)

where ${\sigma }_{ij}^{\prime }$ is the effective stress of solid skeleton (Terzaghi effective stress), MPa; ${\sigma }_{ij}$ is the total stress, MPa; $\varnothing$ is the porosity of porous media; p is the pore water pressure, MPa; ${\delta }_{ij}$ is the Kronecker delta, when i = j, ${\delta }_{ij}$ = 1, i ≠ j, ${\delta }_{ij}$ = 0.

According to the strain–displacement relationship, the geometric equation can be expressed as follows.

$$\left\{\begin{array}{cc}{\epsilon }_x& =\frac{\partial u_x}{\partial x}\\ {\epsilon }_y& =\frac{\partial u_y}{\partial y}\\ {\epsilon }_z& =\frac{\partial u_z}{\partial z}\end{array}\right.$$

(4)

where ${\epsilon }_x$, ${\epsilon }_y$, and ${\epsilon }_z$ are the strain components in the x, y, and z directions; $u_x$, $u_y$, $u_z$ are the displacement components in the x, y, z directions, respectively.

The stress balance equation can be expressed as the relationship between the stress component and the body force component.

$$\left\{\begin{array}{c}\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}+f_x=0\\ \frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+\frac{\partial {\tau }_{xy}}{\partial x}+f_y=0\\ \frac{\partial {\sigma }_z}{\partial z}+\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+f_z=0\end{array}\right.$$

(5)

where $f_x$, $f_y$, and $f_z$ are the body force components in x, y, and z directions, respectively, N/m³. In practical engineering, $f_x$ = $f_y$ = 0, $f_z$ = ρ_sg, ρ_s is the density of broken rock mass, kg/m³; g is gravitational acceleration, m/s². ${\tau }_{yx}$, ${\tau }_{xy}$, ${\tau }_{zx}$, ${\tau }_{xz}$, ${\tau }_{zy}$, ${\tau }_{yz}$ are shear stress components in different directions, respectively, MPa. According to the shear stress equality theorem, ${\tau }_{yx}$ = ${\tau }_{xy}$, ${\tau }_{zx}$ = ${\tau }_{xz}$, ${\tau }_{zy}$ = ${\tau }_{yz}$.

The physical equation can be expressed as the relationship between the shear stress component and the displacement component.

$$\left\{\begin{array}{cc}{\tau }_{yx}& ={\tau }_{xy}=\frac{E}{2(1+\nu )}(\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x})\\ {\tau }_{zx}& ={\tau }_{xz}=\frac{E}{2(1+\nu )}(\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x})\\ {\tau }_{zy}& ={\tau }_{yz}=\frac{E}{2(1+\nu )}(\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y})\end{array}\right.$$

(6)

where E is the elastic modulus, MPa; v is Poisson ‘s ratio, dimensionless.

Upon joining Equations (3), (5) and (6), the following equations can be obtained.

$$\left\{\begin{array}{c}\frac{\partial {\sigma }_x^{\prime }}{\partial x}+\frac{\partial \varnothing p}{\partial x}+\frac{E}{2\left(1+\nu \right)}\left(\frac{{\partial }^2{u}_x}{\partial y^2}+\frac{{\partial }^2{u}_y}{\partial x\partial y}\right)+\frac{E}{2\left(1+\nu \right)}\left(\frac{{\partial }^2{u}_x}{\partial z^2}+\frac{{\partial }^2{u}_z}{\partial x\partial z}\right)=0\\ \frac{\partial {\sigma }_y^{\prime }}{\partial y}+\frac{\partial \varnothing p}{\partial y}+\frac{E}{2\left(1+\nu \right)}\left(\frac{{\partial }^2{u}_y}{\partial z^2}+\frac{{\partial }^2{u}_z}{\partial y\partial z}\right)+\frac{E}{2\left(1+\nu \right)}\left(\frac{{\partial }^2{u}_y}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial y\partial x}\right)=0\\ \frac{\partial {\sigma }_z^{\prime }}{\partial z}+\frac{\partial \varnothing p}{\partial z}+\frac{E}{2\left(1+\nu \right)}\left(\frac{{\partial }^2{u}_z}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial z\partial x}\right)+\frac{E}{2\left(1+\nu \right)}\left(\frac{{\partial }^2{u}_z}{\partial y^2}+\frac{{\partial }^2{u}_y}{\partial z\partial y}\right)+\rho g=0\end{array}\right.$$

(7)

Assuming that the solid skeleton of porous media is isotropic elastic, the effective stress–strain constitutive relation can be expressed as follows.

$$\left\{\begin{array}{c}{\sigma }_x^{\prime }={\epsilon }_V\frac{E\nu }{(1+\nu )(1-2\nu )}+\frac{E}{(1+\nu )}\cdot {\epsilon }_x-\varnothing p\\ {\sigma }_y^{\prime }={\epsilon }_V\frac{E\nu }{(1+\nu )(1-2\nu )}+\frac{E}{(1+\nu )}\cdot {\epsilon }_y-\varnothing p\\ {\sigma }_z^{\prime }={\epsilon }_V\frac{E\nu }{(1+\nu )(1-2\nu )}+\frac{E}{(1+\nu )}\cdot {\epsilon }_z-\varnothing p\end{array}\right.$$

(8)

where ${\epsilon }_V$ is the volumetric strain of the broken rock mass of the overlying strata, dimensionless; v is Poisson ‘s ratio, dimensionless; E is the elastic modulus of the overlying strata after coal seam mining (the mining of coal seam will disturb the overlying strata, and the elastic modulus is about half of that before mining), MPa.

The volumetric strain is equal to the sum of the strain components in three directions and is also affected by the stress of the overlying strata. In engineering, the volume strain can also be expressed by the relative change of volume.

$${\epsilon }_V={\epsilon }_x+{\epsilon }_y+{\epsilon }_z=\frac{1-2\nu }{E}{\sigma }_V$$

(9)

where ${\sigma }_V$ is the overburden stress, ${\sigma }_V={\sigma }_x^{\prime }+{\sigma }_y^{\prime }+{\sigma }_z^{\prime }$.

By combining Equations (4), (8), and (9), we can obtain the following equations.

$$\left\{\begin{array}{c}{\sigma }_x^{\prime }=(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z})\frac{E\nu }{(1+\nu )(1-2\nu )}+\frac{E}{(1+\nu )}\cdot \frac{\partial u_x}{\partial x}-\varnothing p\\ {\sigma }_y^{\prime }=(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z})\frac{E\nu }{(1+\nu )(1-2\nu )}+\frac{E}{(1+\nu )}\cdot \frac{\partial u_y}{\partial y}-\varnothing p\\ {\sigma }_z^{\prime }=(\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z})\frac{E\nu }{(1+\nu )(1-2\nu )}+\frac{E}{(1+\nu )}\cdot \frac{\partial u_z}{\partial z}-\varnothing p\end{array}\right.$$

(10)

Furthermore, by combining Equations (4), (7), (9), and (10), we can obtain Equation (11).

$$\left\{\begin{array}{c}\frac{E}{2(1+v)(1-2v)}\frac{\partial {ℇ}_V}{\partial x}+\frac{E}{2(1+v)}{\nabla }^2{u}_x=0\\ \frac{E}{2(1+v)(1-2v)}\frac{\partial {ℇ}_V}{\partial y}+\frac{E}{2(1+v)}{\nabla }^2{u}_y=0\\ \frac{E}{2(1+v)(1-2v)}\frac{\partial {ℇ}_V}{\partial z}+\frac{E}{2(1+v)}{\nabla }^2{u}_z+\rho g=0\end{array}\right.$$

(11)

where ${\nabla }^2$ is the Laplace operator.

To obtain an analytical solution of the water storage coefficient Q, two assumptions need to be satisfied: (1) before the mine water is injected into the underground reservoir, the pore fluid pressure is equal to the atmospheric pressure; (2) considering the one-dimensional situation, it is assumed that the fractured rock in the reservoir area is in a uniaxial strain state, and its compression is only affected by gravity. Based on these two assumptions, the initial water storage coefficient Q₀ can be obtained and then the water storage coefficient Q can be estimated.

The initial water storage coefficient Q₀ represents the water storage capacity of the fractured rock mass before the roof collapse of the goaf is compacted. The initial void space includes the void space of the caving zone and the volume of coal seam to be mined. Considering the original pores of overlying strata before coal mining, according to the definition of water storage coefficient, Q₀ can be determined by Equation (12).

$$Q_0=\frac{V_k+V_t\phi }{V_k+V_t}\times 100\%$$

(12)

where $V_k$ is the space volume of coal seam to be mined, m³; $V_t$ is the spatial volume of the collapse zone after mining, m³; φ is the porosity of the overlying strata before mining.

$V_k$ is determined by Equation (13).

$$V_k=MWL$$

(13)

where W is the advance distance of the working face, m; L is the width of working face, m; M is the thickness of coal, m.

The shape of the caving zone after mining can be approximately determined to be parabolic [30,31]. The shape of the collapse zone can be roughly fitted by using a quadratic function. Then, the cross-sectional area in the range of caving zone can be obtained by definite integral (Figure 2). According to Equation (14), the spatial volume of caving zone can be calculated.

$$V_t=L{\int }_{-\frac{W}{2}}^{\frac{W}{2}}\left(-0.3x^2+h_1\right)dx$$

(14)

where h₁ is the height of the caving zone, which can be determined by Equation (1). Equations (13) and (14) are introduced into Equation (12), and then the initial water storage coefficient Q₀ can be estimated by Equation (15) as below.

$$Q_0=\frac{M+\phi (h_1-\frac{W^2}{40})}{M+h_1-\frac{W^2}{40}}$$

(15)

After mining, the overlying strata will collapse. Let V_s, V_b, and V_p be the solid volume of the rock mass skeleton of the overlying strata of the coal seam, the apparent volume of the rock mass, and the void volume of the rock mass, respectively. The corresponding change values are ΔV_s, ΔV_b and ΔV_p, and the water storage coefficient Q can be expressed as follows.

$$Q=\frac{V_p+{∆V}_p}{V_b+{∆V}_b}=1-\frac{V_s(1+{∆V}_s/V_s)}{V_b(1+{∆V}_b/V_b)}$$

(16)

According to the definitions of water storage coefficient and volume strain, Equations (17) and (18) can be obtained.

$$\frac{V_s}{V_b}=1-Q_0$$

(17)

$$\frac{{∆V}_b}{V_b}={\epsilon }_V$$

(18)

In practical engineering, it can be considered that the rock particle of overlying strata of coal seam is linearly elastic. Additionally, the formation is isothermal and the influence of temperature field on deformation can be ignored. The particle volume change of broken rock mass caused by the change of pore fluid pressure can be expressed as follows.

$$\frac{{∆V}_s}{V_s}=-\frac{∆p}{K_s}$$

(19)

where Δp = p − p₀, p₀ is the initial pore water pressure, that is, the atmospheric pressure when the reservoir is anhydrous, MPa; K_s is the bulk elastic compression modulus of skeleton solid particles, MPa. Before the mine water is injected into the goaf, the pore water pressure is a constant, which is equal to the atmospheric pressure, that is, p = p₀, that is, Δp = 0.

According to the assumed conditions, the water storage coefficient of the underground reservoir of the coal mine is calculated from the one-dimensional, that is, t = 0. Then, combining Equations (16)–(19) can obtain a mathematical model of water storage coefficient of the coal mine underground reservoir.

$$Q=\frac{Q_0+{\epsilon }_V}{1+{\epsilon }_V}$$

(20)

According to Equation (11), the effective stress in x, y, and z directions is solved.

$${\sigma }_x^{\prime }={\sigma }_y^{\prime }=-\frac{\nu }{1-\nu }\rho gH$$

(21)

$${\sigma }_z^{\prime }=-\rho gH$$

(22)

In summary, by combining Equations (1), (9), (15), and (20)–(22), the water storage coefficient Q under the condition of one-dimensional steady state can be described as follows.

$$Q=\frac{\left(1-v\right)E\left[M+\phi \left(\frac{M}{\left(k-1\right)\mathit{cos}\alpha }-\frac{W^2}{40}\right)\right]-(1-2v)(1+v)\rho gH\left[M+\frac{M}{(k-1)\mathit{cos}\alpha }-\frac{W^2}{40}\right]}{\left[(1-v)E-(1-2v)(1+v)\rho gH\right]\left[M+\frac{M}{(k-1)\mathit{cos}\alpha }-\frac{W^2}{40}\right]}$$

(23)

According to the drainage test that was carried out in the goaf of No. 12301 fully mechanized mining face of 1⁻² coal seam in the HJT mining field of the Shendong mining area, the water storage coefficient was approximately 0.2. The average water storage coefficient, calculated by the proposed model of water storage coefficient, was 0.2194 in this area, which is basically consistent with the in situ measured result.

2.3. Effective Safe Thickness from Underlying Coal Seam

There are usually a few coal seams in a coal-bearing strata. Coal seams are generally mined layer by layer from the top down. The underlying coal seam working face may be under an underground reservoir, which may face the problem of repeated damage of overlying strata and the control of mining strata movement [32,33]. The mining-induced fissure of the underlying coal seam may extend upward to the upper underground reservoir, which will lower the water storage performance in the underground reservoir and may result in water gushing in the lower coal seam mining [34,35].

In order to lower the risk of water leakage of underground reservoirs and the inrush of water from floor during mining of underlying coal seams, the safe distance from the underlying coal seams must be considered when selecting the site of underground reservoirs. According to Equation (2), combined with geological drilling data, the depth of floor fracture zone h₂ can be obtained. Based on the key strata theory, the key strata of the overlying strata of the underlying coal seam are identified, and the height of the water flowing fractured zone h₃ can calculated [36,37].

In the mining rock mass, the rock layer that controls all or part of the rock mass activity is called a key stratum. The main basis for distinguishing key layers is their deformation and fracture characteristics, that is, when the key layer is broken, the subsidence deformation of all or local rock layers above it is coordinated and consistent. The former is called the main key layer of rock activity, and the latter is called the inferior key layer. The fracture of key layers will cause overall movement of all or a considerable portion of the rock layers [38]. There may be a few inferior key layers but only one main key layer in the overburden. The hard and thick rock layer may become the main key layer when it meets the requirements of stiffness and strength simultaneously. According to the discriminant formula in the key layer theory, each rock layer in the overlying rock can be distinguished. Based on the position of the key layer, the height of the water-conducting fracture zone can be predicted [39]. The method is as follows.

(1)

Calculate the height of the key layer position from the mining coal seam. If the height is greater than (7~10) M, the mining-induced fractures do not cut through the key layer; if the height is less than (7~10) M, the fracture will cut through the key layer. M is the thickness of coal seam, m;

(2)

Predict the height of water flowing fractured zone. When the main key layer of overlying strata is located above the critical height (7~10) M, the water flowing fracture will develop to the bottom of the nearest key stratum above the critical height (7~10) M, and the height of the water flowing fracture zone is equal to the height of the key layer from the mining coal seam (Figure 3a). When the main key layer of overlying strata is located within the critical height (7~10) M, the water flowing fracture will extend to the top of the bedrock (Figure 3b).

According to drilling data, the distance between two coal seams l can be obtained; the effective safety thickness D can be calculated according to Equation (24). D refers to the safe distance between the upward development fracture of the underlying coal seam mining and the fracture zone of the underground reservoir floor. In the areas with a great D value, the risk of roof water inrush is small during the mining of the underlying coal seam, which will benefit the construction of underground reservoirs.

$$D=l-h_2-h_3$$

(24)

where l is the vertical distance between two coal seams, m; $h_2$ is the depth of floor fracture zone of this coal seam, m; h₃ is the height of the water flowing fractured zone of the underlying coal seam, m.

2.4. Site Selection Assessment Method of a Coal Mine Underground Reservoir

2.4.1. Site Selection Evaluation Parameters

Based on above analysis, the site selection evaluation parameters include: the thickness of coal seam (M), the elevation of coal seam floor (Z), the sand ratio of roof (R), the sand ratio of floor (F), the water storage coefficient (Q), and the effective safety thickness (D).

We defined a suitability index (SI) to evaluate quantitatively the rationality of site selection of coal mine underground reservoir. The higher the SI is, the higher the rationality of the site selection is. The suitability index (SI) is positively related to M, R, Q, and D, and it is negatively related to Z and F.

2.4.2. Determination of the Weight of Parameters Based on an Entropy Weight Method

The entropy weight method is used to determine the weight of evaluation parameters. In order to eliminate the influence of numerical size difference of each evaluation parameter, the data of six variables, such as Z, M, R, F, Q, and D, are normalized, respectively. The matrix, composed of six indexes and n borehole data, is recorded as X, and the elements are recorded as x_ij. The normalizing method is as follows.

$$s_{ij}=\frac{x_{ij}-min\left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}}{max\left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}-min\left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}}$$

(25)

where x and s are the original value and the normalized value, respectively; i and j are the serial number of the borehole and the serial number of variables, respectively, for instance, x_ij is the original value of the ith borehole in the jth index; s_ij is the normalized value of the ith borehole in the jth index.

For the jth variable, the information entropy is calculated by Equation (26).

$$e_j=-\frac{1}{lnn}{\sum }_{i=1}^n{p}_{ij}ln\left(p_{ij}\right)\hspace{1em}\hspace{1em}\hspace{1em}(j=1,2,\cdots ,6)$$

(26)

where e_j is the information entropy of the jth variable, and 1 − e_j is the information utility value. The larger the e_j value is, the less the information of this variable is, and the smaller the information utility value is; $p_{ij}$ is the probability and is equal to the ratio of s_ij of the ith borehole to the sum of s_ij of all the boreholes in the jth variable.

$p_{ij}$ can be calculated by the following equation.

$$p_{ij}=\frac{s_{ij}}{{\sum }_{i=1}^n{s}_{ij}}$$

(27)

The weight W_j of the jth variable is calculated according to the information utility value of each index.

$$W_j=\frac{1-e_j}{\sum _{j=1}^6(1-e_j)}\hspace{1em}\hspace{1em}\hspace{1em}(j=1,2,\cdots ,6)$$

(28)

According to the weight of each variable, a comprehensive site suitability evaluation index SI is calculated by Equation (29).

$${SI}_i={W_{M}M}_i+{W_{R}R}_i+W_Q{Q}_i+W_D{D}_i-W_Z{Z}_i-{W_{F}F}_i\hspace{1em}\hspace{1em}(i=1,2,\cdots ,n)$$

(29)

where M_i, R_i, Q_i, D_i, Z_i, and F_i are the normalized values of the ith borehole.

2.4.3. Grey Relational Analysis

In this research, a grey correlation method was used to analyze the correlation between the influencing factors and the suitability evaluation index SI of the site selection of the underground reservoir in the HJT mining field.

The basic idea of grey correlation analysis is to judge whether the relationship is close according to the similarity of the geometric shape of the sequence curves. The closer the curves are, the greater the correlation between the corresponding sequences is, and vice versa. The grey relational analysis can be performed by the following steps.

(1)

Determine the analysis sequence and pre-treat the variables.

Determine the parent sequence and subsequence to be analyzed, in which the parent sequence is also called the reference sequence, similar to the dependent variable, which can reflect the system behavior characteristics; the subsequence, also known as the comparative sequence, is similar to the independent variable and consists of factors that can affect the behavior of the system. The parent sequence selected in this research is the comprehensive site suitability evaluation index SI, and the subsequences include: coal seam thickness M, coal seam floor elevation Z, roof sand ratio R, floor sand ratio F, water storage coefficient Q, and effective safety thickness D.

In order to eliminate the influence of dimensionality in the sequences and simplify the calculation, the variables should be preprocessed. For each variable in the parent sequence and the subsequences, the average value ${\overline{x}}_j$ of the jth variable is first calculated, and then each element in the index is divided by the average value.

Suppose the normalized matrix is Z, this matrix has 6n elements with n rows and six columns. z_ij denotes the normalized value of the ith borehole in the jth index, and the element in the original matrix X is denoted by x_ij, then z_ij can be calculated by Equation (30).

$$z_{ij}=\frac{x_{ij}}{{\overline{x}}_j}$$

(30)

(2)

Find the grey correlation coefficient y (x₀(k), x_j (k)) and correlation degree r_i.

The correlation degree r_j represents the correlation degree between the parent sequence and the jth subsequence, which is equal to the average value of the grey correlation coefficient y (x₀ (k), x_j (k)) of the jth subsequence. The grey correlation coefficient is calculated by Equation (31):

$$y(x_0(k),x_j(k))=\frac{a+\rho b}{\left|x_0\left(k\right)-x_j\left(k\right)\right|+\rho b}(j=1,2,\dots 6; k=1,2,\dots n)$$

(31)

where a is the minimum difference, b is the maximum difference, a and b are calculated by Equation (32) and Equation (33), respectively, and ρ is the resolution coefficient (generally 0.5).

$$a=\begin{array}{c}min\\ j\end{array}\{\begin{array}{c}min\\ k\end{array}\left|x_0\left(k\right)-x_j\left(k\right)\right|\}$$

(32)

$$b=\begin{array}{c}max\\ j\end{array}\{\begin{array}{c}max\\ k\end{array}\left|x_0\left(k\right)-x_j\left(k\right)\right|\}$$

(33)

2.4.4. Implementation Procedure

The implementation of the method has the following steps (Figure 4).

• First, determine the thickness of main coal seam (M), the elevation of coal seam floor (Z), the sand ratio of roof (R), and the sand ratio of floor (F) according to the drilling data of the mine field;
• Second, calculate the water storage coefficient Q according to the size of the working face, the buried depth of the coal seam, the density of the overlying strata, and the mechanical parameters of the rock mass;
• Third, estimate the effective safety thickness (D), according to the distance between the target coal seam and the underlying coal seam, the depth of the floor fracture zone, and the height of the roof water-conducting fracture zone of the underlying coal seam;
• Fourth, determine the weight (W_j) of each index based on an entropy weight method;
• Fifth, calculate the suitability evaluation index SI of coal mine underground reservoir;
• Sixth, which is optional, analyze the correlation degree r_j between each index and SI based on a grey relational analysis method.

3. A Case Study from a Coal Mine in the Shendong Coal-Mining Area

3.1. Geological Setting

The HJT mine field is located at the junction of Shaanxi Province and Inner Mongolia Autonomous Region, belonging to Daliuta Town Shenmu City Shaanxi Province China. The field covers an area of 63.784 km², with a north–south length of about 9.76 km and an east–west width of about 10.6 km. The northwest boundary of the field is bounded by the main river channel of HJT Gully, the southwest boundary is bounded by the connecting line of Nos. 274, 5, and 46 boreholes, and the southeast boundary is bounded by the connecting line of borehole No. 57 and the triangulation point of Shuji River, which is adjacent to the Zhugaita mine field. The northeast boundary is bounded by the main river channel of Wulanmulun River and adjacent to the Daliuta mine field.

The climate of the mining area is dry and the precipitation is scarce. The annual precipitation is about 300~400 mm. The rainfall is concentrated in summer, and the regional distribution of precipitation is uneven. In general, the groundwater in the mining area is relatively scarce.

No large or medium-sized faults have been discovered in the study area, and rock fractures are poorly developed with simple structures (Figure 5). There is no volcanic activity in this area. The Ordovician, Carboniferous, Permian, Triassic, Jurassic, Cretaceous, and overlying Neogene and Quaternary strata are exposed from east to west in the Yulin area. The middle-lower Jurassic Yan’an Formation is the main coal-bearing strata in this area, with lithologies predominantly composed of fine sandstone, siltstone, and sandy mudstone; and a small amount of mudstone and medium-coarse sandstone. Fractures in the strata are poorly developed, and most rocks belong to the category of semi-hard rocks.

The mining field contains a total of seven coal seams, with an average total thickness of 20.29 m and an average coal-bearing ratio of 10.00%. There are seven coal seams from top to bottom, including Nos. 1⁻² upper, 1⁻², 2⁻² upper, 2⁻², 3⁻¹, 4⁻³, and 5⁻² coal seams. Among them, three coal seams are main minable ones, including Nos. 1⁻², 2⁻², and 5⁻² coal seams. The coal seams are shallow with a burial depth varying from 30 m to approximately 400 m in the study area.

3.2. Site Selection Assessment Results

Taking the HJT mine field as an example, 17 drillings were selected to calculate the elevation Z, coal seam thickness M, roof sand-to-ground ratio R, floor sand-to-ground ratio F, water storage coefficient Q, and effective safety thickness D of No. 2⁻² coal seam floor in the mine field. The method described in Section 2 was used to analyze the site selection prediction of coal mine underground reservoir in No. 2⁻² coal seam.

(1)

The contour map of the elevation of No. 2⁻² coal seam floor was obtained based on the statistical analysis of the drilling data in the study area (Figure 6). On the whole, from the northwest to the southeast of the mine field, the floor elevation of No. 2⁻² coal seam showed a gradually increasing trend. The floor elevation of No. 36 borehole in the north was the lowest, which was 1053 m, and the floor elevation of No. 242 borehole in the southeast was the highest, which was 1118.4 m. The northwest of the connection line of H15, H40, and 247 boreholes, that is, the whole area of area A, area B, and area D, as well as C-1 and C-2 working faces, was more conducive to the realization of the self-flow supply of mine water and suitable for the construction of underground reservoirs.

(2)

The distribution map of coal thickness in the mine field was obtained based on the statistics of the thickness of No. 2⁻² coal seam in the study area, (Figure 7). The average coal thickness in the southeast area of the borehole H15 to the H17 connection line was below 4m, and the thickness of No. 2⁻² coal was only about 1.5m around the No. 242 borehole in the southeastern edge of the mine field. The coal thickness in the northwest was large, was above 5 m in the borehole No. H86, well H63 and H40. The thickness of No. 2⁻² coal seam was larger in the northwest and smaller in the southeast. That is, the effective water storage space was relatively large if the underground reservoirs were located in the A, B, C, D areas and G-1, G-2, and G-3 working faces in the northwest of the mine field.

(3)

The height of the caving zone of No. 2⁻² coal seam can be calculated according to Equation (1). Set the crushing expansion coefficient k = 1.4. At the same time, the thickness of sandstone in the height range of the caving zone was counted, and the contour map of the sand ratio of roof R can be obtained (Figure 8). Due to the great variation of sandstone thickness in the caving zone on plane, there was no obvious distribution law of R. The general trend was that the R value in the south of H127 was mostly below 0.5; the R value was close to 1 in the northeast and northwest. In the whole area of A and C areas, the east of B-1, B-2, B-3 working faces in B area and G-1, G-2, G-3 working faces in G area, it was conducive to water storage and flow and the construction of underground reservoirs. The R value was as low as 0.2 in the H49 and H40 boreholes of the central area where the thickness of roof sandstone was small, and the thickness of mudstone and other strata with good water-proof effect was relatively large, which is not conducive to the construction of underground reservoirs.

(4)

Calculate the sand ratio of floor (F) of No. 2⁻² coal seam. The depth of the floor fracture zone of No. 2⁻² coal seam was determined by Equation (2). Because No. 2⁻² coal was a nearly horizontal coal seam, the dip angle α of the coal seam was 0, and the remaining parameters can be determined by the geological data of the mine field. The contour map of F of the floor was obtained (Figure 9). The F value was larger in the northeast than in the southwest within the mine field, and the peak of greater than o.6 was located at the boreholes H70 and H15 in the northeast, indicating that the sandstone in the floor fracture zone accounted for a large proportion, and the water insulation was poor, which was prone to leakage, which is not conducive to the effective storage of water in the underground reservoir. The F value was close to 0 near the H49 borehole, and near the No. 36 borehole in the northwest, indicating that the lithology of floor fracture zones was mostly mudstone with a good water-resisting property in these two places (A, C and D-1, D-2 areas), which is the favorable condition for the construction of the underground reservoir.

(5)

According to Equation (23), the water storage coefficient Q of No. 2⁻² coal goaf in each region was determined. The elastic modulus of the overlying strata after mining disturbance was about 0.5 times of the original; the buried depth of No. 2⁻² coal seam was obtained by drilling data, and the parameters used are shown in

Table 1. Rock mechanics parameters in the HJT mine field.

Rock Type	ρ (kg/m3)	Bulk Modulus K (GPa)	Shear Modulus G (GPa)
sandy mudstone	2420	5.12	3.5
5−2 coal seam	1410	1.7	0.8
No. 1 siltstone	2460	7.2	4.9
No. 2 siltstone	2500	7.9	5.3
fine sandstone	2790	8	4.43
mudstone	2650	4.39	2.37
feldspathic sandstone	2560	5.4	4.05
Coarse-grained feldspathic sandstone	2620	5.6	4.15
2−2 coal seam	1540	1.45	0.7
eolian sand	1960	0.25	0.28

. The initial water storage coefficient Q₀ of fractured rock mass can be calculated in terms of Equation (12). The water storage coefficient Q of each region was calculated and the contour map of Q in the study area was drawn (Figure 10).

The variation of Q was insignificant in the study area. The Q value varied from 21.35% at the H49 borehole to 21.40% at the H127 borehole. That is, the water storage coefficient of the goaf of No. 2⁻² coal seam was similar in the mine field. The Q value was relatively large in the working face C-5, C-6, G-5, and G-6 and the northern B-4, B-5, B-6 and was relatively small in the A and D areas.

(6)

To calculate the effective safety thickness D, the distance between No. 2⁻² coal seam and No. 5⁻² coal seam (l), the depth of the fracture zone of No. 2⁻² coal seam floor (h₂), and the height of the water-conducting fracture zone of No. 5⁻² coal seam roof (h₃) should be determined.

The l value of each borehole can be obtained according to the drilling data and h₂ can be determined by Equation (2).

h₃ was predicted by the method described in Section 2.3. First, the thickness of No. 5⁻² coal seam of each borehole was obtained according to the drilling data. The thickness, bulk density, and elastic modulus of each stratum of overburden rock were counted, and the position of each key stratum was calculated according to the key stratum theory [21,22]. Considering that the overburden of No. 5⁻² coal seam was mostly medium-hard rock, the height of water-conducting fracture zone was determined by comparing the distance between each key layer and coal seam and 10 times of mining height. Once l, h₂ and h₃ were determined, the effective safety thickness D can be calculated according to Equation (24) and the contour map of D in the mine field can be drawn (Figure 11).

The D value was relatively large in the southeastern (H area working face) and northwestern edges (A area and C area in the west) of the mine field. The risk level of water inrush from roof into No. 5⁻² coal seam was relatively low in these areas. The maximum D value was at no. 242 borehole, reaching 58.66 m.

The D value was low in the northeastern part of the mine field (B-3, B-4, B-5, B-6 working face). The D value was below 20 m north of the connection line of No. H70 and No. H102 boreholes. The minimum value of D was only 5m and was located at the No. 238 borehole. The construction of underground reservoirs in these areas may have a relatively high adverse effect on the safe mining of No. 5⁻² coal seam.

(7)

The weight of each index was calculated according to Equation (28). The results are shown in

Table 2. Weight calculation results.

Variable	Weight (%)
M	10.09
Z	11.93
R	19.61
F	26.53
Q	18.01
D	13.83

. The maximum weight was 26.53% (F), and the minimum was 10.09% (coal thickness M). The suitability evaluation index SI was obtained from Equation (32), and the SI contour map was drawn (Figure 12).

The SI value was generally large in the central and eastern parts of the minefield. It was the largest in the vicinity of No. H63 and No. H70 boreholes, both above 0.35, indicating that the region was relatively suitable for the construction of underground reservoirs. In the vicinity of No. 245 borehole and No. 36 borehole, the SI values were below 0, that is, these two areas were not suitable for the construction of underground reservoirs. Combined with the distribution of 2⁻² coal working face in the minefield, the suitable locations for the construction of underground reservoirs include: B-3 and B-4 working faces in the north; the E-1, E-2, H-1, and H-2 working faces in the east; the G-1 and G-2 working faces in the center.

It was noted that SI is a comprehensive index and its value was determined by many indicator values and their weights, rather than by a single indicator value (see Equation (29)). Therefore, in some areas, the value of a positive index was relatively large, but the SI value may be relatively small.

An existing underground reservoir was located in the goaf of No. 12301 fully mechanized long wall mining face of No. 1⁻² coal seam in the HJT mine field of the Shendong mining area. The drainage test showed that the water storage coefficient of this underground reservoir was approximately 0.2 and its operating effect was rather good. The estimated water storage coefficient Q and suitability index SI using our site selection assessment method were 0.2194 (Q) and 0.544 (SI, at a good level), respectively, which were in good accordance with the actual situation. It may verify the accuracy and reliability of this method to some extent.

3.3. Correlation Analysis

Based on the correlation calculation of each sub-sequence based on 17 borehole data, the correlation coefficient diagram of each sub-sequence was obtained (Figure 13). The correlation coefficient was high between (F, M) and SI in the north, between (R, F) and SI in the center, between (Q, F) and SI in the south of the mine field.

The correlation degree r_j was equal to the average of the grey correlation coefficients of all borehole data in the jth variable (

Table 3. Grey correlation degree between six variables with SI.

Variable	Correlation Degree with SI	Order
F	0.809	1
R	0.746	2
Z	0.735	3
Q	0.734	4
M	0.717	5
D	0.663	6

). Six variables can be arranged in a descending order of correlation degree: F (0.809) > R (0.746) > Z (0.735) > Q (0.734) > M (0.717) > D(0.663) in this study area.

The comprehensive suitability evaluation index SI in the HJT mine field is plotted in Figure 14. According to the mutation point of SI value, the site selection suitability was divided into three grades: good (SI value ≥ 0.3), average (SI value between 0.1~0.3), and poor (SI value ≤ 0.1). According to this grade division, the suitability of coal mine underground reservoir construction in the HJT mine field was evaluated. The evaluation results are as follows (

Table 4. Site suitability index (SI) of underground reservoir in the study area.

Borehole Number	SI	Level
H63	0.387	Good
H70	0.365
247	0.298	Average
H40	0.296
H86	0.263
H49	0.242
H127	0.218
H102	0.215
238	0.211
H15	0.196
H72	0.176
246	0.167
H65	0.156
242	0.147
H17	0.015	Poor
36	−0.052
245	−0.135

).

4. Conclusions

(1)

A mathematical model of water storage coefficient was established and a geological site selection method of a coal mine underground reservoir was proposed. The major evaluation indexes include the elevation of the coal seam floor Z, the coal seam thickness M, the sandstone ratio of the roof R, the sandstone ratio of the floor F, the water storage coefficient Q, and the effective safety thickness D. An entropy weight method was used to obtain the weight of the evaluation indexes.

(2)

The water storage capacity of coal mine underground reservoir was positively correlated with the coal thickness, sandstone ratio of the roof, water storage coefficient, and effective safety thickness, and was negatively correlated with the elevation of the coal seam floor and the sandstone ratio of the floor.

(3)

With an HJT mine field in the Shendong coal mining area as an example, the site selection suitability index (SI) was estimated. The maximum value appeared at boreholes H63 (0.387) and H70 (0.365), which was at a good level of suitability for underground reservoir construction. Combined with the distribution of No. 2⁻² coal seam working face in the mine field, the suitable locations for the construction of underground reservoirs included: B-3 and B-4 working faces in the north; the E-1, E-2, H-1, and H-2 working faces in the east; the G-1 and G-2 working faces in the center.

(4)

The grey correlation degree between each evaluation index and site selection suitability index (SI) was analyzed. Six variables can be arranged in a descending order of grey correlation degree: sand ratio of floor F (0.809) > sand ratio of roof R (0.746) > floor elevation Z (0.735) > water storage coefficient Q (0.734) > coal seam thickness M (0.717) > effective safety thickness D (0.663) in this study area. The predicted results were consistent with the actual situation. The outcomes of this research may benefit the construction of coal mine underground reservoirs in water deficient coal mining areas.