1. Introduction
Groundwater has been identified as a key route for contaminant migration, leading to underground pollution and soil water contamination. Over the last several decades, groundwater contamination has become a significant issue in various countries. A realistic, physically-based mathematical model is necessary to study the extent of the contaminant movement, build a sophisticated groundwater utilization plan, and prevent polluted groundwater from posing high risks to human health. Typically, the groundwater contaminant concentration distribution is modeled using the advection-dispersion equation (ADE). Numerical and analytical solutions of the ADE are commonly used for depicting the plume movement of pollutants in the groundwater system. Several studies have been found to model the groundwater contamination problem using classical one-dimensional (1D), two-dimensional (2D), or three-dimensional (3D) ADEs [
1,
2,
3,
4,
5,
6,
7]. The solutions in these studies were obtained using various state-of-the-art analytical and numerical methods. Although analytical models necessitate the reduction of several assumptions, they are nonetheless required since sensitivity analysis is considerably easier to perform on analytical models than on numerical models for determining characteristic variables that impact pollutant movement. In addition, analytical models can also be used to identify the best grid size for formulating a numerical model or evaluating the accuracy of the numerical solution. In the past, several authors have used different analytical methods (Laplace transform technique, Hankel transform, Green’s function method, etc.) to solve the ADEs with certain complex hydrological parameters such as heterogeneity of the medium and unsteadiness of the medium [
8,
9]. However, analytical approaches are often challenging to solve ADEs, and moreover, their solutions are infeasible to obtain in the case of complicated hydrological parameters and non-linear ADEs. In such situations, semi-analytical or numerical approaches may be suitable.
There is a growing trend toward using semi-analytical methods for solving ADEs with integer or fractional-order derivatives. Solutions to non-linear differential equations can be efficiently obtained using semi-analytical approaches [
10], which are otherwise difficult to obtain using traditional analytical approaches. Suk et al., [
11] solved a 2D ADE subject to variable boundary conditions under tidal fluctuations of subsurface water using the semi-analytical method. The generalized integral transform and matrix exponential techniques were used to obtain the solution of the 2D transport equation, and the results were validated with the semi-analytical method of 1D ADE reported by [
12] and the finite element method (FEM). Also, Kumar et al., [
13] discussed a 1D ADE by homotopy analysis method (HAM) with time-dependent velocity and considered a non-linear time-dependent dispersion coefficient. The solution was validated with the analytical solution and found good agreement. However, semi-analytical approaches give solutions in truncated series form. Convergence of the solution is one of the issues with such solutions. In such cases, numerical approaches prove to be a better alternative than both analytical and semi-analytical approaches in terms of accuracy and computational feasibility.
The numerical method generally translates differential equations specified in continuous space and time into a wide range of discretized equations [
14]. Several numerical methods, such as the finite volume method (FVM), FEM, finite difference method (FDM), boundary element method (BEM), mesh-free method, etc., have been proposed in the literature [
15,
16] to achieve the discretized space. FDM is classical and widely popular among all these methods since it eases computational complexity by translating the set of partial differential equations into a set of algebraic equations. Numerous 1D, 2D, and 3D ADEs have been solved with various schemes of FDM such as backward time-centered space (BTCS), forward time-centered space (FTCS), upwind schemes, Du-Fort Frankel, Crank-Nicolson (CN) scheme, alternating direct implicit (ADI) method, etc. Recently, Appadu et al., [
17] solved an ADE using three different schemes of FDM, i.e., a non-standard finite difference scheme, a third-order upwind scheme, and a fourth-order upwind scheme. It was found that the non-standard finite difference scheme is substantially better than the third- and fourth-order upwind schemes. Also, Johari et al., [
18] employed the ADI methods for 2D ADEs, while Hutomo et al. [
19] applied the Du-Fort Frankel method for solving a 2D ADE with variable coefficients. Singh et al., [
20] solved a non-linear reactive ADE by explicit FDM and calculated the stability of their model using the von Neumann method. The solution was validated with the existing analytical solution and found a substantial similarity between them. FDM was also used in the past for solving fractional-order derivatives (ADEs). Su et al., [
21] solved a fractional-order space derivative ADE by using the fractional CN scheme. Later, Heris et al., [
22] used the fractional backward differential formula method to obtain the solution for a 1D fractional ADE. Several studies exploring fractional-order ADEs for groundwater contamination transport modeling have been exhaustively reviewed by [
23]. The article discusses the various challenges and recommendations for fractional-order ADEs to be used as a real-world tool to predict groundwater contaminant transport more effectively and accurately. ADI and CN methods are more suitable among various FDM schemes since both are implicit methods and unconditionally first-order and second-order accurate, respectively. Several authors have implemented these methods to solve their problems.
Tian and Ge, [
24] applied the ADI method to the unsteady ADE problem. The von Neuman analysis method was used to verify the proposed method’s stability. The authors found their solution to be unconditionally stable and accurate as fourth-order and second-order with respect to space and time, respectively. Later, Tian, [
25] solved a 2D ADE in the transient system using the rational high-order compact ADI technique. The method was found to be unconditionally stable, having fourth-order and second-order accuracy with respect to space-time, respectively. Recently, Chew et al., [
26] applied the Half-sweep Newton Successive Over Relaxation numerical method for dealing with a 1D non-linear porous medium equation. The authors found that their method gave an unconditionally stable solution and, hence, was a suitable numerical method for non-linear partial differential equations.
In the context of groundwater contaminant transport problems, predicting the contaminant migration profile is a key challenge due to several limitations and model assumptions about the underlying physical phenomenon. There have been continuous efforts by several researchers to improve the accuracy of the prediction. A few of the critical parameters that affect the model’s accuracy are the assumed nature of the contaminant input source and the nature of porous media. In most of the research on contaminant concentration distribution profiles, the input source was considered a point source [
27,
28]. Although the point source assumption eases the calculations from a computational perspective, it doesn’t yield a satisfactory prediction of the contaminant trajectory. Point pollutant sources are generated or found from a single source, whereas non-point pollutant sources are generated from diffused sources, resulting in the release of pollutants over a wide area. Excess fertilizer and pesticides from cropland, oil, grease, and toxic chemicals from urban runoff are examples of non-point pollutant sources. The innate heterogeneity of porous media is well known and thus warrants inclusion in the groundwater contaminant transport modeling exercise [
29]. Various studies in the literature indicate that the assumption of a heterogeneous medium offers enhanced capabilities to account for scale-dependent dispersion and characterize abnormal transport [
30]. Thus, the axial input source assumption and heterogeneous medium present a resemblance to the realistic scenarios and governing physics of the transport problem. In this study, non-point pollutant sources are considered along the coordinate axes, typically known as axial input or line sources. Such input sources can be commonly found in angular-type agricultural lands [
31]. The authors studied solute transport with axial input sources for uniform flow. However, their treatment of contaminant transport phenomena assuming a homogenous medium would be a limitation in realistic scenarios.
With these research gaps discussed so far, we propose a model for analyzing the contaminant transport with the axial input sources having non-linear sorption, decay, and production terms in a heterogeneous medium. The approximate solution of the model was achieved by employing the CN and ADI methods. Because of the heterogeneous medium, the present work is more realistic in nature and gives an accurate prediction of the contaminant concentration migration profile in groundwater reservoirs. To the authors’ best knowledge, no such type of problem has been solved previously in the heterogeneous medium case. Further, several test cases were formulated to broaden the analysis of the impacts of different parameters influencing the contamination process. To this effect, the impact of different types of axial input sources, such as exponential, sinusoidal, and asymptotical, is obtained. In particular, sinusoidally varying time-dependent axial sources might be of interest to study the contaminant transport process in hilly regions. Further, we also characterized the contaminant transport in different soil mediums and the non-linearity power for Langmuir sorption for all the axial input sources considered in this paper. All the graphical solutions in the present study were obtained using the CN method for different geological formations and hydrological input data. Finally, a PDEtool-based validation strategy (a partial differential solver package in MATLAB software based on FEM) is chosen to compare the numerical approximations obtained for the proposed model problem.
2. Contaminant Transport Model (CTM)
The governing contaminant transport equation is derived based on the mass conservation law and Fick’s law. Under the consideration of contaminant sorption in the porous medium, the solid and liquid phase concentrations (i.e.,
and
, respectively) take place in the process of transportation. The 2D contaminant transport in a heterogeneous and anisotropic porous medium having a decay rate
, constant porosity
, bulk density
, and production rate
, is expressed as [
3]:
where,
and
are seepage velocities,
and
are the dispersion coefficients down the horizontal and vertical directions, respectively.
Periodic initial input problems exist in both natural and human-designed systems. In the case of natural groundwater contaminant analysis, a periodic pattern in the concentration levels may typically be caused by seasonal variations. On the other hand, pollutants can also be discharged at fixed intervals in man-made discharges. Such periodicity is found to be best represented by a sinusoidally varying, space-dependent background distribution [
32]. Thus, in this paper, initially, a sinusoidally varying space-dependent background concentration is considered in the non-uniform porous medium as [
33]:
where
is a constant background concentration,
and
are heterogeneity parameters,
is the arbitrary constant,
and
denotes the finite lengths in the
directions, respectively.
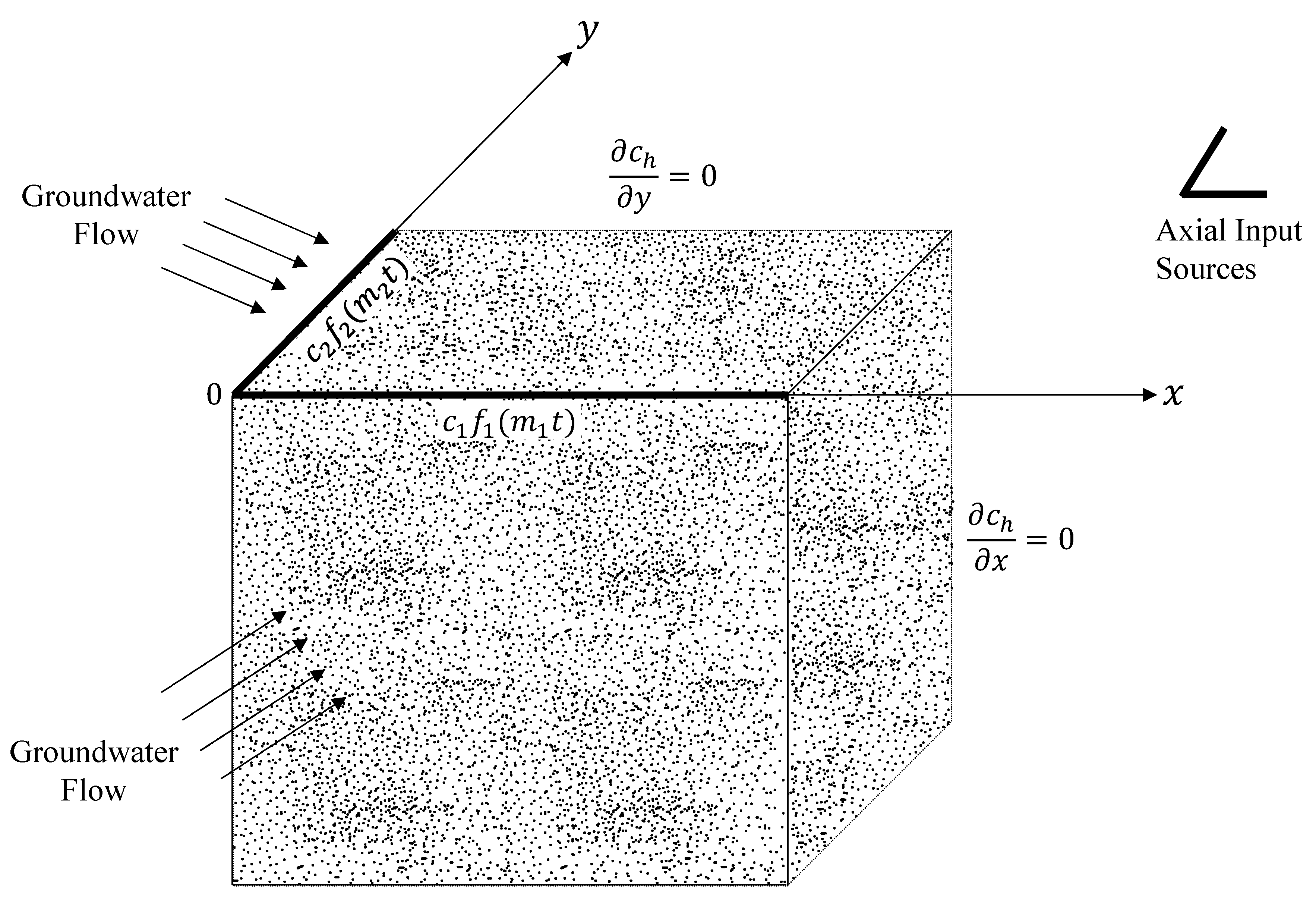
Figure 1 depicts the geometry of the proposed model, in which the axial input sources assigned along the
- and
-directions follow the Dirichlet boundary conditions. In the present study, periodic, exponential, and asymptotic [
32,
34,
35] axial input sources are considered. The boundary conditions for the proposed model are specified as follows:
where,
and
are the constants denoting the sources of input concentrations down the
and
directions, respectively,
and
are decay constant parameters along the
- and
-directions, respectively.
At the outlet boundaries, the boundary conditions are defined as follows:
The conceptual model corresponding to the 2D contaminant dispersion in a porous soil medium with axial input sources and Neumann boundary conditions [
31] is depicted in
Figure 1.
The relationship between the solid and liquid phase contaminant concentrations sorbed onto the soil particles at a constant temperature is known as the isotherm. When the sorption process occurs very quickly compared to the flow velocity, it attains an equilibrium state known as the equilibrium sorption isotherm. The present study uses the equilibrium-state sorption isotherm. The sorption isotherm may be either linear or non-linear. The linear sorption isotherm applies to low solute concentrations and absorption. In the linear sorption isotherm, there is no upper limit to the solute sorption onto the soil particles. However, the solute transport is more realistic for the non-linear sorption model as compared to the linear sorption model [
36,
37]. There are two types of non-linear sorption: Freundlich and Langmuir. The Freundlich sorption is defined as
, where
is the sorption coefficient and
is the empirically determined non-linearity parameter varying from 0 to 1. The Freundlich sorption isotherm is the most preferable and widely used isotherm so far, but it also does not have an upper limit on the solute sorption onto the soil particles. The Langmuir sorption, which specifies an upper limit of the solute sorption onto the soil particle, is defined as
where
is known as the Langmuir constant and
denotes the maximum sorption capacity [
38,
39,
40,
41]. Using the relationships of either Freundlich or Langmuir sorption isotherms between
and
in Equation (1) yields
where,
is known as the retardation factor.
Due to the heterogeneity of the medium, the horizontal and transversal seepage velocities depend on space, and according to [
8], the velocities are defined as follows:
where,
and
are initial groundwater velocities, and
,
are heterogeneity parameters. The idea of classical dispersion theory [
42], is as follows:
where,
and
are initial dispersion coefficients. Using Equations (8) and (9) for
, Equation (7) becomes
where,
,
, and
.
Using transformations
and
[
8] in Equation (10) yields:
where,
and
.
The new space domain following the transformation of the geometrical conditions is given as:
2.1. FDM-Based Solution of the Proposed CTM
The derivation of the solution begins by first splitting into subintervals of different sizes. Similarly, and are split into and subintervals, with each subinterval having and size respectively. Initially, the CN and ADI methods are used for obtaining the numerical approximations of the proposed model described in Equation (11), along with the conditions described by Equations (12)–(16). Following the initial approximation, a penta-diagonal structure of linear algebraic equations for the CN and two batches of the tri-diagonal structure of linear algebraic equations for the ADI method at each discrete time interval are obtained. In the next stage, the set of algebraic equations obtained in the previous step is solved at fixed time intervals using MATLAB scripts to obtain graphical solutions. The mathematical formulations of the proposed numerical approximations are discussed in the following sub-sections.
2.2. CN method-Based Approximate Solution
The time derivative of the ADE (Equation (11)) is estimated using the CN finite difference scheme at the grid point
, while the space derivative is estimated by their central approximations at the
th and
th levels. To ensure that the resultant finite difference approximations are linearized, the retardation factor
given in Equation (11) is calculated using the previous time level (
th time level) [
40]. This yields the following approximation of Equation (11):
Equation (17) is rearranged in the following form:
where,
,
,
,
,
, and
.
Further, Equations (15) and (16) at the time levels
and
can be written as follows:
Applying Equations (19) and (21) to Equation (18) yields:
where,
and
.
Applying Equations (20) and (22) to Equation (18) yields:
where,
and
.
Further, applying Equations (19)–(22) in Equation (18) gives:
where,
and
.
The numerical approximation of the transport equation given by Equation (11) is derived using the combined set of coupled Equations (19) and (23)–(25). Specifically, equating these sets of coupled equations result in a penta-diagonal form of linear algebraic equations for each iteration. In this paper, graphical visualizations of the final numerical derivations, which have been obtained using MATLAB codes, for different cases are presented and discussed in the result section.
2.3. ADI Method-Based Approximate Solution of CTM
Crank-Nicolson (CN) is the conventional approach for obtaining numerical approximations to generic transport equations. However, they result in a complicated multi-dimensional system of equations and are often infeasible for complex transport phenomena with many parameters. On the other hand, the ADI method involves solving a system of equations with a simple structure at each iteration. A generic approach to solving PDEs using the ADI method involves approximating and derivatives in two stages. In the first stage, the derivative is approximated by an implicit scheme, and the derivative is approximated by an explicit scheme. In the second stage, the derivative is approximated by an implicit scheme, and the derivative is approximated by an explicit scheme. Solving the two stages results in tridiagonal matrices, which are then solved to get the final approximate solution.
Similar to solving PDEs using the generic approach of the ADI method, in this paper too, the overall process of approximation using the ADI method is carried out in two steps. In the first step, the entire spatio-temporal derivatives of Equation (11) are substituted by the second-order central difference estimations such that the derivatives of
x-terms are estimated at the
time level with unknown concentration and
y-terms are estimated at the
time level with known concentration. The resultant equation after the substitution in Equation (11) is given as:
After rearrangement, Equation (26) yields:
where,
;
;
;
;
;
,
goes form
to
for every value of
.
In the second phase, the method is reversed for the next half-time interval. Using Equation (11), the
derivative components are approximated by the implicit scheme (i.e.,
time step) with an unknown concentration, whereas
derivative components are approximated by the explicit scheme (i.e.,
time step) with a known concentration. Consequently, at this point, Equation (11) is represented as:
where,
and
.
Further, the estimation of the derivative boundary conditions described in Equations (15) and (16) for the endpoints, i.e., for
and
, is given as:
At the
time level and boundary point
, the estimation of Equation (16) is produced as:
Using Equation (29) in Equation (27) and Equation (30) in Equation (28), we obtain, respectively, the following:
where,
, and
, and
where,
,
.
Similarly, using Equation (29) in Equation (28) and Equation (31) in Equation (27), we obtain the following:
where,
,
, and
where,
, and
.
Using Equation (29) and Equation (31) in Equation (27) yields:
Using Equation (29) and Equation (30) in Equation (28) yields:
On solving the two sets of coupled Equations (27), (28), (32)–(37) for
, two separate tridiagonal systems of linear equations are obtained. For illustration, graphical solutions to these systems are obtained using MATLAB scripts and further discussed in the following section. Further, to summarize all the steps, we present an algorithm (Algorithm 1) below that contains the step-wise description of obtaining the solutions presented in this paper.
| Algorithm 1: Axial Input Source Contaminant Transport System |
Input
: Dispersion coefficients
: Advection coefficients
: initial background source
: constant input sources
: porosity of soil medium
: space domains length
: time interval
: Number of spatial nodes in and directions
: Number of time steps
: Decay parameters
Output
: Concentration distribution matrix
Step 1: Spatial transformation:
Transform old transformation of space variable into new transformation
Step 2: Mesh formation:
Construct mesh size of the space domain and time interval
Step 3: Initialize the initial and axial boundary condition concentration matrix
as follows:
a) for
for
end for
end for
b) for
for
end for
for
end for
end for
Step 4: Repeat this step for P time steps to compute the following:
- A)
Retardation matrix R (Freundlich and Langmuir) - B)
The penta-diagonal coefficient matrices A and B for calculating concentration values for each time step - C)
Compute the unknowns and solve the system of equations C = B1_inv × B × Z as follows:
End |
3. Results and Discussions
In this study, the 2D ADE, taking into account the non-linear sorption, decay, and source terms with periodic initial conditions and three forms of time-varying axial input boundary conditions (given in
Table 1) is solved by CN and ADI methods for a heterogeneous medium. The temporally dependent axial sources
and
are defined as shown in
Table 1.
Dispersion and advective coefficients are taken as space-dependent (i.e.,
,
,
,
). Periodic initial and boundary conditions with identical input values of the advection and dispersion coefficients in the horizontal and vertical directions are considered. Input data from [
43] are used for obtaining the graphical form of the solutions to the governing equation and are given as follows:
The pollutant distribution patterns by CN and ADI methods, assuming periodic initial and boundary conditions in the gravel-type soil medium at time
year are presented in
Figure 2 and
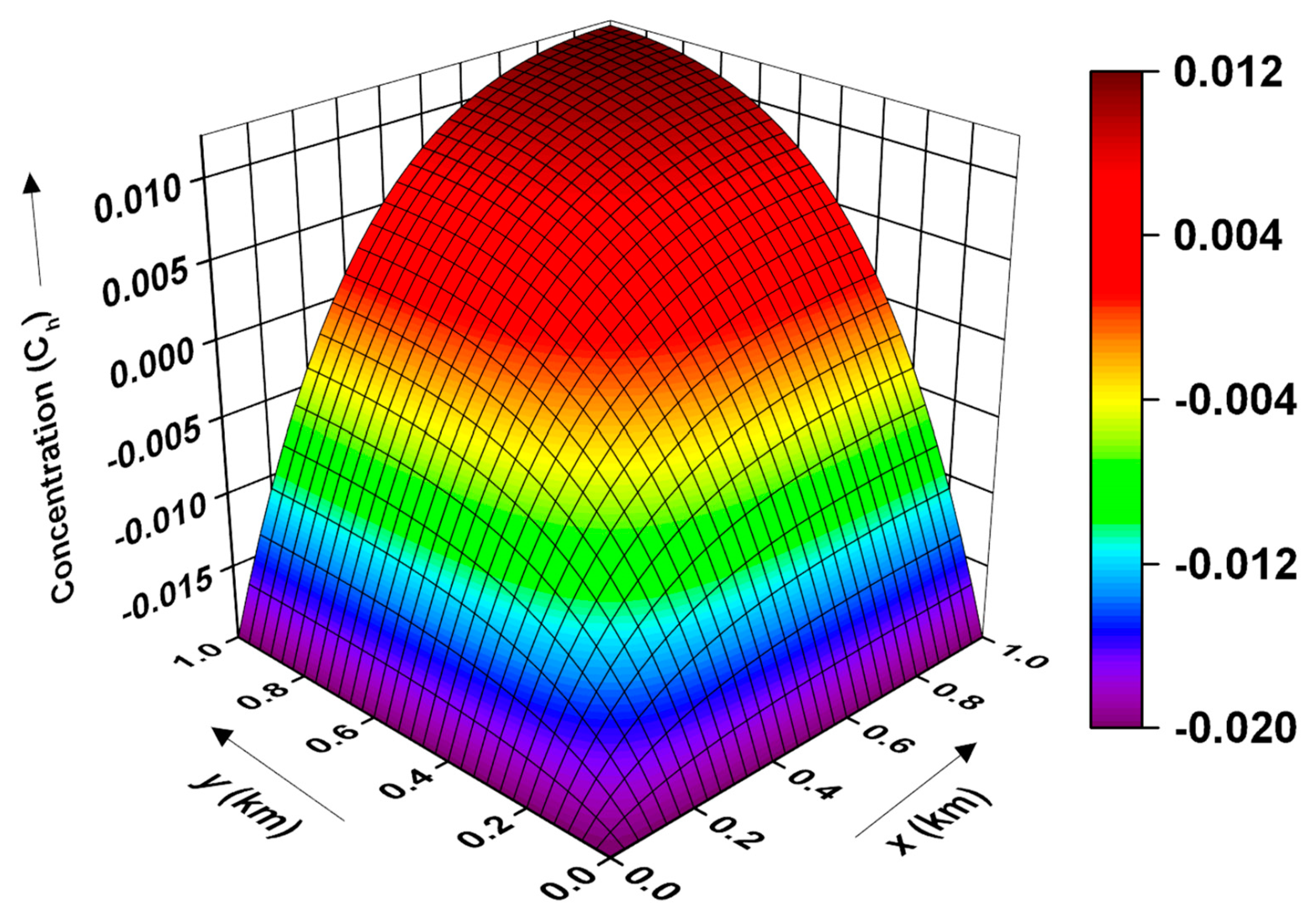
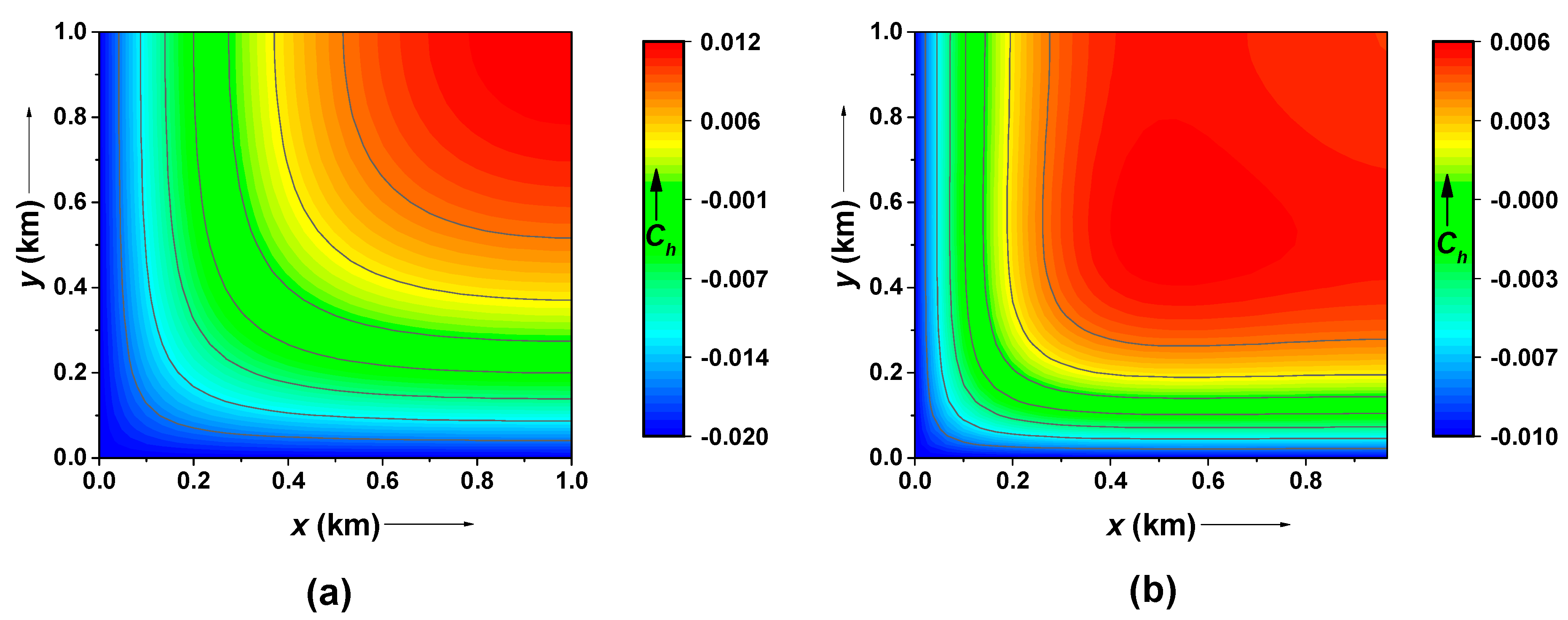
Figure 3. As evident from the figures, the pollutant concentration attains the highest level at the origin and gradually decreases with respect to distance to reach the lowest level near the extreme boundaries. Further, it is observed that the spread of the pollutant concentration is mirror-imaged around the diagonal line, possibly caused by the assumption of an identical distribution profile of input pollutant concentration along the coordinate axes.
Figure 4 depicts the contour of the pollutant distribution pattern obtained using the CN and ADI methods under the assumption of linear sorption. For the present case, periodic initial and boundary conditions with a gravel-type soil medium for the time period
are considered. As evident, the pollutant concentration is maximum along the coordinate axes and decreases with respect to distance towards the extreme boundaries. It may be noted in
Figure 2,
Figure 3 and
Figure 4 that the concentration could be negative since the assumed sinusoidal initial and boundary conditions in this work are known to manifest fluctuations in the concentration and thus output a few negative values [
33].
An earlier study by [
31] elaborated on the efficacy of the CN method over the ADI method for solving contaminant transport for axial input sources. A paucity of such research analyses in the literature prompted us to carry out a similar comparative analysis for our case too. In addition, for the generalizability of the results, findings based on the numerical results must be compared in different cases. Since the cases in the literature and the proposed problem in this work are different, presenting ADI and CN would further help to generalize the conclusions. We found a similarity in the results with the literature; hence, for the cases reported in
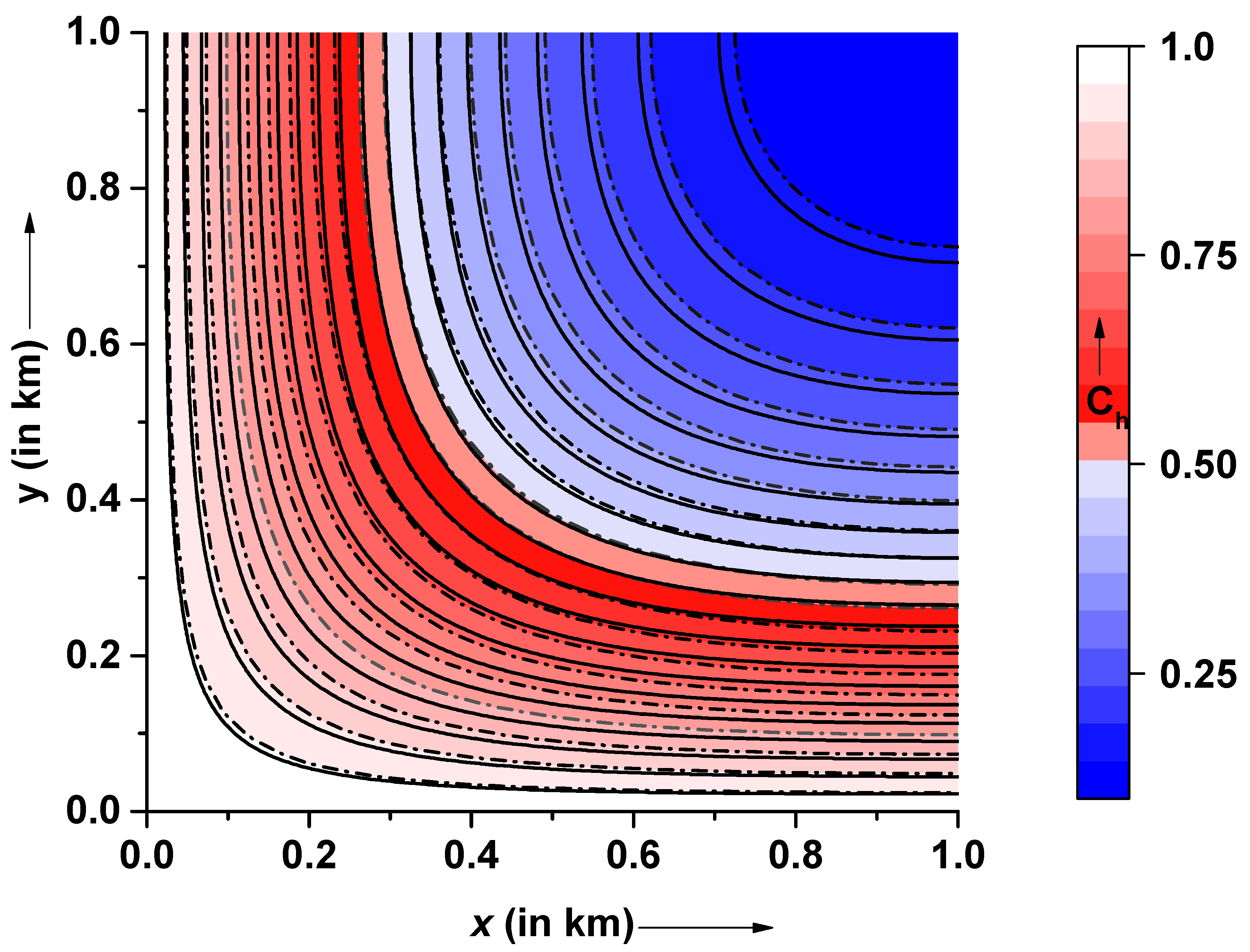
Figure 5 and subsequent cases, the CN method-based graphical solutions alone are reported in this paper. Typically, the accuracy and error of a numerical solution are obtained by validating it against the analytical solutions of the given model problem. However, for the model problem considered in this paper, obtaining an analytical solution is complicated and computationally infeasible. Hence, for the present work, the numerical solution of the proposed model obtained using the CN method is validated using the PDEtool box, as it is generally considered a benchmark for validating numerical solutions of PDEs. The approximate solution to the model problem considered in this paper is obtained for a special case using the following data:
;
as shown in
Figure 5. As evident from
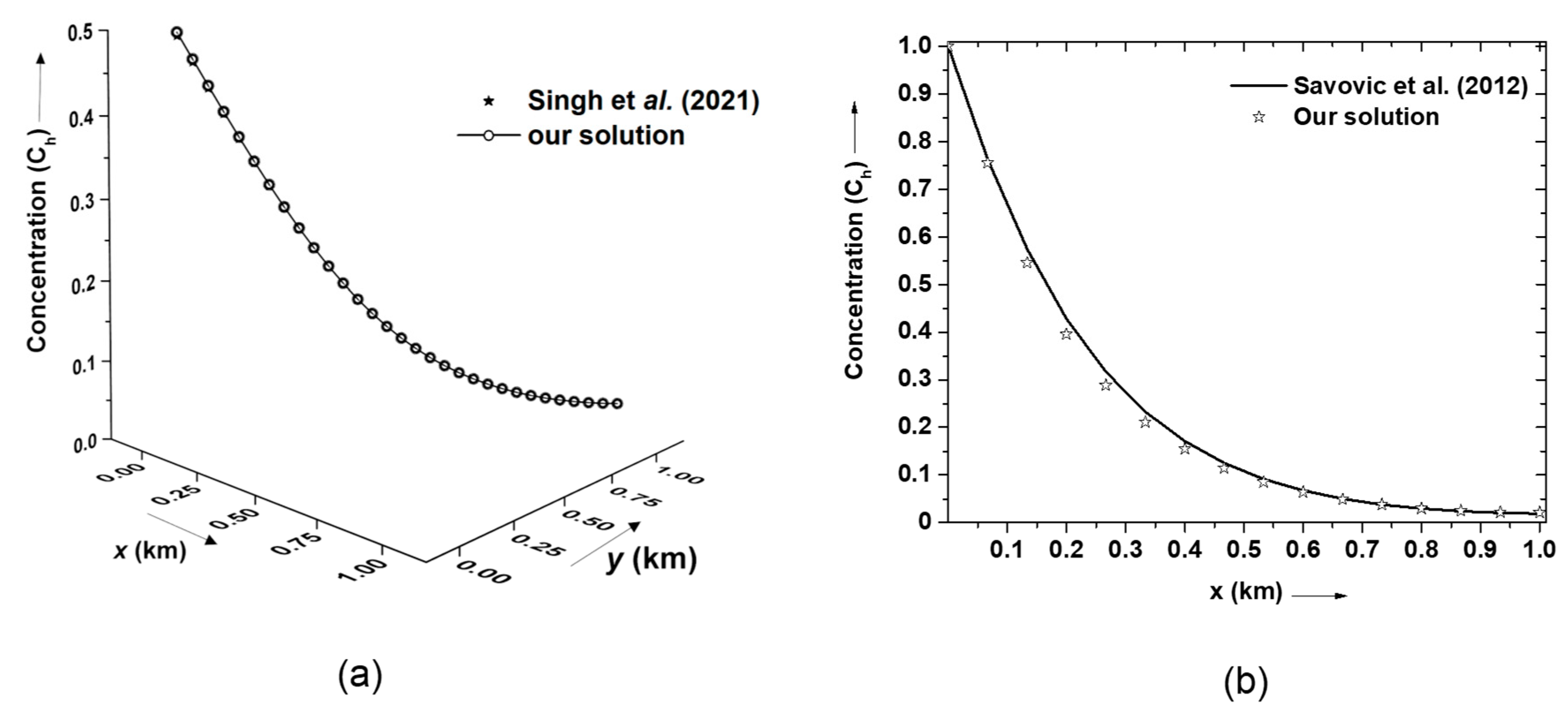
Figure 5, a satisfactory agreement is observed between the proposed numerical solution (CN-based) and the PDEtool-based solution. As observed from the figure, concentration patterns are nearly identical near the inlet and outlet boundaries, whereas a marginal gap is found near the middle of the domain. Further, an apparent uniformity in the contaminant concentration pattern beyond 0.5 km is observed, which becomes constant towards the final boundary. The overall trend suggests that the contaminant concentration reaches a maximum level at the inlet boundary, decays with space, and hits a minimum level near the outlet boundary.
Figure 6(a) illustrates the graphical comparison of the numerical solution for the proposed model with the data (
,
,
,
,
,
,
,
,
,
,
,
) taken from the previous literature given by [
31]. To this effect, the proposed model is transformed into a homogeneous medium without source-sink terms by taking dispersion coefficients and velocities as constants. Also, the initial condition is taken as a constant, and the Dirichlet boundaries are taken as an exponential type. It is found that the pollutant concentration strength of the proposed model solution is identical and shows close agreement with that of [
31].
The proposed numerical solution was compared graphically with the previous existing numerical solution [
44] for 1D contaminant transport with spatially varying transport parameters. The proposed 2D ADE model in this work was reduced to a 1D ADE transport problem by setting all the
-directional terms to zero and subsequently taking the input source as a single point source. The input data considered for comparison is as follows:
,
,
,
,
,
,
,
. We have used the above data in our model with previous numerical solutions. As observed, both solutions match closely, as shown in
Figure 6b. Statistically, the relative match for the proposed solution with the numerical methods shown in
Figure 6a,b is found to be 99.7% and 97.2%, respectively.
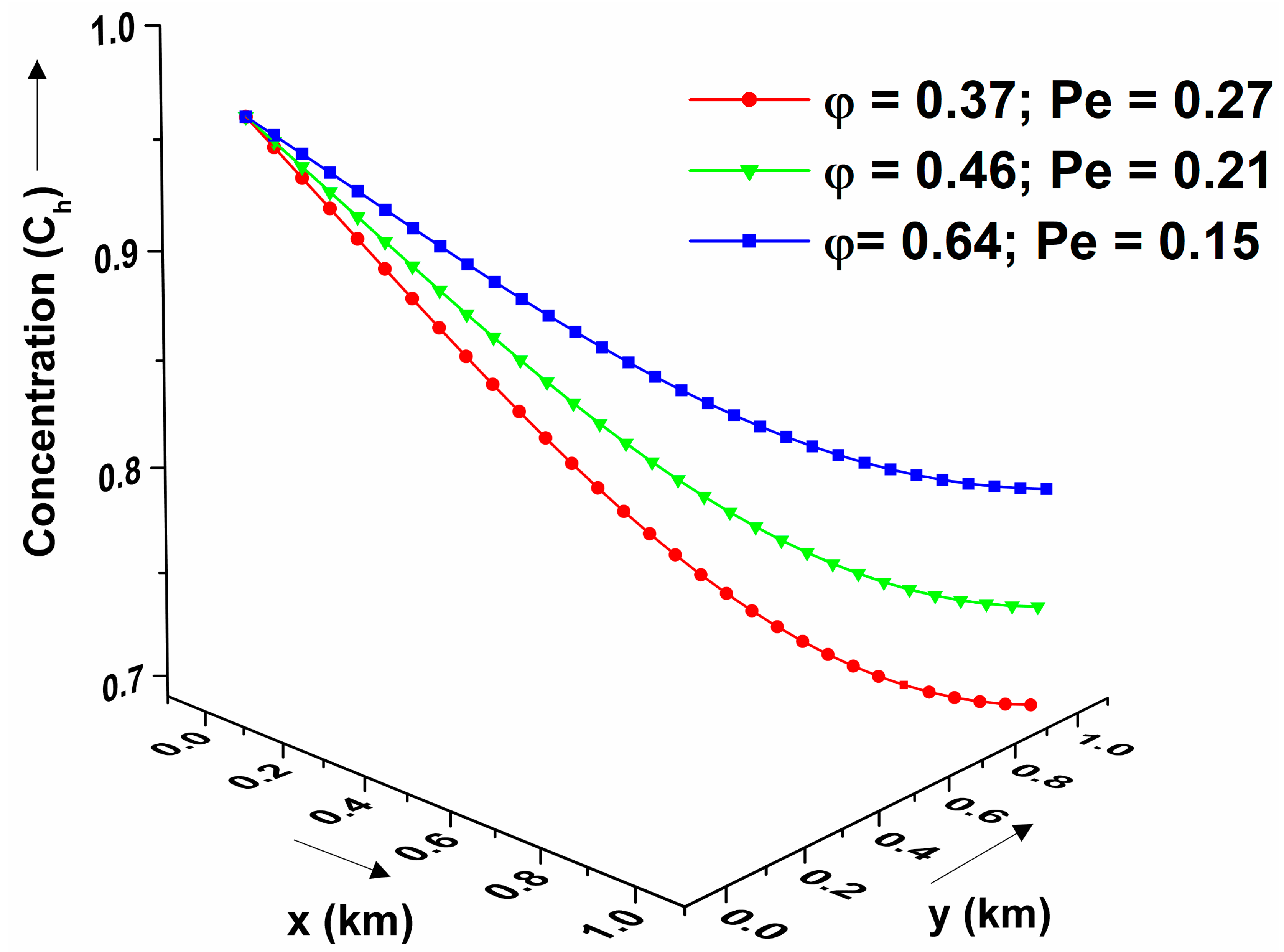
In general, the level of contaminant concentration is a factor of different geological formations in the 2D heterogeneous porous medium; hence, the pattern of pollutant concentration levels in geological formulations of different porosities is investigated in the present study. For this case, different soil mediums, such as clayey sand, fine sand, and silty, represented by porosity,
are considered.
Figure 7a shows the pollutant distribution profiles in various soil mediums at time
years estimated using the CN method, assuming linear sorption for periodic initial and axial boundaries. The pollutant concentration is highest for silty sand compared to clayey sand and fine sand. In contrast, the pollutant concentration hits the minimum level in the clayey sand. The effect of different soil mediums on the concentration distribution is shown in
Figure 7b for exponential axial input sources subject to a constant initial concentration value at a given time
years. The contaminant level decreases with the decrease in the soil’s medium porosity.
Figure 7c depicts the concentration distribution pattern for different soil mediums for asymptotically varying axial input sources with a constant initial concentration value under non-linear sorption for time
year. It is observed that the contaminant concentration level in the silty medium is higher than in the fine sand. In contrast, the contaminant concentration reaches the lowest level in the clayey sand for asymptotically varying axial input sources. Also, concentration reaches its minimum value at the final boundary. Also, it is observed that the distribution of contaminant concentration patterns is similar in the sinusoidal and asymptotic cases but opposite in nature in the exponential case. Since the exponential input source typically represents a sorption-dominated flow process, a higher porosity (more pore space) causes more retardation of the contaminant particles, and hence a slower decay rate is observed.
Figure 8 shows the pollutant transport profile at time
years for different bulk densities of contaminant concentrations (
) in the gravel medium assumed to be in a solid matrix-type packing. To characterize the concentration profile in this case, periodic boundary conditions are considered. It is observed that the initial pollutant concentration for both bulk densities considered is similar near the inlet boundaries. However, as evident from
Figure 8, contaminant concentration diminishes relatively fast for a higher bulk density (
) compared to a low bulk density (
).
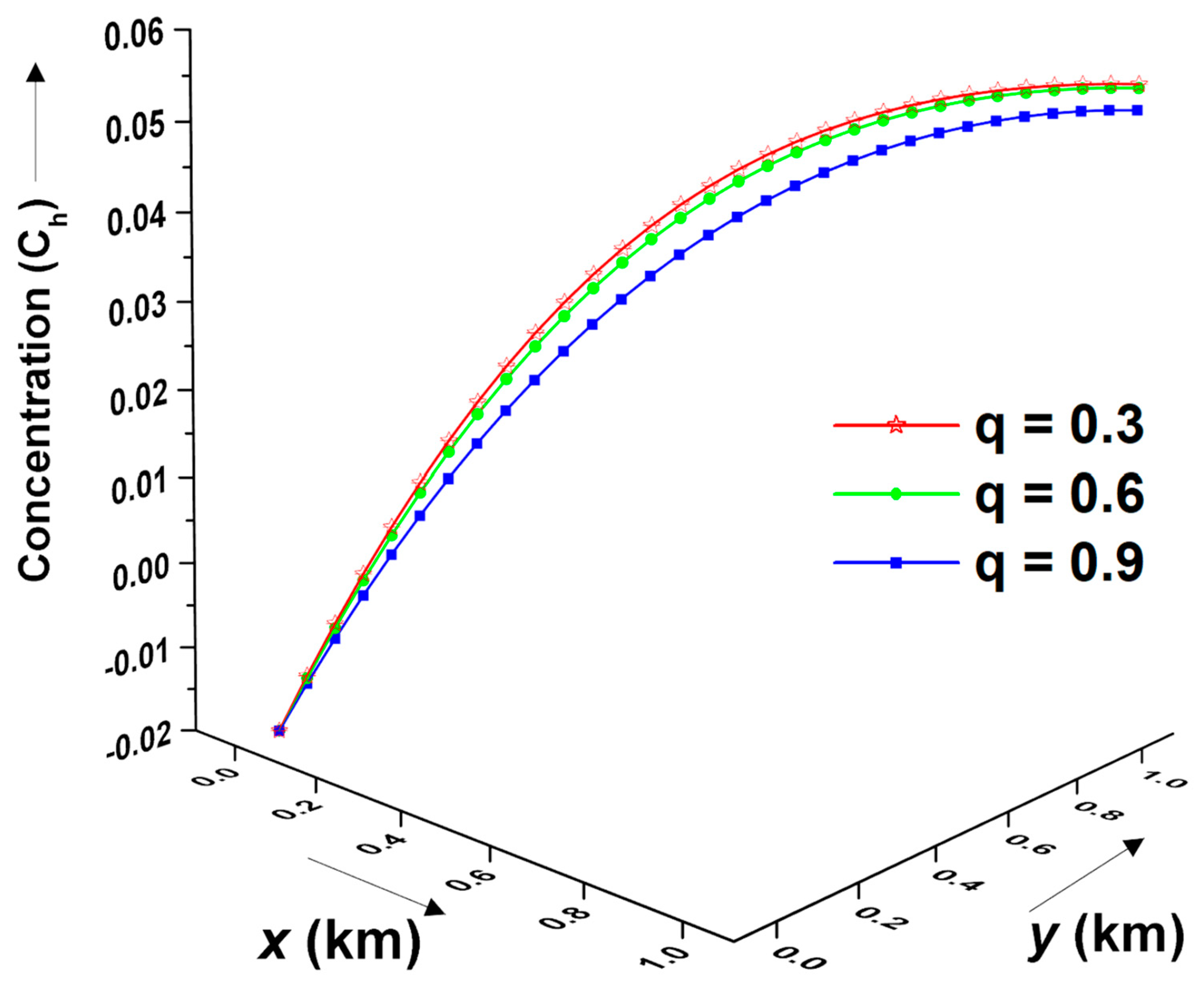
Figure 9 illustrates the effects of the fractional power of
over non-linear Freundlich sorption of contaminant distribution at time
years in the gravel medium. For this case, constant initial conditions and periodic boundary conditions are considered. It is evident from
Figure 9 that with rising values of
, which represent the nonlinearity of the model, the contaminant concentration decreases.
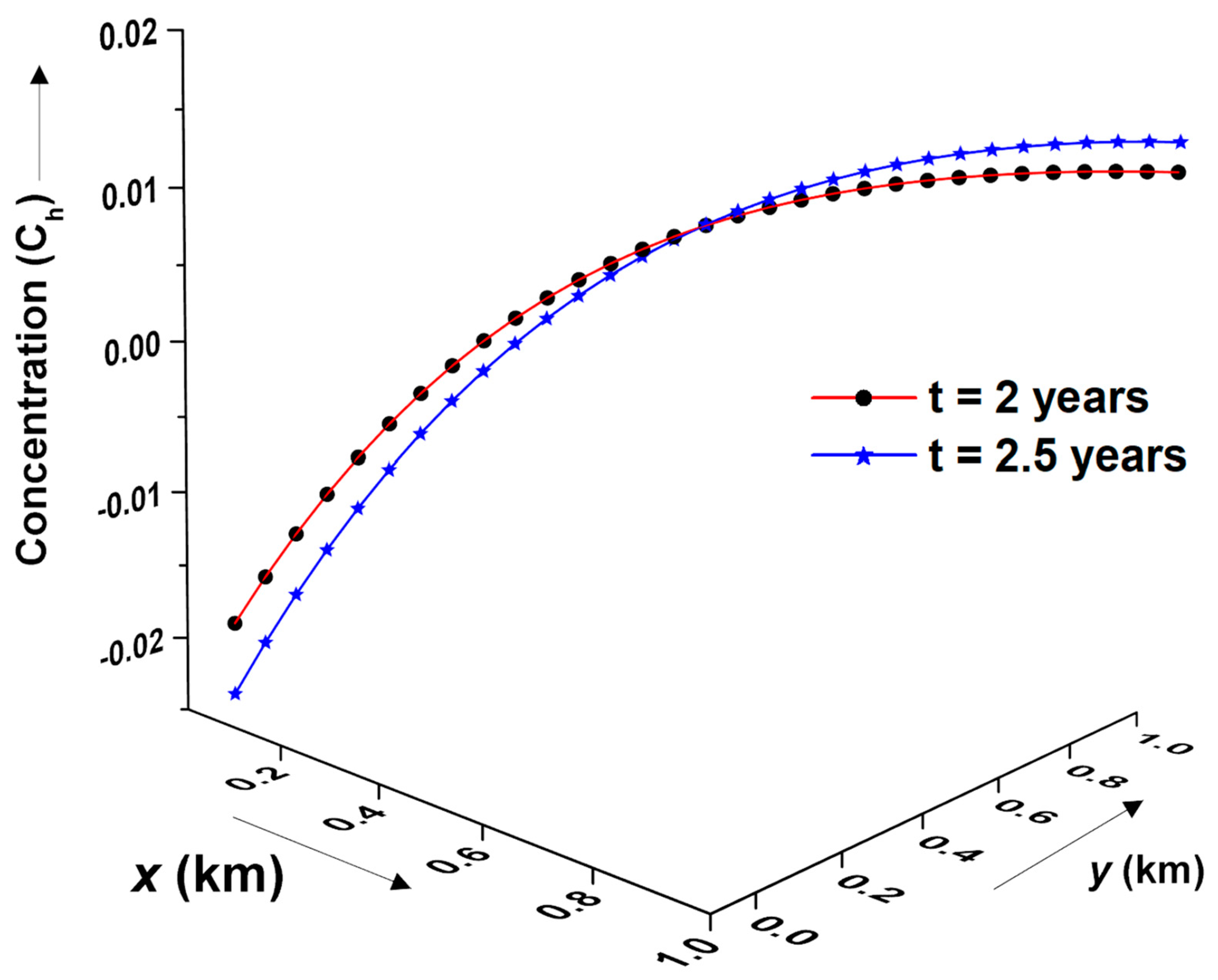
Figure 10 presents the concentration distribution profile at different times (
years) subject to periodic initial conditions in a heterogeneous groundwater flow system. Initial and boundary conditions are assumed to be periodic for both time domains. In general, it is observed that the concentration distribution decreases with increasing time domain up to some spatial distance. However, beyond a certain threshold distance, the concentration distribution increases with increasing time. It is observed that the concentration distribution profile depends on the nature of the initial and boundary conditions.
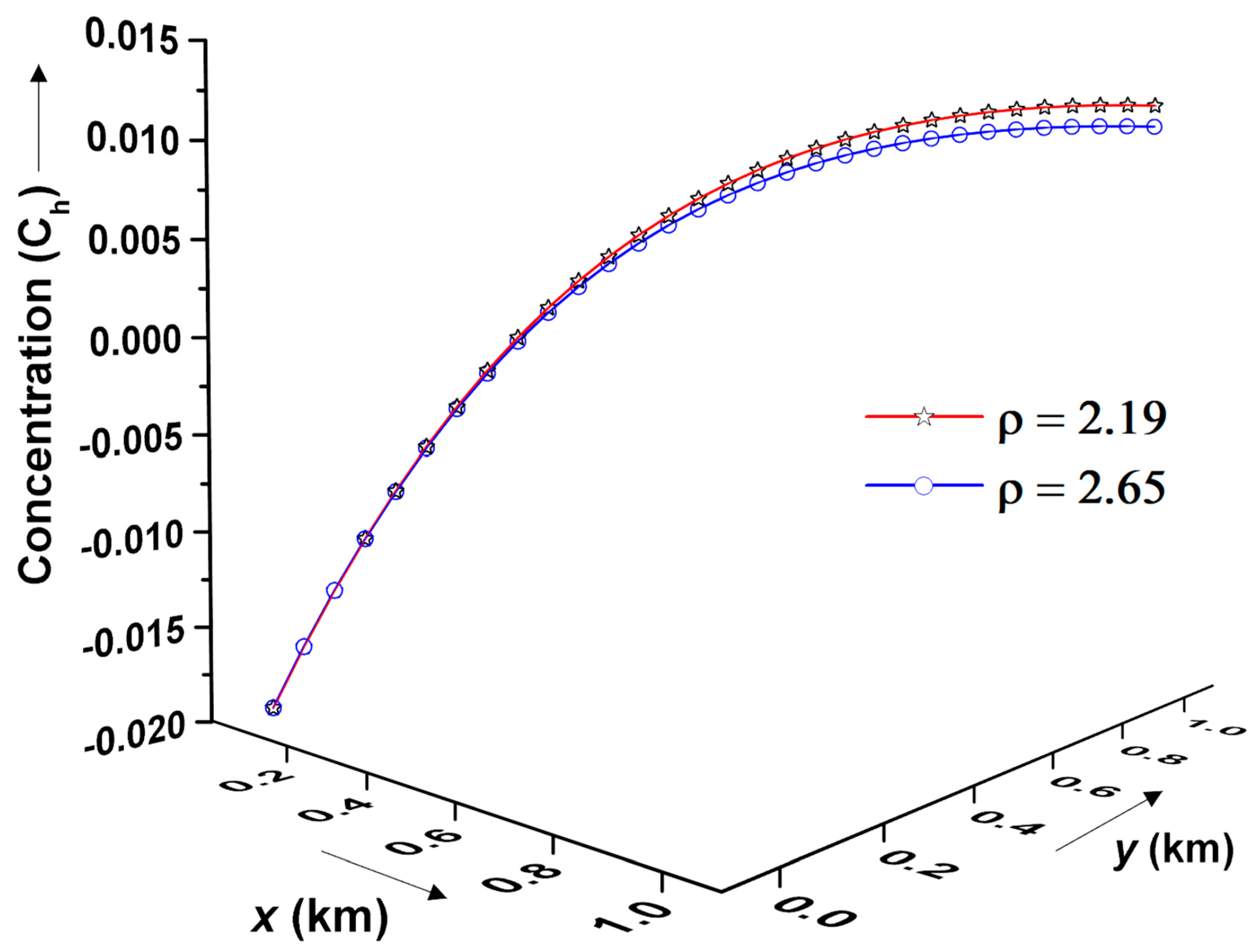
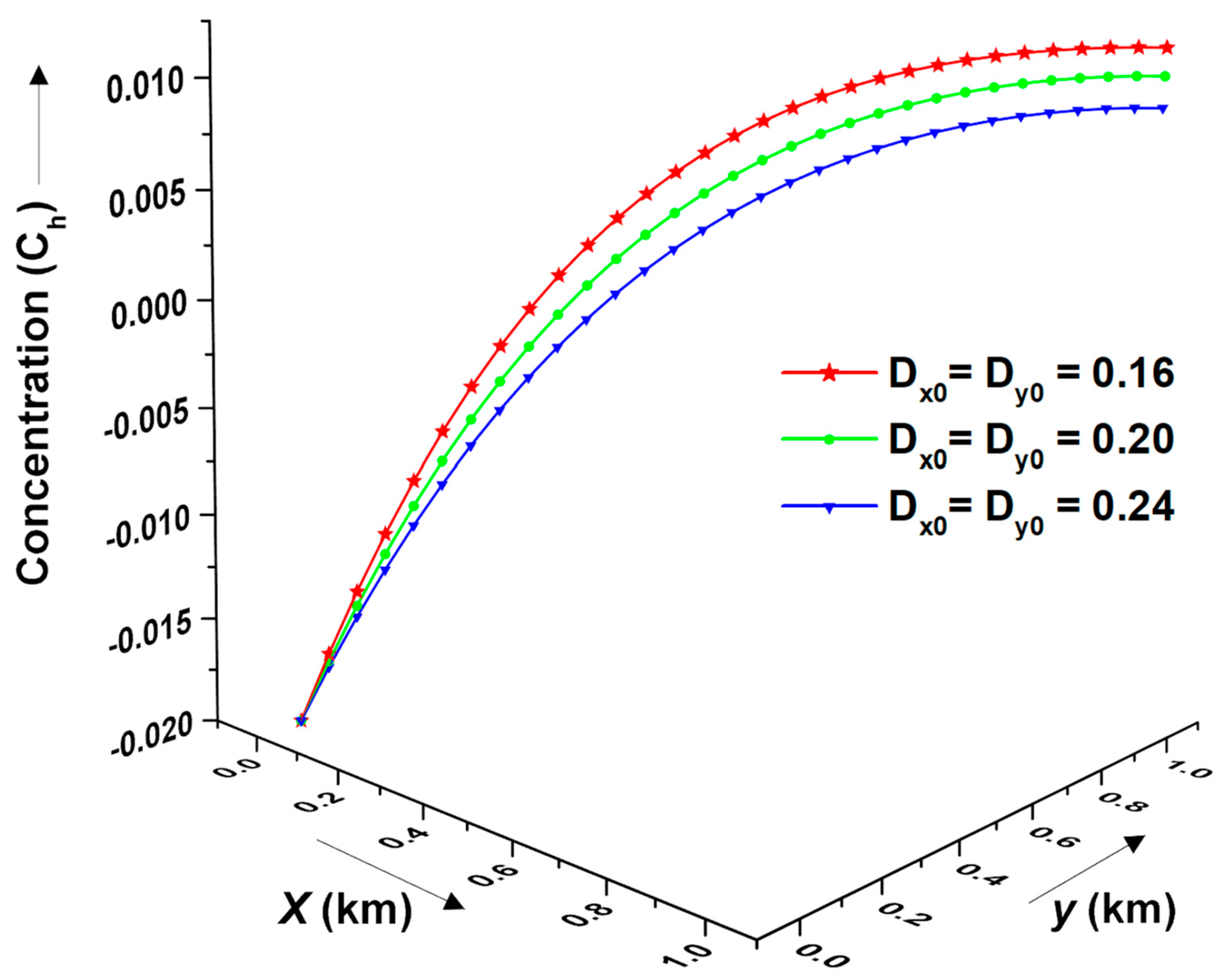
Figure 11 presents the effect of the dispersion coefficients
in the longitudinal and transversal directions over the concentration distribution profiles. It is observed that even with a marginal fluctuation in the dispersion coefficients, the resultant concentration distribution profile varies significantly at each point of the domain. The possible reason for such behavior may be attributed to the critical balance of the advection-dispersion flow process, which is altered by the change in the dispersion coefficients. Overall, the concentration value increases as the dispersion coefficients decrease for any given fixed time domain.
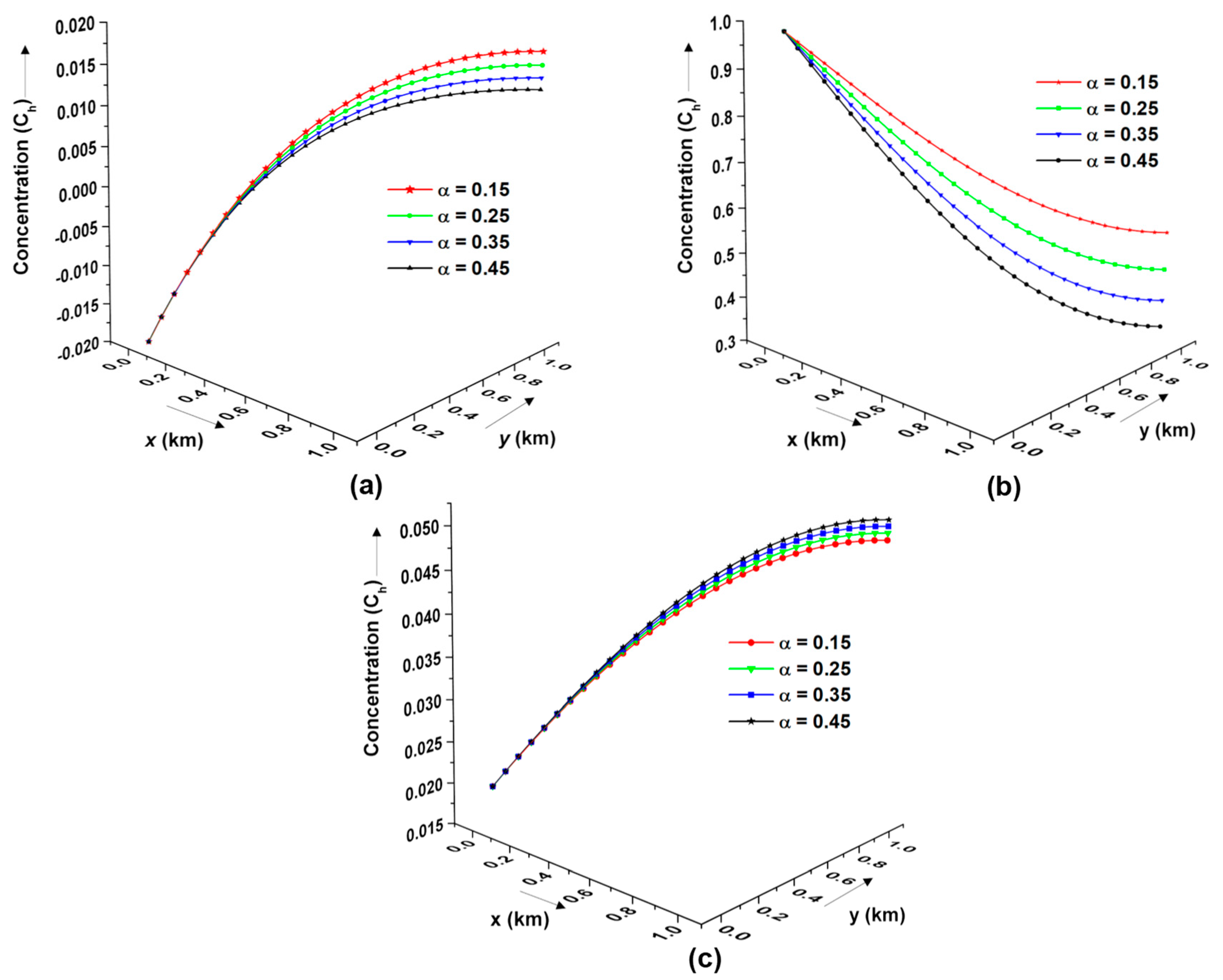
The dependency of the contaminant concentration profile on the non-linearity power
under Langmuir sorption is illustrated in
Figure 12. Different forms of axial input sources, such as sinusoidal, exponential, and asymptotic, are depicted in
Figure 12a–c, respectively. It is observed that the non-linearity terms for the sinusoidal and exponential cases are similar in nature, whereas they are the opposite in nature for the asymptotic case. This difference in contaminant distribution is possibly caused by the underlying physical phenomenon. In sinusoidal and exponential cases, the dispersion phenomenon is dominant and causes a gradual decrease in the contaminant concentration. In contrast, in the asymptotical case, the contaminant concentration reaches a saturation point where it does not change significantly. In addition, the dispersion process for the asymptotical case is relatively weaker compared to the other two cases. These factors may cause different distribution patterns, as observed in
Figure 12a–c. The contaminant concentration for the sinusoidal and exponential axial input sources decreases with increasing values of the non-linearity term. However, in asymptotic cases, contaminant concentration increases with an increase in the non-linearity power
.
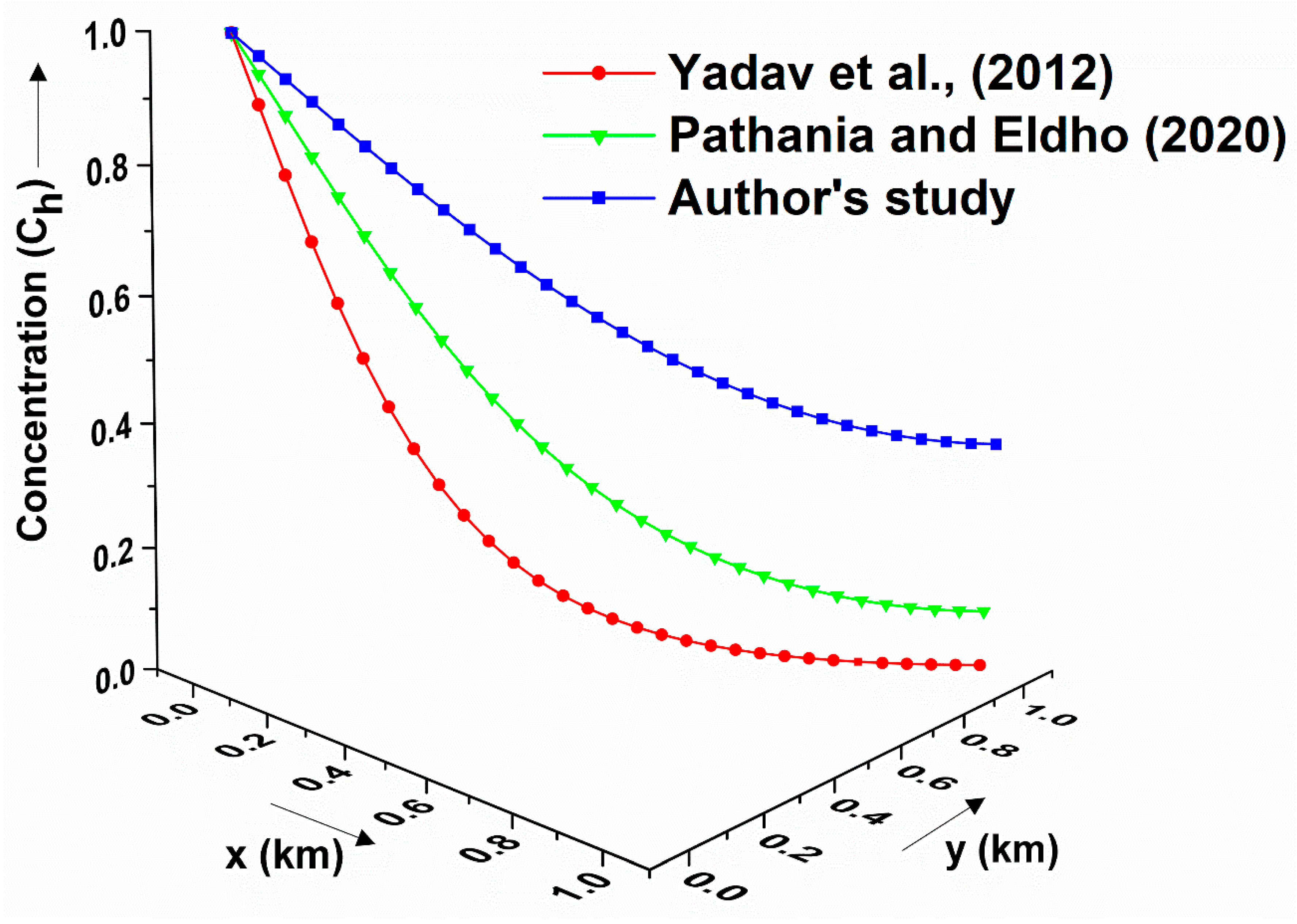
Figure 13 shows the graphical validation of the proposed model for the heterogeneous silty (i.e.,
) type porous medium. For this case, the input source is considered to be a point source, and hence we set
at the Dirichlet boundaries. Further, the initial background source concentration is assumed to be zero (i.e.,
). Data from [
45] (
,
,
,
,
,
) and [
46] (
,
,
,
,
,
) were fed into the proposed model, and its output was compared to the output obtained by the data considered by the authors. As evident, a similar overall trend of the contaminant profile—a spatially diminishing concentration trend towards the edge of the domain, is observed between the various existing models and the proposed model for the respective datasets considered. The rationale behind this graphical comparison was to establish the correctness of the input data considered in this work.
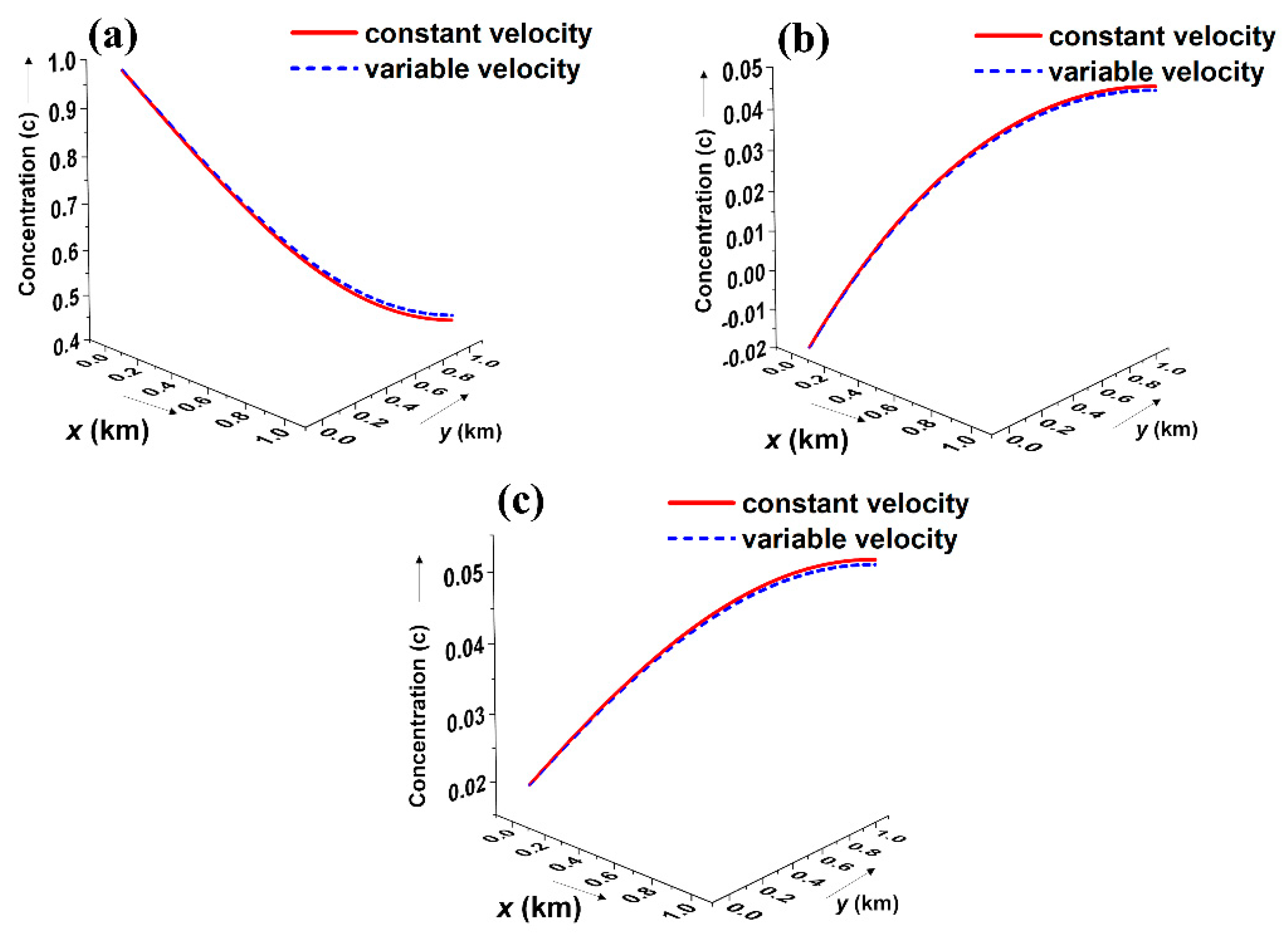
Figure 14, presented in this study, provides a comparative analysis between the constant velocity and variable velocity of groundwater flow conditions. The constant velocity assumption implicitly refers to a homogenous medium, whereas variable velocity refers to a heterogeneous medium. For constant velocities, the advection and dispersion coefficients were kept constant without any spatial dependence, as expressed in Equation (1). In general, it is observed that the overall contaminant concentration may either increase or decrease depending on the specific initial or boundary conditions. As observed from
Figure 14a, which represents the exponential boundary condition, contaminant concentration decreases for both the constant and variable velocities; however, the dip in the constant velocity case is greater than the variable velocity case toward the end of the boundary. In contrast, for sinusoidal (
Figure 14b) and asymptotic (
Figure 14c), there is an overall trend of increasing contaminant concentration, albeit at different rates for constant and variable groundwater flow velocities. A higher peak concentration is observed for the constant velocity condition compared to the variable velocity condition.
Peclet and courant numbers are often used in the context of groundwater contamination phenomena to explain the transport dynamics, i.e., establish a relation between the advection-diffusion processes, and quantify the flow rate of contaminants for various geological formations [
9]. Mathematically, the Peclet number and Courant number are defined as:
A high Peclet number shows that the advection process is the cardinal transport mechanism, while a low Peclet number shows that the dispersion mechanism dominates the transport phenomenon. The courant number gives the number of particles in the medium that are transported in a given time interval. The ideal value of the Courant number must be less than 0.7 [
47].
The relationship between the Peclet number and the porosity of the various geological formations is also addressed. As evident from
Figure 15, the Peclet number increases as the porosity decreases, and vice versa. With a decrease in the Peclet number (increase in porosity), the overall contaminant concentration is found to be higher. The pollutant concentration decreases with space and approaches its lowest value near the extremes of the boundary. Similarly, in the case of the Courant number, the contaminant concentration is also predicted for the different geological formations.
Figure 16 depicts the contaminant concentration in various media with distinct Courant numbers at a specific time period. We observed that as porosity values decreased, the Courant number increased. The nature of the contaminant concentration is also demonstrated, and it is noted that concentration values rise as the courant number decreases at each of the positions. These concentration levels decrease with distance and approach their lowest value near the final boundary.
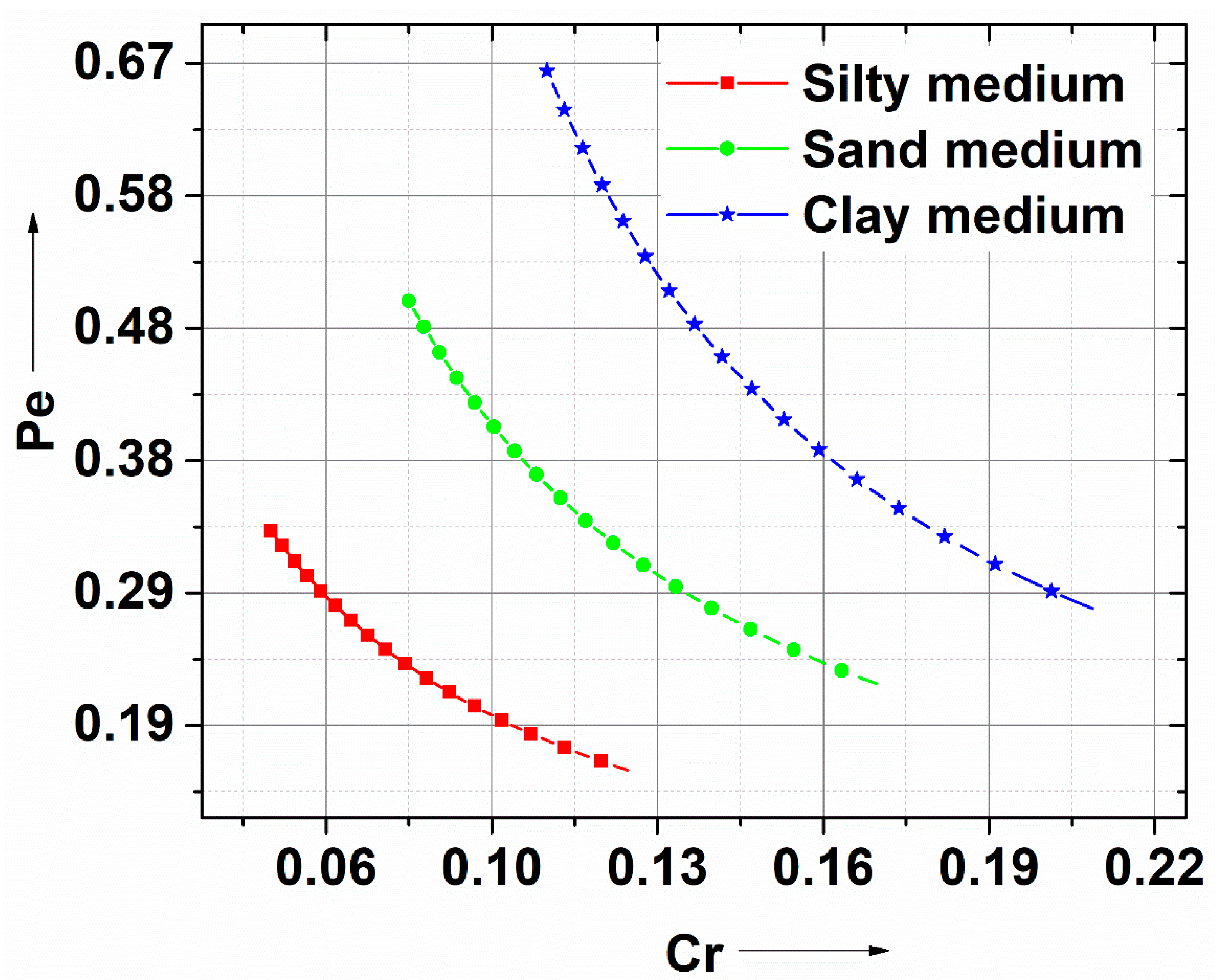
Figure 17 shows the contaminant transport dynamics using a plot between the Peclet and Courant numbers for various transport mediums with different inter-porosity ranges. As observed from
Figure 17, the general trend within a given medium indicates a non-linear relationship between Pe and Cr with an increase in the inter-medium porosity. For advection-dispersion problems, the stability of the numerical solution can be inferred using the Peclet number. The solution will oscillate when the absolute value of the Peclet number is greater than two [
48]. In the present problem, since the Peclet number is less than two, the proposed numerical solution is stable and hence not discussed in the manuscript.