Determining Groundwater Drought Relative to the Opening of a River Barrage in Korea
Abstract
:1. Introduction
2. Methods
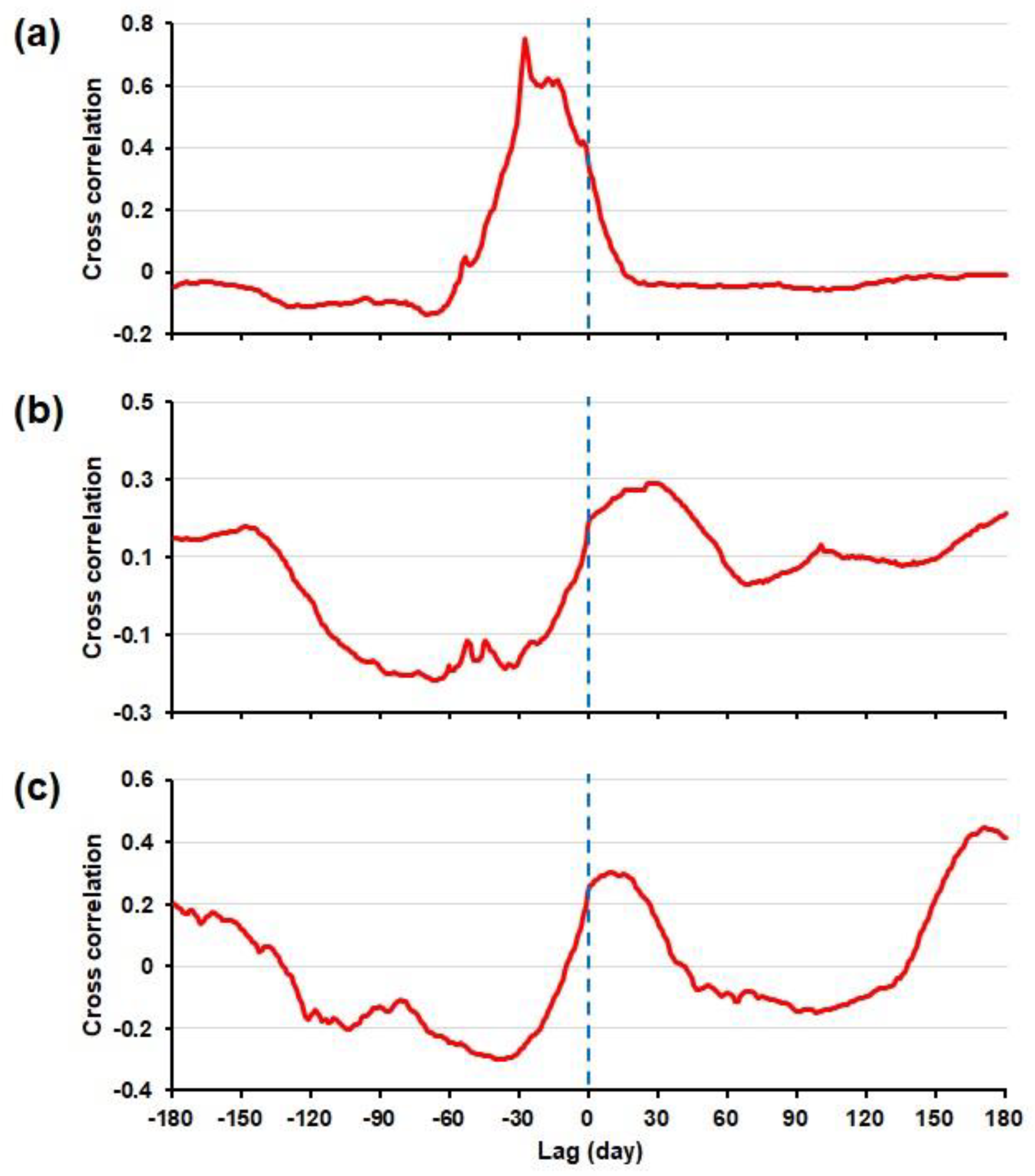
2.1. Cross-Correlation Analysis
2.2. K-Means Cluster Analysis
2.3. Standardized Groundwater Level Index (SGLI)
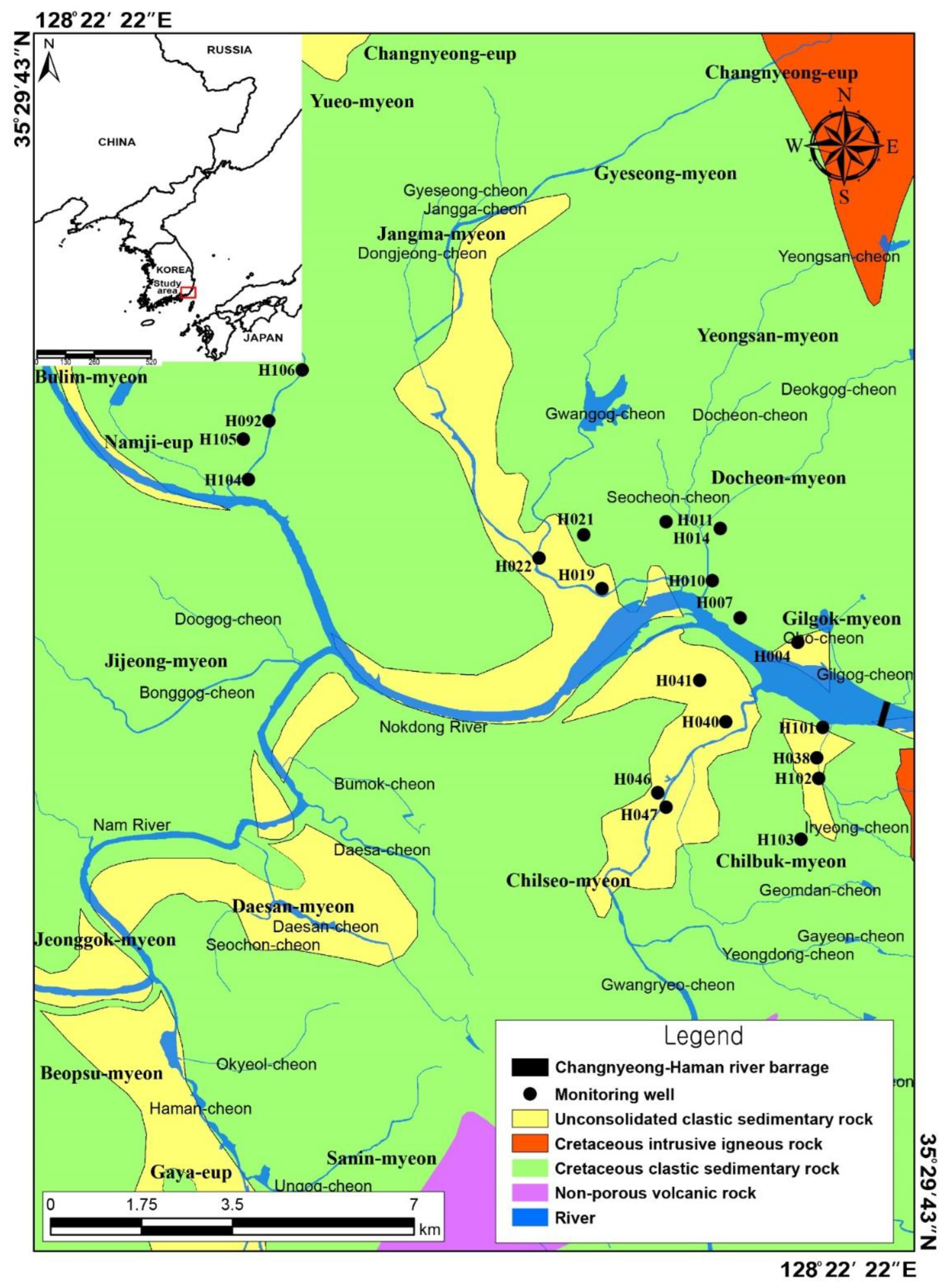
3. Study Area
3.1. Data Acquisition
3.2. Geological and Hydrological Settings
4. Results
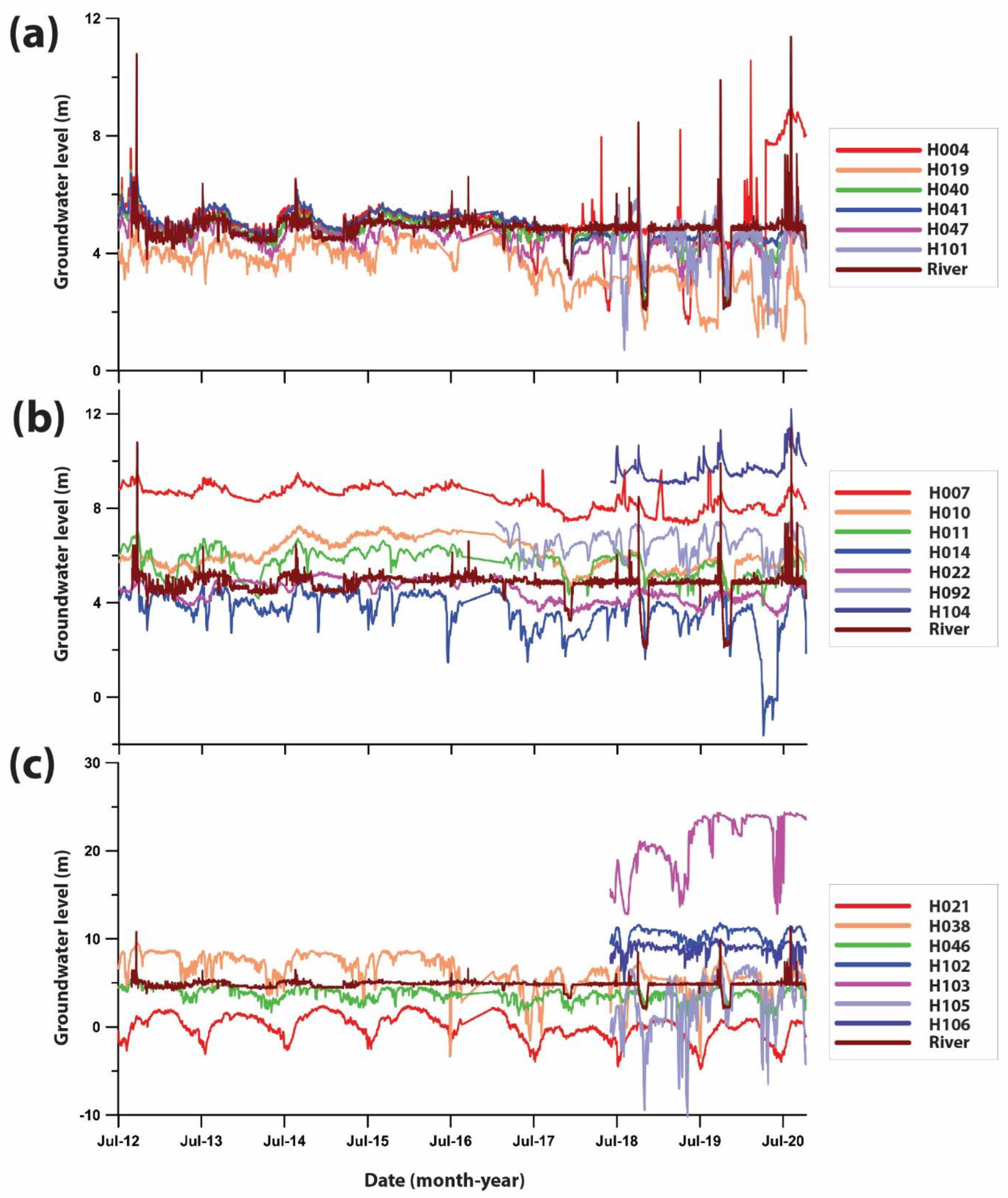
4.1. Characteristics of Groundwater Level and River Stage Fluctuation
4.2. Clustering of Groundwater Levels
4.3. KDE and CKDE of Groundwater Level
4.4. Estimation of the SGLI Values
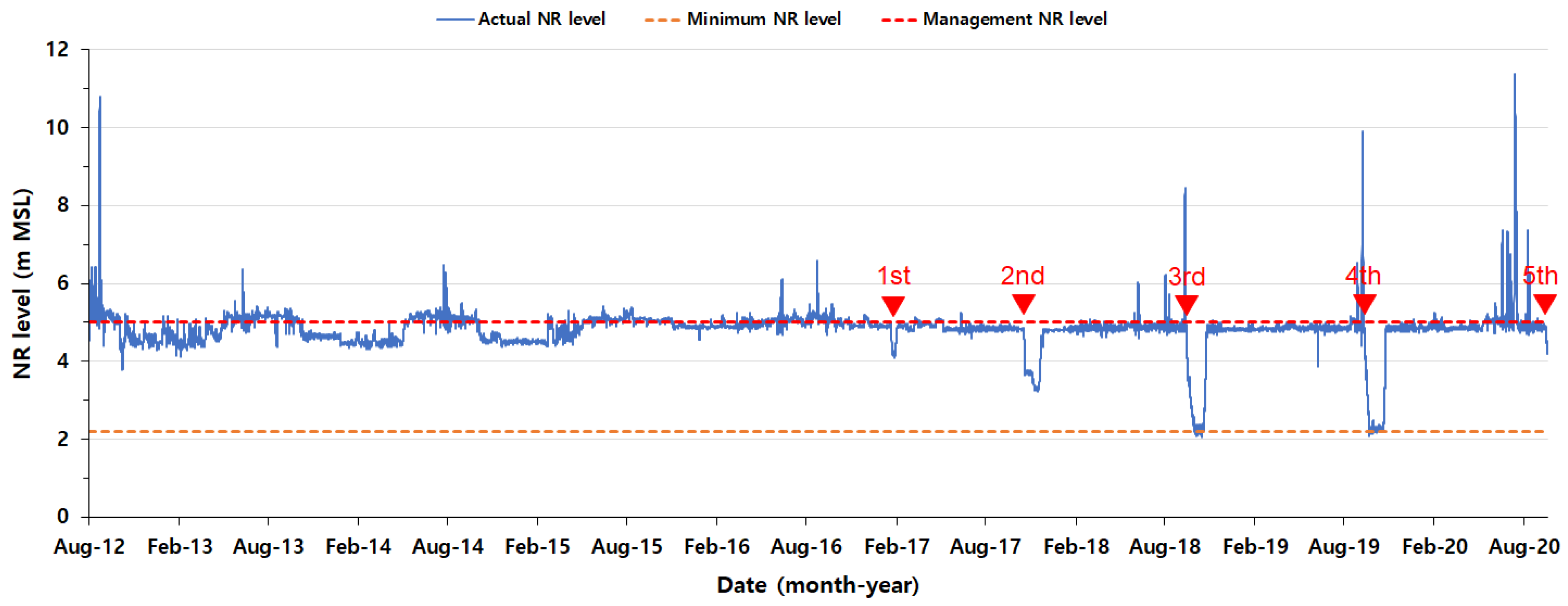
SGLI Values Depending on the Opening of the Changnyeong–Haman River Barrage
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Meteorological Organization (WMO). Manual on Estimation of Probable Maximum Precipitation (PMP); WMO-No. 1045; World Meteorological Organization (WMO): Geneva, Switzerland, 2009; 259p. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Van Lanen, H.A.; Peters, E. Definition, Effects and Assessment of Groundwater Droughts. In Drought and Drought Mitigation in Europe; Springer: Berlin/Heidelberg, Germany, 2000; pp. 49–61. [Google Scholar]
- Peters, E.; Van Lanen, H.A.J.; Torfs, P.J.J.F.; Bier, G. Drought in groundwater-drought distribution and performance indicators. J. Hydrol. 2005, 306, 302–317. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci. 2013, 17, 4769–4787. [Google Scholar] [CrossRef] [Green Version]
- Rahim, A.; Khan, K.; Akif, A.; Jamal, R. The geostatistical approach to assess the groundwater drought by using standardized water level index (SWI) and standardized precipitation index (SPI) in the Peshawar regime of Pakistan. Sci. Int. 2015, 27, 4111–4117. [Google Scholar]
- Mendicino, G.; Senatore, A.; Versace, P. A groundwater resource index (GRI) for drought monitoring and forecasting in a Mediterranean climate. J. Hydrol. 2008, 357, 282–302. [Google Scholar] [CrossRef]
- Kumar, R.; Musuuza, J.L.; Van Loon, A.F.; Teuling, A.J.; Barthel, R.; Ten Broek, J.; Mai, J.; Samaniego, L.; Attinger, S. Multiscale Evaluation of the standardized precipitation index as a groundwater drought indicator. Hydrol. Earth Syst. Sci. 2016, 20, 1117–1131. [Google Scholar] [CrossRef] [Green Version]
- Bidwell, V.J. Realistic forecasting of groundwater level, based on the eigenstructure of aquifer dynamics. Math. Comput. Simulat. 2005, 69, 12–20. [Google Scholar] [CrossRef] [Green Version]
- Goodarzi, M.; Fatehifar, A.; Avazpoor, F. Bivariate analysis of the impact of climate change on drought with SPEI index and Coppola functions (Case study: Dugonbadan). Iran-Water Resour. Res. 2019, 15, 352–365. [Google Scholar]
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Osman, A.I.A.; Ahmed, A.N.; Huang, Y.F.; Kumar, P.; Birima, A.H.; Sherif, M.; Sefelnasr, A.; Ebraheemand, A.A.; El-Shafie, A. Past, present and perspective methodology for groundwater modeling-based machine learning approaches. Arch. Compu. Methods Eng. 2022, 29, 3843–3859. [Google Scholar] [CrossRef]
- Song, S.H.; Lee, H.S.; Choi, K.J.; Kim, J.S.; Kim, G.P. Evaluation of drought effect on groundwater system using groundwater level data in Jeju Island. J. Environ. Sci. Int. 2014, 23, 637–647. [Google Scholar] [CrossRef]
- Yang, J.S.; Par, J.H.; Kim, N.K. Development of drought vulnerability index using trend analysis. Korean Soc. Civ. Eng. 2014, 32, 185–192. [Google Scholar]
- Kim, G.-B.; Yun, H.-H.; Kim, D.-H. Relationship between standardized precipitation index and groundwater levels: A proposal for establishment of drought index wells. J. Soil Groundwater Environ. 2006, 11, 31–42. [Google Scholar]
- Huntington, J.L.; Niswonger, R.G. Role of surface-water and groundwater interactions on projected summertime streamflow in snow dominated regions: An integrated modeling approach. Water Resour. Res. 2012, 48, W11524. [Google Scholar] [CrossRef] [Green Version]
- Menció, A.; Galán, M.; Boix, D.; Mas-Pla, J. Analysis of stream-aquifer relationships: A comparison between mass balance and Darcy’s law approaches. J. Hydrol. 2014, 517, 157–172. [Google Scholar] [CrossRef]
- Oh, Y.-Y.; Hamm, S.-Y.; Kim, G.B.; Lee, C.-M.; Chung, S.Y. Statistical approach to river–aquifer interaction in the Lower Nakdong River Basin, Republic of Korea. Irrig. Drain. 2016, 65, 36–47. [Google Scholar] [CrossRef]
- Oh, Y.-Y.; Hamm, S.-Y.; Ha, K.; Yoon, H.; Chung, I.M. Characterising the impact of river barrage construction on stream–aquifer interactions, Korea. Water. 2016, 8, 137. [Google Scholar] [CrossRef] [Green Version]
- Oh, Y.-Y.; Hamm, S.-Y.; Ha, K.; Yoon, H.; Kim, G.-B. Analytical approach for evaluating the effects of river barrages on river aquifer interactions. Hydrol. Process. 2016, 30, 3932–3948. [Google Scholar] [CrossRef]
- Oh, Y.-Y.; Yun, S.-T.; Yu, S.; Hamm, S.-Y. The combined use of dynamic factor analysis and wavelet analysis to evaluate latent factors controlling complex groundwater level fluctuations in a riverside alluvial aquifer. J. Hydrol. 2017, 555, 938–955. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; LaBaugh, J.W. Field Techniques for Estimating Water Fluxes between Surface Water and Ground Water: U.S. Geological Survey Techniques and Methods; USGS: Reston, VA, USA, 2008; 128p.
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, S.; Kong, X.; Zheng, W.; Feng, W.; Zhang, X.; Yuan, R.; Song, X.; Sprenger, M. Interaction of surface water and groundwater influenced by groundwater over-extraction, wastewater discharge, and water transfer in Xiong’an New Area, China. Water 2019, 11, 539. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, G.M.; Watt, D.G. Spectral Analysis and Its Application; Holden-Day Inc.: San Francisco, CA, USA, 1968; 525p. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994; 598p. [Google Scholar]
- Larocque, M.; Mangin, A.; Razack, M.; Banton, O. Contribution of correlation and spectral analyses to the regional study of a large karst aquifer (Charente, France). J. Hydrol. 1998, 205, 217–231. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process 1978, 26, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986; p. 26. [Google Scholar]
- Bolstad, B.M.; Irizarry, R.A.; Åstrand, M.; Speed, T.P.A. Comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ministry of Land, Transportation, and Maritime Affairs (MLTM). The Detail Design of Development of Residential Sites for Nakdong River District; MLTM: Seoul, Republic of Korea, 2009. [Google Scholar]
- Chang, S.; Chung, I.-M.; Kim, Y.; Moon, S.-H. Long-term groundwater budget analysis based on integrated hydrological model for water curtain cultivation site: Case study of Cheongweon, Korea. J. Geol. Soc. Korea 2016, 52, 201–210. [Google Scholar] [CrossRef]
- Kim, N.J.; Lee, H.K. Explanatory Text of the Geological Map of Yongsan Sheet (1:50,000); Geological Survey Korea: Seoul, Republic of Korea, 1964; 52p. [Google Scholar]
- Choi, S.O.; Yeo, S.C. Explanatory Text of the Geological Map of Namji Sheet (1:50,000), Sheet-6820-II; Geological Survey Korea: Seoul, Republic of Korea, 1972; 27p. [Google Scholar]
- Choi, Y.K.; Kim, T.Y. Explanatory Text of the Geological Map of Uiryong Sheet (1:50,000); Geological Survey Korea: Seoul, Republic of Korea, 1963; 29p. [Google Scholar]
- Economics. British Columbia Drought Response Plan; British Columbia: Victoria, BC, Canada, 2015; p. 35. [Google Scholar]
- Lee, J.; Kang, S.; Jeong, J.; Chun, G. Development of groundwater level monitoring and forecasting technique for drought analysis (I)—Groundwater drought monitoring using standardized groundwater level index (SGI). J. Korea Water Resour. Assoc. 2018, 51, 1011–1020. [Google Scholar]
- Guo, M.; Weifeng Yue, W.; Wang, T.; Zheng, N.; Wu, L. Assessing the use of standardized groundwater index for quantifying groundwater drought over the conterminous US. J. Hydrol. 2021, 598, 126227. [Google Scholar] [CrossRef]
- Laimighofer, J.; Laaha, G. How standard are standardized drought indices? Uncertainty components for the SPI & SPEI case. J. Hydrol. 2022, 613, 128385. [Google Scholar]



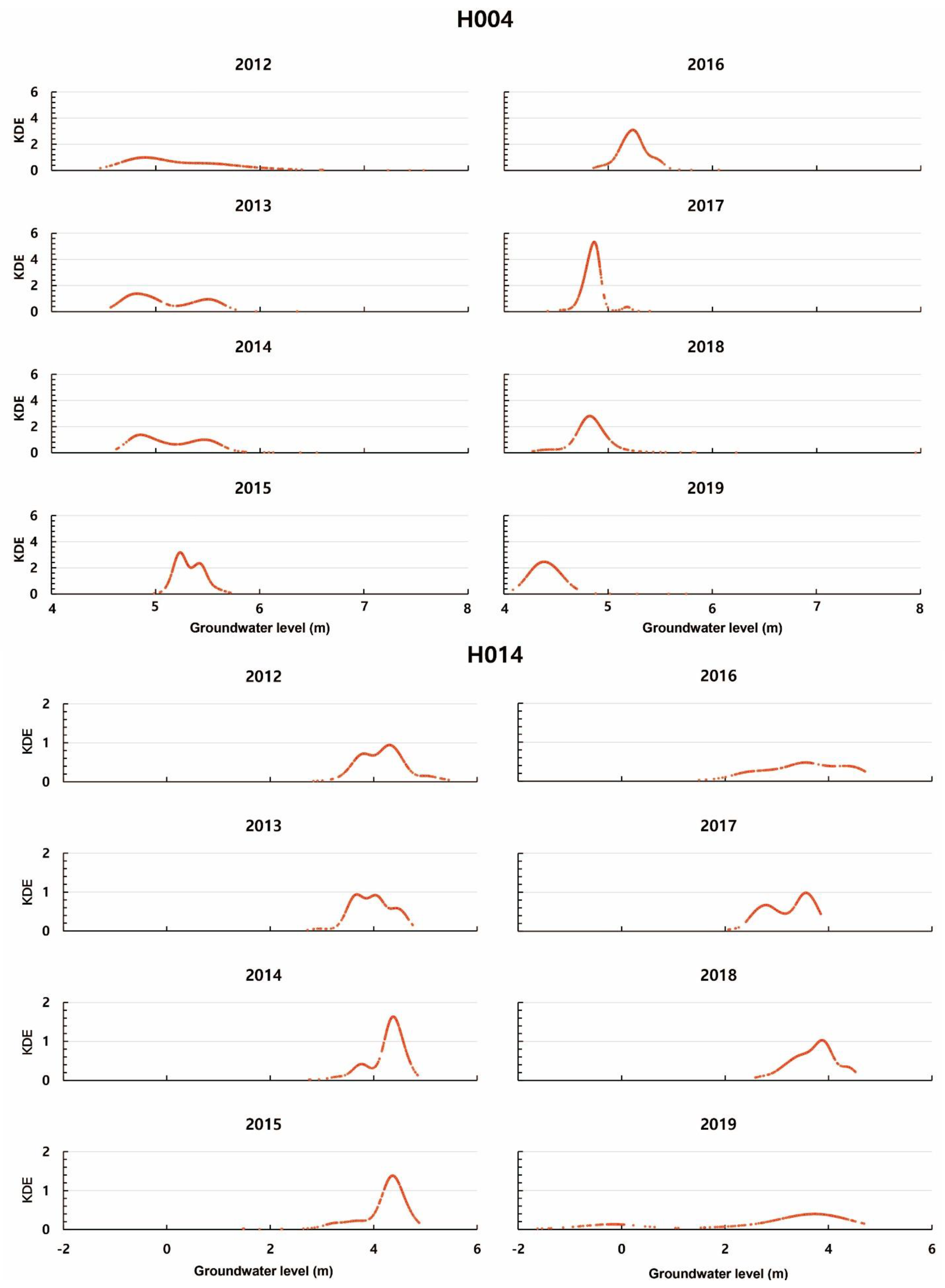
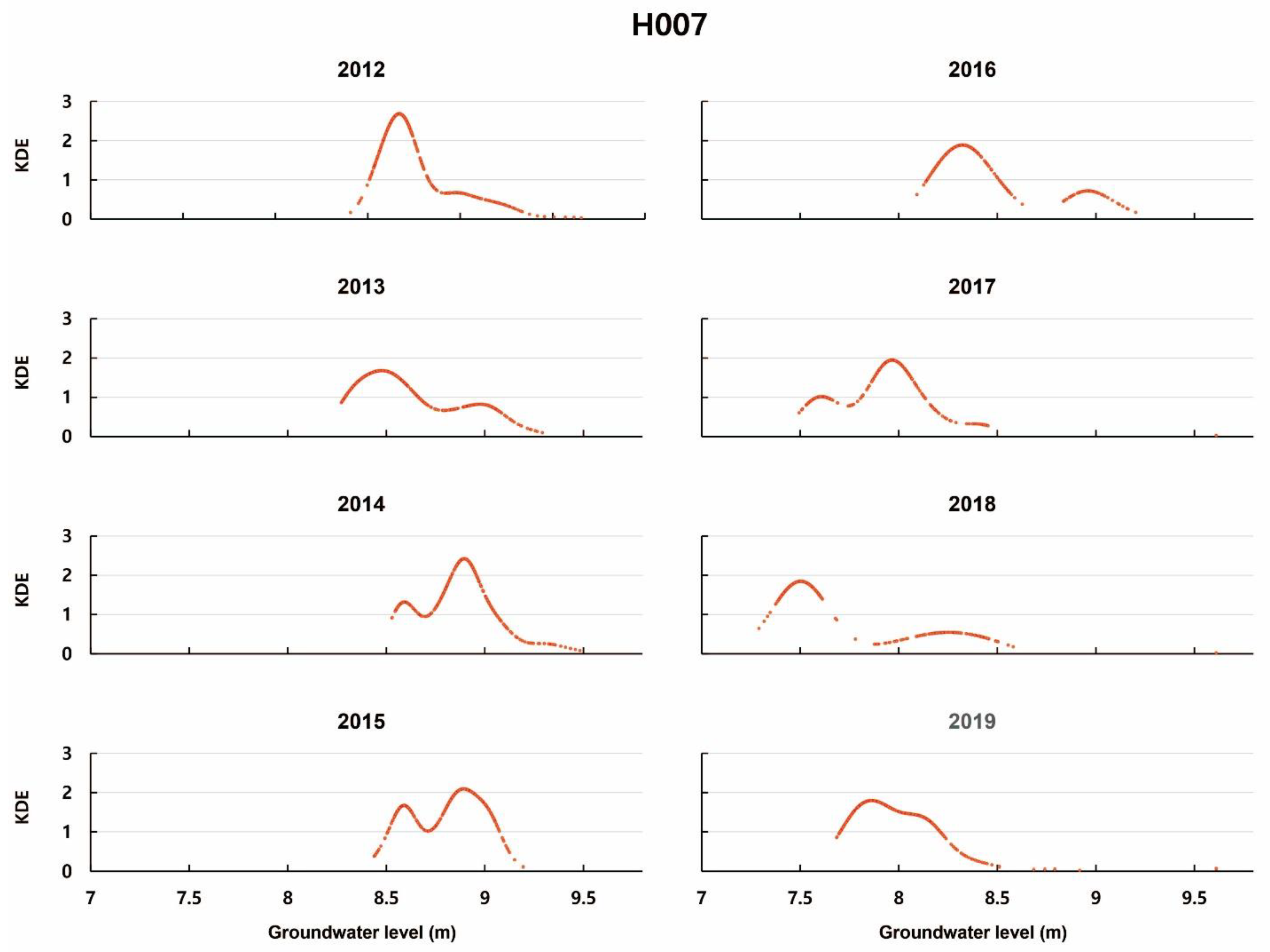
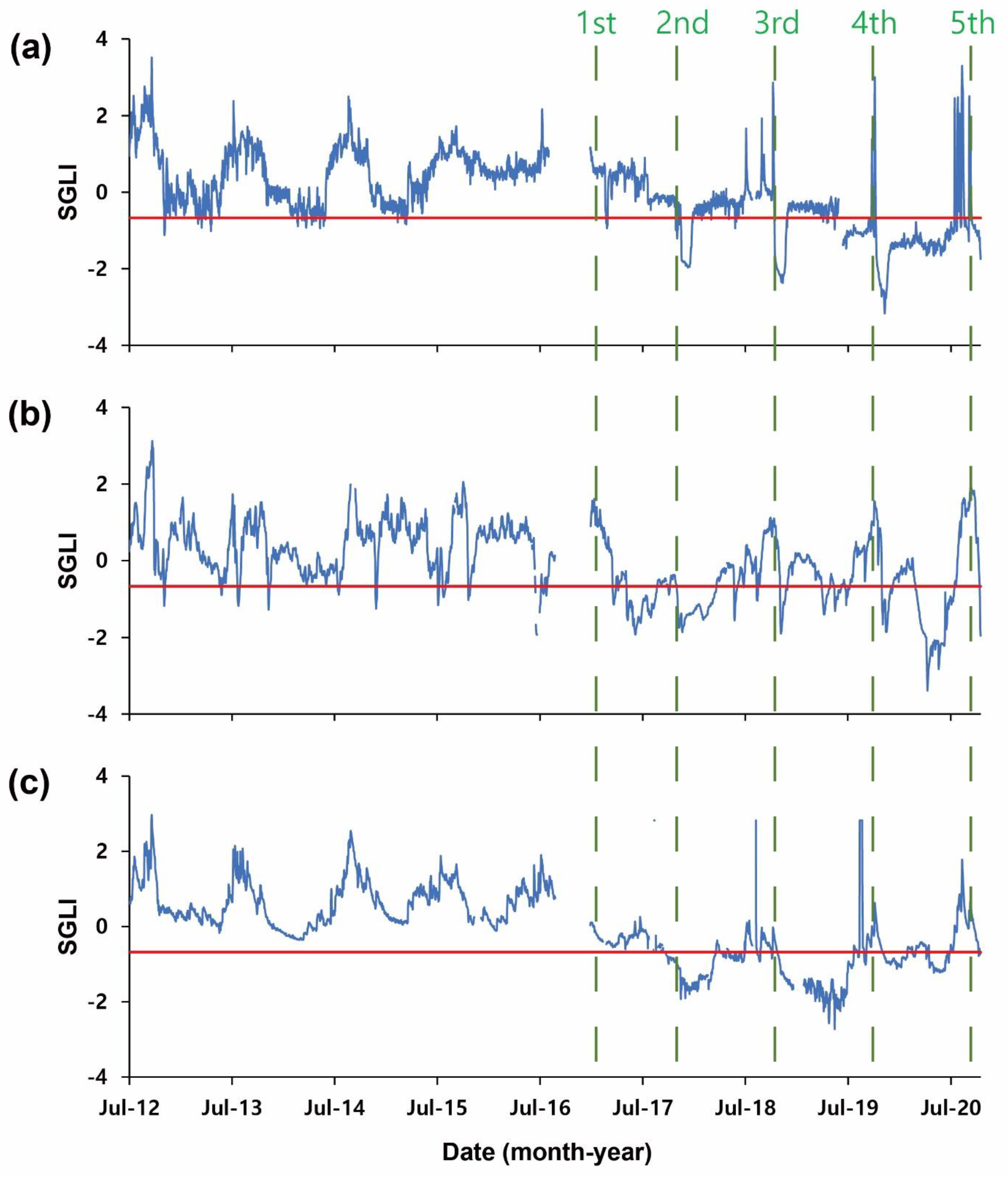
| Cluster | Monitoring Wells |
|---|---|
| Cluster 1 | H004, H010, H011, H022, H040, H041, H047, H092, H101 |
| Cluster 2 | H014, H019, H038, H046, H105 |
| Cluster 3 | H007, H102, H104, H106 |
| Cluster 4 | H021 |
| Cluster 5 | H103 |
| Static. | H004 | H007 | H010 | H011 | H014 | H019 | H021 | H022 | H038 | H040 |
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | −1.34 | −0.46 | −1.59 | −2.52 | −1.92 | −0.90 | −1.82 | −1.17 | −3.15 | −1.48 |
| Max. | 3.54 | 2.95 | 2.42 | 3.10 | 3.10 | 3.55 | 2.18 | 2.42 | 2.79 | 3.54 |
| Mean | 0.46 | 0.59 | 0.42 | 0.39 | 0.41 | 0.58 | 0.40 | 0.56 | 0.51 | 0.47 |
| Static. | H041 | H046 | H047 | H092 | H101 | H102 | H103 | H104 | H105 | H106 |
| Min. | −0.85 | −2.33 | −1.54 | 1.29 | - | - | - | - | - | - |
| Max. | 3.40 | 3.56 | 3.56 | 1.90 | - | - | - | - | - | - |
| Mean | 0.54 | 0.32 | 0.49 | 1.62 | - | - | - | - | - | - |
| Static. | H004 | H007 | H010 | H011 | H014 | H019 | H021 | H022 | H038 | H040 |
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | −2.93 | −2.73 | −3.05 | −3.23 | −3.37 | −3.02 | −3.19 | −3.06 | −3.26 | −3.55 |
| Max. | 3.27 | 2.81 | 0.74 | 1.46 | 1.93 | 3.12 | 1.42 | 1.63 | 0.70 | 3.27 |
| Mean | −0.60 | −0.83 | −0.59 | −0.51 | −0.56 | −0.81 | −0.55 | −0.74 | −0.73 | −0.64 |
| Static. | H041 | H046 | H047 | H092 | H101 | H102 | H103 | H104 | H105 | H106 |
| Min. | −3.19 | −3.37 | −3.41 | −3.04 | −3.02 | −2.97 | −2.15 | −1.48 | −3.03 | −3.17 |
| Max. | 3.35 | 2.46 | 3.11 | 2.81 | 3.18 | 2.48 | 1.10 | 3.18 | 2.40 | 2.53 |
| Mean | −0.72 | −0.42 | −0.67 | −0.04 | −0.01 | −0.03 | −0.04 | 0.03 | −0.02 | −0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, S.-M.; Jeong, J.-H.; Jeon, H.-T.; Cheong, J.-Y.; Hamm, S.-Y. Determining Groundwater Drought Relative to the Opening of a River Barrage in Korea. Water 2023, 15, 2658. https://doi.org/10.3390/w15142658
Yun S-M, Jeong J-H, Jeon H-T, Cheong J-Y, Hamm S-Y. Determining Groundwater Drought Relative to the Opening of a River Barrage in Korea. Water. 2023; 15(14):2658. https://doi.org/10.3390/w15142658
Chicago/Turabian StyleYun, Sul-Min, Ji-Hye Jeong, Hang-Tak Jeon, Jae-Yeol Cheong, and Se-Yeong Hamm. 2023. "Determining Groundwater Drought Relative to the Opening of a River Barrage in Korea" Water 15, no. 14: 2658. https://doi.org/10.3390/w15142658
APA StyleYun, S.-M., Jeong, J.-H., Jeon, H.-T., Cheong, J.-Y., & Hamm, S.-Y. (2023). Determining Groundwater Drought Relative to the Opening of a River Barrage in Korea. Water, 15(14), 2658. https://doi.org/10.3390/w15142658








