1. Introduction
Gravity-driven, inclined flows of particle–fluid mixtures are often observed in geophysical and in industrial applications, leading to the need to develop appropriate and reliable descriptions and prediction tools. This type of natural phenomenon, e.g., debris flow, develops and propagates under the influence of gravity, generally involving a granular concentration that can exceed 0.50 and a wide range of particle sizes, leading to the formation of granular segregation patterns under the effect of both gravity and granular temperature gradients.
Multiple interpretation schemes of such flows were proposed within the scientific literature, involving both phenomenological and rational argumentation. Nonlocal extensions [
1,
2,
3] of the
μ-
I rheology [
4] for the description of particle interactions dominated by viscosity [
5] belong to the first type. An example of a rational method is, instead, represented by kinetic theory, which, however, was developed for uncorrelated binary collisions among pairs of particles. In order to be applied to dense flows, kinetic theory must be extended to account, in a phenomenological way, for the existence of velocity correlations [
6,
7,
8,
9]. In fact, a relation between the two approaches has been shown [
10,
11], although they were developed independently. In this manuscript, we phrase boundary value problems for a fully developed, steady, gravity-driven, dense flow of a mixture of identical, inelastic particles and a liquid over an erodible bed confined between frictional sidewalls using kinetic theory.
The description of the model for the flow of the particles and fluid is identical to that of Jenkins and Larcher [
12], in which the predictions for inclined flows of plastic cylinders and water over an erodible bed were compared with experimental data of Armanini et al. [
13]. The new features in this manuscript consist in the focus on the bimodal mixtures of particles of different sizes and specific gravities; the inclusion of predictions for flows over rigid, bumpy bases; and a discussion of segregation when the particles are of two different sizes, when the material of the spheres is the same or different, in flows over erodible beds and rigid, bumpy bases.
The manuscript is structured as follows: In the second chapter, we describe the theoretical model for the calculation of the velocity profile of water and particles, of particle velocity fluctuations, and of granular concentration and provide boundary conditions for the solution of the system of equations. In the third chapter, we provide and comment on numerical solutions to the boundary value problem for the liquid–granular mixture. In the fourth chapter, we introduce the segregation equations for a binary mixture of spheres and provide the profile of the relative concentration of the two species in three core cases: (i) temperature gradient-driven segregation for particles made of the same material; (ii) mass ratios leading to gravity alone driven segregation; and (iii) mass ratios leading to temperature gradients and gravity-driven segregation being roughly equal. The last chapter is devoted to general comments and conclusions.
2. Model
As do Jenkins and Larcher [
14], in phrasing a kinetic theory for the liquid–granular mixture, we focus on flows that involve a single dense, collisional region in which the fluid and particle phase have the same depth. Such flows are observed in laboratory experiments on debris flows [
13]. Consideration of a single region in which the volume fraction exceeds 0.49 permits significant simplification of the transport coefficients of kinetic theory: there is a common dependence on the concentration that permits it to be eliminated in favor of the granular temperature and the particle pressure. Then, for dense, dry flows, analytic solutions for the profiles of concentration, mean velocity, and velocity fluctuations may be obtained [
15]. In addition, we consider the viscosity of the fluid to be due to velocity fluctuations of the fluid induced by those of the particles [
16]. This is consistent with the observation by Bagnold that turbulent velocity fluctuations of the fluid are suppressed by the particles.
In the model, we calculate the profiles of particle,
u, and fluid,
U, velocity; the strength of particle velocity fluctuations,
T, as one-third of their mean squared value; and the solid fraction,
c, for dense, fully developed, dense, steady flows of a mixture of frictional, inelastic, mono-dispersed spheres characterized by a mass density
a particle diameter
d, a restitution coefficient
e, and a coefficient of sliding friction
μ immersed in a fluid characterized by a mass density
ρf and a viscosity
η. We consider a gravity-driven flow, either over an erodible bed [
12] or over a rigid, bumpy base, inclined at a slope angle
ϕ, confined by two vertical sidewalls separated by a distance
W. In our analysis, we consider only fully saturated flows, i.e., in which the height of the interstitial fluid and the particles coincide.
In our notation, we take the longitudinal x-coordinate in the flow direction and an upward-directed y-coordinate normal to the flow, while g represents the gravitational acceleration. We denote the derivatives with respect to the y-axis with a prime. We will introduce proper scales making use of the density ratio and of the buoyant gravity in order to make lengths dimensionless by d, velocity by stresses by and energy flux by .
The energy dissipated at interparticle collisions is evaluated by means of an effective coefficient of restitution,
ε, which accounts both for the particle friction,
through the friction coefficient
μ [
17,
18], and for the viscosity of the interstitial fluid
η, by means of the Stokes number
in which
represents the Reynolds number [
19,
20]:
In our model, extended kinetic theory is implemented for describing the particle phase flow in a boundary value problem involving the gradients of the average fields across the flow. The numerical solution of these equations is obtained employing two sets of boundary conditions: one appropriate for inclined erodible beds and one for rigid, bumpy bases. We finally use this solution in order to predict the granular segregation of a bimodal mixture of particles having d as the sum of their radii.
2.1. Flow Momentum
The gradient of the pure fluid pressure,
, is governed by the component of the fluid momentum balance in direction
y, orthogonal to the flow:
similarly, the gradient of the average fluid shear stress,
S, can be evaluated through the component of the fluid momentum balance in longitudinal direction
x:
in which
D represents the drag coefficient,
where
the average of the fluid velocity,
U, across the flow is introduced in order to account for the zero value of the fluid velocity at the sidewalls, while the particles have a slip velocity.
The average collisional pressure,
given as the product of the granular concentration,
c, and of the excess of total pure particle pressure,
over the pure fluid pressure,
, exercised by the fluid upon the particles, is governed by the
y-component of the momentum balance of the particles:
or, in combination with (2),
The normal derivative of the average collisional shear stress of the grains,
s, is finally present in the longitudinal balance of particle momentum:
in which the last term represents the influence of sidewall friction on the flow resistance [
21].
Consistent with field and laboratory observations on debris flow, we assume that the granular phase is so dense that the granular concentration c exceeds the value 0.49 everywhere within the flow. With this hypothesis, only terms resulting from the collisional transfer of momentum can be retained in the expressions for the granular stress, and those resulting from transport can be ignored. We finally include a term describing the influence of the elasticity of the particles on the duration and frequency of the collisions.
With these assumptions [
21],
in which
k represents the stiffness of the linear elastic contacts and
is related to the radial distribution function, where the critical volume fraction,
cc, at which particles first touch along the axes of greatest compression and the collisional interactions become singular, is expressed by [
17]
Equation (5) can be rewritten, making use of Equation (8), and employed in order to determine the granular concentration,
c:
Moreover, an expression for the particle shear stress can be obtained upon considering the influence of the contact elasticity on the frequency of collisions,
in which [
22]
The frequency of collisions is independent of elasticity in most of the flow domain; however, because G is singular at cc in (9), the influence of elasticity becomes crucial in the proximity of the bed.
A dependence of shear stress on pressure can be introduced instead of the dependence on the volume fraction:
which, after being inverted, gives a first-order differential equation that can be solved in order to obtain the average particle velocity
u:
The interstitial fluid is assumed to be turbulent, with a viscosity resulting from fluctuations of the fluid velocity that are correlated with the granular temperature and incorporate added mass [
16]:
In the above,
U is uniform across the cell; however, because the fluid has zero velocity at the walls, we approximate the fluid velocity across the flow by means of the Trapezoidal Rule, leading to an average fluid velocity value which is roughly, half of the maximum value. With this,
and
2.2. Particle Fluctuating Energy
The balance of fluctuation energy in the flow relates the gradient of the energy flux
q, the working of the shear stress, and the rate of collisional dissipation
γ:
Upon retaining only the collisional transfers [
22],
in which
or
which, upon inversion, is
and [
22]
or
where
L is the correlation length [
23]
in which
With Equations (15), (22) and (24), the energy Equation (19) becomes
It should be observed that by employing Equation (22) in Equation (28) and introducing the square root of the granular temperature as fluctuation velocity,
we obtain
a second-order, linear differential equation including a variable coefficient, which is a function of the variation of
s/
p and
L with
c.
2.3. Boundary Conditions
2.3.1. Erodible Bed
The erodible bed conditions were already introduced in [
12]. When the granular concentration exceeds the critical value,
cc, more persistent elastic interactions between spheres are observed, occurring in an ever-changing network of contacts. As a consequence, rate-independent components of the stresses result from force transmission through the contact network. However, kinetic energy can be suddenly released when contacts are broken and generate collisions, which also lead to the generation of rate-dependent components of the stresses.
The energy associated with the velocity fluctuations, which is supplied at the erodible bed interface, is transported away from the surface, dissipated through collisions, and eventually disappears. The fluctuation energy production associated with it will be ignored since, in the bed, the shear rate is negligible, and the divergence of the flux,
q, of fluctuation energy is taken to balance its dissipation rate
γ:
in which
and
where
Lc represents the correlation length evaluated at the critical solid fraction
cc. If
c and
ε are taken constant within the bed, Equation (30) becomes
Within the bed, where the
y-coordinate is negative,
in which
represents the velocity fluctuations at the bed and
. Then, at the bed surface,
Equation (34) gives a boundary condition that can be used for the flow above the bed. Moreover, we assume the critical concentration, , at the bed, and, as approximations, we consider both the fluid and particle velocities to vanish.
2.3.2. Rigid, Bumpy Base
At a rigid, bumpy base, the flow momentum balance gives the slip velocity [
24],
where the slip coefficient
F is given by
in which
θ is the bumpiness of the boundary, defined in terms of the diameter of the boundary spheres and the average separation of their edges
by
.
The energy balance at the base relates to the energy flux, the rate of working of the shear stress through the slip velocity, and the rate of collisional dissipation
D [
24]:
where
with
Using
the energy balance at the base may then be written as
When there is a rigid base, the dimensionless measure of the number of particles per unit area of the base,
m, must be specified. This is implemented as a boundary condition for the differential equation for the partial holdup
with
I(0) = 0 and
I(
h) =
m.
Finally, the fluid velocity is taken to be zero at the base.
2.3.3. Free Surface
At the free surface of the flow, we take the particle pressure to be the buoyant weight of a layer of particles at the same concentration as the top of the flow:
and make the rough approximations that the energy flux and the particle and fluid shear stresses vanish.
3. Numerical Solutions
We make use of the MATLAB solver bvp4c in order to obtain solutions for the two-point boundary value problem for a flow over an erodible base and a flow over a rigid, bumpy base for the same particle properties at the same angle of inclination and for the same holdup. It should be noted that all input data for the model consist of geometrical or mechanical properties of the particles, of the fluid, and of the channel, without any ad hoc adjusted or calibrated parameter. For the flow over an erodible bed, the seven first-order differential Equations (3), (7), (11), (15), (18), (23) and (28) are solved for S, s, c, u, U, T, and q, with the eight boundary conditions: four at the bed and four at the free surface. In this way, there is one more boundary condition than differential equations; therefore, the thickness of the flow, h, can be evaluated as a parameter.
For the flow over a rigid bumpy base, there is the additional differential Equation (42) and the two additional boundary conditions associated with it. Also, in this case, because there is one more boundary condition than differential equations, the thickness of the flow can be calculated as part of the solution.
We employ values of the parameters
e,
μ, and
μw that permit the calculation of profiles of flow and fluctuation velocity for smaller plastic particles [
12]. All of the parameters have an effect on the flow depth and on the particle and fluid velocities. The sensitivity of the solution to the mass holdup,
m, is due to its influence on
cc. Moreover, as indicated in Equation (7), the flow slope and the wall friction have competing influences on the solution. The mass holdup,
m, over the rigid base is taken to be the same as that over the erodible bed.
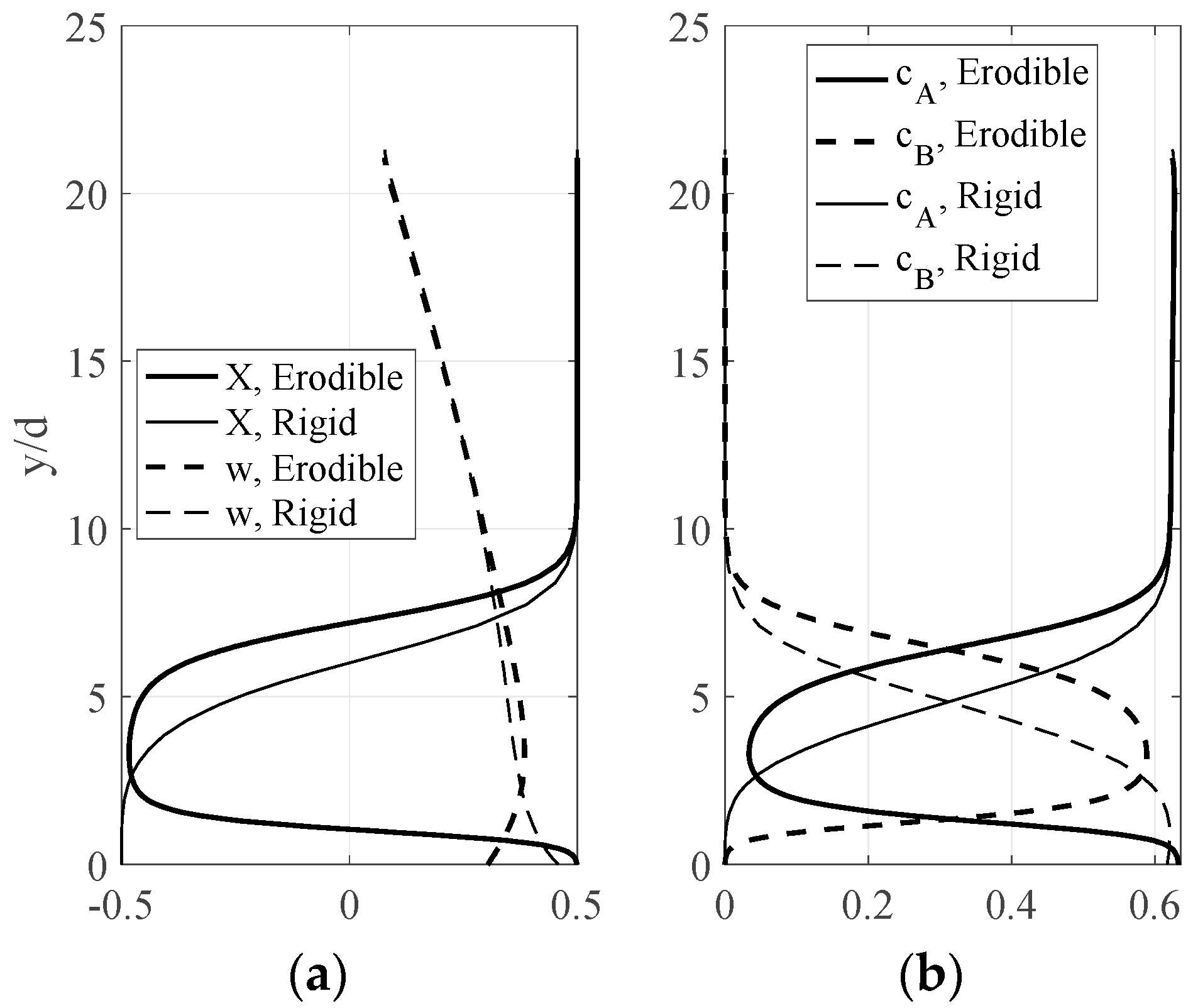
In
Figure 1a, we show the predicted profiles for
c and
w over the two types of boundaries. The difference in the boundaries results in pronounced differences in these. The erodible bed dissipates fluctuation energy from the flow, while the rigid, bumpy base produces it. This is clearly seen in the profiles of velocity fluctuations, which decrease approaching the bed in erodible conditions while showing an opposite trend on a rigid, bumpy base. The granular concentration evolves accordingly when approaching the bed, increasing when the velocity fluctuations increase and vice versa. In
Figure 1b, we show profiles of
u and
U. Apart from the slip in the particle velocity at the rigid, bumpy base, the profiles are similar, with the particle velocity exceeding the fluid velocity everywhere.
4. Segregation
We next suppose that the particle phase consists of a mixture of spheres of different radii rA and rB, masses mA and mB, and number densities nA and nB that are made of the same or different materials and indicate how the two types of spheres would segregate differently in flows over erodible beds and rigid, bumpy bases.
Larcher and Jenkins [
25] characterize the segregation of the two types of spheres using the measure
across the flow and show that when the differences
in mass and
in radii are small,
X is governed by the dimensionless equation
in which
where, in the first approximation,
G is given by Equation (9) and [
25]. So,
Although this equation is approximate, we believe that it captures the physical mechanisms of segregation and results in predictions that are likely to be both qualitatively and, perhaps to a lesser extent, quantitatively correct.
At the erodible bed, we might assume that the value of X in the flow at the bed is the same as a known value of X0 in the bed. However, for a rigid, bumpy bed, the situation is more complicated. In this case, what completes the solution is the knowledge of the total numbers of NA and NB of spheres of types A and B.
We implement the knowledge of the total numbers through an additional differential equation, phrased in terms of the variable
where
n =
nA +
nB, and the over-bar indicates an average through the flow depth. Then, the depth average of
z is given in terms of the total numbers of the two sizes of spheres through the depth of the flow by
where
fA =
NA/
N, with
N = NA + NB, is the total number fraction of spheres
A, and
is their total volume fraction.
The variables
and
X are related through known quantities by
With this, the additional differential equation is
and the boundary conditions are
K(0) = 0 and
K(
h) =
fA − 1/2 [
18].
Here, for simplicity, we do not include the small influence that the differences in size and mass of the two types of spheres have on the profiles of mixture concentration, velocity, and temperature [
18]. Then, the mixture profiles for these quantities are those given in
Figure 1.
In this manuscript, we intended to focus on three core cases, which, in our view, are of fundamental importance for understanding the nature of granular segregation and that can be driven by granular temperature gradients, by gravity alone, or by a combination of the two mechanisms: (i) temperature gradient-driven segregation for particles made of the same material; (ii) mass ratios leading to gravity alone driven segregation; (iii) mass ratios leading to temperature gradients and gravity-driven segregation being roughly equal. To the best of our knowledge, experimental and numerical simulations in analogous conditions are not yet available to provide comparisons. However, the general capability of kinetic theory in predicting, both qualitatively and quantitatively, pure particles [
18,
25] and particle–liquid flows [
12,
14] has previously been established.
4.1. Same Material, Temperature Gradient-Driven Segregation
When the spheres are made of the same material, 2
δm = 3
δr, and Equation (46) reduces to
In this situation, granular segregation is driven only by temperature gradients. We include this equation with those for the other profiles. Because there is a singularity in G at cc, Equation (9), in implementing this, in place of G, we employ an expression with the duration of contact taken into account: .
We again solve the extended boundary value problems for the flow of a mixture of two sizes,
rA = 12.5 cm and
rB = 7.5 cm, so that the average diameter,
rA +
rB, is 20 cm. At both the erodible boundary and the rigid base, we assume that the total number of the two types of spheres above the bed or base is the same,
NA =
NB, or
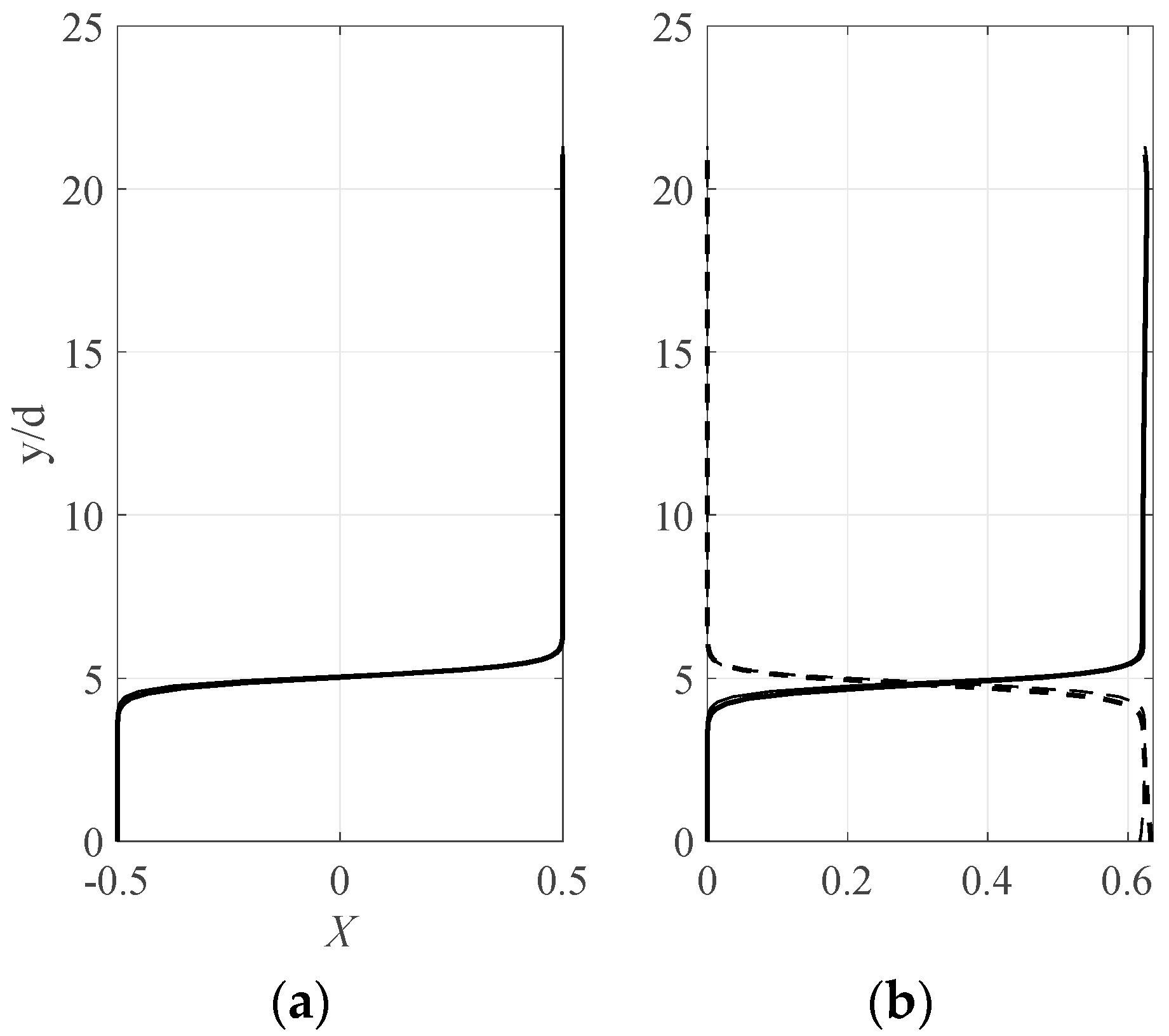
fA = 1/2. This provides equivalency for the two problems. In
Figure 2a, we show profiles of
X that result over the two boundaries.
We next calculate the concentrations,
cA and
cB, of the two types of spheres using the definitions of the concentrations, e.g.,
and
in the definition of
X:
and
Using these, in
Figure 2b, we show profiles of the concentrations of the two sizes of spheres over the two boundaries. On a rigid, bumpy bed, large particles are localized in the upper part of the flow and small particles close to the bottom, with a diffuse region in between. This prediction is similar to those of other models dealing with gravity-driven segregation. However, on an erodible bed, we predict a qualitatively different regime, with a double-segregation profile consisting of large particles localized both at the top and bottom of the flow and small particles in the middle. Similar profiles were previously predicted [
26].
4.2. Mass Ratios Such That Gravity Alone Drives Segregation
As indicated in Equation (46), when 6.2
δm = 4.4
δr, or
δm = 0.71
δr, temperature gradients do not influence segregation. In this case, with
δr = 0.50, as before,
We again incorporate this equation in the system and integrate it over an erodible bed and a rigid bumpy base. The results for the measure of integration
X for the two types of bottom boundaries are shown in
Figure 3a, and the associated concentration profiles are shown in
Figure 3b.
The influence of temperature is present but minimal, and because the greatest influence of the boundaries is on the temperature gradients, the segregation profiles are nearly identical.
4.3. Mass Ratio Such That the Temperature Gradients and Gravity Segregation Mechanisms Are Roughly Equal
When
δm = 1.3345
δr, the value of X at the erodible bed is zero, midway between the extremes of 0.50 and −0.50 for the two different segregation mechanisms. In this case, with
δr = 0.50, we incorporate Equation (46) and integrate. We show the resulting segregation profiles in
Figure 4. From several diameters above the bottom boundaries, the segregation profiles are equal.
The three situations considered indicate that the temperature gradient mechanism for segregation is important for incremental mass differences above 1.34 times the incremental difference in radii. This includes the common case of spheres of two sizes made of the same material. In this case, the profiles of concentrations of the two types of spheres above an erodible bed are not monotone and are somewhat complicated. For incremental mass differences below 1.34 times the incremental difference in radii, gravity dominates segregation, and the concentration profiles above both types of bottom boundaries are similar above several average diameters above the boundaries and involve larger spheres at the top of the flow and smaller spheres at the bottom.
5. Conclusions
The extended kinetic theory employed here has the capability to predict features seen in natural particle–fluid flows. Differences in the profiles of concentration and velocity are predicted to exist over erodible beds and rigid, bumpy bases.
For bimodal mixtures of spheres of the same material, gradients in the strength of the particle velocity fluctuations are responsible for segregation. In this case, the concentration of large spheres over a rigid, bumpy base is monotone, increasing from zero at the bed to the maximum value at the top; that over an erodible bed is not monotone but involves the maximum concentration of larger spheres at both the bed and the top of the flow. The latter is sometimes referred to as inverse grading.
These differences are due to the creation of velocity fluctuations by collisions induced by slip over the rigid, bumpy base. Because the mechanism of particle segregation is driven by gradients in the strength of the particle velocity fluctuations, the difference in the profiles of fluctuation velocity over the two boundaries has an important influence on the concentration profiles of particles of different sizes in the two types of flow. The gravitational mechanism for segregation is insensitive to the nature of the bottom boundary and is active only for spheres made of different materials, with the larger spheres made of a lighter material.