Water Quality Prediction Based on the KF-LSTM Encoder-Decoder Network: A Case Study with Missing Data Collection
Abstract
:1. Introduction
- (1)
- In this article, a Kalman filter is used to process raw data from monitoring stations, perform optimal estimation on missing values in the original data, fill in missing data, and smooth noise reduction on the original data to fully exploit all data features and improve the accuracy of model prediction.
- (2)
- In the traditional encoder-decoder architecture, an attention mechanism is introduced to capture long-range dependent features and multi-dimensional covariate information in sequences. This helps to overcome the shortcoming of traditional RNN models, which forget long-range data information and fully exploit interactive information from high-dimensional data.
- (3)
- We compare several traditional time series prediction models. The model proposed in this article performs better than other comparative models in predicting dissolved oxygen in the Lianjiang River in Guangdong, China.
2. Related Work
2.1. Machine Learning Methods
2.2. Missing Data Processing
2.3. Encoder-Decoder Architecture and Attention
3. Materials and Methods
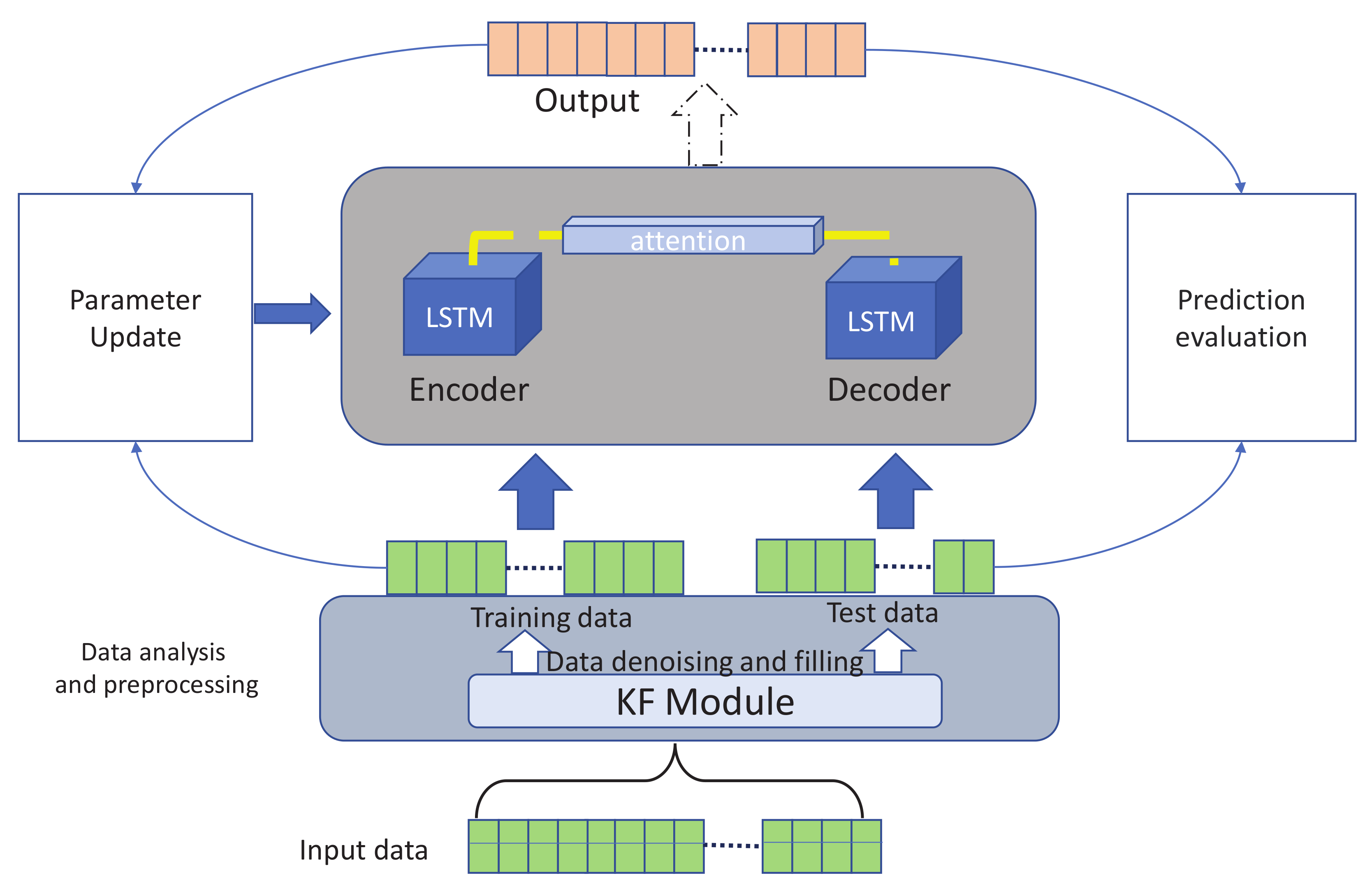
3.1. Overall Framework
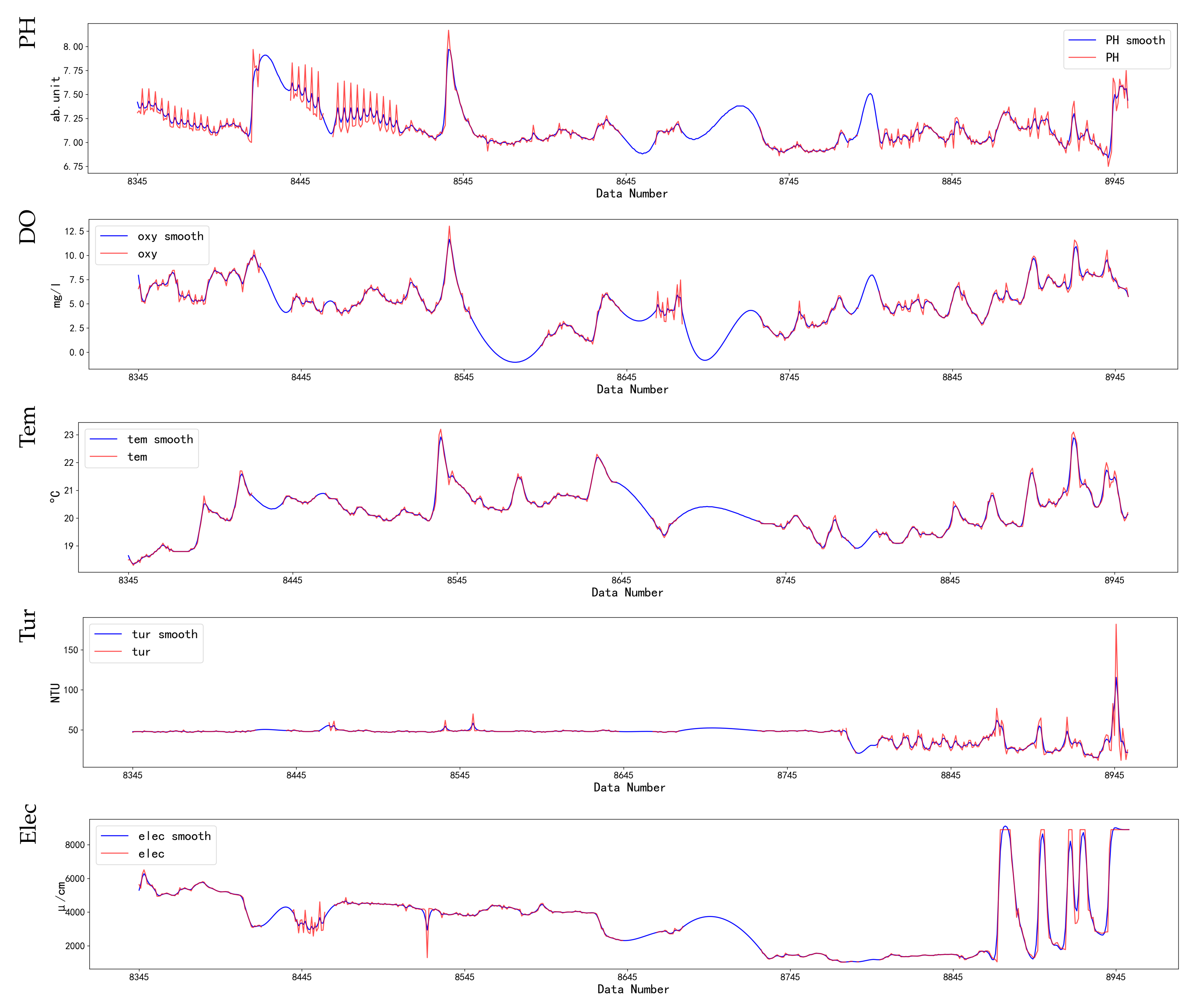
3.2. Data Preprocessing Based on Kalman Filter
| Algorithm 1: Kalman Filter Algorithm |
|
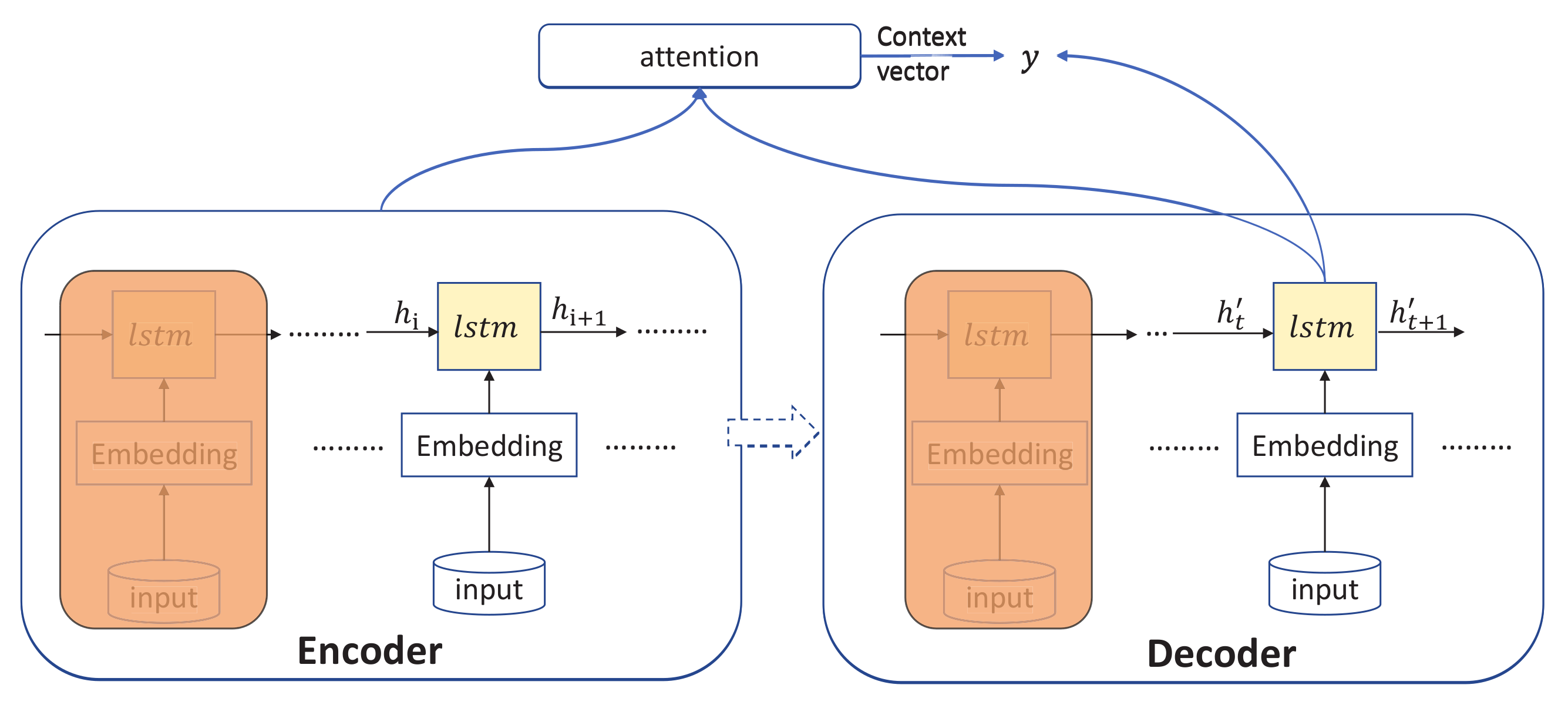
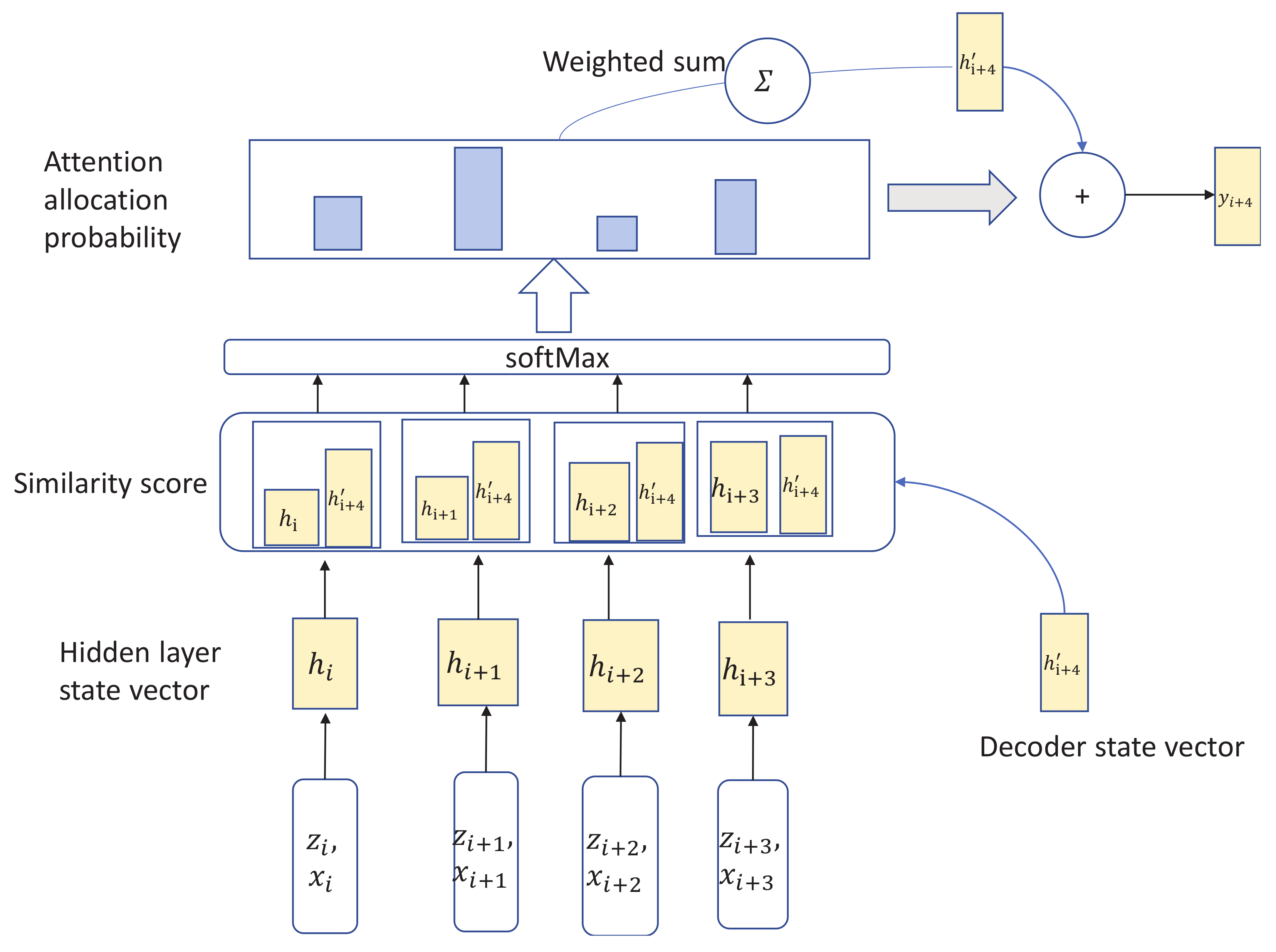
3.3. Attention with Encoder and Decoder
- (1)
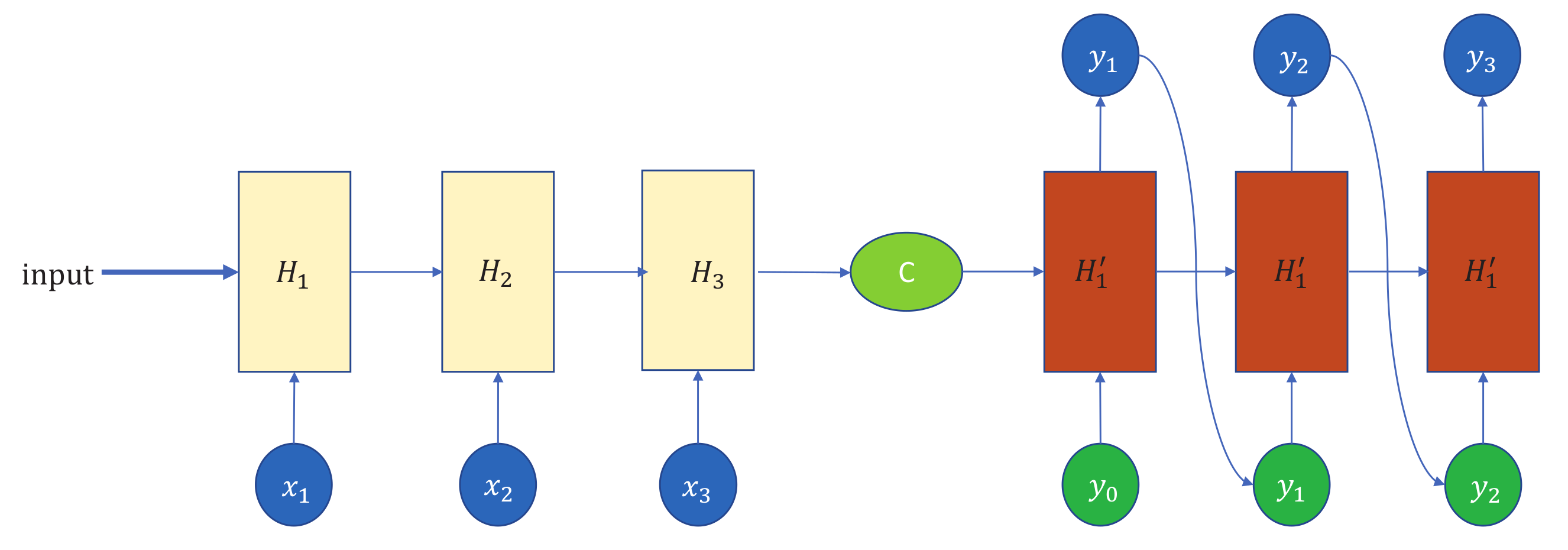
- The encoder LSTM only outputs the state at the last time step, which is used as the initial state for the decoder LSTM. This indicates that the model cannot fully use information from all time steps for prediction. For example, input from the last time step of a sequence cannot capture features from earlier in the sequence.
- (2)
- Although LSTM can handle long sequence data, when dealing with multi-dimensional covariate data, it will compress it into a context vector of fixed length. This causes the decoder to lose interactive information in multi-dimensional data, so that the decoder cannot obtain output information corresponding to different dimensional data.
3.4. KF-LSTM Based Water Quality Prediction Model
| Algorithm 2: Algorithm for the prediction of water quality based on KF-LSTM |
|
4. Experiment
4.1. Experimental Settings
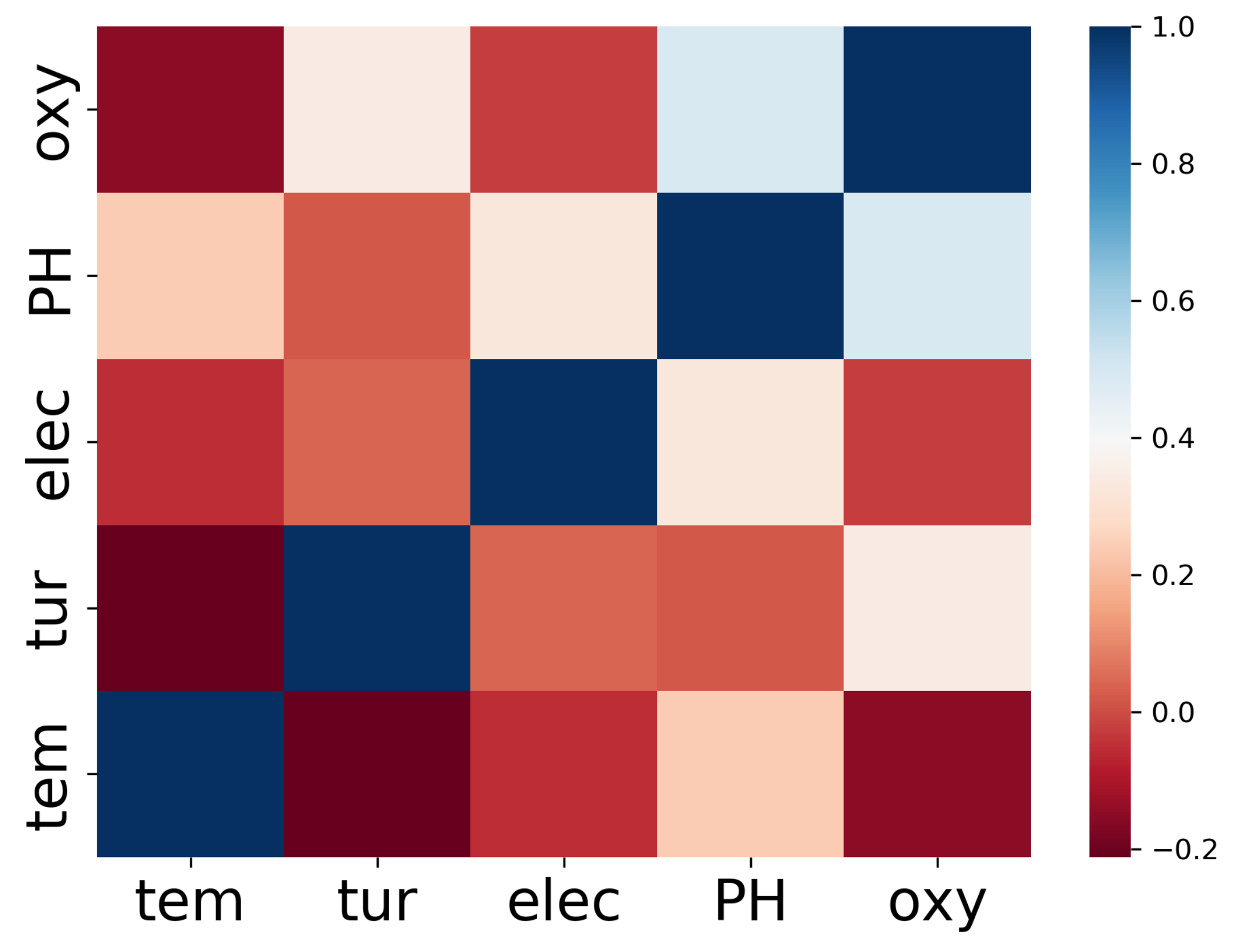
4.2. Data Analysis and Preprocessing
4.3. Model Evaluation Metrics
Hyperparameter Optimization and Cross-Validation
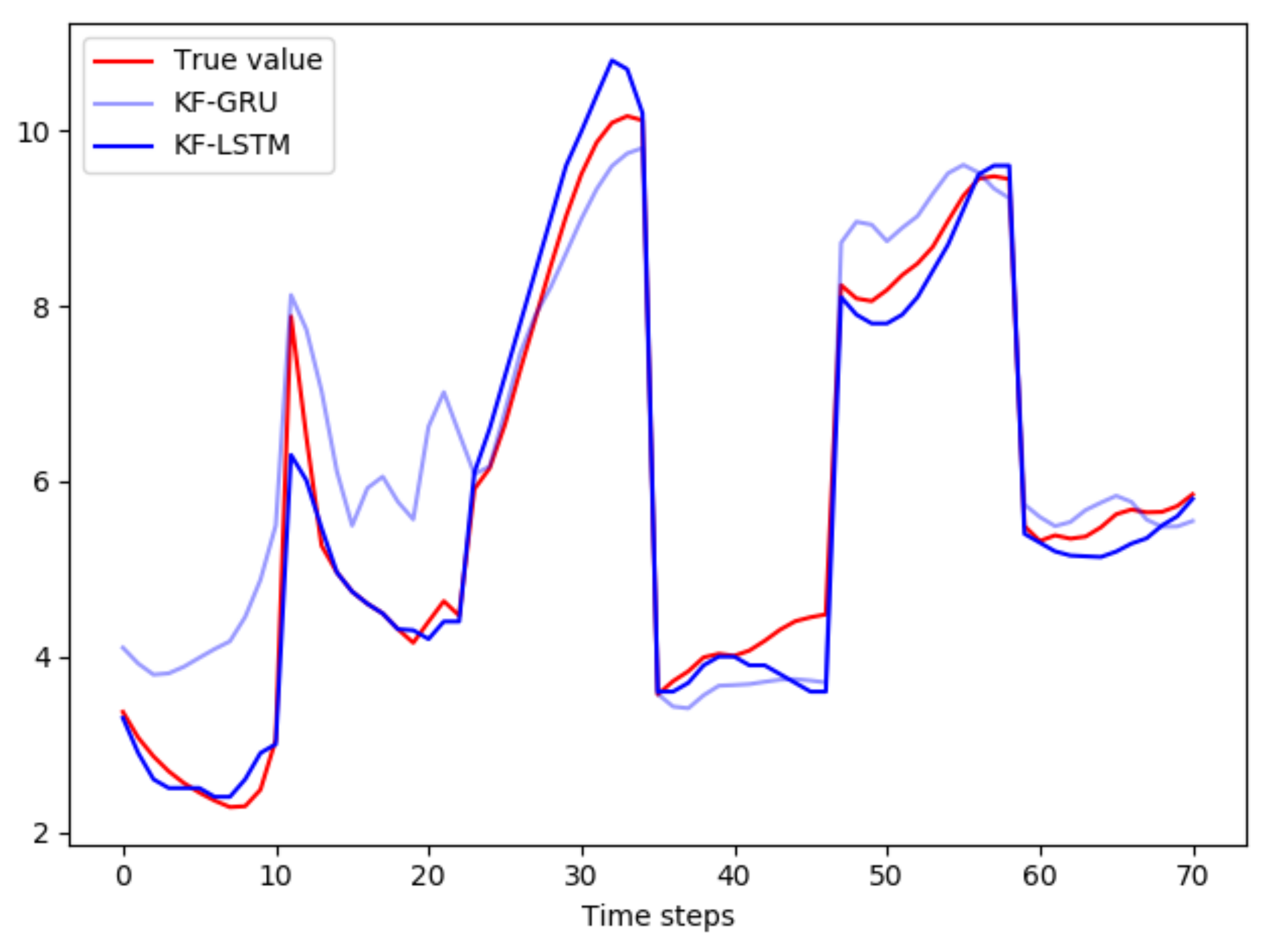
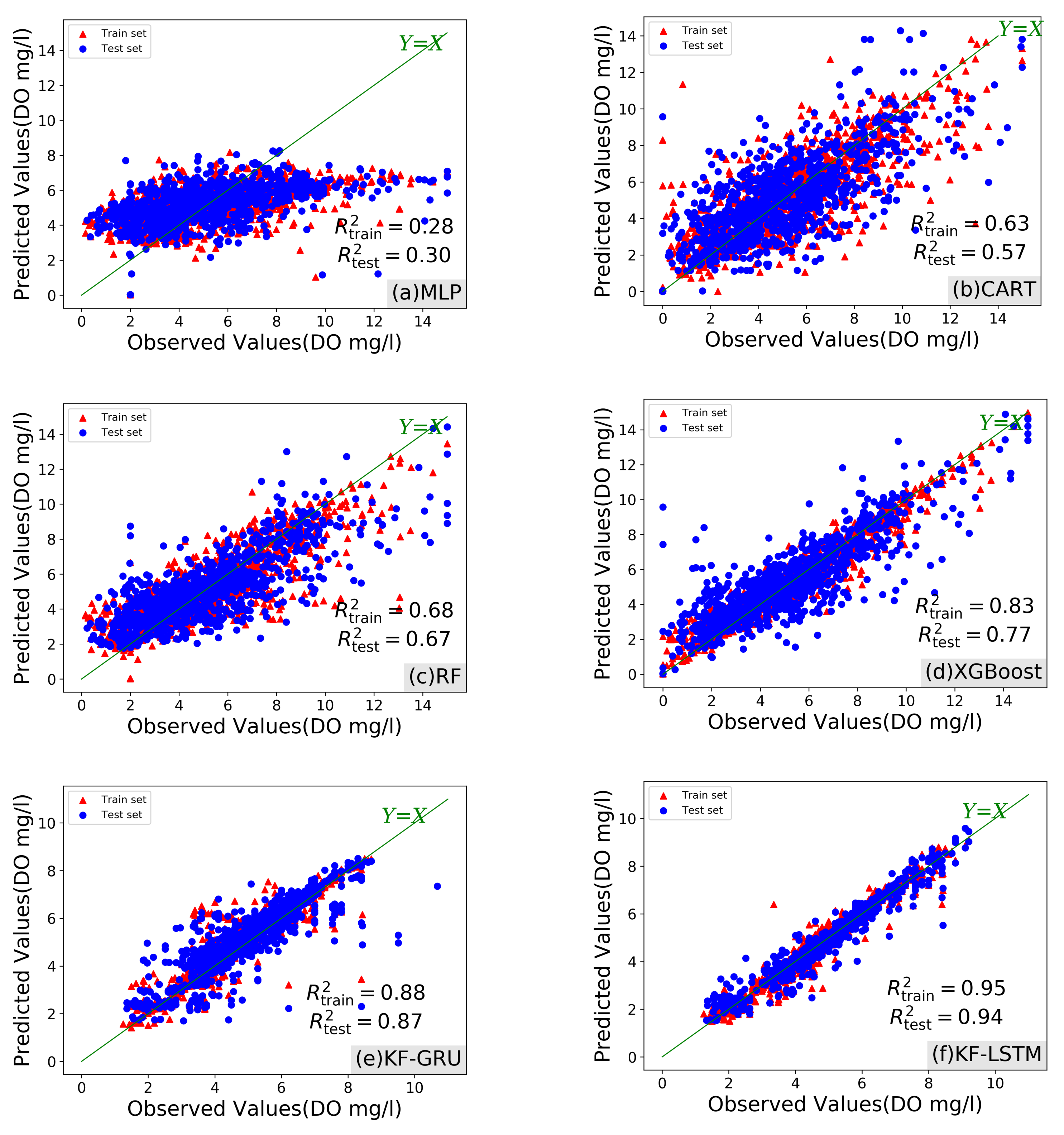
4.4. Experiment Results
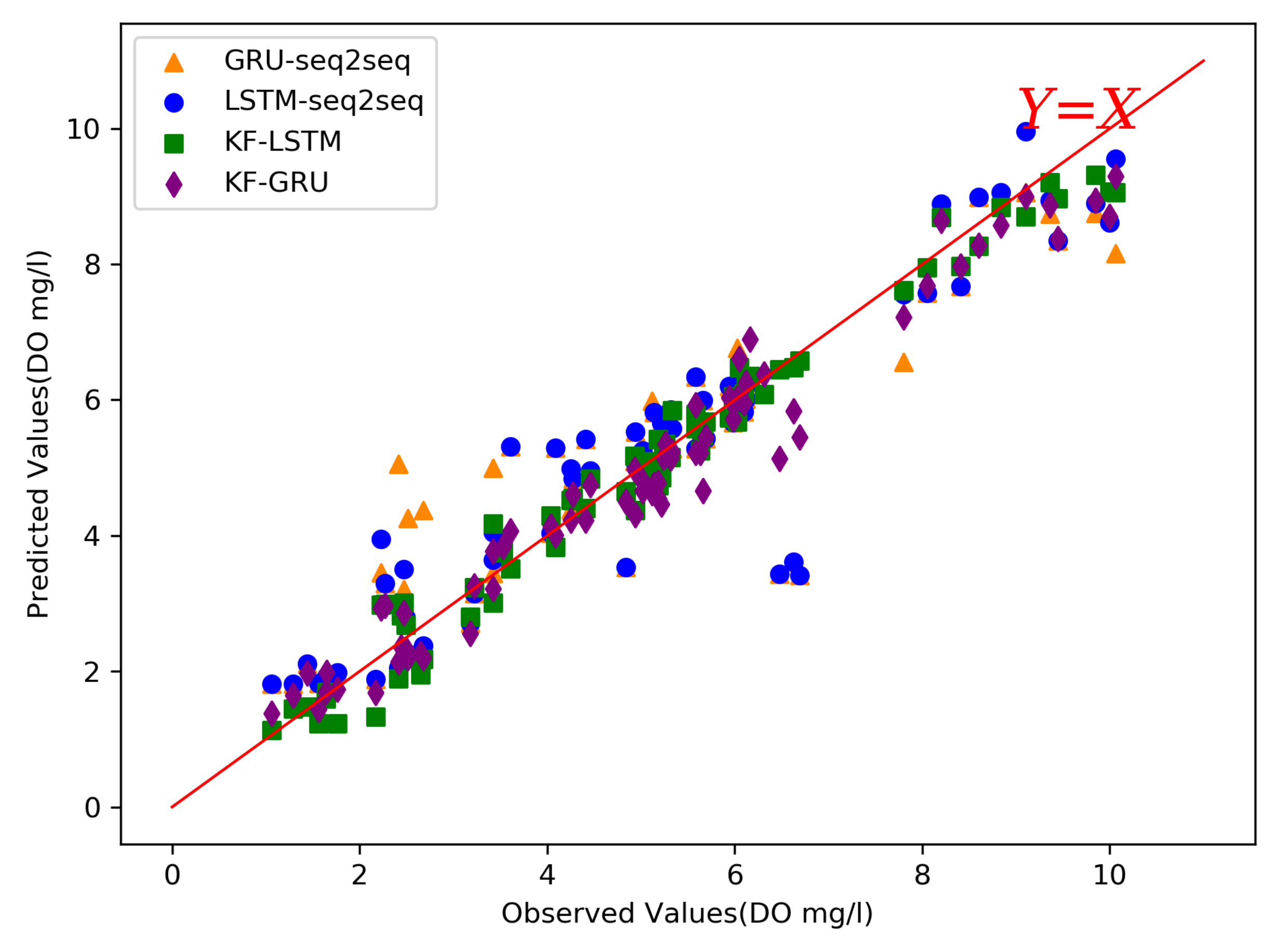
4.5. Ablation Experiment
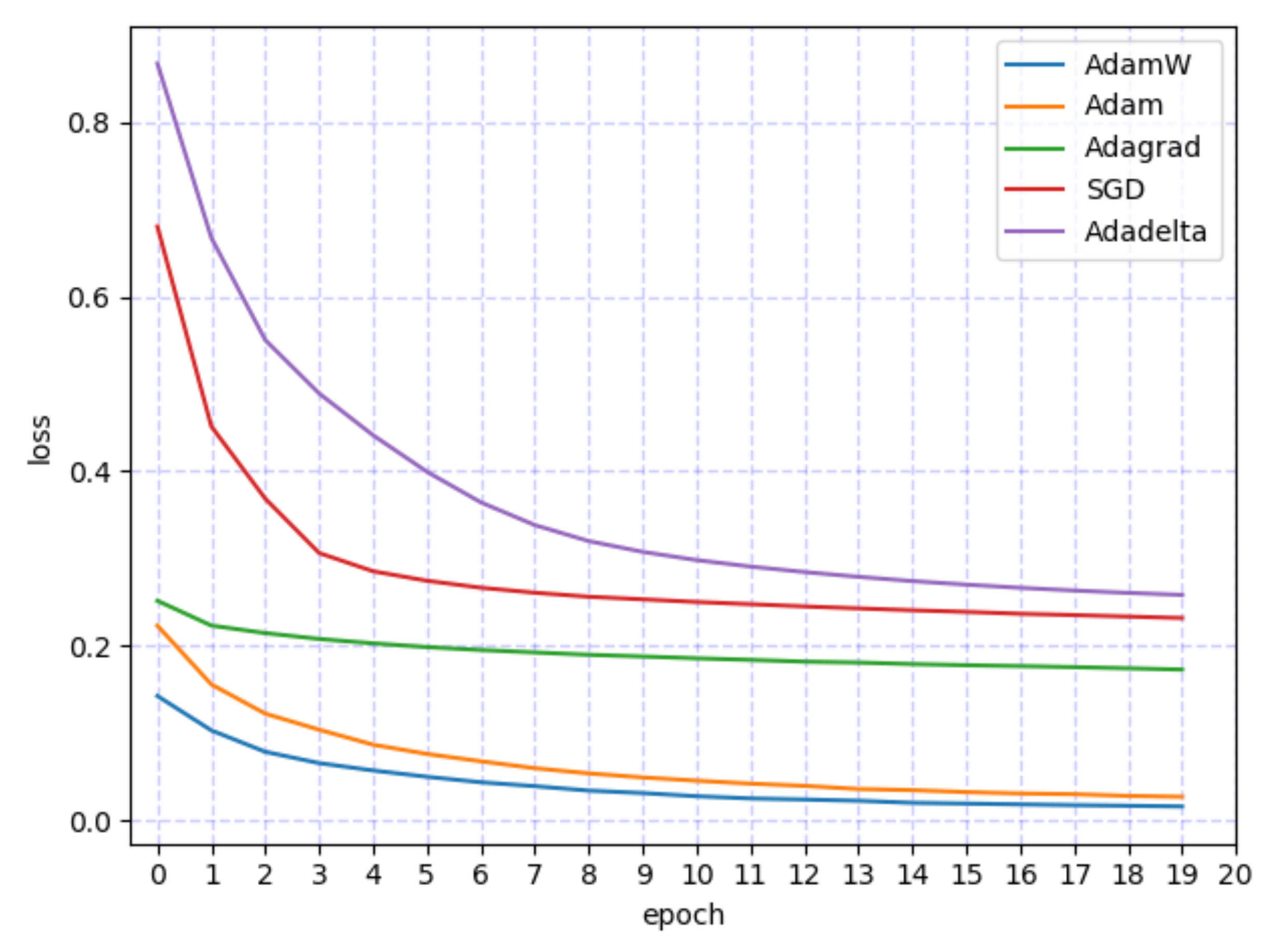
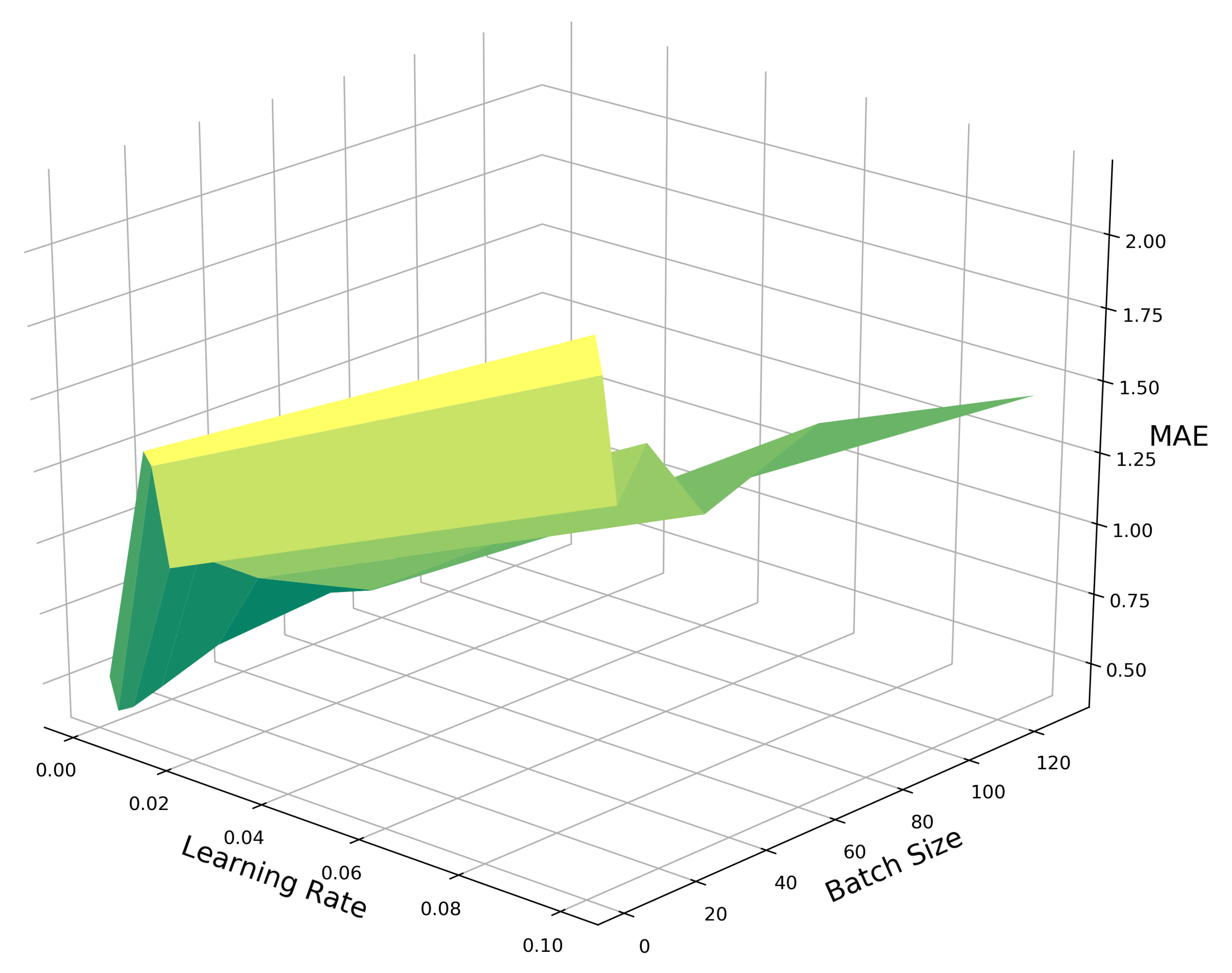
4.6. Optimizer Selection and Parameter Optimization
5. Conclusions and Future Work
- 1.
- Compared with existing machine models, the method proposed in this study has the most accurate prediction of dissolved oxygen content in the water quality of Haimen Bay, with results of 0.95 and 0.94 on the training and test sets, respectively, both higher than other models, while results of 0.31 and 0.30 on the training and test sets, respectively, are lower than other models.
- 2.
- On the one hand, the treatment of missing values in the original data is different from the previous treatment, but the Kalman filter is used to best estimate the data to fill in the missing values in the data, which reduces the harshness of the model for water quality test data and improves the wide applicability of the model.
- 3.
- On the other hand, the model uses the traditional encoder and decoder architecture, using the attention mechanism combined with LSTM neural networks to effectively alleviate the forgetting problem arising from long sequence inputs and to capture the feature interaction information of multi-dimensional covariates, thus reducing the limitations of the traditional decoder-encoder architecture.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morin-Crini, N.; Lichtfouse, E.; Liu, G.; Balaram, V.; Ribeiro, A.R.L.; Lu, Z.; Stock, F.; Carmona, E.; Teixeira, M.R.; Picos-Corrales, L.A.; et al. Worldwide Cases of Water Pollution by Emerging Contaminants: A Review. Environ. Chem. Lett. 2022, 20, 2311–2338. [Google Scholar] [CrossRef]
- Tang, W.; Pei, Y.; Zheng, H.; Zhao, Y.; Shu, L.; Zhang, H. Twenty Years of China’s Water Pollution Control: Experiences and Challenges. Chemosphere 2022, 295, 133875. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Wang, Q.; Zhang, M. A Review of Non-Point Source Water Pollution Modeling for the Urban–Rural Transitional Areas of China: Research Status and Prospect. Sci. Total Environ. 2022, 826, 154146. [Google Scholar] [CrossRef] [PubMed]
- Alasri, T.M.; Ali, S.L.; Salama, R.S.; Alshorifi, F.T. Band-Structure Engineering of TiO2 Photocatalyst by AuSe Quantum Dots for Efficient Degradation of Malachite Green and Phenol. J. Inorg. Organomet. Polym. Mater. 2023. [Google Scholar] [CrossRef]
- Mostafa, M.M.M.; Alshehri, A.A.; Salama, R.S. High performance of supercapacitor based on alumina nanoparticles derived from Coca-Cola cans. J. Energy Storage 2023, 64, 107168. [Google Scholar] [CrossRef]
- Kutty, A.A.; Wakjira, T.G.; Kucukvar, M.; Abdella, G.M.; Onat, N.C. Urban Resilience and Livability Performance of European Smart Cities: A Novel Machine Learning Approach. J. Clean. Prod. 2022, 378, 134203. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A Review of the Artificial Neural Network Models for Water Quality Prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Tian, X.; Wang, Z.; Taalab, E.; Zhang, B.; Li, X.; Wang, J.; Ong, M.C.; Zhu, Z. Water Quality Predictions Based on Grey Relation Analysis Enhanced LSTM Algorithms. Water 2022, 14, 3851. [Google Scholar] [CrossRef]
- Ye, Q.; Yang, X.; Chen, C.; Wang, J. River Water Quality Parameters Prediction Method Based on LSTM-RNN Model. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 3024–3028. [Google Scholar] [CrossRef]
- Hussein, A.M.; Abd Elaziz, M.; Abdel Wahed, M.S.; Sillanpää, M. A New Approach to Predict the Missing Values of Algae during Water Quality Monitoring Programs Based on a Hybrid Moth Search Algorithm and the Random Vector Functional Link Network. J. Hydrol. 2019, 575, 852–863. [Google Scholar] [CrossRef]
- Najah Ahmed, A.; Binti Othman, F.; Abdulmohsin Afan, H.; Khaleel Ibrahim, R.; Ming Fai, C.; Shabbir Hossain, M.; Ehteram, M.; Elshafie, A. Machine Learning Methods for Better Water Quality Prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Shahriari, S.; Sisson, S.; Rashidi, T. Copula ARMA-GARCH Modelling of Spatially and Temporally Correlated Time Series Data for Transportation Planning Use. Transp. Res. Part C Emerg. Technol. 2023, 146, 103969. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhai, M.; Li, G.; Gao, X.; Song, W.; Wang, X.; Ren, H.; Cui, Y.; Qiao, Y.; Ren, J.; et al. Study on the Prediction Effect of a Combined Model of SARIMA and LSTM Based on SSA for Influenza in Shanxi Province, China. BMC Infect. Dis. 2023, 23, 71. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H. VAR-tree Model Based Spatio-Temporal Characterization and Prediction of O3 Concentration in China. Ecotoxicol. Environ. Saf. 2023, 257, 114960. [Google Scholar] [CrossRef] [PubMed]
- Kurani, A.; Doshi, P.; Vakharia, A.; Shah, M. A Comprehensive Comparative Study of Artificial Neural Network (ANN) and Support Vector Machines (SVM) on Stock Forecasting. Ann. Data Sci. 2023, 10, 183–208. [Google Scholar] [CrossRef]
- Alim, M.; Ye, G.H.; Guan, P.; Huang, D.S.; Zhou, B.S.; Wu, W. Comparison of ARIMA Model and XGBoost Model for Prediction of Human Brucellosis in Mainland China: A Time-Series Study. BMJ Open 2020, 10, e039676. [Google Scholar] [CrossRef]
- Gai, R.; Zhang, H. Prediction Model of Agricultural Water Quality Based on Optimized Logistic Regression Algorithm. EURASIP J. Adv. Signal Process. 2023, 2023, 21. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Ho, J.Y.; Afan, H.A.; El-Shafie, A.H.; Koting, S.B.; Mohd, N.S.; Jaafar, W.Z.B.; Lai Sai, H.; Malek, M.A.; Ahmed, A.N.; Mohtar, W.H.M.W.; et al. Towards a Time and Cost Effective Approach to Water Quality Index Class Prediction. J. Hydrol. 2019, 575, 148–165. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid Decision Tree-Based Machine Learning Models for Short-Term Water Quality Prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef] [PubMed]
- Wakjira, T.G.; Rahmzadeh, A.; Alam, M.S.; Tremblay, R. Explainable Machine Learning Based Efficient Prediction Tool for Lateral Cyclic Response of Post-Tensioned Base Rocking Steel Bridge Piers. Structures 2022, 44, 947–964. [Google Scholar] [CrossRef]
- Giri, S.; Kang, Y.; MacDonald, K.; Tippett, M.; Qiu, Z.; Lathrop, R.G.; Obropta, C.C. Revealing the Sources of Arsenic in Private Well Water Using Random Forest Classification and Regression. Sci. Total Environ. 2023, 857, 159360. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Xu, Z.; Kuang, J.; Lin, C.; Xiao, L.; Huang, X.; Zhang, Y. An Alternative to Laboratory Testing: Random Forest-Based Water Quality Prediction Framework for Inland and Nearshore Water Bodies. Water 2021, 13, 3262. [Google Scholar] [CrossRef]
- Ghose, D.K.; Panda, S.S.; Swain, P.C. Prediction of Water Table Depth in Western Region, Orissa Using BPNN and RBFN Neural Networks. J. Hydrol. 2010, 394, 296–304. [Google Scholar] [CrossRef]
- Wang, H.Y.; Chen, B.; Pan, D.; Lv, Z.A.; Huang, S.Q.; Khayatnezhad, M.; Jimenez, G. Optimal Wind Energy Generation Considering Climatic Variables by Deep Belief Network (DBN) Model Based on Modified Coot Optimization Algorithm (MCOA). Sustain. Energy Technol. Assessments 2022, 53, 102744. [Google Scholar] [CrossRef]
- Sharif, S.M.; Kusin, F.M.; Asha’ari, Z.H.; Aris, A.Z. Characterization of Water Quality Conditions in the Klang River Basin, Malaysia Using Self Organizing Map and K-means Algorithm. Procedia Environ. Sci. 2015, 30, 73–78. [Google Scholar] [CrossRef] [Green Version]
- Csábrági, A.; Molnár, S.; Tanos, P.; Kovács, J. Application of Artificial Neural Networks to the Forecasting of Dissolved Oxygen Content in the Hungarian Section of the River Danube. Ecol. Eng. 2017, 100, 63–72. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J. Predicting Inflow Rate of the Soyang River Dam Using Deep Learning Techniques. Water 2021, 13, 2447. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Liu, C.; Liu, D.; Mu, L. Improved Transformer Model for Enhanced Monthly Streamflow Predictions of the Yangtze River. IEEE Access 2022, 10, 58240–58253. [Google Scholar] [CrossRef]
- Tao, Q.; Liu, F.; Li, Y.; Sidorov, D. Air Pollution Forecasting Using a Deep Learning Model Based on 1D Convnets and Bidirectional GRU. IEEE Access 2019, 7, 76690–76698. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long Short-Term Memory Neural Network for Traffic Speed Prediction Using Remote Microwave Sensor Data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Sangaiah, A.; Xie, Y.; Yin, X. Analysis and Prediction of Water Quality Using LSTM Deep Neural Networks in IoT Environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhao, K.; Yu, X.; Yan, Y.; He, Z.; Lai, Y.; Zhou, Y. Crack Classification of Fiber-Reinforced Backfill Based on Gaussian Mixed Moving Average Filtering Method. Cem. Concr. Compos. 2022, 134, 104740. [Google Scholar] [CrossRef]
- Ahmed, H.; Ullah, A. Exponential Moving Average Extended Kalman Filter for Robust Battery State-of-Charge Estimation. In Proceedings of the 2022 International Conference on Innovations in Science, Engineering and Technology (ICISET), Chittagong, Bangladesh, 26–27 February 2022; pp. 555–560. [Google Scholar] [CrossRef]
- Hamzah, F.B.; Mohd Hamzah, F.; Mohd Razali, S.F.; Samad, H. A Comparison of Multiple Imputation Methods for Recovering Missing Data in Hydrological Studies. Civ. Eng. J. 2021, 7, 1608–1619. [Google Scholar] [CrossRef]
- Banerjee, K.; Bali, V.; Nawaz, N.; Bali, S.; Mathur, S.; Mishra, R.K.; Rani, S. A Machine-Learning Approach for Prediction of Water Contamination Using Latitude, Longitude, and Elevation. Water 2022, 14, 728. [Google Scholar] [CrossRef]
- Xu, J.; Wang, K.; Lin, C.; Xiao, L.; Huang, X.; Zhang, Y. FM-GRU: A Time Series Prediction Method for Water Quality Based on Seq2seq Framework. Water 2021, 13, 1031. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, W.; Xie, J.; Huang, W.; Xin, K. LSTM-Based Model-Predictive Control with Rationality Verification for Bioreactors in Wastewater Treatment. Water 2023, 15, 1779. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Bakibillah, A.; Tan, Y.H.; Loo, J.Y.; Tan, C.P.; Kamal, M.; Pu, Z. Robust Estimation of Traffic Density with Missing Data Using an Adaptive-R Extended Kalman Filter. Appl. Math. Comput. 2022, 421, 126915. [Google Scholar] [CrossRef]
- Cai, L.; Zhang, Z.; Yang, J.; Yu, Y.; Zhou, T.; Qin, J. A Noise-Immune Kalman Filter for Short-Term Traffic Flow Forecasting. Phys. A Stat. Mech. Its Appl. 2019, 536, 122601. [Google Scholar] [CrossRef]
- Momin, K.A.; Barua, S.; Jamil, M.S.; Hamim, O.F. Short Duration Traffic Flow Prediction Using Kalman Filtering. In Proceedings of the 6th International Conference on Civil Engineering for Sustainable Development (ICCESD 2022), Khulna, Bangladesh, 10–12 February 2022; p. 040011. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. arXiv 2014, arXiv:1409.3215. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of Gated Recurrent Unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar] [CrossRef] [Green Version]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:cs/1706.03762. [Google Scholar]
- Pan, M.; Zhou, H.; Cao, J.; Liu, Y.; Hao, J.; Li, S.; Chen, C.H. Water Level Prediction Model Based on GRU and CNN. IEEE Access 2020, 8, 60090–60100. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Willmott, C.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Abobakr Yahya, A.S.; Ahmed, A.N.; Binti Othman, F.; Ibrahim, R.K.; Afan, H.A.; El-Shafie, A.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Water Quality Prediction Model Based Support Vector Machine Model for Ungauged River Catchment under Dual Scenarios. Water 2019, 11, 1231. [Google Scholar] [CrossRef] [Green Version]
- Aklilu, E.G.; Adem, A.; Kasirajan, R.; Ahmed, Y. Artificial Neural Network and Response Surface Methodology for Modeling and Optimization of Activation of Lactoperoxidase System. S. Afr. J. Chem. Eng. 2021, 37, 12–22. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Ibrahim, M.; Ebead, U.; Alam, M.S. Explainable Machine Learning Model and Reliability Analysis for Flexural Capacity Prediction of RC Beams Strengthened in Flexure with FRCM. Eng. Struct. 2022, 255, 113903. [Google Scholar] [CrossRef]
- You, Y.; Li, J.; Reddi, S.; Hseu, J.; Kumar, S.; Bhojanapalli, S.; Song, X.; Demmel, J.; Keutzer, K.; Hsieh, C.J. Large Batch Optimization for Deep Learning: Training BERT in 76 Minutes. arXiv 2020, arXiv:1904.00962. [Google Scholar]
| Model | Hyperparameter | Optimal Value |
|---|---|---|
| Multilayer Perceptron | Learning rate | 0.001 |
| Hidden layers Sizes | 32 | |
| Maximum number of iterations | 700 | |
| Classification and Regression Tree | Maximum depth of tree | 20 |
| Minimum number of samples required to be at a leaf node | 8 | |
| Minimum number of samples required to split an internal node | 4 | |
| Divisive strategy | Best | |
| Random Forest | Maximum depth | 10 |
| Maximum number of estimators | 90 | |
| XGBoost | Learning Rate | 0.1 |
| Maximum depth of tree | 7 | |
| Maximum number of estimators | 300 | |
| KF-GRU | Timing structure of the Kalman filter | level_trend |
| Target size | 1 | |
| Feature size | 4 | |
| Hidden layers Sizes | 128 | |
| The number of layers in GRU | 2 | |
| Dropout rate | 0.2 | |
| Encode steps | 24 | |
| Forcast steps | 12 | |
| Batch size | 6 | |
| Learning rate | 0.001 | |
| KF-LSTM | Timing structure of the Kalman filter | level_trend |
| Target size | 1 | |
| Feature size | 4 | |
| Hidden layers Sizes | 128 | |
| The number of layers in LSTM | 3 | |
| Dropout rate | 0.3 | |
| Encode steps | 24 | |
| Forcast steps | 12 | |
| Batch size | 8 | |
| Learning rate | 0.001 |
| Water Data | Count | Mean | Number of Missing Values | Minimum Value | Maximum Value | Unit |
|---|---|---|---|---|---|---|
| Temperature | 12,757 | 24.655 | 371 | 15 | 35 | °C |
| PH | 12,752 | 7.4012 | 376 | 3.63 | 9.86 | - |
| Electrical | 12,763 | 4596.68 | 365 | 4 | 46,878 | μs/cm |
| Turbidity | 12,764 | 55.19 | 364 | 1 | 500 | NTU |
| DO | 12,710 | 5.2366 | 418 | 0.05 | 15 | mg/L |
| Data | Metrics | Model | |||||
|---|---|---|---|---|---|---|---|
| MLP | CART | RF | XGBoost | KF-GRU | KF-LSTM | ||
| Train set | 1.75 | 1.15 | 1.12 | 0.87 | 0.44 | 0.31 | |
| 5.27 | 2.71 | 2.32 | 1.54 | 0.43 | 0.15 | ||
| 2.29 | 1.64 | 1.52 | 1.24 | 0.65 | 0.38 | ||
| 0.28 | 0.63 | 0.68 | 0.83 | 0.88 | 0.95 | ||
| Test set | 1.73 | 1.35 | 1.16 | 0.95 | 0.47 | 0.30 | |
| 5.27 | 3.30 | 2.51 | 1.81 | 0.41 | 0.16 | ||
| 2.29 | 1.81 | 1.58 | 1.34 | 0.62 | 0.40 | ||
| 0.30 | 0.57 | 0.67 | 0.77 | 0.87 | 0.94 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, H.; Zhang, C.; Xu, J.; Wang, F.; Xiao, L.; Huang, S.; Zhang, Y. Water Quality Prediction Based on the KF-LSTM Encoder-Decoder Network: A Case Study with Missing Data Collection. Water 2023, 15, 2542. https://doi.org/10.3390/w15142542
Cai H, Zhang C, Xu J, Wang F, Xiao L, Huang S, Zhang Y. Water Quality Prediction Based on the KF-LSTM Encoder-Decoder Network: A Case Study with Missing Data Collection. Water. 2023; 15(14):2542. https://doi.org/10.3390/w15142542
Chicago/Turabian StyleCai, Hao, Chen Zhang, Jianlong Xu, Fei Wang, Lianghong Xiao, Shanxing Huang, and Yufeng Zhang. 2023. "Water Quality Prediction Based on the KF-LSTM Encoder-Decoder Network: A Case Study with Missing Data Collection" Water 15, no. 14: 2542. https://doi.org/10.3390/w15142542





