1. Introduction
Floods occur frequently in China, and have seriously hindered the country’s socioeconomic development [
1]. Although floods can have various causes, rainfall is by far the most common and immediate [
2]. In the face of increasingly serious flash flood disasters, many countries have developed or are developing effective flash flood monitoring and early warning systems to enhance flood management capabilities, such as the American Hydrological Research Center (HRC) flash flood guidance system (FFGS) [
3], which has been widely used in Central America, South Korea and other regions; China’s independent research and development of China Flash Flood Hydrological model (CNFF) [
4], which strives to minimize the severity of flash floods. As the most active element of the hydrological cycle, rainfall is the main driver of terrestrial hydrological processes and the most important input for flood forecasting models [
5]. However, observation data from a single source contain significant uncertainties due to spatiotemporal variabilities in rainfall [
6] and cannot meet the requirements for high-precision and high-resolution rainfall data in the fields of hydrology, agriculture, and ecology. Therefore, accurate spatial estimation of rainfall has been a popular research topic in various fields [
7,
8].
Since the 1990s, the spatial estimation of rainfall has developed to the multi-source data-fusion stage [
9]. This technique involves merging two or more types of rainfall data, producing rainfall products with high precision and high resolution. One widely used method for rainfall-data fusion is Bayesian model averaging (BMA), which was first proposed by Raftery et al. [
10] in 2005. Since the output statistics of the model should not be applied to a single set member when the BMA method calibrates the set, which reduces the propagation of the set, Schmeits M J et al. corrected the pre-precipitation probability equation (POP) and additive bias, so that it has become more reliable than traditional methods with these improvements [
11]. A newer method for merging rainfall data, the fast Bayesian regression kriging (FBRK) method, was proposed by Yang and Ng in 2019 [
12]. Unlike other methods, FBRK merges radar, gauge, and crowdsourced data and analyzes the differences in errors of the various data types, leading to accurate estimations of actual rainfall fields. Additionally, its speed makes it suitable for real-time rainfall estimation [
13].
The optimal interpolation (OI) method ensures the accuracy of rainfall data measured at the grid points of monitoring stations and reflects the spatial distribution characteristics of rainfall in remote sensing data. However, its accuracy is affected by the density of the monitoring station network [
14]. Presently, kriging with external drift (KED) is the most widely applied and practical method for rainfall-data fusion. In KED, the radar quantitative precipitation estimation (QPE) field is used as auxiliary information to normalize interpolation weights and the spatial correlation between rainfall stations and radar values [
15].
Although rainfall-data fusion can be used to obtain accurate and wide-ranging data, it is still affected by the accuracy of the rainfall station data [
16,
17]. Rainfall monitoring is a critical aspect of hydrological monitoring and is key to the mitigation of rainstorm-induced flooding disasters [
18]. However, owing to the poor construction standards of some rainfall stations, it is challenging to maintain stations in mountainous areas. This has made it difficult to ensure that the data produced by these stations are of high quality. Consequently, some rainfall stations produce anomalous data (e.g., overestimates, underestimates, and missing measurements) [
19]. Moreover, the topographic conditions of small watersheds in hilly areas are complex and changeable, which has a great impact on the prediction results of hydrological models [
20]. Furthermore, owing to the extreme randomity of these anomalies, it is impractical to completely exclude certain stations for rainfall analysis. To ensure that the data from all rainfall stations can be utilized effectively, it is necessary to identify the stations that produced accurate rainfall data in each period, and to exclude the stations with data quality problems [
21]. Pegram G used a covariance biplot to screen for outlier sites and an efficient PEM algorithm to repair missing data by combining with singular value decomposition, which was experimentally found to be effective in identifying outliers and repairing missing data [
22]. Arumugam P found an effective way of excluding outliers from the rainfall data by using the residuals from the fitted SARIMA model to find outliers and distinguish them from other events [
23]. Chao Zhao introduced a robust skewed box plot to remove outliers from skewed data and found that it was possible to robustly identify rainfall outliers as well as retain outliers incorrectly identified by the e standard box plot [
24].
To address the data anomalies caused by poorly maintained rainfall stations in mountainous regions, we developed a three-step method to exclude anomalous stations. First, Hampel’s method and Grubbs’ test were used to screen for stations with anomalous rainfall data, and to select “reference” stations with stable, high-quality rainfall data. Next, adjacent-station comparisons and radar-assisted validation were used to identify anomalous stations, which were subsequently excluded to improve the quality of the rainfall station data. Finally, KED, OI, and an interpolation method based on distance and radar rainfall station data were used to fuse radar QPE data with rainfall station data (for the purposes of this study, this was performed before and after the anomalous stations were excluded). The effects of our anomaly identification method on rainfall-data fusion were analyzed using leave-one-out cross-validation (LOOCV).
4. Results
4.1. Effects of Anomaly Identification and Exclusion
When Hampel’s method and the Grubbs’ test were used to identify anomalous stations during four typical rainfall events, it was found that the 08:00–19:00 July 3 event had the highest number of anomalous stations (11.5% of the total). The event from 01:00 to 17:00 on August 9 had the lowest number of anomalous stations (7.8% of the total) (
Figure 3). By comparing the number of anomalous stations detected for each rainfall event to the actual anomalous stations, it was found that the accuracy of reference station determination was 94.2% (
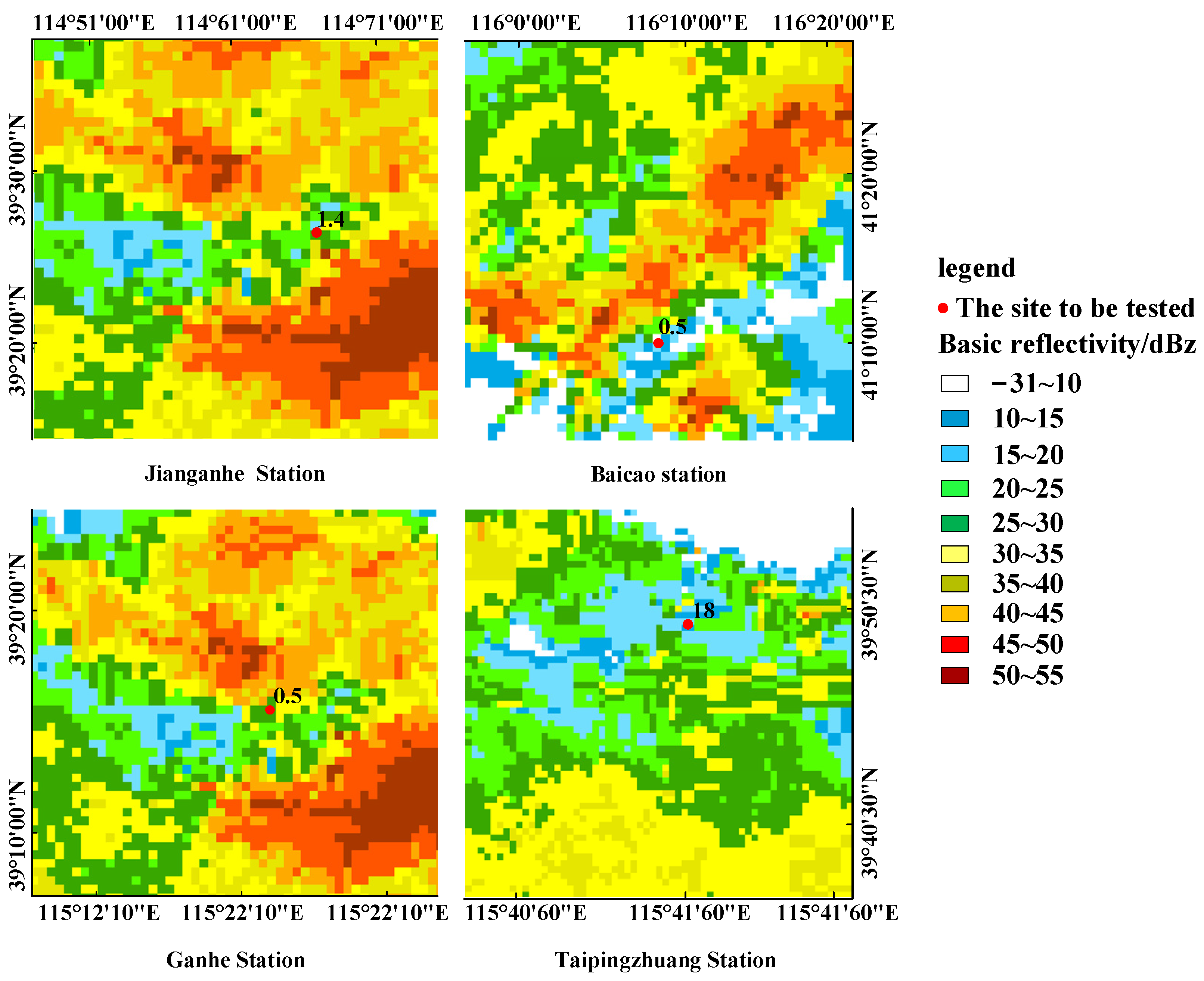
Table 3). The anomalous stations were comprised of three types: (i) those that reported a cumulative rainfall of 0 (no data); (ii) those with rainfalls much smaller than those of their adjacent stations (underestimation); and (iii) those with rainfalls much greater than those of their adjacent stations (overestimation). An example is shown in
Figure 4, which corresponds to the 08:00–19:00 July 3 event.
It was found that eastern, western, and southern Hebei had many anomalous stations, with the most common being underestimation, “no data,” and overestimation, respectively. Northern Hebei only had a small number of anomalous stations, which occasionally reported a cumulative rainfall of zero (“no data” anomaly).
Next, stations that were deemed anomalous at 08:00 and 17:00 during each rainfall event were manually checked; the accuracy of anomaly detection was >90% in most cases (
Table 4).
Radar-assisted validation was performed on the anomalous stations that were detected by reference station determination and adjacent-station analysis. Four stations deemed to be anomalous (Baicao, Jianganhe, Ganhe, and Taipingzhuang) at 17:00 on 3 July 2012, were selected for manual validation, which was performed by superimposing the rain gauge-derived rainfall map onto a radar-echo map. Although the four stations were previously determined to be anomalous, it was discovered that the cumulative rainfalls of the Baicao, Jianganhe, Ganhe, and Taipingzhuang stations during the 16:00–17:00 period were 0.5, 1.4, 0.5, and 18.0 mm, respectively. Radar reflectivity was measured every 6 min from 16:00 to 17:00, and the average radar reflectivity values at the four stations (Baicao, Jianganhe, Ganhe, and Taipingzhuang) were 15, 23, 28, and 19 dBZ, respectively. By comparing the hourly rainfall and radar reflectivity at each station, it was found that the Jianganhe and Baicao stations were accurate. The Ganhe station underestimated rainfall, whereas the Taipingzhuang station overestimated rainfall.
During the month of July, large areas of Hebei are rainy, and many rainfall stations report rain. Therefore, radar-assisted validation was performed on three rainfall events in July, at 08:00 and 17:00 (
Figure 5 and
Table 5). The average accuracy rates of anomaly identification before and after radar verification were 89.7 and 93.7%, respectively.
4.2. Performances of Rainfall Data-Fusion Methods
Three data-fusion methods were used to fuse radar QPE and rainfall station data, before and after anomaly detection, which resulted in several fused rainfall products. The performance of each rainfall data-fusion method was evaluated by calculating the BIAS, RMSE, and MRTE of each method for the four typical rainfall events (
Table 6). BIAS was analyzed by comparing the fused data products to rainfall station data. It was found that OI had strongly negative BIAS values, while the other methods had BIAS values close to 0. For the 08:00–19:00 event on July 3, all three data-fusion methods exhibited large RMSE values (4.65 (OI), 3.16 (FAR) and 2.11 (KED)), but near-zero values for other indicators.
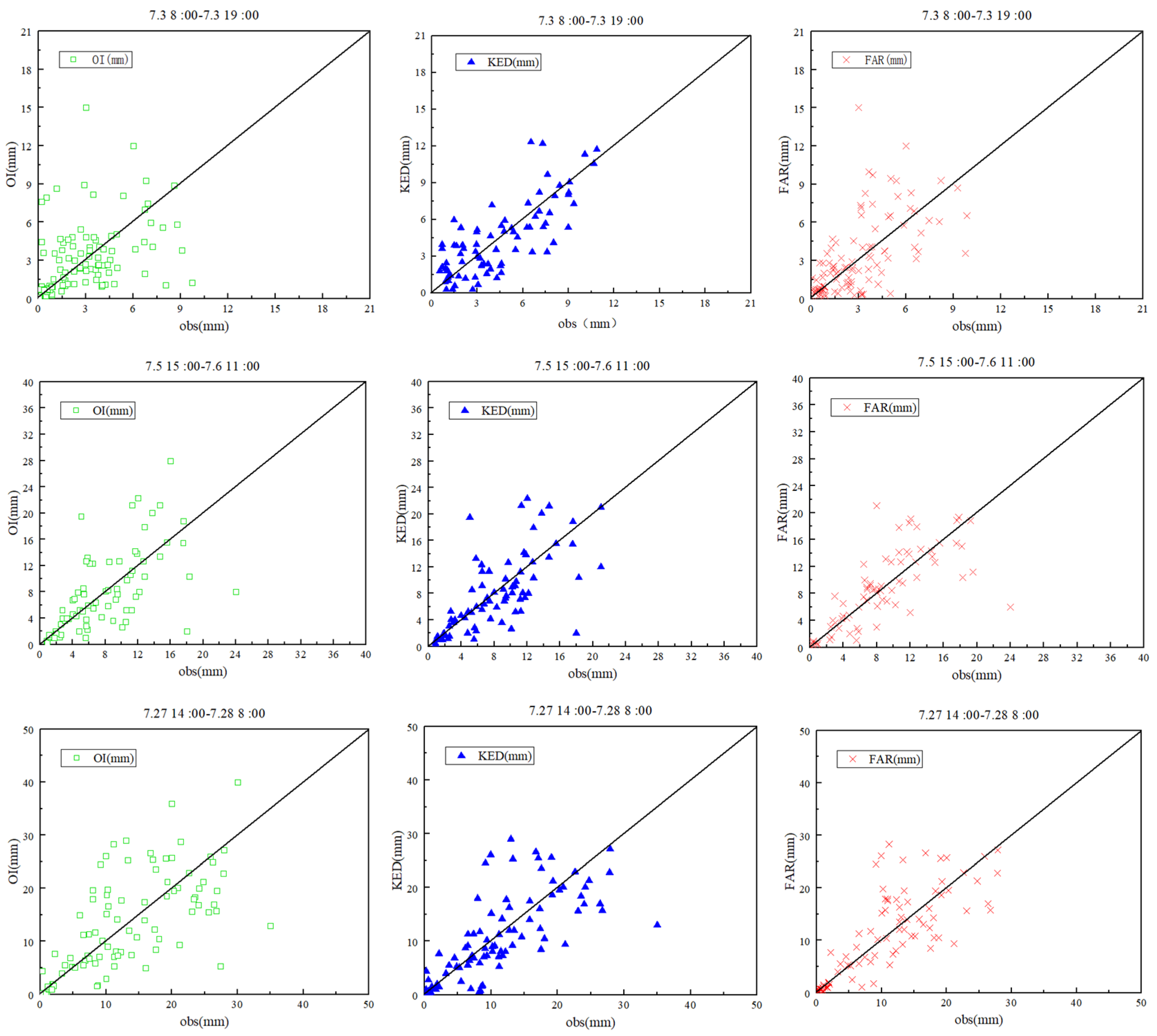
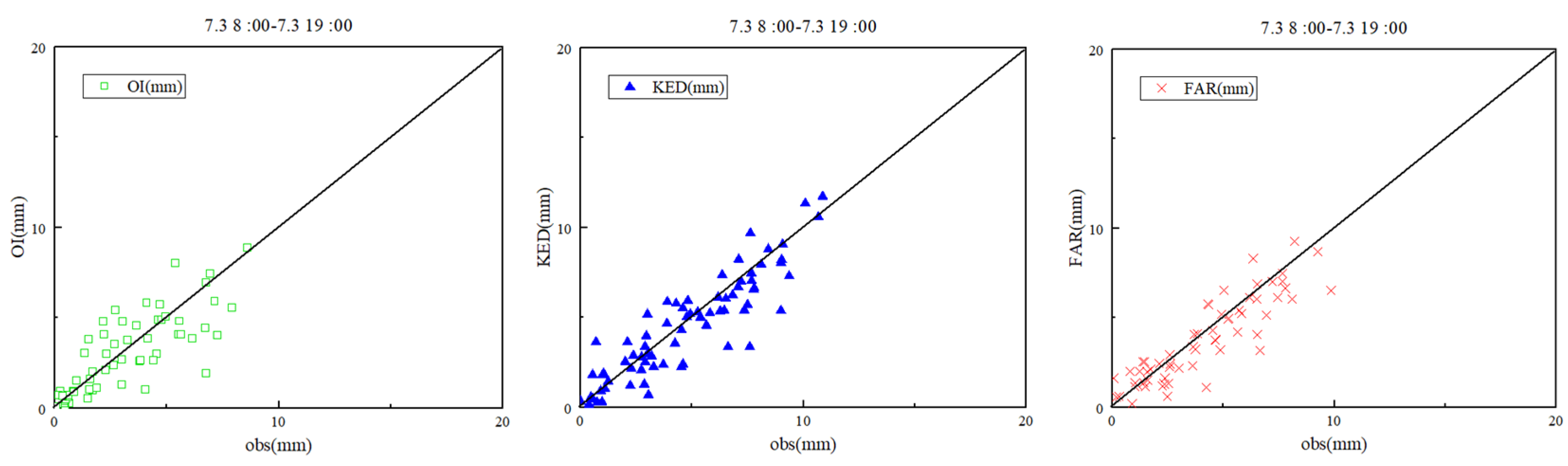
Figure 6 shows the observed rainfall data plotted against the rainfall estimates derived from the three rainfall data-fusion methods without anomalous station identification.
Next, data fusion was performed using the three different data-fusion methods after anomalous stations were identified and excluded. The performance of each method for the four typical rainfall events is shown in
Table 7. By comparing
Table 6 and
Table 7, it is clear that there are noticeable differences in the quality of the fused rainfall products before and after the exclusion of anomalous stations. We found that 95% of the indicator values showed significant improvement after the exclusion of anomalous rainfall data.
After anomalous station exclusion, for the 08:00–19:00 event on July 3, the BIAS and MRTE values were closer to 0, and RMSE decreased by approximately 1.0. For the 15:00 July 5–11:00 July 6 event, all three indicators decreased by approximately 0.1. The indicators corresponding to the 14:00 July 27–08:00 July 28 event did not change significantly after anomaly identification, which indicates that the removal of anomalies only had a small effect on this set of data. For the 01:00–17:00 August 9 event, the indicator values decreased by 0.2–0.5.
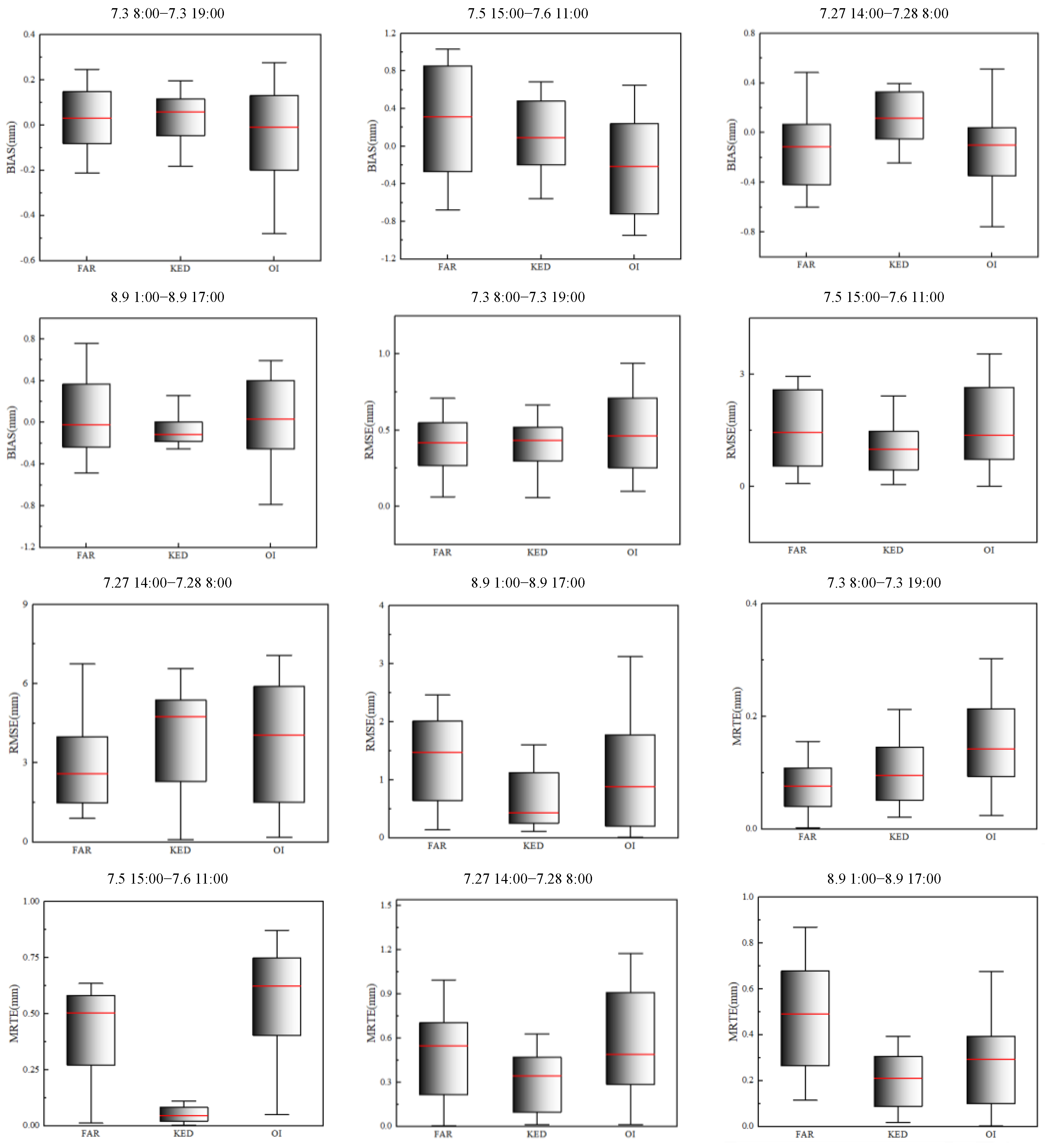
The box plots in
Figure 7 depict the values of the performance indicators for the three rainfall data-fusion methods during the four rainfall events. According to the results, KED was the most effective method, followed closely by FAR. The evaluation of the indicators for the four rainfall sessions showed that KED performed slightly better than FAR, while OI was the least effective method. However, FAR performed better than KED for the session 01:00–17:00 h, August 9.
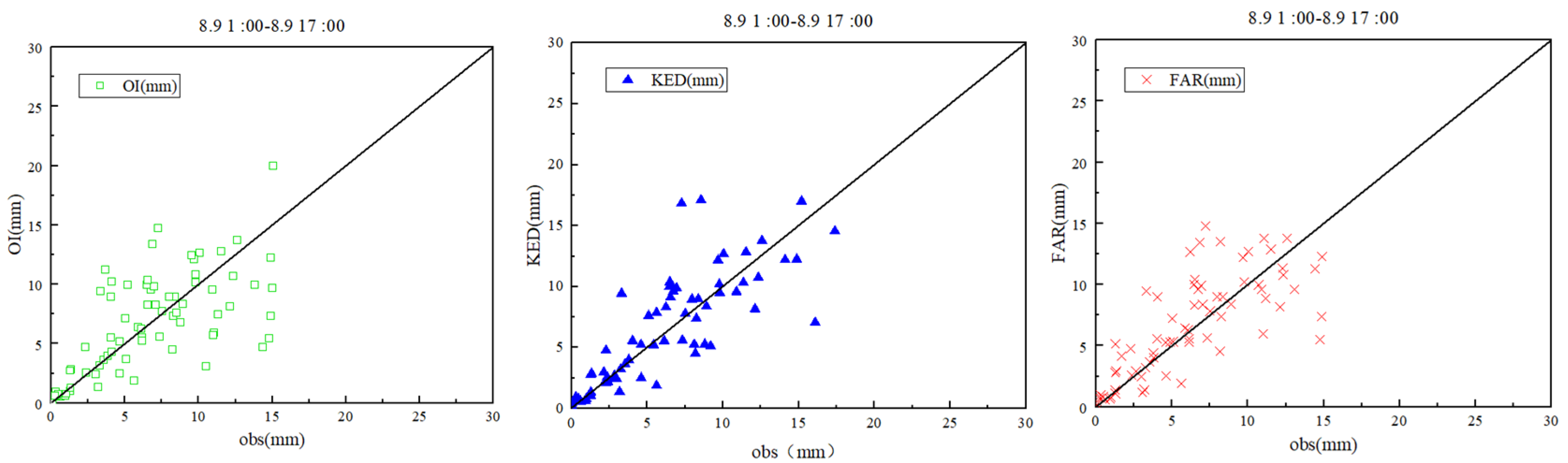
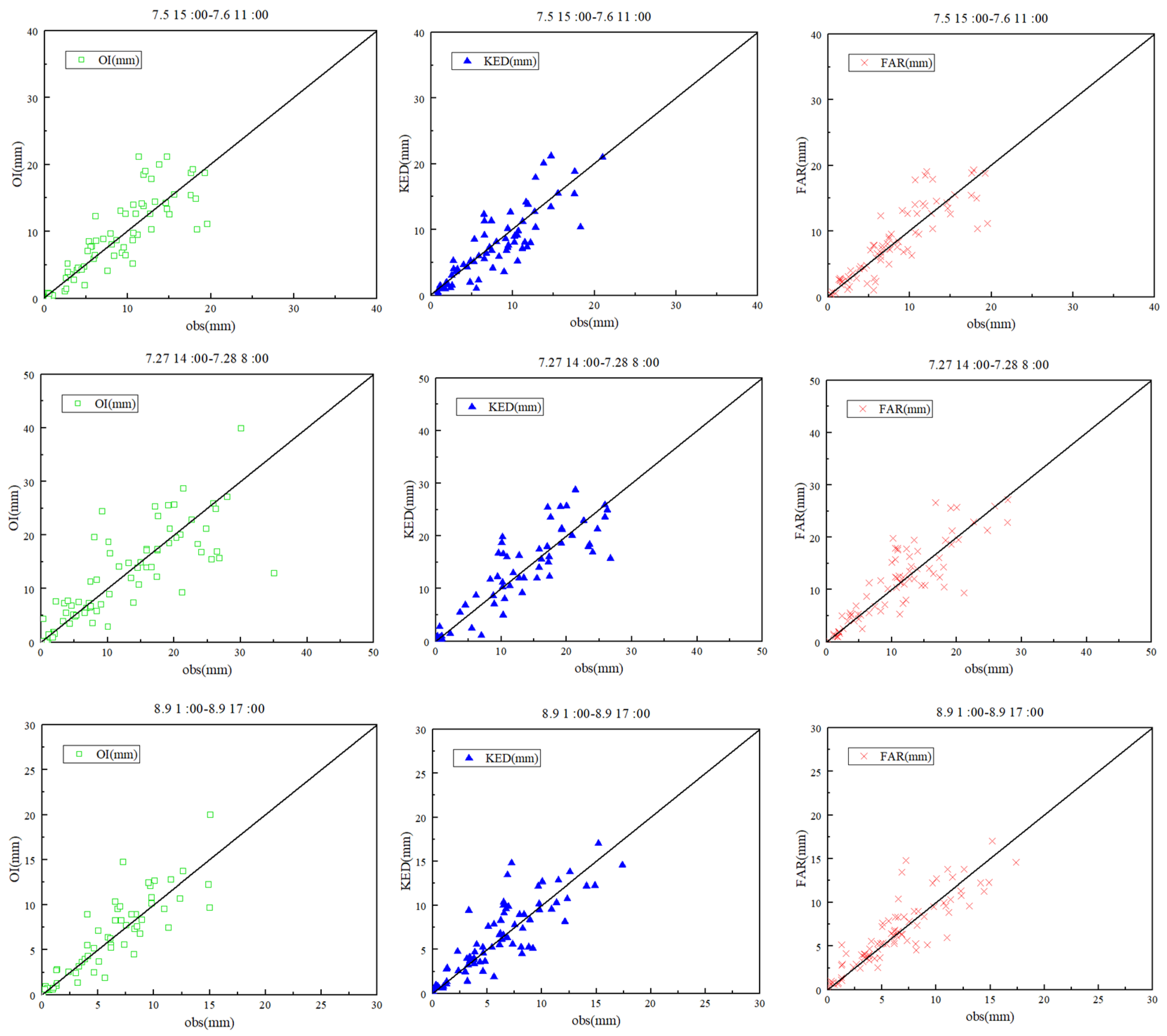
Figure 8 contains scatter diagrams that compare rainfall estimates derived from the three rainfall data-fusion methods plotted against observed rainfall data, after anomalous stations were excluded. As before, OI still had strongly negative BIAS values, while the other methods had average BIAS values close to 0.
By comparing
Figure 6 and
Figure 8, it is clear that the exclusion of anomalous stations significantly improved the performance of all three rainfall data-fusion methods. This is especially true for the OI and KED methods, as their scatter points became much closer to the 1/1 line after the exclusion of anomalous data. The spreads of the FAR product also became smaller after this step.
5. Discussion
The identification of anomalous rainfall stations in four typical rainfall events using Hampel’s method and Grubbs’ test showed that eastern, western, and southern Hebei have many anomalous stations. This can be attributed to the dense distribution of rainfall stations in those regions. The number of anomalous stations decreased for the later rainfall sessions due to the intensified operation and maintenance of gauge stations after the flood season. However, there was an increase in the number of anomalous stations for the session 01:00–17:00 h, August 9. Manual verification showed that the accuracy rate of the reference station was 94.2%, indicating that the Hampel method and Grubbs criterion had significant effects on the identification of anomalous stations and extreme values. Overall, these methods were helpful in improving the quality of monitoring data [
29].
Manual validation performed after the first two steps (reference station determination and adjacent-station analysis) showed that normal stations located at the boundary between rainy and non-rainy areas or areas with significant variations in rainfall intensity were often wrongly classified as anomalous. Hence, the anomalous stations that were detected at 08:00 and 17:00 during three rainfall events in July were selected for radar-assisted validation. The average accuracy of anomaly identification before and after radar-assisted validation were 89.7 and 93.7%, respectively. Hence, radar-assisted validation is suitable for identifying false positives in challenging areas.
The merged rainfall–gauge data were obtained through the application of three different methods before and after the determination of anomalous data. The OI results consistently exhibited strong negative values, regardless of whether the analysis was based on the box diagram or the table of performance indicators, while the average deviations of the other methods were around 0. KED had the best performance, consistent with previous research that shows this method is relatively stable and universal for evaluating most rainfall data merging methods [
30,
31]. The performance gap between FAR and KED was not large, with FAR occasionally performing better than KED. The excellent performance of FAR was due to its greater suitability for calculating and analyzing the merged rainfall data of hilly regions.
After anomalous stations were excluded, the BIAS and MRTE values of all three data-fusion methods became closer to 0 for the 08:00–19:00 July 3 event; their RMSE values also decreased by approximately 1.0. For the session 15:00 h, July 5–11:00 h, July 6, the results of the three indicators generally decreased by approximately 0.1. There was no significant change in the indicators and anomaly identification for the session 14:00 h, July 27–08:00 h, July 28, and the optimization effect was small. For the session 01:00–17:00 h, August 9, the results of the various indicators generally reduced by 0.2–0.5 compared to those before the identification of anomalous stations. This shows that identifying anomalous stations could eliminate anomalous data and improve the quality of rainfall monitoring data, effectively improving the accuracy of the merged rainfall data. The scatter diagrams used for comparing and analyzing the merged products before and after eliminating anomalous rainfall monitoring data show that the overall correction effects improved significantly after anomaly identification, indicating that the quality of rainfall data at gauge stations determines that of the merged rainfall products [
17,
32].