Influence of Rainfall Pattern on Wetness Index for Infinite Slope Stability Analysis
Abstract
:1. Introduction
2. Methodology
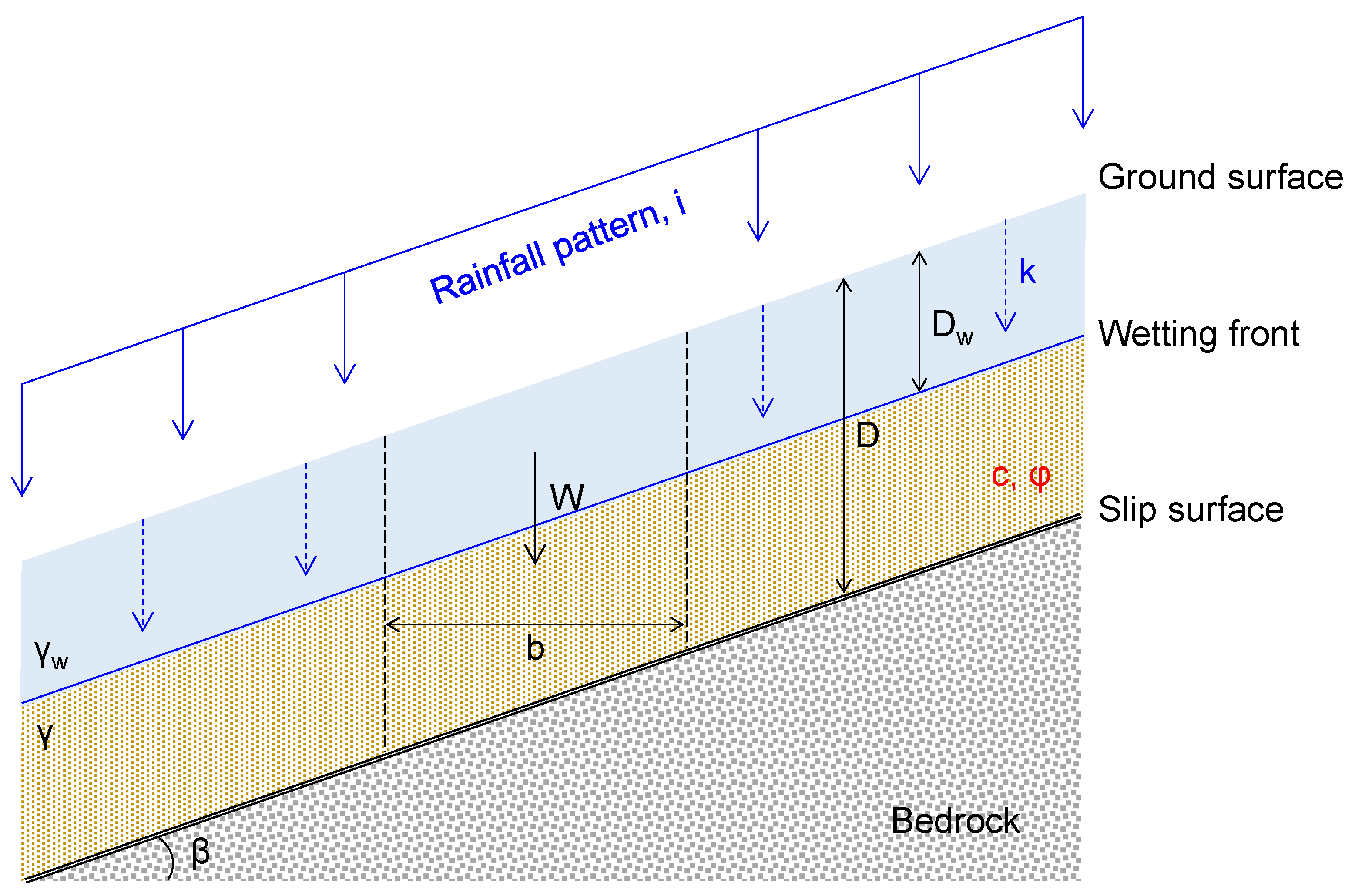
2.1. Slope Stability
2.2. Temporal Distribution of Design Rainfall
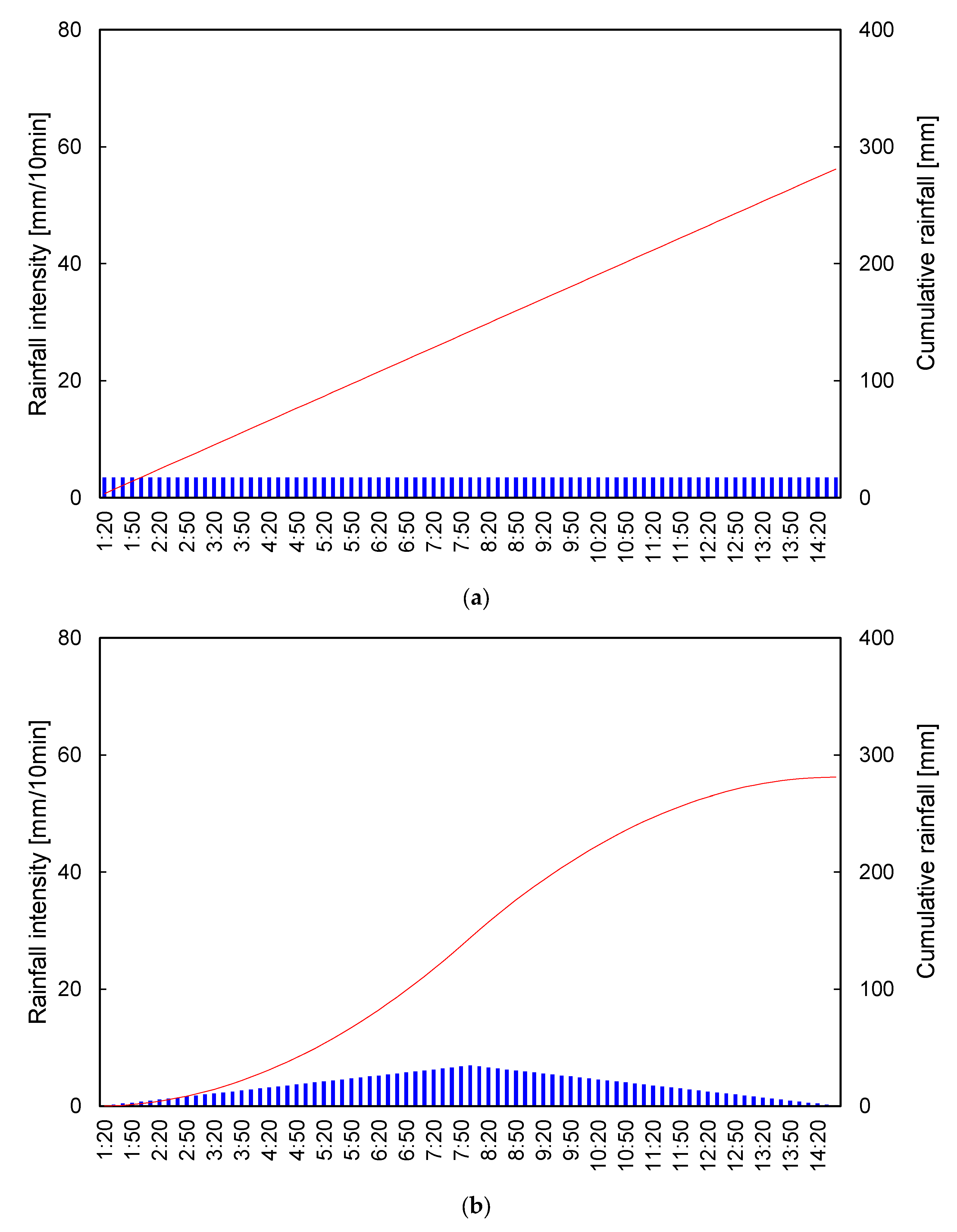
2.2.1. The Yen and Chow Model
2.2.2. The Mononobe Model
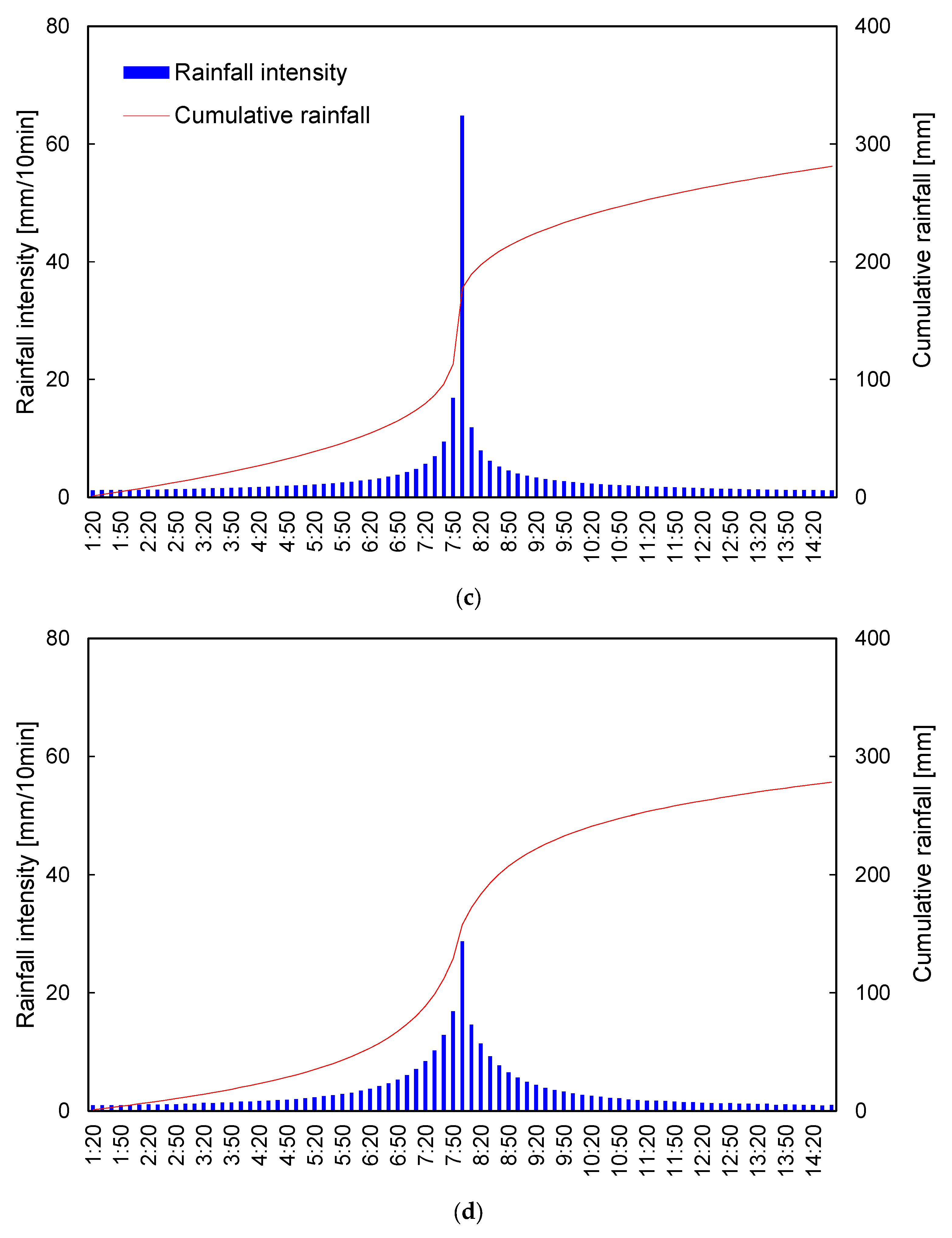
2.2.3. The Alternating Block Method
2.2.4. The Huff Model
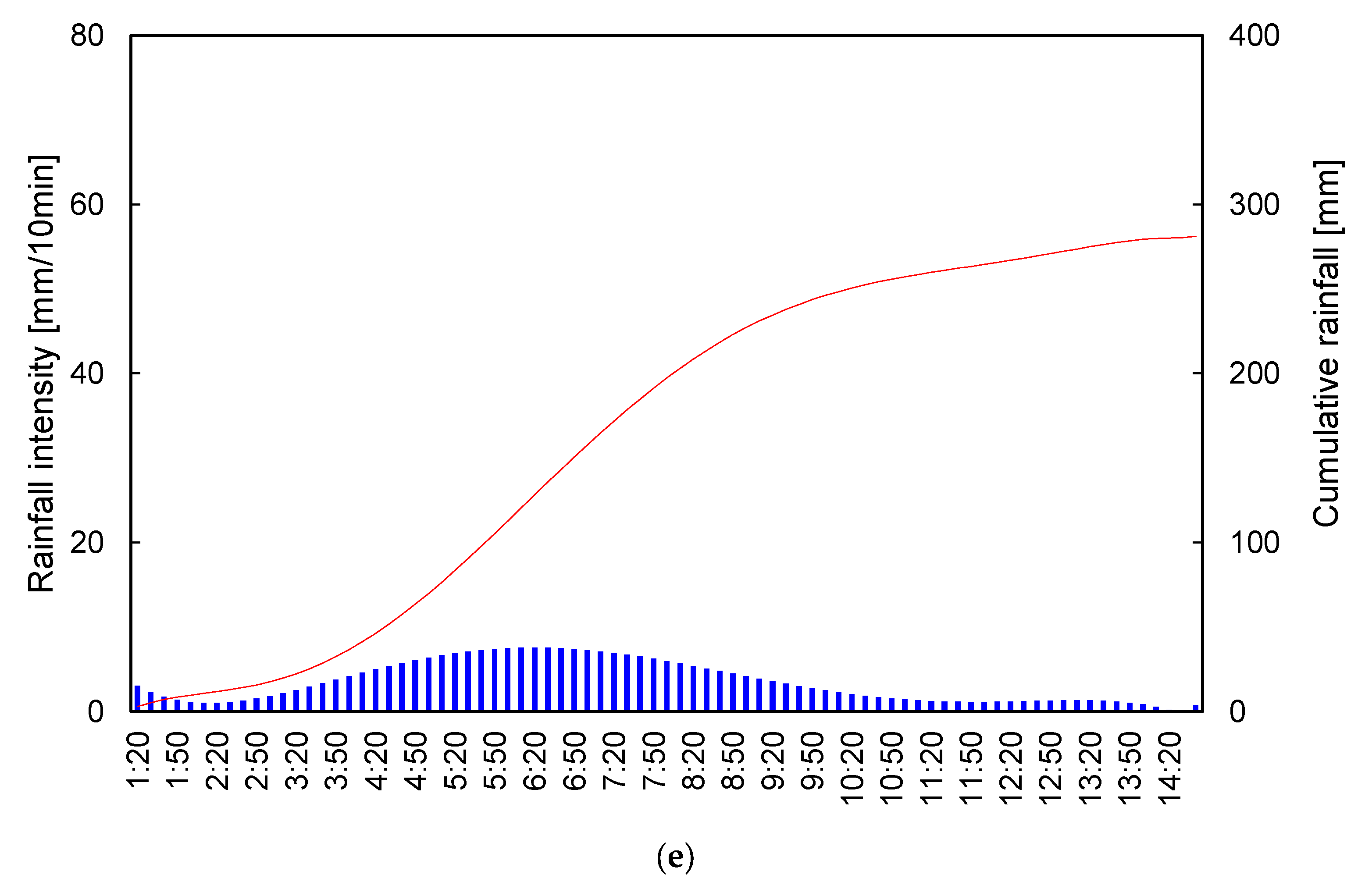
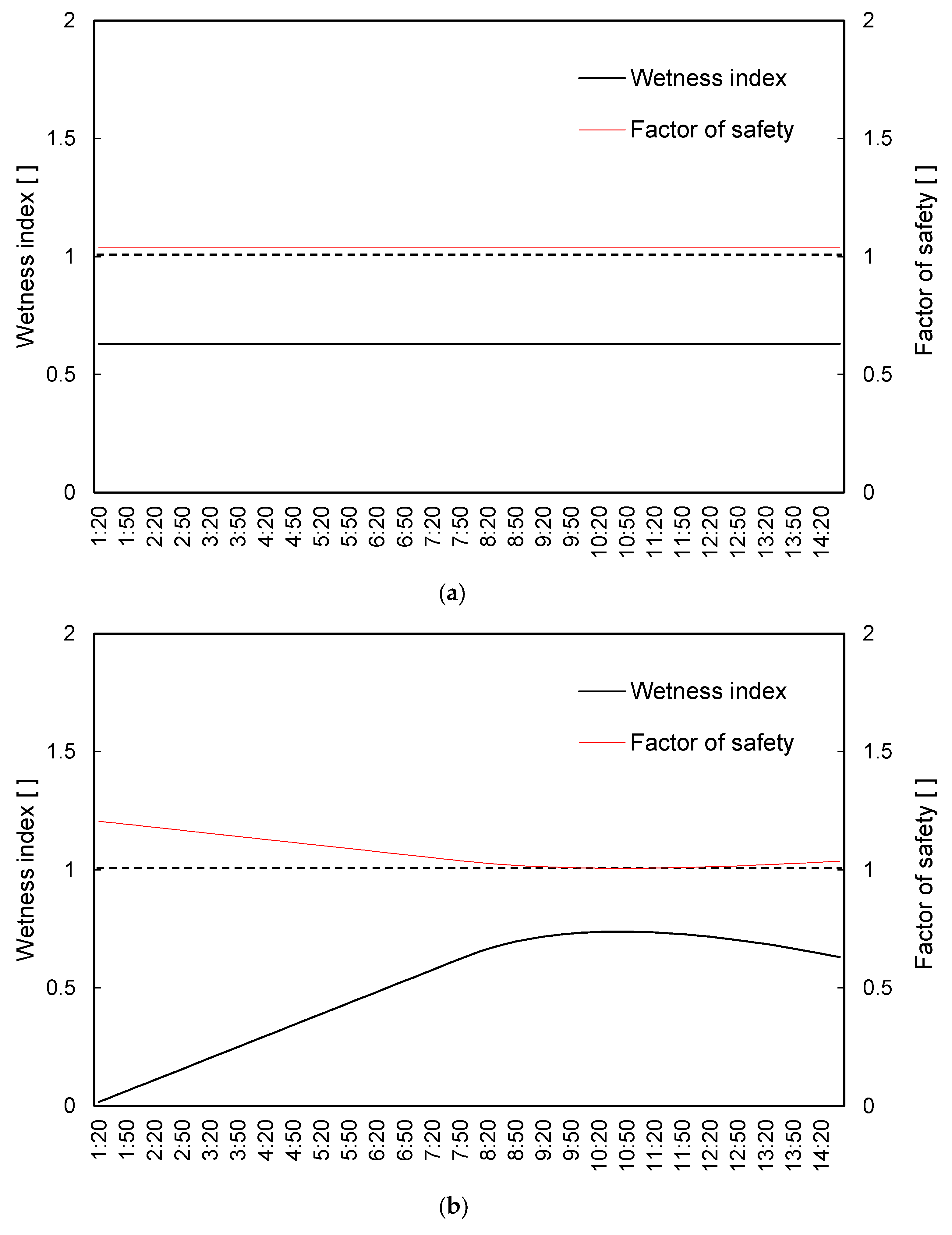
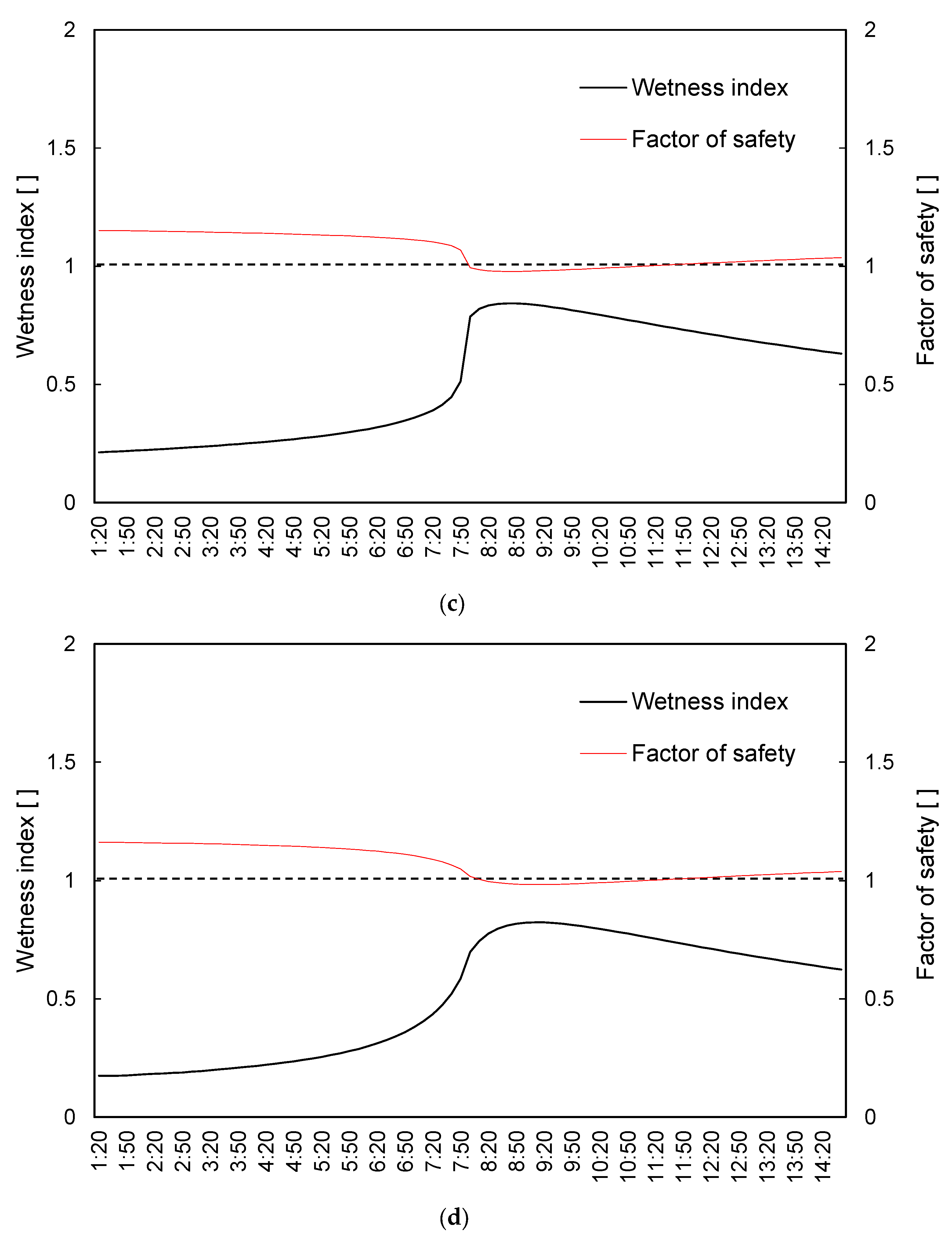
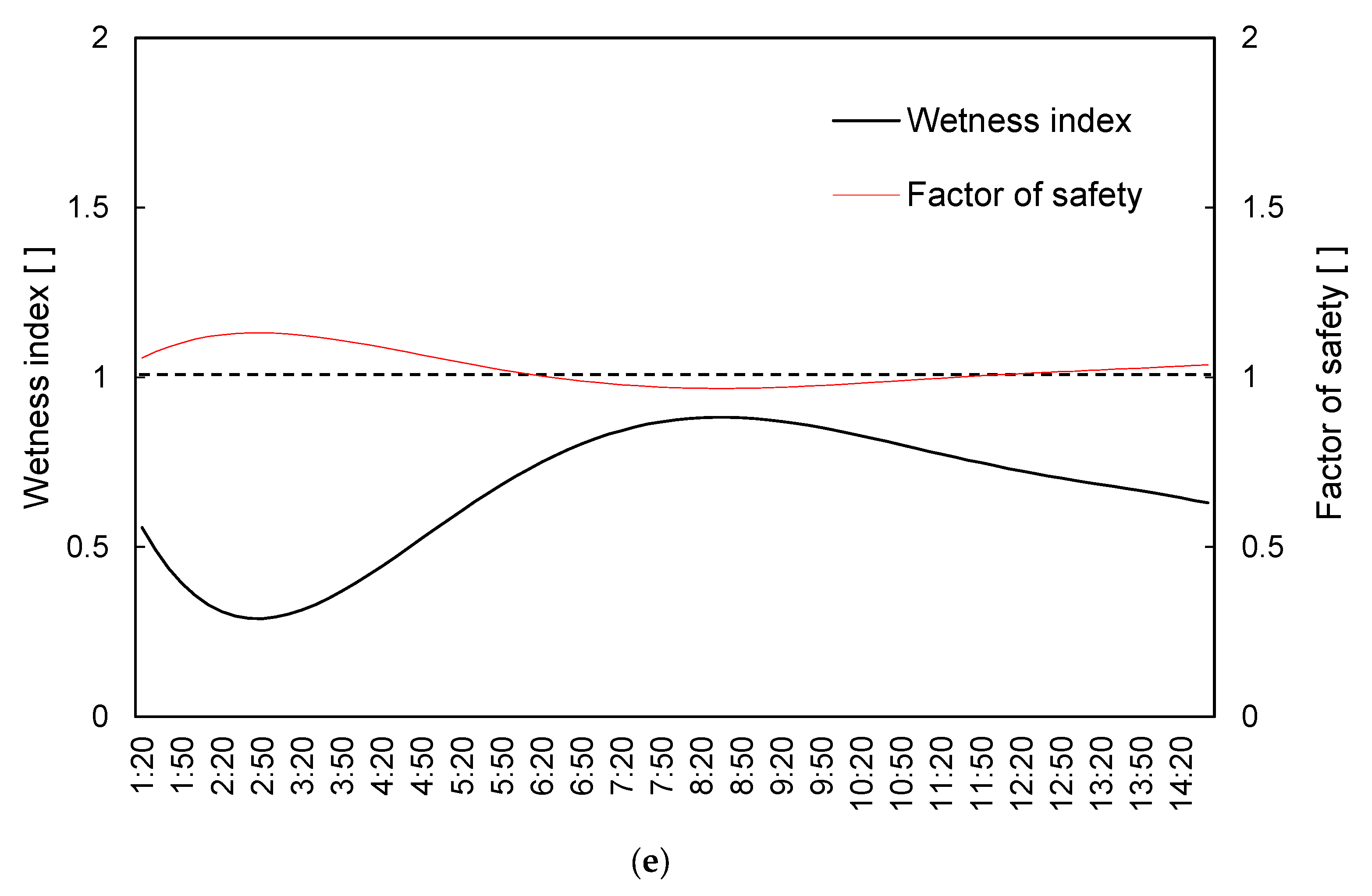
3. Results and Analyses
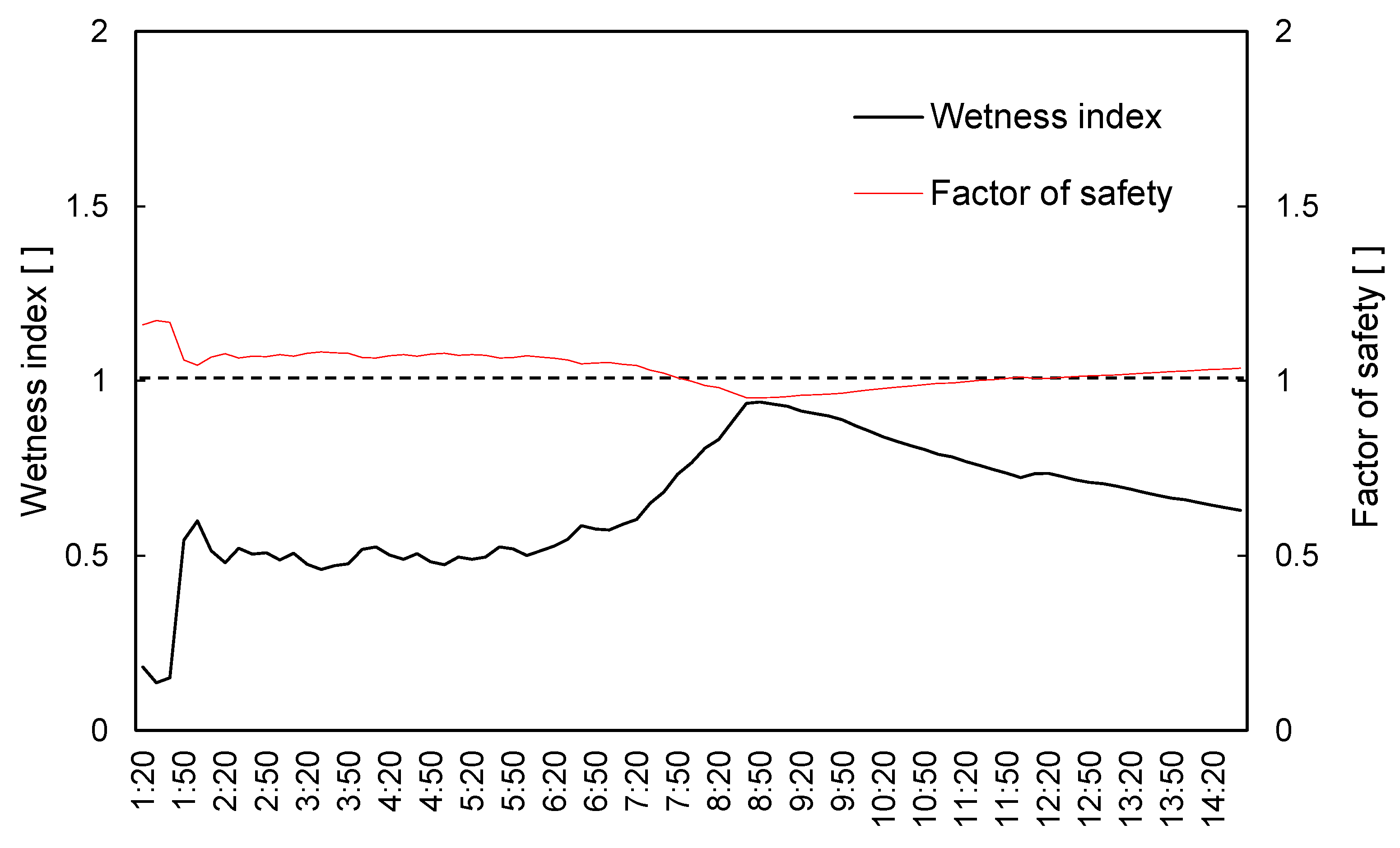
3.1. Landslides in July 2011 in Seoul, Korea
3.2. Impact of Rainfall Pattern on Slope Stability
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oh, S.R.; Lee, G.H. Slope stability analysis at catchment scale using spatially-distributed wetness index. J. Korean Geogr. 2014, 3, 111–126. [Google Scholar]
- Rahardjo, H.; Lim, T.T.; Chang, M.F.; Fredlund, D.G. Shear-strength characteristics of a residual soil. Can. Geotech. J. 1995, 32, 60–77. [Google Scholar] [CrossRef]
- Fourie, A.B. Predicting rainfall-induced slope instability. Proc. Inst. Civ. Eng. Geotech. Eng. 1996, 119, 211–218. [Google Scholar] [CrossRef]
- Borga, M.; Dalla Fontana, G.; Da Ros, D.; Marchi, L. Shallow landslide hazard assessment using a physically based model and digital elevation data. Environ. Geol. 1998, 35, 81–88. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. Influence of rainfall intensity and duration on slope stability in unsaturated soils. Q. J. Eng. Geol. Hydrogeol. 1998, 31, 105–113. [Google Scholar]
- Kim, S.Y.; Park, J.; Cha, W.; Lee, J.S.; Carlos Santamarina, J. Soil response during globally drained and undrained freeze–thaw cycles under deviatoric loading. J. Geotech. Geoenviron.l Eng. 2021, 147, 06020030. [Google Scholar] [CrossRef]
- Chae, B.G.; Lee, J.H.; Park, H.J.; Choi, J. A method for predicting the factor of safety of an infinite slope based on the depth ratio of the wetting front induced by rainfall infiltration. Nat. Hazards Earth Syst. Sci. 2015, 15, 1835–1849. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Barling, R.D.; Moore, I.D.; Grayson, R.B. A quasi-dynamic wetness index for characterizing the spatial distribution of zones of surface saturation and soil water content. Water Resour. Res. 1994, 30, 1029–1044. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Han, D.; Zhang, J.; Zhuo, L.; Berti, M. Application of hydrological model simulations in landslide predictions. Landslides 2020, 17, 877–891. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Muntohar, A.S.; Liao, H.J. Rainfall infiltration: Infinite slope model for landslides triggering by rainstorm. Nat. Hazards 2010, 54, 967–984. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. A physically based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- Cardinali, M.; Galli, M.; Guzzetti, F.; Ardizzone, F.; Reichenbach, P.; Bartoccini, P. Rainfall induced landslides in December 2004 in south-western Umbria, central Italy: Types, extent, damage and risk assessment. Nat. Hazards Earth Syst. Sci. 2006, 6, 237–260. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Deganutti, A.M.; Marchi, L.; Arattano, M. Rainfall and debris-flow occurrence in the Moscardo basin (Italian Alps). In Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment; Millpress Science Publishers: Rotterdam, The Netherlands, 2000; pp. 67–72. [Google Scholar]
- Zhou, W.; Tang, C.; Van Asch, T.W.; Zhou, C. Rainfall-triggering response patterns of post-seismic debris flows in the Wenchuan earthquake area. Nat. Hazards 2014, 70, 1417–1435. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Segoni, S.; Leoni, L.; Benedetti, A.I.; Catani, F.; Righini, G.; Falorni, G.; Rebora, N. Towards a definition of a real-time forecasting network for rainfall induced shallow landslides. Nat. Hazards Earth Syst. Sci. 2009, 9, 2119–2133. [Google Scholar] [CrossRef] [Green Version]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Park, H.-J.; Jang, J.-Y.; Lee, J.-H. Physically based susceptibility assessment of rainfall-induced shallow landslides using a fuzzy point estimate method. Remote Sens. 2017, 9, 487. [Google Scholar] [CrossRef] [Green Version]
- Zêzere, J.L.; Pereira, S.; Melo, R.; Oliveira, S.C.; Garcia, R.A. Mapping landslide susceptibility using data-driven methods. Sci. Total Environ. 2017, 589, 250–267. [Google Scholar] [CrossRef] [PubMed]
- Medina, V.; Hürlimann, M.; Guo, Z.; Lloret, A.; Vaunat, J. Fast physically-based model for rainfall-induced landslide susceptibility assessment at regional scale. Catena 2021, 201, 105213. [Google Scholar] [CrossRef]
- Van Westen, C.J. The modelling of landslide hazards using GIS. Surv. Geophys. 2000, 21, 241–255. [Google Scholar] [CrossRef]
- Huabin, W.; Gangjun, L.; Weiya, X.; Gonghui, W. GIS-based landslide hazard assessment: An overview. Prog. Phys. Geogr. 2005, 29, 548–567. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Park, H.J.; Lee, J.H.; Woo, I.K. Assessment of rainfall-induced shallow landslide susceptibility using a GIS-based probabilistic approach. Eng. Geol. 2013, 161, 1–15. [Google Scholar] [CrossRef]
- Burton, A.; Bathurst, J.C. Physically based modelling of shallow landslide sediment yield at a catchment scale. Environ. Geol. 1998, 35, 89–99. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F. Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Yilmaz, I.; Keskin, I. GIS based statistical and physical approaches to landslide susceptibility mapping (Sebinkarahisar, Turkey). Bull. Eng. Geol. Environ. 2009, 68, 459–471. [Google Scholar]
- Gutierrez-Martin, A. A GIS-physically-based emergency methodology for predicting rainfall-induced shallow landslide zonation. Geomorphology 2020, 359, 107121. [Google Scholar] [CrossRef]
- Ji, J.; Cui, H.; Zhang, T.; Song, J.; Gao, Y. A GIS-based tool for probabilistic physical modelling and prediction of landslides: GIS-FORM landslide susceptibility analysis in seismic areas. Landslides 2022, 19, 2213–2231. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Saito, H.; Nakayama, D.; Matsuyama, H. Relationship between the initiation of a shallow landslide and rainfall intensity—Duration thresholds in Japan. Geomorphology 2010, 118, 167–175. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: Proposing hydro-meteorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Ma, T.; Li, C.; Lu, Z.; Wang, B. An effective antecedent precipitation model derived from the power-law relationship between landslide occurrence and rainfall level. Geomorphology 2014, 216, 187–192. [Google Scholar] [CrossRef]
- Pennington, C.; Dijkstra, T.; Lark, M.; Dashwood, C.; Harrison, A.; Freeborough, K. Antecedent precipitation as a potential proxy for landslide incidence in South West United Kingdom. In Landslide Science for a Safer Geoenvironment: Vol. 1: The International Programme on Landslides (IPL); Springer International Publishing: New York, NY, USA, 2014; pp. 253–259. [Google Scholar]
- Zhao, B.; Dai, Q.; Han, D.; Dai, H.; Mao, J.; Zhuo, L.; Rong, G. Estimation of soil moisture using modified antecedent precipitation index with application in landslide predictions. Landslides 2019, 16, 2381–2393. [Google Scholar] [CrossRef]
- Hong, M.; Kim, J.; Jeong, S. Rainfall intensity-duration thresholds for landslide prediction in South Korea by considering the effects of antecedent rainfall. Landslides 2018, 15, 523–534. [Google Scholar] [CrossRef]
- De Luca, D.L.; Versace, P. A comprehensive framework for empirical modeling of landslides induced by rainfall: The Generalized FLaIR Model (GFM). Landslides 2017, 14, 1009–1030. [Google Scholar] [CrossRef]
- Sirangelo, B.; Versace, P. A real time forecasting model for landslides triggered by rainfall. Meccanica 1996, 31, 73–85. [Google Scholar] [CrossRef]
- Capparelli, G.; Biondi, D.; De Luca, D.L.; Versace, P. Hydrological and complete models for forecasting landslides triggered by rainfalls. Proc. First Ital. Workshop Landslides 2009, 1, 162–173. [Google Scholar]
- Capparelli, G.; Versace, P. FLaIR and SUSHI: Two mathematical models for early warning of landslides induced by rainfall. Landslides 2011, 8, 67–79. [Google Scholar] [CrossRef]
- Na, W.; Yoo, C. Evaluation of rainfall temporal distribution models with annual maximum rainfall events in Seoul, Korea. Water 2018, 10, 1468. [Google Scholar] [CrossRef] [Green Version]
- Alfieri, L.; Laio, F.; Claps, P. A simulation experiment for optimal design hyetograph selection. Hydrol. Process. Int. J. 2008, 22, 813–820. [Google Scholar] [CrossRef]
- D’Odorico, P.; Fagherazzi, S.; Rigon, R. Potential for landsliding: Dependence on hyetograph characteristics. J. Geophys. Res. Earth Surf. 2005, 110, F01007. [Google Scholar] [CrossRef] [Green Version]
- Ibsen, M.-L.; Casagli, N. Rainfall patterns and related landslide incidence in the Porretta-Vergato region, Italy. Landslides 2004, 1, 143–150. [Google Scholar] [CrossRef]
- Tsai, T.-L. The influence of rainstorm pattern on shallow landslide. Environ. Geol. 2008, 53, 1563–1569. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Wang, J.-K. Examination of influences of rainfall patterns on shallow landslides due to dissipation of matric suction. Environ. Earth Sci. 2011, 63, 65–75. [Google Scholar] [CrossRef]
- Ran, Q.; Hong, Y.; Li, W.; Gao, J. A modelling study of rainfall-induced shallow landslide mechanisms under different rainfall characteristics. J. Hydrol. 2018, 563, 790–801. [Google Scholar] [CrossRef]
- Fan, L.; Lehmann, P.; Zheng, C.; Or, D. Rainfall intensity temporal patterns affect shallow landslide triggering and hazard evolution. Geophys. Res. Lett. 2020, 47, e2019GL085994. [Google Scholar] [CrossRef]
- Acharya, G.; De Smedt, F.; Long, N.T. Assessing landslide hazard in GIS: A case study from Rasuwa, Nepal. Bull. Eng. Geol. Environ. 2006, 65, 99–107. [Google Scholar] [CrossRef]
- Yen, B.C.; Chow, V.T. Design hyetographs for small drainage structures. J. Hydraul. Div. 1980, 106, 1055–1076. [Google Scholar] [CrossRef]
- Mononobe, N. Hydraulics; Iwanami Shoten: Chiyoda, Japan, 1993; pp. 351–356. [Google Scholar]
- Jeong, J.H.; Yoon, Y.N. Design Practices for Water Resources; Goomi Press: Seoul, Republic of Korea, 2007. (In Korean) [Google Scholar]
- Danasla, M.A.; Kusuma, G.J.; Tuheteru, E.J.; Gautama, R.S. Hydrology model establishment of pit Lake: Extreme event rainfall data analysis. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bandung, Indonesia, 23–24 June 2021; Volume 883, p. 012048. [Google Scholar]
- Yoo, C.; Jun, C.; Park, C. Effect of rainfall temporal distribution on the conversion factor to convert the fixed-interval into true-interval rainfall. J. Hydrol. Eng. 2015, 20, 04015018. [Google Scholar] [CrossRef]
- Prayuda, D.D. Temporal and spatial analysis of extreme rainfall on the slope area of Mt. Merapi. J. Civ. Eng. Forum 2015, 21, 1285–1290. [Google Scholar]
- Priambodo, S.; Montarcih, L.; Suhartanto, E. Hourly rainfall distribution patterns in Java island. MATEC Web Conf. 2019, 276, 04012. [Google Scholar] [CrossRef] [Green Version]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, International ed.; MacGraw-Hill, Inc.: Singapore, 1988; Volume 149. [Google Scholar]
- Viessman, W.; Lewis, G.L.; Knapp, J.W.; Harbaugh, T.E. Introduction to Hydrology; Prentice Hall, Pearson Education, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Azli, M.; Rao, A.R. Development of Huff curves for peninsular Malaysia. J. Hydrol. 2010, 388, 77–84. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, S.; Regueiro, R.A. Instability of partially saturated soil slopes due to alteration of rainfall pattern. Eng. Geol. 2012, 147, 28–36. [Google Scholar] [CrossRef]
- KGS (Korean Geotechnical Society). Final Report on the Cause of Landslides in Umyeonsan(Mt.) Area and the Establishment of Restoration Measures; Report No. KGS11-250; Korean Geotechnical Society: Seoul, Republic of Korea, 2011. (In Korean) [Google Scholar]
- SI (The Seoul Institute). Final Report on the Cause of Landslides in Umyeonsan(Mt.)—Complementary Investigation; Report No. 51-6110000-000649-01; The Seoul Institute: Seoul, Republic of Korea, 2014. (In Korean)
- Ministry of Construction and Transportation (MOCT). 1999 Report on the Development of Water Resources Management Techniques: Design Rainfall Temporal Distribution; Ministry of Construction and Transportation: Seoul, Republic of Korea, 2000. (In Korean)
- Ministry of Land, Transport and Maritime Affairs (MLTM). Research on the Improvement of Probability Rainfall; Ministry of Land, Transport and Maritime Affair: Seoul, Republic of Korea, 2019. (In Korean)
- Yoo, C.; Na, W. Analysis of a Conventional Huff Model at Seoul Station and Proposal of an Improvisation Method. J. Korean Soc. Hazard. Mitig. 2019, 19, 43–55. (In Korean) [Google Scholar] [CrossRef]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wiley Interdiscip. Rev. Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Tsai, T.L.; Yang, J.C. Modeling of rainfall-triggered shallow landslide. Environ. Geol. 2006, 50, 525–534. [Google Scholar] [CrossRef]
- Yang, W.Y.; Li, D.; Sun, T.; Ni, G.H. Saturation-excess and infiltration-excess runoff on green roofs. Ecol. Eng. 2015, 74, 327–336. [Google Scholar] [CrossRef]
- Wicki, A.; Lehmann, P.; Hauck, C.; Seneviratne, S.I.; Waldner, P.; Stähli, M. Assessing the potential of soil moisture measurements for regional landslide early warning. Landslides 2020, 17, 1881–1896. [Google Scholar] [CrossRef] [Green Version]
- Jungerius, P.D.; Ten Harkel, M.J. The effect of rainfall intensity on surface runoff and sediment yield in the grey dunes along the Dutch coast under conditions of limited rainfall acceptance. Catena 1994, 23, 269–279. [Google Scholar] [CrossRef] [Green Version]

| Factor of Safety | Slope Stability | Remarks |
|---|---|---|
| FS > 1.5 | Stable | Only major destabilizing factors lead to instability |
| 1.25 < FS < 1.5 | Moderately stable | Moderate destabilizing factors lead to instability |
| 1 < FS < 1.25 | Quasi-stable | Minor destabilizing factors can lead to instability |
| FS < 1 | Unstable | Stabilizing factors are needed for stability |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, W.; Jun, C.; Kim, S.Y. Influence of Rainfall Pattern on Wetness Index for Infinite Slope Stability Analysis. Water 2023, 15, 2535. https://doi.org/10.3390/w15142535
Na W, Jun C, Kim SY. Influence of Rainfall Pattern on Wetness Index for Infinite Slope Stability Analysis. Water. 2023; 15(14):2535. https://doi.org/10.3390/w15142535
Chicago/Turabian StyleNa, Wooyoung, Changhyun Jun, and Sang Yeob Kim. 2023. "Influence of Rainfall Pattern on Wetness Index for Infinite Slope Stability Analysis" Water 15, no. 14: 2535. https://doi.org/10.3390/w15142535





