Application of the Standardised Streamflow Index for Hydrological Drought Monitoring in the Western Cape Province, South Africa: A Case Study in the Berg River Catchment
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Streamflow Data
2.3. Rainfall Data
3. Methods
3.1. SSI Calculation
3.2. PDFs Considered for SSI Calculation
| Probability Distribution Function (PDF) Used for SSI Calculation in the BRC | PDF Equations | |
|---|---|---|
| Log-logistic [40,46] | (2) | |
| , , | ||
| Log-Normal [40,46] | (3) | |
| θ ≈ standard normal cumulative distribution function. such that . is the Gauss error function such that and . | ||
| Pearson Type III [40,46] | (4) | |
| If , then , leading to If , then ; such that , and | ||
| Weibull [40,46] | (5) | |
| , , | ||
| Gamma [34,38] | (6) | |
| α > 0 and β > 0 are the estimated shape and scale parameters, x > 0 is the streamflow (m3/s), and Γ (α) is the Gamma PDF such that, . | ||
3.3. SSI Computation Using R Software Package
3.4. Evaluation of Best Fitting PDFs for SSI Computation
3.5. Evaluation of the Correlation between the SSI Computed Using the Selected PDFs
4. Results
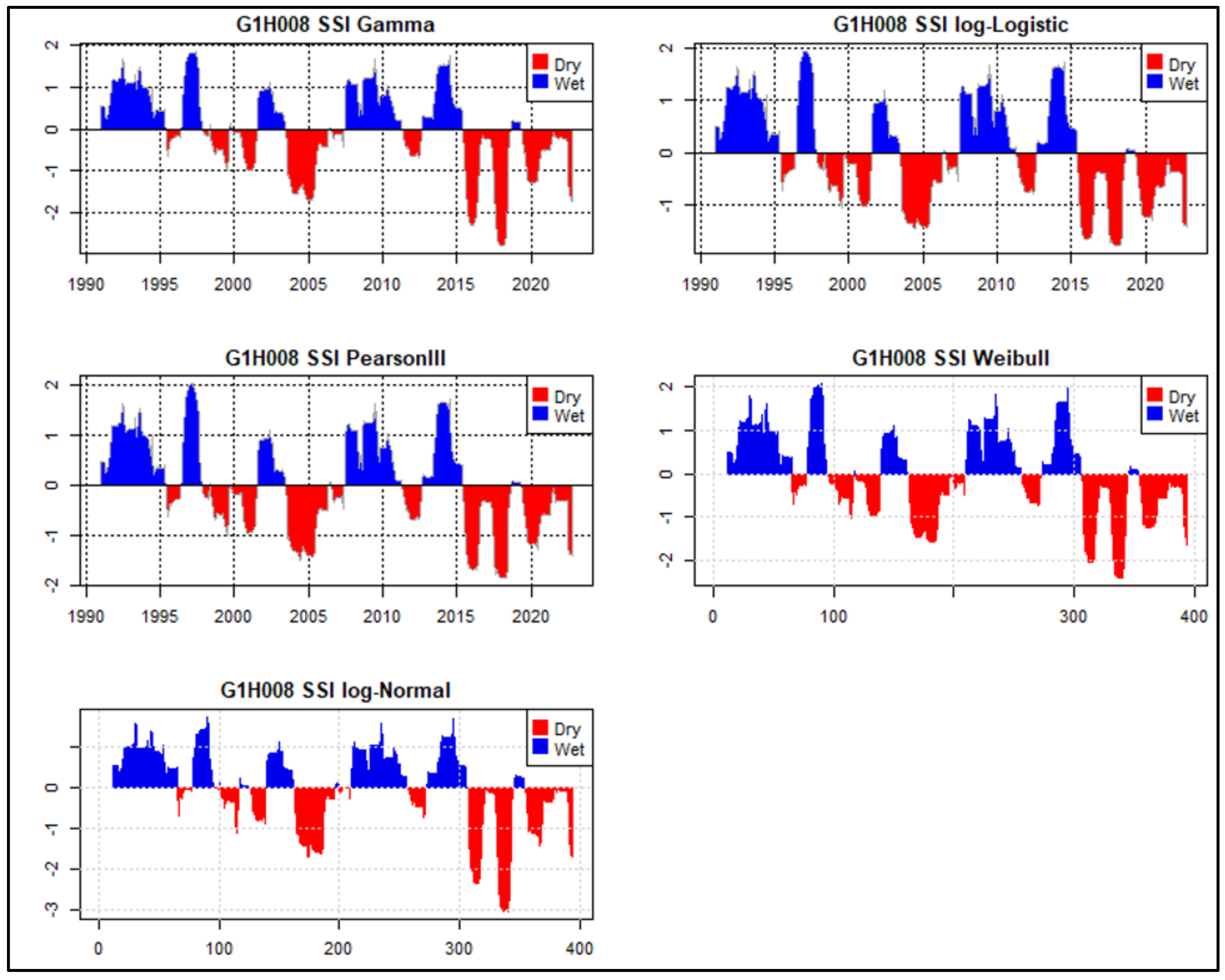
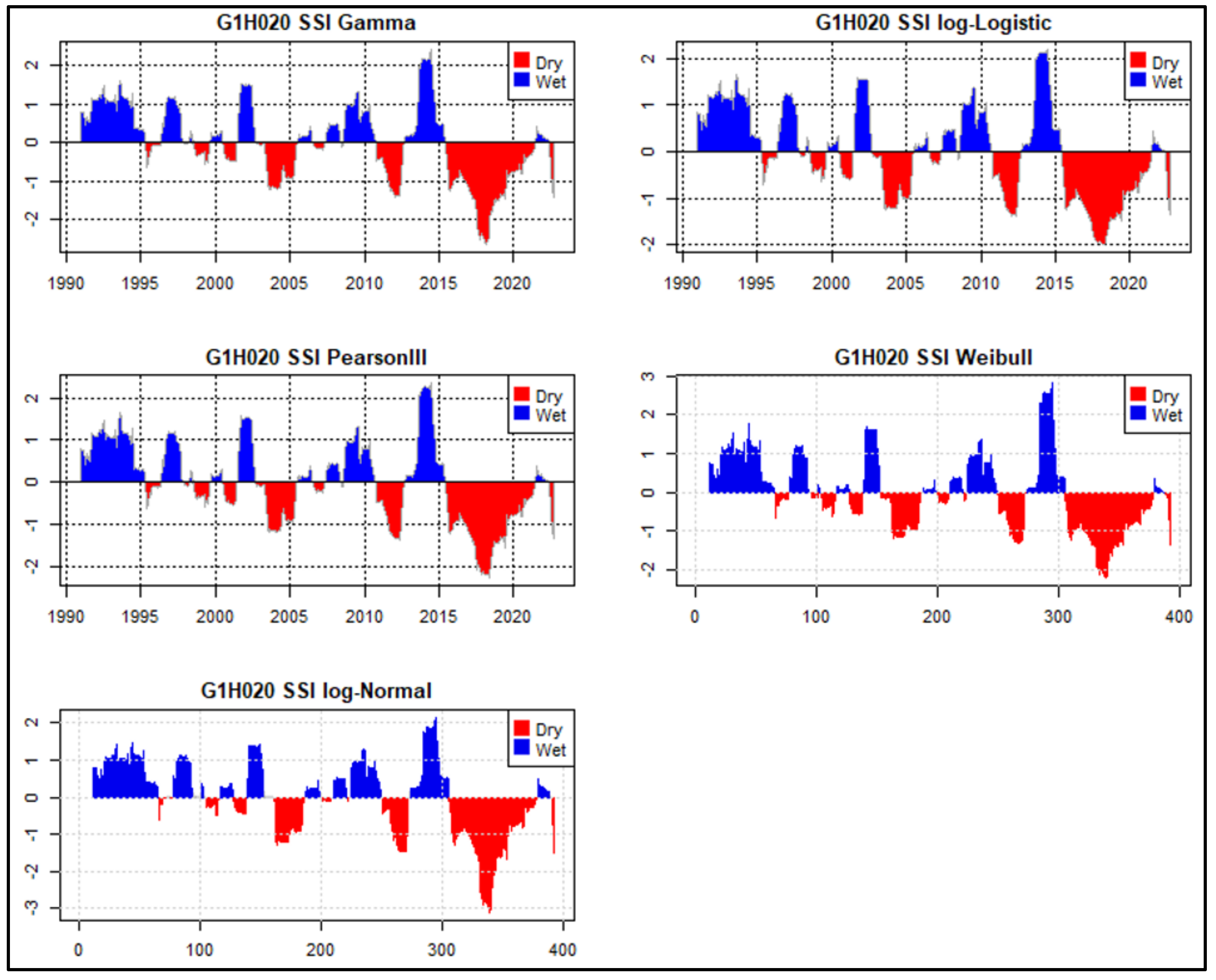
4.1. SSI Calculation Using the Selected PDFs
4.2. The S-W Test for Normality on the SSI Calculated Using the Selected PDFs
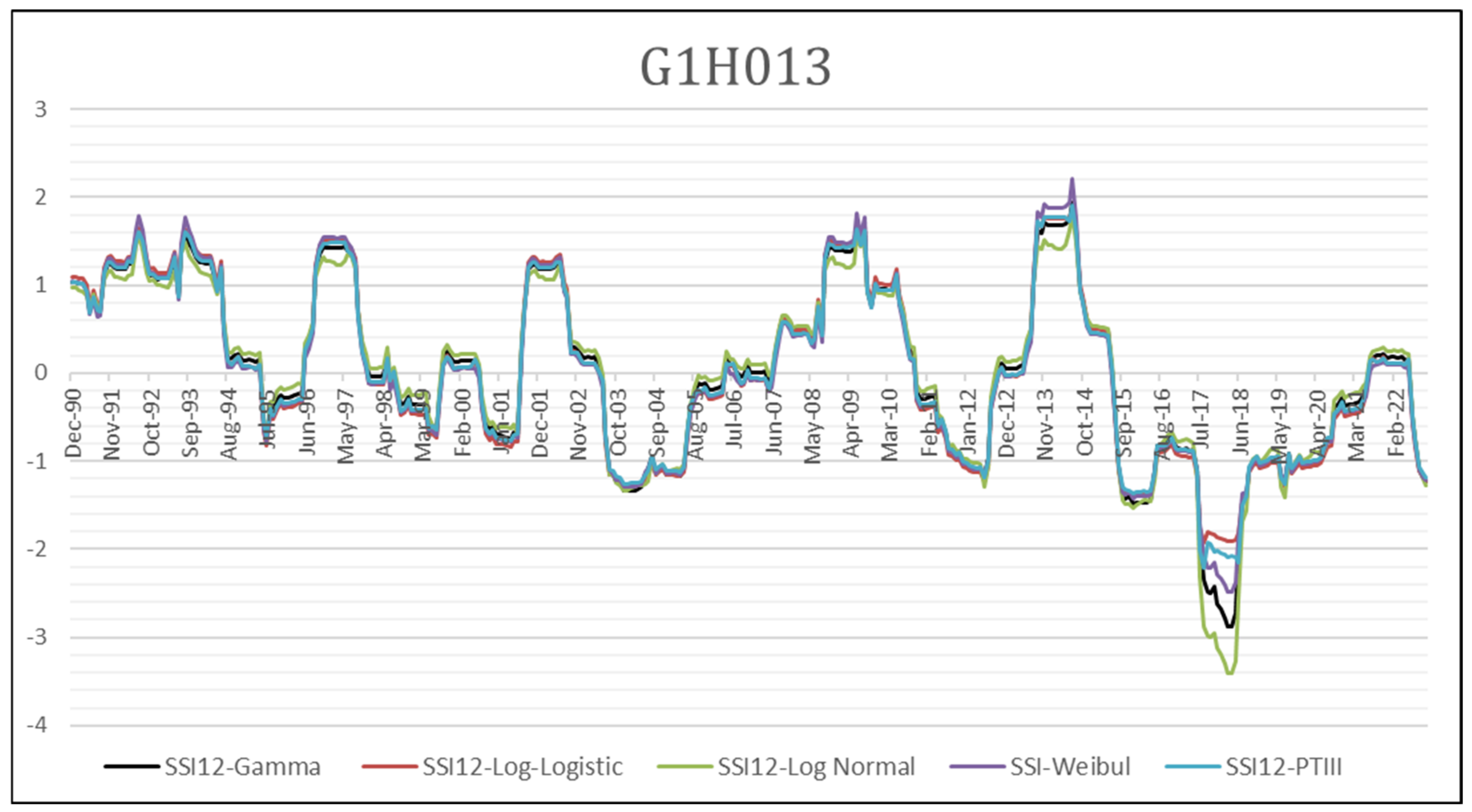
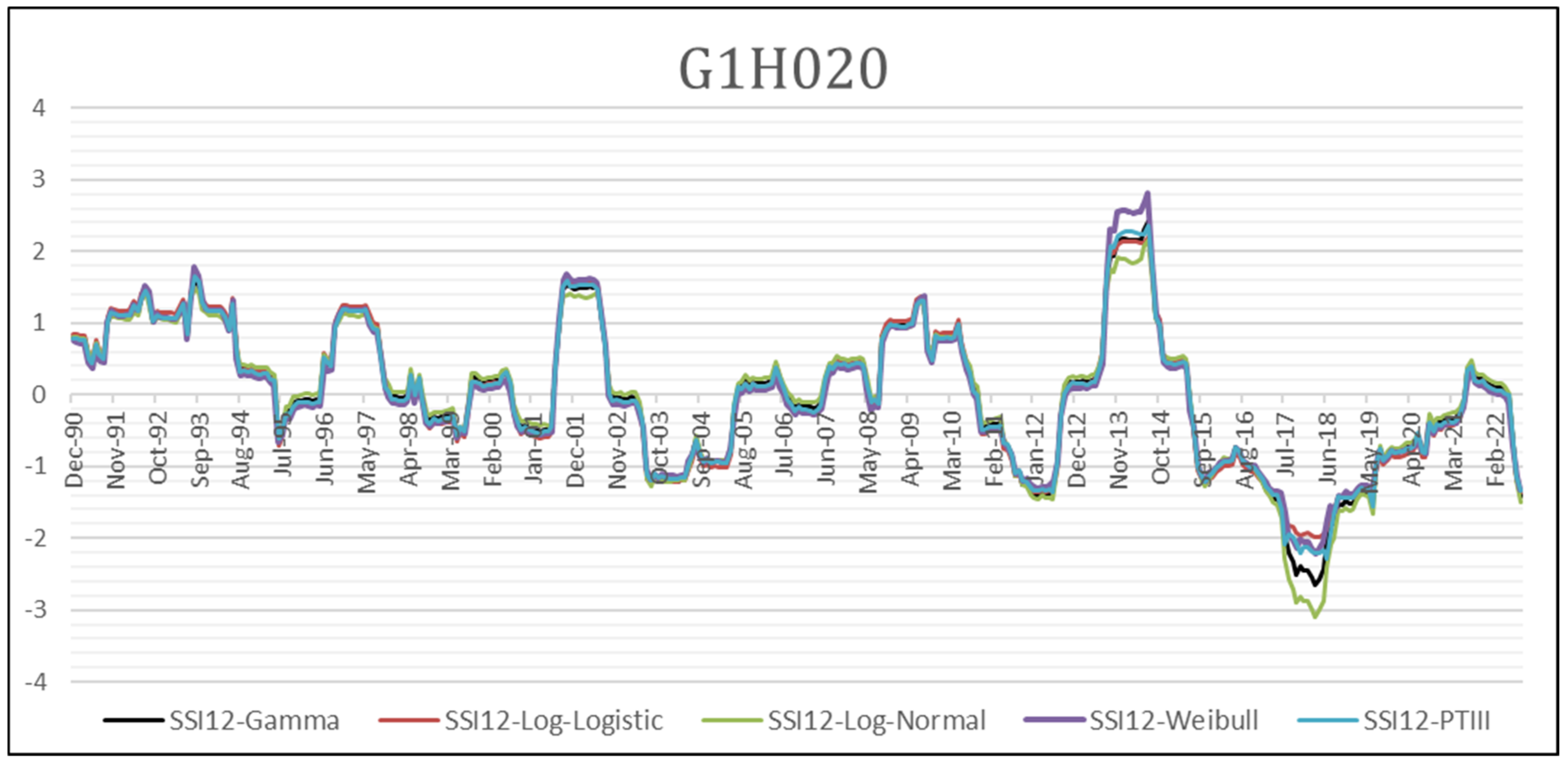
4.3. Visual Inspection of the SSI Calculated Using the Selected PDFs
4.4. Evaluation of the Correlation between the SSI Computed Using the Selected PDFs
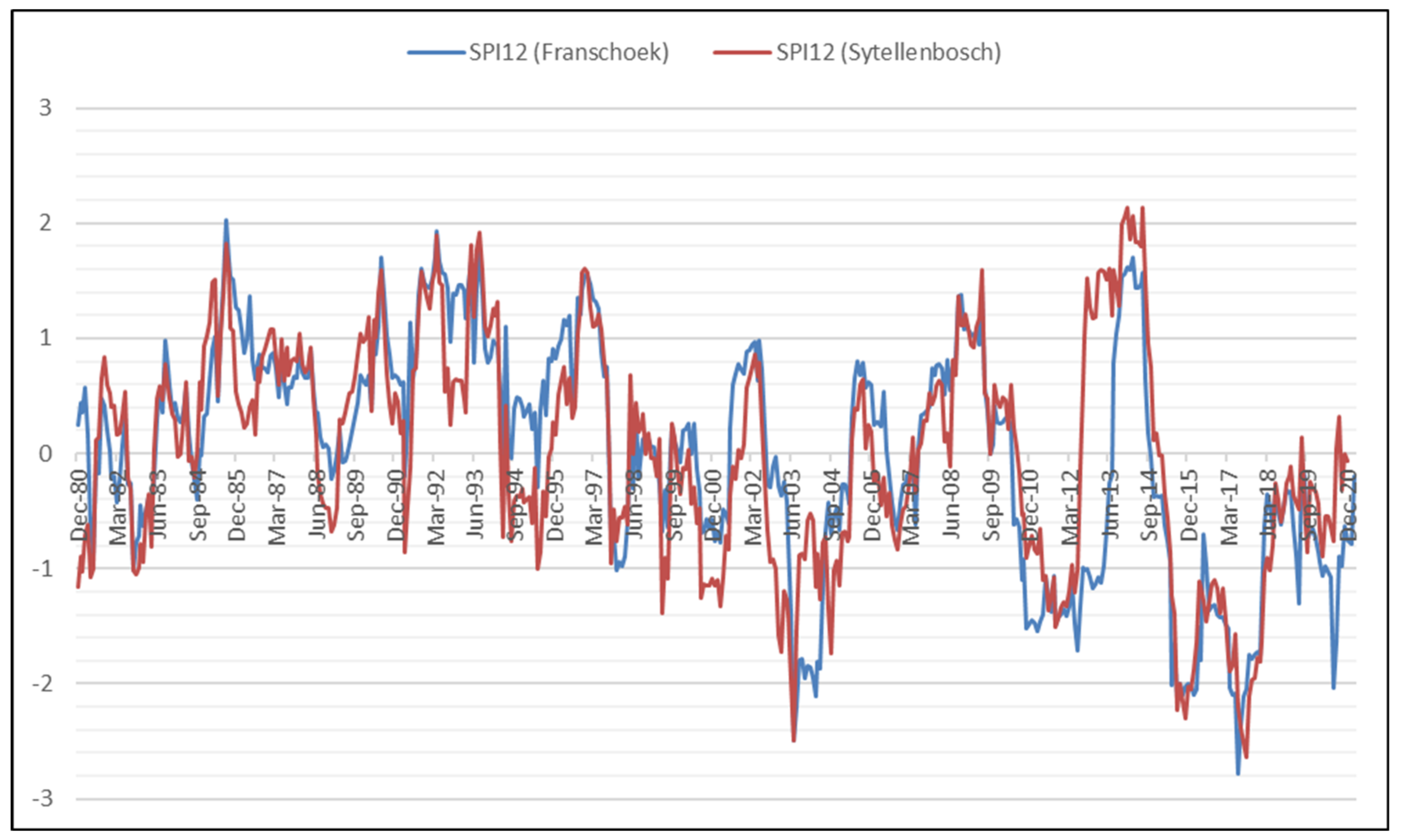
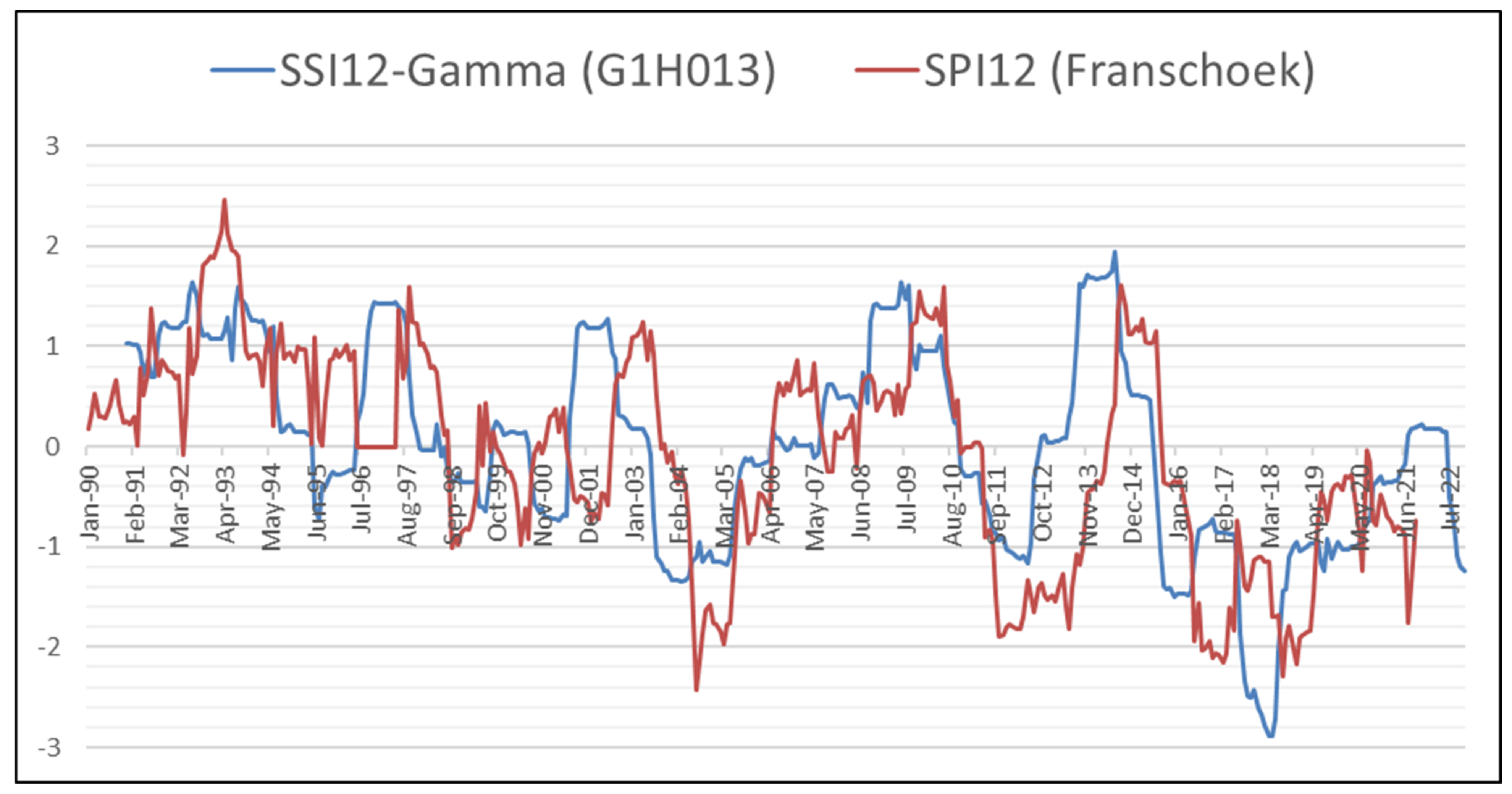
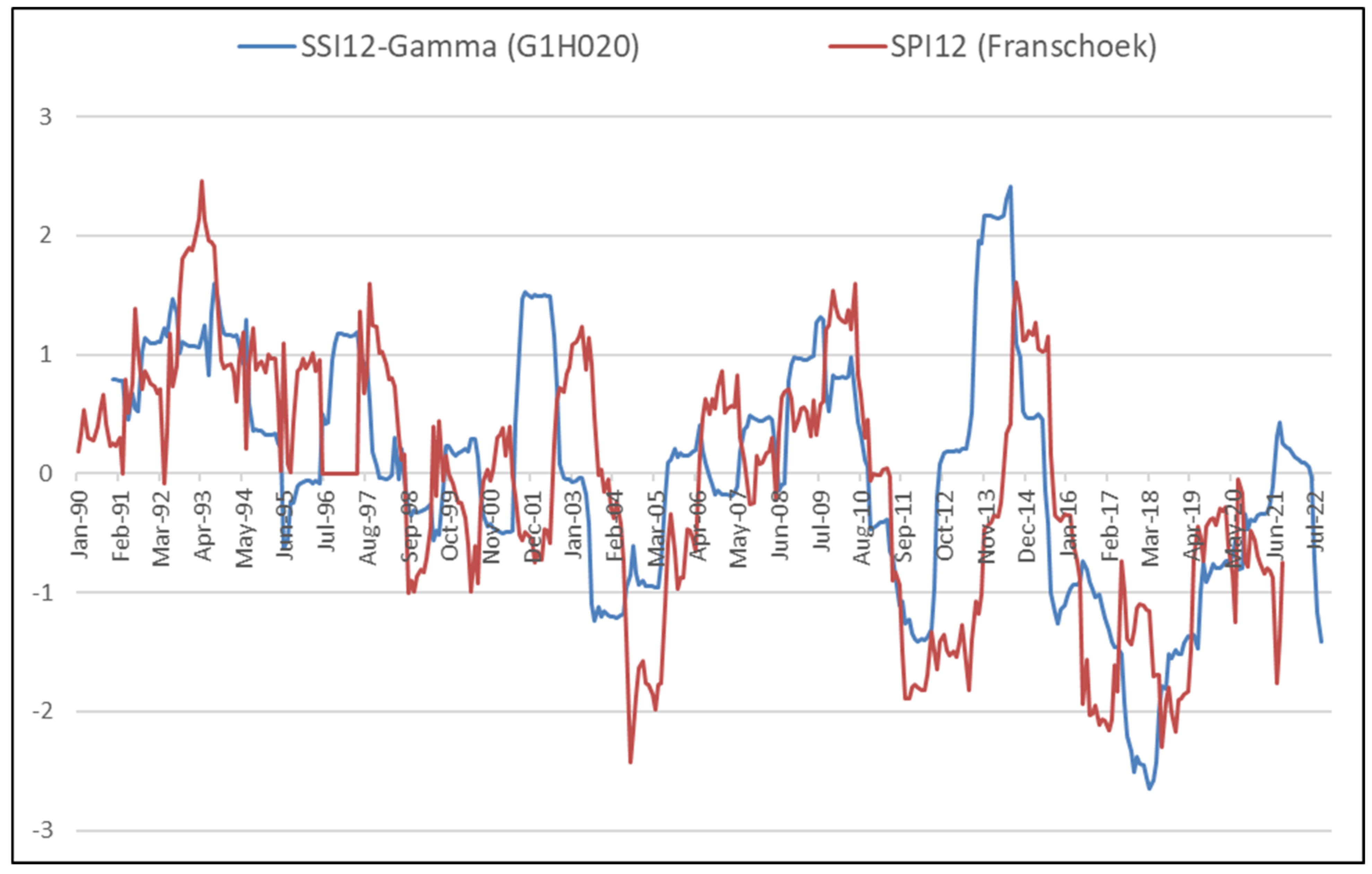
4.5. Comparison of the SSI with SPI Results
4.6. Drought Assessment Using the SSI Calculated Using the Gamma, Log-Normal and Weibull PDFs
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mukhawana, M.B.; Kanyerere, T.; Kahler, D. Review of In-Situ and Remote Sensing-Based Indices and Their Applicability for Integrated Drought Monitoring in South Africa. Water 2023, 15, 240. [Google Scholar] [CrossRef]
- Baker, L.J.; Hannaford, J.; Parry, S.; Smith, K.A.; Tanguy, M.; Prudhomme, C. Historic hydrological droughts 1891–2015: Systematic characterization for a diverse set of catchments across the UK. Hydrol. Earth Syst. Sci. Discuss. 2019, 23, 4583–4602. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Hong, Y.; Bednarczyk, C.N.; Yong, B.; Shafer, M.A.; Riley, R.; Hocker, J.E. Hydro-Climatological Drought Analyses and Projections Using Meteorological and Hydrological Drought Indices: A Case Study in Blue River Basin, Oklahoma. Water Resour. Manag. 2012, 26, 2761–2779. [Google Scholar] [CrossRef]
- Botai, J.O.; Botai, C.M.; de Wit, J.P.; Muthoni, M.; Adeola, A.M. Analysis of Drought Progression Physiognomies in South Africa. Water 2019, 11, 299. [Google Scholar] [CrossRef] [Green Version]
- Botai, C.M.; Botai, J.O.; De Wit, J.P.; Ncongwane, K.P.; Adeola, A.M. Drought Characteristics over the Western Cape Province, South Africa. Water 2017, 9, 876. [Google Scholar] [CrossRef] [Green Version]
- Luetkemeier, R.; Stein, L.; Drees, L.; Liehr, S. Blended Drought Index: Integrated Drought Hazard Assessment in the Cuvelai-Basin. Climate 2017, 5, 51. [Google Scholar] [CrossRef] [Green Version]
- Van Zyl, K. Lessons on Drought in South Africa. Discussion Paper for Drought Dialogue at Elsenburg. 2016. Available online: https://www.greenagri.org.za/assets/documents-/Drought-dialogue-2016-/Mnr-Kosie-van-Zyl.pdf (accessed on 23 April 2020).
- Serdeczny, O.; Adams, S.; Baarsch, F.; Coumou, D.; Robinson, A.; Hare, W.; Schaeffer, M.; Perrette, M.; Reinhardt, J. Climate change impacts in Sub-Saharan Africa: From physical changes to their social repercussions. Reg. Environ. Chang. 2017, 17, 1585–1600. [Google Scholar] [CrossRef]
- Hao, Z.; Aghakouchak, A. A Nonparametric Multivariate Multi-Index Drought Monitoring Framework. Special Advances in Drought Monitoring Collection. J. Hydrometeorol. 2014, 15, 89–101. [Google Scholar] [CrossRef]
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef] [Green Version]
- Cairns, J.E.; Hellin, J.; Sonder, K.; Araus, J.L.; MacRobert, J.F.; Thierfelder, C.; Prasanna, B.M. Adapting maize production to climate change in sub-Saharan Africa. Food Secur. 2013, 5, 345–360. [Google Scholar] [CrossRef] [Green Version]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef] [Green Version]
- Yihdego, Y.; Vaheddoost, B.; Al-Weshah, R.A. Drought indices and indicators revisited. Arab. J. Geosci. 2019, 12, 69. [Google Scholar] [CrossRef]
- Chang, J.; Li, Y.; Wang, Y.; Yuan, M. Copula-based drought risk assessment combined with an integrated index in the Wei River Basin, China. J. Hydrol. 2016, 540, 824–834. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; Dlamini, L.C.; Zwane, N.S.; Phaduli, E. Characteristics of Droughts in South Africa: A Case Study of Free State and Northwest Provinces. Water 2016, 8, 439. [Google Scholar] [CrossRef] [Green Version]
- Pathak, A.A.; Dodamani, B.M.C. Department Comparison of two hydrological drought indices. Perspect. Sci. 2016, 8, 626–628. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Hao, Z.; Aghakouchak, A. Multivariate Standardized Drought Index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Zalokar, L.; Kobold, M.; Šraj, M. Investigation of Spatial and Temporal Variability of Hydrological Drought in Slovenia Using the Standardised Streamflow Index (SSI). Water 2021, 13, 3197. [Google Scholar] [CrossRef]
- Svensson, C.; Hannaford, J.; Prosdocimi, I. Statistical distributions for monthly aggregations of precipitation and streamflow in drought indicator applications. Water Resour. Res. 2017, 53, 999–1018. [Google Scholar] [CrossRef] [Green Version]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef] [Green Version]
- Water Research Commission (WRC). Vulnerability, Adaptation to and Coping with Drought: The Case of Commercial and Subsistence Rain Fed Farming in the Eastern Cape. Deliverable 2: Drought Hazard Assessment; KSA4/1002947/2280; Water Research Commission: Lynnwood, WA, USA, 2014. [Google Scholar]
- World Meteorological Organization (WMO); Global Water Partnership (GWP). Handbook of Drought Indicators and Indices; Svoboda, M., Fuchs, B.A., Eds.; Integrated Drought Management Tools and Guidelines Series 2; Integrated Drought Management Programme (IDMP): Geneva, Switzerland, 2016. [Google Scholar]
- Nkamisa, M.; Ndhleve, S.; Nakin, M.D.; Mngeni, A.; Kabiti, H.M. Analysis of trends, recurrences, severity and frequency of droughts using standardised precipitation index: Case of OR Tambo District Municipality, Eastern Cape, South Africa. Jàmbá J. Disaster Risk Stud. 2022, 14, a1147. [Google Scholar] [CrossRef]
- Adeola, O.M.; Masinde, M.; Botai, J.O.; Adeola, A.M.; Botai, C.M. An Analysis of Precipitation Extreme Events Based on the SPI and EDI Values in the Free State Province, South Africa. Water 2021, 13, 3058. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; Adeola, A.M.; de Wit, J.P.; Ncongwane, K.P.; Zwane, N.N. Drought Risk Analysis in the Eastern Cape Province of South Africa: The Copula Lens. Water 2020, 12, 1938. [Google Scholar] [CrossRef]
- Tfwala, C.; van Rensburg, L.; Schall, R.; Dlamini, P. Drought dynamics and interannual rainfall variability on the Ghaap plateau, South Africa, 1918–2014. Phys. Chem. Earth 2018, 107, 1–7. [Google Scholar] [CrossRef]
- Smith, T.; Fitchett, J.M. Drought challenges for nature tourism in the Sabi Sands Game Reserve in the eastern region of South Africa. Afr. J. Range Forage Sci. 2020, 37, 107–117. [Google Scholar] [CrossRef]
- Mathivha, F.I.; Tshipala, N.N.; Nkuna, Z. The relationship between drought and tourist arrivals: A case study of Kruger National Park, South Africa. Jàmbá J. Disaster Risk Stud. 2017, 9, a471. [Google Scholar] [CrossRef] [Green Version]
- Mazibuko, S.; Mukwada, G.; Moeletsi, M. Assessing the frequency of drought/flood severity in the Luvuvhu River catchment, Limpopo Province, South Africa. Water SA 2021, 47, 172–184. [Google Scholar] [CrossRef]
- Rouault, M.; Richard, Y. Intensity and spatial extension of drought in South Africa at different time scales. Water SA 2004, 29, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Yue, W.; Wang, T.; Zheng, N.; Wu, L. Assessing the use of standardized groundwater index for quantifying groundwater drought over the conterminous US. J. Hydrol. 2021, 598, 126227. [Google Scholar] [CrossRef]
- Guttman, N.B. Accepting the Standardized Precipitation Index: A Calculation Algorithm. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- World Meteorological Organisation (WMO). Handbook of Drought Indicators and Indices; WMO-No. 1173; WMO: Geneva, Switzerland, 2016. [Google Scholar]
- Wu, J.; Chen, X.; Yao, H.; Zhang, D. Multi-timescale assessment of propagation thresholds from meteorological to hydrological drought. Sci. Total. Environ. 2021, 765, 144232. [Google Scholar] [CrossRef] [PubMed]
- Salimi, H.; Asadi, E.; Darbandi, S. Meteorological and hydrological drought monitoring using several drought indices. Appl. Water Sci. 2021, 11, 1–10. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; de Wit, J.P.; Ncongwane, K.P.; Murambadoro, M.; Barasa, P.M.; Adeola, A.M. Hydrological Drought Assessment Based on the Standardized Streamflow Index: A Case Study of the Three Cape Provinces of South Africa. Water 2021, 13, 3498. [Google Scholar] [CrossRef]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Kargar, K.; Mosavi, A.; Nabipour, N.; Chau, K.W. Predicting Standardized Streamflow index for hydrological drought using machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Begueria, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; Lopez-Moreno, J.I.; Azorin-Molina, C.; Revuelto, J.; Moran-Tejeda, E.; Sanchez-Lorenzo, A. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Interact. 2012, 16, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Sutanto, S.J.; Van Lanen, H.A.J. Streamflow drought: Implication of drought definitions and its application for drought forecasting. Hydrol. Earth Syst. Sci. 2021, 25, 3991–4023. [Google Scholar] [CrossRef]
- Tijdeman, E.; Stahl, K.; Tallaksen, L.M. Drought Characteristics Derived Based on the Standardized Streamflow Index: A Large Sample Comparison for Parametric and Nonparametric Methods. Water Resour. Res. 2020, 56, e2019WR026315. [Google Scholar] [CrossRef]
- Li, Q.; He, P.; He, Y.; Han, X.; Zeng, T.; Lu, G.; Wang, H. Investigation to the relation between meteorological drought and hydrological drought in the upper Shaying River Basin using wavelet analysis. Atmos. Res. 2018, 234, 104743. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Clim. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Singh, V.P.; Guo, F.X.Y. Parameter estimation for 3-parameter log-logistic distribution (LLD3) by Pome. Stoch. Hydrol. Hydraul. 2013, 7, 163–177. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the Correlation Coefficient: A Basic Review. J. Diagn. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef] [Green Version]
- Brühl, J.; Visser, M. The Cape Town drought: A study of the combined effectiveness of measures implemented to prevent “Day Zero”. Water Resour. Econ. 2021, 34, 100177. [Google Scholar] [CrossRef]

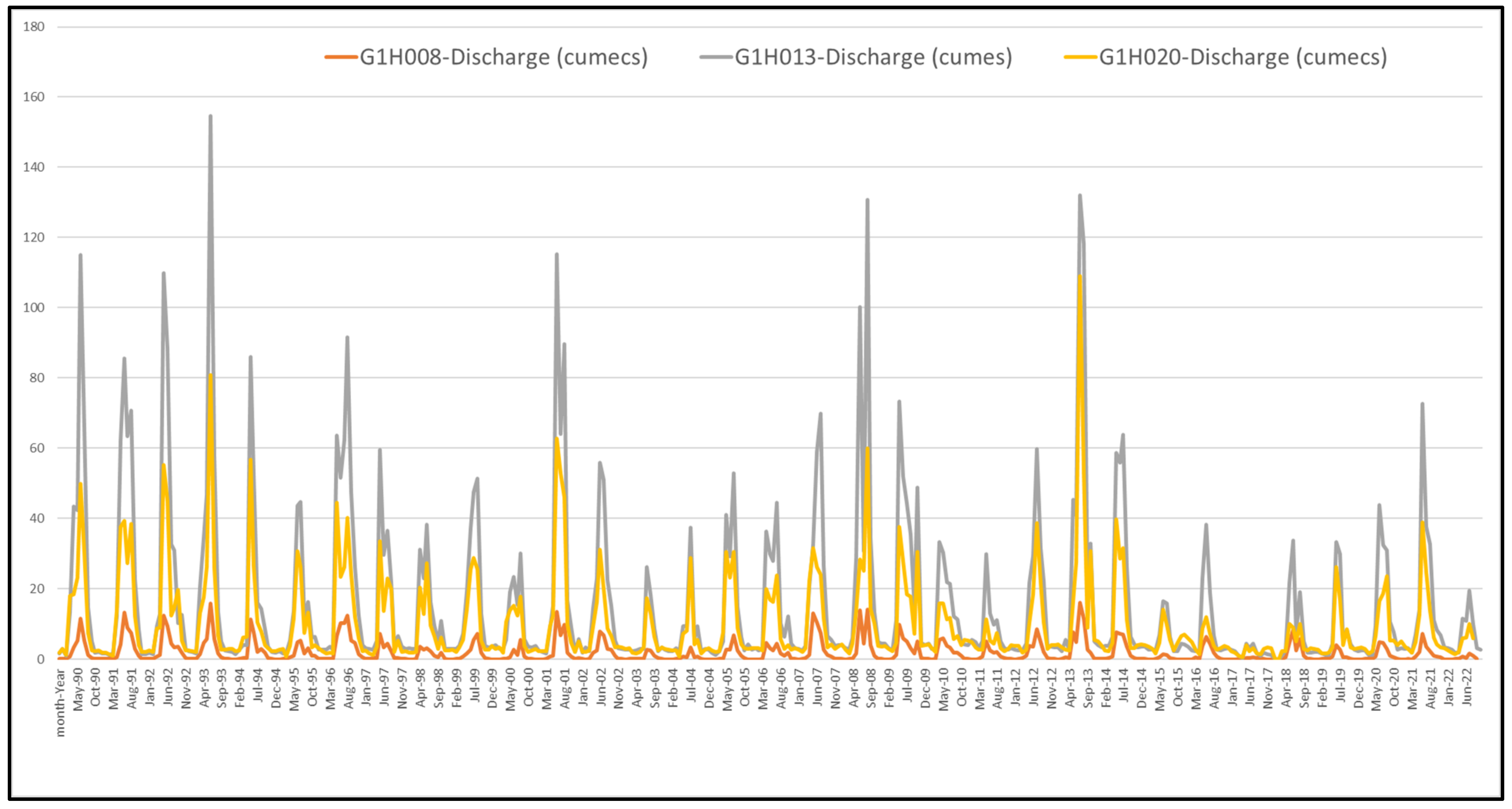
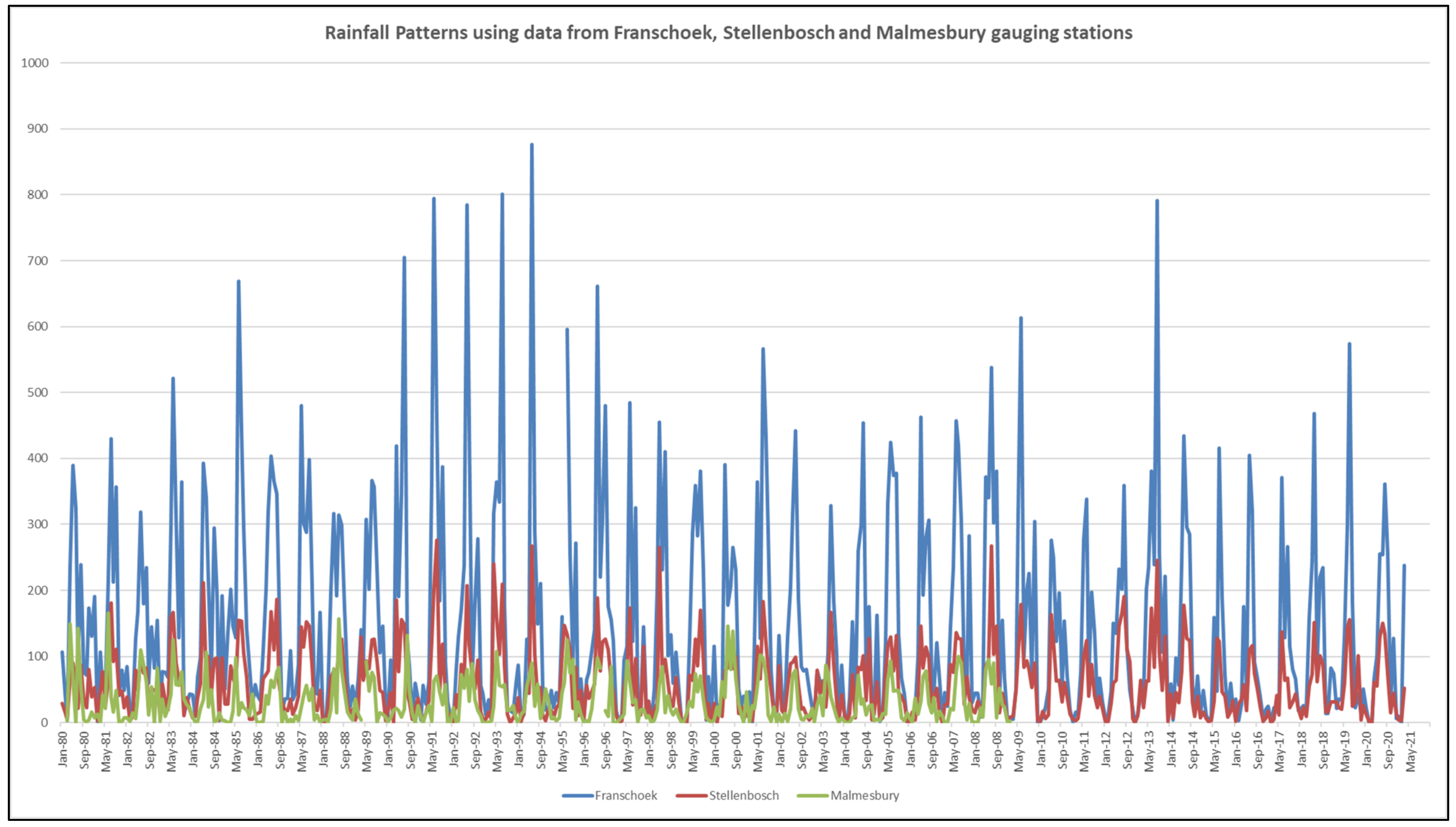




| Streamflow Gauging Station Identity | River | Location Coordinates (Latitude: Longitude) | Period (Years) |
|---|---|---|---|
| G1H008 | Klein Berg | −33.313889:19.074722 | 1990 to 2022 (32 Years) |
| G1H013 | Berg | −33.130833:18.862778 | 1990 to 2022 (32 Years) |
| G1H020 | Berg | −33.707778:18.991111 | 1990 to 2022 (32 Years) |
| SPI/SSI Values | Drought Classification |
|---|---|
| ≥2.00 | Extremely Wet |
| 1.50 to 1.99 | Severely Wet |
| 1.00 to 1,49 | Moderately Wet |
| 0.00 to 0.99 | Mildly Wet |
| 0.00 to −0.99 | Mild Drought |
| −1.00 to −1.49 | Moderate Drought |
| −1.5 to −1.99 | Severe Drought |
| ≤−2.00 | Extreme Drought |
| G1H008 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month-Year | SSI12 Gamma | Drought Classification | SSI12 Log-Logistic | Drought Classification | SSI12 Log-Normal | Drought Classification | SSI12 PTIII | Drought Classification | SSI12 Weibull | Drought Classification |
| November 2004 | −1.6 | Severe | −1.4 | Moderate | −1.5 | Severe | −1.3 | Moderate | −1.5 | Severe |
| December 2004 to April 2005 | −1.6 | Severe | −1.4 | Moderate | −1.6 | Severe | −1.4 | Moderate | −1.6 | Severe |
| May 2005 | −1.6 | Severe | −1.4 | Moderate | −1.6 | Severe | −1.4 | Moderate | −1.5 | Severe |
| June 2005 | −1.6 | Severe | −1.4 | Moderate | −1.5 | Severe | −1.3 | Moderate | −1.5 | Severe |
| Average | −1.6 | Severe | −1.4 | Moderate | −1.6 | Severe | −1.4 | Moderate | −1.6 | Severe |
| G1H008 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month-Year | SSI12 Gamma | Drought Classification | SSI12 Log-Logistic | Drought Classification | SSI1 Log-Normal | Drought Classification | SSI12 PTIII | Drought Classification | SSI12 Weibull | Drought Classification |
| December 2015 to March 2016 | −2.2 | Extreme | −1.6 | Severe | −2.3 | Extreme | −1.6 | Severe | −2.0 | Extreme |
| April 2016 | −2.1 | Extreme | −1.6 | Severe | −2.2 | Extreme | −1.6 | Severe | −1.9 | Severe |
| Average | −2.2 | Extreme | −1.6 | Severe | −2.3 | Extreme | −1.6 | Severe | −2.0 | Extreme |
| G1H013 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month-Year | SSI12 Gamma | Drought Classification | SSI12 Log-Logistic | Drought Classification | SSI12 Log-Normal | Drought Classification | SSI12 PTIII | Drought Classification | SSI12 Weibull | Drought Classification |
| November 2003 | −1.2 | Moderate | −1.2 | Moderate | −1.3 | Moderate | −1.2 | Moderate | −1.2 | Moderate |
| December 2003 to May 2004 | −1.3 | Moderate | −1.3 | Moderate | −1.3 | Moderate | −1.3 | Moderate | −1.3 | Moderate |
| June 2004 | −1.1 | Moderate | −1.2 | Moderate | −1.3 | Moderate | −1.2 | Moderate | −1.1 | Moderate |
| July 2004 | −1.1 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| August 2004 | −1.0 | Moderate | −1.0 | Moderate | −1.0 | Moderate | −1.0 | Moderate | −1.0 | Moderate |
| September 2004 | −1.1 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| October 2004 | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| November 2004 | −1.0 | Moderate | −1.1 | Moderate | −1.0 | Moderate | −1.0 | Moderate | −1.0 | Moderate |
| December 2004 to April 2005 | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| May 2005 | −1.2 | Moderate | −1.1 | Moderate | −1.0 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| Average | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.2 | Moderate |
| G1H013 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month-Year | SSI12 Gamma | Drought Classification | SSI12 Log-Logistic | Drought Classification | SSI12 Log-Normal | Drought Classification | SSI12 PTIII | Drought Classification | SSI12 Weibull | Drought Classification |
| August 2017 | −2.3 | Extreme | −1.9 | Severe | −2.9 | Extreme | −2.2 | Extreme | −2.1 | Extreme |
| September 2017 to October 2017 | −2.5 | Extreme | −1.8 | Severe | −3.0 | Extreme | −1.9 | Severe | −2.2 | Extreme |
| November 2017 | −2.4 | Extreme | −1.8 | Severe | −3.0 | Extreme | −2.0 | Extreme | −2.2 | Extreme |
| December 2017 | −2.6 | Extreme | −1.9 | Severe | −3.1 | Extreme | −2.0 | Extreme | −2.3 | Extreme |
| January 2018 | −2.7 | Extreme | −1.9 | Severe | −3.2 | Extreme | −2.0 | Extreme | −2.3 | Extreme |
| February 2018 | −2.8 | Extreme | −1.9 | Severe | −3.3 | Extreme | −2.1 | Extreme | −2.4 | Extreme |
| March 2018 to April 2018 | −2.9 | Extreme | −1.9 | Severe | −3.4 | Extreme | −2.1 | Extreme | −2.5 | Extreme |
| May 2018 | −2.7 | Extreme | −1.9 | Severe | −3.3 | Extreme | −2.1 | Extreme | −2.4 | Extreme |
| Average | −2.6 | Extreme | −1.9 | Severe | −3.2 | Extreme | −2.1 | Extreme | −2.3 | Extreme |
| G1H013 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month-Year | SSI12 Gamma | Drought Classification | SSI12 Log-Logistic | Drought Classification | SSI12 Log-Normal | Drought Classification | SSI12 PTIII | Drought Classification | SSI12 Weibull | Drought Classification |
| July 2003 | −1.1 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.0 | Moderate |
| August 2003 | −1.2 | Moderate | −1.2 | Moderate | −1.3 | Moderate | −1.2 | Moderate | −1.2 | Moderate |
| September 2003 | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| October 2003 | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate |
| November 2003 | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| December 2003 to May 2004 | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate |
| June 2004 | −1.0 | Moderate | −1.0 | Moderate | −1.0 | Moderate | −1.0 | Moderate | −0.9 | Mild |
| Average | −1.2 | Moderate | −1.2 | Moderate | −1.2 | Moderate | −1.1 | Moderate | −1.1 | Moderate |
| G1H013 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month-Year | SSI12 Gamma | Drought Classification | SSI12 Log-Logistic | Drought Classification | SSI12 Log-Normal | Drought Classification | SSI12 PTIII | Drought Classification | SSI12 Weibull | Drought Classification |
| July 2017 | −1.9 | Severe | −1.8 | Severe | −2.3 | Extreme | −2.1 | Extreme | −1.7 | Severe |
| August 2017 | −2.2 | Extreme | −1.8 | Severe | −2.6 | Extreme | −2.0 | Extreme | −1.9 | Severe |
| September 2017 | −2.3 | Extreme | −1.9 | Severe | −2.7 | Extreme | −2.0 | Extreme | −2.0 | Extreme |
| October 2017 | −2.5 | Extreme | −1.9 | Severe | −2.9 | Extreme | −2.1 | Extreme | −2.1 | Extreme |
| November 2017 | −2.4 | Extreme | −2.0 | Severe | −2.8 | Extreme | −2.2 | Extreme | −2.0 | Extreme |
| December 2017 to January 2018 | −2.4 | Extreme | −1.9 | Severe | −2.9 | Extreme | −2.1 | Extreme | −2.1 | Extreme |
| February 2018 | −2.6 | Extreme | −2.0 | Extreme | −3.0 | Extreme | −2.2 | Extreme | −2.1 | Extreme |
| March 2018 | −2.7 | Extreme | −2.0 | Extreme | −3.1 | Extreme | −2.2 | Extreme | −2.2 | Extreme |
| April 2018 | −2.6 | Extreme | −2.0 | Extreme | −3.0 | Extreme | −2.2 | Extreme | −2.2 | Extreme |
| May 2018 | −2.4 | Extreme | −1.9 | Severe | −2.9 | Extreme | −2.2 | Extreme | −2.1 | Extreme |
| Average | −2.4 | Extreme | −1.9 | Severe | −2.8 | Extreme | −2.1 | Extreme | −2.0 | Extreme |
| Shapiro-Wilk Test for Normality | |||||
|---|---|---|---|---|---|
| Gamma | Log-Logistic | PTIII | Log-Normal | Weibull | |
| G1H008 | W = 0.97464 p-value = 3.06× 10−6 | W = 0.96785 p-value = 1.83× 10−7 | W = 0.97958 p-value = 3.062× 10−5 | W = 0.94277 p-value = 5.416× 10−11 | W = 0.94277 p-value = 5.416× 10−11 |
| G1H013 | W = 0.9717 p-value = 8.386× 10−7 | W = 0.95804 p-value = 5.186× 10−9 | W = 0.97103 p-value = 6.346× 10−7 | W = 0.94802 p-value = 2.293× 10−10 | W = 0.97389 p-value = 2.14× 10−6 |
| G1H020 | W = 0.99019 p-value = 0.01188 | W = 0.98243 p-value = 0.0001341 | W = 0.99018 p-value = 0.01177 | W = 0.97238 p-value = 1.186× 10−6 | W = 0.98534 p-value = 0.0006527 |
| G1H008 | ||||||
|---|---|---|---|---|---|---|
| SSI Gamma | SSI log-Logistic | SSI log-Normal | SSI PTIII | SSI Weibull | Franschoek SPI12 (Gamma) | |
| SSI Gamma | 1 | |||||
| SSI log-Logistic | 0.98223 | 1 | ||||
| SSI log-Normal | 0.984512 | 0.947839 | 1 | |||
| SSI PTIII | 0.986172 | 0.998936 | 0.953691 | 1 | ||
| SSI Weibull | 0.991315 | 0.98774 | 0.977377 | 0.990254 | 1 | |
| Franschoek SPI12 (Gamma) | 0.741493 | 0.750306 | 0.715999 | 0.752611 | 0.754136 | 1 |
| G1H013 | ||||||
| SSI Gamma | SSI log-Logistic | SSI log-Normal | SSI PTIII | SSI Weibull | Franschoek SPI12 (Gamma) | |
| SSI Gamma | 1 | |||||
| SSI log-Logistic | 0.989213 | 1 | ||||
| SSI log-Normal | 0.991976 | 0.965913 | 1 | |||
| SSI PTIII | 0.994384 | 0.998255 | 0.976084 | 1 | ||
| SSI Weibull | 0.995609 | 0.995802 | 0.977003 | 0.998044 | 1 | |
| Franschoek SPI12 (Gamma) | 0.803445 | 0.81042 | 0.782366 | 0.811022 | 0.810208 | 1 |
| G1H020 | ||||||
| SSI Gamma | SSI log-Logistic | SSI log-Normal | SSI PTIII | SSI Weibull | Franschoek SPI12 (Gamma) | |
| SSI Gamma | 1 | |||||
| SSI log-Logistic | 0.994149 | 1 | ||||
| SSI log-Normal | 0.994499 | 0.980957 | 1 | |||
| SSI PTIII | 0.997659 | 0.997659 | 0.987417 | 1 | ||
| SSI Weibull | 0.992818 | 0.993924 | 0.975533 | 0.996049 | 1 | |
| Franschoek SPI12 (Gamma) | 0.817348 | 0.827468 | 0.804458 | 0.82031 | 0.816487 | 1 |
| Streamflow Gauging Station | Drought Period | Average SSI12 | Drought Classification | ||
|---|---|---|---|---|---|
| Gamma | Log-Normal | Weibull | |||
| G1H008 | June 2000 to June 2001 | −0.7 | −0.7 | −0.8 | Mild Drought |
| September 2004 to May 2005 | −1.6 | −1.6 | −1.5 | Severe Drought | |
| September 2015 to April 2016 | −2.1 | −2.2 | −2.0 | Extreme Drought | |
| August 2017 to May 2018 | −2.6 | −2.9 | −2.3 | Extreme Drought | |
| September 2019 to July 2020 | −1.3 | −1.3 | −1.2 | Moderate Drought | |
| Streamflow Gauging Station | Drought Period | Average SSI12 | Drought Classification | ||
|---|---|---|---|---|---|
| Gamma | Log-Normal | Weibull | |||
| G1H013 | August 2000 to June 2001 | −0.6 | −0.6 | −0.7 | Mild Drought |
| August 2003 to May 2005 | −1.2 | −1.2 | −1.2 | Moderate Drought | |
| October 2011 to July 2012 | −1.0 | −1.0 | −1.0 | Moderate Drought | |
| August 2015 to June 2016 | −1.4 | −1.4 | −1.3 | Moderate Drought | |
| July 2017 to June 2018 | −2.5 | −3.0 | −2.2 | Extreme Drought | |
| July 2018 to February 2019 | −1.1 | −1.1 | −1.1 | Moderate Drought | |
| Streamflow Gauging Station | Drought Period | Average SSI12 | Drought Classification | ||
|---|---|---|---|---|---|
| Gamma | Log-Normal | Weibull | |||
| G1H020 | August 2000 to June 2001 | −0.4 | −0.4 | −0.5 | Mild Drought |
| July 2003 to June 2004 | −1.2 | −1.2 | −1.1 | Moderate Drought | |
| August 2011 to July 2012 | −1.3 | −1.3 | −1.2 | Moderate Drought | |
| August 2015 to January 2016 | −1.1 | −1.1 | −1.1 | Moderate Drought | |
| July 2017 to June 2018 | −2.4 | −2.8 | −2.0 | Extreme Drought | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhawana, M.B.; Kanyerere, T.; Kahler, D.; Masilela, N.S. Application of the Standardised Streamflow Index for Hydrological Drought Monitoring in the Western Cape Province, South Africa: A Case Study in the Berg River Catchment. Water 2023, 15, 2530. https://doi.org/10.3390/w15142530
Mukhawana MB, Kanyerere T, Kahler D, Masilela NS. Application of the Standardised Streamflow Index for Hydrological Drought Monitoring in the Western Cape Province, South Africa: A Case Study in the Berg River Catchment. Water. 2023; 15(14):2530. https://doi.org/10.3390/w15142530
Chicago/Turabian StyleMukhawana, Mxolisi Blessing, Thokozani Kanyerere, David Kahler, and Ndumiso Siphosezwe Masilela. 2023. "Application of the Standardised Streamflow Index for Hydrological Drought Monitoring in the Western Cape Province, South Africa: A Case Study in the Berg River Catchment" Water 15, no. 14: 2530. https://doi.org/10.3390/w15142530
APA StyleMukhawana, M. B., Kanyerere, T., Kahler, D., & Masilela, N. S. (2023). Application of the Standardised Streamflow Index for Hydrological Drought Monitoring in the Western Cape Province, South Africa: A Case Study in the Berg River Catchment. Water, 15(14), 2530. https://doi.org/10.3390/w15142530





