Assimilation of Sentinel-2 Biophysical Variables into a Digital Twin for the Automated Irrigation Scheduling of a Vineyard
Abstract
:1. Introduction
2. Materials and Methods
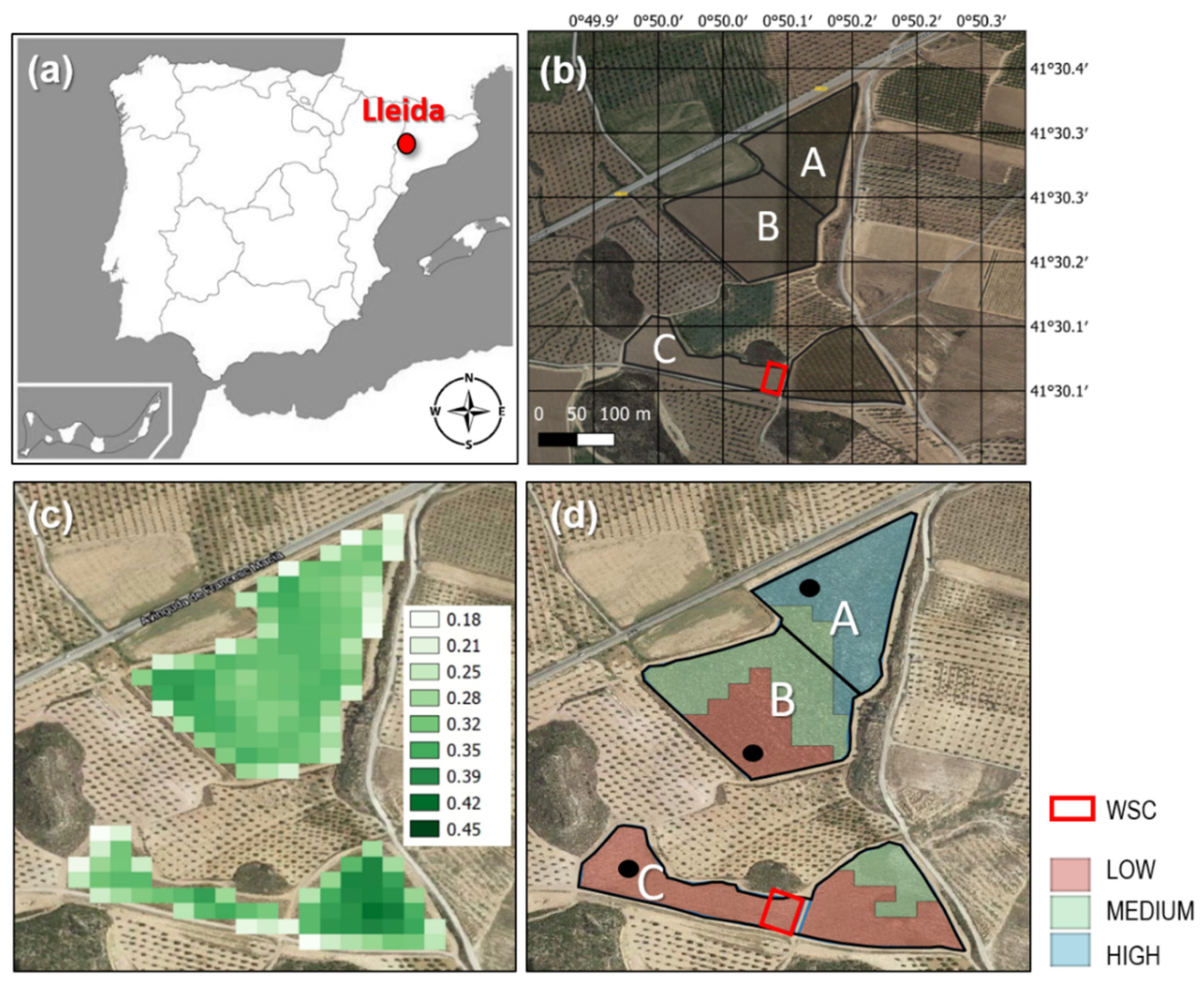
2.1. Study Site
2.2. Selection of the Location for Installing Sensors
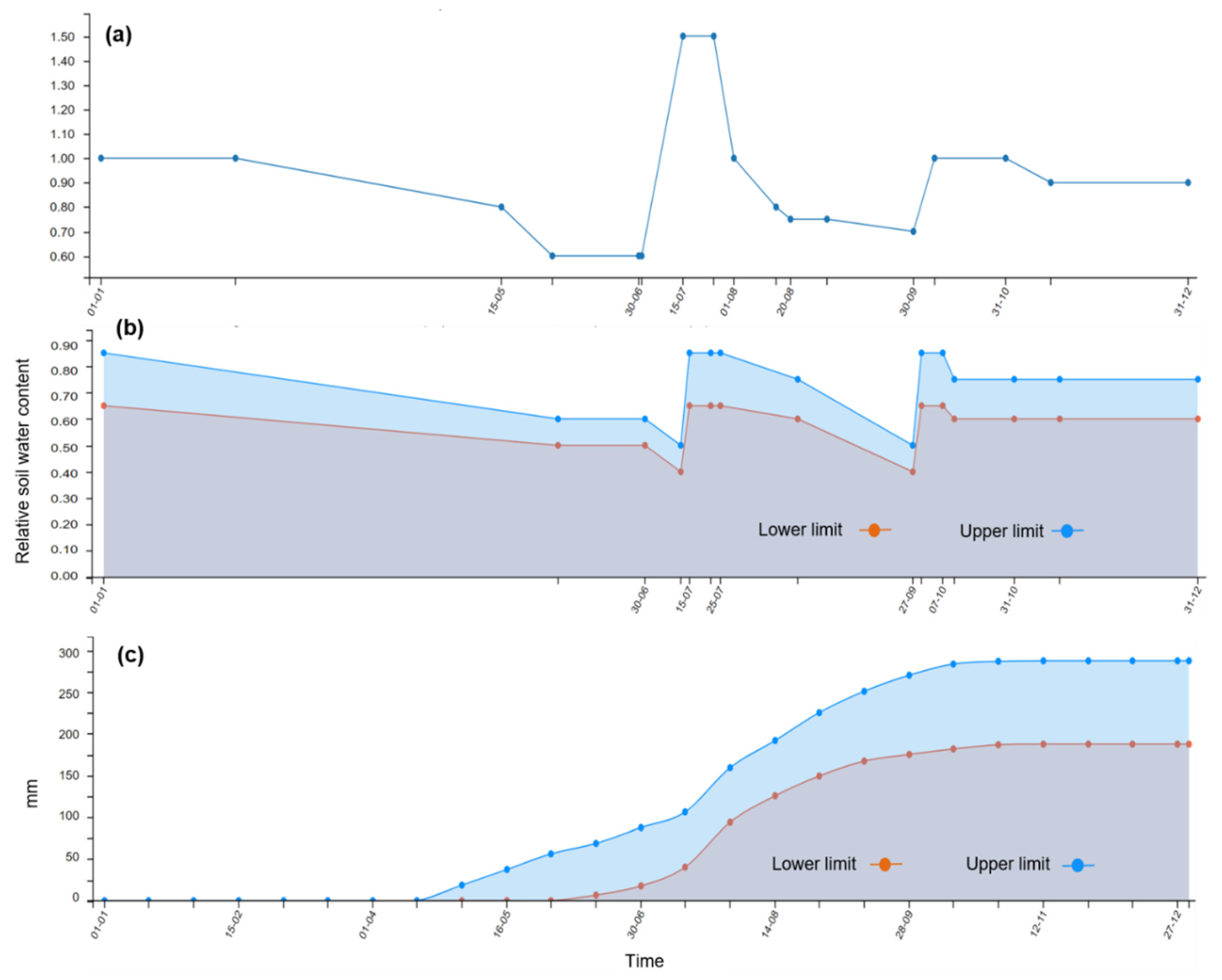
2.3. IrriDesk® and Definition of the Irrigation Seasonal Plan
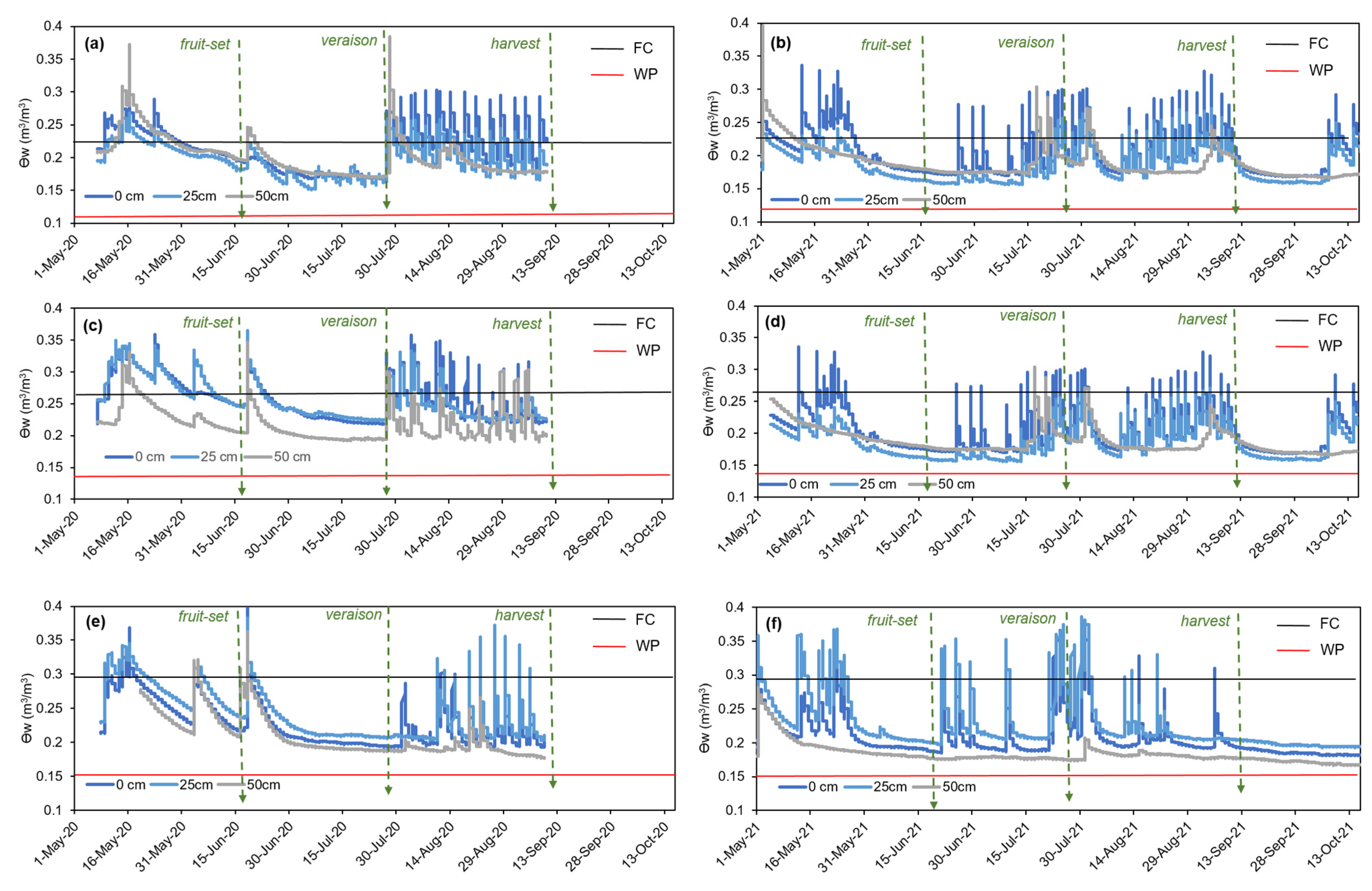
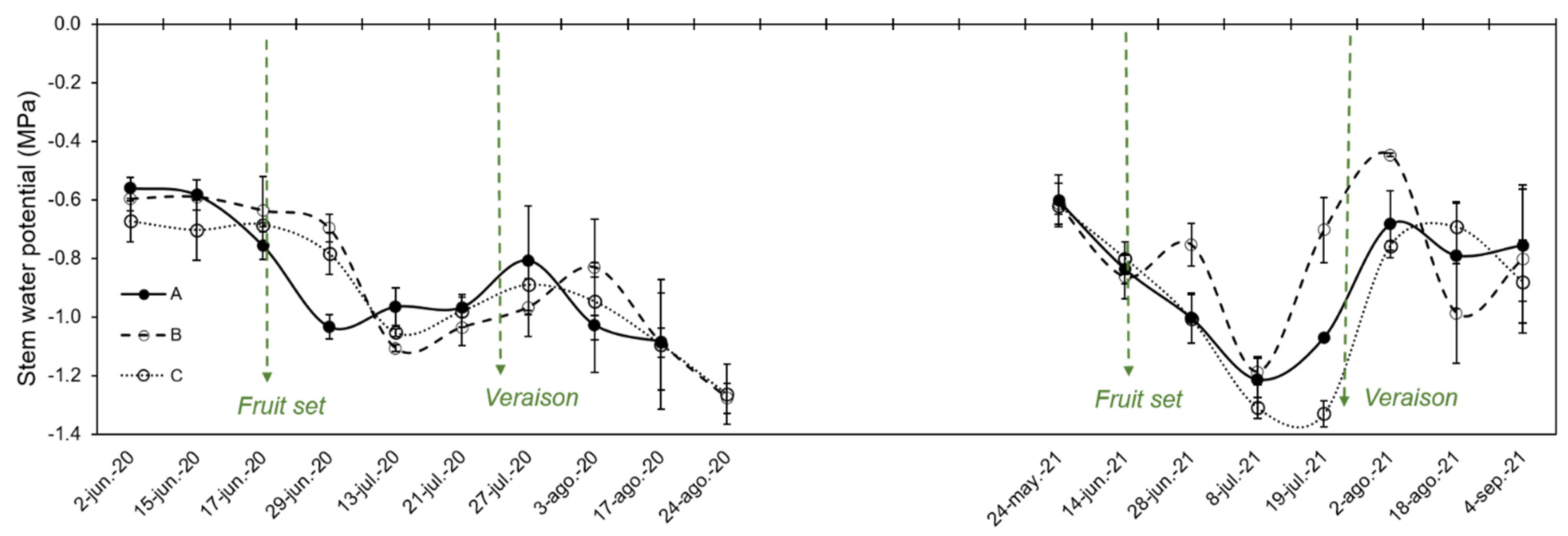
2.4. Field Measurements
2.5. Satellite Imagery and Biophysical Variables
2.6. Actual and Potential Evapotranspiration Using Copernicus-Based Inputs
3. Results and Discussion
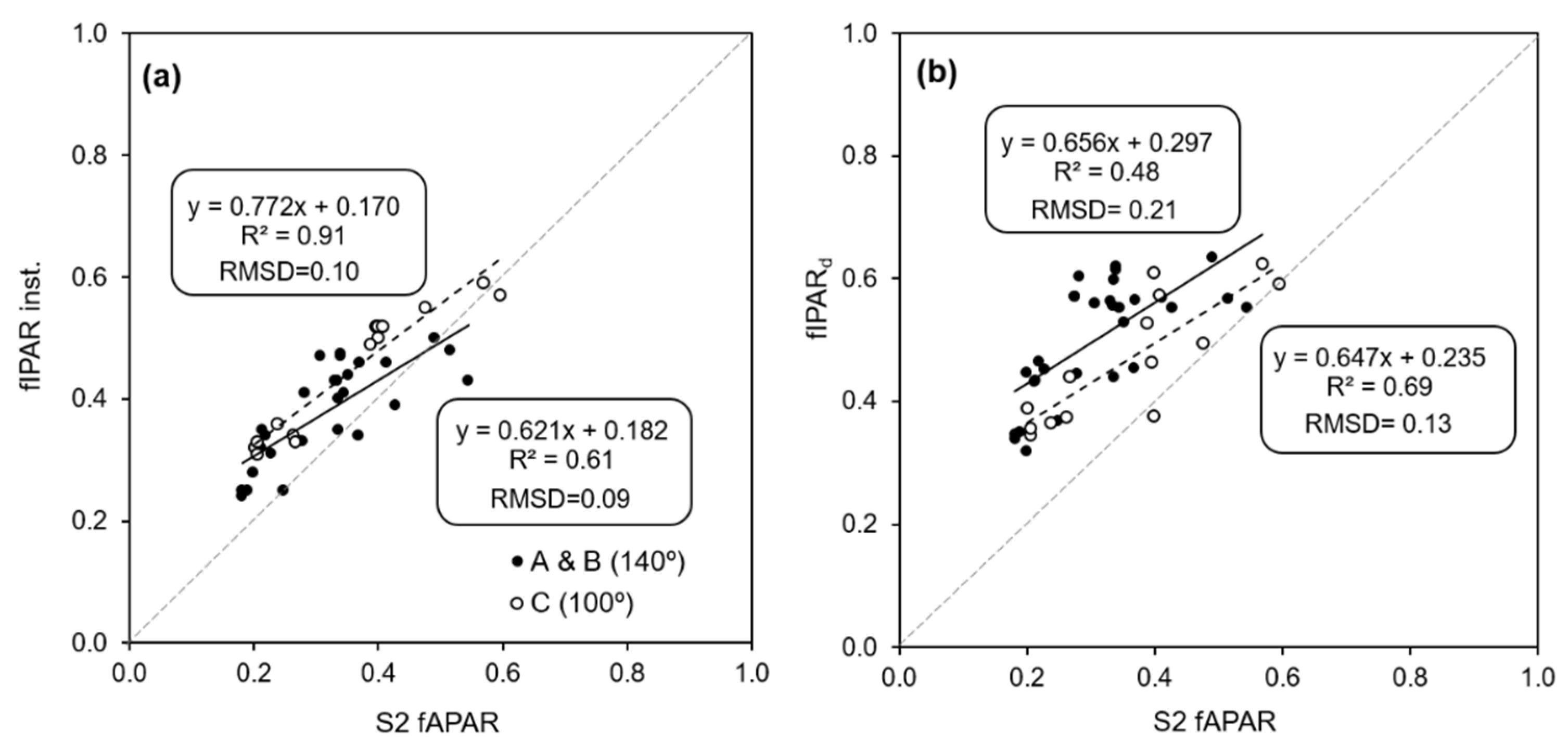
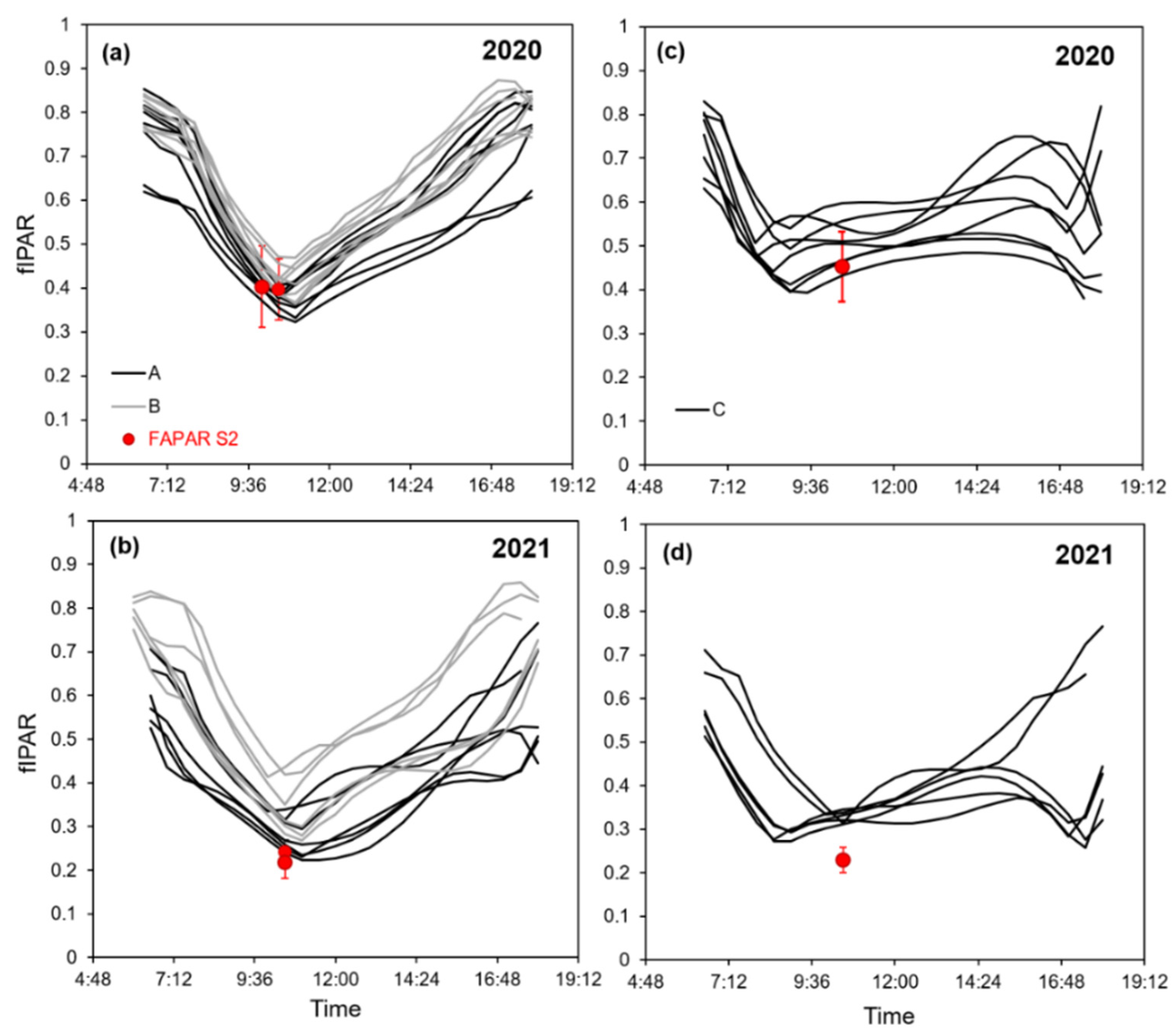
3.1. Sentinel-2 fAPAR
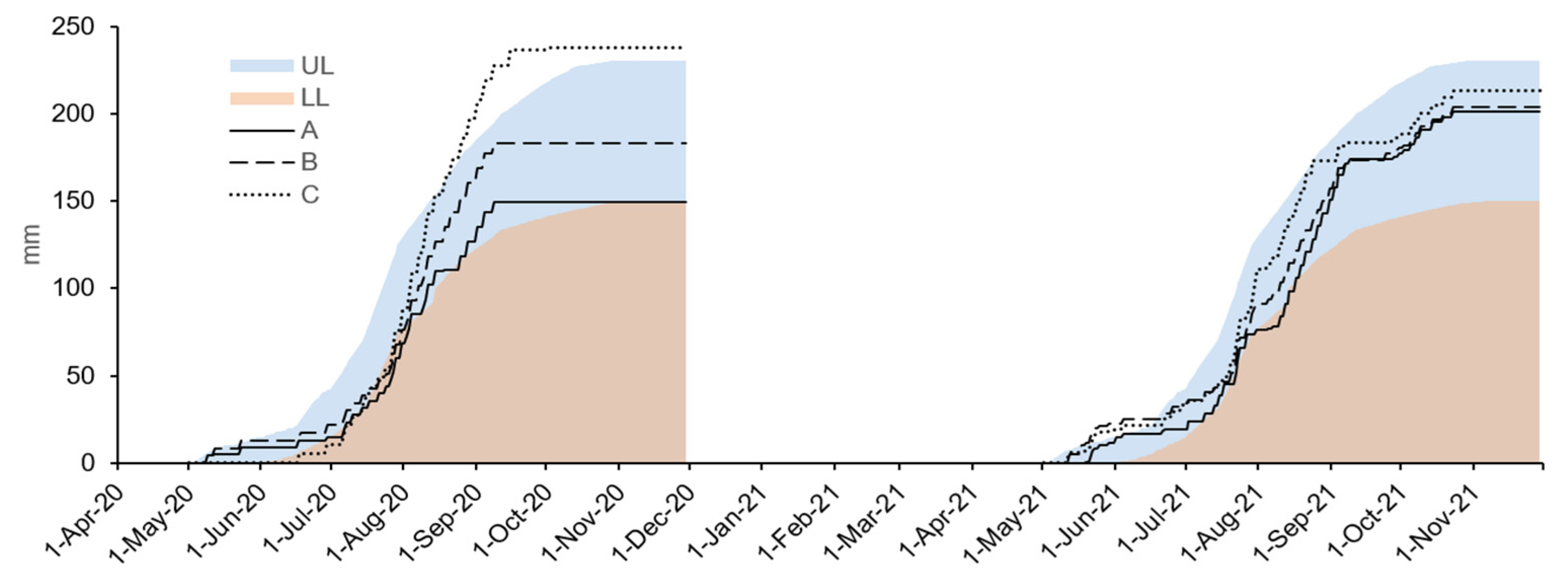
3.2. Performance of the Automated Decision Support System for Irrigation Scheduling
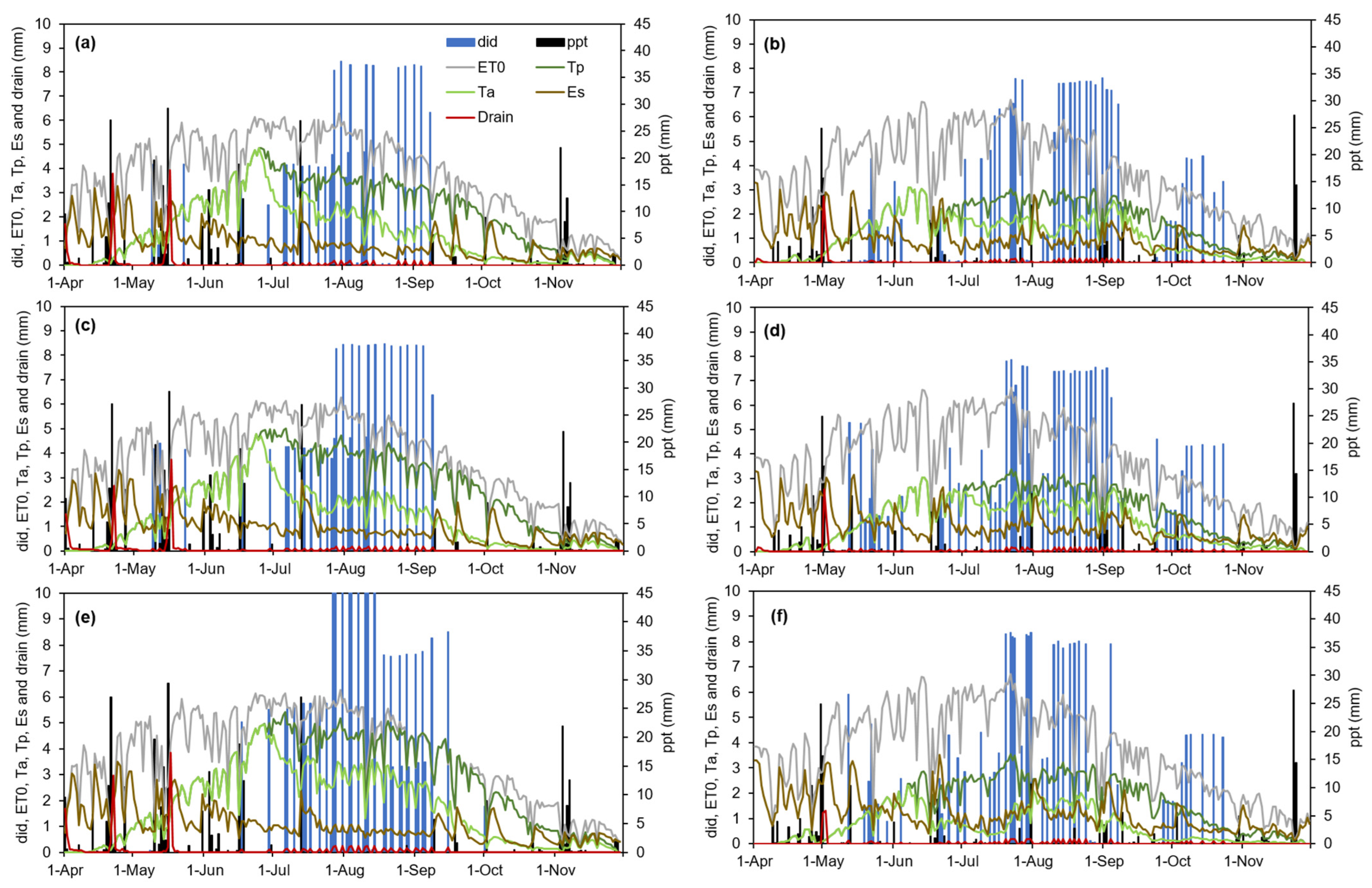
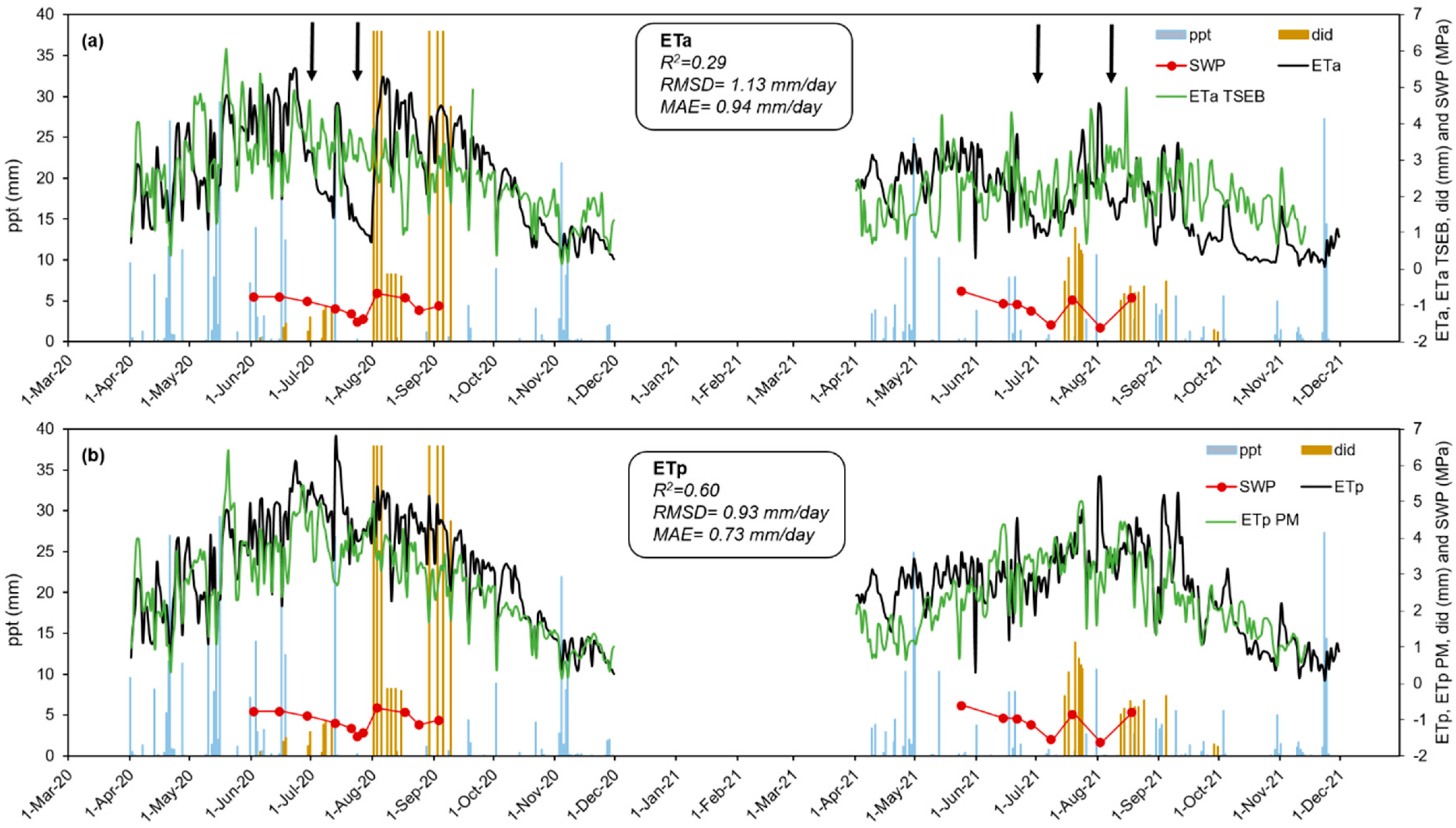
3.3. Simulations of the Water Balance Variables through the Digital Twin
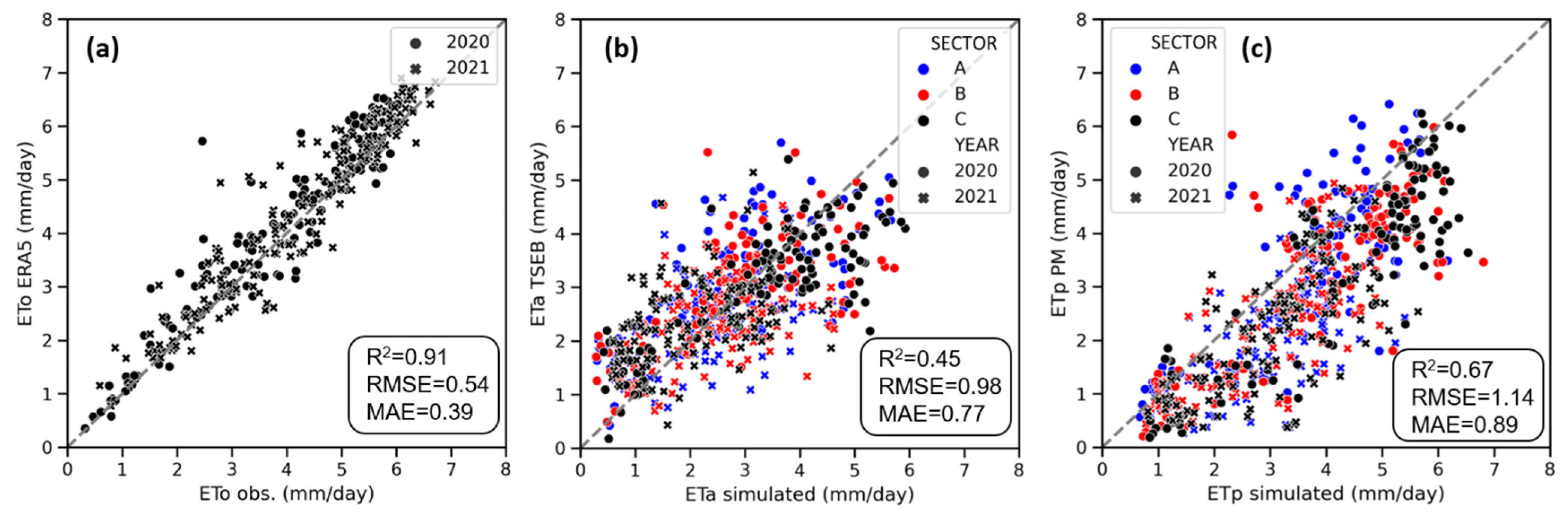
3.4. Comparison of Digital Twin Simulations of ET with Values Estimated with Remote Sensing
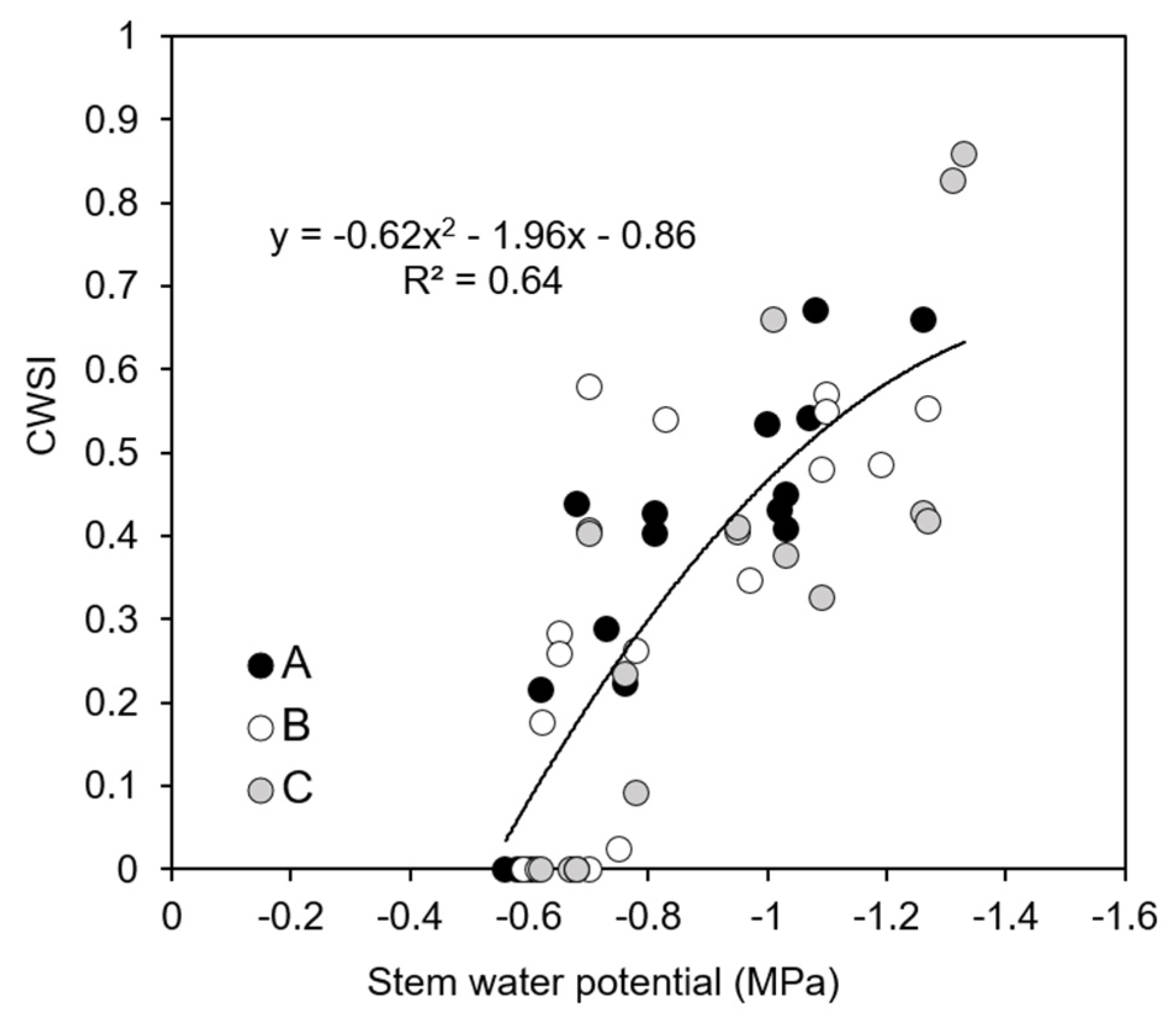
3.5. Comparison of the Response of ET in Vines under Water Stress Cycles (WSC)
4. Conclusions and Perspective
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Calzadilla, A.; Rehdanz, K.; Tol, R.S.J. The GTAP-W Model: Accounting for Water Use in Agriculture; Kiel Working Paper, 2011, No. 1745; Kiel Institute for the World Economy (IfW): Kiel, Germany, 2011; Available online: http://hdl.handle.net/10419/54939 (accessed on 20 February 2023).
- ISPA. 2020. Available online: https://www.ispag.org/about/definition (accessed on 21 October 2022).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration—Guidelines for computing crop water requirements. In FAO Irrigation and Drainage; Paper No. 56; Food and Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Intrieri, C.; Poni, S.; Rebucci, B.; Magnanini, E. Row orientation effects on whole-canopy gas exchange of potted and field-grown grapevines. Vitis 1998, 37, 147–154. [Google Scholar] [CrossRef]
- Marsal, J.; Johnson, S.; Casadesus, J.; Lopez, G.; Girona, J.; Stöckle, C. Fraction of canopy intercepted radiation relates differently with crop coefficient depending on the season and the fruit tree species. Agric. For. Meteorol. 2014, 184, 1–11. [Google Scholar] [CrossRef]
- Ayars, J.E.; Johnson, R.S.; Phene, C.J.; Trout, T.J.; Clark, D.A.; Mead, R.M. Water use by drip-irrigated late-season peaches. Irrig. Sci. 2003, 22, 187–194. [Google Scholar] [CrossRef]
- Auzmendi, I.; Mata, M.; del Campo, J.; Lopez, G.; Girona, J.; Marsal, J. Intercepted radiation by apple canopy can be used as a basis for irrigation scheduling. Agric. Water Manag. 2011, 98, 886–892. [Google Scholar] [CrossRef]
- Girona, J.; del Campo, J.; Mata, M.; Lopez, G.; Marsal, J. A comparative study of apple and pear tree water consumption measured with two weighing lysimeters. Irrig. Sci. 2011, 29, 55–63. [Google Scholar] [CrossRef]
- Egea, G.; Nortes, P.A.; González-Real, M.M.; Baille, A.; Domingo, R. Agronomic response and water productivity of almond trees under contrasted deficit irrigation regimes. Agric. Water Manag. 2010, 97, 171–181. [Google Scholar] [CrossRef]
- Memmi, H.; Gijón, M.C.; Couceiro, J.F.; Pérez-López, D. Water stress thresholds for regulated deficit irrigation in pistachio trees: Rootstock influence and effects on yield quality. Agric. Water Manag. 2016, 164, 58–72. [Google Scholar] [CrossRef] [Green Version]
- Moñino, M.J.; Blanco-Cipollone, F.; Vivas, A.; Bodelón, O.G.; Prieto, M.H. Evaluation of different deficit irrigation strategies in the late-maturing Japanese plum cultivar ‘Angeleno’. Agric. Water Manag. 2020, 234, 106111. [Google Scholar] [CrossRef]
- Intrigliolo, D.; Castel, J.R. Response of plum trees to deficit irrigation under two crop levels: Tree growth, yield and fruit quality. Irrig. Sci. 2010, 28, 525–534. [Google Scholar] [CrossRef]
- Basile, B.; Marsal, J.; Mata, M.; Vallverdú, X.; Bellvert, J.; Girona, J. Phenological Sensitivity of Cabernet Sauvignon to Water Stress: Vine Physiology and Berry Composition. Am. J. Enol. Vitic. 2011, 62, 452–461. [Google Scholar] [CrossRef] [Green Version]
- Lipan, L.; Martín-Palomo, M.J.; Sánchez-Rodríguez, L.; Cano-Lamadrid, M.; Sendra, E.; Hernández, F.; Burló, F.; Vázquez-Araújo, L.; Andreu, L.; Carbonell-Barrachina, A.A. Almond fruit quality can be improved by means of deficit irrigation strategies. Agric. Water Manag. 2019, 217, 236–242. [Google Scholar] [CrossRef]
- Jones, H.G. Irrigation scheduling: Advantages and pitfalls of plant-based methods. J. Exp. Bot. 2004, 55, 2427–2436. [Google Scholar] [CrossRef] [Green Version]
- Goldhamer, D.A.; Fereres, E. Irrigation scheduling of almond trees with trunk diameter sensors. Irrig. Sci. 2004, 23, 11–19. [Google Scholar] [CrossRef]
- Dukes, M.D.; Zotarelli, L.; Morgan, K.T. Use of irrigation technologies for vegetable crops in Florida. HortTechnology 2010, 20, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Soulis, K.X.; Elmaloglou, S.; Dercas, N. Investigating the effects of soil moisture sensors positioning and accuracy on soil moisture based drip irrigation scheduling Systems. Agric. Water Manag. 2015, 148, 258–268. [Google Scholar] [CrossRef]
- Osroosh, Y.; Peters, R.T.; Campbell, C.S.; Zhang, Q. Comparison of Irrigation Automation Algorithms for Drip-Irrigated Apple Trees. Comput. Electron. Agric. 2016, 128, 87–99. [Google Scholar] [CrossRef] [Green Version]
- Dukes, M.D.; Scholberg, J.M. Soil moisture controlled subsurface drip irrigation on sandy soils. Appl. Eng. Agric. 2005, 21, 89–101. [Google Scholar] [CrossRef]
- Millán, S.; Campillo, C.; Casadesús, J.; Pérez-Rodríguez, J.M.; Prieto, M.H. Automatic irrigation scheduling on a hedgerow olive orchard using an algorithm of water balance readjusted with soil moisture sensors. Sensors 2020, 20, 2526. [Google Scholar] [CrossRef]
- Casadesús, J.; Mata, M.; Marsal, J.; Girona, J. A general algorithm for automated scheduling of drip irrigation in tree crops. Comput. Electron. Agric. 2012, 83, 11–20. [Google Scholar] [CrossRef]
- Domínguez-Niño, J.M.; Oliver-Manera, J.; Girona, J.; Casadesús, J. Differential irrigation scheduling by an automated algorithm of water balance tuned by capacitance- type soil moisture sensors. Agric. Water Manag. 2020, 228, 105880. [Google Scholar] [CrossRef]
- Millán, S.; Casadesús, J.; Campillo, C.; Moñino, M.J.; Prieto, M.H. Using Soil Moisture Sensors for Automated Irrigation Scheduling in a Plum Crop. Water 2019, 11, 2061. [Google Scholar] [CrossRef] [Green Version]
- Grieves, M. Digital Twin: Manufacturing Excellence through Virtual Factory Replication. Florida Institute of Technology. Digit. Twin White Pap. 2014, 1, 1–7. [Google Scholar]
- ESA. Sentinel-2 User Handbook; ESA Standard Document, Issue 1, Rev. 2.; ESA: Peris, France, 2015; Available online: www.copernicus.eu (accessed on 15 May 2022).
- Bausch, W.C.; Neale, C.M.U. Crop coefficients derived from reflected canopy radiation: A concept. Trans. ASAE 1987, 30, 703–709. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinífera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Kamble, B.; Kilic, A.; Hubbard, K. Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index. Remote Sens. 2013, 5, 1588–1602. [Google Scholar] [CrossRef] [Green Version]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Delalieux, S.; Somers, B.; Hereijgers, S.; Verstraeten, W.W.; Keulemans, W.; Coppin, P. A near-infrared narrow-waveband ratio to determine Leaf Area Index in orchards. Remote Sens. Environ. 2008, 112, 3762–3772. [Google Scholar] [CrossRef]
- Hall, F.G.; Huemmrich, K.F.; Goetz, S.J.; Sellers, P.J.; Nickerson, J.E. Satellite remote sensing of surface energy balance, failures, and unresolved issues in FIFE. J. Geophys. Res. 1992, 97, 19061–19089. [Google Scholar] [CrossRef]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Leolini, L.; Moriondo, M.; Rossi, R.; Bellini, E.; Brilli, L.; López-Bernal, Á.; Santos, J.A.; Fraga, H.; Bindi, M.; Dibari, C.; et al. Use of Sentinel-2 Derived Vegetation Indices for Estimating fPAR in Olive Groves. Agronomy 2022, 12, 1540. [Google Scholar] [CrossRef]
- Leolini, L.; Bregaglio, S.; Ginaldi, F.; Costafreda-Aumedes, S.; Di Gennaro, S.F.; Matese, A.; Maselli, F.; Caruso, G.; Palai, G.; Bajocco, S.; et al. Use of remote sensing-derived fPAR data in a grapevine simulation model for estimating vine biomass accumulation and yield variability at sub-field level. Precis. Agric. 2022, 24, 705–726. [Google Scholar] [CrossRef]
- Huete, A.R. Soil influences in remotely sensed vegetation-canopy spectra. In Theory and Application of Optical Remote Sensing; Asrar, G., Ed.; Wiley Series in Remote Sensing; Wiley: New York, NY, USA, 1989; pp. 107–141. [Google Scholar]
- Kempeneers, P.; Zarco-Tejada, P.J.; North, P.R.J.; De Backer, S.; Delalieux, S.; Sepulcre-Cantó, G.; Morales, F.; Van Aardt, J.A.N.; Sagardoy, R.; Coppin, P.; et al. Model inversion for chlorophyll estimation in open canopies from hyperspectral imagery. Int. J. Remote Sens. 2008, 29, 5093–5111. [Google Scholar] [CrossRef]
- Guillén-Climent, M.L.; Zarco-Tejada, P.J.; Villabobos, F.J. Estimating radiation interception in an olive orchard using physical models and multispectral airborne imagery. Isr. J. Plant Sci. 2012, 60, 107–121. [Google Scholar] [CrossRef] [Green Version]
- Weiss, M.; Baret, F. S2ToolBox Level 2 Products: LAI, FAPAR, FCOVER—Version 1.1. Sentinel2 ToolBox Level2 Products; INRA: Paris, France, 2016; pp. 1–53. Available online: https://step.esa.int/docs/extra/ATBD_S2ToolBox_L2B_V1.1.pdf (accessed on 19 August 2022).
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and Indirect Estimation of Leaf Area Index, fAPAR, and Net Primary Production of Terrestrial Ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Li, W.; Fang, H.; Wei, S.; Weiss, M.; Baret, F. Critical analysis of methods to estimate the fraction of absorbed or intercepted photosynthetically active radiation from ground measurements: Application to rice crops. Agric. For. Meteorol. 2021, 297, 108273. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.; Humes, K. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng.-Asce 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Merlin, O.; Duchemin, B.; Hagolle, O.; Jacob, F.; Coudert, B.; Chehbouni, G.; Dedieu, G.; Garatuza, J.; Kerr, Y. Disaggregation of MODIS surface temperature over an agricultural area using a time series of Formosat-2 images. Remote Sens. Environ. 2010, 114, 2500–2512. [Google Scholar] [CrossRef] [Green Version]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, S.; Li, M.; Zhan, W.; Xu, Z.; Xu, T. Quantification of the Scale Effect in Downscaling Remotely Sensed Land Surface Temperature. Remote Sens. 2016, 8, 975. [Google Scholar] [CrossRef] [Green Version]
- Bisquert, M.; Sánchez, J.M.; Caselles, V. Evaluation of Disaggregation Methods for Downscaling MODIS Land Surface Temperature to Landsat Spatial Resolution in Barrax Test Site. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1430–1438. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef] [Green Version]
- Guzinski, R.; Nieto, H.; Sandholt, I.; Karamitilios, G. Modelling High-Resolution Actual Evapotranspiration through Sentinel-2 and Sentinel-3 Data Fusion. Remote Sens. 2020, 12, 1433. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sánchez, J.M.; López-Urrea, R.; Boujnah, D.M.; Boulet, G. Utility of Copernicus-Based Inputs for Actual Evapotranspiration Modeling in Support of Sustainable Water Use in Agriculture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11466–11484. [Google Scholar] [CrossRef]
- Bellvert, J.; Jofre-Čekalović, C.; Pelechá, A.; Mata, M.; Nieto, H. Feasibility of Using the Two-Source Energy Balance Model (TSEB) with Sentinel-2 and Sentinel-3 Images to Analyze the Spatio-Temporal Variability of Vine Water Status in a Vineyard. Remote Sens. 2020, 12, 2299. [Google Scholar] [CrossRef]
- Jofre-Čekalović, C.; Nieto, H.; Girona, J.; Pamies-Sans, M.; Bellvert, J. Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs. Remote Sens. 2022, 14, 2106. [Google Scholar] [CrossRef]
- Oyarzun, R.A.; Stöckle, C.O.; Whiting, M.D. A simple approach to modeling radiation interception by fruit-tree orchards. Agric. For. Meteorol. 2007, 142, 12–24. [Google Scholar] [CrossRef]
- Steduto, P.; Raes, D.; Theodore Hsiao, C.; Fereres, E.; Heng, L.K.; Hower, T.A.; Evett, S.R.; RojasLara, B.A.; Farahani, H.J.; Izzi, G.; et al. Concepts and Applications of AquaCrop: The FAO Crop Water Productivity Model. In Crop Modelling and Decision Support; Cao, W., White, J.W., Wang, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 175–191. [Google Scholar] [CrossRef] [Green Version]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J., Jr. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- McCutchan, H.; Shackel, K.A. Stem water potential as a sensitive indicator of water stress in prune trees (Prunus domestica L. cv French). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar] [CrossRef] [Green Version]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kustas, W.P.; Nieto, H.; Morillas, L.; Anderson, M.C.; Alfieri, J.G.; Hipps, L.E.; Villagarcía, L.; Domingo, F.; Garcia, M. Revisiting the paper “Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective”. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef] [Green Version]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Chapter 13: Steady state heat balance. In Principles of Environmental Physics, 3rd ed.; Academic Press: Burlington, VT, USA, 2008; pp. 250–255. [Google Scholar]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B.; et al. A recommendation on standardized surface resistance for hourly calculation of reference ET0 by the FAO56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Andrieu, B.; Baret, F. Indirect methods of estimating crop structure from optical measurements. In Crop Structure and Light Microclimate—Characterization and Applications; Varlet-Grancher, R.B.C., Sinoquet, H., Eds.; INRA: Paris, France, 1993; pp. 285–322. [Google Scholar]
- Li, W.; Weiss, M.; Waldner, F.; Defourny, P.; Demarez, V.; Morin, D.; Hagolle, O.; Baret, F. A Generic Algorithm to Estimate LAI, FAPAR and FCOVER Variables from SPOT4_HRVIR and Landsat Sensors: Evaluation of the Consistency and Comparison with Ground Measurements. Remote Sens. 2015, 7, 15494–15516. [Google Scholar] [CrossRef] [Green Version]
- Wojnowski, W.; Wei, S.; Li, W.; Yin, T.; Li, X.-X.; Ow, G.L.F.; Mohd Yusof, M.L.; Whittle, A.J. Comparison of Absorbed and Intercepted Fractions of PAR for Individual Trees Based on Radiative Transfer Model Simulations. Remote Sens. 2021, 13, 1069. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Kizito, F.; Campbell, C.S.; Campbell, G.S.; Cobos, D.R.; Teare, B.L.; Carter, B.; Hopmans, J.W. Frequency, electrical conductivity and temperature analysis of a low-cost capacitance soil moisture sensor. J. Hydrol. 2008, 352, 3–4. [Google Scholar] [CrossRef]
- Nolz, R.; Loiskandl, W. Evaluating soil water content data monitored at different locations in a vineyard with regard to irrigation control. Soil Water Res. 2017, 12, 152–160. [Google Scholar] [CrossRef] [Green Version]
- Domínguez-Niño, J.M.; Oliver-Manera, J.; Arbat, G.; Girona, J.; Casadesús, J. Analysis of the Variability in Soil Moisture Measurements by Capacitance Sensors in a Drip-Irrigated Orchard. Sensors 2020, 20, 5100. [Google Scholar] [CrossRef]
- Cancela, J.J.; Fandiño, M.; Rey, B.J.; Rosa, R.; Pereira, L.S. Estimating transpiration and soil evaporation of vineyards from the fraction of ground cover and crop height—Application to ‘Albariño’ vineyards of Galicia. Acta Hortic. 2012, 931, 227–234. [Google Scholar] [CrossRef]
- Phogat, V.; Skewes, M.A.; McCarthy, M.G.; Cox, J.W.; Simunek, J.; Petrie, P.R. Evaluation of crop coefficients, water productivity, and water balance components for wine grapes irrigated at different deficit levels by a sub-surface drip. Agric. Water Manag. 2017, 180, 22–34. [Google Scholar] [CrossRef] [Green Version]
- Bellvert, J.; Mata, M.; Vallverdú, X.; Paris, C.; Marsal, L. Optimizing precision irrigation of a vineyard to improve water use efficiency and profitability by using a decision-oriented vine water consumption model. Precis. Agric. 2021, 22, 319–334. [Google Scholar] [CrossRef]
- Bellvert, J.; Marsal, J.; Girona, J.; Zarco-Tejada, P.J. Seasonal evolution of crop water stress index in varieties determined with high-resolution remote sensing thermal imagery. Irrig. Sci. 2015, 33, 81–93. [Google Scholar] [CrossRef]
- Burchard-Levine, V.; Nieto, H.; Riaño, D.; Migliavacca, M.; El-Madany, T.S.; Guzinski, R.; Carrara, A.; Martín, M.P. The effect of pixel heterogeneity for remote sensing based retrievals of evapotranspiration in a semi-arid tree-grass ecosystem. Remote Sens. Environ. 2021, 260, 112440. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J. An Introduction to Environmental Biophysics, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]

| Soil Properties in Points of Each Irrigation Sector 1 | A | B | C | WSC |
|---|---|---|---|---|
| Soil depth (m) | 2.0 | 1.8 | 0.8 | 0.8 |
| Silt | 0.35 | 0.34 | 0.36 | 0.35 |
| Clay | 0.42 | 0.56 | 0.58 | 0.62 |
| Sand | 0.24 | 0.09 | 0.05 | 0.03 |
| USDA Soil Classification | Clay | |||
| Soil water content at field capacity (33 KPa) m3 m−3 | 0.22 | 0.26 | 0.29 | 0.28 |
| Soil water content at wilting point (−1500 KPa) m3 m−3 | 0.11 | 0.13 | 0.15 | 0.14 |
| Saturated hydraulic conductivity (mm/h) | 1.3 | 1.3 | 1.3 | 1.3 |
| Apparent bulk density (kg m−3) | 1.25 | 1.4 | 1.37 | 1.41 |
| Year | Irrig. Sector | Variables | ||||||
|---|---|---|---|---|---|---|---|---|
| ET0 (mm) | R (mm) | ETp (mm) | ETa (mm) | (R + IR)/ETp | E/ETa | ETa/ETp | ||
| 2020 | A | 895 | 323 | 731.3 | 553.5 | 0.65 | 0.42 | 0.76 |
| B | 799.5 | 574.1 | 0.63 | 0.43 | 0.72 | |||
| C | 865.1 | 675.0 | 0.65 | 0.38 | 0.78 | |||
| 2021 | A | 902 | 207 | 605.7 | 502.8 | 0.67 | 0.49 | 0.83 |
| B | 611.5 | 526.4 | 0.72 | 0.49 | 0.86 | |||
| C | 646.9 | 455.6 | 0.65 | 0.65 | 0.70 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellvert, J.; Pelechá, A.; Pamies-Sans, M.; Virgili, J.; Torres, M.; Casadesús, J. Assimilation of Sentinel-2 Biophysical Variables into a Digital Twin for the Automated Irrigation Scheduling of a Vineyard. Water 2023, 15, 2506. https://doi.org/10.3390/w15142506
Bellvert J, Pelechá A, Pamies-Sans M, Virgili J, Torres M, Casadesús J. Assimilation of Sentinel-2 Biophysical Variables into a Digital Twin for the Automated Irrigation Scheduling of a Vineyard. Water. 2023; 15(14):2506. https://doi.org/10.3390/w15142506
Chicago/Turabian StyleBellvert, Joaquim, Ana Pelechá, Magí Pamies-Sans, Jordi Virgili, Mireia Torres, and Jaume Casadesús. 2023. "Assimilation of Sentinel-2 Biophysical Variables into a Digital Twin for the Automated Irrigation Scheduling of a Vineyard" Water 15, no. 14: 2506. https://doi.org/10.3390/w15142506
APA StyleBellvert, J., Pelechá, A., Pamies-Sans, M., Virgili, J., Torres, M., & Casadesús, J. (2023). Assimilation of Sentinel-2 Biophysical Variables into a Digital Twin for the Automated Irrigation Scheduling of a Vineyard. Water, 15(14), 2506. https://doi.org/10.3390/w15142506









