Analysis of the Behavior of Groundwater Storage Systems at Different Time Scales in Basins of South Central Chile: A Study Based on Flow Recession Records
Abstract
:1. Introduction
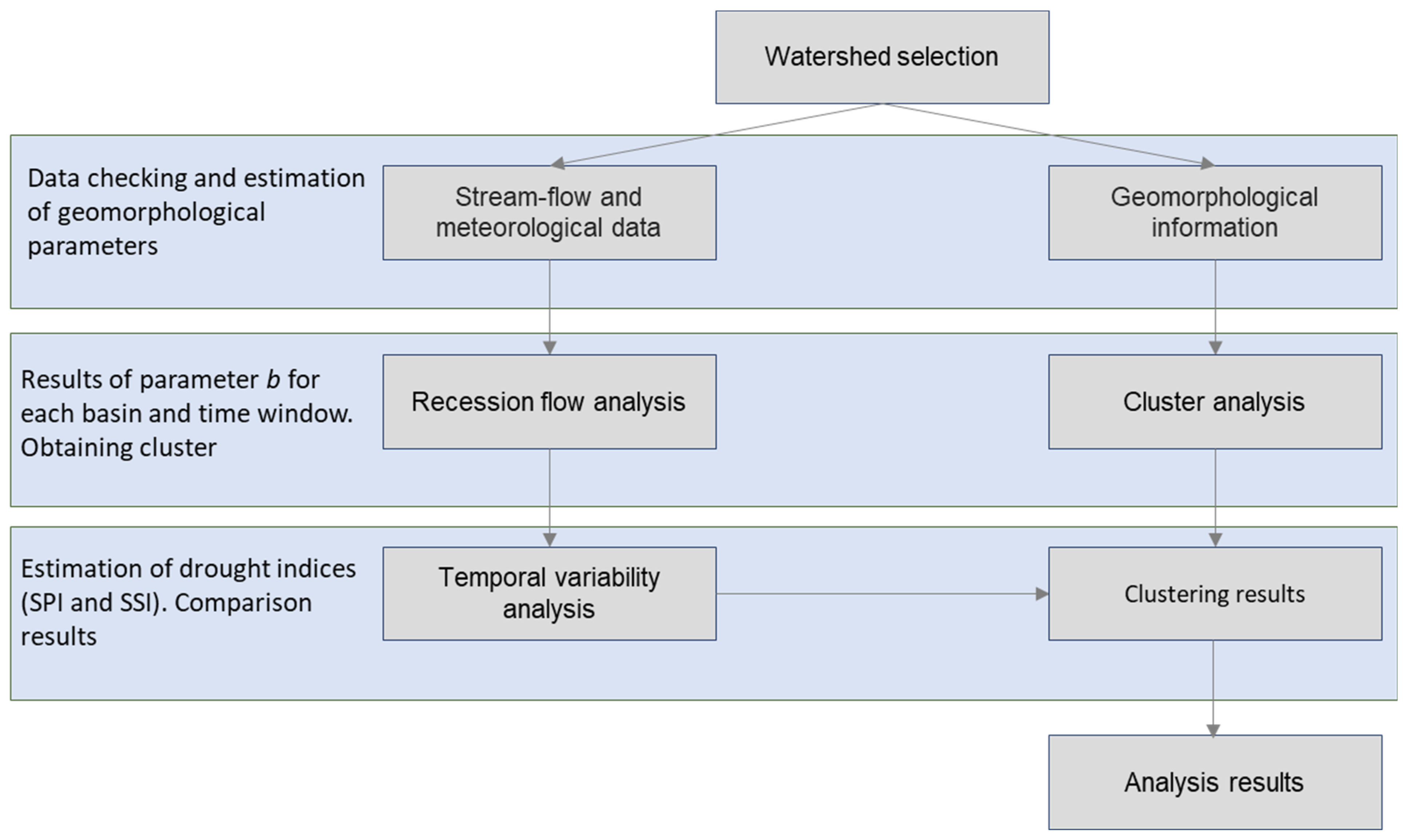
2. Materials and Methods
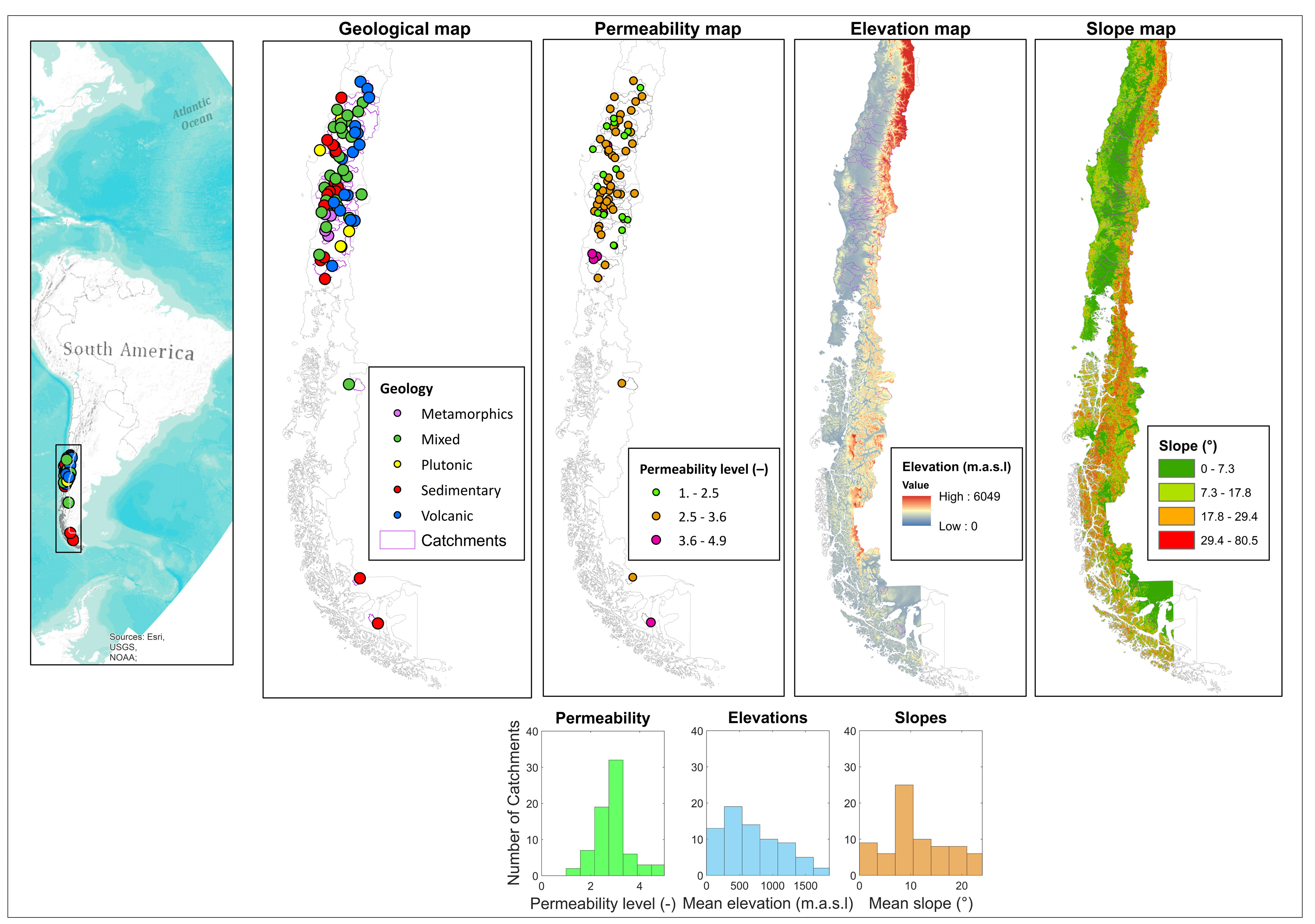
2.1. Study Area and Data
2.2. Recession Flow Analysis
2.3. Temporal Variability in Recession Flows
2.4. Cluster Analysis
3. Results and Discussion
3.1. Basin-Scale Spatial Distribution of Characteristics
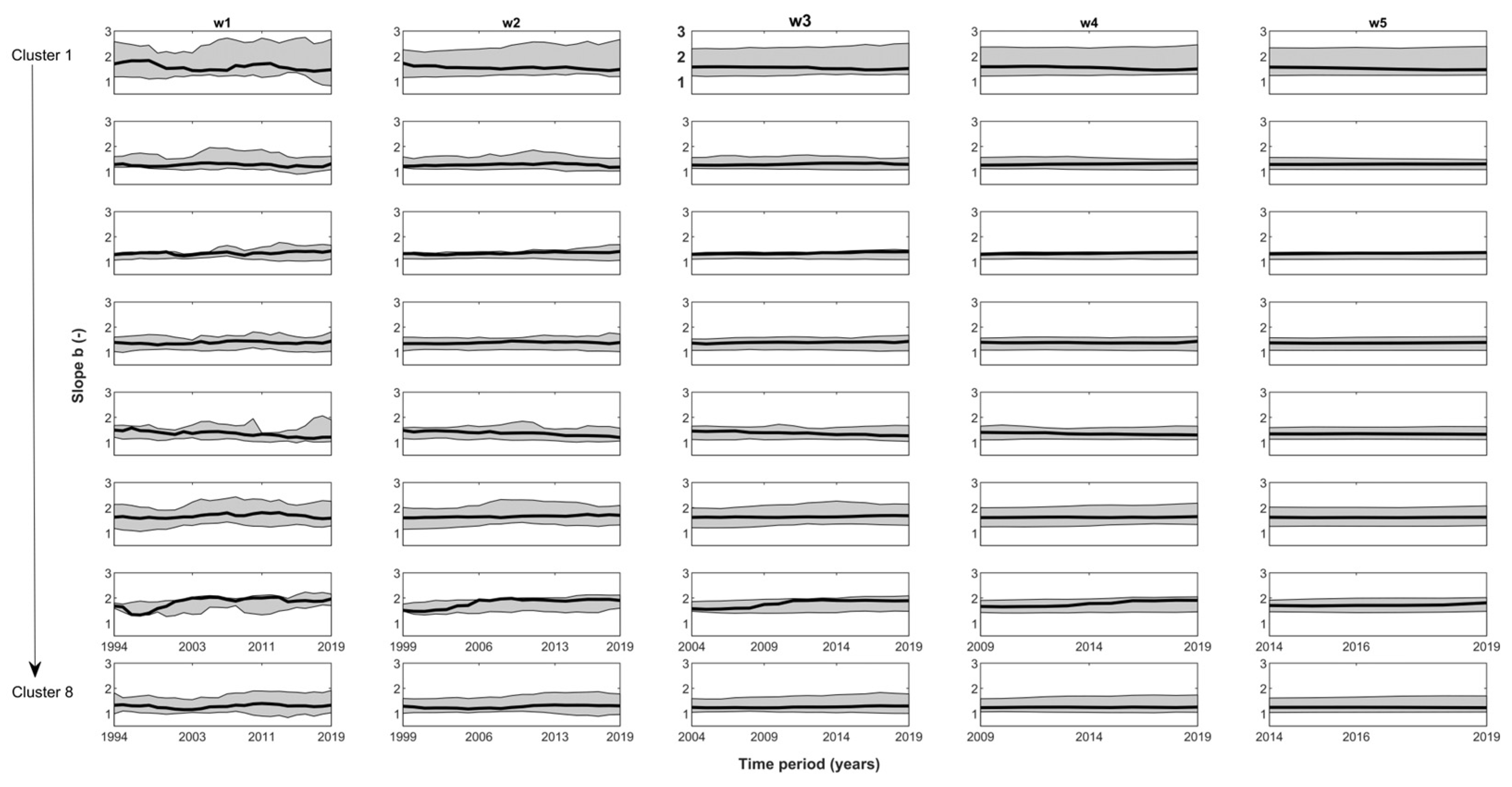
3.2. Temporal Variability of Recession Parameter b
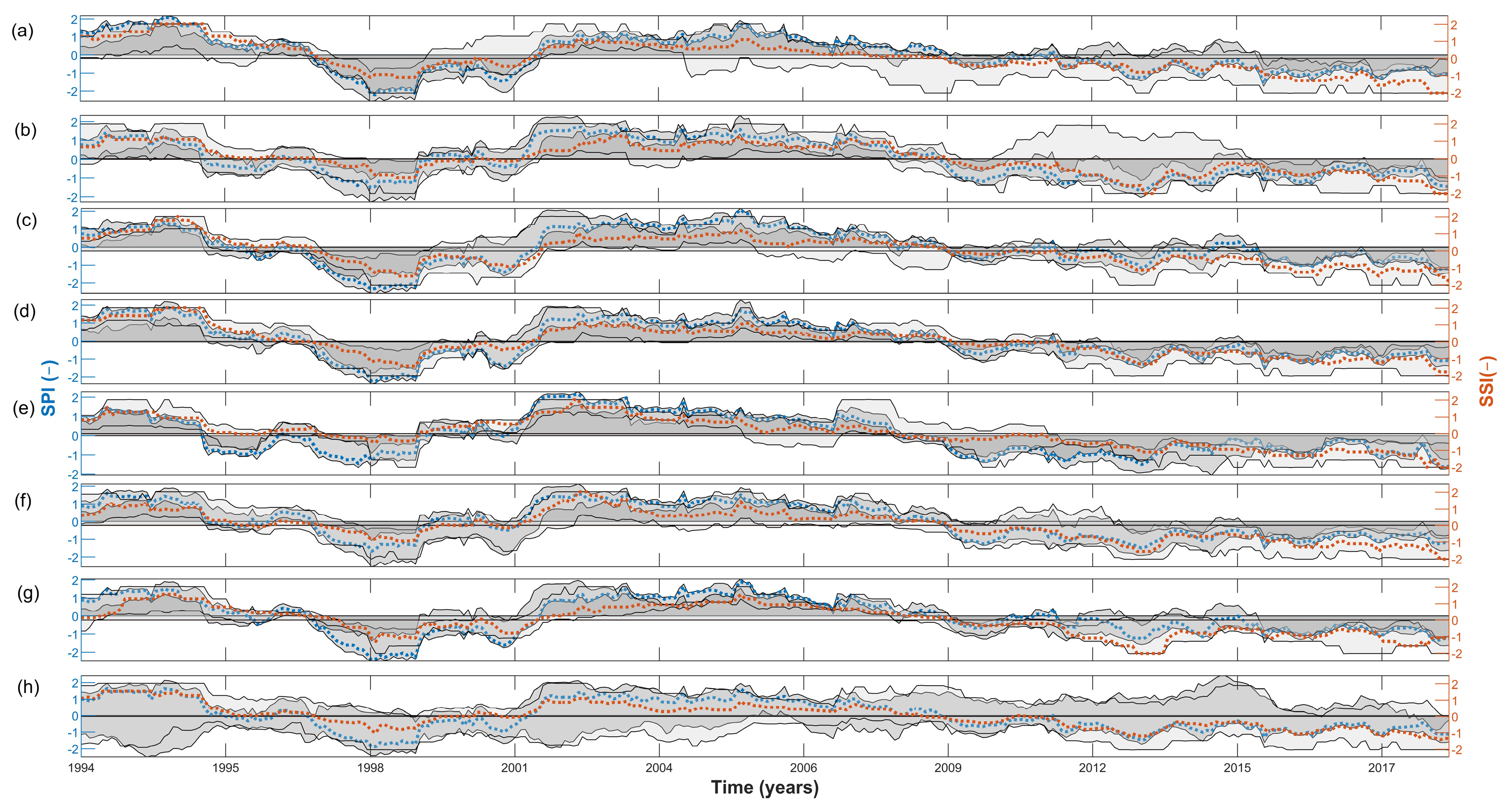
3.3. Influence of Climate Behavior on S-Q Behavior
3.4. Implications of the Study and Future Research
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Gauge Name | Gauge Latitude (°) | Gauge Longitude (°) | Area (km2) | Mean Elevation (m) | Mean Slope (°) | Geologic Class | Degree of Permeability (-) | Aridity Index (-) |
|---|---|---|---|---|---|---|---|---|
| Estero Zamorano En Puente El Niche | −34.4 | −71.2 | 1023 | 672 | 13.2 | MiG | 3.1 | 1.6 |
| Rio Quepe En Quepe | −38.9 | −72.6 | 1666 | 506 | 7.3 | MiG | 3.2 | 0.5 |
| Rio Cauquenes En El Arrayan | −36.0 | −72.4 | 622 | 308 | 8.3 | MiG | 1.8 | 1.2 |
| Rio Purapel En Sauzal | −35.8 | −72.1 | 404 | 294 | 7.0 | PG | 1.7 | 1.5 |
| Rio Andalien Camino A Penco | −36.8 | −73.0 | 750 | 210 | 7.7 | PG | 1.0 | 1.0 |
| Rio Lumaco En Lumaco | −38.2 | −72.9 | 853 | 341 | 9.7 | MiG | 1.7 | 1.0 |
| Estero Curipeumo En Lo Hernandez | −36.0 | −72.0 | 217 | 137 | 0.7 | SG | 3.2 | 1.6 |
| Rio Loncomilla En Bodega | −35.8 | −71.8 | 7079 | 398 | 7.1 | MiG | 2.7 | 1.1 |
| Rio Mininco En Longitudinal | −37.9 | −72.4 | 440 | 450 | 3.3 | SG | 3.0 | 0.6 |
| Rio Malleco En Collipulli | −38.0 | −72.4 | 415 | 801 | 13.8 | MiG | 3.0 | 0.4 |
| Rio Traiguen En Victoria | −38.2 | −72.3 | 94 | 513 | 2.1 | SG | 3.0 | 0.6 |
| Rio Dumo En Santa Ana | −38.2 | −72.3 | 393 | 485 | 2.4 | SG | 3.0 | 0.7 |
| Rio Quino En Longitudinal | −38.3 | −72.4 | 277 | 581 | 3.6 | SG | 3.0 | 0.5 |
| Estero Chufquen En Chufquen | −38.3 | −72.7 | 854 | 429 | 2.7 | SG | 3.0 | 0.7 |
| Rio Quillen En Galvarino | −38.4 | −72.8 | 710 | 285 | 3.7 | SG | 3.1 | 0.9 |
| Rio Larqui En Santa Cruz De Cuca | −36.7 | −72.4 | 636 | 150 | 1.7 | SG | 5.0 | 1.1 |
| Rio Lirquen En Cerro El Padre | −37.8 | −71.9 | 103 | 668 | 13.7 | MiG | 3.5 | 0.5 |
| Rio Donguil En Gorbea | −39.1 | −72.7 | 770 | 206 | 5.1 | MG | 4.2 | 0.6 |
| Rio Negro En Chahuilco | −40.7 | −73.2 | 2280 | 152 | 3.2 | SG | 4.6 | 0.6 |
| Rio Damas En Tacamo | −40.6 | −73.1 | 467 | 132 | 1.6 | SG | 4.8 | 0.7 |
| Rio Negro En Las Lomas | −41.4 | −73.1 | 253 | 118 | 1.8 | SG | 3.6 | 0.4 |
| Rio Cholchol En Cholchol | −38.6 | −72.8 | 5048 | 342 | 7.0 | MiG | 2.6 | 0.8 |
| Rio Puyehue En Quitratue | −39.2 | −72.7 | 153 | 200 | 8.9 | MG | 2.2 | 0.6 |
| Rio Mahuidanche En Santa Ana | −39.1 | −72.9 | 384 | 189 | 10.2 | MG | 2.2 | 0.6 |
| Rio Collileufu En Los Lagos | −39.9 | −72.8 | 626 | 197 | 8.1 | MG | 2.5 | 0.7 |
| Rio Inaque En Mafil | −39.7 | −73.0 | 539 | 204 | 8.6 | MG | 2.9 | 0.6 |
| Rio Cauquenes En Desembocadura | −35.9 | −72.1 | 1637 | 246 | 5.9 | MiG | 2.0 | 1.3 |
| Rio Loncomilla En Las Brisas | −35.6 | −71.8 | 9924 | 489 | 8.7 | MiG | 2.8 | 1.0 |
| Rio Vergara En Tijeral | −37.7 | −72.6 | 2537 | 375 | 8.1 | MiG | 2.2 | 0.8 |
| Rio Muco En Puente Muco | −38.6 | −72.4 | 650 | 537 | 7.1 | MiG | 3.1 | 0.6 |
| Rio Cruces En Rucaco | −39.6 | −72.9 | 1803 | 282 | 7.9 | MiG | 3.4 | 0.5 |
| Rio Longavi En El Castillo | −36.3 | −71.3 | 467 | 1564 | 24.4 | VG | 2.7 | 0.5 |
| Rio Achibueno En La Recova | −36.0 | −71.4 | 894 | 1329 | 23.0 | VG | 2.9 | 0.6 |
| Rio Itata En Cholguan | −37.2 | −72.1 | 860 | 834 | 12.1 | VG | 3.1 | 0.6 |
| Rio Diguillin En San Lorenzo (Atacalco) | −36.9 | −71.6 | 204 | 1511 | 22.8 | VG | 2.7 | 0.4 |
| Rio Coihueco Antes Junta Pichicope | −40.9 | −72.7 | 313 | 608 | 14.1 | VG | 3.0 | 0.3 |
| Rio Perquilauquen En Gniquen | −36.2 | −72.0 | 1209 | 647 | 11.2 | MiG | 2.6 | 0.7 |
| Rio Perquilauquen En Quella | −36.1 | −72.1 | 1687 | 505 | 8.6 | MiG | 2.9 | 0.9 |
| Rio Itata En General Cruz | −36.9 | −72.4 | 1662 | 613 | 7.9 | SG | 3.2 | 0.7 |
| Rio Itata En Trilaleo | −37.1 | −72.2 | 1148 | 752 | 10.2 | MiG | 3.2 | 0.7 |
| Rio Diguillin En Longitudinal | −36.9 | −72.3 | 1300 | 785 | 10.1 | SG | 3.2 | 0.6 |
| Rio Itata En Balsa Nueva Aldea | −36.7 | −72.5 | 4510 | 504 | 7.0 | SG | 3.3 | 0.8 |
| Rio Itata En Coelemu | −36.5 | −72.7 | 10,405 | 616 | 9.0 | SG | 3.3 | 0.8 |
| Rio Renaico En Longitudinal | −37.9 | −72.4 | 688 | 833 | 16.0 | MiG | 2.6 | 0.4 |
| Rio Huichahue En Faja 24000 | −38.9 | −72.3 | 348 | 605 | 12.9 | MiG | 3.1 | 0.4 |
| Rio Cautin En Almagro | −38.8 | −72.9 | 5547 | 553 | 7.4 | SG | 3.1 | 0.5 |
| Estero Upeo En Upeo | −35.2 | −71.1 | 367 | 1197 | 19.8 | MiG | 2.9 | 0.8 |
| Rio Mataquito En Licanten | −35.0 | −72.0 | 5700 | 1230 | 15.2 | SG | 3.0 | 0.9 |
| Rio Perquilauquen En San Manuel | −36.4 | −71.6 | 502 | 1100 | 20.5 | MiG | 2.0 | 0.5 |
| Rio Longavi En La Quiriquina | −36.2 | −71.5 | 669 | 1401 | 23.0 | VG | 2.5 | 0.5 |
| Rio Lircay En Puente Las Rastras | −35.5 | −71.3 | 382 | 1052 | 14.4 | MiG | 3.1 | 0.6 |
| Rio Duqueco En Villucura | −37.6 | −72.0 | 818 | 1023 | 16.4 | MiG | 2.3 | 0.5 |
| Rio Tolten En Teodoro Schmidt | −39.0 | −73.1 | 7927 | 702 | 11.1 | MiG | 2.8 | 0.4 |
| Rio Rahue En Forrahue | −40.5 | −73.3 | 5603 | 234 | 4.9 | MiG | 4.1 | 0.5 |
| Rio Ñirehuao En Villa Mañihuales | −45.2 | −72.1 | 1997 | 926 | 9.7 | MiG | 3.5 | 1.1 |
| Rio Claro En El Valle | −34.7 | −70.9 | 349 | 1605 | 20.0 | VG | 2.5 | 0.7 |
| Rio Claro En Los QueñEs | −35.0 | −70.8 | 354 | 1857 | 23.8 | VG | 2.7 | 0.6 |
| Rio Sauces Antes Junta Con Ñuble | −36.7 | −71.3 | 607 | 1683 | 22.8 | VG | 2.9 | 0.6 |
| Rio Blanco En Curacautin | −38.5 | −71.9 | 171 | 1297 | 13.4 | VG | 2.9 | 0.3 |
| Rio Cautin En Rari-Ruca | −38.4 | −72.0 | 1306 | 1125 | 13.5 | VG | 2.9 | 0.4 |
| Rio Allipen En Los Laureles | −39.0 | −72.2 | 1675 | 1021 | 14.7 | VG | 2.5 | 0.4 |
| Rio Nilahue En Mayay | −40.3 | −72.2 | 309 | 914 | 14.5 | VG | 2.5 | 0.3 |
| Rio Liucura En Liucura | −39.3 | −71.8 | 349 | 1038 | 19.4 | MiG | 1.9 | 0.4 |
| Rio Liquine En Liquine | −39.7 | −71.8 | 368 | 1122 | 19.8 | PG | 1.5 | 0.3 |
| Rio Calcurrupe En Desembocadura | −40.3 | −72.3 | 1726 | 936 | 20.5 | PG | 1.6 | 0.3 |
| Rio San Juan En Desembocadura | −53.7 | −71.0 | 864 | 342 | 8.8 | SG | 4.0 | 0.8 |
| Rio Maule En Forel | −35.4 | −72.2 | 20,515 | 890 | 11.8 | MiG | 2.8 | 0.9 |
| Rio Lonquimay Antes Junta Rio Bio Bio | −38.4 | −71.2 | 467 | 1359 | 15.6 | MiG | 2.6 | 0.4 |
| Rio Cautin En Cajon | −38.7 | −72.5 | 2756 | 763 | 9.2 | VG | 3.0 | 0.5 |
| Rio Trancura En Curarrehue | −39.4 | −71.6 | 357 | 1195 | 20.2 | VG | 2.3 | 0.3 |
| Rio Trancura Antes Rio Llafenco | −39.3 | −71.8 | 1379 | 1147 | 18.3 | VG | 2.4 | 0.3 |
| Rio Rubens En Ruta N 9 | −52.0 | −71.9 | 504 | 415 | 7.4 | SG | 3.5 | 0.7 |
References
- Condon, L.E.; Atchley, A.L.; Maxwell, R.M. Evapotranspiration depletes groundwater under warming over the contiguous United States. Nat. Commun. 2020, 11, 873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patnaik, S.; Biswal, B.; Kumar, D.N.; Bellie Sivakumar, B. Regional variation of recession flow power-law exponent. Hydrol. Process. 2018, 32, 866–872. [Google Scholar] [CrossRef]
- Jachens, E.R.; Rupp, D.E.; Roques, C.; Selker, J.S. Recession analysis revisited: Impacts of climate on parameter estimation. Hydrol. Earth Syst. Sci. 2020, 24, 1159–1170. [Google Scholar] [CrossRef] [Green Version]
- Shao, C.; Liu, Y. Analysis of Groundwater Storage Changes and Influencing Factors in China Based on GRACE Data. Atmosphere 2023, 14, 250. [Google Scholar] [CrossRef]
- Karimi, S.; Seibert, S.; Laudon, H. Evaluating the effects of alternative model structures on dynamic storage simulation in heterogeneous boreal catchments. Hydrol. Res. 2022, 53, 562–583. [Google Scholar] [CrossRef]
- Adams, K.H.; Reager, J.T.; Rosen, P.; Wiese, D.N.; Farr, T.G.; Rao, S.; Haines, B.J.; Argus, D.F.; Liu, Z.; Smith, R.; et al. Remote sensing of groundwater: Current capabilities and future directions. Water Resour. Res. 2022, 58, e2022WR032219. [Google Scholar] [CrossRef]
- Brutsaert, W.; Nieber, J.L. Regionalized drought flow hydrographs from a mature glaciated plateau. Water Resour. Res. 1977, 13, 637–643. [Google Scholar] [CrossRef]
- Tallaksen, L. A review of baseflow recession analysis. J. Hydrol. 1995, 65, 349–370. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, W02429. [Google Scholar] [CrossRef] [Green Version]
- Biswal, B.; Marani, M. Universal recession curves and their geomorphological interpretation. Adv. Water Resour. 2014, 65, 34–42. [Google Scholar] [CrossRef]
- Parra, V.; Arumí, J.L.; Muñoz, E.I. Characterization of the Groundwater Storage Systems of South-Central Chile: An Approach Based on Recession Flow Analysis. Water 2019, 11, 1506. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Yeh, H. Impact of climate and NDVI changes on catchment storage–discharge dynamics in southern Taiwan. Hydrol. Sci. J. 2022, 67, 1834–1845. [Google Scholar] [CrossRef]
- Mendoza, G.F.; Steenhuis, T.S.; Walter, M.T.; Parlange, J.Y. Estimating basin-wide hydraulic parameters of a semi-arid mountainous watershed by recession-flow analysis. J. Hydrol. 2003, 279, 57–69. [Google Scholar] [CrossRef]
- Oyarzún, R.; Godoy, R.; Núñez, J.; Fairley, J.P.; Oyarzún, J.; Maturana, H.; Freixas, G. Recession flow analysis as a suitable tool for hydrogeological parameter determination in steep, arid basins. J. Arid. Environ. 2014, 105, 1–11. [Google Scholar] [CrossRef]
- Brutsaert, W. Long-term groundwater storage trends estimated from streamflow records: Climatic perspective. Water Resour. Res. 2008, 44, W02409. [Google Scholar] [CrossRef]
- Lin, K.T.; Yeh, H.F. Baseflow recession characterization and groundwater storage trends in northern Taiwan. Hydrol. Res. 2017, 48, 1745–1756. [Google Scholar] [CrossRef]
- Yan, H.; Hu, H.; Liu, Y.; Tudaji, M.; Yang, T.; Wei, Z.; Chen, L.; Ali Khan, M.Y.; Chen, Z. Characterizing the groundwater storage–discharge relationship of small catchments in China. Hydrol. Res. 2022, 53, 782–794. [Google Scholar] [CrossRef]
- Lin, L.; Gao, M.; Liu, J.; Wang, J.; Wang, S.; Chen, X.; Liu, H. Understanding the effects of climate warming on streamflow and active groundwater storage in an alpine catchment: The upper Lhasa River. Hydrol. Earth Syst. Sci. 2020, 24, 1145–1157. [Google Scholar] [CrossRef] [Green Version]
- Buttle, J.M. Dynamic storage: A potential metric of inter-basin differences in storage properties. Hydrol. Process. 2016, 30, 4644–4653. [Google Scholar] [CrossRef]
- Fan, Y.; Clark, M.; Lawrence, D.; Swenson, S.; Band, L.E.; Brantley, S.; Brooks, P.; Dietrich, W.; Flores, A.; Grant, G.; et al. Hillslope Hydrology in Global Change Research and Earth System Modeling. Water Resour. Res. 2019, 55, 1737–1772. [Google Scholar] [CrossRef] [Green Version]
- Shaw, S.B.; Riha, S.J. Examining individual recession events instead of a data cloud: Using a modified interpretation of dQ/dt -Q streamflow recession in glaciated watersheds to better inform models of low flow. J. Hydrol. 2012, 434, 46–54. [Google Scholar] [CrossRef]
- Sánchez-Murillo, R.; Brooks, E.S.; Elliot, W.J.; Gazel, E.; Boll, J. Baseflow recession analysis in the in land Pacific Northwest of the United States. Hydrogeol. J. 2015, 23, 287–303. [Google Scholar] [CrossRef]
- Brutsaert, W.; Lopez, J.P. Basin-scale geohydrologic drought Flow features of riparian aquifers in the southern Great Plains. Water Resour. Res. 1998, 34, 233–240. [Google Scholar] [CrossRef]
- Ceola, S.; Botter, G.; Bertuzzo, E.; Porporato, A.; Rodriguez-Iturbe, I.; Rinaldo, A. Comparative study of ecohydrological streamflow probability distributions. Water Resour. Res. 2010, 46, W09502. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Li, H.; Huang, M.; Ali, M.; Leng, G.; Leung, L.R.; Sivapalan, M. Regionalization of subsurface stormflow parameters of hydrologic models: Derivation from regional analysis of streamflow recession curves. J. Hydrol. 2014, 519, 670–682. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Krajewski, W. Analysing individual recession events: Sensitivity of parameter determination to thecalculation procedure. Hydrol. Sci. J. 2016, 61, 2887–2901. [Google Scholar] [CrossRef] [Green Version]
- Santos, A.C.; Portela, M.M.; Rinaldo, A.; Schaefli, B. Estimation of streamflow recession parameters: New insights from an analytic streamflow distribution model. Hydrol. Process. 2019, 33, 1595–1609. [Google Scholar] [CrossRef]
- Jachens, E.R.; Roques, C.; Rupp, D.E.; Selker, J.S. Streamflow recession analysis using water height. Water Resour. Res. 2020, 56, e2020WR027091. [Google Scholar] [CrossRef]
- Huang, C.C.; Yeh, H.F. Evaluation of seasonal catchment dynamic storage components using an analytical streamflow duration curve model. Sustain. Environ. Res. 2022, 32, 49. [Google Scholar] [CrossRef]
- DGA. Atlas del Agua: Chile 2016; DGA: Santiago, Chile, 2016; Available online: https://snia.mop.gob.cl/repositoriodga/handle/20.500.13000/4371 (accessed on 16 March 2023).
- Garreaud, R.; Vuille, M.; Compagnucci, R.; Marengo, J. Present-day South American climate. Palaeogeogr. Palaeoclim. Palaeoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Mendoza, P.A.; Boisier, J.P.; Addor, N.; Galleguillos, M.; Zambrano-Bigiarini, M.; Lara, A.; Puelma, C.; Cortes, G.; Garreaud, R.; et al. The CAMELS-CL dataset: Catchment attributes and meteorology for large sample studies—Chile dataset. Hydrol. Earth Syst. Sci. 2018, 22, 5817–5846. [Google Scholar] [CrossRef] [Green Version]
- Sernageomin. Mapa Geológico de Chile: Versión Digital; Servicio Nacional de Geología y Minería; Publicación Geológica Digital: Santiago, Chile, 2003.
- Rubio-Álvarez, E.; McPhee, J. Patterns of spatial and temporal variability in streamflow records in south central Chile in the period 1952–2003. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Voeckler, H.; Allen, D.M. Estimating regional-scale fractured bedrock hydraulic conductivity using discrete fracture network (DFN) modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Roques, C.; Rupp, D.; Selker, J. Improved streamflow recession parameter estimation with attention to calculation of −dQ/dt. Adv. Water Resour. 2017, 108, 29–43. [Google Scholar] [CrossRef]
- Troch, P.A.; De Troch, F.P.; Brutsaert, W. Effective water-table depth to describe initial conditions prior to storm rainfall in humid regions. Water Resour. Res. 1993, 29, 427–434. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, L.; Liu, T.; Li, J.; Feng, P. A Non-stationary Standardized Streamflow Index for hydrological drought using climate and human-induced indices as covariates. Sci. Total Environ. 2019, 699, 134278. [Google Scholar] [CrossRef]
- World Meteorological Organization. Standardized Precipitation Index User Guide. Available online: https://library.wmo.int/index.php?lvl=notice_display&id=13682 (accessed on 16 January 2023).
- Castro, L.; Gironás, J. Precipitation, Temperature and Evaporation. In Water Resources of Chile; Fernández, B., Gironás, J., Eds.; Springer: Cham, Switzerland, 2021; Volume 8. [Google Scholar] [CrossRef]
- Savenije, H.H. HESS opinions “topography driven conceptual modelling (FLEX-topo)”. Hydrol. Earth Syst. Sci. 2010, 14, 2681–2692. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Ameli, A. A statistical approach for identifying factors governing streamflow recession behaviour. Hydrol. Process. 2022, 36, e14718. [Google Scholar] [CrossRef]
- Fenta, M.C.; Anteneh, Z.L.; Szanyi, J.; Walker, D. Hydrogeological framework of the volcanic aquifers and groundwater quality in Dangila Town and the surrounding area, Northwest Ethiopia. Groundw. Sustain. Dev. 2020, 11, 100408. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Boisier, J.P.; Rondanelli, R.; Montecinos, A.; Sepúlveda, H.H.; Veloso-Aguila, D. The Central Chile Mega Drought (2010–2018): A climate dynamics perspective. Int. J. Climatol. 2019, 40, 421–439. [Google Scholar] [CrossRef]
- McNamara, J.P.; Tetzlaff, D.; Bishop, K.; Soulsby, C.; Seyfried, M.; Peters, N.E.; Aulenbach, B.T.; Hooper, R. Storage as a metric of catchment comparison. Hydrol. Process. 2011, 25, 3364–3371. [Google Scholar] [CrossRef]
- Dralle, D.N.; Hahm, W.J.; Rempe, D.M.; Karst, N.J.; Thompson, S.E.; Dietrich, W.E. Quantification of the seasonal hillslope water storage that does not drive streamflow. Hydrol Process. 2018, 32, 1978–1992. [Google Scholar] [CrossRef]
- Staudinger, M.; Stoelzle, M.; Seeger, S.; Seibert, J.; Weiler, M.; Stahl, K. Catchment water storage variation with elevation. Hydrol. Process. 2017, 31, 2000–2015. [Google Scholar] [CrossRef]
- Balocchi, F.; Flores, N.; Arumí, J.L.; Iroumé, A.; White, D.A.; Silberstein, R.P.; Ramírez de Arellano, P. Comparison of streamflow recession between plantations and native forests in small catchments in Central-Southern Chile. Hydrol. Process. 2021, 35, e14182. [Google Scholar] [CrossRef]
- Mutzner, R.; Bertuzzo, E.; Tarolli, P.; Weijs, S.V.; Nicotina, L.; Ceola, S.; Rinaldo, A. Geomorphic signatures on brutsaert base flow recession analysis. Water Resour. Res. 2013, 49, 5462–5472. [Google Scholar] [CrossRef] [Green Version]
- Sharma, D.; Patnaik, S.; Biswal, B.; Reager, J.T. Characterization of Basin-Scale Dynamic Storage–Discharge Relationship Using Daily GRACE Based Storage Anomaly Data. Geosciences 2020, 10, 404. [Google Scholar] [CrossRef]
- Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.-F.; Ducharne, A.; Yang, Z. Divergent effects of climate change on future groundwater availability in key mid-latitude aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef]



| SPI/SSI Values (*) | Category |
|---|---|
| 2 and above | Extremely wet |
| 1.5 a 1.99 | Severely wet |
| 1.0 a 1.49 | Moderately wet |
| −0.99 a 0.99 | Normal or near normal |
| −1.0 a −1.49 | Moderate drought |
| −1.5 a −1.99 | Severe drought |
| −2 and below | Extreme drought |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra, V.; Muñoz, E.; Arumí, J.L.; Medina, Y. Analysis of the Behavior of Groundwater Storage Systems at Different Time Scales in Basins of South Central Chile: A Study Based on Flow Recession Records. Water 2023, 15, 2503. https://doi.org/10.3390/w15142503
Parra V, Muñoz E, Arumí JL, Medina Y. Analysis of the Behavior of Groundwater Storage Systems at Different Time Scales in Basins of South Central Chile: A Study Based on Flow Recession Records. Water. 2023; 15(14):2503. https://doi.org/10.3390/w15142503
Chicago/Turabian StyleParra, Víctor, Enrique Muñoz, José Luis Arumí, and Yelena Medina. 2023. "Analysis of the Behavior of Groundwater Storage Systems at Different Time Scales in Basins of South Central Chile: A Study Based on Flow Recession Records" Water 15, no. 14: 2503. https://doi.org/10.3390/w15142503
APA StyleParra, V., Muñoz, E., Arumí, J. L., & Medina, Y. (2023). Analysis of the Behavior of Groundwater Storage Systems at Different Time Scales in Basins of South Central Chile: A Study Based on Flow Recession Records. Water, 15(14), 2503. https://doi.org/10.3390/w15142503






