Abstract
Vegetation in rivers and streams plays an important role in preventing erosion and improving bank stability. Comparison between emergent vegetation (bank vegetation) and submerged vegetation, in terms of velocity and Reynolds stress distributions, for the same aspect ratio and flow discharge, has received limited attention in the literature. This study investigates the velocity and Reynolds stress, as well as the log law for submerged and emergent vegetation in a laboratory flume and compares the results for a different set up with different sediment size and aspect ratio but the same discharge. The results indicate that the influence of submerged vegetation on the secondary currents generation is less than emergent vegetation. In addition, the log law application is valid for both submerged and emergent vegetation cases, however, it is valid up to y/h = 0.75 for emergent vegetation (in which the vegetation cover in banks is partly out of the water) but up to y/h = 0.25 for vegetation bank. For both submerged and emergent vegetation, Reynolds stress distribution presents a convex form but with a different turning point. Comparison of the results with those in an artificial pool over submerged vegetation and low aspect ratio (<5) keeps almost the same form for velocity and Reynolds stress distributions but decreases the turning point in Reynolds stress distribution. For the submerged vegetation cover, the location of zero shear stress superposes that of maximum velocity, but for the emergent vegetation approaching the bank vegetation and shifting the maximum velocity towards the bed, the location of zero shear stress approaches the bed.
1. Introduction
Environmental aquatic currents are rarely free of vegetative effects. Moreover, vegetation over the bed or banks exercises a dominant influence on the fluvial hydraulic studies, including drag coefficient, stable channel design, river plan and bed-forms characteristics [1,2,3,4,5,6,7]. Despite considerable investigations on the influence of vegetation in hydraulic projects, there are not many comparative studies for submerged and emergent vegetation in literature. The effect of vegetation can be better considered if one knows that about $1 billion was spent annually during 1990–2003 in USA to manage degraded streams [8,9]. Knowledge of the interaction of flow and vegetation enhances our understanding of sediment transport and resistance to flow because it influences the velocity and turbulent flow characteristics, including bed shear stress estimation. Stream flows over a vegetated bed channel can be observed in river floodplains during floods, or during drought when weeds grow on the bare bed [6,10,11]. Therefore, it is important to understand the impact of vegetation on the velocity and Reynolds stress distributions, which are the key parameters in almost all fluvial hydraulic studies. In fact, floodplain vegetation plays an important role in preventing erosion and improving bank stability. The influence of vegetation depends on many complex interacting factors, including distance from the bank vegetation to the measurement point and spacing of the vegetation, as well as the physical properties including the space of vegetation [12,13]. A survey of the literature suggests that many studies have focused on different aspects of velocity turbulent characteristics of vegetated channels [3]. There are two ways to investigate the effect of vegetation on flow structure: one is an application of rigid and cylindrical roughness and the other is natural vegetation application to simulate at the laboratory scale. Huai et al. investigated a vegetated channel using submerged rigid vegetation, while Stephan and Gutknecht used flexible vegetation in their investigation in a laboratory [14,15].
Kummu performed their laboratory experiments to investigate the relation between vegetation and flow resistance [16]. They found that the vertical velocity profile is logarithmically distributed between 0.1–0.6 water depths over vegetation. This means that some points near the top of the vegetation do not follow the log law. Stephan and Gutknecht presented a modified logarithmic velocity profile for flow over aquatic vegetation. They did not observe a decrease in turbulent intensity with decreasing relative submergence (h/yp) where h is water depth and yp is the deflected plant height in vegetated flow [15]. However, Shucksmith et al. carried out their experiments in various submerged and emergent natural vegetation. They found that vegetation causes uniform velocity distribution in vertical direction, and the velocity shear in submerged vegetation is more than an emergent one due to faster flow conditions over submerged vegetation [17]. Kumar and Sharma showed that the vertical velocity reduces in regions of free stream, but at the central axis of channel cross-section and Reynolds shear stress and turbulent intensity are weaker in magnitude at vegetation region. Accordingly, vegetation decreases the flow velocity, Reynolds shear stress and turbulence intensities, showing that vegetation plays an effective role to reduce the resistance in the flow [18]. Much less is understood on the comparison between vegetation in banks and vegetation over the bed for the same aspect ratio (the ratio of the width to flow depth) and flow discharge. Barahimi and Sui [3] found that over submerged vegetation, a high velocity gradient is observed near the bed up to z/h = 0.1, and a decreasing trend towards the water surface. In addition, the Reynolds stress distribution is influenced by the aspect ratio (W/h), showing an irregular distribution in the vertical direction [3].
Afzalimehr and Dey observed that the maximum velocity is located at y/h = 0.2, near the vegetated bank and gravel-bed stream at y/h = 0.56 in center of flume under uniform flow and aspect ratio of (W/h = 3) [19]. The position of maximum velocity in the presence of vegetation cover on the walls was located deeper from the water surface, and the dip distance (the location of the maximum flow velocity from the water surface) was observed to be up to 35%. Further, they found that the Reynolds stress distribution was nonlinear, even if the flow depth was constant along the flume with the maximum value near the bed [19]. Setayesh and Afzalimehr showed that Reynolds stress distribution displays a concave form for emergent vegetation and the best method of shear velocity estimation of application of Reynolds stress [20]. For constant flow depth, and equal water surface and bed slopes for vegetation banks over gravel bed, Afzalimehr et al. found that for the aspect ratio of W/h = 4, the maximum velocity occurs under water at a water depth of y/h = 0.46, and its difference with flow velocity near water surface is 50% [21]. Furthermore, in natural channels and W/h = 7, the maximum velocity in the central axis is located at the water surface, and for the near bank it is located on average at a water depth of y/h = 0.50. Thus, the vegetation cover on channel/flume banks may considerably affect the location of maximum velocity even for W/h > 5, due to development of secondary currents. In addition, Afzalimehr et al. found that the maximum Reynolds stress was near the vegetated banks and close to the channel bed at y/h = 0.1 [21].
The influence of aspect ratio was investigated in two parts: less than 5 and greater than 5, showing W/h = 5 as critical value, where the flow reveals different patterns. When W/h < 5, the flow is 3D and corner flows are developed because the banks produce anisotropy of turbulence and the velocity dip (the occurrence of the maximum velocity under the water surface). However, when W/h > 5, the bank effect on the velocity decreases and the maximum velocity occurs at the water surface. Some researchers are pioneers to consider a relation between the aspect ratio and generation of secondary currents [22,23]. They found that nonlinear distribution of shear stress and occurrence of the maximum velocity under the water surface is caused by secondary currents. Accordingly, any change in aspect ratio when it is less than 5 indicates similar patterns. Also, similar patterns are observed when the aspect ratio is larger than 5, indicating that it makes no difference to the velocity and Reynolds stress distributions if W/h is 2 or 4 [24].
In addition, the vegetation covering the bed has small influence on the generation of secondary currents. Huai et al. conducted their experiments over stiff and artificial vegetation cover under uniform flow and found that small aspect ratio did not affect the generation of secondary currents [14]. Carrollo et al. observed an inflection point in velocity profile, which is superposed on the maximum turbulence intensity [25]. Jarvela used wheat stems with a density of 12,000 per square meter and found the occurrence of maximum Reynolds stress (RS) slightly above the top of flexible vegetation [12]. Other investigators have noted that the RS distribution over stiff and flexible vegetation covers is nonlinear in a way that, at the top of vegetation, RS is maximum and then decreases towards the water surface [14,26,27]. Yang et al. found that the Reynolds shear stress in the upper layer of a uniform narrow channel is negative and the zero shear stress would therefore be observed below the free surface [28].
Understanding the difference between submerged and emergent vegetation effects on the velocity and Reynolds stress distributions can improve the estimation of roughness and drag coefficients. The objective of this study is to investigate this comparison for the velocity and the Reynolds stress under similar aspect ratio and discharge, as well as to investigate the limit of the log law application for submerged and bank vegetation (emergent case) in a laboratory flume. To better present the results of this study, the authors compare their results with those of Parvizi et al. [2] in an artificial pool with submerged vegetated cover in laboratory flume.
2. Materials and Methods
Most experimental studies of natural channels and rivers are conducted in straight flumes in a laboratory, so that the flow patterns are studied under controlled conditions (e.g., Nepf [29] and Wang et al. [30]). Moreover, in rivers, a straight reach is considered to study the flow structures ignoring small variations of width (e.g., Julien) [29,30,31].
In this study, the experiments were conducted in a 20 m long, 0.6 m wide and 0.6 m deep glass-walled rectangular flume, at hydraulic laboratory in University of Science and Technology, Tehran, Iran. A movable weir located at the downstream end of the flume was used to obtain quasi-uniform regime conditions along the vegetated zone. The quasi- uniform flow is considered over rough bed such as gravel-bed streams or submerged vegetation where the depth and velocity are constant alone the stream. The slope of the flume was set to 0.005. A limnimeter was used to record the depth of water along the flume and to determine the water surface profile. Experiments were conducted in four runs. Run 1 and run 2 were carried out over submerged vegetation (wheat stems); run 3 and run 4 were investigated in flow over gravel bed and vegetation banks. The bank and bed vegetation have different characters. The bank vegetation is relatively more moisture-demanding. On the other hand, on a typical bed in rivers, light-demanding and shade-tolerant species (i.e., grasses and vegetation cover such as “Arundo donax”) live together.
For runs 1 and 2, sprouts of wheat were planted from 11.5 m to 14.5 m from the entrance of the flume, and the walls were glassy (Figure 1a). The planted wheat over the bed was long enough to have high flexibility and wavy motion. The rest of the flume bed was covered with gravel, which had a median grain size of = 21 mm with a standard deviation of less than 1.3. Gravel size can only change the results when relative submergence (h/) is less than 3. In these conditions, the log law and the boundary layer theory applications are invalid. This statement was confirmed by other studies (e.g., Afzalimehr, Simons, Graf and Altinakar, and Song and Chiew [23,32,33,34]. These studies show that for all changes in gravel size for (h/) > 3, the Reynolds stress and turbulence intensity distributions remain stable, showing a convex distribution decelerating flow and concave distribution for accelerating flow in open channels.
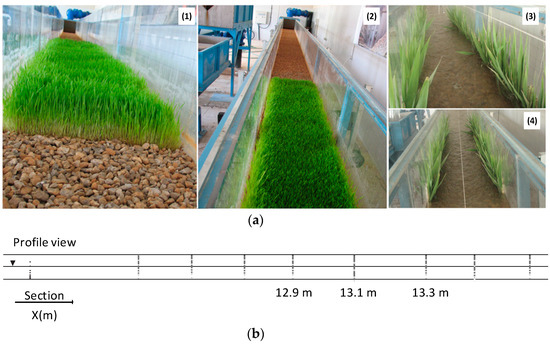
Figure 1.
(a). Experimental set up showing: (1 and 2) Wheat sprout canopy; (3 and 4) Wheat stems on bank. (b). Measured velocity points of experimental set up, at the distance of 12.9, 13.1, 13.3 m from the entrance of the channel.
The height of submerged wheat was not changed during the tests, and density of wheat stems was kept at 45,604 per square meter in both runs. For runs 3 and 4, “Arundo donax”, the selected plant, which was collected from surroundings of a gravel-bed river in Iran, was fixed to the banks of the flume and the bed was covered by gravel (Figure 1). Table 1 shows the hydraulic characteristics of laboratory experiments set up and a summary of experimental data for this study. Flow discharges were selected between 0.037–0.055 m3/s and water depth was fixed between 11 and 15 cm.

Table 1.
Hydraulic conditions of laboratory experiments.
The aspect ratio W/h ≤ 5 has been considered as a criterion for narrow open channels in which the velocity dip (the maximum velocity occurs under water surface) occurs and the banks produce anisotropy of turbulence. The dip phenomenon has been confirmed by using advanced tools such as the High-power laser Doppler anemometer (LDA) system by Nezu, Nakagawa, and the Acoustic Doppler Velocity Profiler ADVP by Graf and Altimakar for W/h ≤ 5 or slightly larger. They used W/h ≤ 5 as a range where the flows are considered 3D [22,23]. Acoustic Doppler Velocimeter (ADV) is a Nortek Vectrino that measures the instantaneous three-dimensional velocity components. The change of flow discharge has no effect on the shape of distribution but leads to higher values of velocity (Afzalimehr and Rennie [35,36]).
Moreover, water depth influences the velocity and Reynolds stress distributions, when the relative submerge changes from (h/) > 3 to (h/) < 3, where h is the flow depth and d50 the median gravel size (Afzalimehr) [32]. Since the experiments in this study were conducted for (h/) > 5, the change of flow depth has no effect on the results. In addition, for runs 1 and 2, yp is the plant height.
A down looking Acoustic Doppler Velocimeter (ADV), 10MHz Nortek Vectrino, was used to measure the instantaneous three-dimensional velocity components. The ADV used in this study has the precision of ±0.1 mm s−1 and a sampling volume with a height of 5.5 mm. After measurements, the data were filtered with a WinADV program. WinADV helps to select suitable series data for velocity to draw reliable results. Accordingly, the coefficiency of determination (R2) for most data collection was over 95 percent, and signal to noise ratio (SNR) was over 15. Data with SNR lower than or equal to 5 and an average correlation of less than 70% were removed from data set. Collecting data with sampling frequency f = 200 Hz and sampling time 120 sec leads to more than 24,000 observations at each point of velocity and Reynolds stress profile. This shows a great repeatability of data at each point. Accordingly, even if 10% of data were not suitable at each point, the analysis was done with more than 21,000 data points, resulting in high certainty in results.
To investigate the occurrence of fully developed flow along the vegetation patch, the measurements of velocity profiles were made in three cross sections: 12.9, 13.1 and 13.30 m (Figure 2), from the beginning of the channel at three different distances of 5, 12 and 30 cm from the bank (D). About 19 to 23 point velocity values were measured in each velocity profile, and approximately 7 points were measured in the region near the bed (y/h < 0.2); where y is distance of each measuring point from the top of vegetation cover. However, for runs, 1 and 2, ADV was not able to measure velocity inside the vegetation cover and the top of gravel for runs 3 and 4. In each case, two runs with selected discharges and flow depths were carried out.
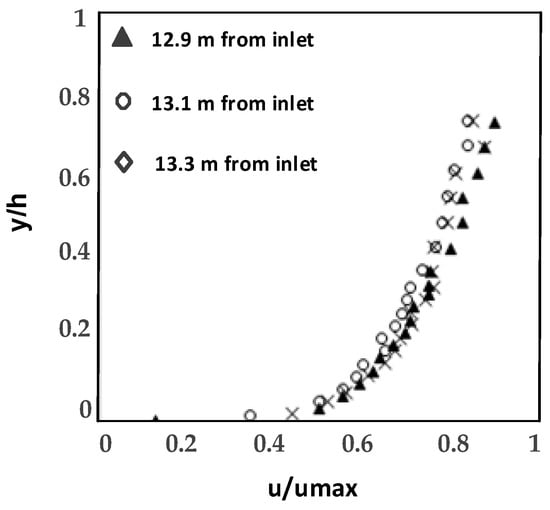
Figure 2.
Fully developed flow presentation at the distance of 12.9 m from the flume entrance.
The vertical dotted line in Figure 1b, before 12.9 m, shows the sections where velocity profiles were measured to check the fully developed flow condition. This condition reached after 12.9 m from the flume entrance. Moreover, the vertical dotted lines shown in Figure 1b, after 13.3 m were considered to be sure that the velocity distributions remain similar toward the end of the flume.
The beginning of the channel was at three different distances of 5, 12 and 30 cm from the bank (D) (Figure 1b). About 19 to 23 point velocity values were measured in each velocity profile, and approximately 7 points were measured in the region near the bed (y/h < 0.2); where y is distance of each measuring point from the top of vegetation cover. However, for runs 1 and 2, ADV was not able to measure velocity inside the vegetation cover and the top of gravel for runs 3 and 4. In each case, two runs with selected discharges and flow depths were carried out. In addition, our results were compared with those of Parvizi et al. [2] who studied the same flow discharge of 0.037 m3/s over an artificially vegetated and non-vegetated pool, with 5° slope in the entrance and exit section of the pool. Their experiments were conducted in a laboratory flume with W = 0.4 m, h = 0.20 m, an aspect ratio of 2, and a d50 of 10.4 mm. The vegetation cover over the examined pool was almost the same as the present grass canopy. The comparison of results of Parvizi et al. [2] with the present study is presented in the discussion section.
The velocity distribution by the log law is presented for flow over vegetation cover as:
where u is the mean point velocity, is the shear velocity, k is the von Karman constant (equal to 0.4), is the roughness scale, and C is a constant. This study applies the following relation developed by Stephan and Gutknecht [15].
where y is a distance from the bed, is the thickness of vegetation cover, which was used on the bed in the laboratory. Since ADV cannot collect data inside the dense vegetation, all measurements of velocity are conducted from the top of vegetation. The constant of 8.5 is the universal value for the flow over the rough boundaries. The following relation for the case of bank vegetation and gravel bed:
where y is the distance from the top of gravel. Due to a micro variation in gravel bed surface, a reference level is defined as 0.1d50 under tops of gravel particles where y = 0. Therefore, addition of 0.1d50 in numerator of (3) causes a better fitness of the log law to the velocity points in the logarithmic region. C is a constant that depends on the flow conditions and roughness size. The value of C has been reported 8.5 by Graf and Altinakar [23], however, there is no universal value for C.
The value of 0.1d50 for this study is different from the one used in other studies. For example, Graf and Altinakar use 0.2d50 in order to show a better presentation of data fitness by the log law. The reason for not using any modification factor in Equation (2) such as 0.1yp is the insignificant change in the presentation of the log- law fitness by this modifying factor.
3. Results
3.1. Comparison of Velocity Distributions for Submerged and Emergent Vegetation Covers
Although the gravel bed from the entrance to x = 11.5 m prompts the fully developed flow in the flume (Figure 2), the variation of bed roughness from gravel to vegetation cover (wheat stems) causes the development of a new boundary layer. Figure 2 reveals that after x = 12.9 m from entrance of the flume in this experimental set up, the new boundary layer reaches a fully developed condition where flow velocity profiles are similar at different distances from the leading end of the flume (where water enters to the flume). The horizontal axis shows the mean point velocity (u) normalized by the maximum velocity () in each profile, and y/h shows the flow depth at each point from the bed (y) normalized by total flow depth (h). Therefore, all results for this experimental set up are presented after x = 12.9 m from the channel entrance. Some deviations from unique curves are observed in Figure 2, which may be ascribed to some uncertainty associated with the definition of reference level where u = 0. Since measurements inside the vegetation cover have considerable limitations with ADV, the flow velocity was measured from the top of submerged vegetation (Figure 1a). Figure 2 shows that for the range of 0 < y/h ≤ 0.2, the velocity gradient is different from y/h > 0.2 (y is the distance of each point velocity from the top of gravel or vegetation). This is due to a strong shear layer effect on the velocity distribution near the top of vegetation (run 2).
Figure 3 confirms the validity of the log law from the top of vegetation up to y/h = 0.23. The mentioned distance of y/h = 0.23 shows the deviation of the log law from the measured data in y/h > 0.23. This means the data above the bed up to y/h = 0.23 follows the log law distribution and from y/h > 0.23 toward the water surface this law is invalid. The reason for deviation of data from this law is inapplicability of mixing length theory to quasi-uniform flow, and resistance to flow due to vegetation and gravel. In fact, deviation of measured velocity points is due to the effect of pressure gradient changes, the boundary layer thickness, and the maximum velocity In Figure 3a,b the change of gradient is clearly observed, however, in Figure 3c, the deviation point is not clearly observed. The general rule for choice of deviation point of the inner and outer regions of the boundary layer is to use the coefficient of determination (R2) between u/umax and Ln(y/d50) or Ln (y/yp). In this study, the value of R2 ≥ 0.98 in the logarithmic zone was considered as the deviation point where the data are deviated from the log law zone. The value of R2 decreases after the selected deviation point towards the water surface.
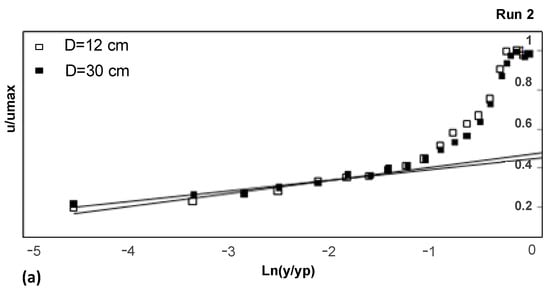
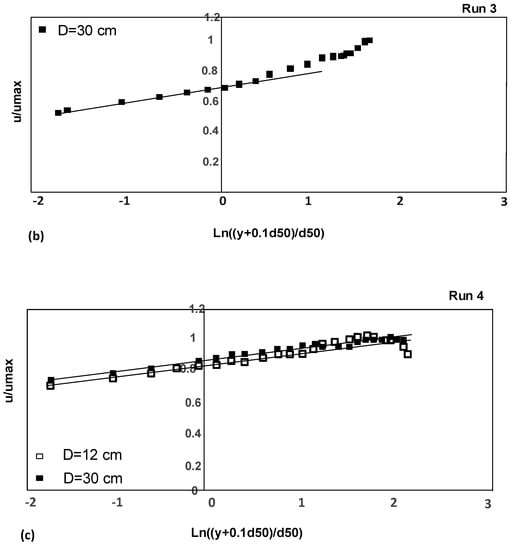
Figure 3.
(a) The log-law validation for different conditions for submerged vegetation (run 2). (b,c) The log-law validation for different conditions: (b) for the gravel bed without vegetation in bed and banks in the central axis (run 3); (c) for the emergent vegetation in banks and gravel bed (run 4).
The maximum velocity occurs under the water surface for 3D flow in which bank effect causes a strong lateral velocity component (v). This component is directed near the water surface from the bank to the flume center, and a down flow (w < 0) occurs from the water surface. This difference of velocity components v and w generates the secondary currents. The larger is this difference, the stronger will be deviation of the log law in velocity data far from the bed (Figure 3a). The reason for this deviation is invalidity of two assumptions in the log law application: (1) constant shear stress throughout the fluid, and (2) mixing length approximation l = ky, in which k is von Karman constant and y is the distance from the bed. In addition, the choice of 0.1d50 for the gravel bed has some uncertainties. In other words, if one uses a plot with constant particle diameter, there is less uncertainty in application of the log law compared to gravel bed streams.
There are two differences between the case of vegetation on banks and gravel over the bed with the case of vegetation over the bed and bare banks (Figure 4): (1) the former case has lower velocity gradient and the velocity values over vegetation are less than those over gravel with bank vegetation (Figure 4). Since the flow discharge is almost the same for both cases, the reason for decreasing velocity values may be explained by passing some part of flow through the vegetation cover, which causes the diminution of flow velocity. (2) The bank vegetation accelerates the secondary currents, and for a small aspect ratio (W/h < 5) the maximum velocity occurs far from the water surface. The dip phenomenon (the location of the maximum velocity from the water surface) is strengthened when approaching the bank vegetation and the difference between the last measuring point velocity with the maximum velocity reaches 50%. It is noted that such a velocity distribution is not observed for the flow in submerged vegetation (Figure 4a), where the velocity profiles show no significant decreasing trend with approaching to the water surface.
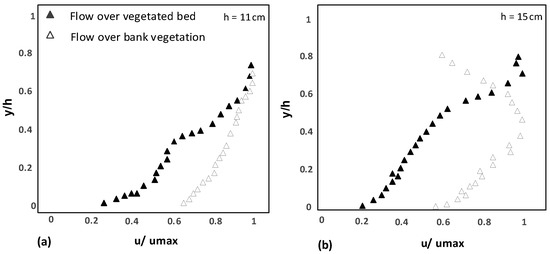
Figure 4.
Velocity distributions: (a) The flow depth of 11 cm; (b) The flow depth of 15 cm.
Considering the equations 2 and 3 for the case W/h = 5.4 (runs 2 and 3), the log-law validity zone is up to y/h = 0.2 for all the velocity profiles at different distances from the vegetation bank. This relative depth (y/h = 0.2) is considered as a classic thickness for validity of log law over gravel and sand bed. However, for run 4, where W/h = 4, the log law can extend up to 0.75 y/h, and for cases near the bank it reaches y/h = 0.25 (Figure 3c).
Figure 4 shows that when aspect ratio is less than 5 the velocity distribution displays different patterns depending on secondary currents power. In Figure 4a,b for submerged vegetation, an irregular velocity profile (flow over vegetated bed) is observed, but for emergent vegetation (bank vegetation) a convex form is observed in which the turning point depends on aspect ratio and pressure gradient. The irregular velocity profile in which a significant change in velocity is observed towards the water surface is due to turbulent structures developed by flow wake around the submerged vegetation and the form-induced stress by vegetation.
3.2. Comparison of Reynolds Shear Stress for Submerged and Emergent Vegetation
Figure 5a shows a convex distribution of RS for flow over gravel with vegetation banks (emergent vegetation). The convex form is due to the interaction of small aspect ratio and decelerating flow near the rough bed. Near the rough bed for decelerating flow in which the velocity decreases and pressure increases, a positive pressure gradient develops in the flow direction. Based on Navier Stocks equation, ∂p/∂x = ∂τ/∂y when pressure gradient increases, the vertical Reynolds stress increases as well. Therefore, an increasing trend is observed near the bed for RS distribution. However, RS should reach zero at the water surface, this leads to convex distribution for RS. This convex form occurs for any roughness, vegetation cover and gravel under decelerating flow, however, in Figure 5a the convex form may be observed near the water surface where ADV needs an additional probe to reveal it.
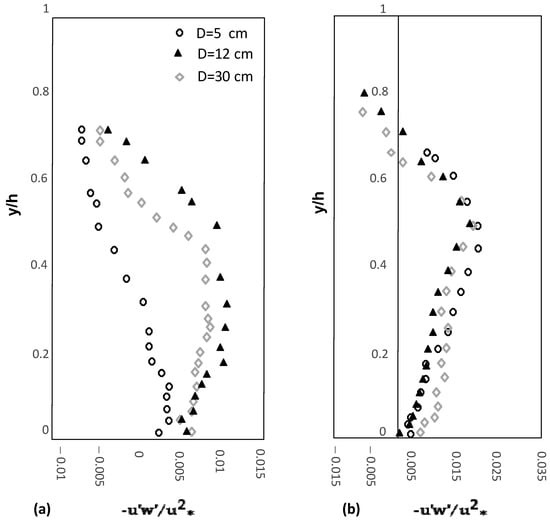
Figure 5.
Reynolds stress distributions: (a) for emergent vegetation with gravel bed; (b) over submerged vegetation. (y) is normalized by the total flow depth (h).
The change in the location of zero RS is due to variations in longitudinal pressure gradient in different distances from the vegetated bank. Figure 5a clearly shows the Reynolds stress distribution changes at different distances from the bank; this is due to a change in longitudinal pressure gradient. Reynolds equation ∂τ/∂y = ∂p/∂x states [36] that a vertical change in Reynolds stress distribution is due to a longitudinal change in pressure gradient. This situation occurs for emergent vegetation due to the considerable effect of bank roughness on the Reynolds stress distribution.
Figure 5b shows the flow over a submerged vegetation. It shows that the RS distribution is nonlinear, but the maximum RS occurs above vegetation at y/h = 0.5. It is noted that above the bed vegetation, there is a strong horizontal shear layer, which diffuses vertically inside of the vegetation cover.
The vegetation over the bed generates high drag force due to additional turbulence, which shifts the maximum turbulent stress to a level above the top of the vegetation cover. In this research, due to high density of vegetation (45,604 wheat stems per square meter), the vertical momentum between flow and vegetation cover decreases and consequently the maximum of RS shifts to the upper flow depth.
The negative values for y/h > 0.7 indicate the effect of secondary flows and the occurrence of the maximum flow velocity under the water surface. The vegetation cover on the bed generates a quasi-uniform flow in which there is a non-zero pressure gradient. This non-uniform pressure gradient should reach equilibrium by the vertical shear stress. Since the vegetation bed decelerates the flow, an unfavorable pressure gradient is developed, with a positive sign demanding a positive pressure gradient. Therefore, Reynolds stress increase up to y/h = 0.5 and then decreases towards the water surface [37]. As Figure 5b shows, the location of Reynolds stress distribution across the flume does not influence the convex distribution, and for all distances from the bank the maximum RS occurs at y/h = 0.5 for submerged vegetation and bare banks.
Comparison of submerged and emergent vegetation covers reveals that for both cases, the Reynolds stress distribution is nonlinear, although the flow depth is constant. This shows that for both submerged and emergent vegetation covers, the change of aspect ratio (W/h) influences the location of the maximum Reynolds stress (Figure 5). In Figure 5a, at a distance of 5 cm from the bank, RS distribution is non-linear, showing the maximum RS at y/h = 0.15. There is a difference between RS at 12 cm from the bank in Figure 5a,b. This can be clearly observed by comparing the slope of RS for 12 cm from the bank in y/h < 0.5 for both figures.
In Figure 5a, with a constant aspect ratio, by approaching the bank vegetation the maximum Reynolds stress location is close to the gravel bed. Moving away from the bank vegetation towards the central axis of the flume, the location of maximum Reynolds stress for both submerged and emergent vegetation becomes almost the same.
In addition, although Figure 5b is presented for W/h = 4, it is observed that the change in the location of Maximum Reynolds stress is less affected by aspect ratio due to different roughness of bank for submerged (glass) vs. emergent (vegetation cover). It is observed that the role of secondary currents for the case where the bank is covered with vegetation is stronger than that of the bank with glass. Comparison of Figure 5 and Figure 6 reveals a convex form for RS distribution. This comparison shows that for the submerged vegetation and different distances from the bank, the location of zero or maximum RS is almost the same. However, for emergent vegetation, the distance from the bank plays a significant role in the RS distribution in a manner that at the distance of 5 cm from the vegetation bank its value decreases considerably, reaching near the gravel bed.
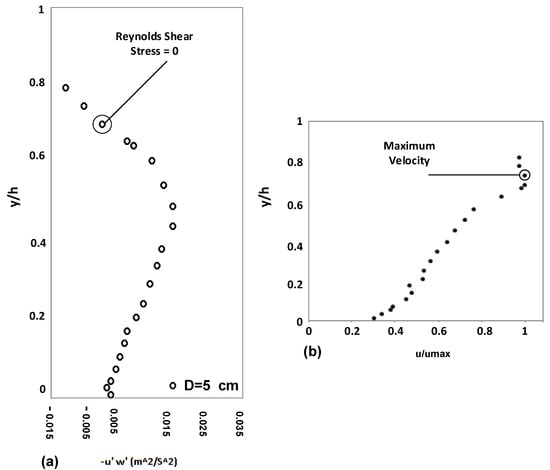
Figure 6.
(a) Location of zero Reynolds stress over submerged vegetation cover. (b) Location of maximum point velocity over submerged vegetation cover.
Since the zero Reynolds shear always corresponds to the zero-velocity gradient or maximum velocity, Figure 6 demonstrates that the location of zero RS in the Reynolds stress profiles is superposed with the location of maximum velocity for the flow over submerged vegetation cover. However, for the flow over gravel with vegetation banks, such a superposition is not considered, but it is possible to observe the change of location of zero Reynolds stress with the maximum velocity location with approaching the vegetated banks.
Comparison of the results of experimental set up to those of Parvizi et al. over an artificial pool [2] shows that the vegetation arrangement (submerged and emergent), and the sediment size and bed geometry influence the flow velocity distribution and Reynolds stress distribution, but not the log law validation and convex form of Reynolds stress distributions (Figure 7 and Figure 8). Interestingly, no irregular velocity profile is observed for submerged vegetation over an artificial pool.
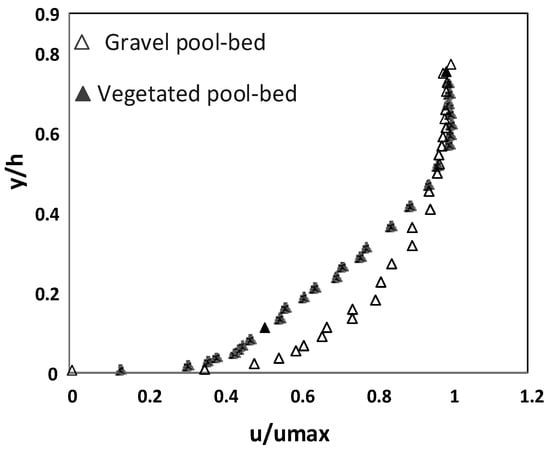
Figure 7.
Velocity distributions in pool bed by Parvizi et al. [2].
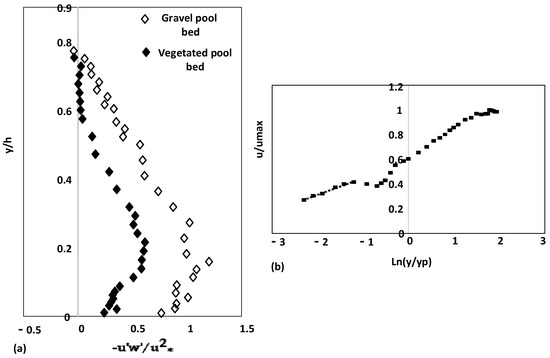
Figure 8.
Flow over Pool with submerged vegetation by Parvizi et al. [2]: (a) Distribution of Reynolds shear stress over gravel bed and vegetated canopy; (b) Validation of logarithmic law in vegetated pool.
In the artificial pool examined by Parvizi et al. [2], the velocity, flow depth and shear stress change at different sections along the pool, generating various flow conditions, including decelerating flow in the entrance region, quasi-uniform flow at the middle section and accelerating flow at the exit region of the pool.
In an artificial pool with an aspect ratio of 2 covered by submerged vegetation, the main difference is the decrease of the turning point keeping the convex distribution of Reynolds shear stress. This difference directly affects estimation of shear velocity and drag coefficiency. The negative values of Reynolds stress are rarely observed for this submerged vegetation over bed form, while it is observed for emergent vegetation due to dip phenomenon (the location from the water surface). The above considerations show that aspect ratio does not play a significant role on the estimation of Reynolds stress, as well as drag coefficient determination in submerged vegetation compared to the emergent vegetation, which plays a significant role. This will help engineers consider the role of distance from wall vegetation in estimation of hydraulic parameters only for emergent vegetation.
4. Discussion
Figure 3 shows that the log law is valid for both submerged and emergent vegetation but with different thickness near the bed. Deviation from the log law is significant in the outer layer for the submerged vegetation; this is due to vegetation roughness, which is different from gravel roughness. The significant deviation in the log law application for submerged vegetation causes the von Karman constant to reduce κ = 0.16 as reported by Afzalimehr et al. [38]. This value (κ) is obtained from the average of many different profiles. The small values of von Karman constant have been reported by Yalin [39] as κ =0.16 for sand-bed streams and as κ =0.21 by Vanoni [40] for suspended sediment. Therefore, submerged vegetation causes the value of von Karman constant decreases making significant difference with the reported value in literature for universal von Karman constant 0.4 in gravel-bed streams. Distance from the bank vegetation does not significantly affect the log law thickness, showing suitable performance of this law across a natural stream with gravel-bed and bank vegetation in emergent cases.
Figure 4 shows that when the aspect ratio decreases (W/h < 5), the velocity distribution is influenced more significantly by the emergent vegetation in banks than the submerged vegetation on the bed. However, this is not observed for the aspect ratio (W/h > 5). This is partly due to certain limitations of ADV to collect data in small aspect ratio. The reason for observing the dip phenomenon for emergent case with (W/h < 5) is a better performance of ADV to reveal the interaction of gravel-bed with the bank vegetation in generation of secondary currents, which forces the location of the maximum velocity reach near the bed. The change of location is important in application of the boundary layer theory to estimate drag coefficient because the emergent vegetation decreases the thickness of the boundary layer zone whose data is used to determine shear velocity. In Figure 4 for h = 11 cm where (W/h > 5), the turning point is not observed in the velocity distribution, showing lack of measuring by ADV probe for shallow flow near the water surface. Experience with ADV shows that near the water surface, data keep the same trend that they have at last points measured by ADV towards the water surface. Using additional probes to collect data near the water surface region may provide potentially useful information but requires additional resources. However, comparison of data obtained near the bed with that near the water surface confirms a good agreement between bottom shear velocities, calculated using the Reynolds stress (using all data in Reynolds stress profile) and the logarithmic law methods, which uses only the near-bed data.
The density of vegetation covering the experimental set up of this study is almost the same as the pool set up built by Parvizi et al. [2], but with a very thin layer of vegetation in comparison to the present work. The authors did not exclude the influence of the aspect ratio (W/h) considering Figure 5b and Figure 8a. In fact, for Figure 5b the aspect ratio is 4 or 5.4 but for Figure 8a, it is 2. This difference forces the location of maximum Reynolds stress approaching the bed for W/h = 2.
The different size of gravel in this study and that used in Parvizi et al. [2] have no significant impact on the shape of RS distribution, as both Figure 5b and Figure 8a show a convex form, and for both cases a polynomial fit can be used to determine bed shear stress. All measurements were conducted over the vegetation patch in the region where flow reached the fully developed condition, and the submerged vegetation front area has no effect in the estimation of hydraulic parameters.
In rivers and natural channels, submerged and emergent vegetation covers are observed in banks frequently. However, no roughness coefficient or sediment transport parameter such as Shields parameter considers the simultaneous effect of submerged and emergent vegetation in their estimations. Many hydraulic models in river engineering are based on the assumptions to simplify the calculation process, which leads to over or under estimation of results, increasing the cost of river restoration projects and decreasing the accuracy of key parameter estimations. Accordingly, in future studies, researchers should apply a mixed estimation of key hydraulic parameters in rivers, which are affected by the presence of vegetation on beds and banks.
The limitation of ADV to detect flow characteristics very near the bed (h < 4 mm) calls to use better instruments such as PIV, which are very suitable for collecting data with more details in laboratory studies.
5. Conclusions
Understanding the effects of submerged and emergent vegetation covers on the velocity and Reynolds stress distribution is important for hydraulic designers and engineers who work in fluvial projects. Using two setups in the presence of submerged and emergent vegetation over flat bed and an artificial bedform, the following results are obtained in this study:
- In emergent vegetation, the velocity distribution is influenced by a small aspect ratio (W/h < 5) forcing the maximum velocity to move towards the bed. However, in the submerged vegetation, the velocity distribution is less influenced by the aspect ratio, showing the location of maximum velocity far from the bed.
- The log law is valid up to y/h = 0.23 for the flow over submerged vegetation in different aspect ratios. However, for emergent vegetation, the validation zone depends on the distance from the vegetation bank; at small aspect ratio and the central axis of the flume, this law is valid up to y/h = 0.75.
- Reynolds stress (RS) distributions show a convex form for submerged and emergent vegetation covers at different aspect ratios. However, approaching the bank vegetation (emergent case), the power of secondary currents increases, forcing the maximum RS shifts towards the bed.
- For the aspect ratio of W/h = 4 and flow over submerged vegetation, the location of zero shear stress superposes that of maximum velocity. However, in emergent vegetation, such a superposition is not considered. Further, approaching the bank vegetation and shifting the maximum velocity towards the bed, the location of zero shear stress approaches the bed.
- The results of this research show that estimation of key parameters of fluvial projects, velocity and Reynolds stress is influenced by the vegetation arrangements, submerged or emergent. Therefore, a better estimation of these parameters influences drag coefficient and sediment determinations, improving bank stability with reasonable channel design, reducing the cost of project and modifying the input data for hydraulic models.
Author Contributions
Methodology, P.P., M.R.T.M. and H.A.; Validation, S.A. and M.R.T.M.; Formal analysis, M.R.T.M.; Investigation, M.R.T.M.; Writing—original draft, M.R.T.M.; Writing—review & editing, P.P., M.R.T.M., H.A. and S.A.; Visualization, M.R.T.M.; Supervision, H.A. and S.A.; Project administration, P.P. and M.R.T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| d50 | Median diameter of sediment particles |
| C | Constant of the log law |
| D | Distance from the wall |
| yp | Plant height (for run 1 and 2) |
| h | Water depth above the vegetation (for run 1 and run 2) and water depth over gravel bed (for run 3 and run 4) |
| W | Flume width |
| ks | Roughness scale (equivalent sand roughness) |
| Q | Flow discharge |
| u | Mean point velocity |
| uave | Average velocity at a section; |
| umax | Maximum velocity |
| u’ | Turbulence intensity in longitudinal direction |
| w’ | Turbulence intensity in vertical direction |
| u* | Shear velocity |
| y | Distance from top of gravel or vegetation cover |
| Y | Distance from the bed |
| κ | von Karman constant |
References
- Shi, H.; Huai, W. Flow structure of open channel flow with partly submerged vegetation. In Proceedings of the 12th International Symposium on Ecohydraulics, Tokyo, Japan, 19–24 August 2018. [Google Scholar]
- Parvizi, P.; Afzalimehr, H.; Sui, J.; Raeisifar, H.R.; Eftekhari, A.R. Characteristics of Shallow Flows in a Vegetated Pool—An Experimental Study. Water 2023, 15, 205. [Google Scholar] [CrossRef]
- Barahimi, M.; Sui, J. Effects of Submerged Vegetation Arrangement Patterns and Density on Flow Structure. Water 2023, 15, 176. [Google Scholar] [CrossRef]
- Soltani, N.; Afzalimehr, H.; Shahiri Tabarestani, E.; Eftekhari, A.; Khabari, M.; Nazari-Sharabian, M.; Karakouzian, M. Turbulence Characteristics in Mild and Steep Entrance Slopes of Pool-Riffle Sequences. Water 2023, 15, 720. [Google Scholar] [CrossRef]
- Kazem, M.; Afzalimehr, H.; Sui, J. Characteristics of Turbulence in the Downstream Region of a Vegetation Patch. Water 2021, 13, 3468. [Google Scholar] [CrossRef]
- Sohrabi, S.; Afzalimehr, H.; Singh, V.P. Estimation of drag coefficient of emergent and submerged vegetation patches with various densities and arrangements in open channel flow. ISH J. Hydraul. Eng. 2022, 29, 297–307. [Google Scholar] [CrossRef]
- Hopkinson, L.; Wynn, T. Vegetation impacts on near bank flow. Ecohydrol Ecosyss Land Water Process. Interact. Ecohydrogeomorpho. 2009, 2, 404–418. [Google Scholar] [CrossRef]
- Bernhardt, E.S.; Palmer, M.A.; Allan, J.D.; Alexander, G.; Barnas, K.; Brooks, S.; Carr, J.; Clayton, S.; Dahm, C.; Follstad-Shah, J.; et al. Synthesizing U.S. river restoration efforts. Science 2005, 308, 636–637. [Google Scholar] [CrossRef] [PubMed]
- Aberle, J.; Järvelä, J. Flow resistance of emergent rigid and flexible floodplain vegetation. J. Hydraul. Res. 2013, 51, 33–45. [Google Scholar] [CrossRef]
- King, A.T.; Tinoco, R.O.; Cowen, E.A. A k–ε turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 2012, 701, 1–39. [Google Scholar] [CrossRef]
- Yagci, O.; Kabdasli, M. The impact of single natural vegetation elements on flow characteristics. Hydrol. Process. 2008, 22, 4310–4321. [Google Scholar] [CrossRef]
- Järvelä, J. Effect of submerged flexible vegetation on flow structure and resistance. J. Hydrol. 2005, 307, 233–241. [Google Scholar] [CrossRef]
- Thorne., C.R. Effects of vegetation on riverbank erosion and stability. In Vegetation and Erosion; Wiley: Chichester, UK, 1990. [Google Scholar]
- Huai, W.X.; Zeng, Y.H.; Xu, Z.G.; Yang, Z.H. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water. Res. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Stephan, U.; Gutknecht, D. Hydraulic resistance of submerged flexible vegetation. J. Hydrol. 2002, 269, 27–43. [Google Scholar] [CrossRef]
- Kummu, M. Roughness Characteristics and Velocity Profile in Vegetated and Nonvegetated Channel. Master’s Thesis, Aalto University, Espoo, The Netherland, 2002. [Google Scholar]
- Shucksmith, J.D.; Boxall, J.B.; Guymer, I. Effects of emergent and submerged natural vegetation on longitudinal mixing in open channel flow. Water Resour. Res. 2010, 46, W04504. [Google Scholar] [CrossRef]
- Kumar, P.; Sharma, A. Experimental investigation of 3D flow properties around emergent rigid vegetation. Ecohydrology 2022, 15, e2474. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Dey, S. Influence of bank vegetation and gravel bed on velocity and Reynolds stress distributions. Int. J. Sediment. Res. 2009, 24, 236–246. [Google Scholar] [CrossRef]
- Setayesh, P.; Afzalimehr, H. Effect of Reedy Emergent Side-Vegetation in Gravel-Bed Streams on Bed Shear Stress: Patch Scale Analysis. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 46, 1375–1392. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Sui, J.; Moghbel, R. Hydraulic parameters in channels with wall vegetation and gravel bed. Int. J. Sediment Res. 2010, 25, 81–90. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulent in open-channel flow. In IAHR MonographSeries; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Graf, W.H.; Altinakar, M.S. Fluvial Hydraulics: Flow and Transport Processes in Channels of Simple Geometry; Willey: New York, NY, USA, 1998. [Google Scholar]
- Hadian, S.; Afzalimehr, H.; Ahmad, S. Effects of Channel Width Variations on Turbulent Flow Structures in the Presence of Three-Dimensional Pool-Riffle. Sustainability 2023, 15, 7829. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Termini, D. Flow Velocity Measurements in Vegetated Channels. J. Hydraul. Eng. 2002, 128, 664–673. [Google Scholar] [CrossRef]
- Nepf, H.M.; Vivoni, E. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. Oceans. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Velasco, D.; Bateman, A.; Redondo, J.M.; Medina, V. An Open Channel Flow Experimental and Theoretical Study of Resistance and Turbulent Characterization over Flexible Vegetated Linings. Flow Turbul. Combust. 2003, 70, 69–88. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Xu, W.-L.; Yu, G.-L. Velocity distribution in a gradually accelerating free surface flow. Adv. Water Resour. 2006, 29, 1969–1980. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Wang, J.; He, G.; Dey, S.; Fang, H. Influence of submerged flexible vegetation on turbulence in an open-channel flow. J. Fluid Mech. 2022, 947, A31. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Afzalimehr, H. Effect of non-uniformity of flow on velocity and turbulence intensities over a cobble-bed. Hydrol. Process. Int. J. 2009, 24, 331–341. [Google Scholar] [CrossRef]
- Simons, D.B.; Şentürk, F. Sediment Transport Technology: Water and Sediment Dynamics; Water Resources Publication: Littleton, CO, USA, 1992. [Google Scholar]
- Song, T.; Chiew, Y. Turbulence measurement in nonuniform open-channel flow using acoustic Doppler velocimeter (ADV). J. Eng. Mech. 2001, 127, 219–232. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Rennie, C.D. Determination of bed shear stress in gravel-bed rivers using boundary-layer parameters. Hydrologic. Sci. J. 2009, 54, 147–159. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Anctil, F. Velocity distribution and shear velocity behavior of decelerating flow over a gravel- bed. J. Can. Civ. Eng. 1999, 26, 468–475. [Google Scholar] [CrossRef]
- Wang, Y. Reynolds stress model for viscoelastic drag-reducing flow induced by polymer solution. Polymers 2019, 11, 1659. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Moghbel, R.; Ghalichand, J.; Sui, J. Investigation of Turbulence characteristics in channel with dense vegetation over bed. Int. J. Sediment Res. 2011, 26, 255–268. [Google Scholar] [CrossRef]
- Yalin, M.S. Mechanics of Sediment Transport, 2nd ed.; Pergamon: New York, NY, USA, 1992. [Google Scholar]
- Vanoni, V. Sedimentation Engineering; ASCE Publications: Reston, VA, USA, 1975. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).