Experimental Study on the Wake Characteristics of Composite Secondary Grooved Cylinder
Abstract
1. Introduction
2. Experimental Apparatus and Details
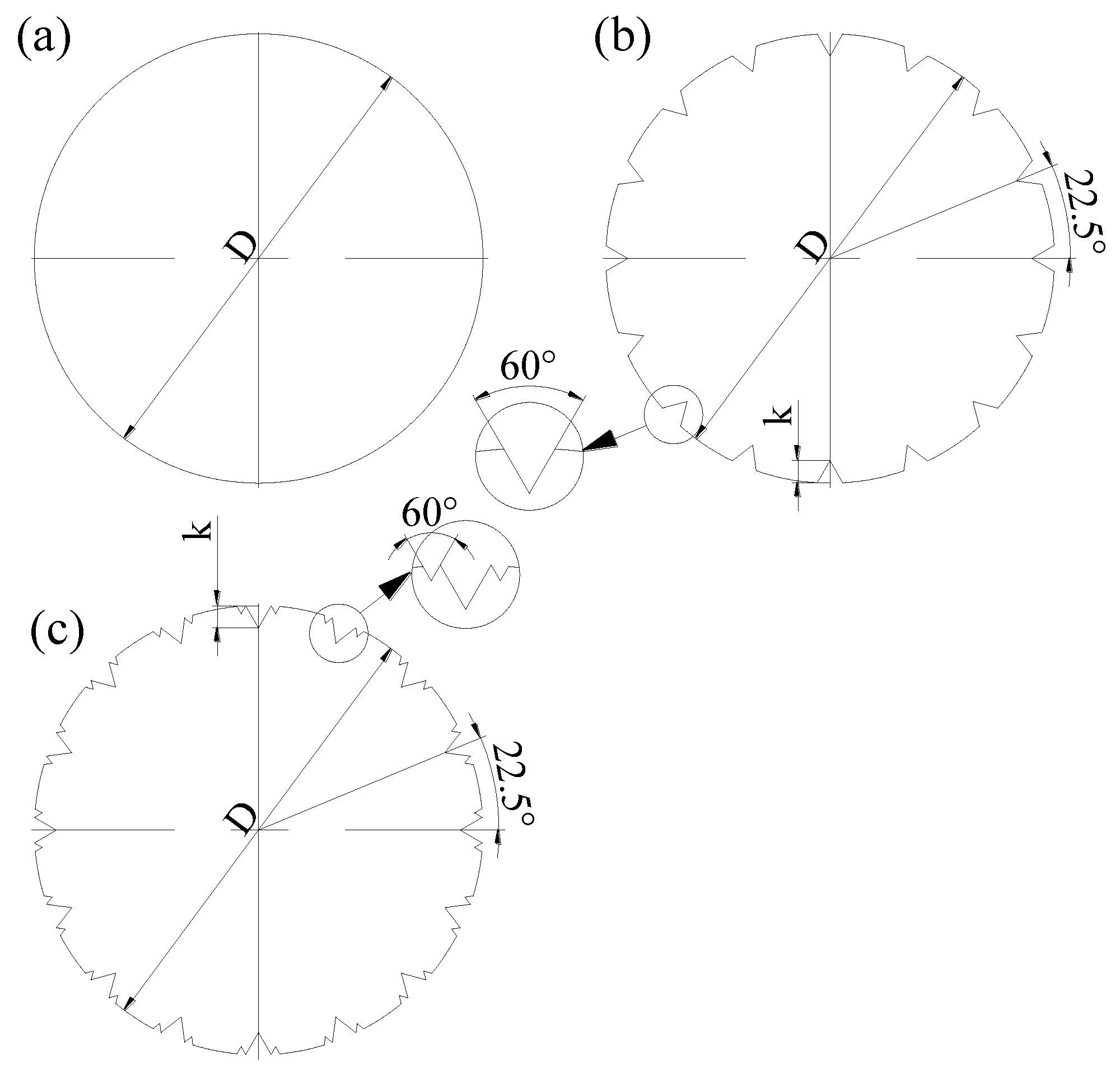
2.1. Experimental Models
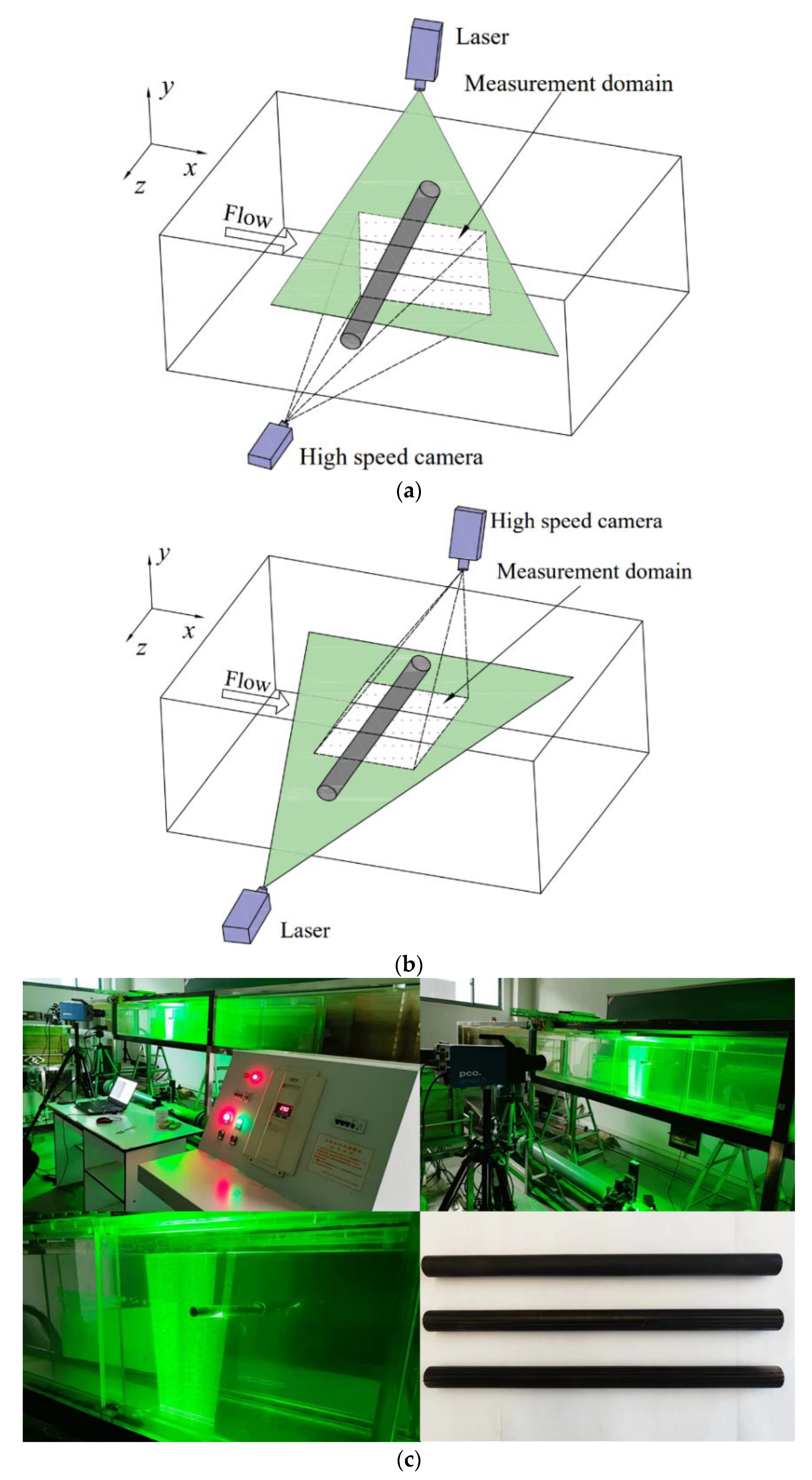
2.2. Experimental Measurement Apparatus
3. Experimental Results and Discussion
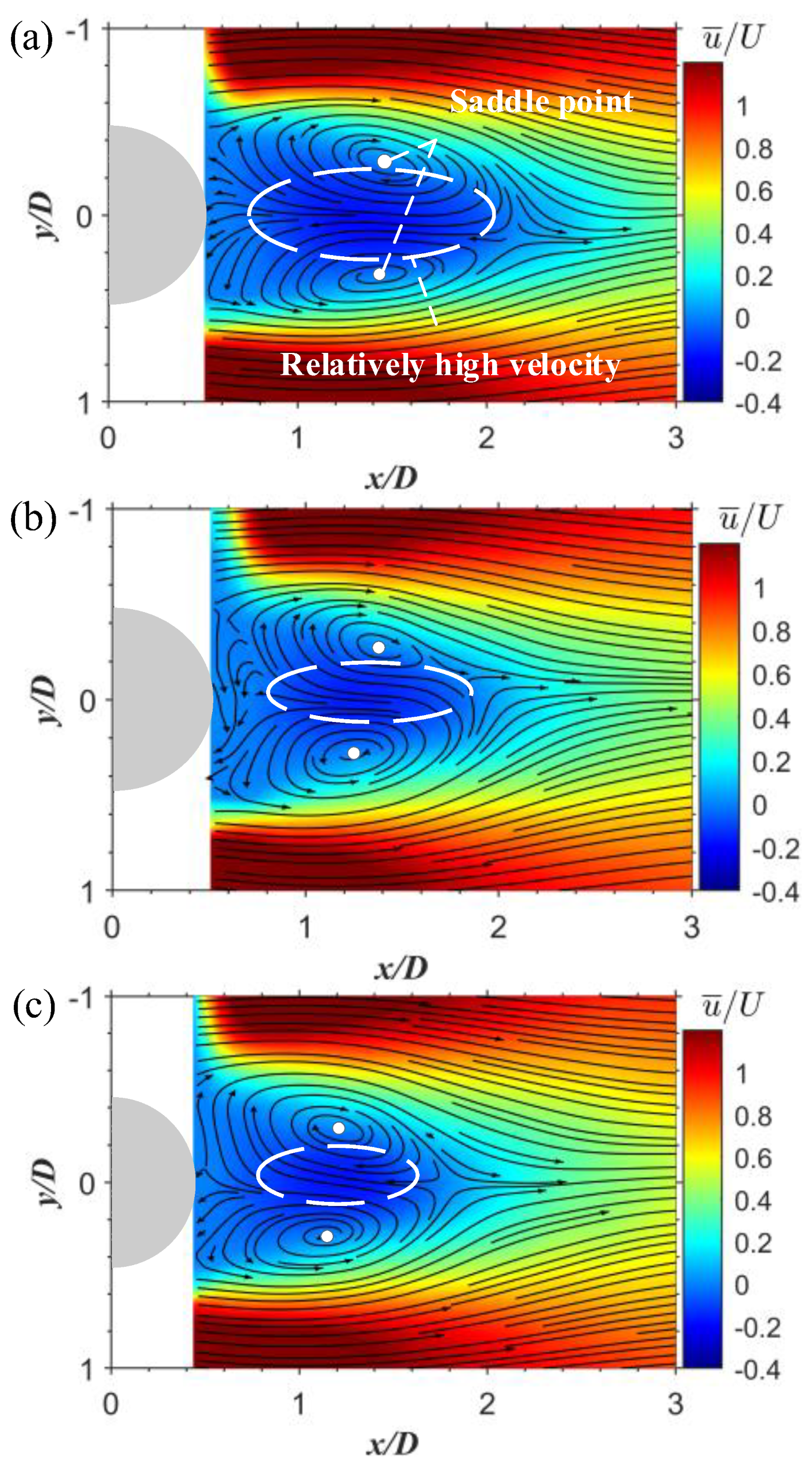
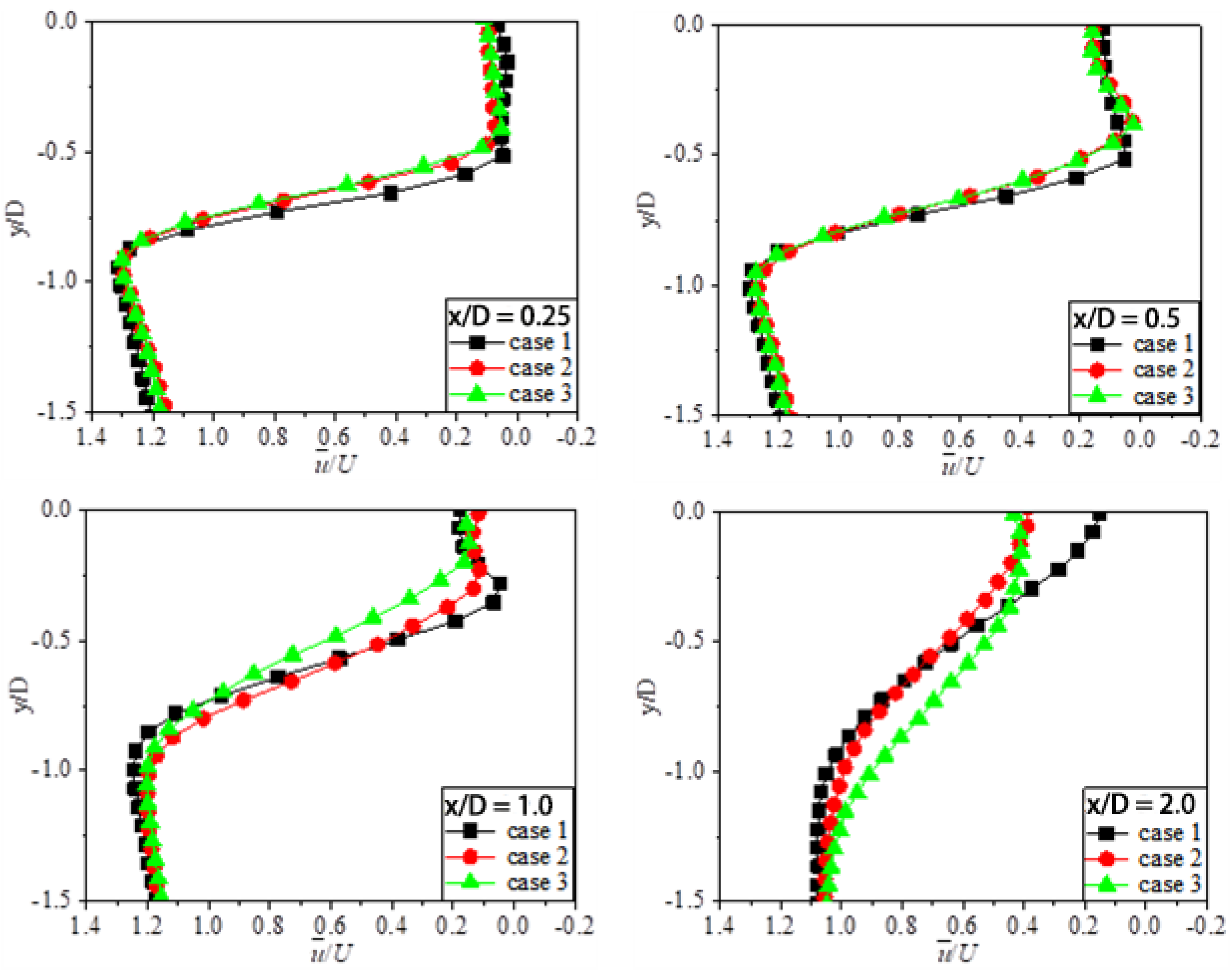
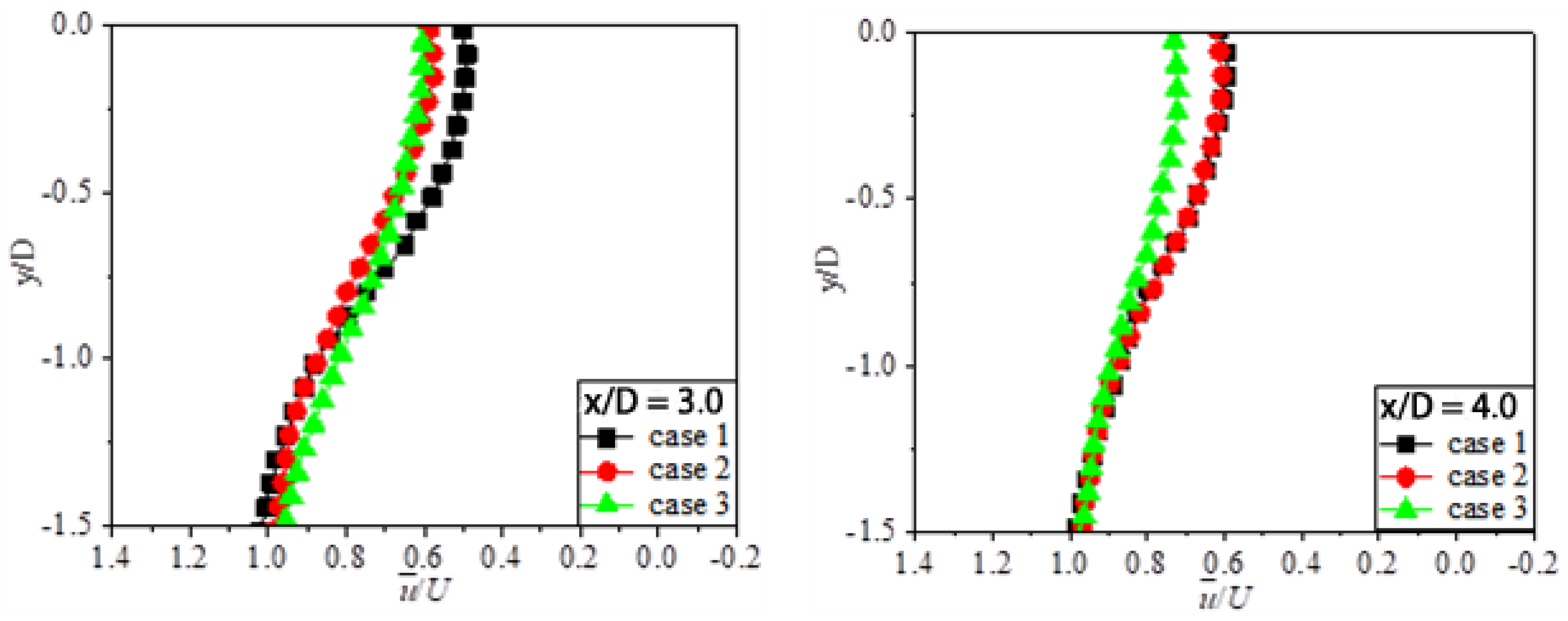
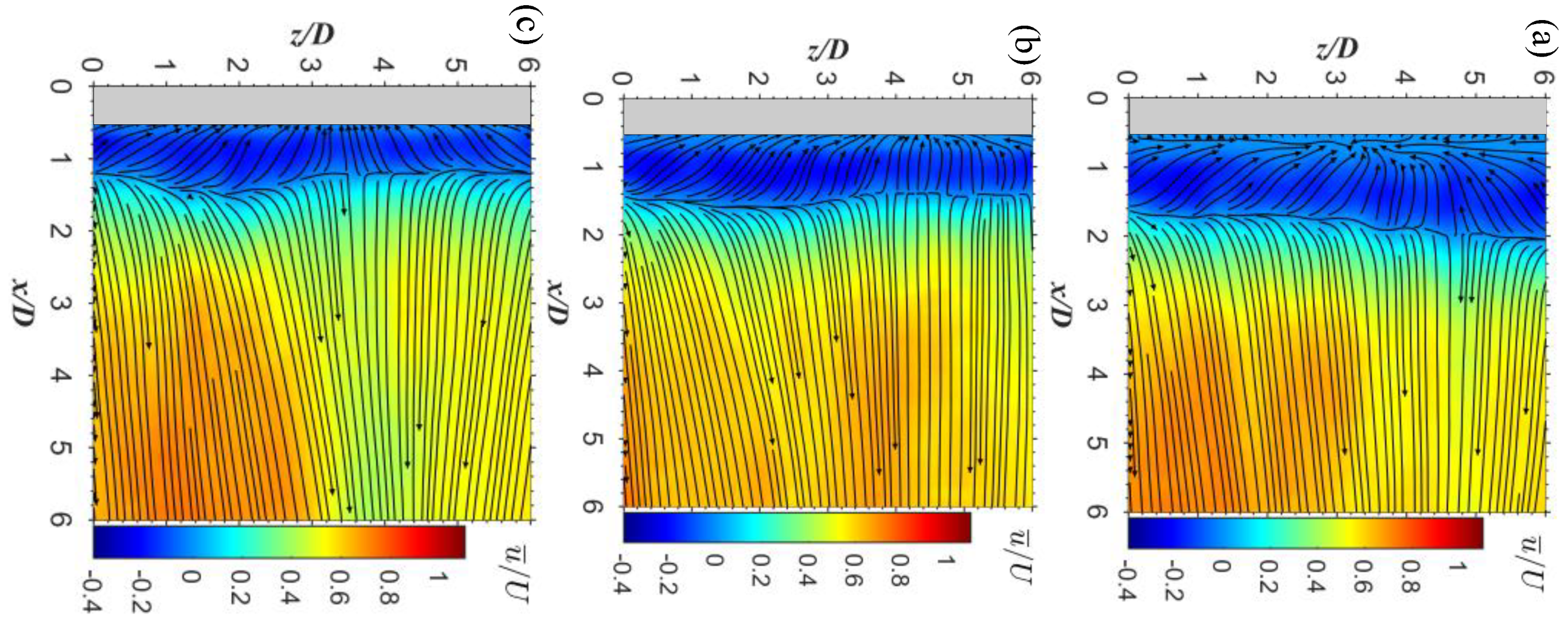
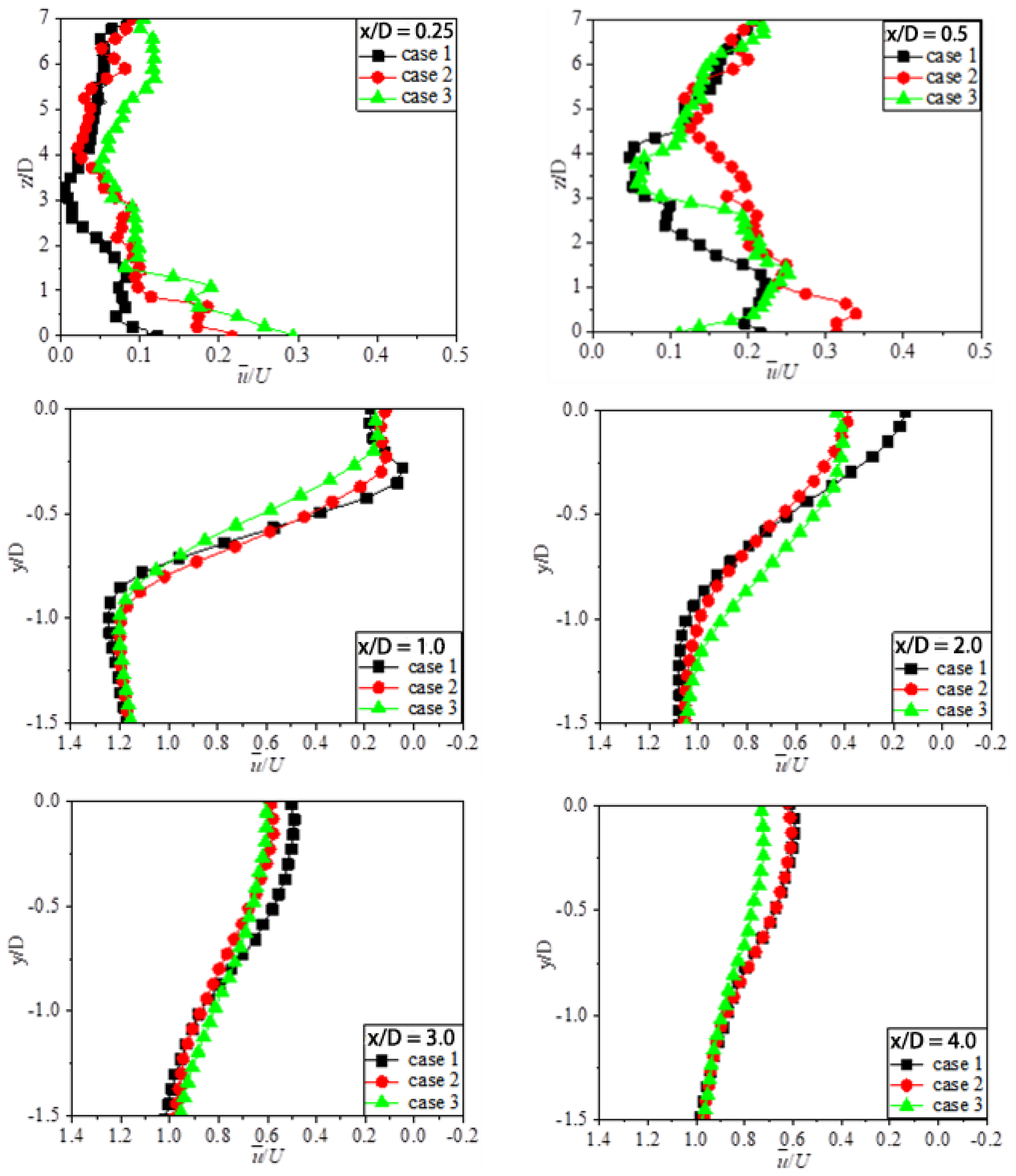
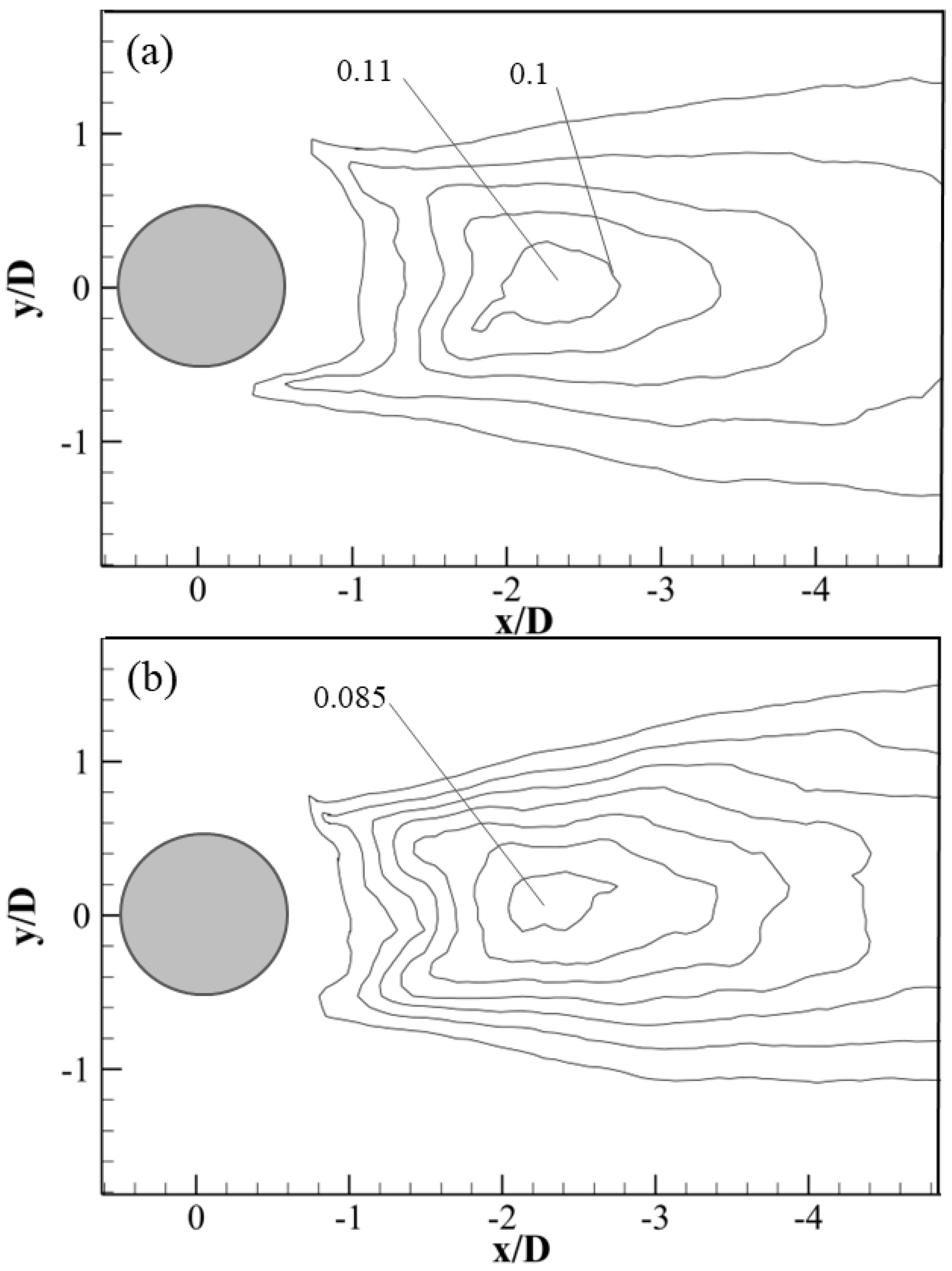
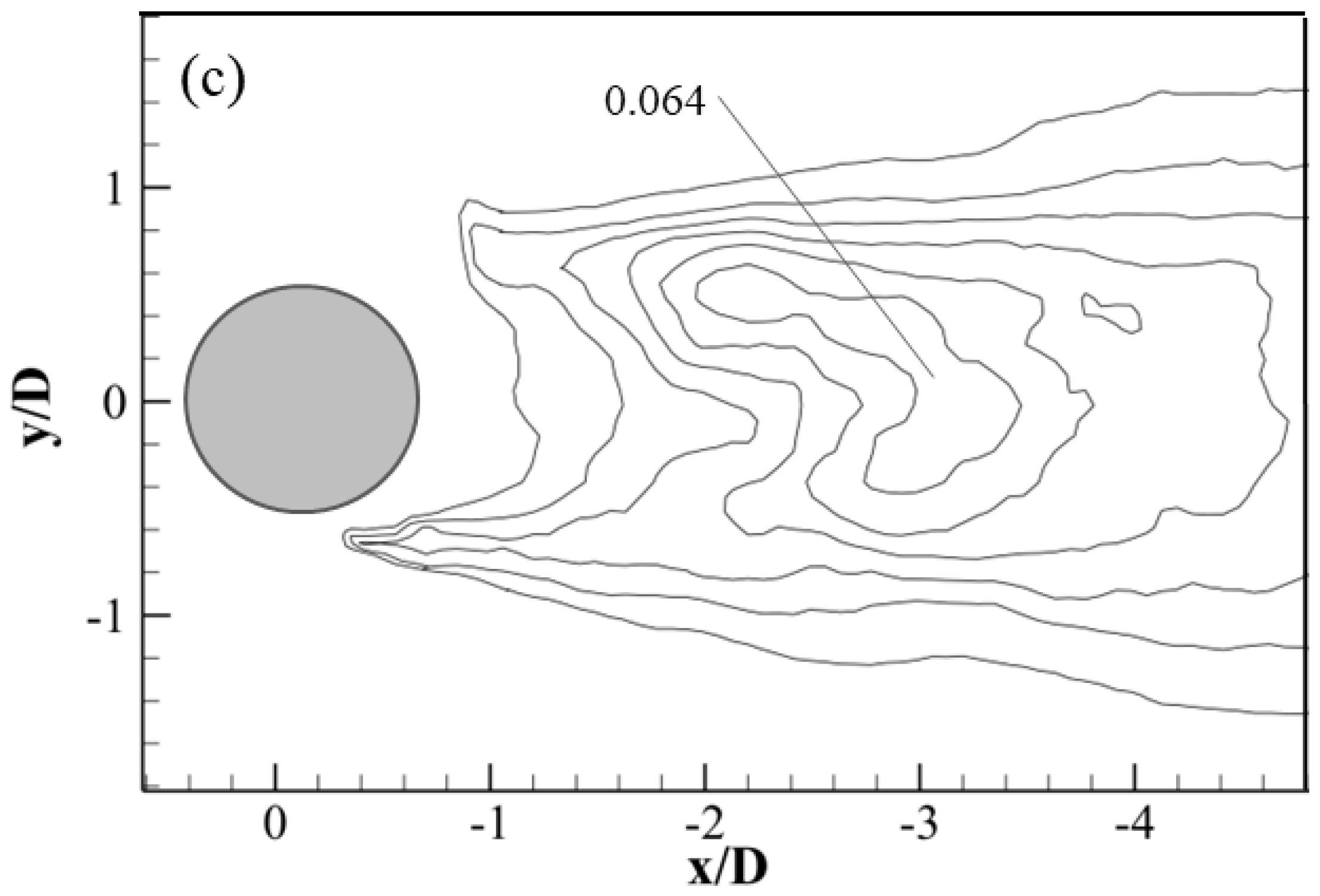
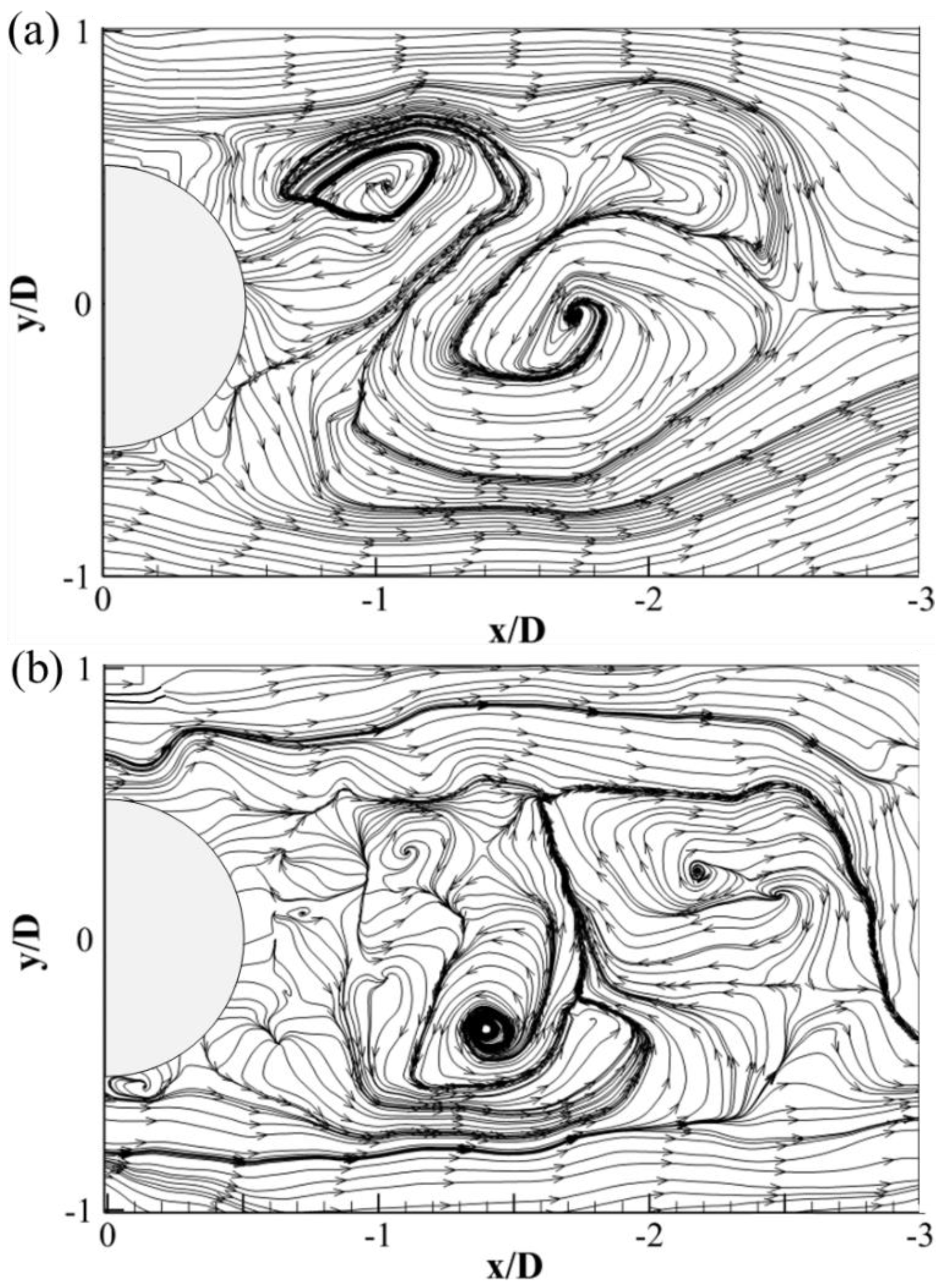
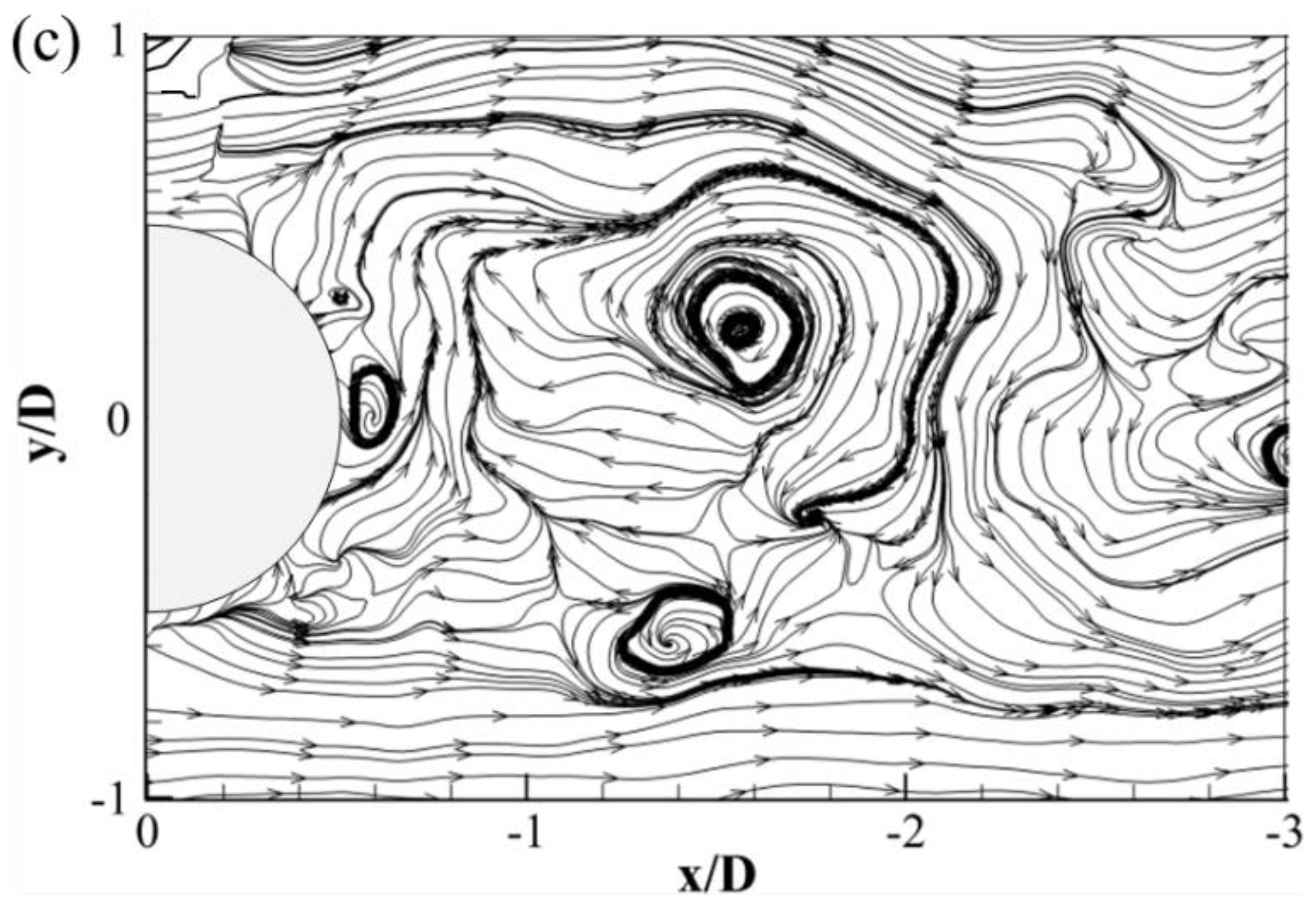
3.1. Streamlines and Velocity Field
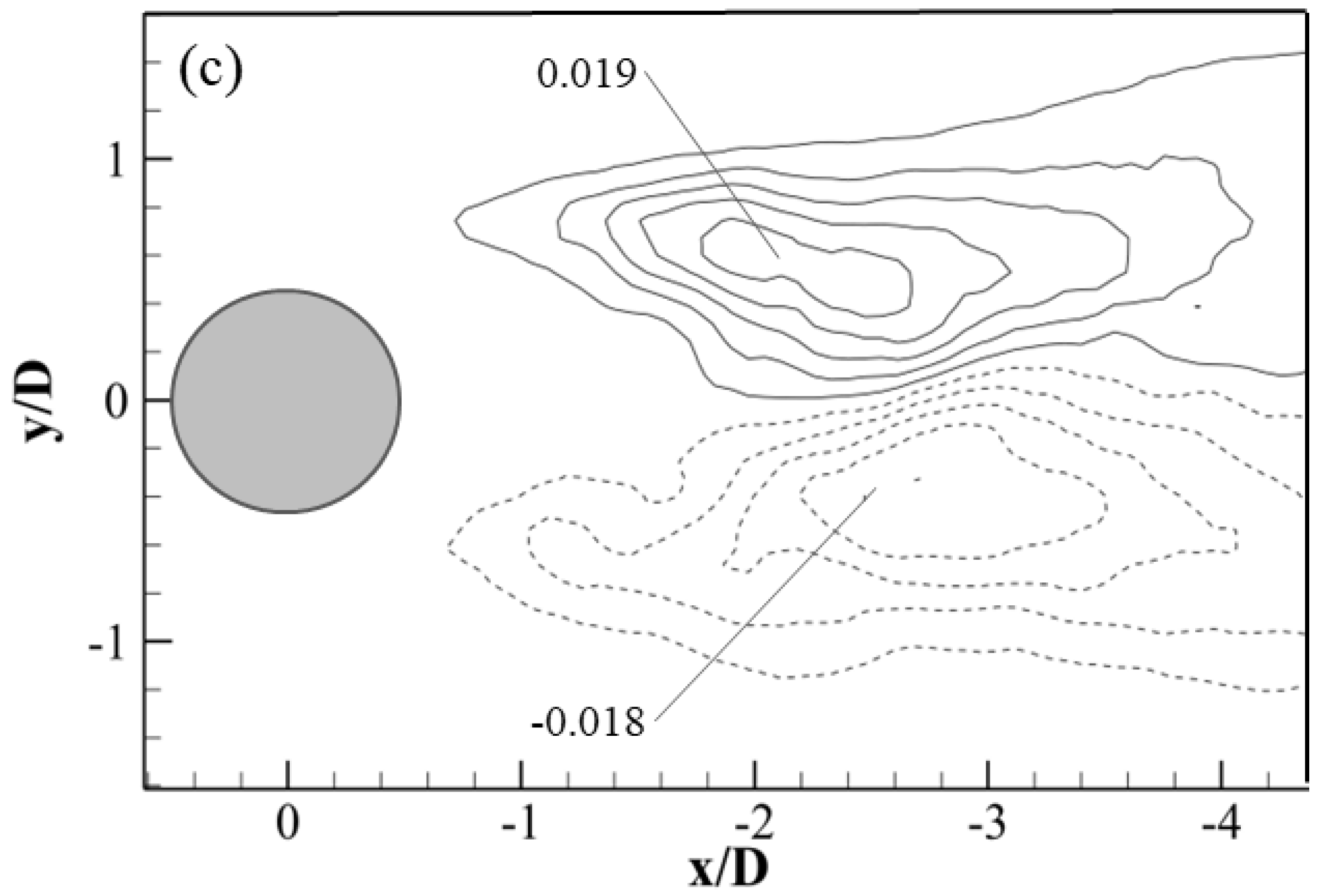
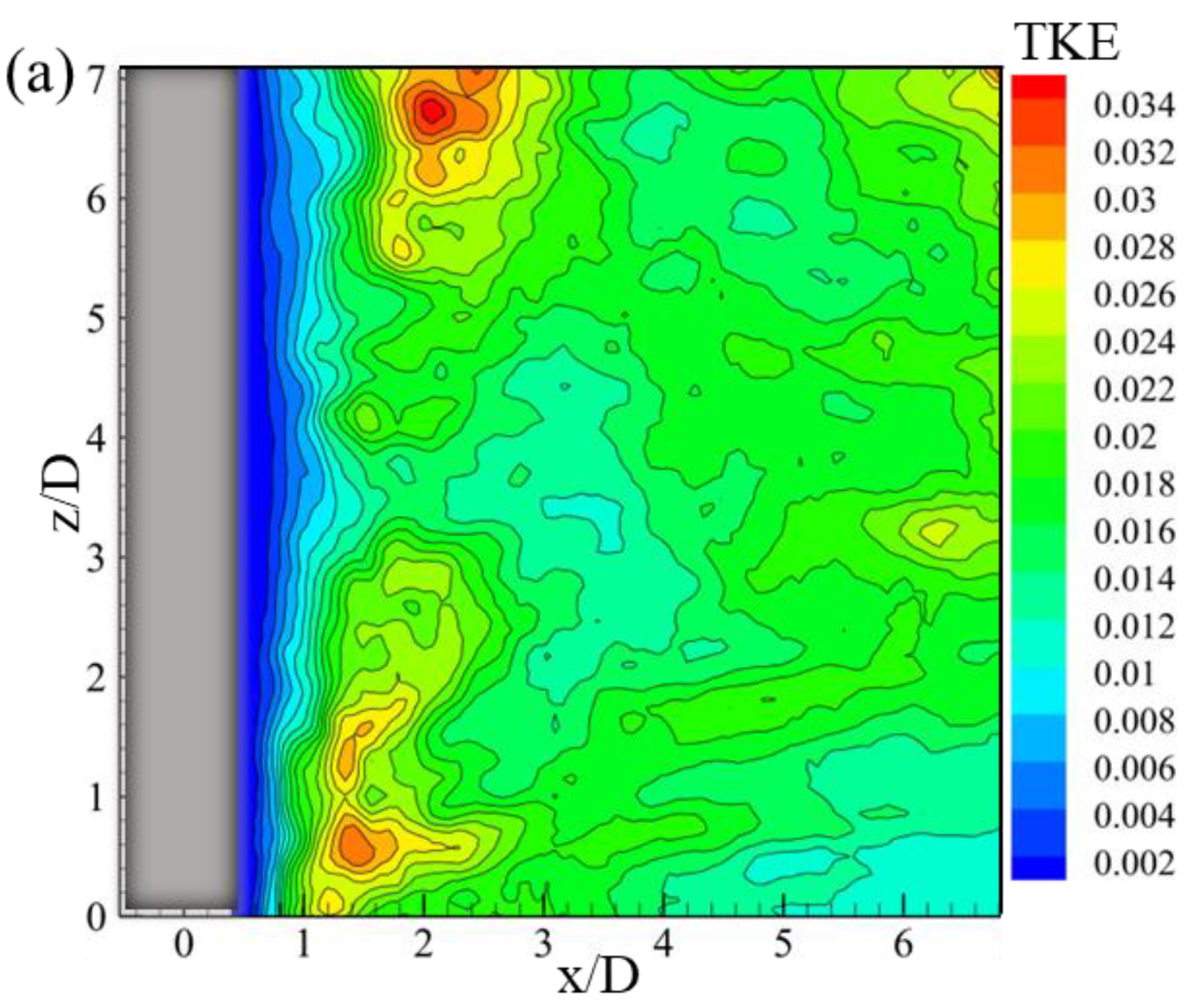
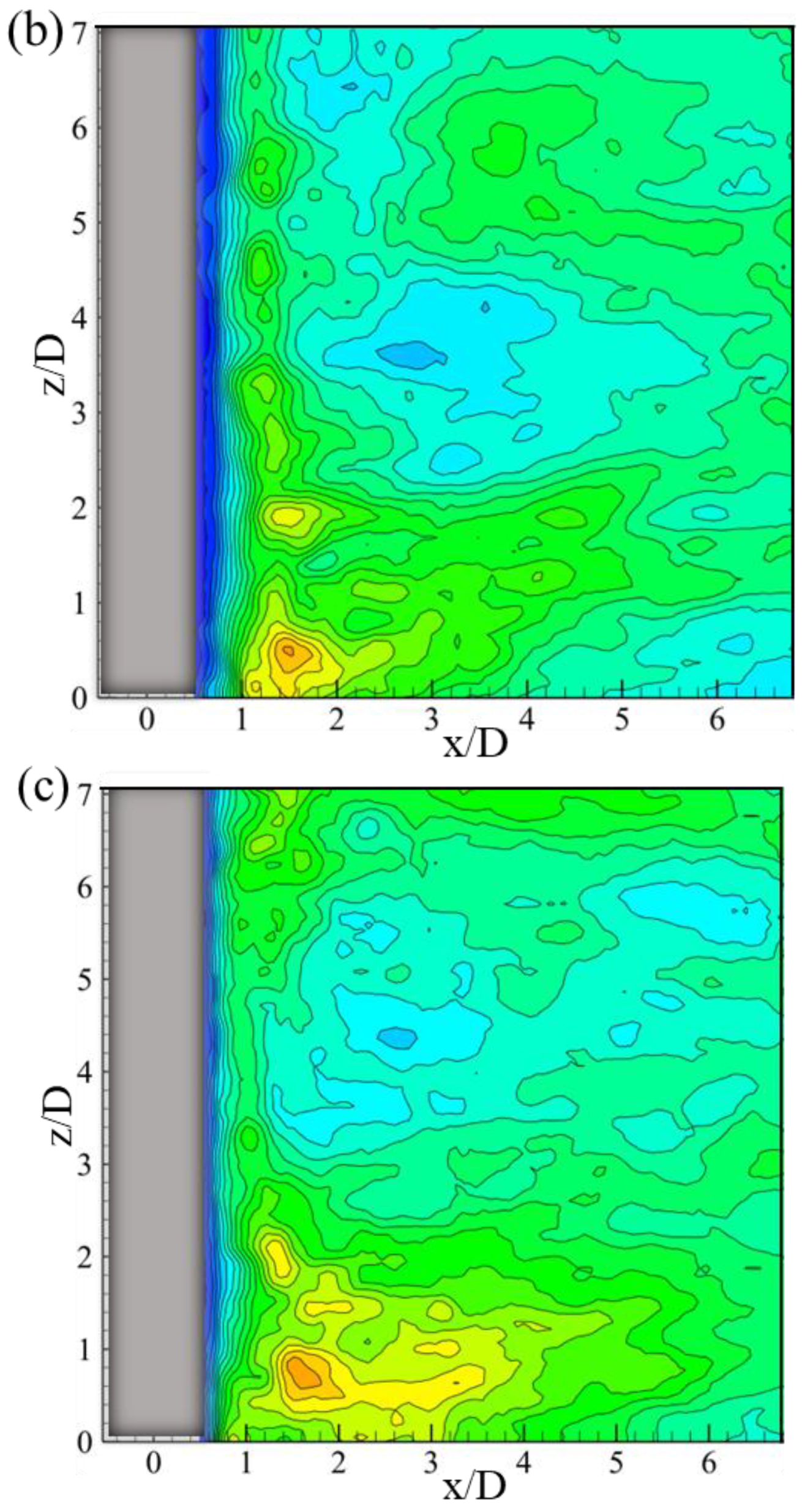
3.2. Reynolds Shear Stress and Turbulent Kinetic Energy
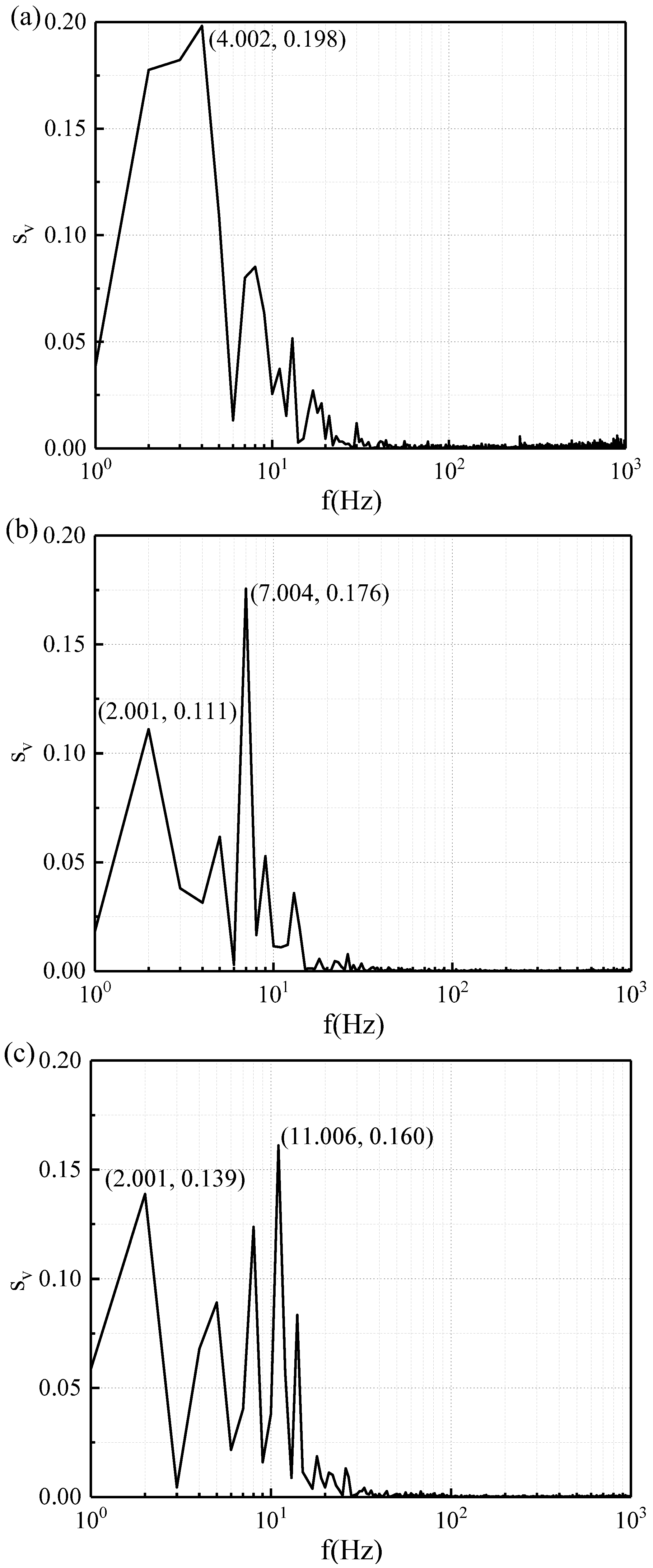
3.3. Spectral Characteristic
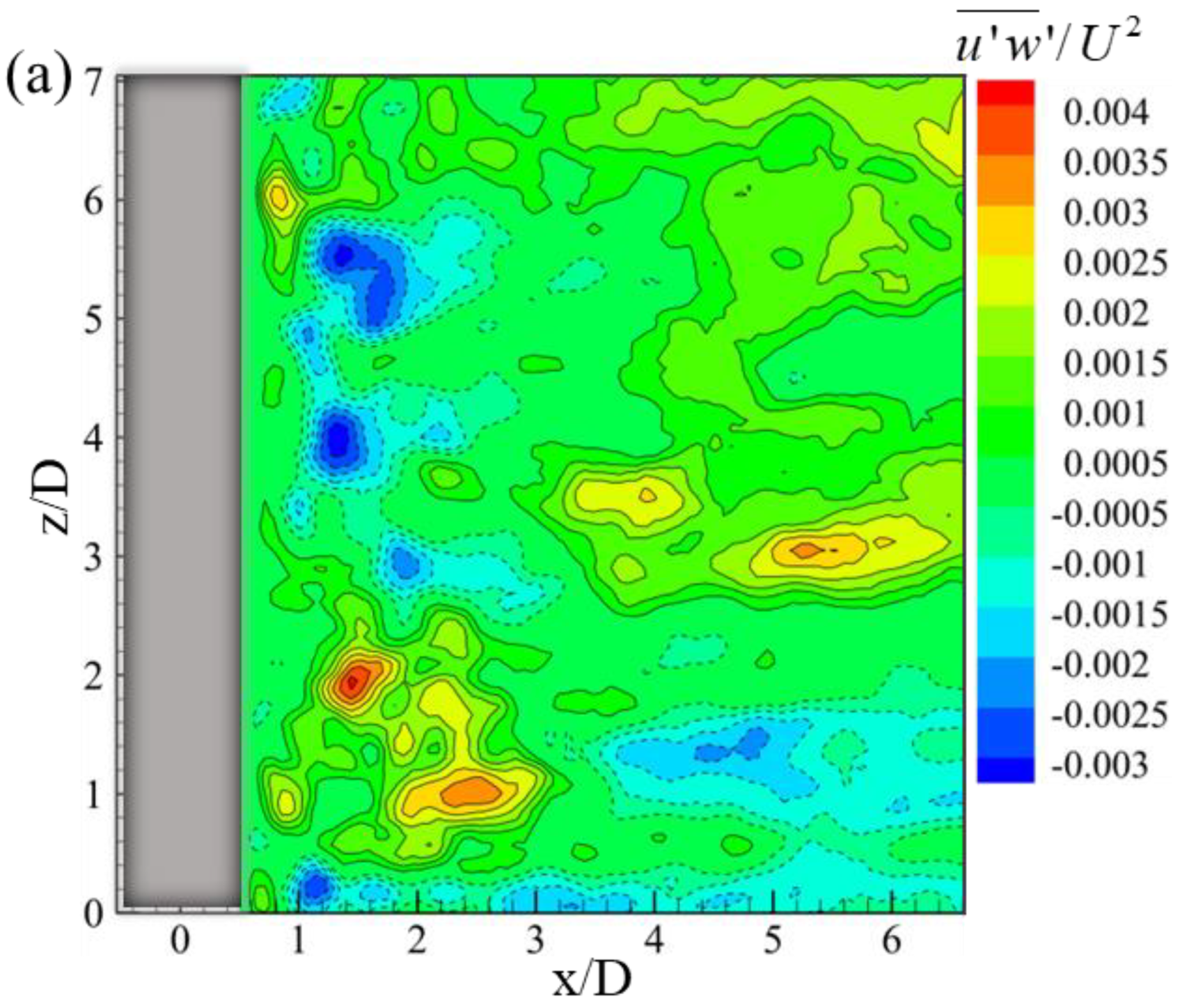
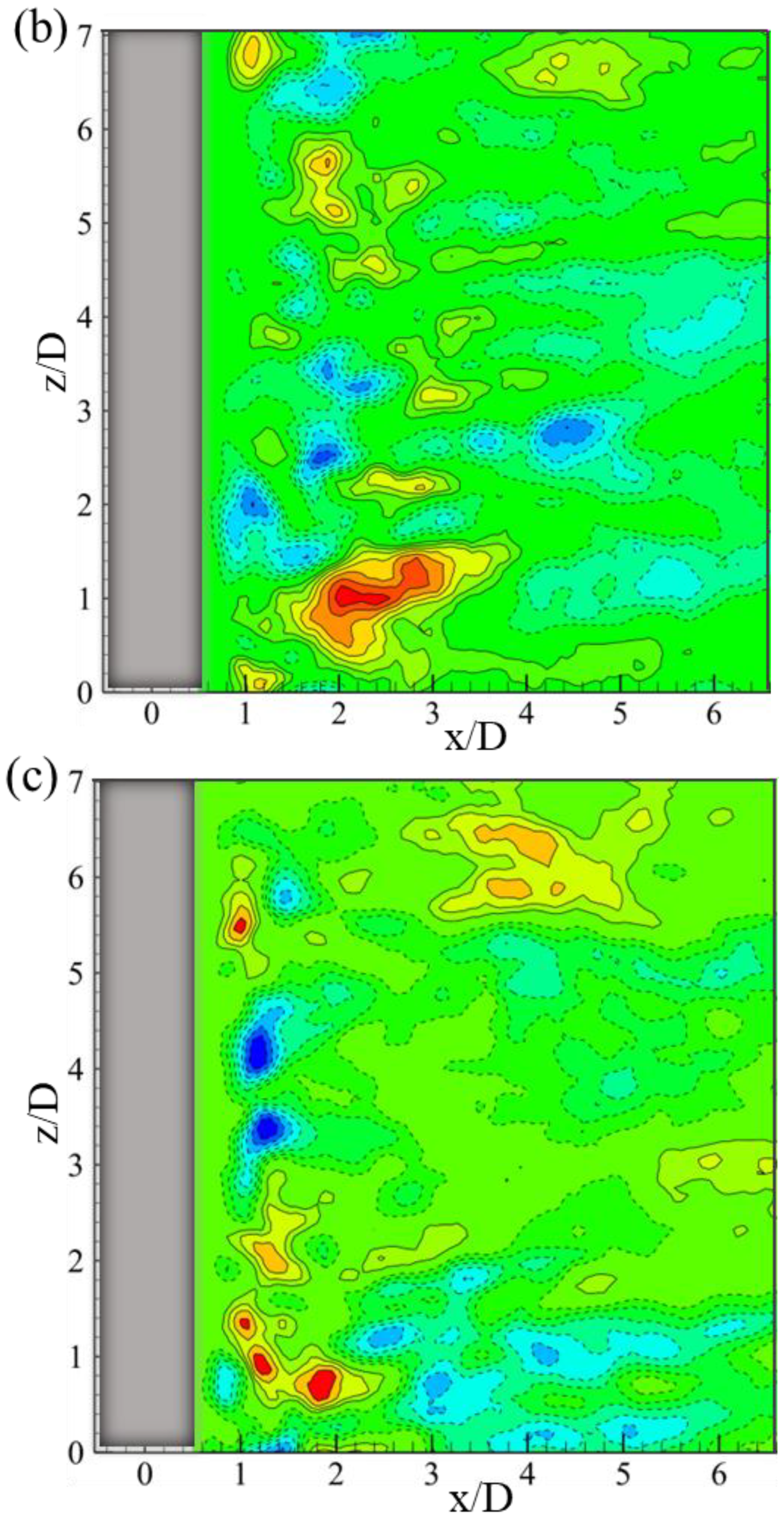
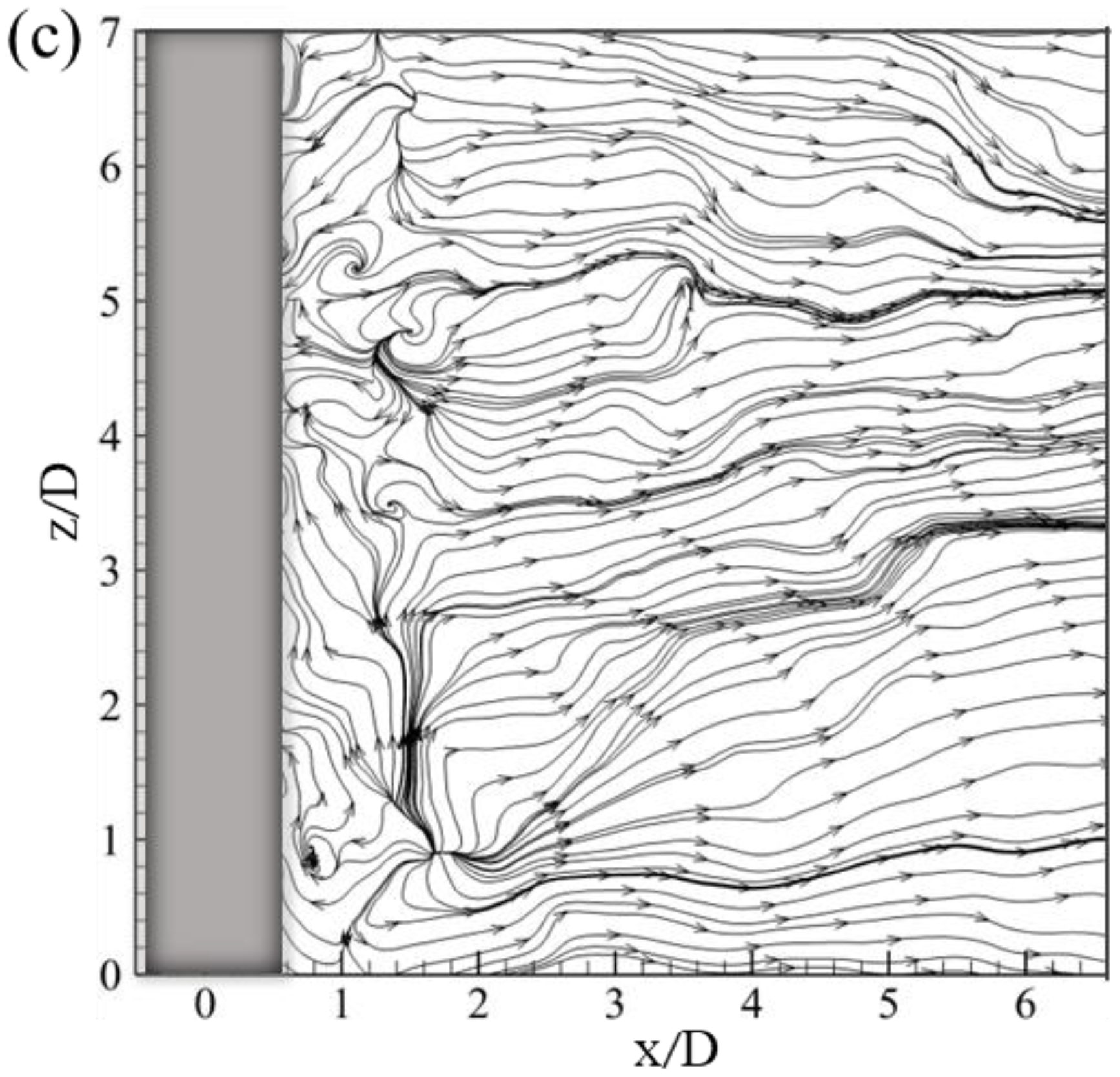
3.4. Instantaneous Flow Structures
4. Conclusions
- (1)
- The wake structure downstream of the cylinder was improved by the groove structure, resulting in the reduction of the recirculation region, especially in the secondary groove structure. The flow-direction velocity gradient of the grooved cylinders was found to be less than that of a smooth cylinder;
- (2)
- The secondary grooved cylinder reduced the turbulent fluctuation within the boundary layer, resulting in the maximum Reynolds shear stress being suppressed. Moreover, compared to a smooth cylinder, the maximum of TKE was reduced by 42% for the secondary grooved cylinder, which indicates that the formation of secondary vortices was suppressed;
- (3)
- For spectral characters of the velocity component, both small-scale and large-scale vortices were present in the wake vortex shedding, while the secondary grooved cylinder reduced the power spectrum;
- (4)
- For the instantaneous flow structures, the spike structure was deemed to be a vortex generator, and directly impacts the generation of small eddies and the dissipation of large vortices.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rashidi, S.; Hayatdavoodi, M.; Esfahani, J.A. Vortex shedding suppression and wake control: A review. Ocean. Eng. 2016, 126, 57–80. [Google Scholar] [CrossRef]
- Zheng, Y.; Rinoshika, H.; Zhang, D.; Rinoshika, A. Analyses on flow structures behind a wavy square cylinder based on continuous wavelet transform and dynamic mode decomposition. Ocean. Eng. 2020, 216, 108117. [Google Scholar] [CrossRef]
- Gu, F.; Wang, J.S.; Qiao, X.Q.; Huang, Z. Pressure distribution, fluctuating forces and vortex shedding behavior of circular cylinder with rotatable splitter plates. J. Fluids Struct. 2012, 28, 263–278. [Google Scholar] [CrossRef]
- Assi, G.; Bearman, P.W.; Tognarelli, M.A. On the stability of a free-to-rotate short-tail fairing and a splitter plate as suppressors of vortex-induced vibration. Ocean Eng. 2014, 92, 234–244. [Google Scholar] [CrossRef]
- Seo, J.; Yun, J.; Lee, J. Control of Turbulent Flow over a Circular Cylinder Using Tabs. Mathematics 2023, 11, 968. [Google Scholar] [CrossRef]
- Xie, F.; Yu, Y.; Constantinides, Y.; Triantafyllou, M.S.; Karniadakis, G.E. U-shaped fairings suppress vortex-induced vibrations for cylinders in cross-flow. J. Fluid Mech. 2015, 782, 300–332. [Google Scholar] [CrossRef]
- Liu, K.; Deng, J.; Mei, M. Experimental study on the confined flow over a circular cylinder with a splitter plate. Flow Meas. Instrum. 2016, 51, 95–104. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Yang, K.S. Drag reduction on a circular cylinder using dual detached splitter plates. J. Wind Eng. Ind. Aerodyn. 2007, 95, 551–564. [Google Scholar] [CrossRef]
- Sahu, Y. Flow-induced vibration of a circular cylinder with rigid splitter plate. J. Fluids Struct. 2019, 89, 244–256. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Guo, W.; Gho, W.M.; Tan, S.K. Experimental study on flow past a circular cylinder with rough surface. Ocean Eng. 2015, 109, 7–13. [Google Scholar] [CrossRef]
- Afroz, F.; Sharif, M.A. Numerical study of cross-flow around a circular cylinder with differently shaped span-wise surface grooves at low Reynolds number. Eur. J. Mech. B/Fluids 2022, 91, 203–218. [Google Scholar] [CrossRef]
- Quintavalla, S.J.; Angilella, A.J.; Smits, A.J. Drag reduction on grooved cylinders in the critical Reynolds number regime. Exp. Therm. Fluid Sci. 2013, 48, 15–18. [Google Scholar] [CrossRef]
- Munendra, C.; Inamdar, A.; Kumar, R.; Science, G. Numerical studies of drag reduction on circular cylinder with V-grooves. Int. J. Eng. Res. 2015, 3. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=e19955455326c2ef162cecb4b8752bce667eedae (accessed on 24 May 2023).
- Sun, C.; Zhou, T.; An, H.; Zhu, H.; Cheng, L.; Flow, F. Experimental studies on wake structures of a circular cylinder with different surface roughness heights. Int. J. Heat 2022, 94, 108941. [Google Scholar] [CrossRef]
- Aleksyuk, A. Analysis of three-dimensional transition mechanisms in the near wake behind a circular cylinder. Eur. J. Mech. B. Fluids 2018, 72, 456–466. [Google Scholar] [CrossRef]
- Xha, B.; Yt, C.; Zm, A.; Fei, F.A.; Aqb, D.; Jian, G.E.; Jw, B. Surface roughness effect on cylinder vortex-induced vibration at moderate Re regimes. Ocean Eng. 2021, 224, 108690. [Google Scholar] [CrossRef]
- Merzkirch, W. Particle Image Velocimetry. In Optical Measurements: Techniques and Applications; Mayinger, F., Feldmann, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 341–357. [Google Scholar] [CrossRef]
- Huang., S. VIV suppression of a two-degree-of-freedom circular cylinder and drag reduction of a fixed circular cylinder by the use of helical grooves. J. Fluids Struct. 2011, 27, 1124–1133. [Google Scholar] [CrossRef]
- Canpolat, C. Characteristics of flow past a circular cylinder with a rectangular groove. Flow Meas. Instrum. 2015, 45, 233–246. [Google Scholar] [CrossRef]
- Levy, B.; Liu, Y. The effects of cactus inspired spines on the aerodynamics of a cylinder. J. Fluids Struct. 2013, 39, 335–346. [Google Scholar] [CrossRef]
- Talley, B.S.; Mungal, G. An Experimental and Computational Investigation of Flow Past Cacti; Annual Research Briefs; Center for Turbulence Research, NASA Ames/Stanford University: Silicon Valley, CA, USA, 2001; pp. 51–63. [Google Scholar]
- Qi, J.; Yue, Q.; Qunyan, C.; Fei, Y. A Study of Drag Reduction on Cylinders with Different V-Groove Depths on the Surface. Water 2021, 14, 36. [Google Scholar] [CrossRef]
- Jiang, S.; Yan, F.; Zhang, J.; Song, B. Multi-Scale Wake Characteristics of the Flow over a Cylinder with Different V-Groove Numbers. Water 2023, 15, 805. [Google Scholar] [CrossRef]
- Feng, B.; Wang, J.; Chen, D.; Liu, Z.; Jiang, S. Drag reduction mechanism of feather-like riblet film. J. Funct. Mater. 2016, 47, 1–4. [Google Scholar] [CrossRef]
- Reif, W.E. Morphogenesis and function of the squamation in sharks. Neues Jahrb. Geol. Paläontologie Abh. 1982, 164, 172–183. [Google Scholar] [CrossRef]
- Wachter, F.; Metelkin, A.; Jovanovi, J.; Pra, J.; Becker, S. Numerical investigation of the effect of convex transverse curvature and concave grooves on the turbulent boundary layer along a cylinder in axial flow. Int. J. Heat Fluid Flow 2021, 92, 108855. [Google Scholar] [CrossRef]
- Cheng, P.; Jiang, C.; Wu, C. Numerical simulation of drag reduction characteristics in bionic secondary micro-grooved surface. China Sci. 2014, 9, 940–943. [Google Scholar]
- Takayama, S.; Aoki, K. Numerical Analysis of Flow Characteristics around Circular Cylinders with Arc Grooves (SCHOOL OF ENGINEERING). Proc. Sch. Eng. Tokai Univ. 2005, 30, 1–5. [Google Scholar]
- Zhou, B.; Wang, X.; Guo, W.; Zheng, J.; Tan, S.K. Experimental measurements of the drag force and the near-wake flow patterns of a longitudinally grooved cylinder. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 30–41. [Google Scholar] [CrossRef]
- Apelt, G. Measurements of Fluctuating Pressures and Forces on a Circular Cylinder in the Reynolds Number Range 104 to 2·5 × 105. J. Fluids Struct. 1993, 7, 227–244. [Google Scholar] [CrossRef]
- Oruç, V.; Akilli, H.; Sahin, B. PIV measurements on the passive control of flow past a circular cylinder. Exp. Therm. Fluid Sci. 2016, 70, 283–291. [Google Scholar] [CrossRef]
- Caliskan, M.; Tantekin, A.; Tumen Ozdil, N.F.; Akilli, H. Investigation of flow characteristics for triangular grooved shape cylinder at different heights in shallow water. Ocean Eng. 2021, 225, 108788. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Shi, L.L.; Yu, J. TR-PIV measurement of the wake behind a grooved cylinder at low Reynolds number. J. Fluids Struct. 2011, 27, 394–407. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, T. Flow around a circular cylinder attached with a pair of fin-shaped strips. Ocean Eng. 2019, 190, 106484. [Google Scholar] [CrossRef]
- Fujisawa, N.; Hirabayashi, K.; Yamagata, T. Aerodynamic noise reduction of circular cylinder by longitudinal grooves. J. Wind. Eng. Ind. Aerodyn. 2020, 199, 104129. [Google Scholar] [CrossRef]
- Rinoshika, H.; Rinoshika, A. Passive control of a front inclined hole on flow structures around a surface-mounted short cylinder. Ocean Eng. 2019, 189, 106383. [Google Scholar] [CrossRef]
- Baek, H.; Karniadakis, G.E. Suppressing vortex-induced vibrations via passive means. J. Fluids Struct. 2009, 25, 848–866. [Google Scholar] [CrossRef]
- Aguedal, L.; Semmar, D.; Berrouk, A.S.; Azzi, A.; Oualli, H. 3D vortex structure investigation using Large Eddy Simulation of flow around a rotary oscillating circular cylinder. Eur. J. Mech. B/Fluids 2018, 71, 113–125. [Google Scholar] [CrossRef]
- Zheng, Y.; Rinoshika, A.; Fujimoto, S. Triangle Cylinder Wake Analysis Based on Wavelet and POD Techniques. Procedia Eng. 2015, 126, 108–112. [Google Scholar] [CrossRef]
- Foo, K.; Liang, Y.Y.; Tan, C.K.; Fimbres Weihs, G.A. Coupled effects of circular and elliptical feed spacers under forced-slip on viscous dissipation and mass transfer enhancement based on CFD. J. Membr. Sci. 2021, 637, 119599. [Google Scholar] [CrossRef]
- Lim, H.C.; Lee, S.J. PIV measurements of near wake behind a U-grooved cylinder. J. Fluids Struct. 2003, 18, 119–130. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, P.; Zhong, S.; Zhang, X.; Huang, X.; So, R.C.-H. An experimental investigation of drag and noise reduction from a circular cylinder using longitudinal grooves. Phys. Fluids 2021, 33, 115110. [Google Scholar] [CrossRef]
- Qi, J.; Shao, Y.; Chen, Q.; Liu, P.; Chen, C.; Wang, D.; Yang, H.; Yan, F. Dynamic Analysis of Wake Characteristics of the Circular Cylinder with a Dimpled Surface. Water 2021, 13, 2197. [Google Scholar] [CrossRef]
- Wang, H.F.; Zhou, Y. The finite-length square cylinder near wake. J. Fluid Mech. 2009, 638, 453–490. [Google Scholar] [CrossRef]
- Sakamoto, H.; Arie, M. Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer. J. Fluid Mech. 1983, 126, 147–165. [Google Scholar] [CrossRef]
- Zhou, T.; Razali, S.; Hao, Z.; Cheng, L. On the study of vortex-induced vibration of a cylinder with helical strakes. J. Fluids Struct. 2011, 27, 903–917. [Google Scholar] [CrossRef]

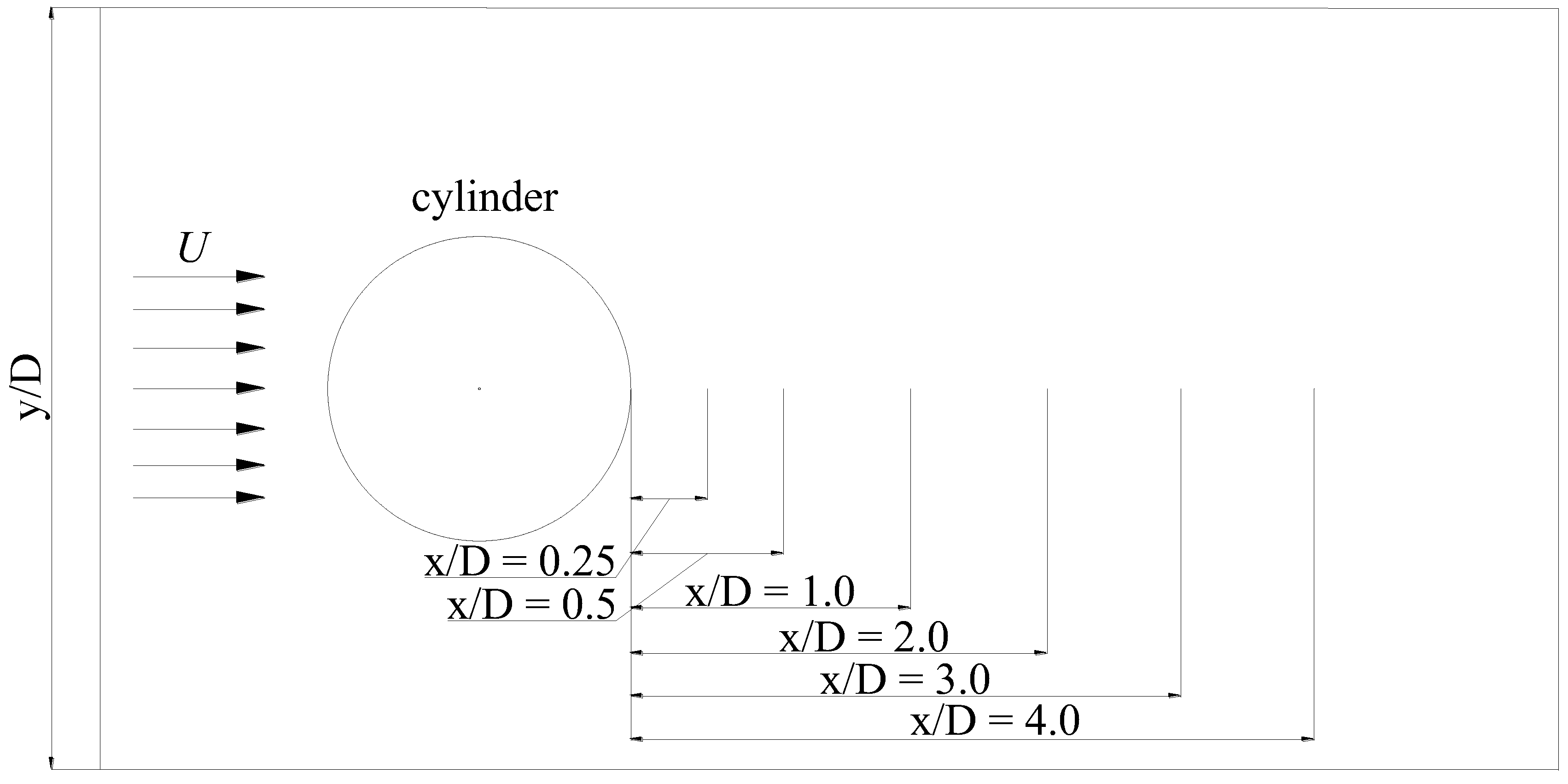


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Luo, X.; Wang, J.; Shi, Z.; Yan, F. Experimental Study on the Wake Characteristics of Composite Secondary Grooved Cylinder. Water 2023, 15, 2073. https://doi.org/10.3390/w15112073
Liu L, Luo X, Wang J, Shi Z, Yan F. Experimental Study on the Wake Characteristics of Composite Secondary Grooved Cylinder. Water. 2023; 15(11):2073. https://doi.org/10.3390/w15112073
Chicago/Turabian StyleLiu, Liangqing, Xiaoyuan Luo, Jianzheng Wang, Zhisai Shi, and Fei Yan. 2023. "Experimental Study on the Wake Characteristics of Composite Secondary Grooved Cylinder" Water 15, no. 11: 2073. https://doi.org/10.3390/w15112073
APA StyleLiu, L., Luo, X., Wang, J., Shi, Z., & Yan, F. (2023). Experimental Study on the Wake Characteristics of Composite Secondary Grooved Cylinder. Water, 15(11), 2073. https://doi.org/10.3390/w15112073




