Mathematic Modelling of a Reversible Hydropower System: Dynamic Effects in Turbine Mode
Abstract
1. Introduction
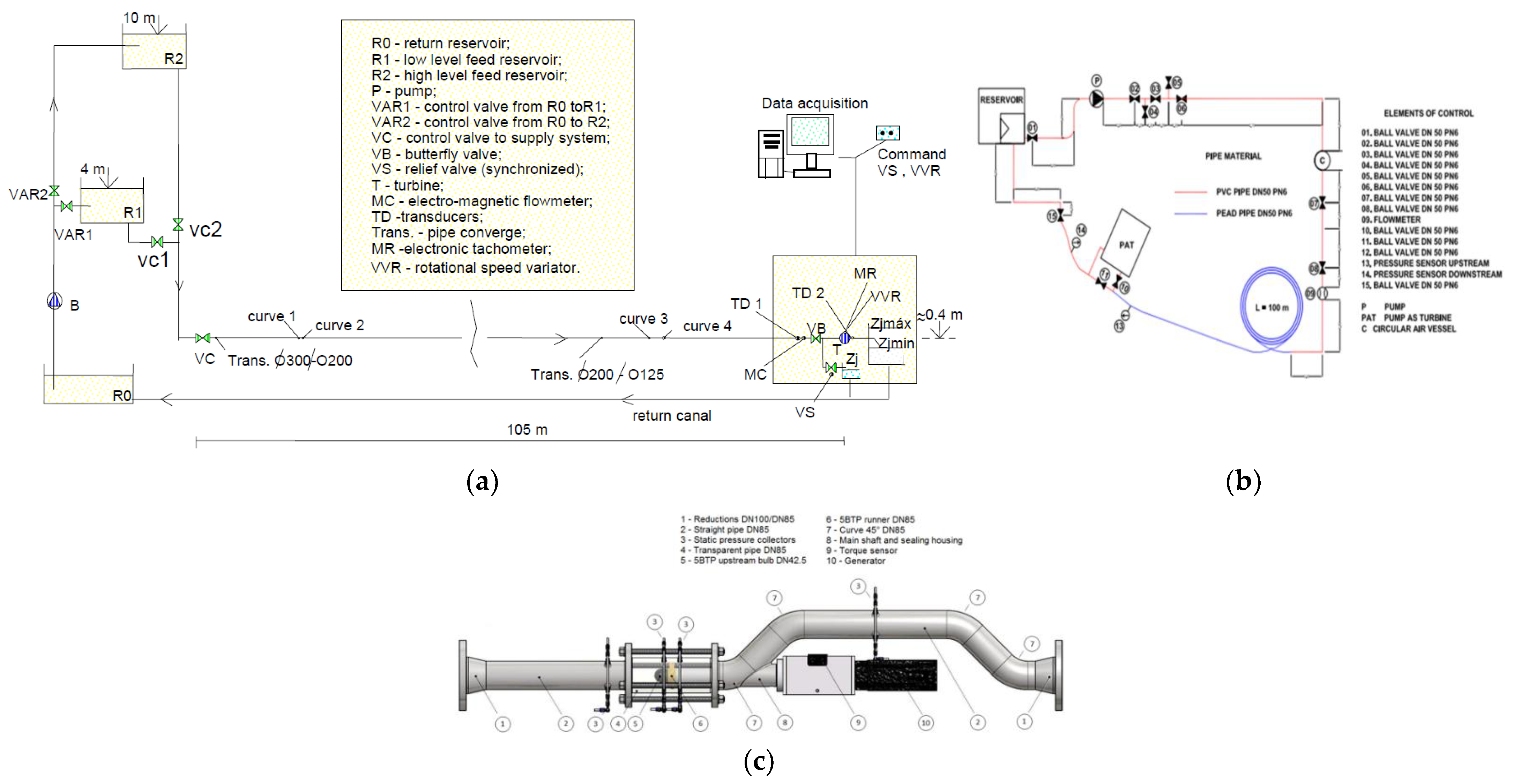
2. Methods and Materials
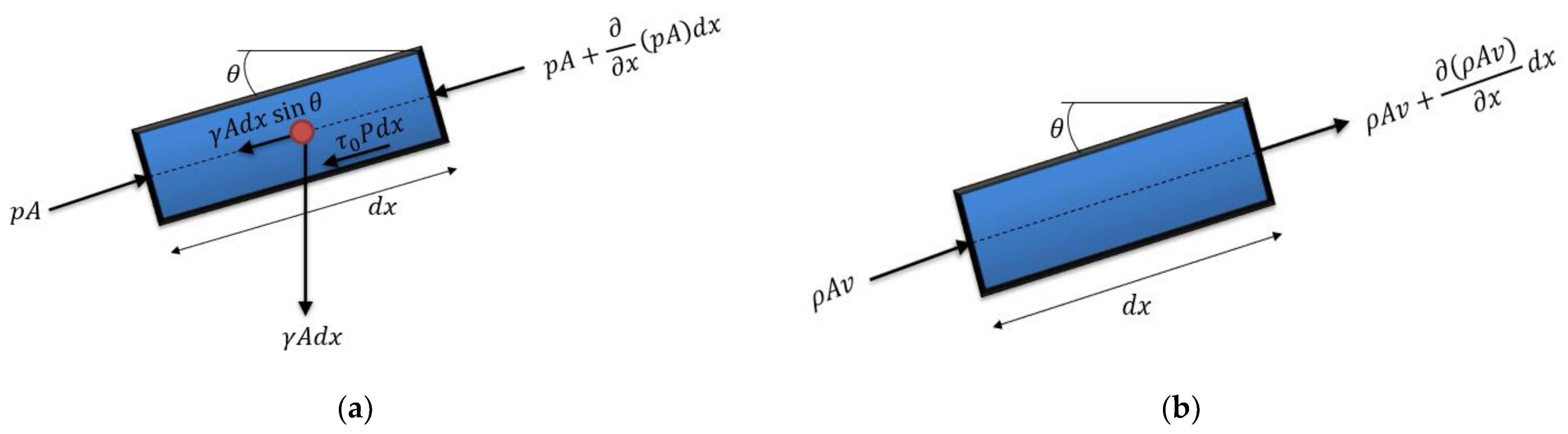
2.1. Water Hammer Modelling
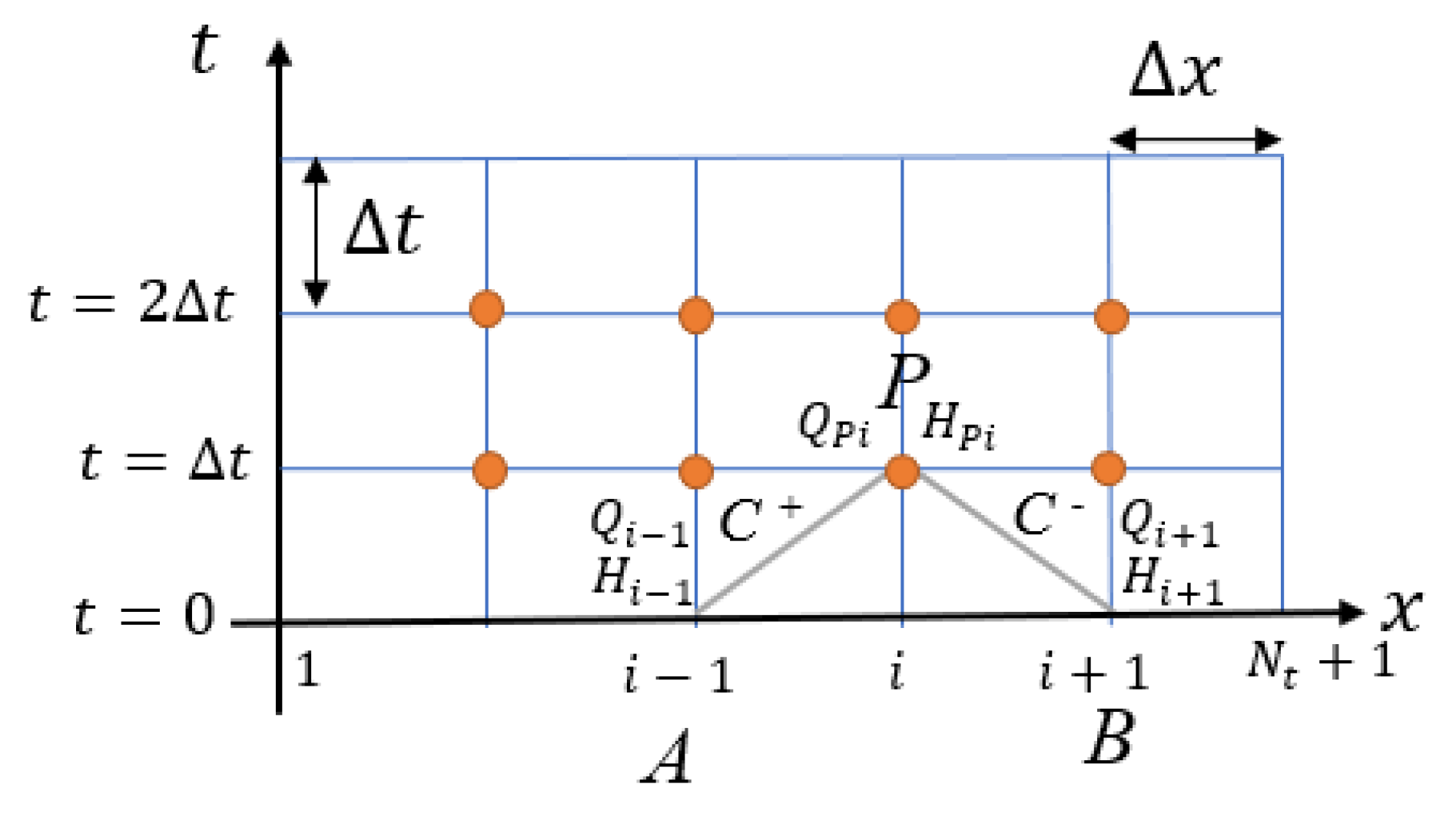
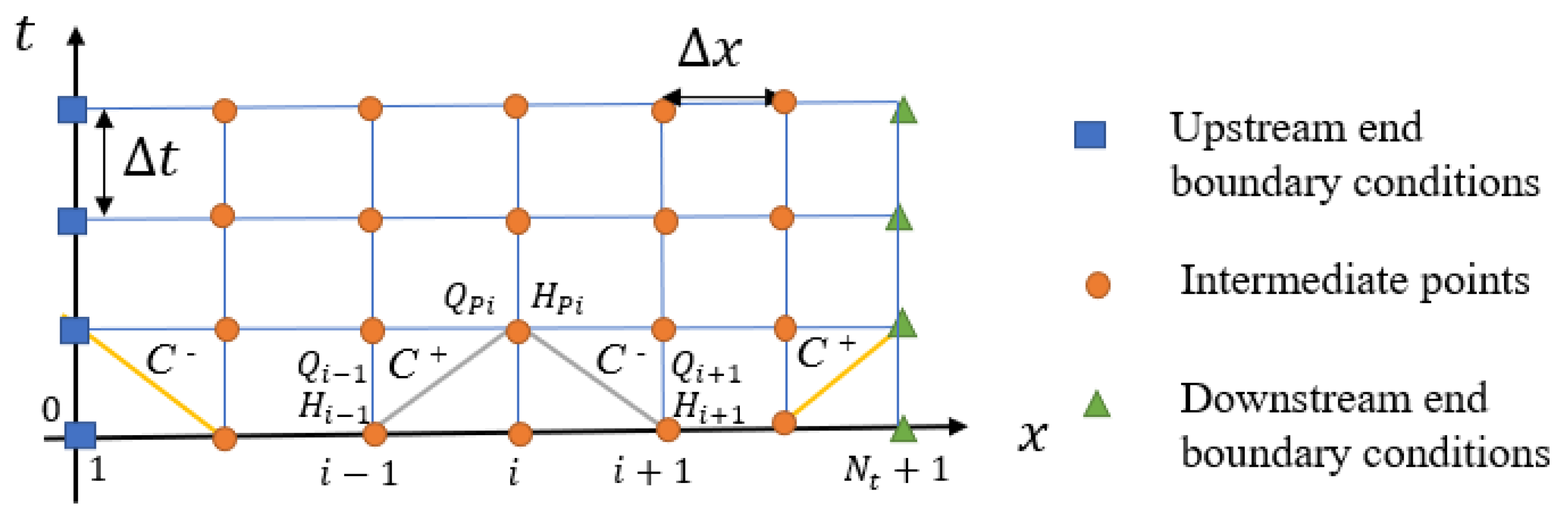
2.2. Boundary Conditions for MOC
2.3. Turbine Modelling
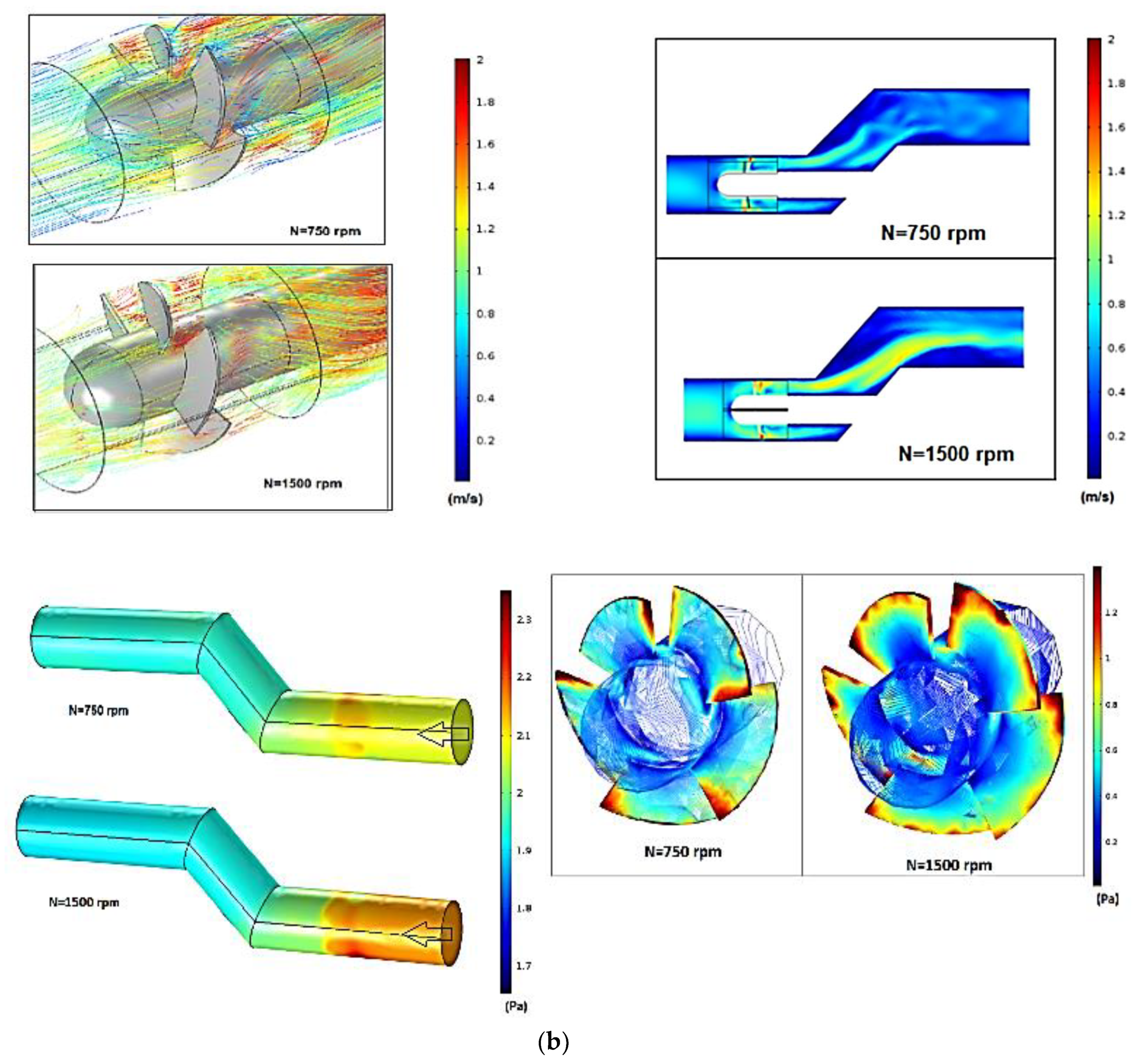
2.4. CFD Model Description and Mesh
3. Dynamic Effects in Hydropower Systems
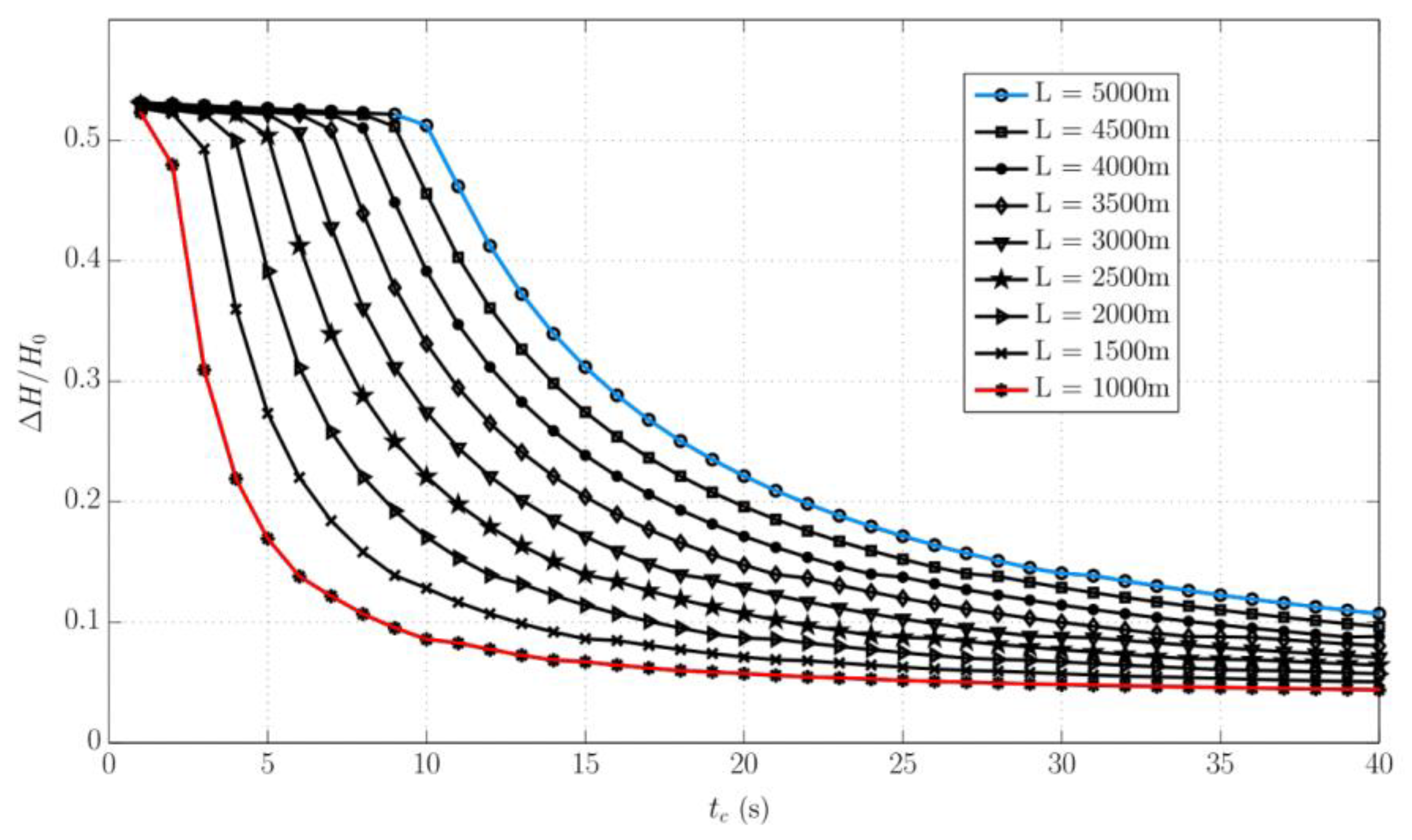
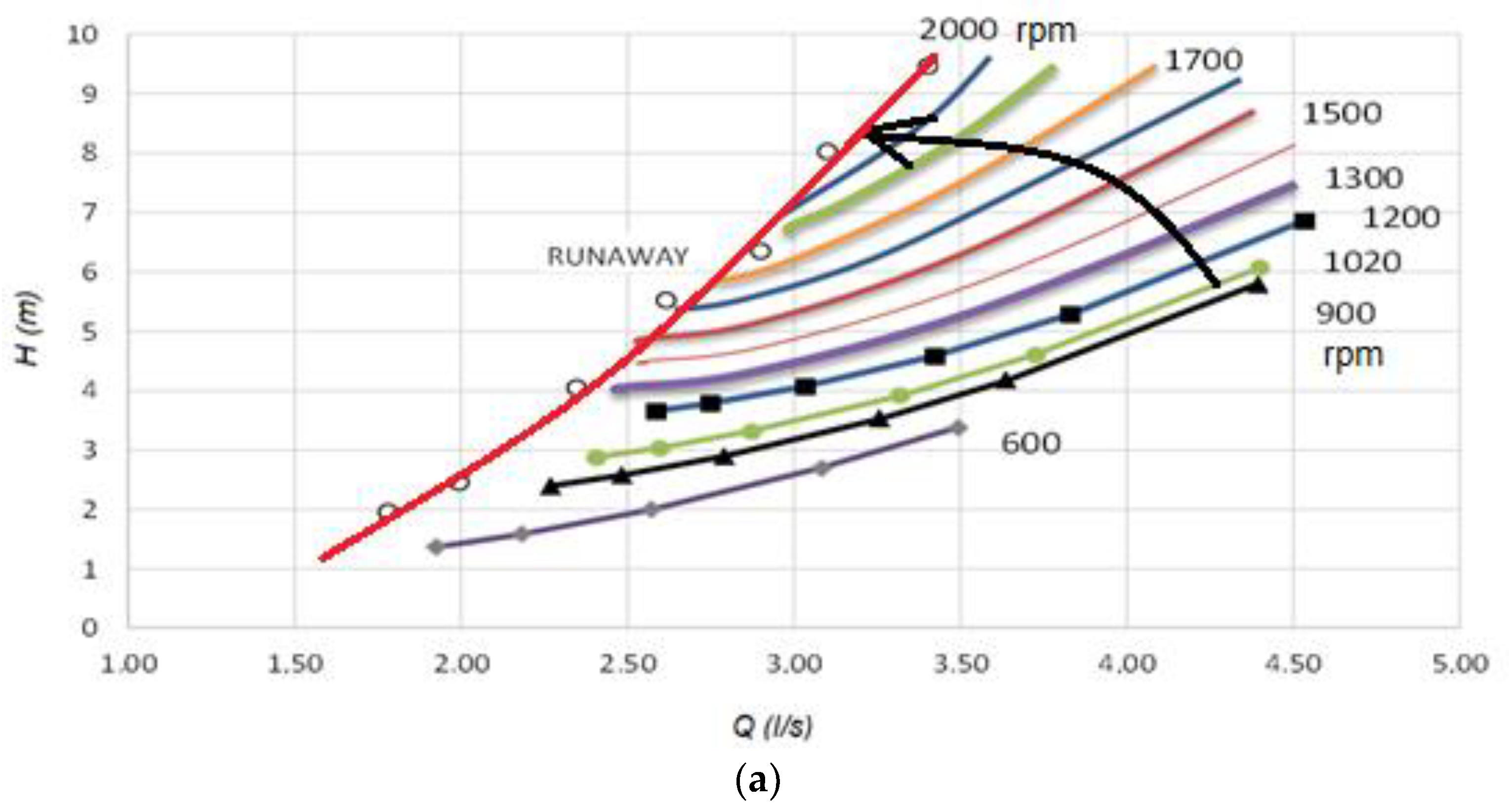
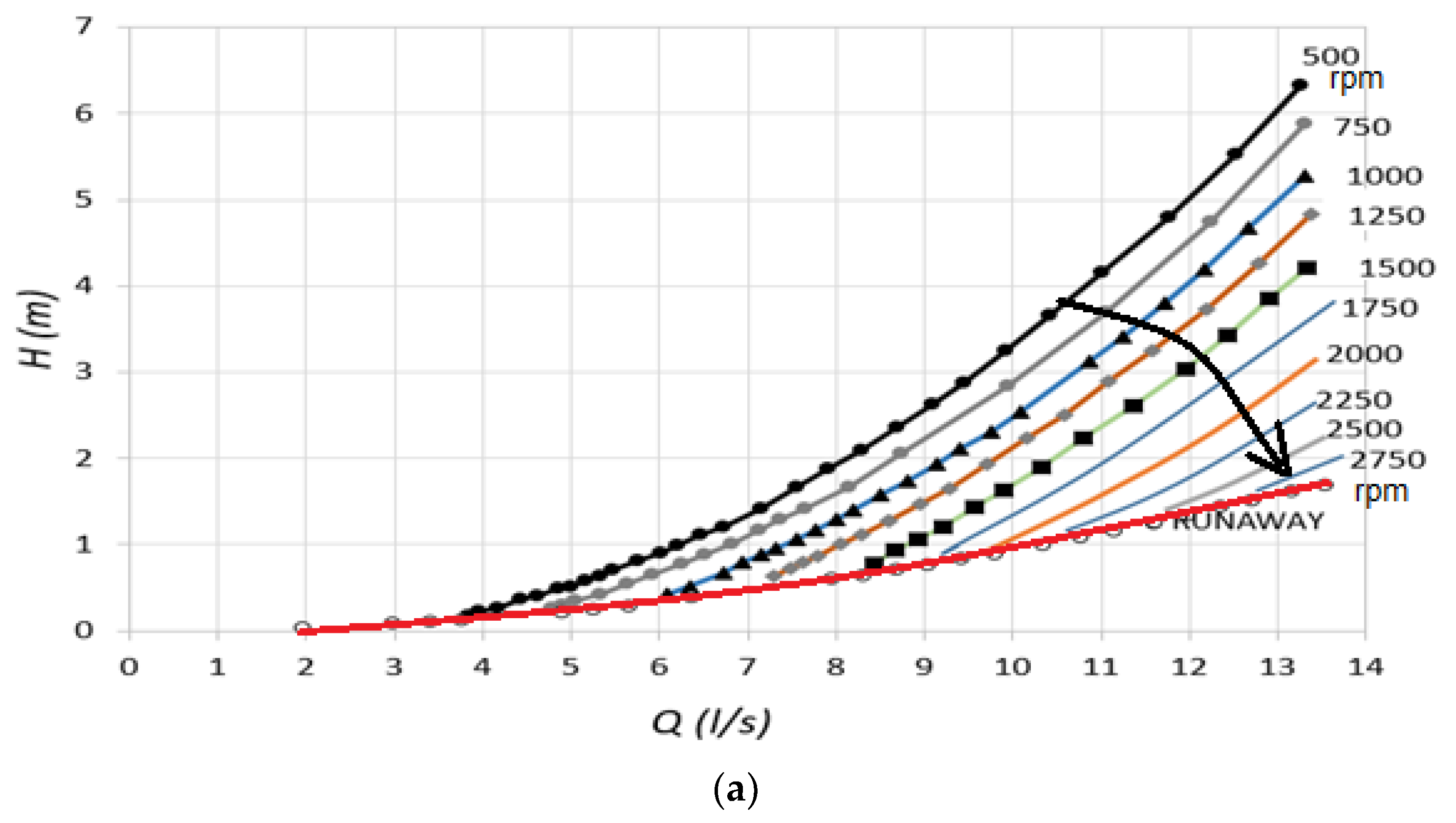
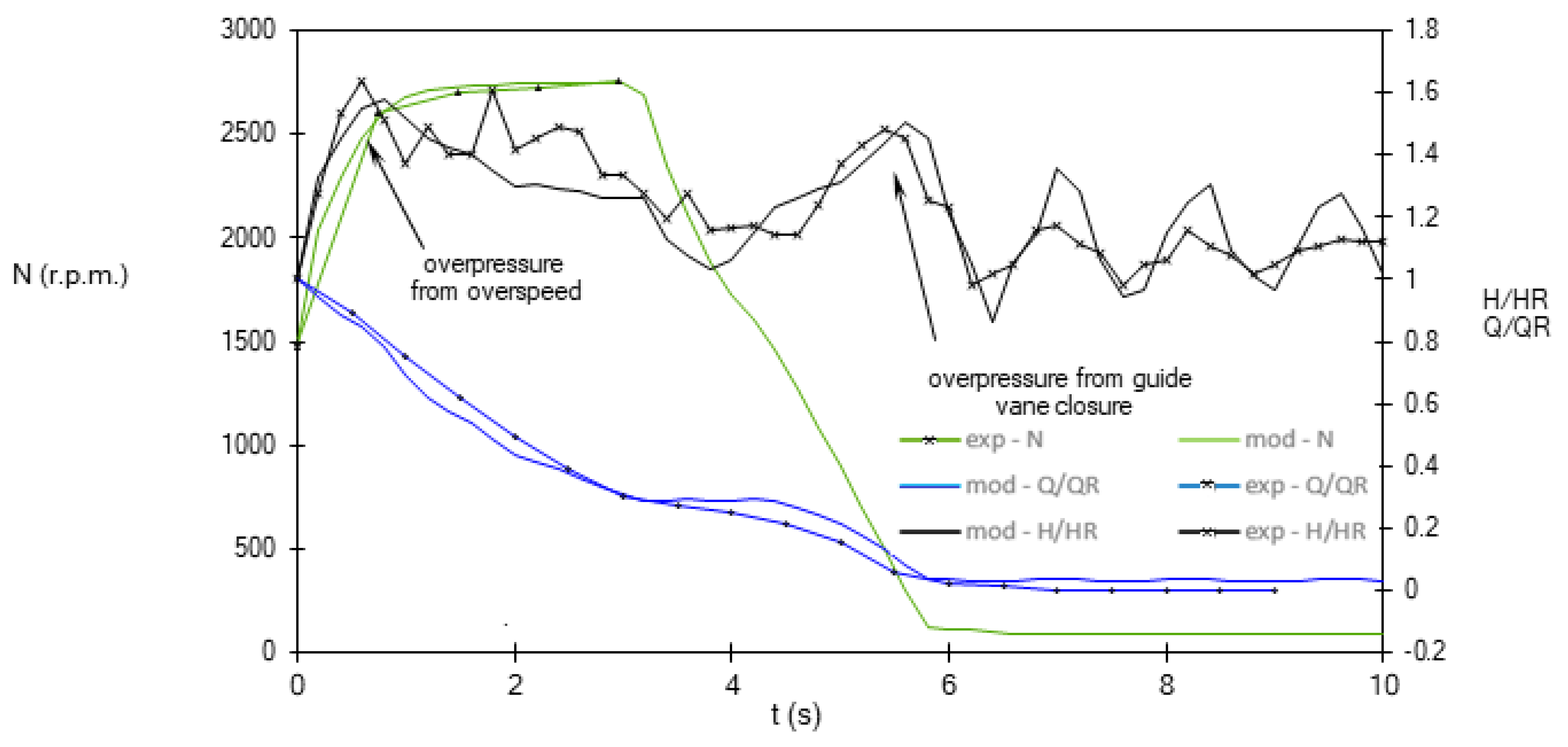
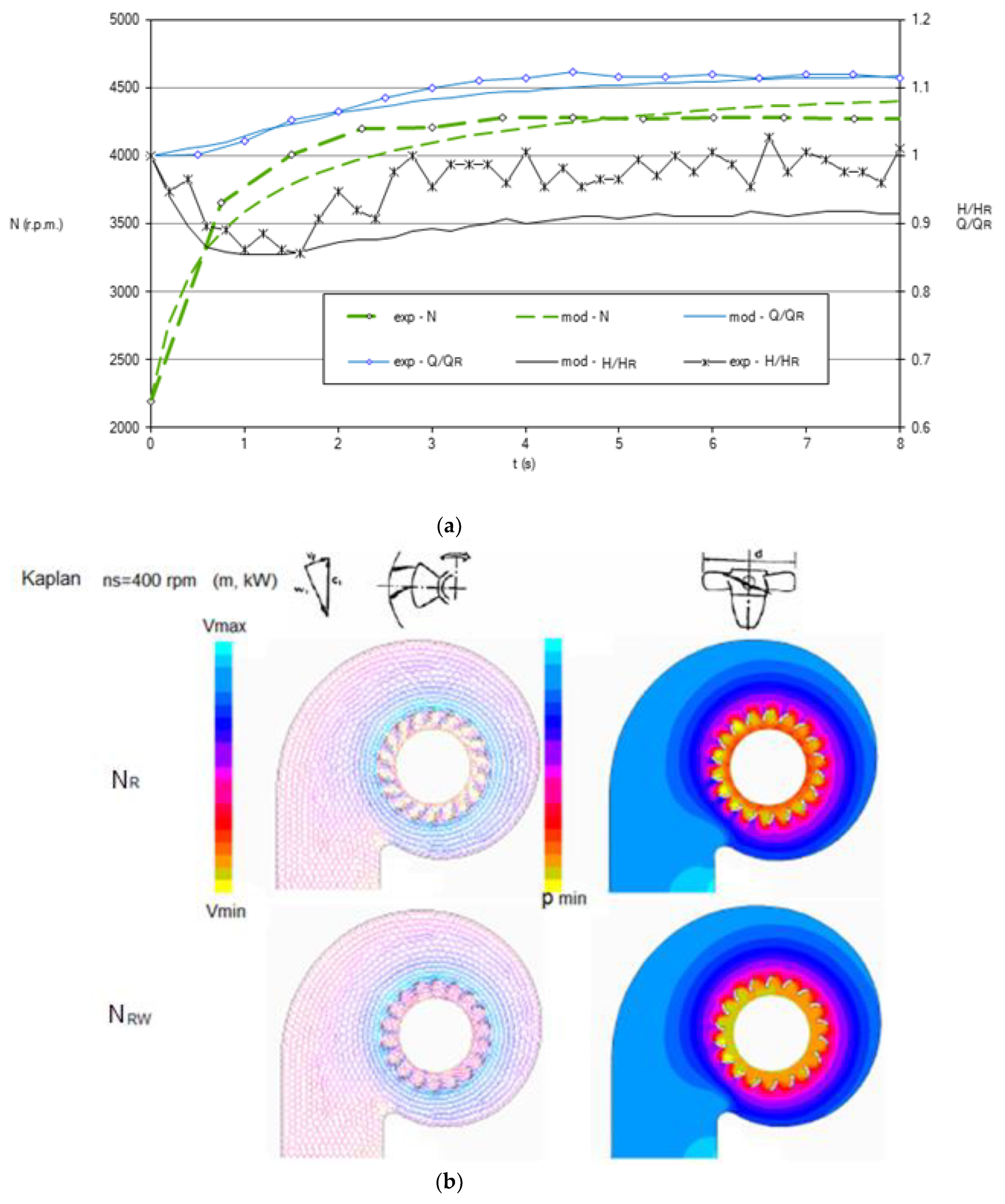
3.1. Overspeed Effect Due to Full-Load Rejection
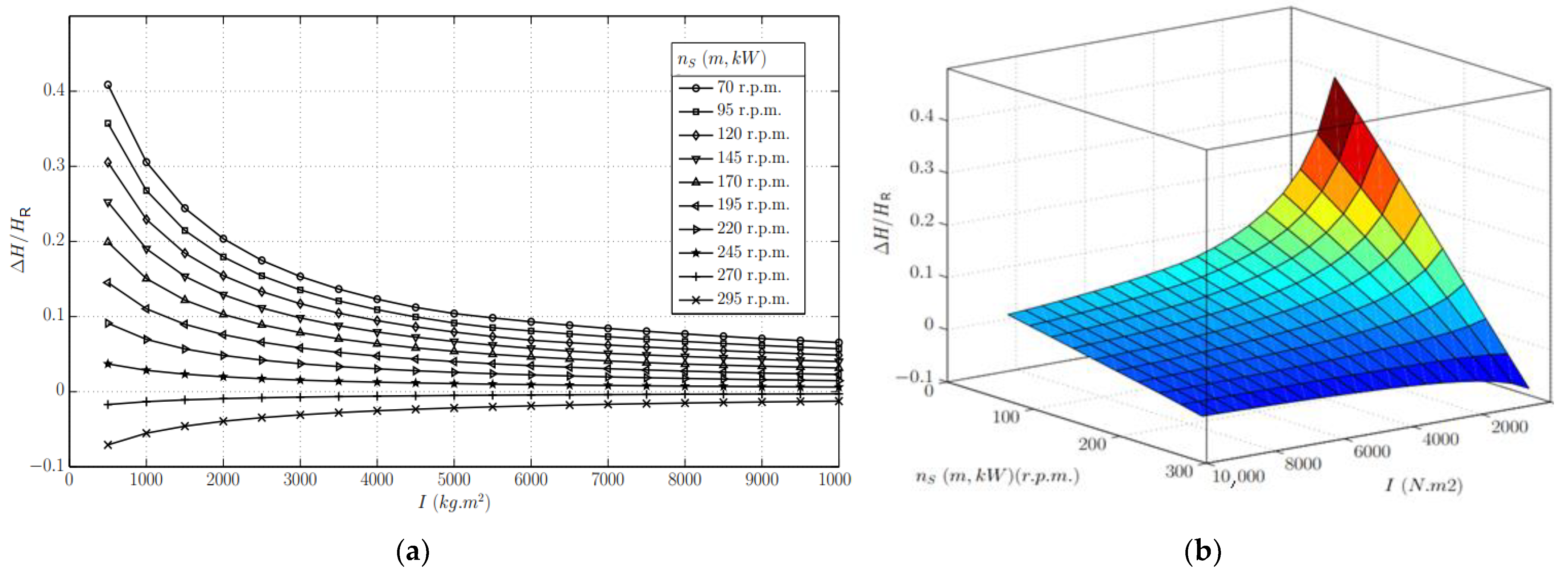
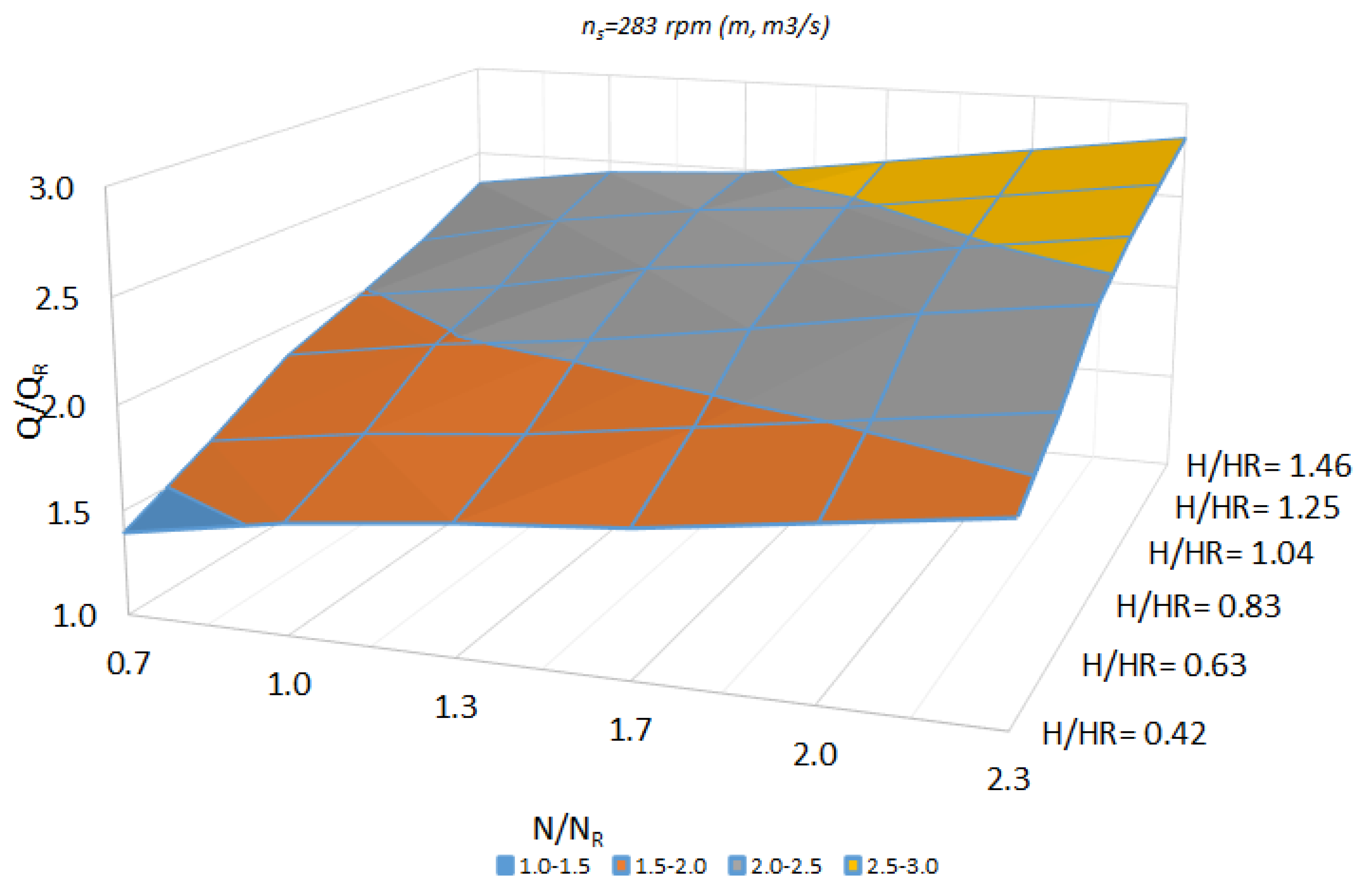
3.2. Influence of Other Characteristic Parameters
4. Comparisons between Modelling and Laboratory Tests for Different Type of Turbines and Specific Speeds
- -
- For Francis and Kaplan with fixed blades (propeller)
- -
- For radial PAT
- -
- For axial PAT
4.1. PAT Radial Runners—Low ns
4.2. PAT Axial Runners—High ns
4.3. Francis Turbine—Low
4.4. Kaplan Turbine—High
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Wave celerity (m/s) | |
| , , | Constants of a pump head curve |
| Cross-sectional area of a pipe (m2) | |
| Cross-sectional area of an orifice (m2) | |
| Cross section of an air vessel (m2) | |
| Constant computed in the initial condition of an air vessel | |
| Relationship between , , and | |
| Negative characteristic equation (-) | |
| Positive characteristic equation (-) | |
| Contraction coefficient (-) | |
| Opening gate coefficient (-) | |
| Negative characteristic constant (-) | |
| Positive characteristic constant (-) | |
| Runner’s rotational speed (-) | |
| Constant of the turbulent eddy viscosity coefficient | |
| Internal pipe diameter (m) | |
| Friction factor (-) | |
| Turbulent viscosity factor | |
| Forces in x direction (N) | |
| Gravitational acceleration (m/s2) | |
| Iteration number (-) | |
| Position in a pipe (-) | |
| Relative turbine head (-) | |
| Hydraulic grade line (m) | |
| Piezometric head on section A (m) | |
| Piezometric head on section B (m) | |
| Barometric pressure (m) | |
| Piezometric head at section P (m) | |
| Pressure head at the end of an analyzed time step in an air vessel (m) | |
| Piezometric head on an analyzed side of section P (m) | |
| Piezometric head on the upstream side of section P (m) | |
| Piezometric head on the downstream side of section P (m) | |
| Turbine/pump rated head (m) | |
| Water level of a reservoir (m) | |
| Rotating mass inertia (kgm2) | |
| Turbulent kinetic energy (m2/s2) | |
| Valve head loss coefficient (-) | |
| Pipe length (m) | |
| Water mass (kg) | |
| Relative rotating speed (-) | |
| Rotational speed | |
| Number of segments (-) | |
| Turbine rated speed (-) | |
| Runaway turbine rotating speed (r.p.m. | |
| Nominal runner speed (r.p.m.) | |
| Specific velocity (r.p.m.). | |
| Pump power (kW) | |
| Reference power (kW) | |
| Pipe perimeter (m) | |
| Pressure force (N) | |
| Polytropic coefficient (-) | |
| Discharge (m3/s) | |
| Relative flow through the turbine (-) | |
| Relative discharge (-) | |
| Discharge at section A (m3/s) | |
| Discharge at section B (m3/s) | |
| Discharge at section P (m3/s) | |
| Air vessel orifice discharge (m3/s) | |
| Turbine/pump rated discharge (m3/s) | |
| Turbine discharge at runaway speed (m3/s) | |
| Time (s) | |
| Turbine torque (N·m) | |
| Electromagnetic resistance torque (N·m) | |
| Actuating hydraulic torque (N·m | |
| Guide-vane or valve closing time (s) | |
| Elastic time constant (s) | |
| Hydraulic turbine torque (N·m) | |
| Start-up time of rotating masses (s) | |
| Hydraulic inertia time (s) | |
| Water velocity in a pipe (m/s) | |
| Volume of the air enclosed in the vessel of an analyzed time step (m3) | |
| Distance along the main direction of a pipe system (m) | |
| Distance from the wall (m) | |
| Initial elevation of the free surface inside an air vessel (m) | |
| Free surface elevation at the end of the time step (m) | |
| Inertial weight of rotating mass (N·m2) | |
| Relative runaway discharge (-) | |
| Relative runaway rotating speed (-) | |
| Turbulent dissipation | |
| Pipe slope (m/m) | |
| Time step (s) | |
| Overpressure (m) | |
| Water density (kg/m3) | |
| Water unit weight (N/m3) | |
| Dynamic viscosity coefficient (-) | |
| Turbulent eddy viscosity coefficient (-) | |
| Shear stress (N/m2) | |
| Viscous shear stress tensor | |
| Reynolds-stress tensor | |
| Kronecker delta function (-) | |
| Angular speed (rad/s) | |
| Unit rated efficiency (-) |
References
- Burek, P.; Satoh, Y.; Fischer, G.; Kahil, T.; Jimenez, L.; Scherzer, A.; Tramberend, S.; Wada, Y.; Eisner, S.; Flörke, M.; et al. Water Futures and Solution: Fast Track Initiative (Final Report); IIASA: Laxemburg, Austria, 2016. [Google Scholar]
- Ferroukhi, R.; Nagpal, D.; Lopez-Peña, A.; Hodges, T.; Mohtar, R.H.; Daher, B.; Mohtar, S.; Keulertz, M. Renewable Energy in the Water, Energy and Food Nexus; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2015. [Google Scholar]
- Simão, M.; Ramos, H.M. Hybrid Pumped Hydro Storage Energy Solutions towards Wind and PV Integration: Improvement on Flexibility, Reliability and Energy Costs. Water 2020, 12, 2457. [Google Scholar] [CrossRef]
- Rogner, M.; Troja, N. The World’s Water Battery: Pumped Hydropower Storage and the Clean Energy Transition; International Hydropower Association: London, UK, 2018. [Google Scholar]
- Ramos, H.M.; Amaral, M.P.; Covas, D.I.C. Pumped-Storage Solution towards Energy Efficiency and Sustainability: Portugal Contribution and Real Case Studies. J. Water Resour. Prot. 2014, 6, 1099–1111. [Google Scholar] [CrossRef]
- Carravetta, A.; Houreh, S.D.; Ramos, H.M. Pumps as Turbines: Fundamentals and Applications; Springer International Publishing AG: Cham, Switzerland, 2018; ISBN 978-3-319-67506-0. [Google Scholar] [CrossRef]
- Kougias, I.; Patsialis, T.; Zafirakou, A.; Theodossiou, N. Exploring the potential of energy recovery using micro hydropower systems in water supply systems. Water Util. J. 2014, 7, 25–33. [Google Scholar]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Carravetta, A.; Del~Giudice, G.; Fecarotta, O.; Gallagher, J.; Morani, M.C.; Ramos, H.M. Potential Energy, Economic, and Environmental Impacts of Hydro Power Pressure Reduction on the Water-Energy-Food Nexus. J. Water Resour. Plan. Manag. 2022, 148, 04022012. [Google Scholar] [CrossRef]
- Fontanella, S.; Fecarotta, O.; Molino, B.; Cozzolino, L.; Della Morte, R. A Performance Prediction Model for Pumps as Turbines (PATs). Water 2020, 12, 1175. [Google Scholar] [CrossRef]
- De Marchis, M.; Milici, B.; Volpe, R.; Messineo, A. Energy Saving in Water Distribution Network through Pump as Turbine Generators: Economic and Environmental Analysis. Energies 2016, 9, 877. [Google Scholar] [CrossRef]
- Lima, G.M.; Luvizotto, E., Jr.; Brentan, B.M. Selection and location of Pumps as Turbines substituting pressure-reducing valves. Renew. Energy 2017, 109, 392–405. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water 2020, 12, 468. [Google Scholar] [CrossRef]
- Ramos, H.; Almeida, A.B. Dynamic orifice model on waterhammer analysis of high or medium heads of small hydropower schemes. J. Hydraul. Res. 2001, 39, 429–436. [Google Scholar] [CrossRef]
- Ramos, H.; Almeida, A.B. Parametric analysis of waterhammer effects in small hydropower schemes. J. Hydraul. Eng. 2002, 128, 689–697. [Google Scholar] [CrossRef]
- Ramos, H.M.; Almeida, A.B.; Portela, M.M.; Almeida, H.P. Guidelines for Design of Small Hydropower Plants; Western Regional Energy Agency & Network: Enniskillen, Northern Ireland; Department of Economic Development: Belfast, Northern Ireland, 2000. [Google Scholar]
- Pothof, I.; Karney, B. Guidelines for transient analysis in water transmission and distribution systems. In Water Supply System Analysis—Selected Topics; Ostfeld, A., Ed.; InTech: Rijeka, Croatia, 2012; pp. 1–21. [Google Scholar]
- Boulos, P.; Karney, B.; Wood, D.; Lingireddy, S. Hydraulic transient guidelines for protecting water distribution systems. J. Am. Water Work. Assoc. 2005, 97, 111–124. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L. Fluid Transients; FEB Press: Ann Arbor, MI, USA, 1983. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. PATs Operating in Water Networks under Unsteady Flow Conditions: Control Valve Manoeuvre and Overspeed Effect. Water 2018, 10, 529. [Google Scholar] [CrossRef]
- Lima, G.M.; Luvizotto, E., Jr. Method to Estimate Complete Curves of Hydraulic Pumps through the Polymorphism of Existing Curves. J. Hydraul. Eng. 2017, 143, 04017017. [Google Scholar] [CrossRef]
- Ramos, H.; Almeida, A.B. Experimental and Computational Analysis of Hydraulic Transients Induced by Small Reaction Turbomachines; APRH, LNEC.: Lisboa, Portugal, 2001. (In Portuguese) [Google Scholar]
- Ramos, H.M. Simulation and Control of Hydrotransients at Small Hydroelectric Power Plants. Ph.D. Thesis, Technical University of Lisbon, Lisbon, Portugal, 1995. (In Portuguese). [Google Scholar]
- Ramos, H.; Borga, A. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Hanna, K.; Parry, J. Back to the Future: Trends in Commercial CFD. In Proceedings of the NAFEMS World Congress 2011, Boston, MA, USA, 23–26 May 2011. [Google Scholar]
- Solid Works 2011. Flow Simulation. Available online: https://www.gsc-3d.com/training-solutions/ (accessed on 12 November 2022).
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; López-Jiménez, P.; Ramos, H.M. Velocities in a Centrifugal PAT Operation: Experiments and CFD Analyses. Fluids 2018, 3, 3. [Google Scholar] [CrossRef]
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; Ramos, H.M. Flow Conditions for PATs Operating in Parallel: Experimental and Numerical Analyses. Energies 2019, 12, 901. [Google Scholar] [CrossRef]
- Simão, M.; López-Jiménez, P.A.; Ramos, H.M. CFD Analyses and Experiments in a PAT Modeling: Pressure Variation and System Efficiency. Fluids 2017, 2, 51. [Google Scholar] [CrossRef]
- Liu, K.; Yang, F.; Yang, Z.; Zhu, Y.; Cheng, Y. Runner Lifting-Up during Load Rejection Transients of a Kaplan Turbine: Flow Mechanism and Solution. Energies 2019, 12, 4781. [Google Scholar] [CrossRef]
- Zhang, M.; Feng, J.; Zhao, Z.; Zhang, W.; Zhang, J.; Xu, B. A 1D-3D Coupling Model to Evaluate Hydropower Generation System Stability. Energies 2022, 15, 7089. [Google Scholar] [CrossRef]
- Li, S.; Yang, Y.; Xia, Q. Dynamic Safety Assessment in Nonlinear Hydropower Generation Systems. Complexity 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Morgado, P.A.L. Mathematical Modelling to Simulate Dynamic Effects in Reversible Hydro Systems. Master’s Thesis, Instituto Superior Técnico, Universidade Técnica de Lisboa, Lisboa, Portugal, 2010. [Google Scholar]
- Morgado, P.A.; Ramos, H.M. Pump as turbine: Dynamic effects in small hydro. In Proceedings of the World Renewable Energy Congress, Linkoping, Sweden, 8–13 May 2011; Hydropower Applications: Linkoping, Sweden, 2011. [Google Scholar]
- Mahfoud, R.J.; Alkayem, N.F.; Zhang, Y.; Zheng, Y.; Sun, Y.; Alhelou, H.H. Optimal operation of pumped hydro storage-based energy systems: A compendium of current challenges and future perspectives. Renew. Sustain. Energy Rev. 2023, 178, 113267. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Münch-Alligné, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blades tubular propeller turbine for pipe inline installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]









| Element | Scheme | Considerations and Additional Equations | Equations System | Notation |
|---|---|---|---|---|
| Constant-head reservoir | 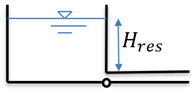 | The boundary condition for a constant-head reservoir is computed neglecting entrance head losses as: | (10) | is the water level of a reservoir. |
| Pump | 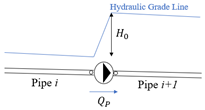 | Based on pump characteristic curve for each time step as: | (11) | , , and are constants of a pump curve, and is the rotational speed. |
| Valve | 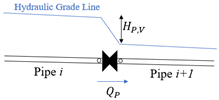 | The boundary condition in a regulating valve is obtained based on steady-state head loss equation as: | (12) | is the head loss coefficent obtained experiment20ally. |
| Air vessel |  | The equation of an air vessel is obtained considering the polytropic law , which needs to be solved simultaneously with the following five equations: | (13) | is the absolute pressure head at the end of an analysed time step, is the air volumne at the end of an analysed time step, is the air volume, is the flow through the orifice, is the cross-section of the orifice, is the discharge coefficient of the orifice, is the polytropic coefficient (usually takes a value of 1.2), is the initial elevation of the free surface, is the barometric pressure, is the constant computed in the initial condition of the air vessel, is the free surface elevation at the end of the time step, and is the cross-section of the air vessel. |
| Mesh | Number of Fluid Mesh Cells | Number of Solid Mesh Cells | H | Error (%) | Duration |
|---|---|---|---|---|---|
| Mesh 1 | 35,888 | 25,378 | 9.8 | 0.15 h | |
| Mesh 2 | 60,381 | 30,229 | 6.4 | 34% | 0.49 h |
| Mesh 3 | 110,691 | 60,088 | 5.8 | 9% | 2.23 h |
| Mesh 4 | 121,936 | 71,162 | 5.4 | 6% | 2.52 h |
| Mesh 5 | 134,152 | 81,291 | 5.2 | 3% | 3.28 h |
| Mesh 6 | 135,472 | 88,364 | 5.1 | 1% | 3.33 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, H.M.; Coronado-Hernández, O.E.; Morgado, P.A.; Simão, M. Mathematic Modelling of a Reversible Hydropower System: Dynamic Effects in Turbine Mode. Water 2023, 15, 2034. https://doi.org/10.3390/w15112034
Ramos HM, Coronado-Hernández OE, Morgado PA, Simão M. Mathematic Modelling of a Reversible Hydropower System: Dynamic Effects in Turbine Mode. Water. 2023; 15(11):2034. https://doi.org/10.3390/w15112034
Chicago/Turabian StyleRamos, Helena M., Oscar E. Coronado-Hernández, Pedro A. Morgado, and Mariana Simão. 2023. "Mathematic Modelling of a Reversible Hydropower System: Dynamic Effects in Turbine Mode" Water 15, no. 11: 2034. https://doi.org/10.3390/w15112034
APA StyleRamos, H. M., Coronado-Hernández, O. E., Morgado, P. A., & Simão, M. (2023). Mathematic Modelling of a Reversible Hydropower System: Dynamic Effects in Turbine Mode. Water, 15(11), 2034. https://doi.org/10.3390/w15112034








