Fast Prediction of Solitary Wave Forces on Box-Girder Bridges Using Artificial Neural Networks
Abstract
:1. Introduction
2. Numerical Model and Validation
2.1. Governing Equations
2.2. Solitary Wave Generation and Elimination
2.3. Validation of Numerical Wave Flume
2.4. Validation of Numerical Wave Force
3. Numerical Results and Parametric Study
3.1. Solitary Wave Force on Bridge Deck
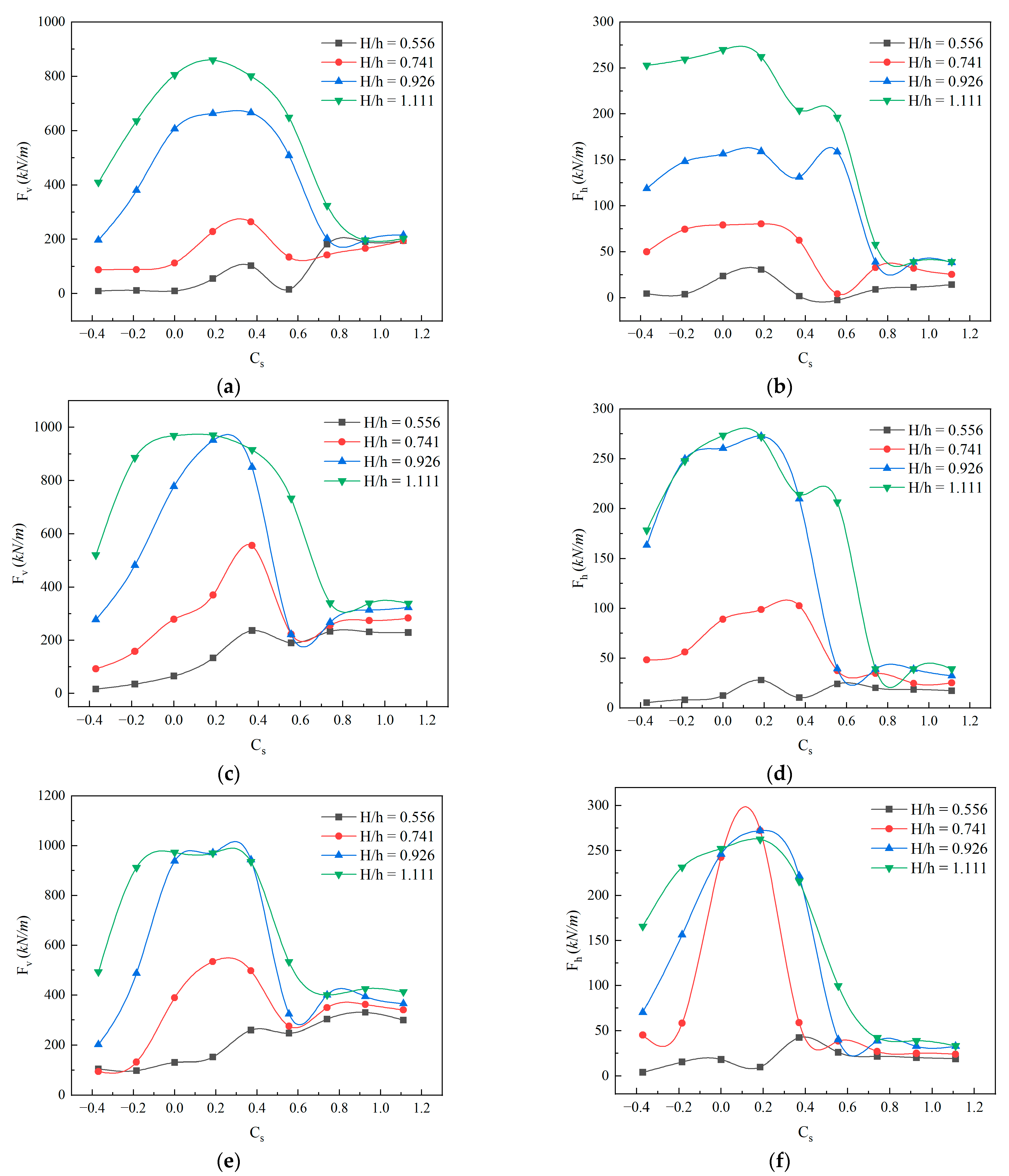
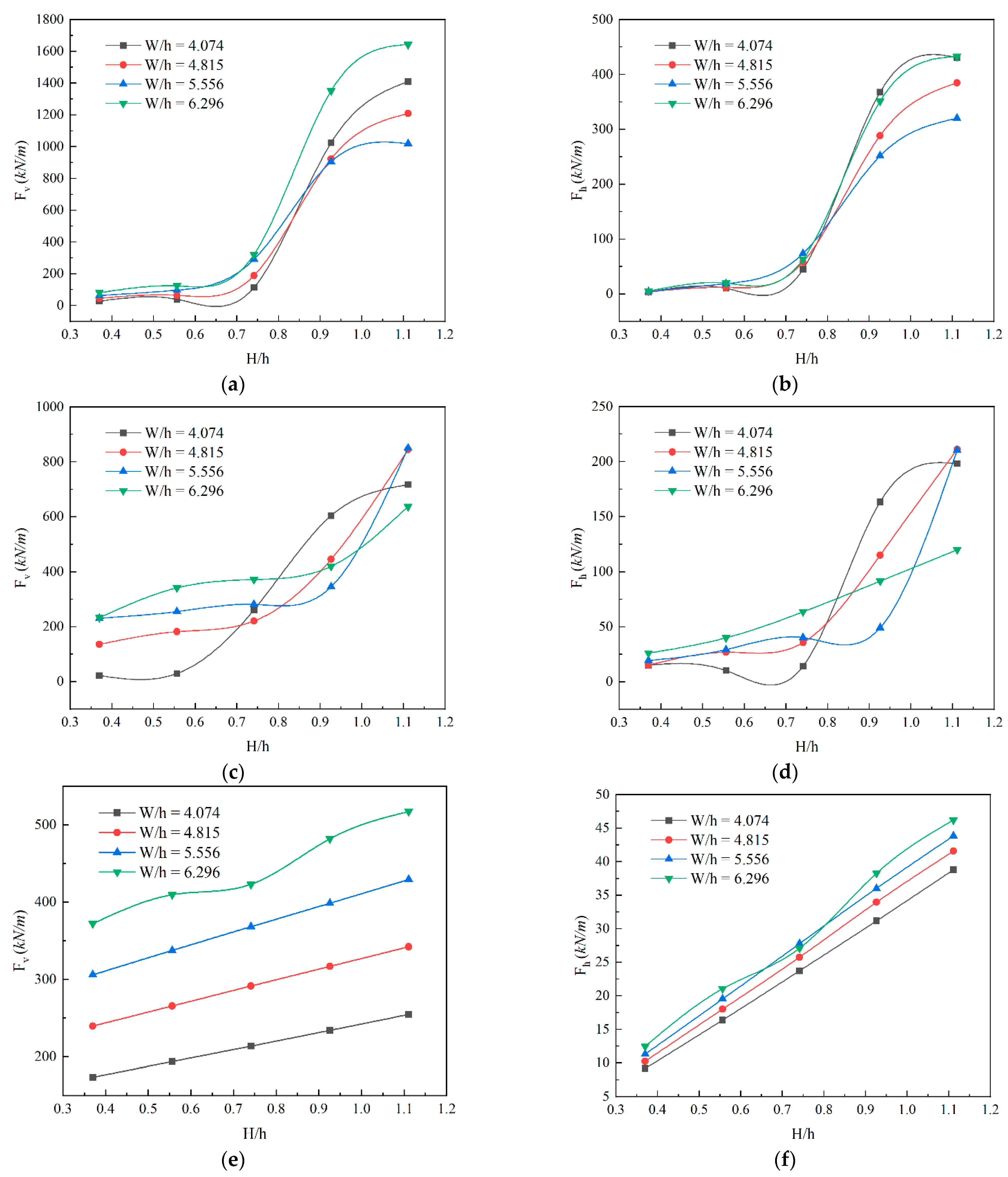
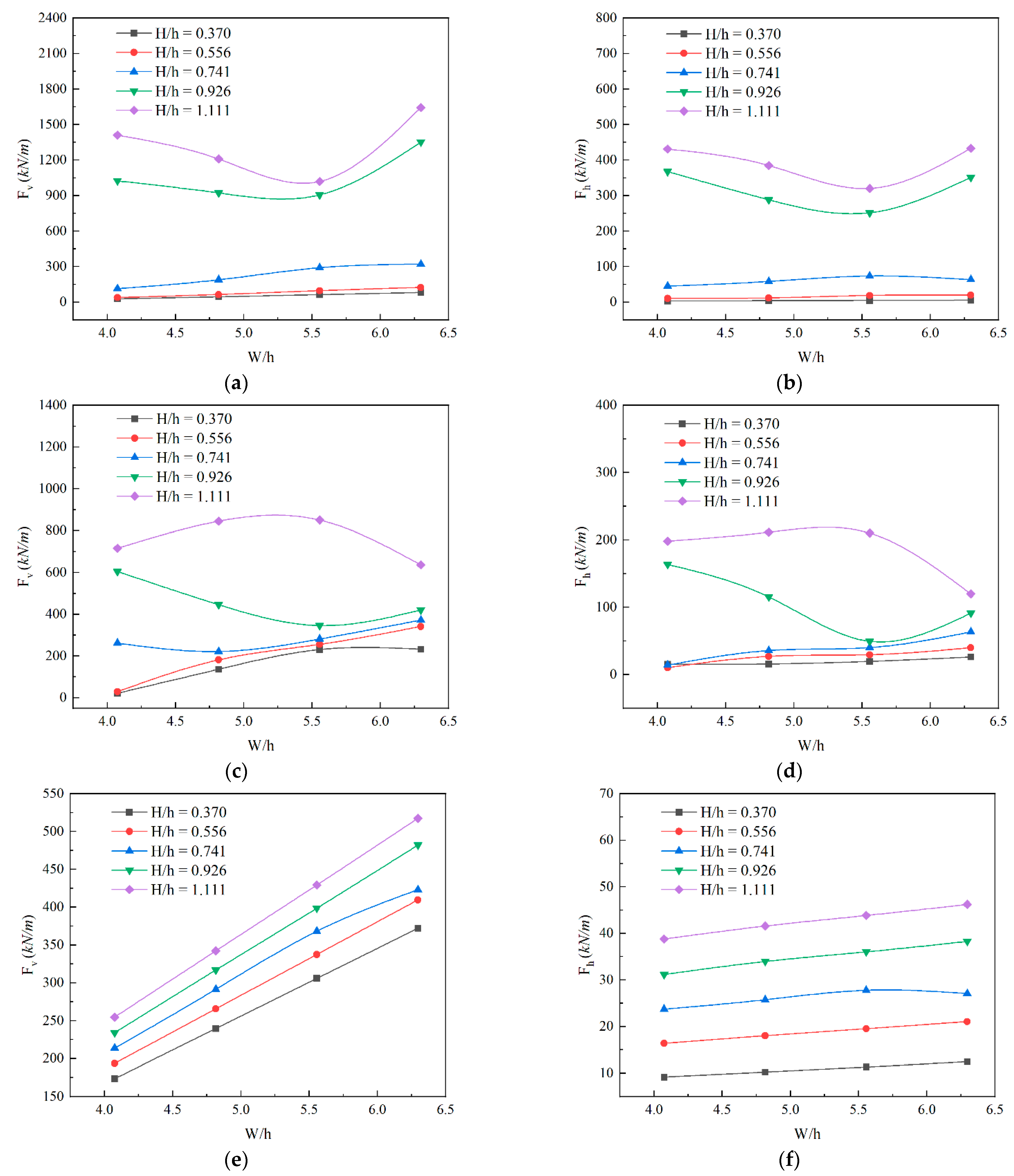
3.2. Parametric Study on Wave Force
4. Artificial Neural Network for Fast Prediction of Wave Force
4.1. Datasets
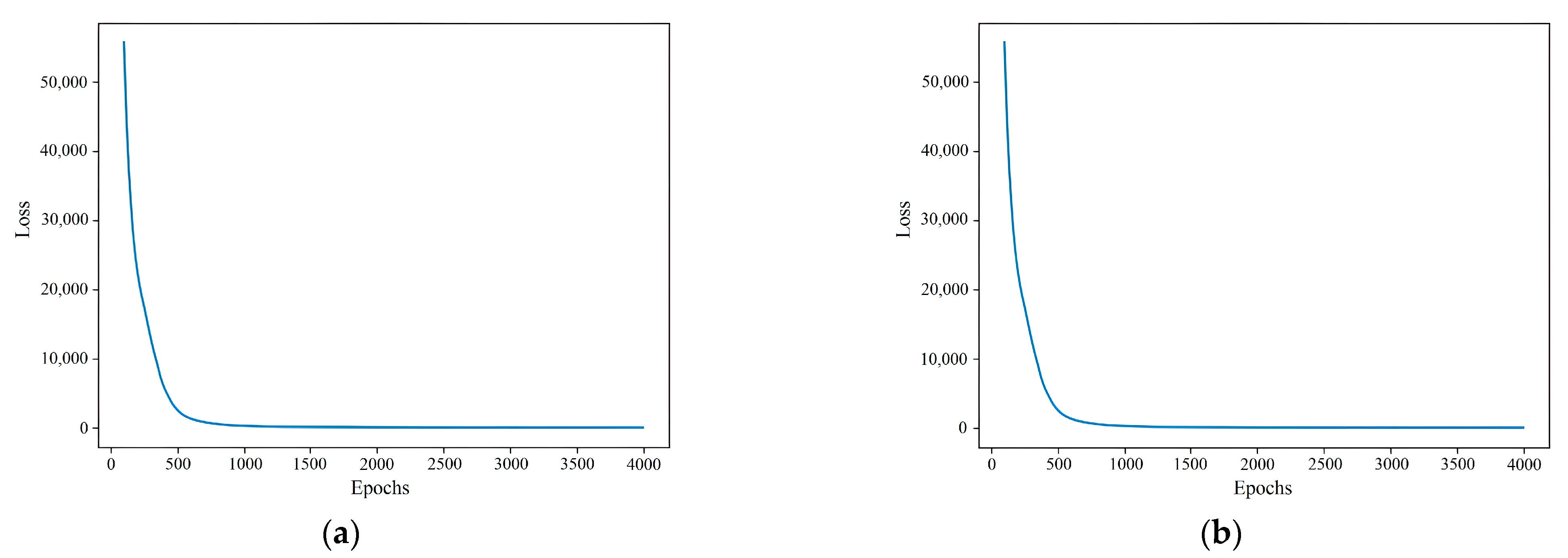
4.2. Training Process
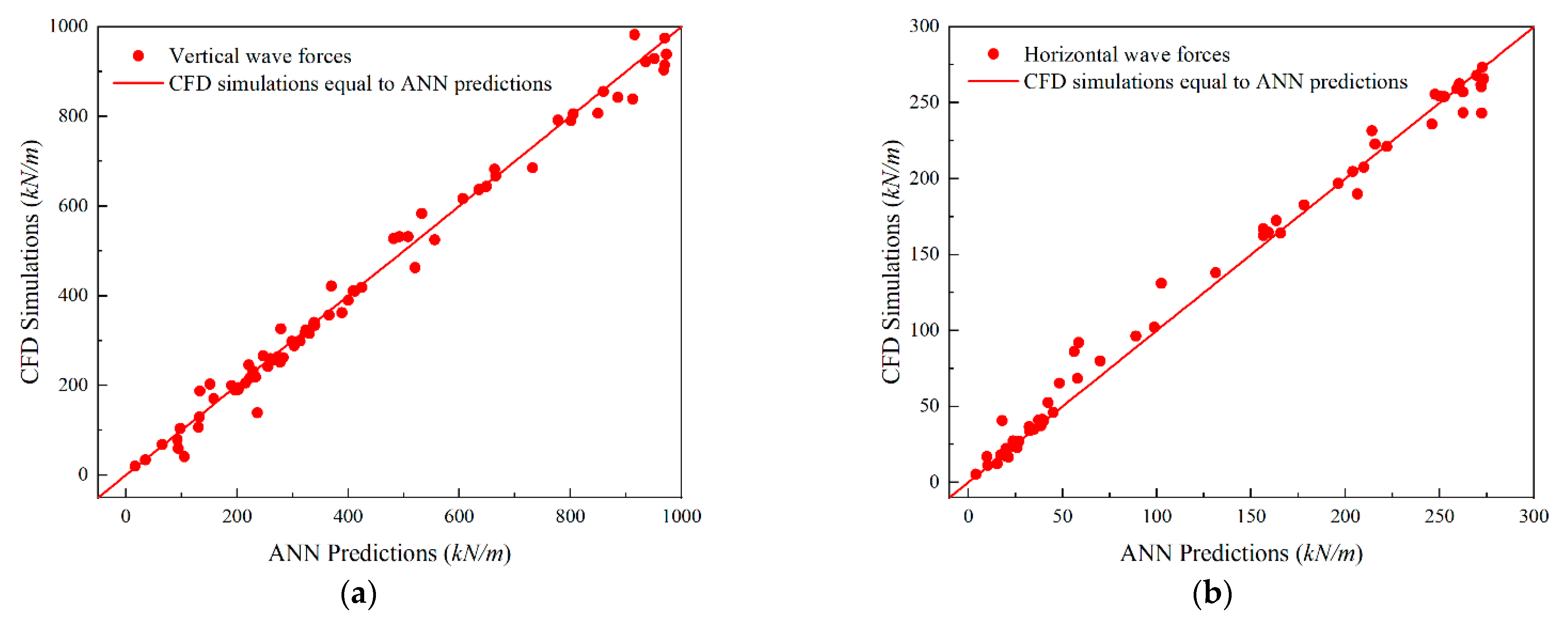
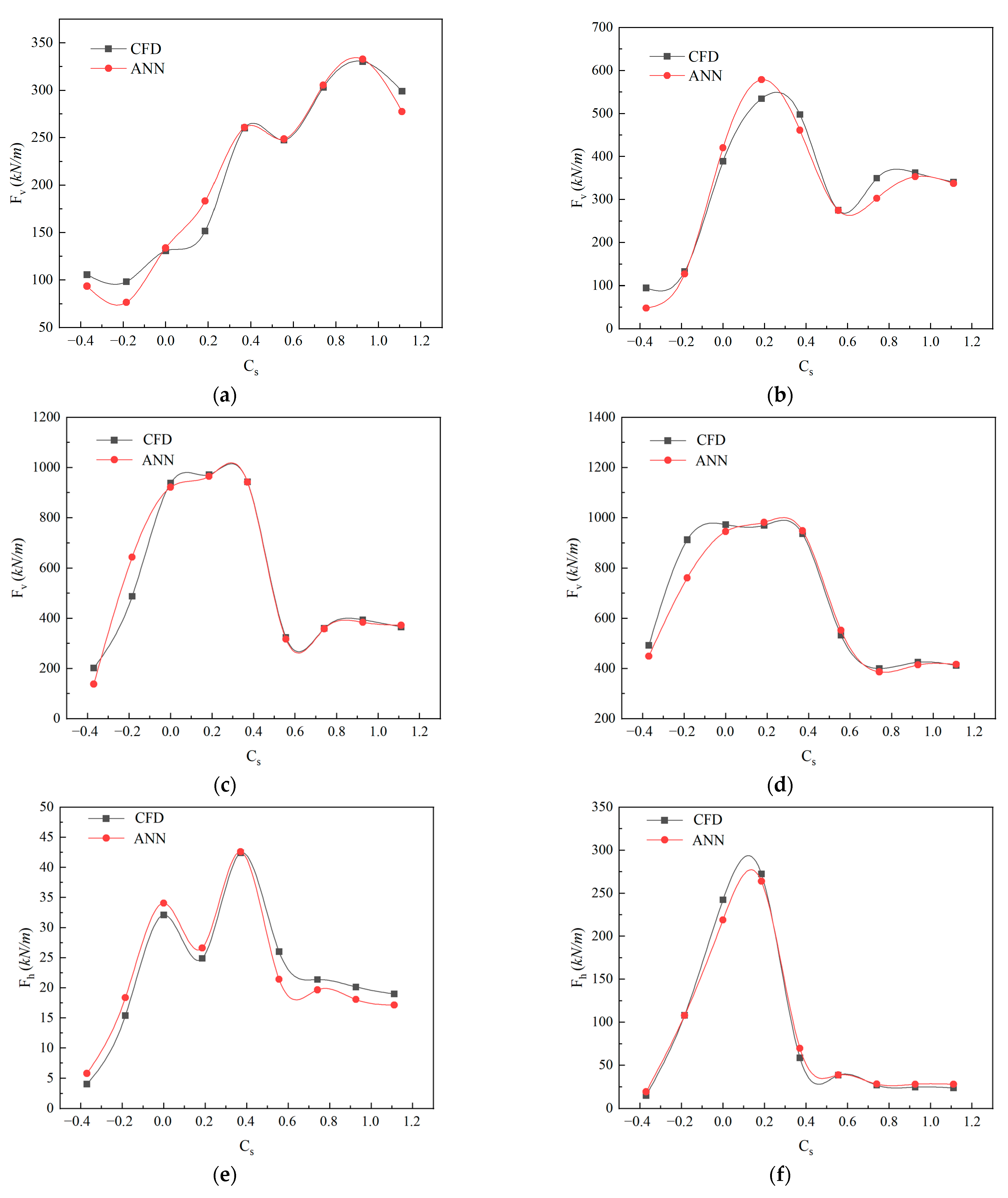
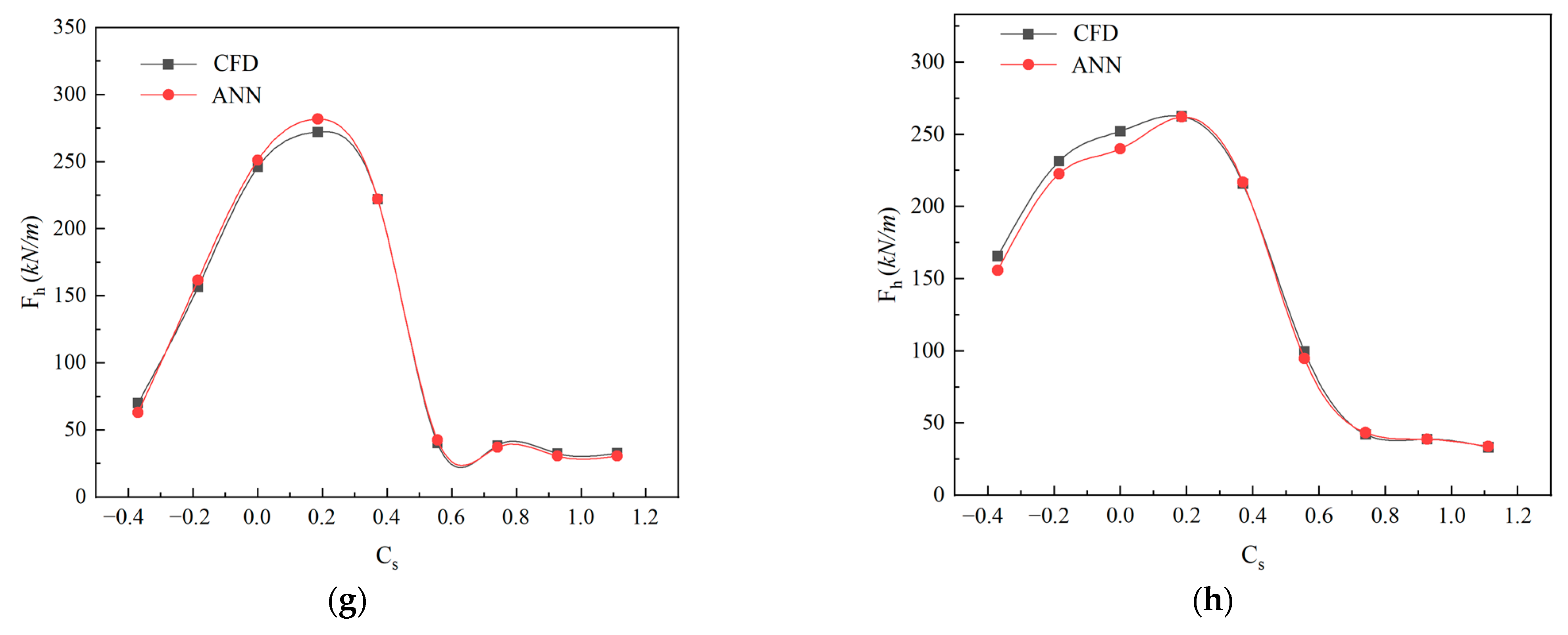
4.3. Prediction Accuracy
5. Conclusions and Future Directions
- (1)
- Both the maximum vertical and horizontal wave forces first increased and then decreased with the submersion coefficient Cs, and finally converged around Cs = 0.8. The peak values of maximum vertical wave forces were achieved in the range of Cs equal to 0.2–0.35, depending on the relative wave height (H/h) and the deck aspect ratio (W/h). For the maximum positive horizontal wave forces, the peak values were obtained in the range of Cs equal to 0–0.2.
- (2)
- Both the maximum vertical and horizontal wave forces monotonically increased with respect to H/h. The relationship between the maximum wave forces and relative wave heights presented strong nonlinearities for small Cs. On the other hand, the maximum wave force increased with H/h following an approximately linear relationship for large Cs. Both the maximum vertical and horizontal wave forces linearly increased with W/h for relatively small H/h and large Cs values. For relatively large H/h and small Cs values, however, the relationship between the maximum wave forces and deck aspect ratios presented strong nonlinearities.
- (3)
- The ANN model efficiently and accurately predicted wave forces on bridge decks for various Cs, H/h, and W/h values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Submergence coefficients | |
| Wave height | |
| Height of bridge deck | |
| Width of bridge deck | |
| Relative wave height | |
| Deck aspect ratio | |
| Root mean squared error | |
| Mean values for the maximum vertical wave force | |
| Mean values for the maximum horizontal wave force | |
| Still water depth | |
| Average velocity in the i direction | |
| Average velocity in the j direction | |
| Fluctuation velocity along the i direction | |
| Fluctuation velocity along the j direction | |
| Coordinate axis along the i direction | |
| Coordinate axis along the j direction | |
| Average pressure | |
| Density of fluid | |
| Viscosity of fluid | |
| Time | |
| Turbulence kinetic energy | |
| Dissipation | |
| y+ | Nondimensional wall-coordinate |
| Distance from the wave surface to the still water level | |
| Wave celerity | |
| Axis of horizontal direction | |
| Axis of vertical direction | |
| Gravity acceleration | |
| Damping coefficient | |
| Length of the wave elimination zone | |
| Start coordinates of the wave elimination zone | |
| End coordinates of the wave elimination zone | |
| Empirical parameter of the damping coefficient | |
| Maximum vertical wave force | |
| Maximum horizontal wave force | |
| Deck length | |
| Height of rail | |
| Clearance of bridge deck | |
| Bottom elevation of the bridge superstructure | |
| Angle of incidence to the structure | |
| Submergence depths | |
| t1 | Time of maximum slamming force |
| t2 | Time of maximum quasi-static force |
| t3 | Time of maximum downward force |
| Weights from the input layer neurons to the ith neurons in the first hidden layer | |
| bi | Bias for the ith neurons in the first hidden layer |
| The “activated” value of the ith neurons in the first hidden layer | |
| Target value | |
| Output value | |
| Correlation coefficient | |
| Mean of the target value | |
| Mean of the output value |
References
- Roeber, V.; Bricker, J.D. Destructive tsunami-like wave generated by surf beat over a coral reef during Typhoon Haiyan. Nat. Commun. 2015, 6, 7854. [Google Scholar] [CrossRef] [PubMed]
- Hansom, J.D.; Switzer, A.D.; Pile, J. Extreme waves: Causes, characteristics, and impact on coastal environments and society. In Coastal and Marine Hazards, Risks, and Disasters; Shroder, J.F., Ellis, J.T., Sherman, D.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 307–334. [Google Scholar]
- Yin, J.; Griffies, S.M.; Winton, M.; Zhao, M.; Zanna, L. Response of Storm-Related Extreme Sea Level along the U.S. Atlantic Coast to Combined Weather and Climate Forcing. J. Clim. 2020, 33, 3745–3769. [Google Scholar] [CrossRef]
- Hansom, J.; Barltrop, N.; Hall, A. Modelling the processes of cliff-top erosion and deposition under extreme storm waves. Mar. Geol. 2008, 253, 36–50. [Google Scholar] [CrossRef]
- Wang, D.-P.; Oey, L.-Y. Hindcast of Waves and Currents in Hurricane Katrina. Bull. Am. Meteorol. Soc. 2008, 89, 487–496. [Google Scholar] [CrossRef]
- Wang, D.W.; Mitchell, D.A.; Teague, W.J.; Jarosz, E.; Hulbert, M.S. Extreme waves under hurricane Ivan. Science 2005, 309, 896. [Google Scholar] [CrossRef]
- Chen, H.C.; Liu, L.; Liu, X.D.; Zhou, S.S. Overall Design of East Man-Made Island Junction Bridge of Hongkong-Zhuhai-Macao Bridge. World Bridge 2016, 3, 1–5. [Google Scholar]
- Ge, L.-Z.; Chen, H.-B.; Chen, S.-G.; Liu, H.Y. Experimental Study on Wave Forces Acting on Bridge at the Junction of Island and Bridge in the Shenzhen-Zhongshan Channel West Artificial Island. In Proceedings of the the 30th International Ocean and Polar Engineering Conference, Virtual, 11–16 October 2020. [Google Scholar]
- Okeil, A.M.; Cai, C. Survey of short-and medium-span bridge damage induced by Hurricane Katrina. J. Bridge Eng. 2008, 13, 377–387. [Google Scholar] [CrossRef]
- Padgett, J.; DesRoches, R.; Nielson, B.; Yashinsky, M.; Kwon, O.-S.; Burdette, N.; Tavera, E. Bridge damage and repair costs from Hurricane Katrina. J. Bridge Eng. 2008, 13, 6–14. [Google Scholar] [CrossRef]
- Huang, W.; Xiao, H. Numerical modeling of dynamic wave force acting on Escambia Bay Bridge deck during Hurricane Ivan. J. Waterw. Port Coast. Ocean Eng. 2009, 135, 164–175. [Google Scholar] [CrossRef]
- Bozorgnia, M.; Lee, J.-J. Wave Structure Interaction during Hurricane Ivan Simulated by Two-Phase Flow Model. In Proceedings of the Engineering Mechanics Conference, Los Angeles, CA, USA, 8–11 August 2011; pp. 33–44. [Google Scholar]
- Bradner, C.; Schumacher, T.; Cox, D.; Higgins, C. Experimental setup for a large-scale bridge superstructure model subjected to waves. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 3–11. [Google Scholar] [CrossRef]
- Hayatdavoodi, M.; Seiffert, B.; Ertekin, R.C. Experiments and calculations of cnoidal wave loads on a flat plate in shallow-water. J. Ocean Eng. Mar. Energy 2015, 1, 77–99. [Google Scholar] [CrossRef]
- Huang, B.; Zhu, B.; Cui, S.; Duan, L.; Zhang, J. Experimental and numerical modelling of wave forces on coastal bridge superstructures with box girders, Part I: Regular waves. Ocean Eng. 2018, 149, 53–77. [Google Scholar] [CrossRef]
- Jin, J.; Meng, B. Computation of wave loads on the superstructures of coastal highway bridges. Ocean Eng. 2011, 38, 2185–2200. [Google Scholar] [CrossRef]
- Marin, J.; Sheppard, D.M. Storm surge and wave loading on bridge superstructures. In Proceedings of the Structures Congress 2009, Austin, TX, USA, 30 April–2 May 2009; pp. 1–10. [Google Scholar]
- Seiffert, B.R.; Hayatdavoodi, M.; Ertekin, R.C. Experiments and calculations of cnoidal wave loads on a coastal-bridge deck with girders. Eur. J. Mech. B/Fluids 2015, 52, 191–205. [Google Scholar] [CrossRef]
- Xu, G.; Cai, C. Numerical investigation of the lateral restraining stiffness effect on the bridge deck-wave interaction under Stokes waves. Eng. Struct. 2017, 130, 112–123. [Google Scholar] [CrossRef]
- Yuan, P.; Xu, G.; Chen, Q.; Cai, C. Framework of practical performance evaluation and concept of interface design for bridge deck–wave interaction. J. Bridge Eng. 2018, 23, 04018048. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Dong, Y. Reliability-based retrofit assessment of coastal bridges subjected to wave forces using 3D CFD simulation and metamodeling. Civ. Eng. Environ. Syst. 2021, 38, 59–83. [Google Scholar] [CrossRef]
- Douglass, S.L.; Chen, Q.; Olsen, J.; Edge, B.; Brown, D. Wave Forces on Bridge Decks; Department of Transportation, Federal Highway Administration, Office of Bridge Technology: Washington, DC, USA, 2006. [Google Scholar]
- McPherson, R.L. Hurricane Induced Wave and Surge Forces on Bridge Decks; Texas A & M University: College Station, TX, USA, 2010. [Google Scholar]
- Kulicki, J.M.; Mertz, D.R. Guide Specifications for Bridges Vulnerable to Coastal Storms; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2008. [Google Scholar]
- Azadbakht, M.; Yim, S.C. Simulation and estimation of tsunami loads on bridge superstructures. J. Waterw. Port Coast. Ocean Eng. 2015, 141, 04014031. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami loads on a representative coastal bridge deck: Experimental study and validation of design equations. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Xu, G.; Cai, C.; Deng, L. Numerical prediction of solitary wave forces on a typical coastal bridge deck with girders. Struct. Infrastruct. Eng. 2017, 13, 254–272. [Google Scholar] [CrossRef]
- Yim, S.C.; Boon-Intra, S.; Nimmala, S.B.; Winston, H.M.; Azadbakht, M.; Cheung, K.F. Development of a Guideline for Estimating Tsunami Forces on Bridge Superstructures; OR-RD-12-03; Oregon Department of Transportation, Research Section: Multnomah, WA, USA, 2011; pp. 35–38. [Google Scholar]
- Zhu, D.; Dong, Y. Experimental and 3D numerical investigation of solitary wave forces on coastal bridges. Ocean Eng. 2020, 209, 107499. [Google Scholar] [CrossRef]
- Xu, F.; Wu, T.; Ying, X.; Kareem, A. Higher-order self-excited drag forces on bridge decks. J. Eng. Mech. 2016, 142, 06015007. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W.; Rehman, K.U.; Shatnawi, T.A. Velocity and thermal slips impact on boundary layer flow of micropolar nanofluid over a vertical nonlinear stretched Riga sheet. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2023, 1. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, T.; Xu, F. Vortex-induced vibration of bridge decks: Describing function-based model. J. Wind Eng. Ind. Aerodyn. 2019, 195, 104016. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W.; Shatnawi, T.A. Theoretical analysis of modified non-Newtonian micropolar nanofluid flow over vertical Riga sheet. Int. J. Mod. Phys. B 2023, 37, 2350016. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A. Modelling of nonlinear bridge aerodynamics and aeroelasticity: A convolution based approach. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2012; Volume 1, p. 03004. [Google Scholar]
- Abbas, N.; Malik, M.Y.; Nadeem, S. Stagnation flow of hybrid nanoparticles with MHD and slip effects. Heat Transf.Asian Res. 2020, 49, 180–196. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A.; Li, S. On the excitation mechanisms of rain–wind induced vibration of cables: Unsteady and hysteretic nonlinear features. J. Wind Eng. Ind. Aerodyn. 2013, 122, 83–95. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A. Modeling hysteretic nonlinear behavior of bridge aerodynamics via cellular automata nested neural network. J. Wind Eng. Ind. Aerodyn. 2011, 99, 378–388. [Google Scholar] [CrossRef]
- Li, S.; Snaiki, R.; Wu, T. A knowledge-enhanced deep reinforcement learning-based shape optimizer for aerodynamic mitigation of wind-sensitive structures. Comput. -Aided Civ. Infrastruct. Eng. 2021, 36, 733–746. [Google Scholar] [CrossRef]
- Wu, T.; Snaiki, R. Applications of machine learning to wind engineering. Front. Built Environ. 2022, 8, 811460. [Google Scholar] [CrossRef]
- Li, L.; Gao, Z.; Yuan, Z.-M. On the sensitivity and uncertainty of wave energy conversion with an artificial neural-network-based controller. Ocean Eng. 2019, 183, 282–293. [Google Scholar] [CrossRef]
- Lotfollahi-Yaghin, M.; Pourtaghi, A.; Sanaaty, B.; Lotfollahi-Yaghin, A. Artificial neural network ability in evaluation of random wave-induced inline force on a vertical cylinder. China Ocean Eng. 2012, 26, 19–36. [Google Scholar] [CrossRef]
- Mase, H.; Kitano, T. Prediction model for occurrence of impact wave force. Ocean Eng. 1999, 26, 949–961. [Google Scholar] [CrossRef]
- Xu, G.; Chen, Q.; Chen, J. Prediction of solitary wave forces on coastal bridge decks using artificial neural networks. J. Bridge Eng. 2018, 23, 04018023. [Google Scholar] [CrossRef]
- Xu, G.; Ji, C.; Wei, H.; Wang, J.; Yuan, P. A novel ensemble model using artificial neural network for predicting wave-induced forces on coastal bridge decks. Eng. Comput. 2022, 1–24. [Google Scholar] [CrossRef]
- Jia, L.; Zhang, Y.; Zhu, D.; Dong, Y. 3D Numerical Modeling and Quantification of Oblique Wave Forces on Coastal Bridge Superstructures. J. Mar. Sci. Eng. 2022, 10, 860. [Google Scholar] [CrossRef]
- Berryman, J.G. Stability of solitary waves in shallow water. Phys. Fluids 1976, 19, 771–777. [Google Scholar] [CrossRef]
- Zdyrski, T.; Feddersen, F. Wind-induced changes to surface gravity wave shape in shallow water. J. Fluid Mech. 2021, 913, A27. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Chen, M.; Huang, B.; Yang, Z.; Ren, Q.; Zhu, B. The Influence of Lateral Restraining Stiffness on the Box-Girder Superstructure under Unbroken Solitary Waves. J. Mar. Sci. Eng. 2022, 10, 1019. [Google Scholar] [CrossRef]
- Park, J.C.; Kim, M.H.; Miyata, H. Fully non-linear free-surface simulations by a 3D viscous numerical wave tank. Int. J. Numer. Methods Fluids 1999, 29, 685–703. [Google Scholar] [CrossRef]
- Seiffert, B.; Hayatdavoodi, M.; Ertekin, R.C. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part I: Flat plate. Coast. Eng. 2014, 88, 194–209. [Google Scholar] [CrossRef]
- Seiffert, B.R.; Cengiz Ertekin, R.; Robertson, I.N. Effect of Entrapped Air on Solitary Wave Forces on a Coastal Bridge Deck with Girders. J. Bridge Eng. 2016, 21, 04015036-1–04015036-14. [Google Scholar] [CrossRef]
- Sheppard, D.M.; Marin, J. Wave Loading on Bridge Decks; BD545-58; Florida Department of Transportation: Tallahassee, FL, USA, 2009; p. 63. [Google Scholar]

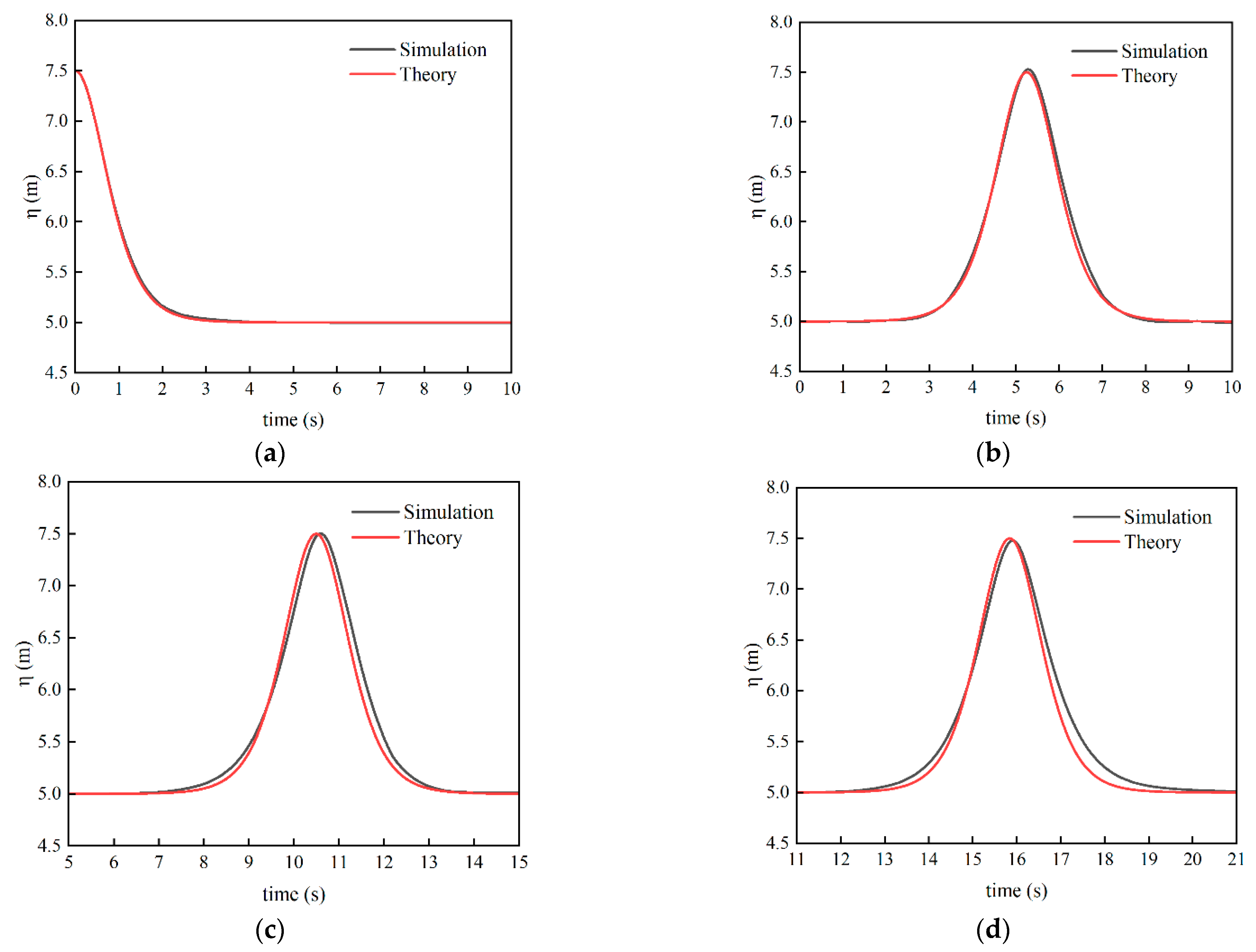

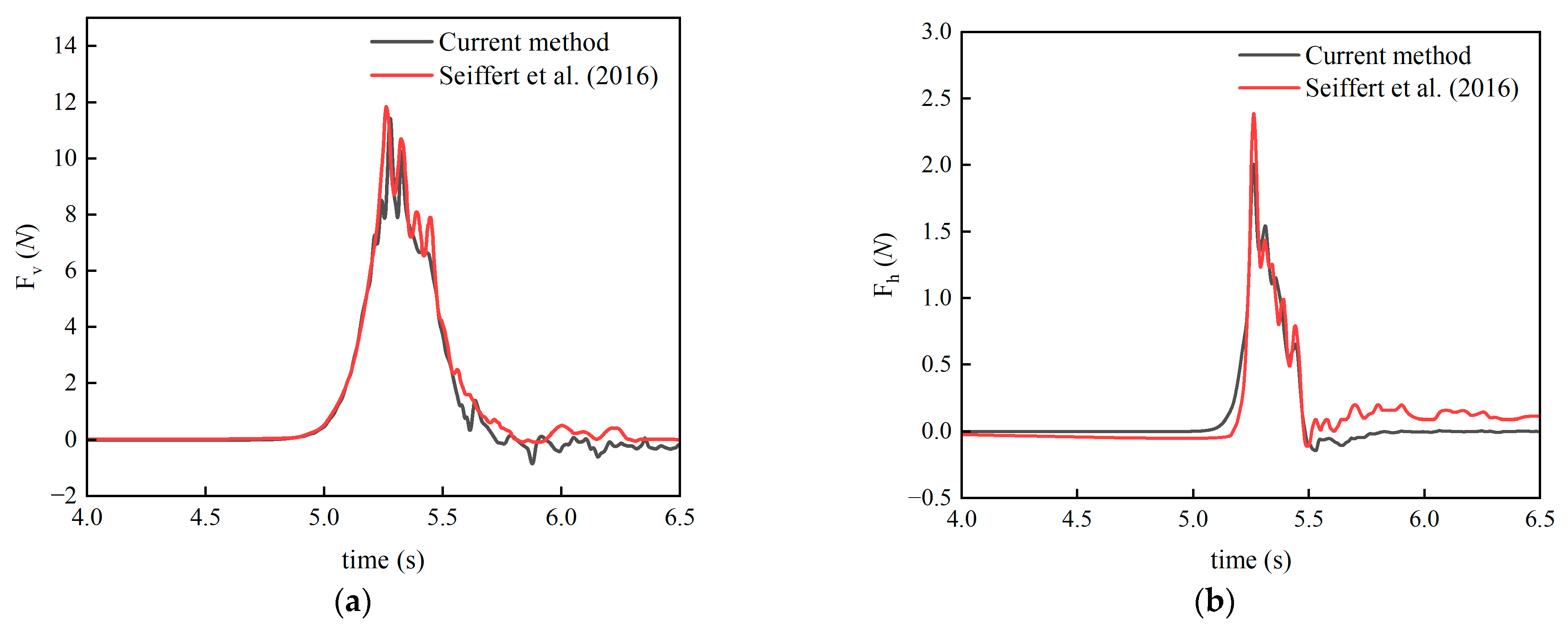
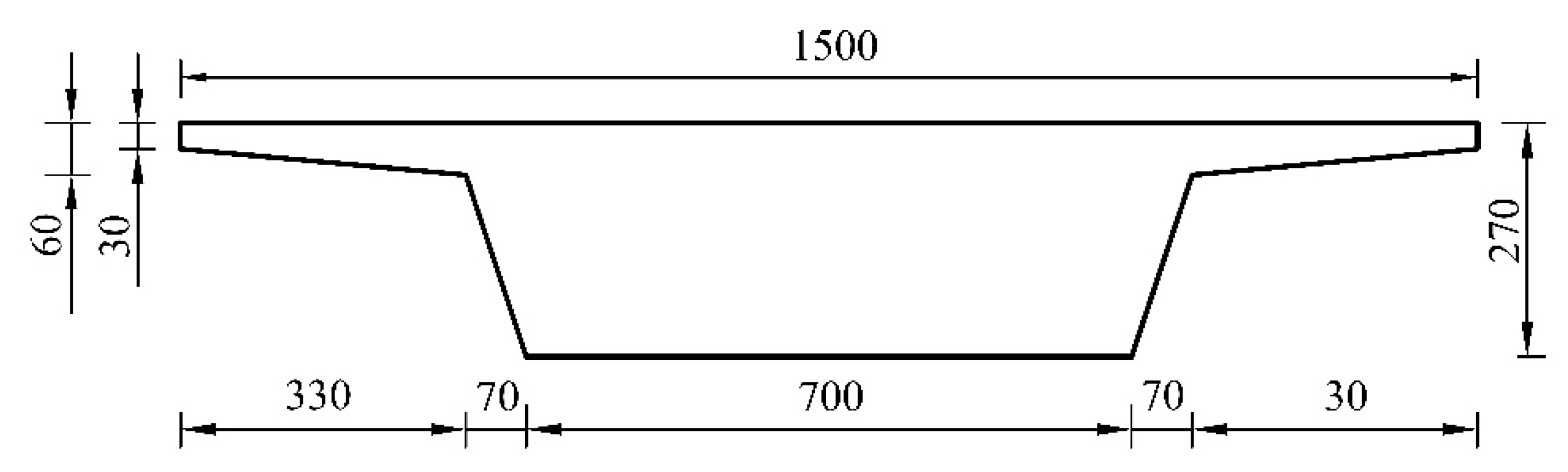

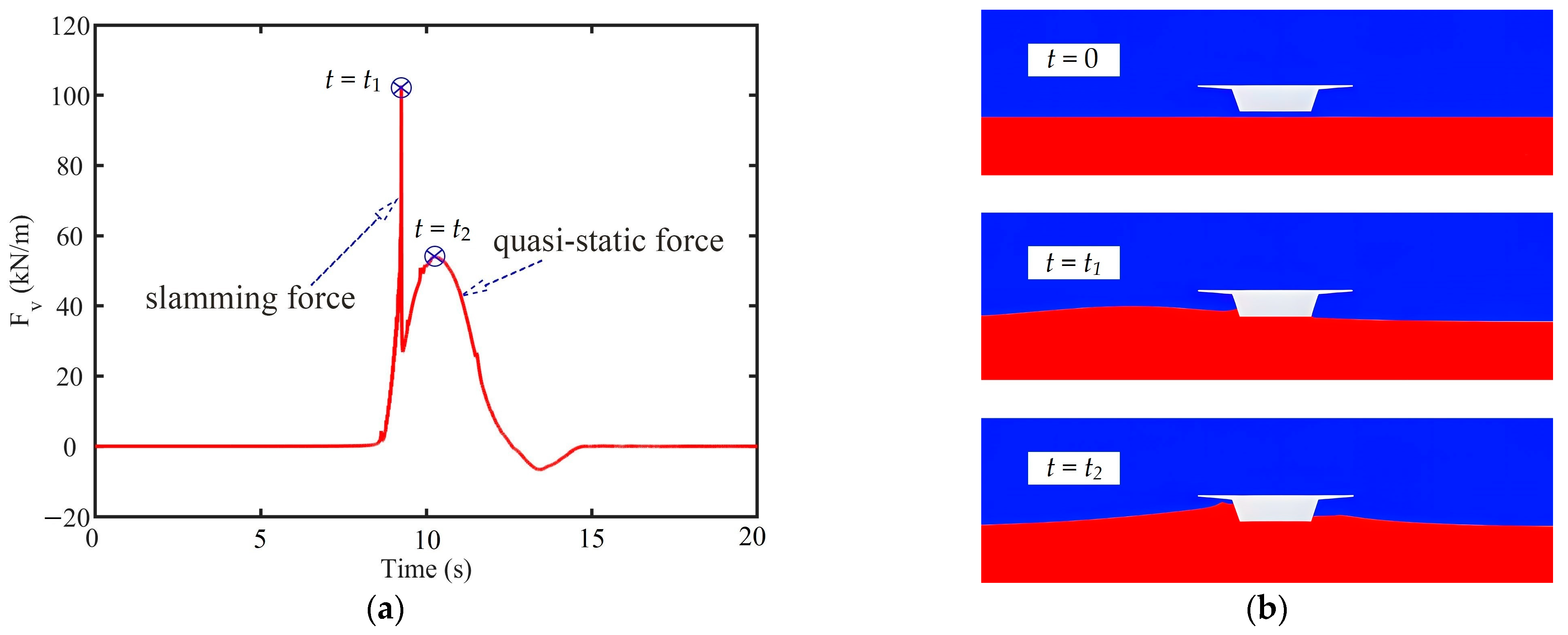


| Location | Numerical Wave Height | Theoretical Wave Height | Error |
|---|---|---|---|
| 45 m | 2.528 m | 2.5 m | 1.12% |
| 90 m | 2.502 m | 2.5 m | 0.08% |
| 135 m | 2.477 m | 2.5 m | 0.92% |
| Parameter | Minimum | Maximum |
|---|---|---|
| Submersion coefficient | −0.370 | 1.111 |
| Relative wave height | 0.370 | 1.111 |
| Aspect ratio | 4.074 | 6.296 |
| Vertical force | 9.200 kN/m | 1643.2 kN/m |
| Horizontal force | 1.720 kN/m | 654.77 kN/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, M.; Li, S.; Wu, T. Fast Prediction of Solitary Wave Forces on Box-Girder Bridges Using Artificial Neural Networks. Water 2023, 15, 1963. https://doi.org/10.3390/w15101963
Lu M, Li S, Wu T. Fast Prediction of Solitary Wave Forces on Box-Girder Bridges Using Artificial Neural Networks. Water. 2023; 15(10):1963. https://doi.org/10.3390/w15101963
Chicago/Turabian StyleLu, Minglong, Shaopeng Li, and Teng Wu. 2023. "Fast Prediction of Solitary Wave Forces on Box-Girder Bridges Using Artificial Neural Networks" Water 15, no. 10: 1963. https://doi.org/10.3390/w15101963




