Prediction of Rainfall Time Series Using the Hybrid DWT-SVR-Prophet Model
Abstract
:1. Introduction
2. Methodology
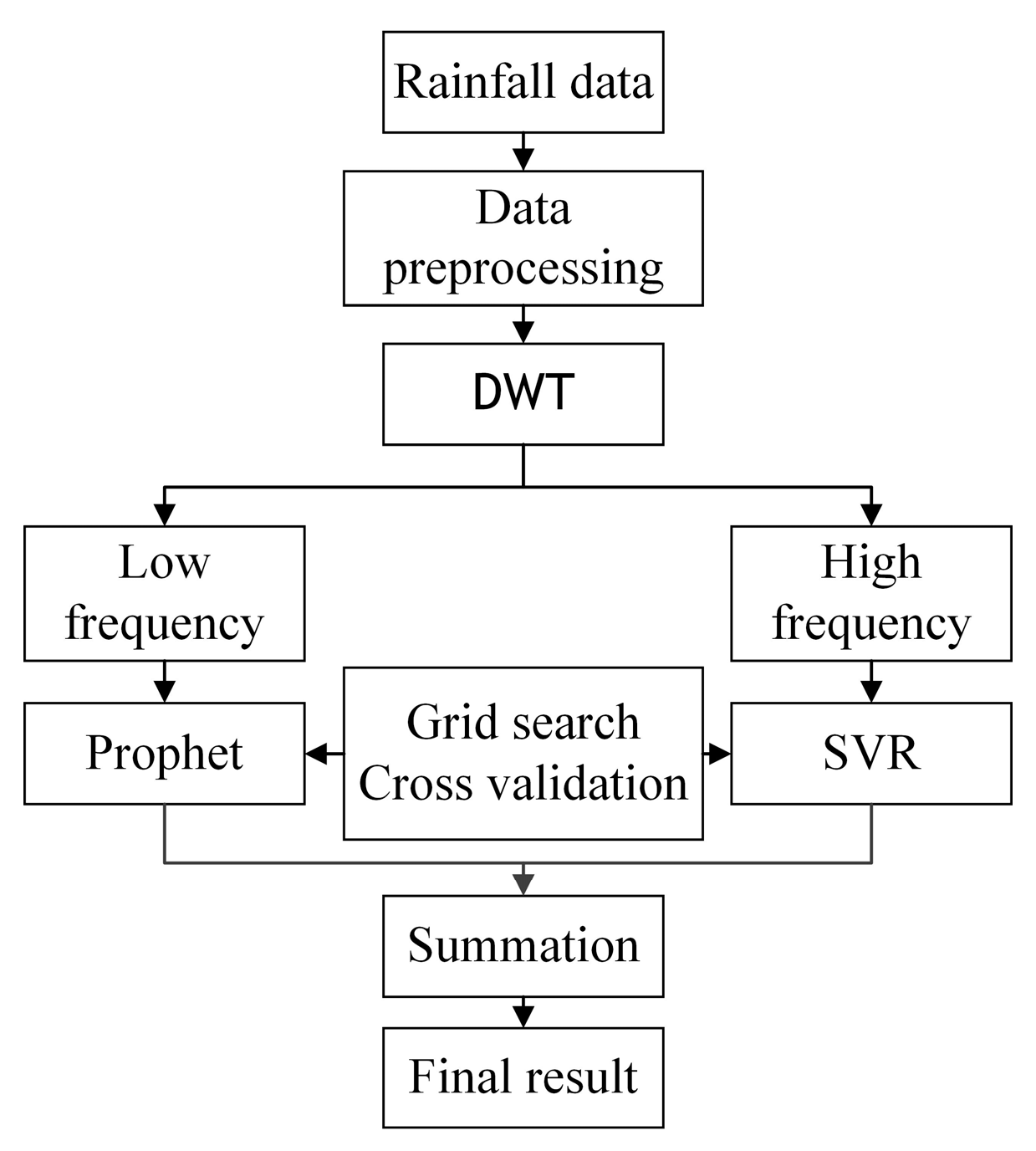
2.1. Hybrid Model Based on DWT-SVR-Prophet
- (i)
- Data preparation and preprocessing: We construct a dataset with daily rainfall data from the National Meteorological Center. The validity and superiority of the model introduced in this paper are verified using this dataset. We preprocess the measured rainfall data to ensure the fitting effect of the applied machine learning model. This process is described in detail in Section 2.2.
- (ii)
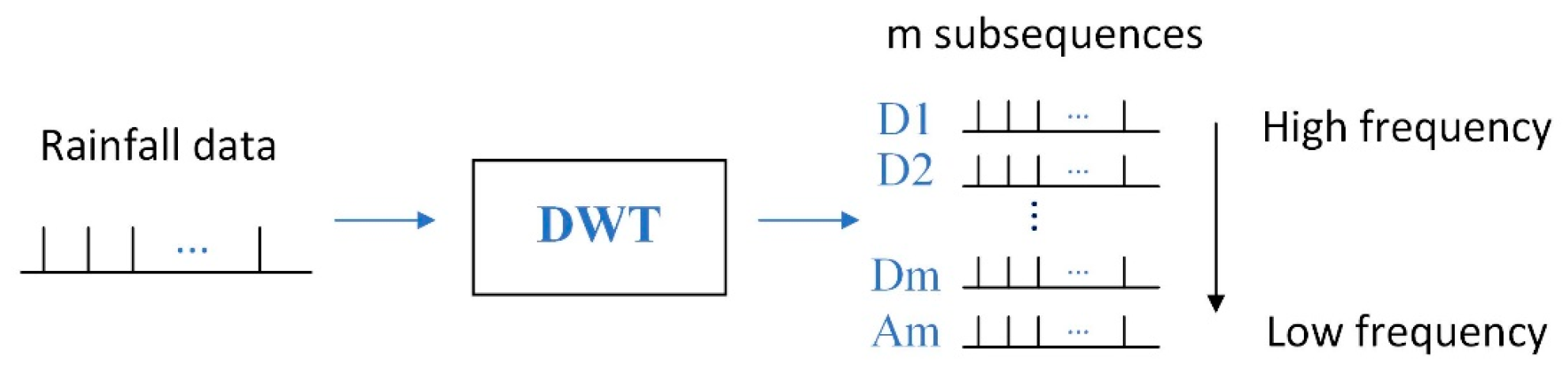
- DWT processing: The rainfall time series are decomposed using DWT to obtain high-frequency subsequences with high randomness and volatility and low-frequency subsequences with high periodicity (see Section 2.3.1). This approach allows us to choose forecasting models based on the characteristics of each subseries.
- (iii)
- Hyperparameter optimization: The hyperparameters of the three methods in the coupled model are optimized to obtain the optimal prediction effect. Notably, the parameters of the DWT method are determined by referring to the previous literature, and a grid search method is used to set the hyperparameters of the SVR and Prophet models. The specific process of parameter selection is described in detail in Section 2.5.
- (iv)
- Rainfall prediction: The optimized SVR model and Prophet model are used to predict high-frequency subseries and low-frequency subseries, respectively. The prediction results for each subseries are summed to obtain the final prediction results.
2.2. Data Preprocessing
2.3. Methods Used in the DSP Model
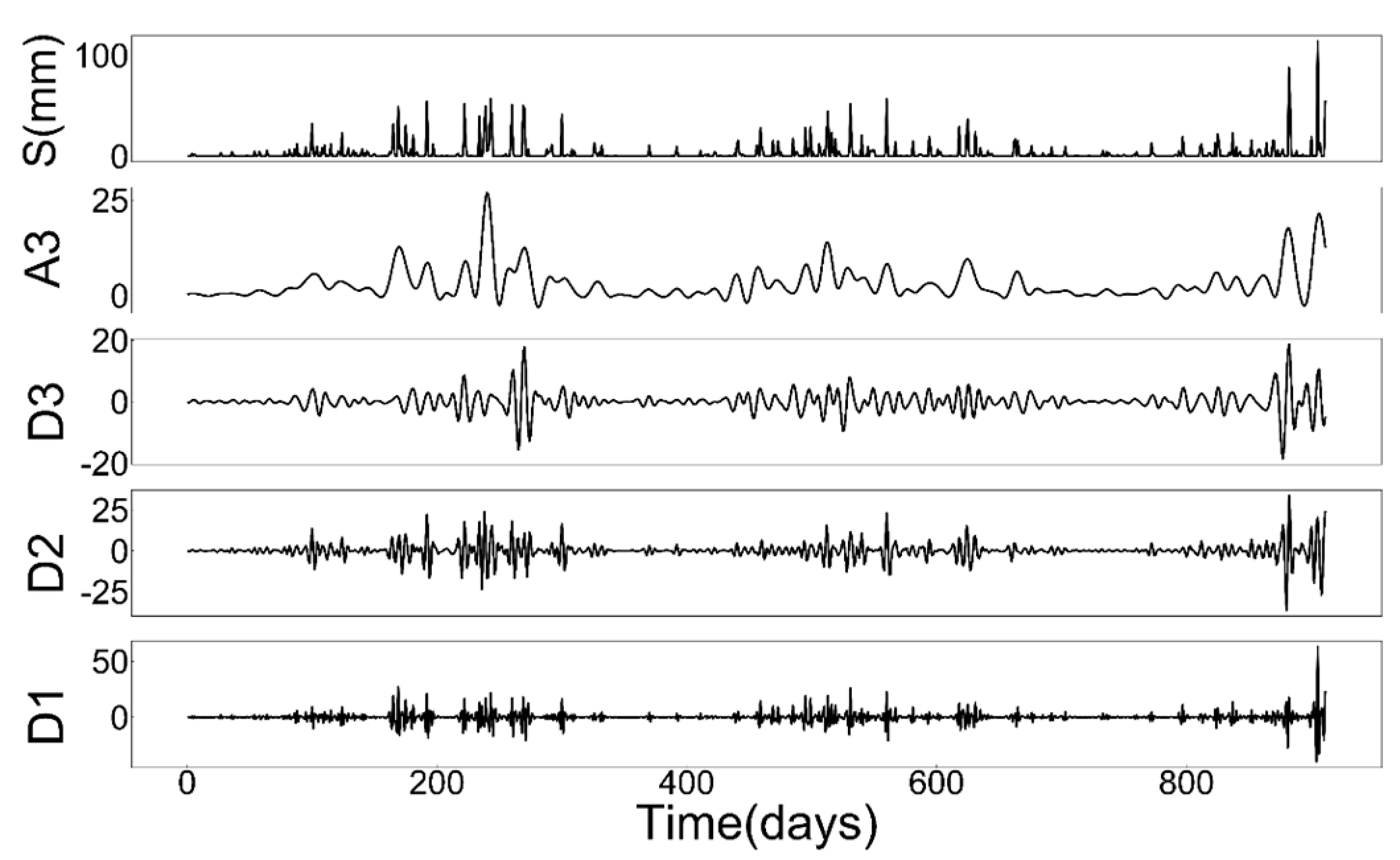
2.3.1. Discrete Wavelet Transform
2.3.2. Support Vector Regression Model
2.3.3. Prophet Model
2.4. Hyperparameter Optimization
2.4.1. DWT
2.4.2. SVR
- (i)
- The radial basis function (rbf) is chosen as the kernel function of the SVR model. First, the ranges of values and search steps are set for the main parameters C and γ, and all parameter combinations within the given ranges are obtained .
- (ii)
- All parameter combinations are applied to rainfall predictions, and the best parameter combination is selected based on effect evaluation .
- (iii)
- To ensure the stability of the search result, the adjacent interval of the optimal parameter combination is selected as the new search range . Then, the search step size is reduced by a factor of 2 (or another multiple), and the optimal parameter combination is again obtained. If the result is unstable, the process is continued until a stable result, i.e., the optimal combination of parameters, is obtained.
2.4.3. Prophet Model
- (i)
- Both linear and logistic “Growth” parameters, and additive and multiplicative “Seasonality mode” parameters are considered.
- (ii)
- The monthly period term is summed with the “Add_seasonality” function in the Prophet model, with “period” = 30.5. Then, the initial range of “Year_seasonality” and “Seasonality_prior_scale” is set to with a step size of 5.
- (iii)
- The “Changepoint_prior_scale” parameter has a range of , and the corresponding step size is 0.5.
2.5. Evaluation Metrics
2.6. Open-Source Libraries
3. Results
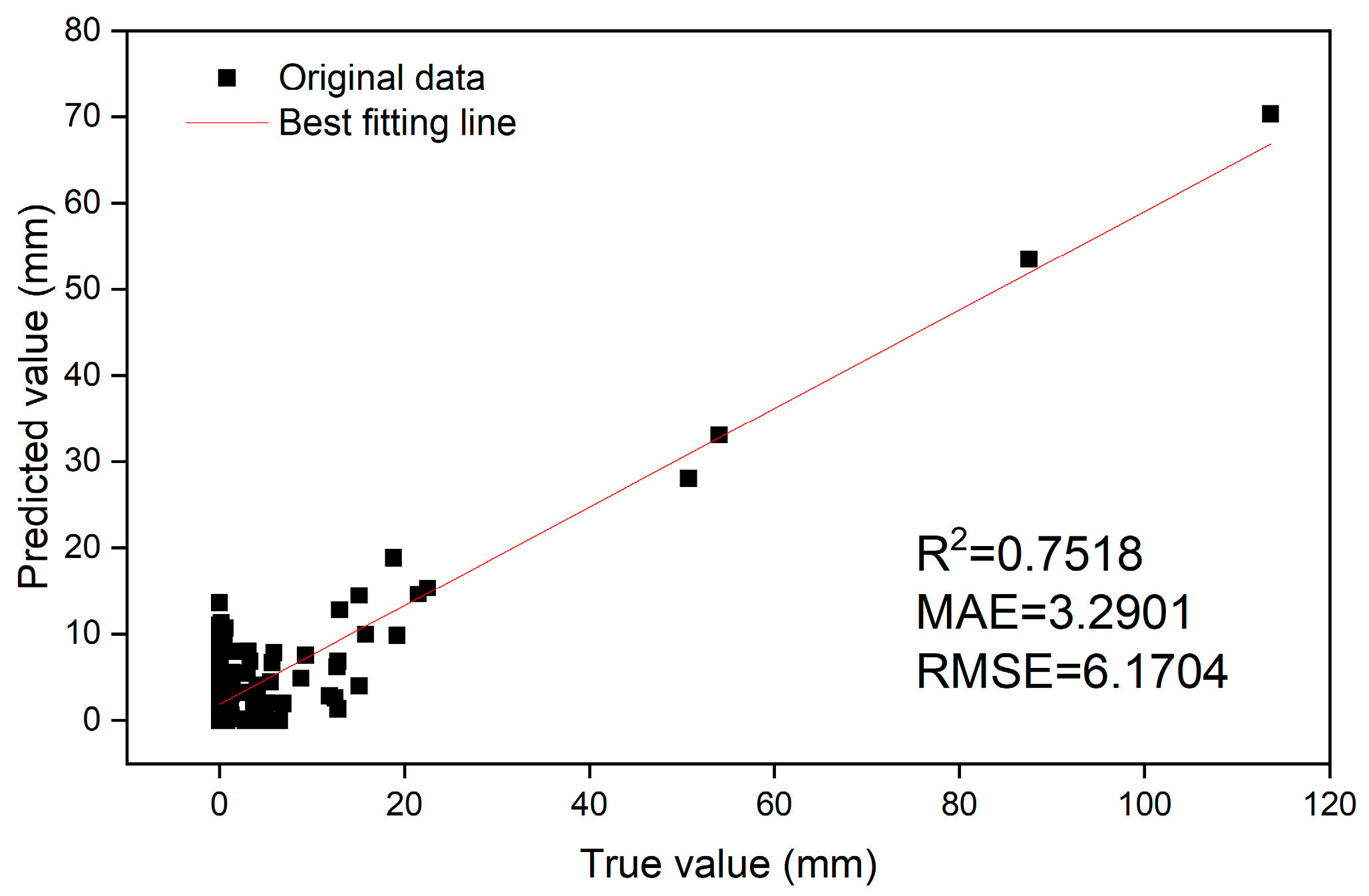
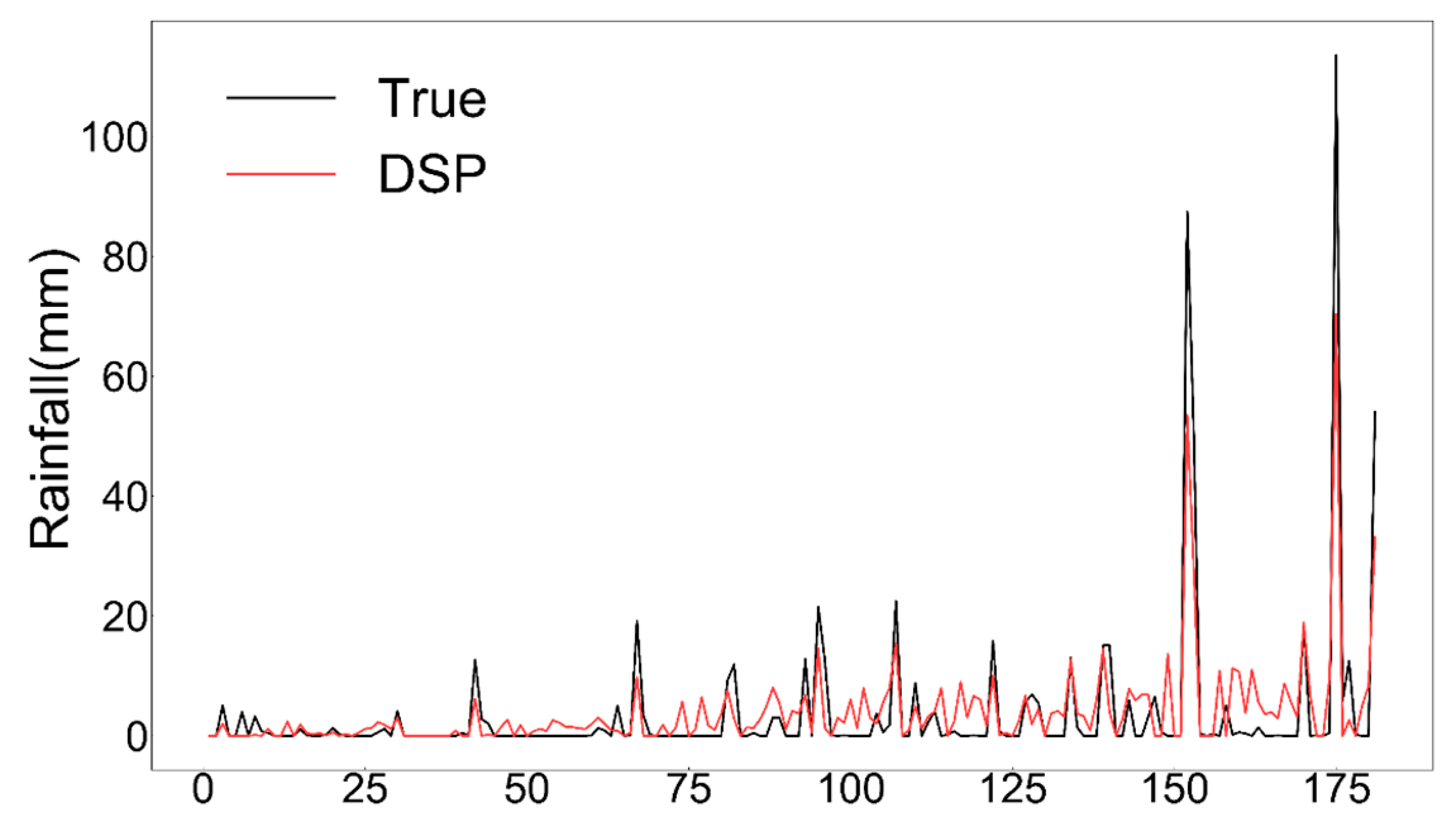
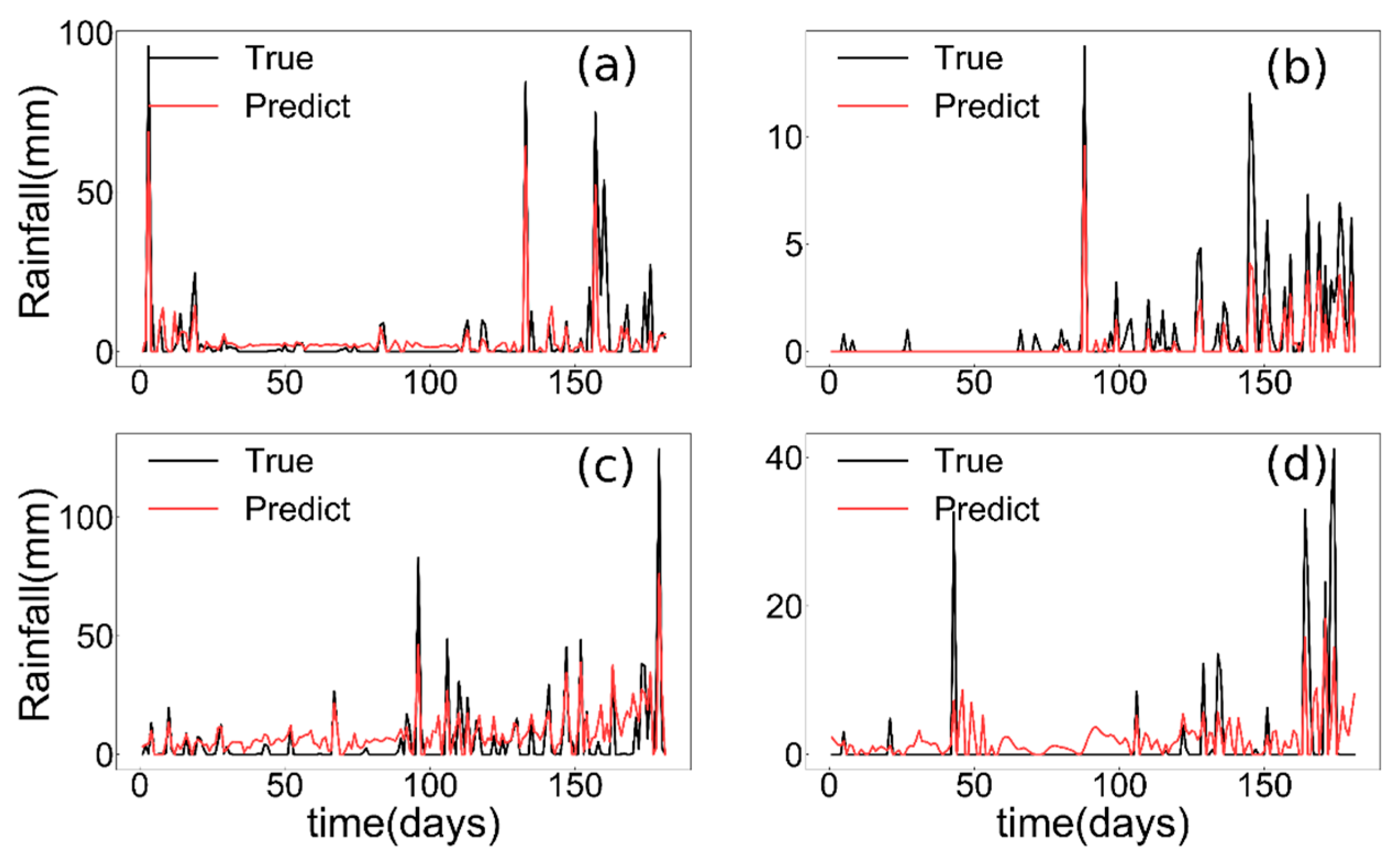
3.1. The DSP Model Provides Accurate Predictions of Rainfall
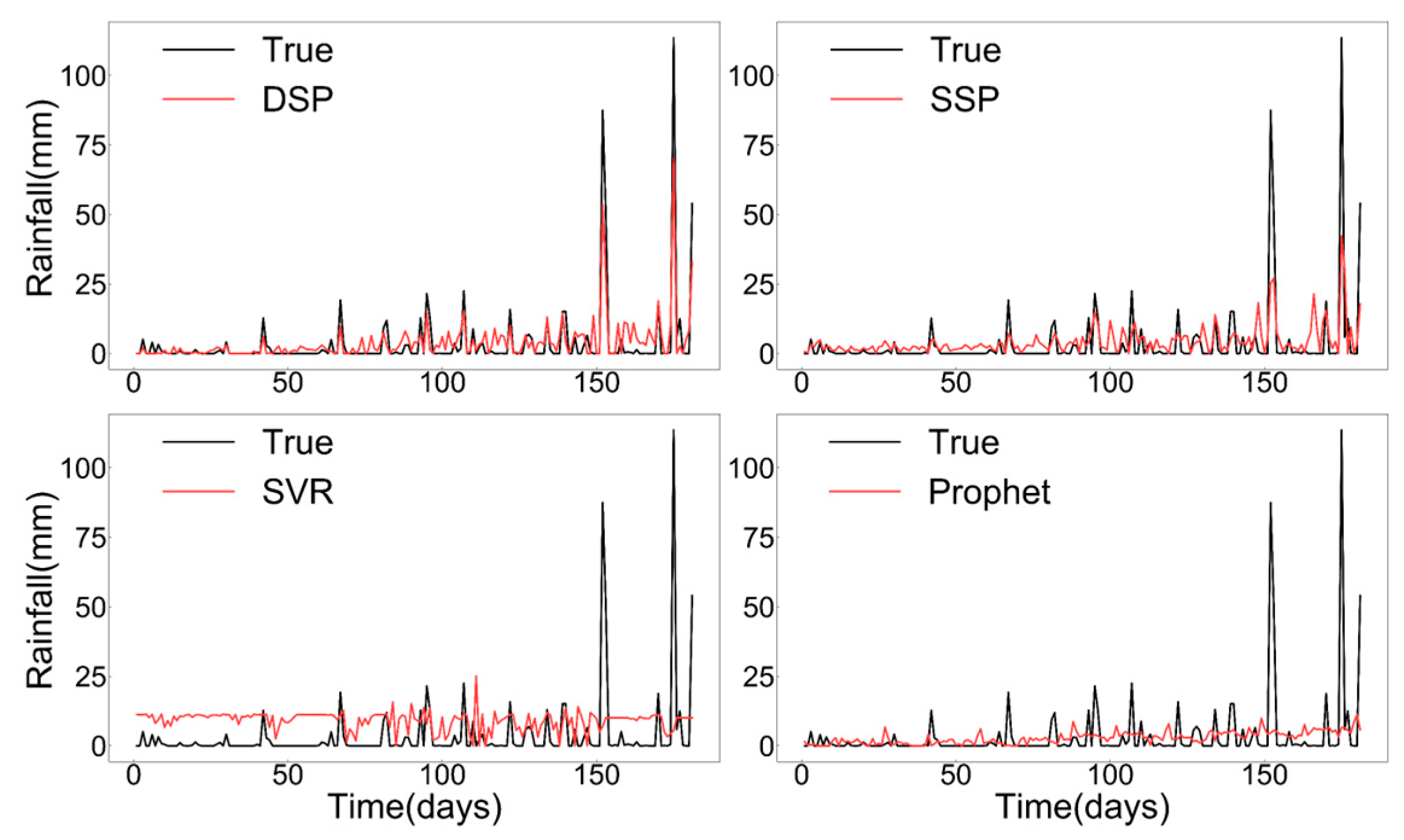
3.2. The Prediction Accuracy of the DSP Model Is Higher Than That of the Baseline Models
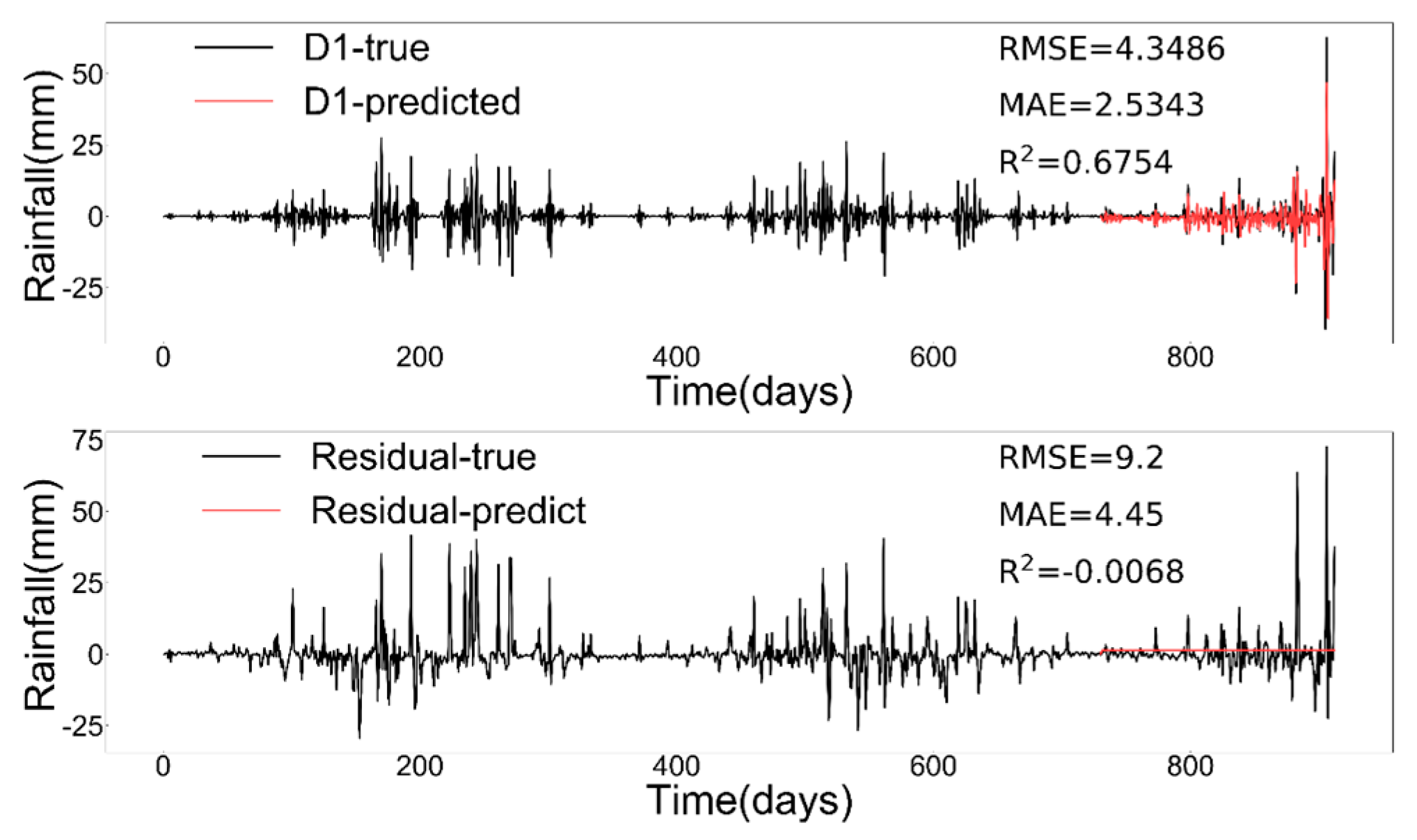
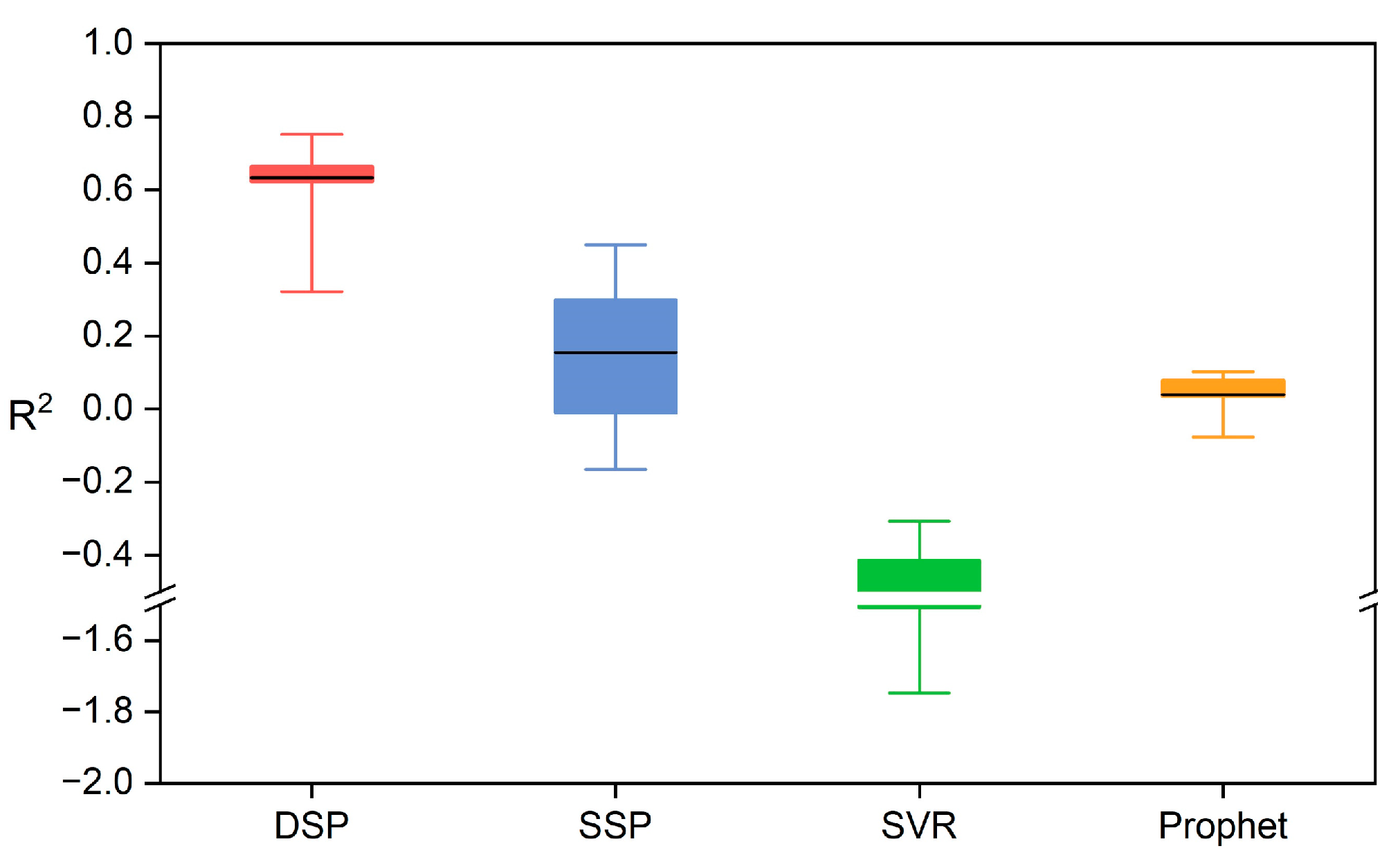
3.3. The DSP Model Displays Outstanding Stability
4. Discussion
4.1. The DSP Model Achieves Accurate Forecasts of Rainfall Time Series
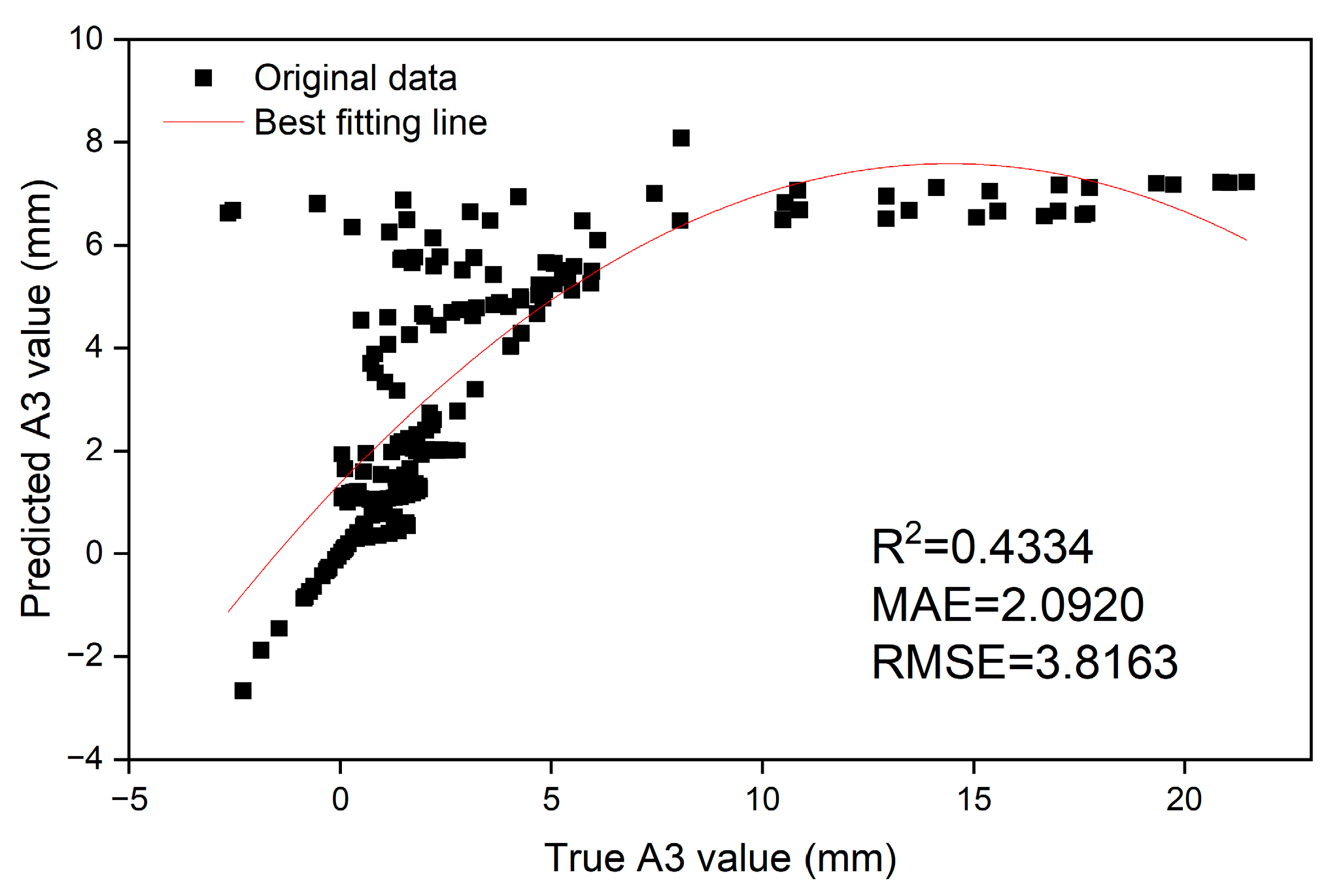
4.2. The DSP Model Effectively Captures the Detailed Features of Rainfall Time Series
4.3. Generalization of DSP Models
4.4. Disadvantages and Direction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poornima, S.; Pushpalatha, M.; Jana, R.B.; Patti, L.A. Rainfall Forecast and Drought Analysis for Recent and Forthcoming Years in India. Water 2023, 15, 592. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Rao, M.U.M.; Patra, K.C.; Sasmal, S.K.; Sharma, A.; Oliveto, G. Forecasting of Rainfall across River Basins Using Soft Computing Techniques: The Case Study of the Upper Brahmani Basin (India). Water 2023, 15, 499. [Google Scholar] [CrossRef]
- Adaryani, F.R.; Jamshid Mousavi, S.; Jafari, F. Short-term rainfall forecasting using machine learning-based approaches of PSO-SVR, LSTM and CNN. J. Hydrol. 2022, 614, 128463. [Google Scholar] [CrossRef]
- He, X.; Guan, H.; Qin, J. A hybrid wavelet neural network model with mutual information and particle swarm optimization for forecasting monthly rainfall. J. Hydrol. 2015, 527, 88–100. [Google Scholar] [CrossRef]
- Zhang, F.H.; Shao, Z.G. ST-GRF: Spatiotemporal graph neural networks for rainfall forecasting. Digit. Signal Process. 2023, 136, 103989. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Zhang, C.; Wang, B. Are hybrid models integrated with data preprocessing techniques suitable for monthly streamflow forecasting? Some experiment evidences. J. Hydrol. 2015, 530, 137–152. [Google Scholar] [CrossRef]
- Chong, K.L.; Lai, S.H.; Yao, Y.; Ahmed, A.N.; Jaafar, W.Z.W.; El-Shafie, A. Performance Enhancement Model for Rainfall Forecasting Utilizing Integrated Wavelet-Convolutional Neural Network. Water Resour. Manag. 2020, 34, 2371–2387. [Google Scholar] [CrossRef]
- Zhang, H.; Singh, V.P.; Wang, B.; Yu, Y. CEREF: A hybrid data-driven model for forecasting annual streamflow from a socio-hydrological system. J. Hydrol. 2016, 540, 246–256. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Ojo, O.S.; Ogunjo, S.T. Machine learning models for prediction of rainfall over Nigeria. Sci. Afr. 2022, 16, e01246. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J.A.K. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Netw. 2020, 125, 1–9. [Google Scholar] [CrossRef]
- Aksoy, H.; Dahamsheh, A. Markov chain-incorporated and synthetic data-supported conditional artificial neural network models for forecasting monthly precipitation in arid regions. J. Hydrol. 2018, 562, 758–779. [Google Scholar] [CrossRef]
- Chen, L.; Sun, N.; Zhou, C.; Zhou, J.; Zhou, Y.; Zhang, J.; Zhou, Q. Flood Forecasting Based on an Improved Extreme Learning Machine Model Combined with the Backtracking Search Optimization Algorithm. Water 2018, 10, 1362. [Google Scholar] [CrossRef]
- Barrera-Animas, A.Y.; Oyedele, L.O.; Bilal, M.; Akinosho, T.D.; Delgado, J.M.D.; Akanbi, L.A. Rainfall prediction: A comparative analysis of modern machine learning algorithms for time-series forecasting. Mach. Learn. Appl. 2022, 7, 100204. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, G.; Guo, L. Evaluating a coupled discrete wavelet transform and support vector regression for daily and monthly streamflow forecasting. J. Hydrol. 2014, 519, 2822–2831. [Google Scholar] [CrossRef]
- Aditya-Satrio, C.B.; Darmawan, W.; Nadia, B.U.; Hanafiah, N. Time series analysis and forecasting of coronavirus disease in Indonesia using ARIMA model and PROPHET. Procedia Comput. Sci. 2021, 179, 524–532. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Z.; Liu, X. Short-term offshore wind power forecasting—A hybrid model based on Discrete Wavelet Transform (DWT), Seasonal Autoregressive Integrated Moving Average (SARIMA), and deep-learning-based Long Short-Term Memory (LSTM). Renew. Energy 2022, 185, 611–628. [Google Scholar] [CrossRef]
- Vivas, E.; de Guenni, L.B.; Allende-Cid, H.; Salas, R. Deep Lagged-Wavelet for monthly rainfall forecasting in a tropical region. Stoch. Environ. Res. Risk Assess. 2023, 37, 831–848. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Delkash, M.; Bonakdari, H. A hybrid wavelet–machine learning model for qanat water flow prediction. Acta Geophys. 2022, 1–19. [Google Scholar] [CrossRef]
- Apaydin, H.; Taghi Sattari, M.; Falsafian, K.; Prasad, R. Artificial intelligence modelling integrated with Singular Spectral analysis and Seasonal-Trend decomposition using Loess approaches for streamflow predictions. J. Hydrol. 2021, 600, 126506. [Google Scholar] [CrossRef]
- Ravansalar, M.; Rajaee, T.; Kisi, O. Wavelet-linear genetic programming: A new approach for modeling monthly streamflow. J. Hydrol. 2017, 549, 461–475. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Nejatijahromi, Z.; Etebari, B.; Kisi, O. Groundwater level response identification by hybrid wavelet–machine learning conjunction models using meteorological data. Environ. Sci. Pollut. Res. 2023, 30, 22863–22884. [Google Scholar] [CrossRef]
- Xiang, Y.; Gou, L.; He, L.; Xia, S.; Wang, W. A SVR–ANN combined model based on ensemble EMD for rainfall prediction. Appl. Soft Comput. 2018, 73, 874–883. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Du, Y.; Xu, D. Examining the Applicability of Wavelet Packet Decomposition on Different Forecasting Models in Annual Rainfall Prediction. Water 2021, 13, 1997. [Google Scholar] [CrossRef]
- Wei, M.; You, X.Y. Monthly rainfall forecasting by a hybrid neural network of discrete wavelet transformation and deep learning. Water Resour. Manag. 2022, 36, 4003–4018. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Adib, A.; Zaerpour, A.; Lotfirad, M. On the reliability of a novel MODWT-based hybrid ARIMA-artificial intelligence approach to forecast daily Snow Depth (Case study: The western part of the Rocky Mountains in the U.S.A). Cold Reg. Sci. Technol. 2021, 189, 103342. [Google Scholar] [CrossRef]
- He, R.; Zhang, L.; Chew, A.W.Z. Modeling and predicting rainfall time series using seasonal-trend decomposition and machine learning. Knowl.-Based Syst. 2022, 251, 109125. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, R.; Deng, H. A novel STL-based hybrid model for forecasting hog price in China. Comput. Electron. Agric. 2022, 198, 107068. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petković, D.; Javidnia, H.; Gani, A. Sensor Data Fusion by Support Vector Regression Methodology—A Comparative Study. IEEE Sens. J. 2015, 15, 850–854. [Google Scholar] [CrossRef]
- Huang, Y.-T.; Bai, Y.-L.; Yu, Q.-H.; Ding, L.; Ma, Y.-J. Application of a hybrid model based on the Prophet model, ICEEMDAN and multi-model optimization error correction in metal price prediction. Resour. Policy 2022, 79, 102969. [Google Scholar] [CrossRef]
- Luo, J.; Hong, T.; Fang, S.-C. Benchmarking robustness of load forecasting models under data integrity attacks. Int. J. Forecast. 2018, 34, 89–104. [Google Scholar] [CrossRef]
- Ponnoprat, D. Short-term daily precipitation forecasting with seasonally-integrated autoencoder. Appl. Soft Comput. 2021, 102, 107083. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, H.; Luo, P.; Peng, Y.; Li, Q. Ultra-short-term Railway traction load prediction based on DWT-TCN-PSO_SVR combined model. Int. J. Electr. Power Energy Syst. 2022, 135, 107595. [Google Scholar] [CrossRef]
- Essam, Y.; Huang, Y.F.; Birima, A.H.; Ahmed, A.N.; El-Shafie, A. Predicting suspended sediment load in Peninsular Malaysia using support vector machine and deep learning algorithms. Sci. Rep. 2022, 12, 302. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, X.; Wang, W.; Lu, C.; Zhang, Y.; Qin, W.; Tick, G.R.; Liu, B.; Shu, L. Groundwater level modeling framework by combining the wavelet transform with a long short-term memory data-driven model. Sci. Total Environ. 2021, 783, 146948. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J. A maximal overlap discrete wavelet packet transform integrated approach for rainfall forecasting—A case study in the Awash River Basin (Ethiopia). Environ. Model. Softw. 2021, 144, 105119. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B. Using discrete wavelet transforms to analyze trends in streamflow and precipitation in Quebec and Ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Nigussie, T.A. Prediction of daily rainfall by a hybrid wavelet-season-neuro technique. J. Hydrol. 2015, 529, 287–301. [Google Scholar] [CrossRef]
- Guo, L.; Fang, W.; Zhao, Q.; Wang, X. The hybrid PROPHET-SVR approach for forecasting product time series demand with seasonality. Comput. Ind. Eng. 2021, 161, 107598. [Google Scholar] [CrossRef]
- Fahad, S.; Su, F.; Khan, S.U.; Naeem, M.R.; Wei, K. Implementing a novel deep learning technique for rainfall forecasting via climatic variables: An approach via hierarchical clustering analysis. Sci. Total Environ. 2023, 854, 158760. [Google Scholar] [CrossRef] [PubMed]
- Malik, A.; Tikhamarine, Y.; Souag-Gamane, D.; Rai, P.; Sammen, S.S.; Kisi, O. Support vector regression integrated with novel meta-heuristic algorithms for meteorological drought prediction. Meteorol. Atmos. Phys. 2021, 133, 891–909. [Google Scholar] [CrossRef]
- Hossain, M.M.; Anwar, A.; Garg, N.; Prakash, M.; Bari, M. Monthly Rainfall Prediction at Catchment Level with the Facebook Prophet Model Using Observed and CMIP5 Decadal Data. Hydrology 2022, 9, 111. [Google Scholar] [CrossRef]
- Pihrt, J.; Raevskiy, R.; Šimánek, P.; Choma, M. WeatherFusionNet: Predicting Precipitation from Satellite Data. arXiv 2022, arXiv:2211.16824. [Google Scholar] [CrossRef]

| Station (ID) | Rainfall (mm) | Rainfall Frequency (%) | Climatic Type | ||
|---|---|---|---|---|---|
| Per Year | Per Month | Daily Maximum | |||
| Hainan (59855) | 1972.2 | 182.6 | 253.1 | 41.4 | Northern tropics |
| Jiangsu (58345) | 1362.7 | 126.2 | 154.8 | 36.0 | Northern subtropics |
| Chognqi (57348) | 881.9 | 81.7 | 113.6 | 35.8 | Mid-subtropics |
| Shandon (54823) | 642.5 | 59.5 | 127.1 | 20.7 | Southern temperate |
| Qinghai (56018) | 466.3 | 43.2 | 31.3 | 40.4 | Plateau climate |
| Model | Parameters | Parameters Description | Default Value | Optimization Method |
|---|---|---|---|---|
| DWT | Wavelet name | Wavelet basis function | - | From previous research |
| Level | Wavelet decomposition level | - | ||
| SVR | Kernel | Kernel function | rbf | Grid search |
| C | Penalty coefficient | 1 | ||
| γ | Kernel function coefficient | auto | ||
| Prophet | Growth | Function in the trend model | linear | Grid search |
| Changepoint_prior_scale | Trend flexibility | 0.05 | ||
| Year_seasonality | Year flexibility | 10 | ||
| Seasonality_prior_scale | Seasonality flexibility | 10 | ||
| Seasonality mode | Model learning style | additive |
| Parameter | Parameter Values |
|---|---|
| kernel function | rbf |
| C (penalty variable) | 1024 |
| γ (kernel function parameter) | 0.03125 |
| Parameter | Parameter Values |
|---|---|
| Growth | Linear |
| Changepoint_prior_scale | 1 |
| Year_seasonality | 9 |
| Seasonality_prior_scale | 60 |
| Seasonality mode | Additive |
| Model | Advantages | Disadvantages |
|---|---|---|
| SVR | It displays good generalization ability and is suitable for nonlinear prediction | It has limitations for general data |
| Prophet | It can effectively fit the trend and period variations of time series | Poor fitting ability for complex models |
| DSP | It can extract linear and nonlinear features and fit each component using dominance models, respectively | The parameter selection of DWT affects the prediction accuracy and requires additional optimization |
| SSP | It can extract linear and nonlinear features and fit each component using dominance models, respectively | The residual term is difficult to fit and requires high model performance |
| Metric | DSP | SSP | SVR | Prophet |
|---|---|---|---|---|
| RMSE | 6.1704 | 9.1679 | 14.1779 | 12.1362 |
| MAE | 3.2901 | 4.3931 | 9.5772 | 4.9510 |
| R2 | 0.7518 | 0.4492 | −0.3061 | 0.0348 |
| Station | Metric | DSP | SSP | SVR | Prophet |
|---|---|---|---|---|---|
| 59855 | RMSE | 7.3116 | 13.5961 | 19.9489 | 13.0716 |
| MAE | 3.3035 | 7.4914 | 15.2908 | 4.4126 | |
| R2 | 0.6632 | −0.1647 | −1.5074 | −0.0766 | |
| 56018 | RMSE | 1.2364 | 2.0519 | 2.9356 | 1.9336 |
| MAE | 0.5197 | 0.9194 | 2.7219 | 0.9101 | |
| R2 | 0.6330 | −0.0107 | −1.0688 | 0.1024 | |
| 58345 | RMSE | 8.8391 | 13.2151 | 17.0824 | 13.7878 |
| MAE | 6.1431 | 8.0558 | 12.7209 | 7.1224 | |
| R2 | 0.6217 | 0.1543 | −0.4131 | 0.0794 | |
| 54823 | RMSE | 4.8553 | 4.9367 | 9.7700 | 5.7756 |
| MAE | 2.3643 | 2.8757 | 8.3983 | 2.4138 | |
| R2 | 0.3214 | 0.2985 | −1.7476 | 0.0398 | |
| 57348 | RMSE | 6.1704 | 9.1679 | 14.1779 | 12.1362 |
| MAE | 3.2901 | 4.3931 | 9.5772 | 4.9510 | |
| R2 | 0.7518 | 0.4492 | −0.3061 | 0.0348 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Ma, J.; Rao, K.; Wang, X.; Li, R.; Yang, Y.; Zheng, H. Prediction of Rainfall Time Series Using the Hybrid DWT-SVR-Prophet Model. Water 2023, 15, 1935. https://doi.org/10.3390/w15101935
Li D, Ma J, Rao K, Wang X, Li R, Yang Y, Zheng H. Prediction of Rainfall Time Series Using the Hybrid DWT-SVR-Prophet Model. Water. 2023; 15(10):1935. https://doi.org/10.3390/w15101935
Chicago/Turabian StyleLi, Dongsheng, Jinfeng Ma, Kaifeng Rao, Xiaoyan Wang, Ruonan Li, Yanzheng Yang, and Hua Zheng. 2023. "Prediction of Rainfall Time Series Using the Hybrid DWT-SVR-Prophet Model" Water 15, no. 10: 1935. https://doi.org/10.3390/w15101935





