Spatio-Temporal Heterogeneity of Soil Moisture on Shrub–Grass Hillslope in Karst Region
Abstract
:1. Introduction
2. Materials and Methods
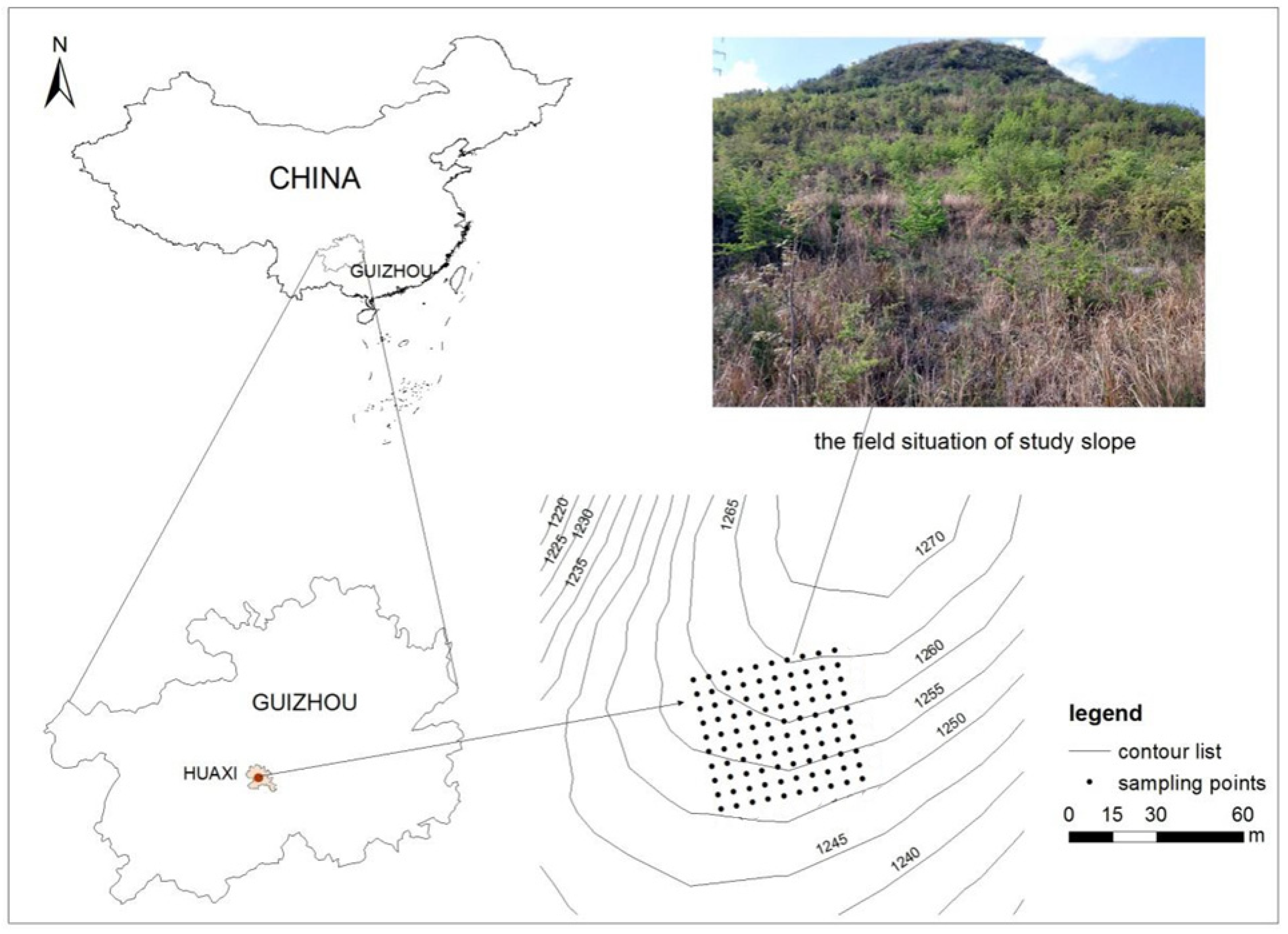
2.1. Study Area
2.2. Sampling Point Layout
2.3. Data Analysis
3. Results
3.1. Statistical Characteristics of Soil Moisture
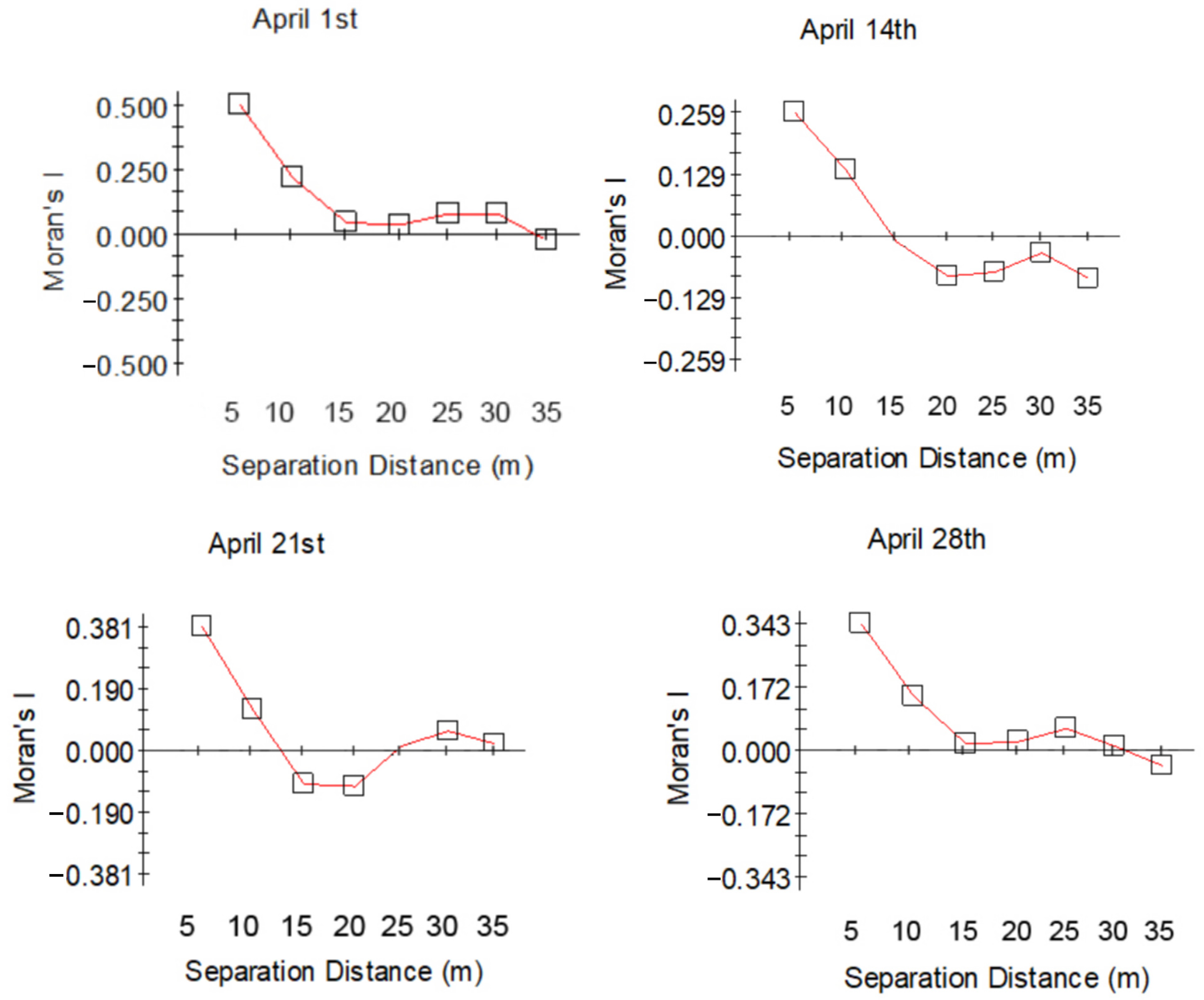
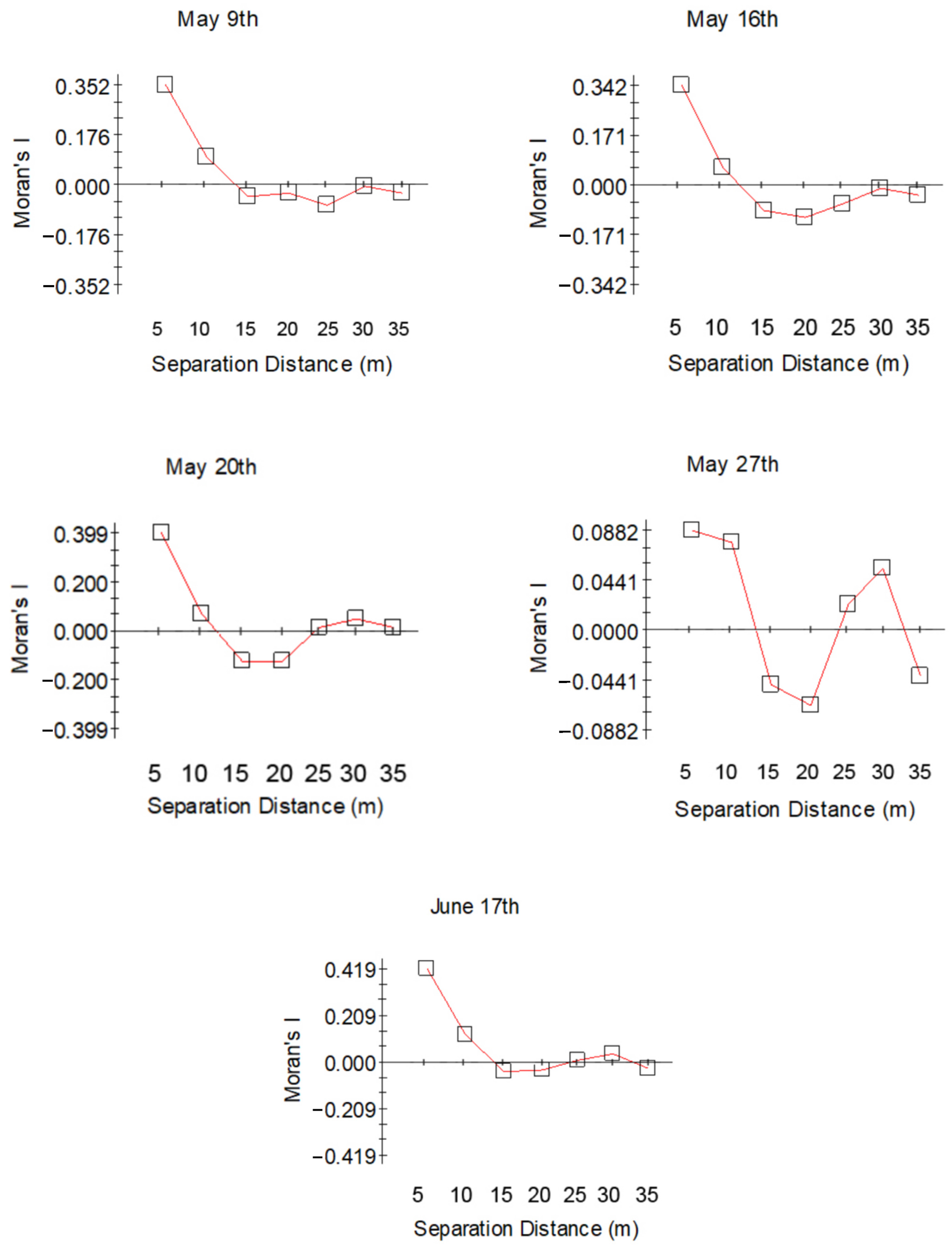
3.2. Spatial Autocorrelation Analysis of Soil Moisture
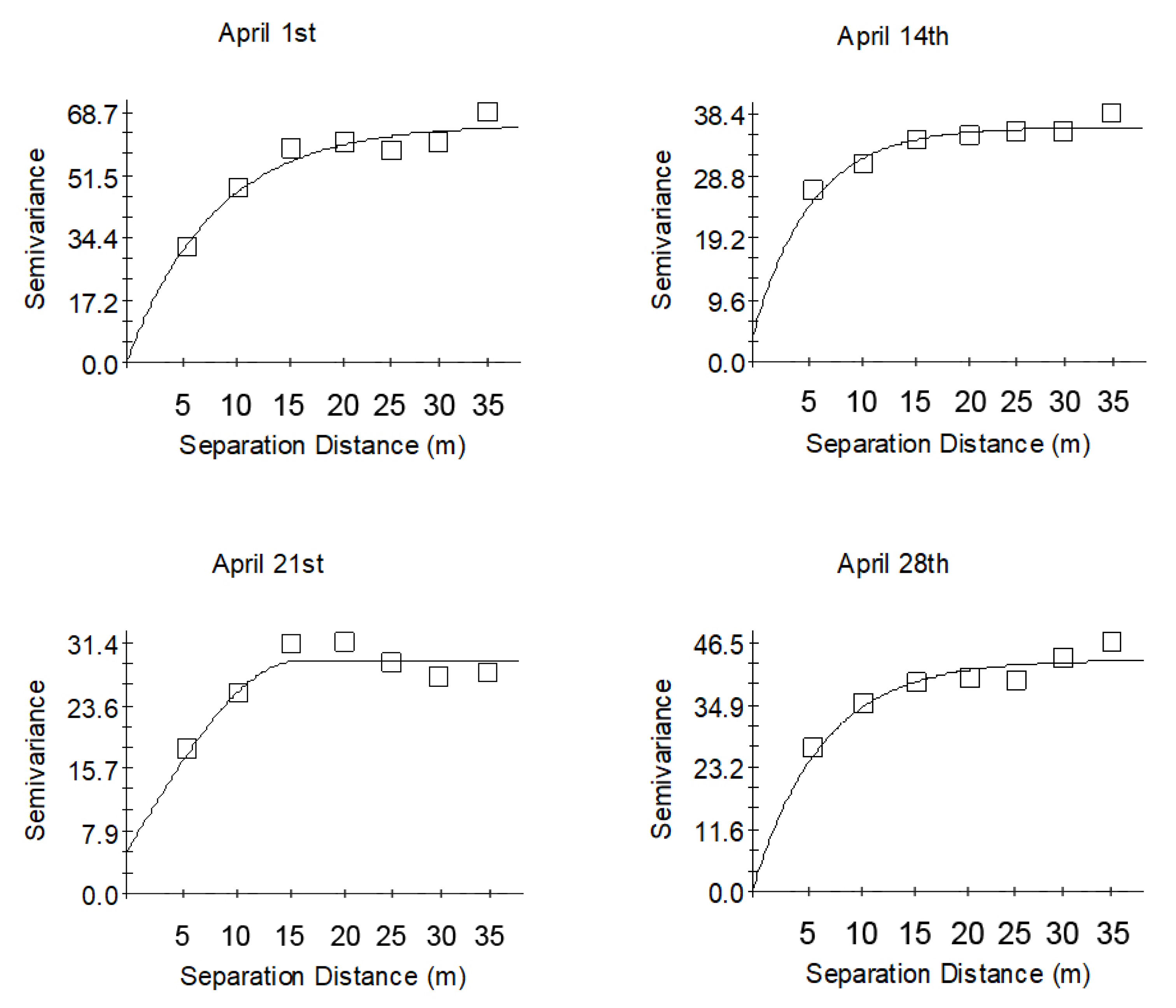
3.3. Spatial Variability of Soil Moisture
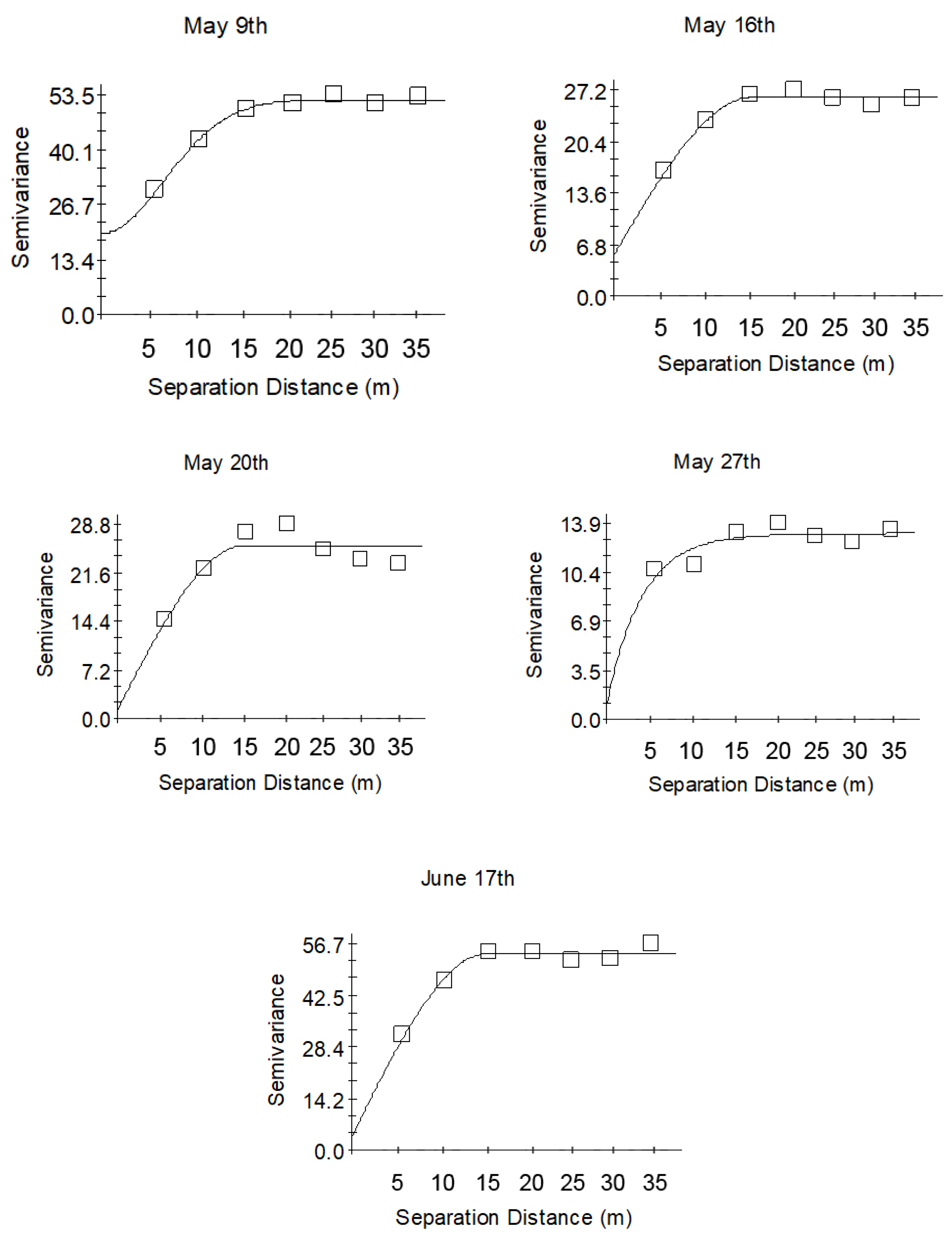
3.4. Changes of Soil Moisture Omnidirectional Experimental Semivariogram Parameters
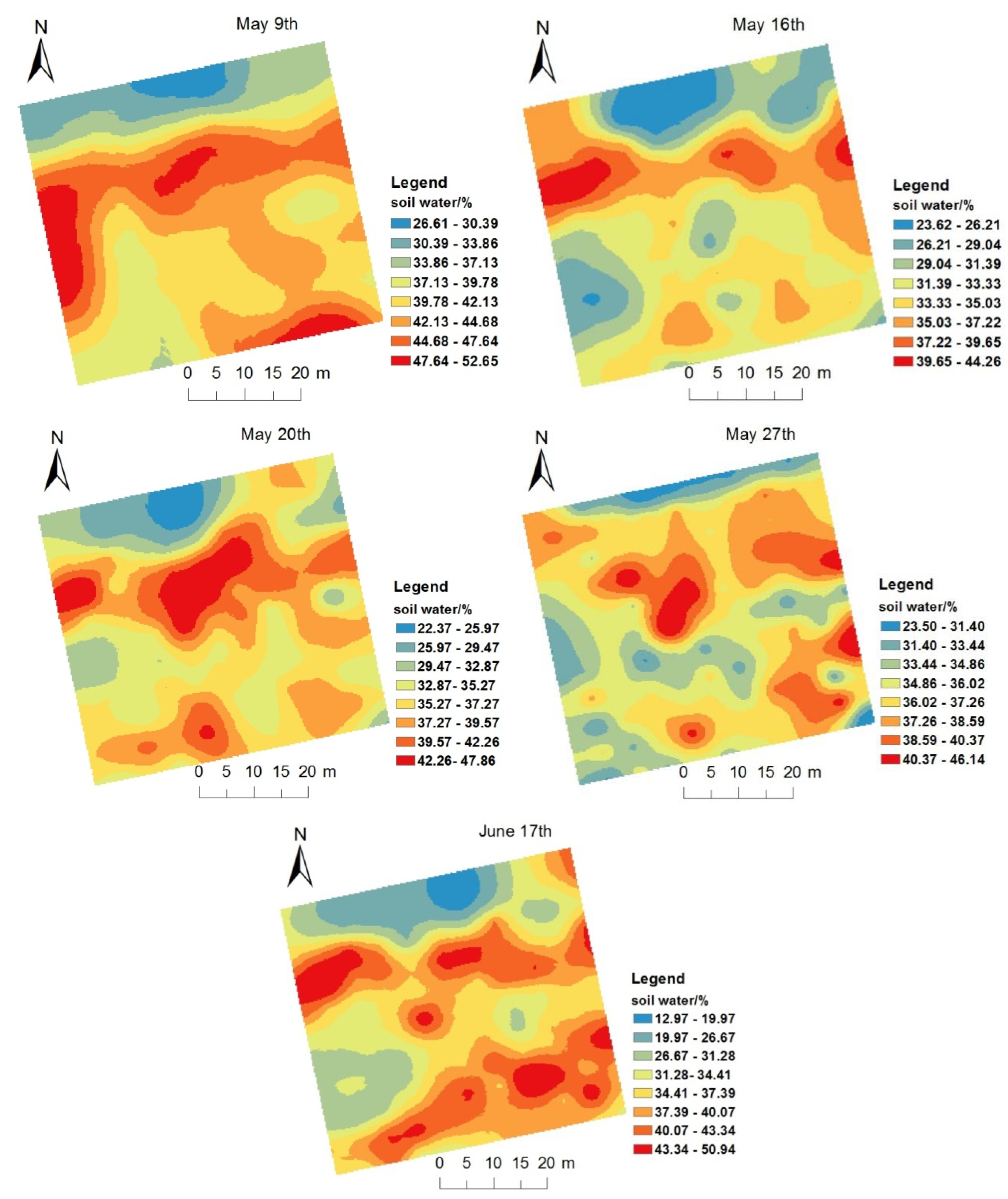
3.5. Spatial Distribution Pattern of Soil Moisture
4. Discussion
4.1. Spatial Autocorrelation of Soil Moisture
4.2. Spatial Distribution of Soil Moisture
4.3. Comparative Analysis of Soil Moisture
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gwak, Y.; Kim, S. Factors affecting soil moisture spatial variability for a humid forest hillslope. Hydrol. Process. 2017, 31, 431–445. [Google Scholar] [CrossRef]
- Lv, L.; Liao, K.; Zhou, Z.; Zhu, Q.; Shen, C. Determining hot moments/spots of hillslope soil moisture variations based on high-resolution spatiotemporal soil moisture data. Catena 2019, 173, 150–161. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, Q.; Tang, X.; Yan, W.; Chen, M. Changes in soil moisture caused solely by vegetation restoration in the karst region of southwest China. J. Hydrol. 2022, 613, 128460. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, C.; Xu, Z.; Wang, Y.; Peng, H. Effect of vegetation on soil water retention and storage in a semi-arid alpine forest catchment. J. Arid Land 2013, 5, 207–219. [Google Scholar] [CrossRef]
- Sun, F.; Lü, Y.; Wang, J.; Hu, J.; Fu, B. Soil moisture dynamics of typical ecosystems in response to precipitation: A monitoring-based analysis of hydrological service in the Qilian Mountains. Catena 2015, 129, 63–75. [Google Scholar] [CrossRef]
- Canton, Y.; Rodríguez-Caballero, E.; Contreras, S.; Villagarcia, L.; Li, X.Y.; Solé-Benet, A.; Domingo, F. Vertical and lateral soil moisture patterns on a Mediterranean karst hillslope. J. Hydrol. Hydromech. 2016, 64, 209–217. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, W.; Wang, K.; Fu, W. Soil moisture dynamics under different land uses on karst hillslope in northwest Guangxi, China. Environ. Earth Sci. 2010, 61, 1105–1111. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Ghadouani, A.; Shi, P. Modelling hydrological processes influenced by soil, rock and vegetation in a small karst basin of southwest China. Hydrol. Process. 2011, 25, 2456–2470. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, F.; Jiang, Z.; Yuan, D.; Jiang, Y. Assessment of water resource carrying capacity in karst area of Southwest China. Environ. Earth Sci. 2016, 75, 37. [Google Scholar] [CrossRef]
- Yan, W.; Zhou, Q.; Peng, D.; Luo, Y.; Chen, M.; Lu, Y. Response of surface-soil quality to secondary succession in karst areas in Southwest China: Case study on a limestone slope. Ecol. Eng. 2022, 178, 106581. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhu, A.X.; Yan, W.; Sun, Z. Impacts of forestland vegetation restoration on soil moisture content in humid karst region: A case study on a limestone slope. Ecol. Eng. 2022, 180, 106648. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, K.; Liu, Z.; Li, K.; Luo, D. Distribution and influencing factors of soil organic carbon in a typical karst catchment undergoing natural restoration. Catena 2022, 212, 106078. [Google Scholar] [CrossRef]
- Bouabdelli, S.; Meddi, M.; Zeroual, A.; Alkama, R. Hydrological drought risk recurrence under climate change in the karst area of Northwestern Algeria. J. Water Clim. Change 2020, 11, 164–188. [Google Scholar] [CrossRef]
- Yan, Y.; Dai, Q.; Yang, Y.; Yan, L.; Yi, X. Epikarst shallow fissure soil systems are key to eliminating karst drought limitations in the karst rocky desertification area of SW China. Ecohydrology 2022, 15, e2372. [Google Scholar] [CrossRef]
- Gan, F.; Diao, X.; Tan, K.; Cao, G.; Zhang, Y.; Zhong, X.; Gao, Y. An evaluation of the use of IMERG products for representing drought in a typical rocky karst region experiencing rocky desertification in Guangxi, China. Remote Sens. Lett. 2022, 13, 1100–1109. [Google Scholar] [CrossRef]
- Yan, W.; Zhou, Q.; Peng, D.; Wei, X.; Tang, X.; Yuan, E.; Wang, Y.; Shi, C. Soil moisture responses under different vegetation types to winter rainfall events in a humid karst region. Environ. Sci. Pollut. Res. 2021, 28, 56984–56995. [Google Scholar] [CrossRef]
- Yuan, E.; Zhou, Q.; Yan, W.; Peng, D.; Wang, Y. Response of the winter soil moisture of different vegetation types to rainfall events in karst slope land. Hydrol. Res. 2022, 53, 1271–1285. [Google Scholar] [CrossRef]
- Zhou, Q.; Sun, Z.; Liu, X.; Wei, X.; Peng, Z.; Yue, C.; Luo, Y. Temporal soil moisture variations in different vegetation cover types in karst areas of southwest China: A plot scale case study. Water 2019, 11, 1423. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Z.; Chen, X.; Shi, P. The impact of land use and land cover changes on soil moisture and hydraulic conductivity along the karst hillslopes of southwest China. Environ. Earth Sci. 2009, 59, 811–820. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Luo, G.; Wu, L.; Chen, F.; Wang, J.; Li, Q.; Li, C.; Yang, Y.; et al. Spatiotemporal dynamics of soil moisture in the karst areas of China based on reanalysis and observations data. J. Hydrol. 2020, 585, 124744. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Luo, G.; Wu, L.; Chen, F.; Wang, J.; Li, Q.; Li, C.; Yang, Y.; et al. Characteristics of soil moisture storage from 1979 to 2017 in the karst area of China. Geocarto Int. 2021, 36, 903–917. [Google Scholar] [CrossRef]
- Yang, J.; Chen, H.; Nie, Y.; Wang, K. Dynamic variations in profile soil water on karst hillslopes in Southwest China. Catena 2019, 172, 655–663. [Google Scholar] [CrossRef]
- Li, C.; Chen, H.; Xu, Q.; Wu, P.; Fu, Z. Spatial variability of soil moisture on hillslope in typical karst peak-cluster depression areas. Carsologica Sin. 2018, 2, 159–167. [Google Scholar]
- Luo, W.; Xu, X.; Liu, W.; Liu, M.; Li, Z.; Peng, T.; Zhang, R. UAV based soil moisture remote sensing in a karst mountainous catchment. Catena 2019, 174, 478–489. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, W.; Chen, H.S.; Nie, Y.P.; Ye, Y.Y.; Wang, K.L. Temporal and spatial variation in surface soil moisture content of karst slopes in the dry season. Acta Ecol. Sin. 2015, 35, 6326–6334. [Google Scholar]
- Wang, S.; Chen, H.S.; Fu, Z.; Wang, K. Temporal stability analysis of surface soil water content on two karst hillslopes in southwest China. Environ. Sci. Pollut. Res. 2016, 23, 25267–25279. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rudnicki, J.W.; Rodell, M. Variability in surface moisture content along a hillslope transect: Rattlesnake Hill, Texas. J. Hydrol. 1998, 210, 259–281. [Google Scholar] [CrossRef]
- Zhang, J.G.; Chen, H.S.; Su, Y.R.; Kong, X.L.; Zhang, W.; Shi, Y.; Liang, H.; Shen, G. Spatial variability and patterns of surface soil moisture in a field plot of karst area in southwest China. Plant Soil Environ. 2011, 57, 409–417. [Google Scholar] [CrossRef]
- Martínez-Murillo, J.F.; Hueso-González, P.; Ruiz-Sinoga, J.D. Topsoil moisture mapping using geostatistical techniques under different Mediterranean climatic conditions. Sci. Total Environ. 2017, 595, 400–412. [Google Scholar] [CrossRef]
- Yang, Q.; Jiang, Z.; Ma, Z.; Li, H. Spatial prediction of soil water content in karst area using prime terrain variables as auxiliary cokriging variable. Environ. Earth Sci. 2014, 72, 4303–4310. [Google Scholar] [CrossRef]
- Tuffour, H.O.; Abubakari, A.; Bashagaluke, J.B.; Djagbletey, E.D. Mapping spatial variability of soil physical properties for site-specific management. Int. Res. J. Eng. Technol. 2016, 3, 149–163. [Google Scholar]
- Mirzaei, R.; Sakizadeh, M. Comparison of interpolation methods for the estimation of groundwater contamination in Andimeshk-Shush Plain, Southwest of Iran. Environ. Sci. Pollut. Res. 2016, 23, 2758–2769. [Google Scholar] [CrossRef]
- Pesquer, L.; Cortes, A.; Pons, X. Parallel ordinary kriging interpolation incorporating automatic variogram fitting. Comput. Geosci. 2011, 37, 464–473. [Google Scholar] [CrossRef]
- Wang, J.; Fu, B.J.; Qiu, Y.; Chen, L.D. Semi-variogram of temporal and spatial variation of soil moisture in a small watershed of the Loess Hills. Acta Geogr. Sin. 2000, 55, 428–437. (In Chinese) [Google Scholar]
- Brooker, P.I. A parametric study of robustness of kriging variance as a function of range and relative nugget effect for a spherical semivariogram. Math. Geol. 1986, 18, 477–488. [Google Scholar] [CrossRef]
- Robert, A.; Richards, K.S. On the modelling of sand bedforms using the semivariogram. Earth Surf. Process. Landf. 1988, 13, 459–473. [Google Scholar] [CrossRef]
- Olea, R.A. Fundamentals of semivariogram estimation, modeling, and usage. In Stochastic Modeling and Geostatistics; Yarus, J.M., Chambers, R.L., Eds.; AAPG Datapages, Inc.: Tulsa, OK, USA, 1994; Volume 3, pp. 27–35. [Google Scholar]
- Murakami, D.; Yoshida, T.; Seya, H.; Griffith, D.A.; Yamagata, Y. A Moran coefficient-based mixed effects approach to investigate spatially varying relationships. Spat. Stat. 2017, 19, 68–89. [Google Scholar] [CrossRef]
- Cardoso, G.G.G.; Wanderley, R.C.; Souza, M.L.C. Physical attributes of a pasture soil in southeast Goiás determined by geostatistics. Eng. Agrícola 2016, 36, 143–151. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, H.; Su, Y.; Wu, J.; Zhang, W. Spatial variability of surface soil moisture content in depression area of karst region under moist and arid conditions. J. Appl. Ecol. 2006, 17, 2277–2282. [Google Scholar]
- Yates, S.R.; Warrick, A.W. Estimating soil water content using cokriging. Soil Sci. Soc. Am. J. 1987, 51, 23–30. [Google Scholar] [CrossRef]
- Korres, W.; Reichenau, T.; Fiener, P.; Koyama, C.; Bogena, H.; Cornelissen, T.; Baatz, R.; Herbst, M.; Diekkrüger, B.; Vereecken, H.; et al. Spatio-temporal soil moisture patterns—A meta-analysis using plot to catchment scale data. J. Hydrol. 2015, 520, 326–341. [Google Scholar] [CrossRef]
- Ries, F.; Lange, J.; Schmidt, S.; Puhlmann, H.; Sauter, M. Recharge estimation and soil moisture dynamics in a Mediterranean, semi-arid karst region. Hydrol. Earth Syst. Sci. 2015, 19, 1439–1456. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, H.; Su, Y.; Shi, Y.; Zhang, W.; Kong, X. Spatial variability of surface soil moisture in a depression area of karst region. Clean–Soil Air Water 2011, 39, 619–625. [Google Scholar] [CrossRef]

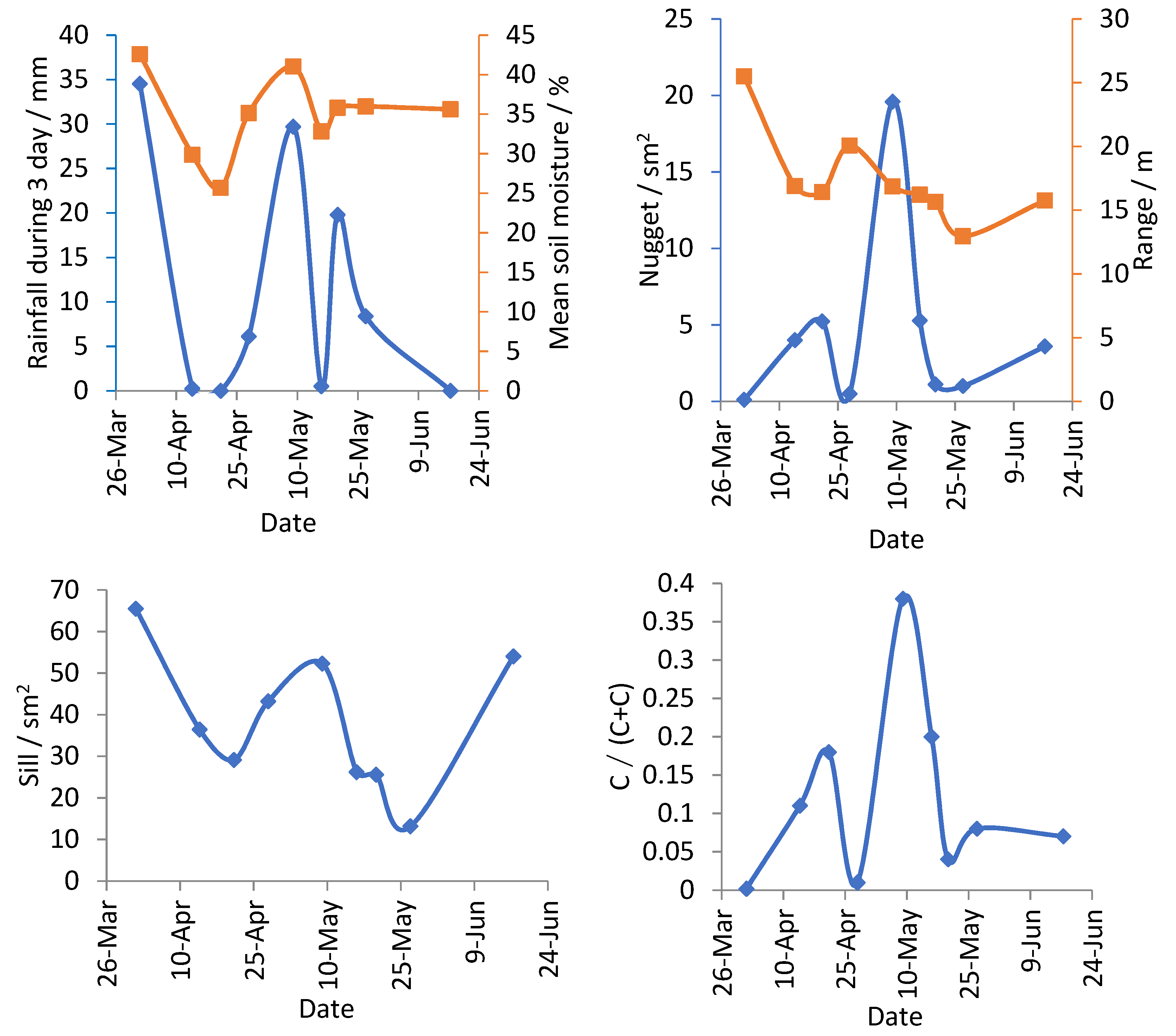

| Sampling Date | Rainfall during 3 Days (mm) | Max (%) | Min (%) | Mean (%) | SD(%) | CV(%) | Skew | Kurtosis | Distribution Type |
|---|---|---|---|---|---|---|---|---|---|
| 1 April | 34.54 | 56.80 | 22 | 42.60 | 8.23 | 19.32 | −0.42 | −0.29 | N |
| 14 April | 0.25 | 47.07 | 20.87 | 29.87 | 5.88 | 19.69 | 0.81 | 0.40 | S |
| 21 April | 0 | 38.17 | 11.63 | 25.67 | 5.37 | 20.91 | −0.33 | −0.02 | N |
| 28 April | 6.10 | 52.2 | 17.50 | 35.15 | 6.72 | 17.35 | −0.07 | 0.57 | N |
| 9 May | 29.72 | 58.37 | 24.80 | 41.03 | 7.24 | 17.65 | 0.15 | −0.36 | N |
| 16 May | 0.51 | 48.37 | 20.27 | 32.82 | 5 | 15.23 | −0.01 | 0.23 | N |
| 20 May | 19.8 | 49.07 | 21.83 | 35.81 | 4.93 | 13.77 | −0.16 | 0.27 | N |
| 27 May | 8.38 | 47.40 | 20.70 | 35.98 | 3.71 | 10.31 | −0.26 | 2.57 | N |
| 17 June | 0 | 53.07 | 11.50 | 35.63 | 7.41 | 20.78 | −0.41 | 0.72 | N |
| Sampling Date | Nugget C0 | Total Sill C0 + C | C0/(C0 + C) | Range (m) | R2 | Residual | Models |
|---|---|---|---|---|---|---|---|
| 1 April | 0.1 | 65.5 | 0.01 | 25.5 | 0.94 | 55.9 | Exponential |
| 14 April | 4 | 36.43 | 0.11 | 16.89 | 0.91 | 8.41 | Exponential |
| 21 April | 5.23 | 29.13 | 0.18 | 16.42 | 0.87 | 16.6 | Spherical |
| 28 April | 0.5 | 43.24 | 0.01 | 20.07 | 0.89 | 26.6 | Exponential |
| 9 May | 19.6 | 52.31 | 0.38 | 16.87 | 0.99 | 3.77 | Gaussian |
| 16 May | 5.28 | 26.21 | 0.20 | 16.22 | 0.98 | 2.04 | Spherical |
| 20 May | 1.1 | 25.6 | 0.04 | 15.65 | 0.80 | 25 | Spherical |
| 27 May | 1 | 13.16 | 0.08 | 12.96 | 0.69 | 2.95 | Exponential |
| 17 June | 3.6 | 54.04 | 0.07 | 15.76 | 0.97 | 15.8 | Spherical |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Meng, X.; Li, H.; Gu, X.; Cai, X.; Li, Y.; Zhou, Q. Spatio-Temporal Heterogeneity of Soil Moisture on Shrub–Grass Hillslope in Karst Region. Water 2023, 15, 1868. https://doi.org/10.3390/w15101868
Li J, Meng X, Li H, Gu X, Cai X, Li Y, Zhou Q. Spatio-Temporal Heterogeneity of Soil Moisture on Shrub–Grass Hillslope in Karst Region. Water. 2023; 15(10):1868. https://doi.org/10.3390/w15101868
Chicago/Turabian StyleLi, Juncai, Xiaorong Meng, Hua Li, Xiaoxiao Gu, Xiaojun Cai, Yuanlong Li, and Qiuwen Zhou. 2023. "Spatio-Temporal Heterogeneity of Soil Moisture on Shrub–Grass Hillslope in Karst Region" Water 15, no. 10: 1868. https://doi.org/10.3390/w15101868






