Wave Buoy Measurements at Short Fetches in the Black Sea Nearshore: Mixed Sea and Energy Fluxes
Abstract
:1. Introduction
2. Materials and Methods
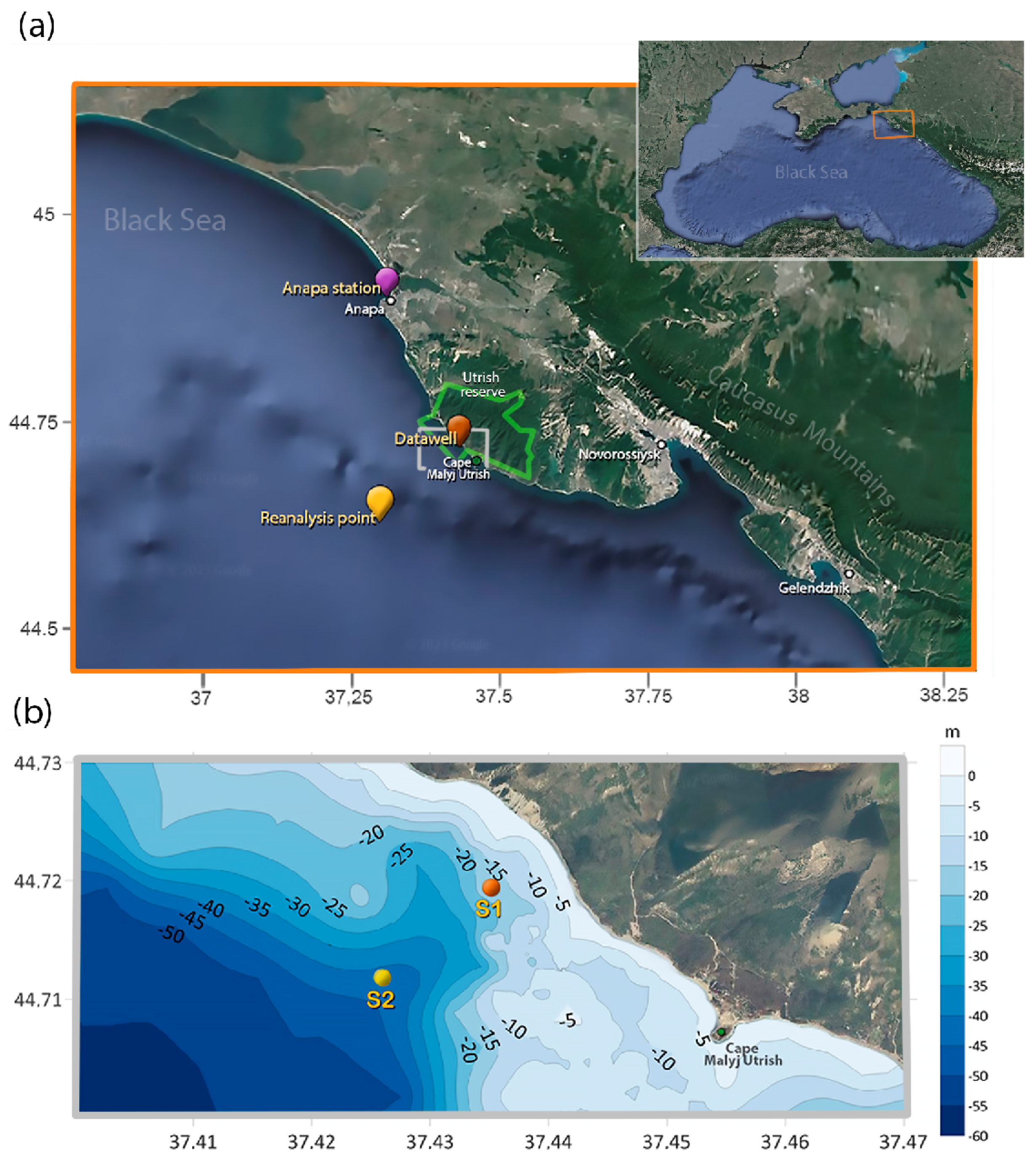
2.1. Study Area General Description
2.2. Wave Buoy Data
2.3. Auxiliary In Situ and Reanalysis Data
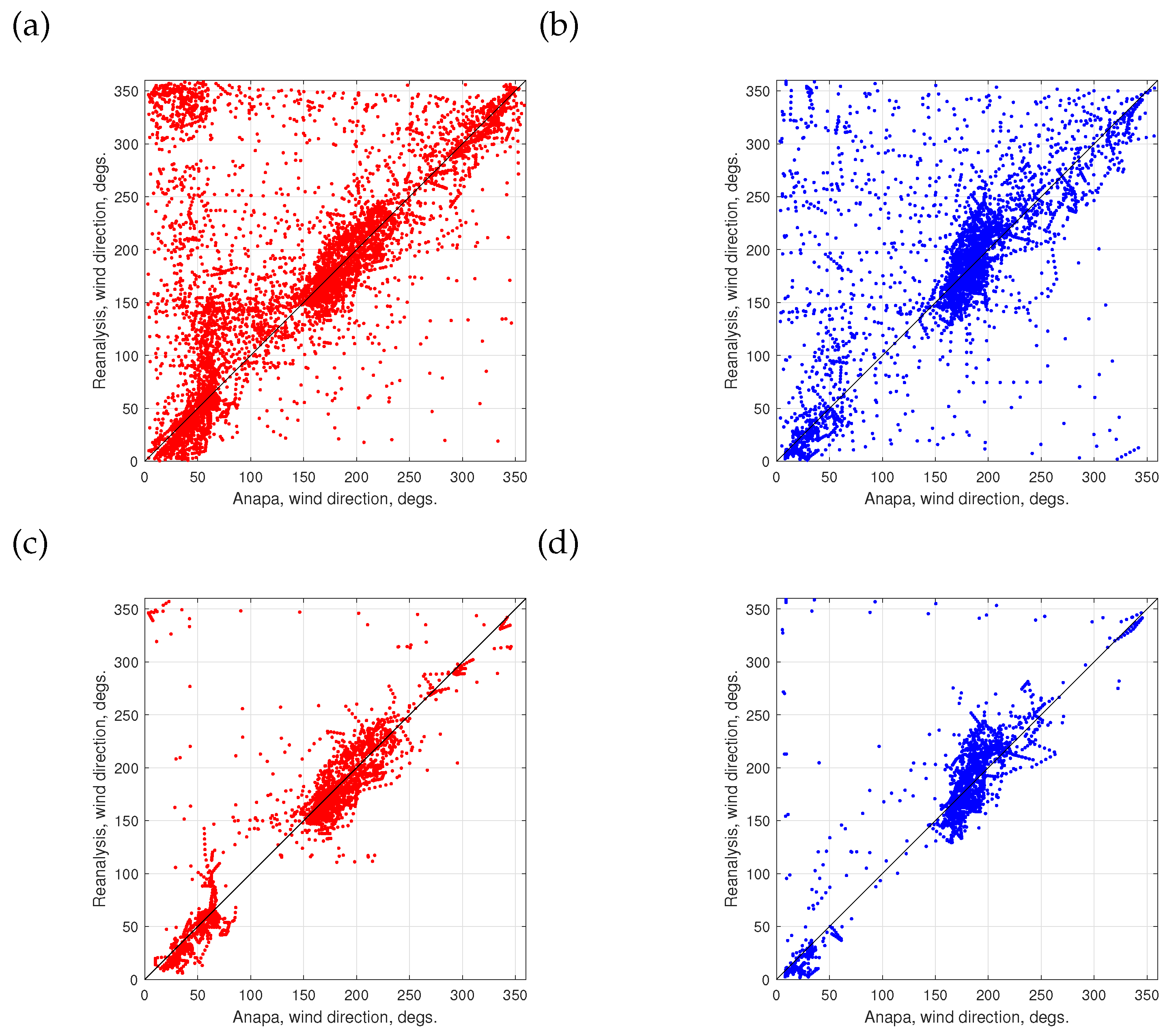
2.3.1. Anapa Weather Station
2.3.2. Wind Reanalysis Data
2.3.3. Wave Model Data
2.4. Theoretical Background of the Data Analysis
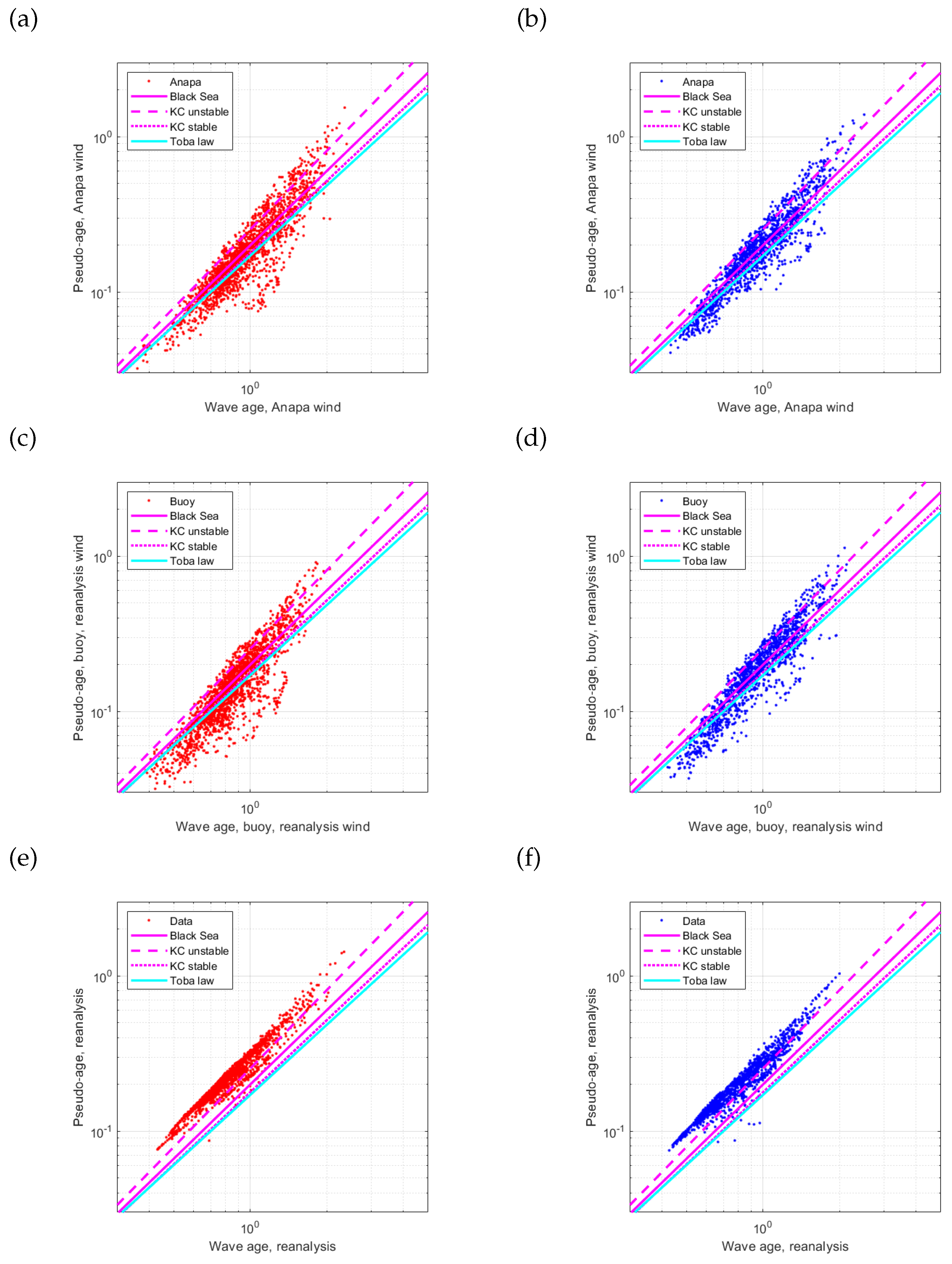
2.4.1. Similarity Approach by Kitaigorodskii [42] for Analysis of Wind–Wave Coupling
2.4.2. Theory of Wave Turbulence for the Analysis of Wind–Wave Coupling
3. Results
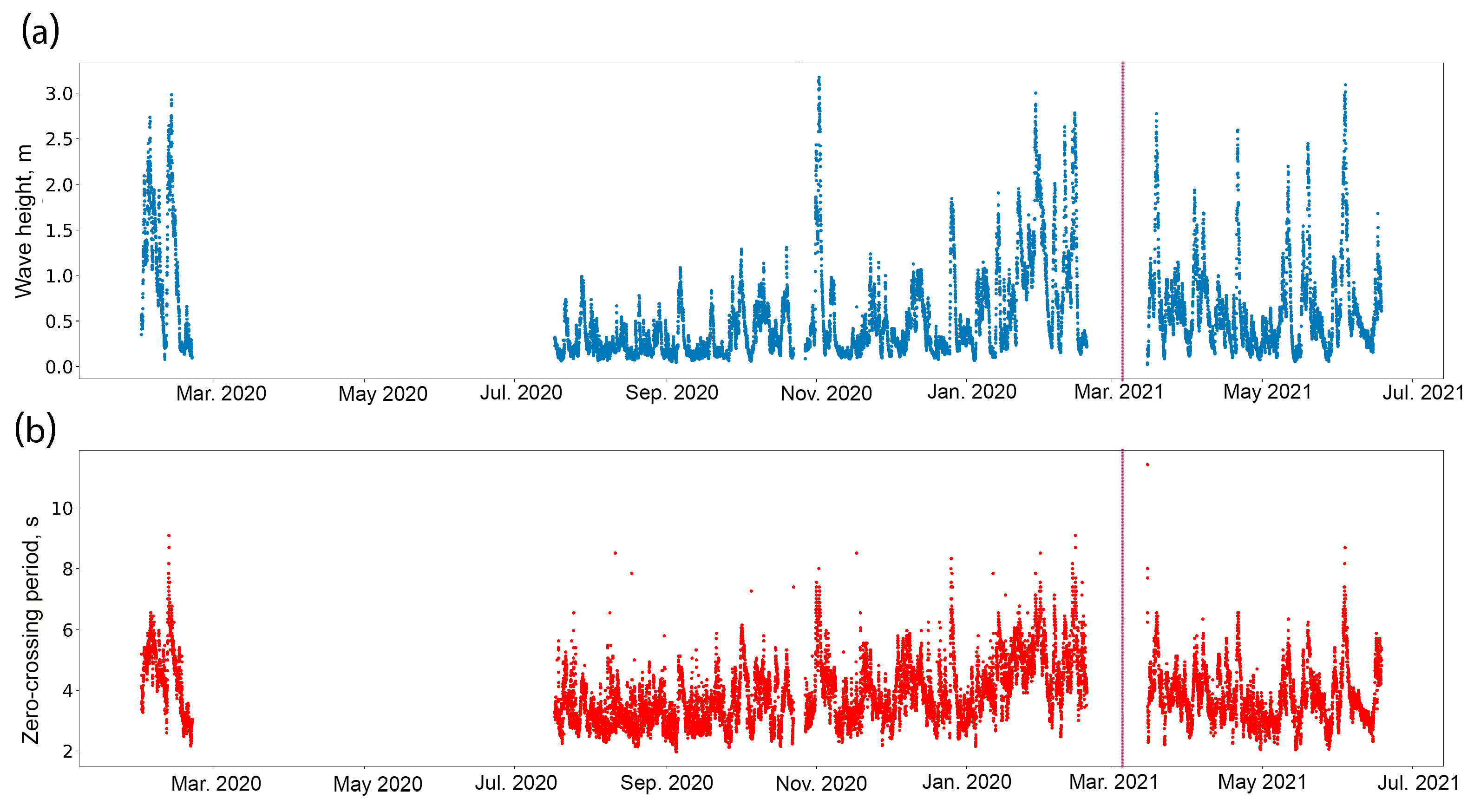
3.1. Utrish Buoy Time Series for Nearshore Wave Dynamics
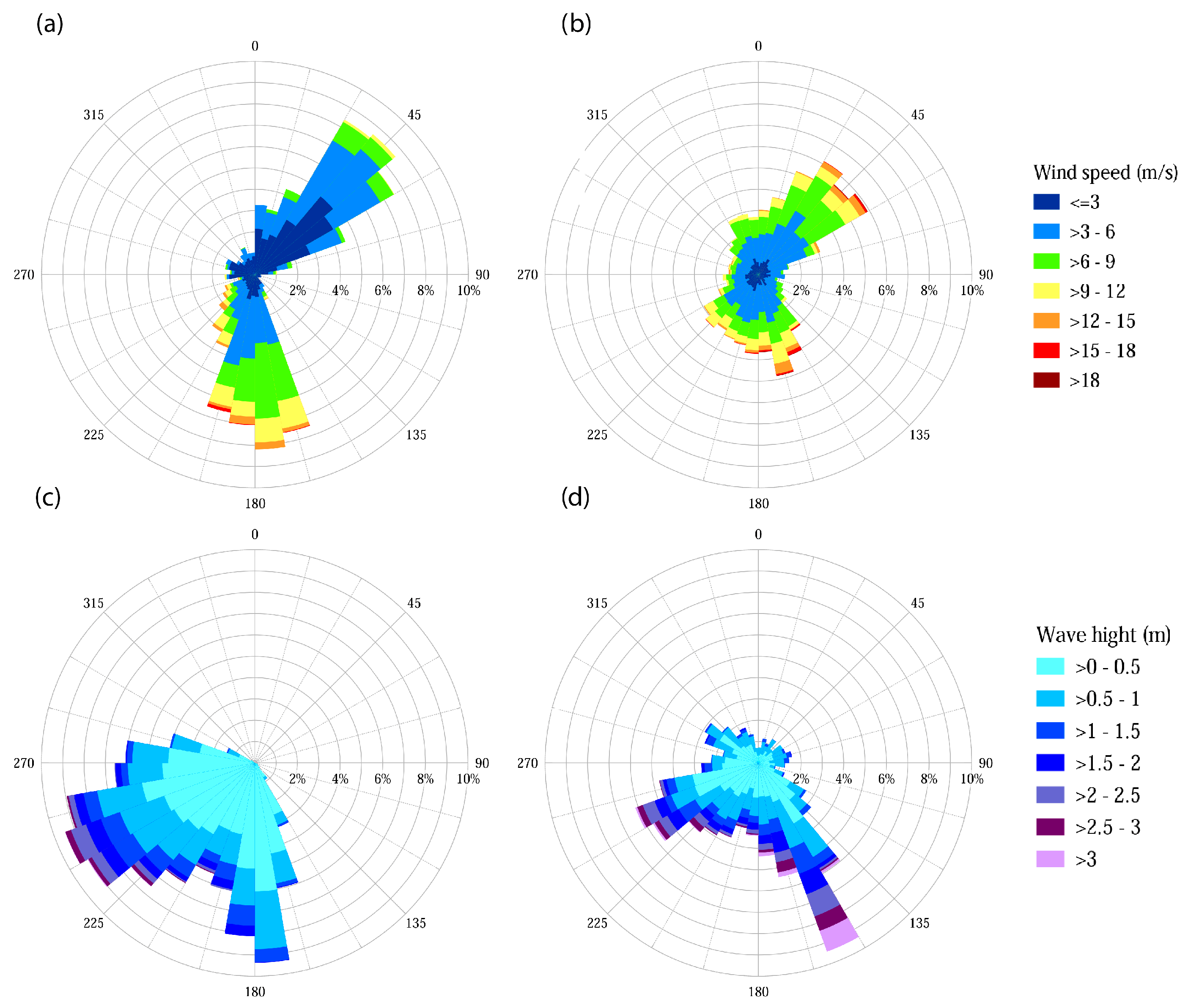
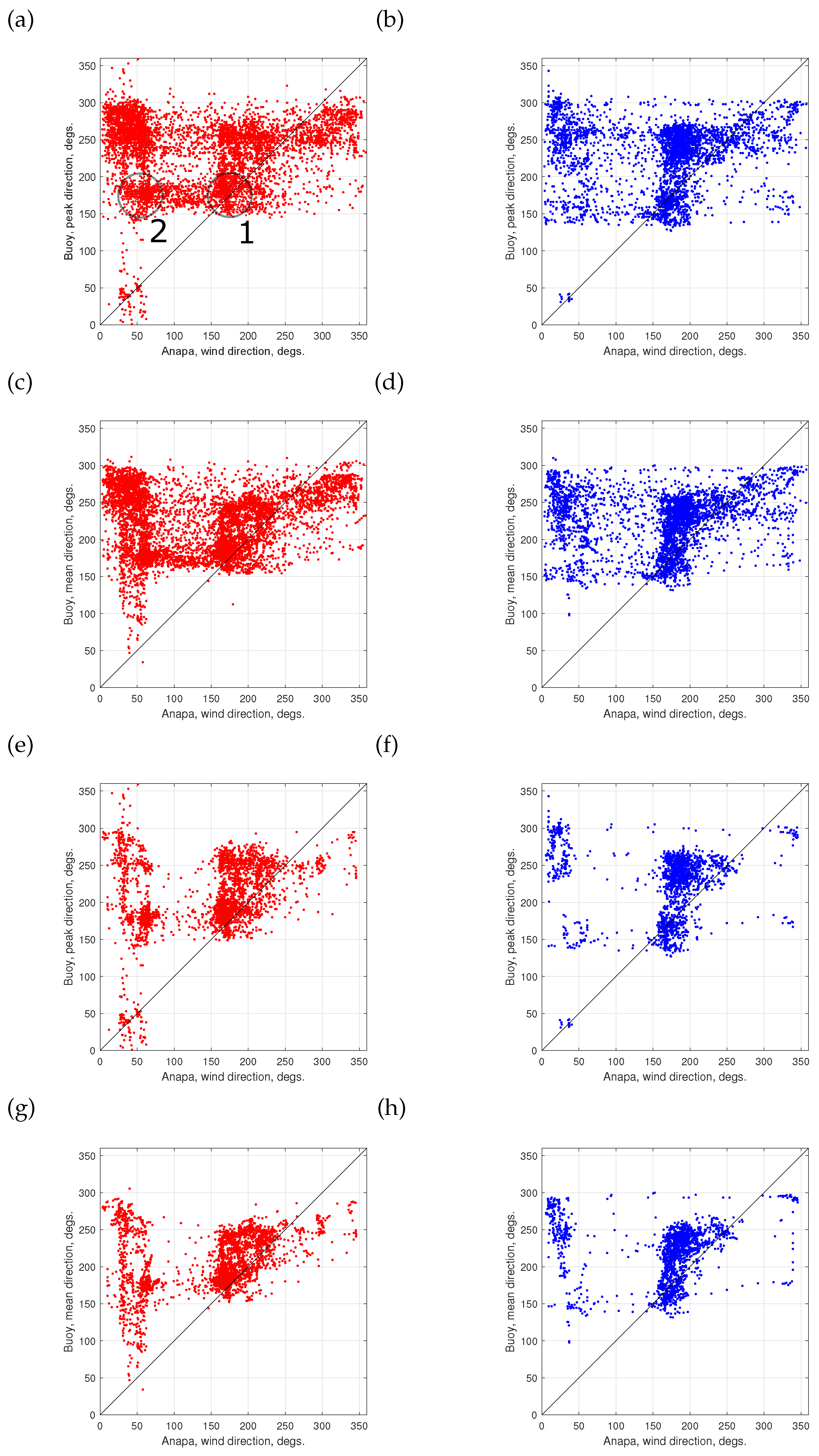
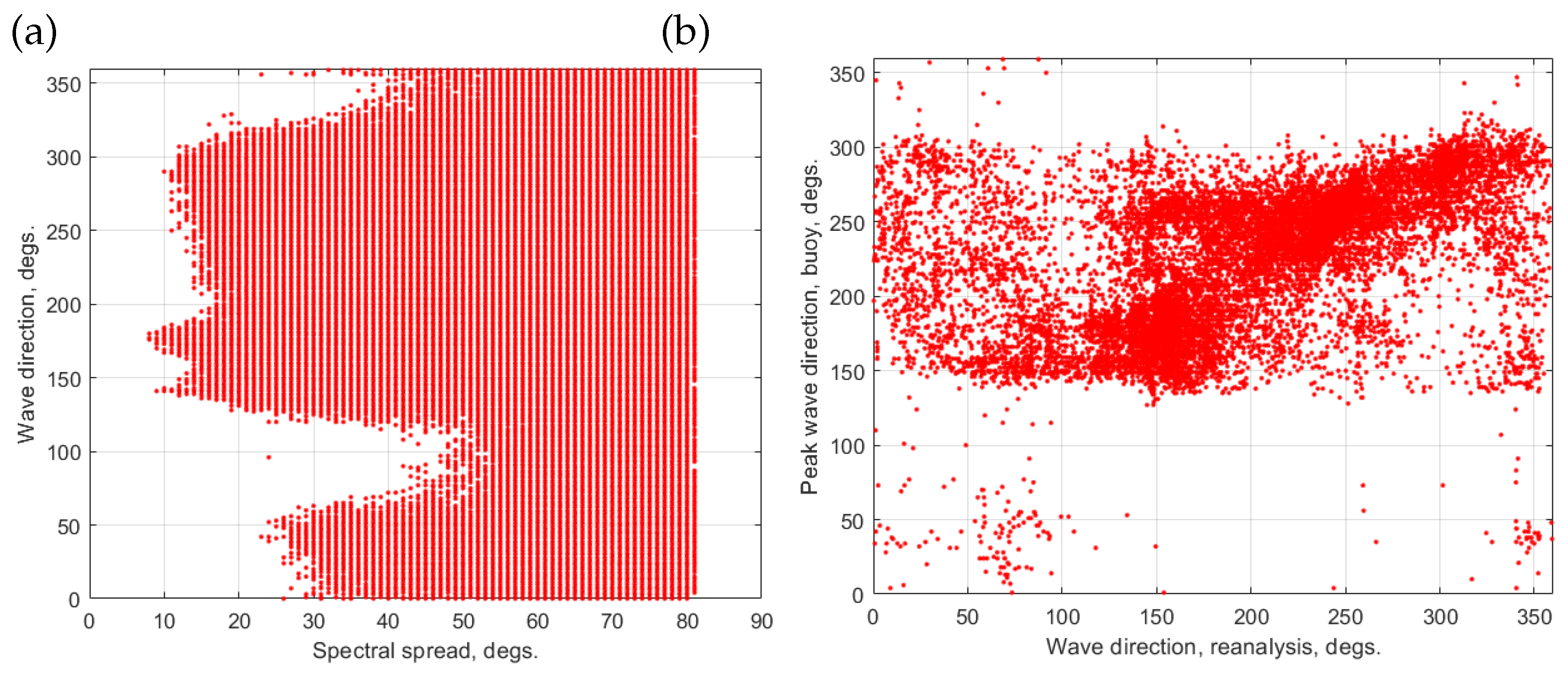
Directionality of Wind and Waves as a Key Feature of Wave Dynamics
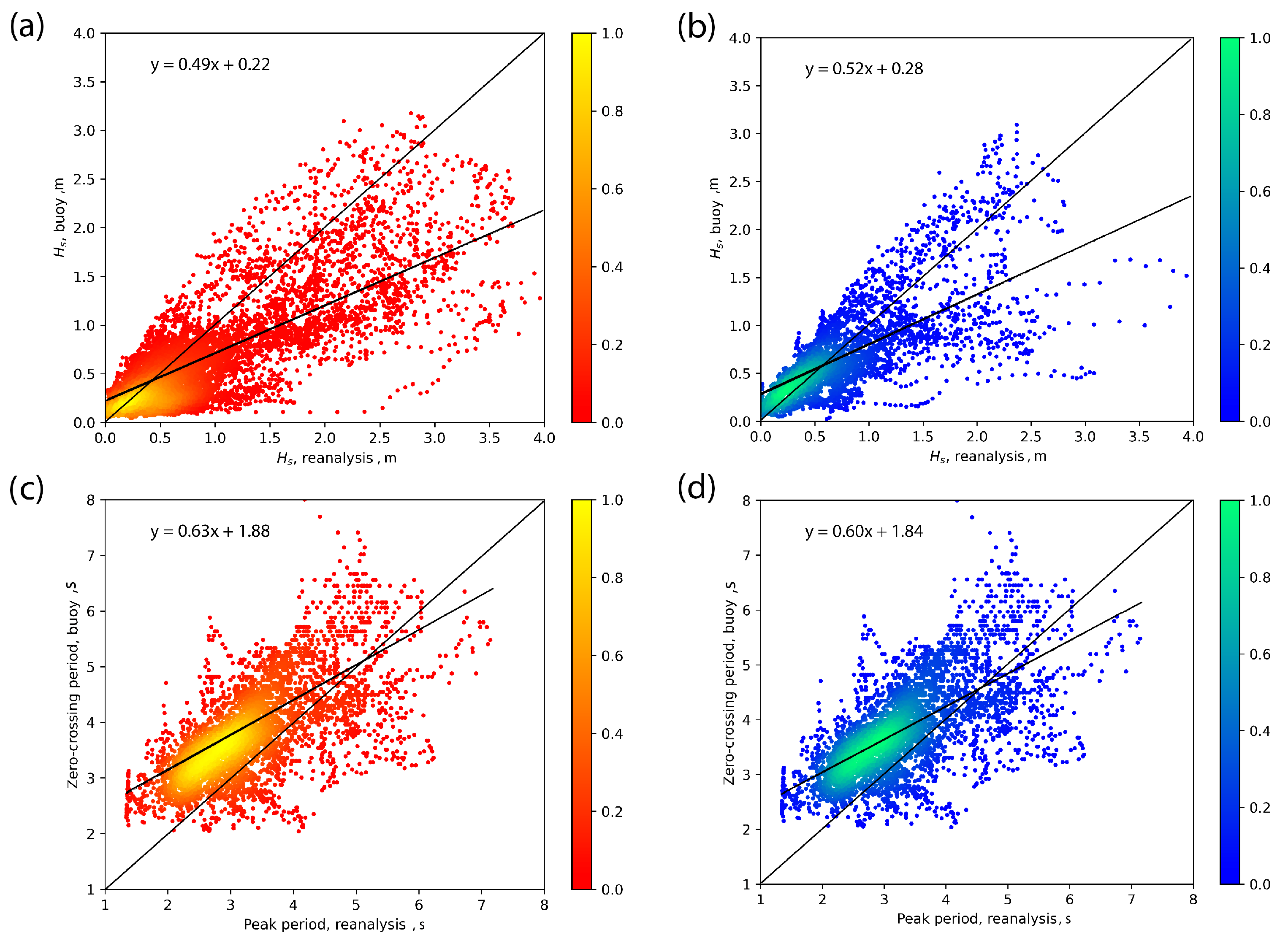
3.2. Conventional Analysis of Wind Speed, Wave Heights, and Periods as Essential Physical Parameters
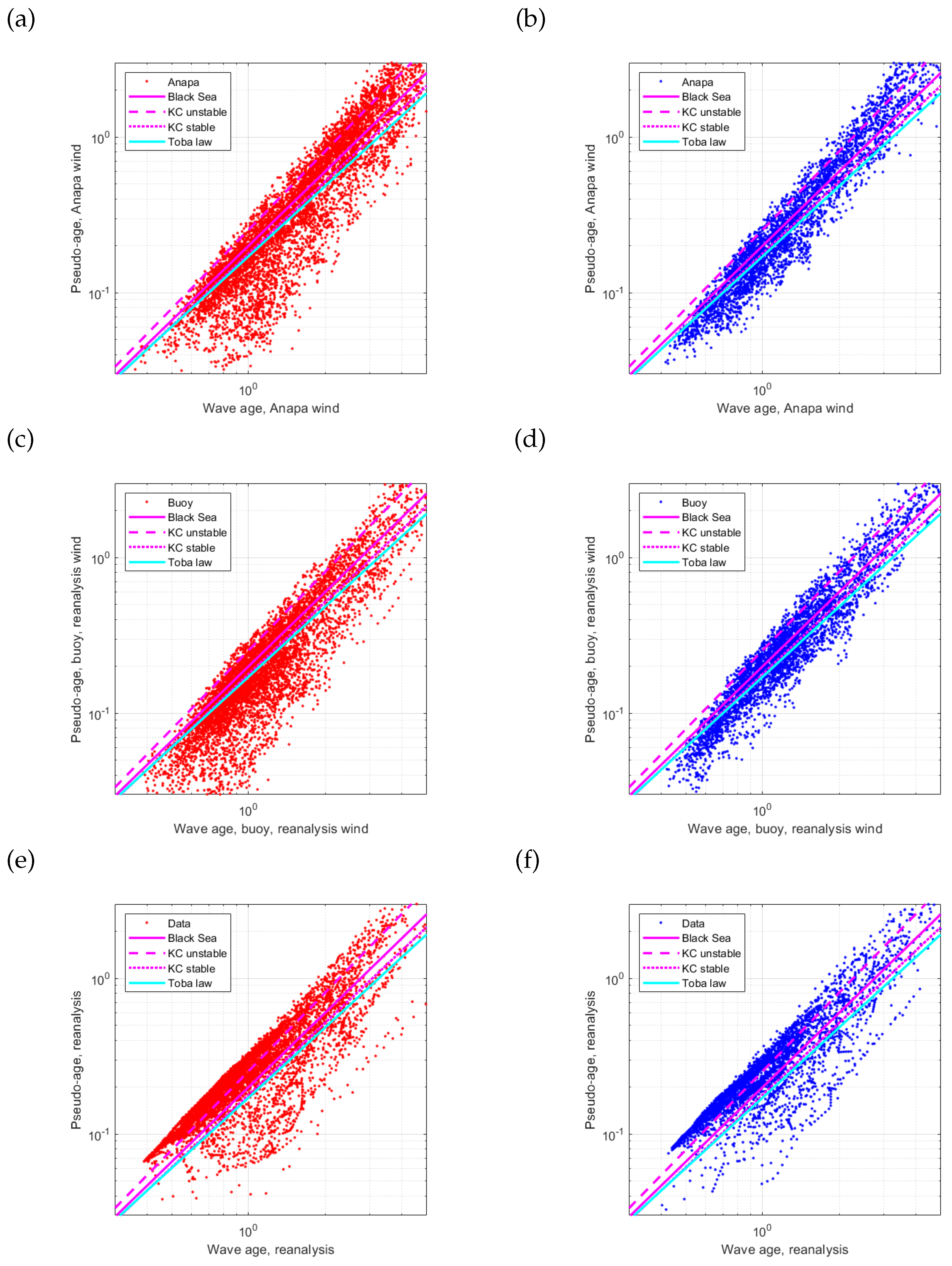
3.3. Theory of Wave Turbulence for Wind–Wave Coupling Diagnostics
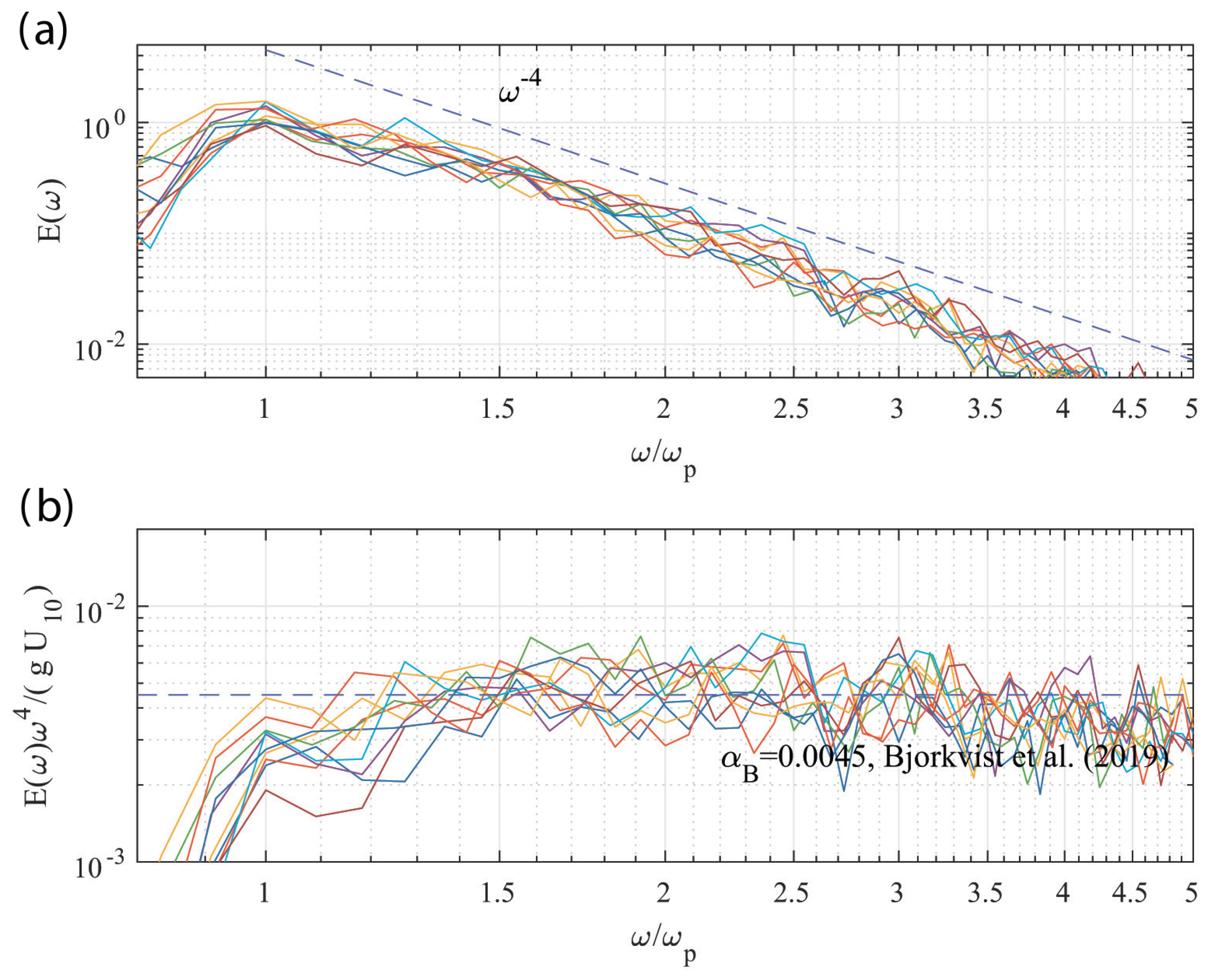
3.3.1. The Equilibrium Range in the Wave Spectra Measured Using the Buoy
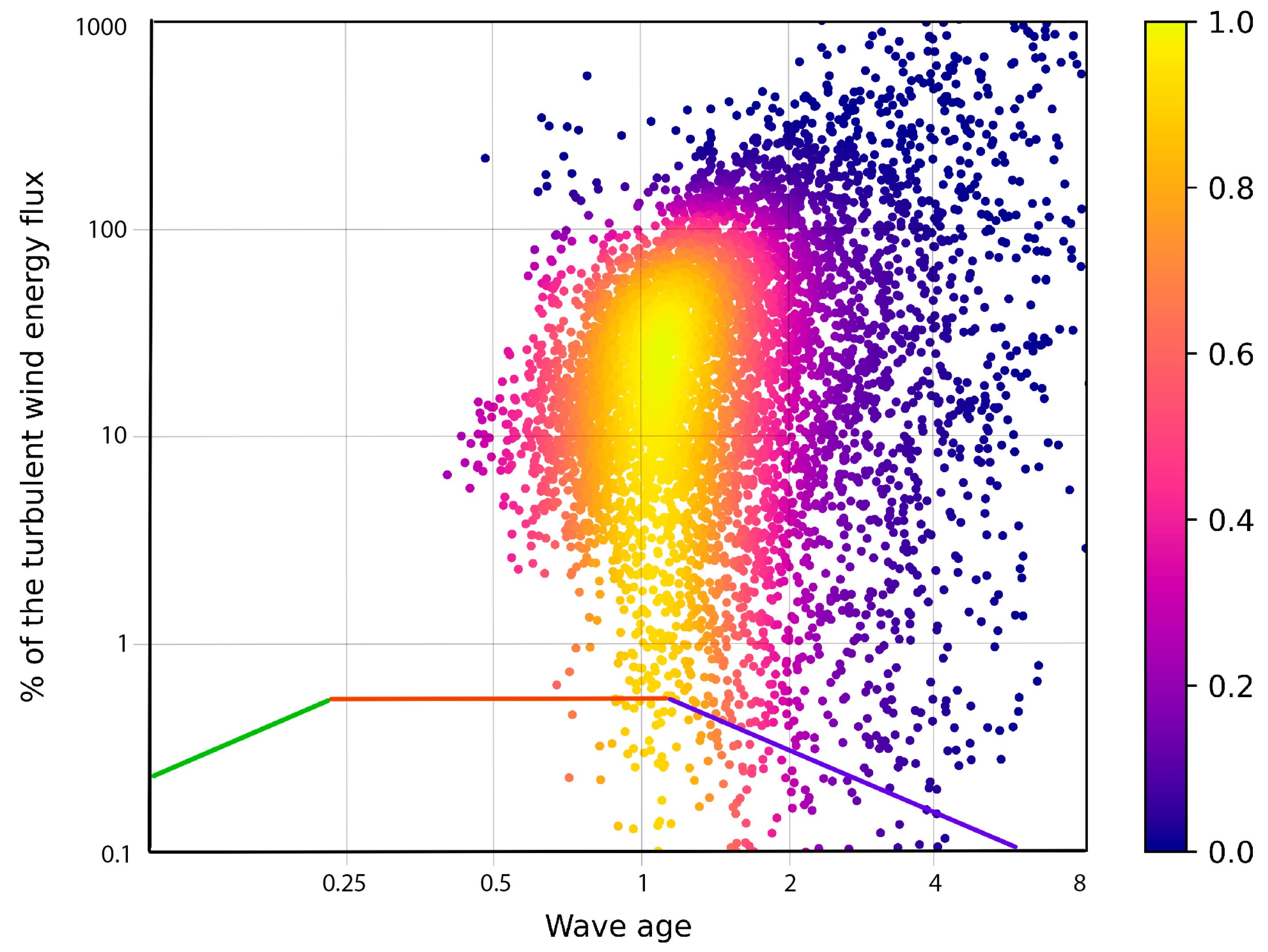
3.3.2. Energy Flux in the Spectral Equilibrium Range
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sverdrup, H.V.; Munk, W.H. Wind, Sea, and Swell: Theory of Relations for Forecasting; Hydrographic Office Pub. 60; U.S. Navy: Washington, DC, USA, 1947. [Google Scholar]
- Li, L.; Haver, S.; Berlin, N. Assessment of operational limits: Effects of uncertainties in sea state description. Mar. Struct. 2021, 77, 102975. [Google Scholar] [CrossRef]
- Bonnefond, P.; Haines, B.; Watson, C. In situ Absolute Calibration and Validation: A link from coastal to open-ocean altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 259–296. [Google Scholar] [CrossRef]
- Abdalla, S.; Abdeh Kolahchi, A.; Ablain, M.; Adusumilli, S.; Aich Bhowmick, S.; Alou-Font, E.; Amarouche, L.; Andersen, O.B.; Antich, H.; Aouf, L.; et al. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Gelci, R.; Cazalé, H.; Vassal, J. Prévision de la houle. La méthode des densités spectroangulaires. Bull. D’Inf. Comité d’Oceanogr. d’Etude Côtes 1957, 9, 416–435. [Google Scholar]
- Cavaleri, L.; Alves, J.H.G.M.; Ardhuin, F.; Babanin, A.; Banner, M.; Belibassakis, K.; Benoit, M.; Donelan, M.; Groeneweg, J.; Herbers, T.H.C.; et al. Wave modelling—The state of the art. Progr. Ocean. 2007, 75, 603–674. [Google Scholar] [CrossRef]
- Hanson, J.L.; Phillips, O.M. Automated analysis of ocean surface directional wave spectra. J. Atmos. Ocean. Technol. 2001, 18, 277–293. [Google Scholar] [CrossRef]
- Munk, W.H.; Miller, G.R.; Snodgrass, F.E.; Barber, N.F. Directional Recording of Swell from Distant Storms. Phil. Trans. R. Soc. Lond. 1963, 255, 505–584. [Google Scholar] [CrossRef]
- Rusu, L. Assessment of the wave energy in the Black Sea based on a 15-year hindcast with data assimilation. Energies 2015, 8, 10370–10388. [Google Scholar] [CrossRef]
- Akpınar, A.; Bingölbali, B. Long-term variations of wind and wave conditions in the coastal regions of the Black Sea. Nat. Hazards 2016, 84, 69–92. [Google Scholar] [CrossRef]
- Myslenkov, S.; Shestakova, A.; Toropov, P. Numerical simulation of storm waves near the northeastern coast of the Black Sea. Russ. Meteorol. Hydrol. 2016, 41, 706–713. [Google Scholar] [CrossRef]
- Onea, F.; Rusu, L. A long-term assessment of the Black Sea wave climate. Sustainability 2017, 9, 1875. [Google Scholar] [CrossRef]
- Gippius, F.N.; Myslenkov, S.A. Black Sea wind wave climate with a focus on coastal regions. Ocean. Eng. 2020, 218, 108–199. [Google Scholar] [CrossRef]
- Divinsky, B.V.; Fomin, V.V.; Kosyan, R.D.; Ratner, Y.D. Extreme wind waves in the Black Sea. Oceanologia 2020, 62, 23–30. [Google Scholar] [CrossRef]
- Divinsky, B.; Kuklev, S. Climate Variations of Certain Wave Parameters at the Inlet of Novorossiysk Bay. Oceanology 2022, 62, 155–161. [Google Scholar] [CrossRef]
- Melnikov, V.; Zatsepin, A.; Kostianoy, A.G. Hydrophysical polygon on the Black Sea. Trudy GOIN Proc. Russ. State Oceanogr. Inst. 2011, 213, 264–278. (In Russian) [Google Scholar]
- Evstigneev, V.; Naumova, V.; Evstigneev, V.P.; Evstigneev, M.P.; Ljubarec, E. Wind-Wave Climate Over the Coastal Zone of the Azov and the Black Seas; INTS: Sevastopol, Ukraine, 2017; ISBN 978-5-6040795-0-8. [Google Scholar]
- Melnikov, V.A.; Moskalenko, L.V.; Kuzevanova, N. Wind cycles and climatic trends of the Black Sea. Trudy GOIN Proc. Russ. State Oceanogr. Inst. 2018, 219, 101–123. (In Russian) [Google Scholar]
- Saprykina, Y.; Kuznetsov, S.; Valchev, N. Multidecadal fluctuations of storminess of black sea due to teleconnection patterns on the base of modelling and field wave data. In Proceedings of the Fourth International Conference in Ocean Engineering (ICOE2018); Lecture Notes in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2019; Volume 22, pp. 773–781. [Google Scholar]
- Badulin, S.I.; Vershinin, V.V.; Levchenko, D.G.; Zatsepin, A.G.; Ostrovskii, A.G.; Lobkovsky, L.I. A project of concrete stabilized spar buoy as a coastal environmental observation and maritime safety platform. J. Ocean Eng. Mar. Energy 2021, 7, 115–127. [Google Scholar] [CrossRef]
- Kos’yan, R.; Divinsky, B.; Pushkarev, O. Measurements of parameters of wave processes in the open sea near Gelendzhik. In Eight Workshop of NATO TU-WAVES/Black Sea; Middle East Technical University: Ankara, Turkey, 1998; pp. 5–6. [Google Scholar]
- Yılmaz, N.; Özhan, E. Characteristics of the frequency spectra of wind-waves in Eastern Black Sea. Ocean. Dyn. 2014, 64, 1419–1429. [Google Scholar] [CrossRef]
- Coastal Dynamics. Available online: https://coastdyn.ru/toppage1.htm (accessed on 11 October 2022).
- Myslenkov, S.A.; Badulin, S.I.; Lopatukhin, L.; Arkhipkin, V.; Akpınar, A.; Bingölbali, B.; Soran, M.B. Quality assessment of wind wave spectra simulation in the Black Sea coastal zone. In Proceedings of the IX International Scientific and Practical Conference Marine Research and Education (MARESEDU-2020), Boston, MA, USA, 7–10 March 2020; pp. 258–261. [Google Scholar]
- Amarouche, K.; Akpınar, A.; Soran, M.B.; Myslenkov, S.; Majidi, A.G.; Kankal, M.; Arkhipkin, V. Spatial calibration of an unstructured SWAN model forced with CFSR and ERA5 winds for the Black and Azov Seas. Appl. Ocean. Res. 2021, 117, 102962. [Google Scholar] [CrossRef]
- Rybalko, A.; Myslenkov, S. Seasonal variability of wave spectra based on simulation and measurement data in the Gelendzhik and Utrish region. In Proceedings of the X International Scientific and Practical Conference Marine Research and Education (MARESEDU-2021), Moscow, Russia, 24–28 October 2021; Volume 1, pp. 121–124. [Google Scholar]
- Amarouche, K.; Akpınar, A.; Rybalko, A.; Myslenkov, S. Assessment of SWAN and WAVEWATCH-III models regarding the directional wave spectra estimates based on Eastern Black Sea measurements. Ocean. Eng. 2023, 272, 113944. [Google Scholar] [CrossRef]
- Baydakov, G.A.; Kandaurov, A.A.; Kuznetsova, A.M.; Sergeev, D.A.; Troitskaya, Y.I. Field Studies of Features of Wind Waves at Short Fetches. Bull. Russ. Acad. Sci. Phys. 2018, 82, 1431–1434. [Google Scholar] [CrossRef]
- Kuznetsova, A.M.; Dosaev, A.S.; Baydakov, G.A.; Sergeev, D.A.; Troitskaya, Y.I. Adaptation of the Parameterization of the Nonlinear Energy Transfer for Short Fetch Conditions in the WAVEWATCH III Wave Prediction Model. Izv. Atmos. Ocean. Phys. 2020, 56, 191–199. [Google Scholar] [CrossRef]
- Walsh, E.J.; Hancock, D.W., III; Hines, D.E.; Swift, R.N.; Scott, J.F. Directional wave spectra measured with the surface contour radar. J. Phys. Oceanogr. 1985, 15, 566–592. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Nakamura, R.; Komori, T. Observations of the wind and waves in Hakata Bay. Rep. Res. Inst. Appl. Mech. Kyushu Univ. 1971, 19, 37–74. [Google Scholar]
- Mitsuyasu, H.; Tasai, H.; Suhara, F.; Mizuno, T.; Honda, S.O.T.; Rikiishi, K. Observation of power spectrum of ocean waves using a clover-leaf buoy. J. Phys. Oceanogr. 1982, 10, 286–296. [Google Scholar] [CrossRef]
- Panahi, R.; Shafieefar, M. Development of a bi-modal directional wave spectrum. Ocean. Eng. 2015, 105, 104–111. [Google Scholar] [CrossRef]
- Akbari, H.; Panahi, R.; Amani, L. A double-peaked spectrum for the northern parts of the Gulf of Oman: Revisiting extensive field measurement data by new calibration methods. Ocean. Eng. 2019, 12, 187–198. [Google Scholar] [CrossRef]
- Akbari, H.; Panahi, R.; Amani, L. Improvement of double-peaked spectra: Revisiting the combination of the Gaussian and the JONSWAP models. Ocean. Eng. 2020, 198, 106965. [Google Scholar] [CrossRef]
- Adibzade, M.; Shafieefar, M.; Akbari, H.; Panahi, R. Multi-peaked directional wave spectra based on extensive field measurement data in the Gulf of Oman. Ocean. Eng. 2021, 230, 109057. [Google Scholar] [CrossRef]
- Official Website of the Utrish Reserve. Available online: https://utrishgpz.ru/ (accessed on 12 December 2022). (In Russian).
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Dtsch. Hydrogh. Z. Suppl. 1973, 2, 2–95. [Google Scholar]
- Hasselmann, K.; Ross, D.B.; Müller, P.; Sell, W. A parametric wave prediction model. J. Phys. Oceanogr. 1976, 6, 200–228. [Google Scholar] [CrossRef]
- Badulin, S.I.; Pushkarev, A.N.; Resio, D.; Zakharov, V.E. Self-similarity of wind-driven seas. Nonlinear Proc. Geophys. 2005, 12, 891–946. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Badulin, S.I.; Hwang, P.A.; Caulliez, G. Universality of Sea Wave Growth and Its Physical Roots. J. Fluid Mech. 2015, 708, 503–535. [Google Scholar] [CrossRef]
- Kitaigorodskii, S.A. Applications of the theory of similarity to the analysis of wind-generated wave motion as a stochastic process. Bull. Acad. Sci. USSR Geophys. Ser. Engl. Transl. 1962, N1, 73–80. [Google Scholar]
- Björkqvist, J.V.; Pettersson, H.; Drennan, W.M.; Kahma, K.K. A New Inverse Phase Speed Spectrum of Nonlinear Gravity Wind Waves. J. Geophys. Res. Ocean. 2019, 124, 6097–6119. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Badulin, S.I.; Geogjaev, V.V.; Pushkarev, A.N. Weak-Turbulent Theory of Wind-Driven Sea. Earth Space Sci. 2019, 6, 540–556. [Google Scholar] [CrossRef]
- Semenov, E.; Sokolikhina, N.; Sokolikhina, E. Meteorological and synoptic aspects of the formation and evolution of the Novorossiysk Bora. Russ. Meteorol. Hydrol. 2013, 38, 661–668. [Google Scholar] [CrossRef]
- Kuharev, I.L. Relief. In Atlas of State Nature Reserve Utrish; Scientific Prossessings: Anapa, Russia, 2013; Volume 2, pp. 24–27. [Google Scholar]
- Tkachenko, Y.; Denisov, V. Climate. In Atlas of State Nature Reserve Utrish; Scientific Prossessings: Anapa, Russia, 2013; Volume 2, pp. 32–37. [Google Scholar]
- Banner, M.L.; Jones, I.S.F.; Trinders, J.C. Wavenumber spectra of short gravity waves. J. Fluid Mech. 1989, 198, 321–344. [Google Scholar] [CrossRef]
- Veselov, V.; Pribylskaya, I.; Mirzeabasov, O. All-Russia Research Institute of Hydrometeorological Information— World Data Center (RIHMI-WDC), Roshydromet. 2023. Available online: http://aisori-m.meteo.ru/waisori/ (accessed on 30 September 2022).
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.y.; Iredell, M.; et al. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Tolman, H.; Abdolali, A.; Accensi, M.; Alves, J.H.; Ardhuin, F.; Babanin, A.; Barbariol, F.; Benetazzo, A.; Bidlot, J. User Manual and System Documentation of WAVEWATCH III (R) Version 6.07; Technical Report 333; NOAA/NWS/NCEP/MMAB: Washington, DC, USA, 2019. [Google Scholar]
- Zieger, S.; Babanin, A.V.; Rogers, W.E.; Young, I.R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean. Model. 2015, 96, 2–25. [Google Scholar] [CrossRef]
- Hasselmann, S.; Hasselmann, K.; Allender, J.H.; Barnett, T.P. Computations and parametrizations of the nonlinear energy transfer in a gravity-wave spectrum. Part II. Parameterizations of the nonlinear energy transfer for application in wave models. J. Phys. Oceanogr. 1985, 15, 1378–1391. [Google Scholar] [CrossRef]
- Zelenko, A.; Strukov, B.; Resnyansky, Y.; Martynov, S.L. A system of wind wave forecasting in the World ocean and seas of Russia. In Zubov State Oceanographic Institute Proceedings; SOI: Moscow, Russia, 2014; pp. 90–101. [Google Scholar]
- Kirezci, C.; Ozyurt Tarakcıoglu, G. Validation of Wavewatch III Model in Black Sea Using Different Re-Analysis Wind Data. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016; Volume 2016, p. A43G-0336. [Google Scholar]
- Myslenkov, S.; Zelenko, A.; Resnyanskii, Y.; Arkhipkin, V.; Silvestrova, K. Quality of the wind wave forecast in the Black Sea including storm wave analysis. Sustainability 2021, 13, 13099. [Google Scholar] [CrossRef]
- Soran, M.B.; Amarouche, K.; Akpınar, A. Spatial calibration of WAVEWATCH III model against satellite observations using different input and dissipation parameterizations in the Black Sea. Ocean. Eng. 2022, 257, 111627. [Google Scholar] [CrossRef]
- Hasselmann, K. On the nonlinear energy transfer in a gravity wave spectrum. Part 1. General theory. J. Fluid Mech. 1962, 12, 481–500. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. The Interaction of Ocean Waves and Wind. Cambridge University Press: New York, NY, USA, 2004; 300p. [Google Scholar]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Donelan, M.A.; Hamilton, J.; Hui, W.H. Directional spectra of wind-generated waves. Phil. Trans. R. Soc. Lond. A 1985, 315, 509–562. [Google Scholar]
- Young, I.R. Wind Generated Ocean Waves; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Zakharov, V.E.; Filonenko, N.N. Energy spectrum for stochastic oscillations of the surface of a fluid. Soviet Phys. Dokl. 1966, 170, 1292–1295. [Google Scholar]
- Zakharov, V.E.; Zaslavsky, M.M. Shape of spectrum of energy carrying components of a water surface in the weak-turbulence theory of wind waves. Izv. Acad. Sci. USSR Atmos. Ocean. Phys. 1983, 19, 207–212. [Google Scholar]
- Pierson, W.J.; Moskowitz, L.A. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Toba, Y. Local balance in the air-sea boundary processes. Part I. On the growth process of wind waves. J. Oceanogr. Soc. Jpn. 1972, 28, 109–121. [Google Scholar] [CrossRef]
- Pushkarev, A.N.; Resio, D.; Zakharov, V.E. Weak turbulent approach to the wind-generated gravity sea waves. Phys. D Nonlinear Phenom. 2003, 184, 29–63. [Google Scholar] [CrossRef]
- Badulin, S.I.; Babanin, A.V.; Resio, D.; Zakharov, V. Weakly turbulent laws of wind-wave growth. J. Fluid Mech. 2007, 591, 339–378. [Google Scholar] [CrossRef]
- Gagnaire-Renou, E.; Benoit, M.; Badulin, S.I. On weakly turbulent scaling of wind sea in simulations of fetch-limited growth. J. Fluid Mech. 2011, 669, 178–213. [Google Scholar] [CrossRef]
- Badulin, S.I. Nonlinear Waves—2018; Collected Papers ABC of Wind-Driven Waves; Institute of Applied Physics, Russian Academy of Sciences: Nizhny Novgorod, Russia, 2019; pp. 121–141. (In Russian) [Google Scholar]
- Phillips, O. The equilibrium range in the spectrum of wind-generated waves. J. Fluid Mech. 1958, 4, 426–434. [Google Scholar] [CrossRef]
- Toba, Y. Local balance in the air-sea boundary processes: III. On the spectrum of wind waves. J. Oceanogr. Soc. Jpn. 1973, 29, 209–220. [Google Scholar] [CrossRef]
- Forristall, G.Z. Measurements of a saturated range in ocean wave spectra. J. Geophys. Res. 1981, 86, 8075–8084. [Google Scholar] [CrossRef]
- Kahma, K.K. A study of the growth of the wave spectrum with fetch. J. Phys. Oceanogr. 1981, 11, 1503–1515. [Google Scholar] [CrossRef]
- Battjes, J.A.; Zitman, T.J.; Holthuijsen, L.H. A reanalysis of the spectra observed in JONSWAP. J. Phys. Oceanogr. 1987, 17, 1288–1295. [Google Scholar] [CrossRef]
- Phillips, O.M. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 1985, 156, 505–531. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Lvov, V.S.; Falkovich, G. Kolmogorov Spectra of Turbulence. Part I; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Zakharov, V.E. Statistical theory of gravity and capillary waves on the surface of a finite-depth fluid. Eur. J. Mech. B Fluids 1999, 18, 327–344. [Google Scholar] [CrossRef]
- Zakharov, V.E. Energy balance in a wind-driven sea. Phys. Scr. 2010, T142, 014052. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Badulin, S.I. On Energy Balance in Wind-Driven Seas. Dokl. Earth Sci. 2011, 440, 1440–1444. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. USSR Acad. Sci. Russ. 1941, 30, 299–303. [Google Scholar]
- Geogjaev, V.V.; Zakharov, V.E. Numerical and analytical calculations of the parameters of power-law spectra for deep water gravity waves. JETP Lett. 2017, 106, 184–187. [Google Scholar] [CrossRef]
- Kats, A.V.; Kontorovich, V.M. Drift stationary solutions in the weak turbulence theory. JETP Lett. 1971, 14, 265–267. [Google Scholar]
- Zakharov, V.E.; Zaslavsky, M.M. Dependence of wave parameters on the wind velocity, duration of its action and fetch in the weak-turbulence theory of water waves. Izv. Acad. Sci. USSR. Atmos. Ocean. Phys. 1983, 19, 300–306. [Google Scholar]
- Badulin, S.I.; Geogdzhaev, V.V. Evaluation of wind wave growth parameters basing on spectral fluxes. Radiophys. Quantum Electron. 2019, 61, 545–552. [Google Scholar] [CrossRef]
- Kahma, K.K.; Pettersson, H. Wave growth in a narrow fetch geometry. Global Atmos. Ocean Syst. 1994, 2, 253–263. [Google Scholar]
- Pettersson, H. Wave Growth in a Narrow Bay. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2004. [Google Scholar]
- Young, I. R Directional spectra of hurricane wind waves. J. Geophys. Res. 2006, 111, C8. [Google Scholar] [CrossRef]
- Badulin, S.I.; Grigorieva, V.G. On discriminating swell and wind-driven seas in Voluntary Observing Ship data. J. Geophys. Res. 2012, 117, C11. [Google Scholar] [CrossRef]
- Toba, Y. Stochastic form of the growth of wind waves in a single-parameter representation with physical implementations. J. Phys. Oceanogr. 1978, 8, 494–507. [Google Scholar] [CrossRef]
- Kahma, K.K.; Calkoen, C.J. Reconciling discreapancies in the observed growth of wind-generated waves. J. Phys. Oceanogr. 1992, 22, 1389–1405. [Google Scholar] [CrossRef]
- Babanin, A.V.; Soloviev, Y.P. Field investigation of transformation of the wind wave frequency spectrum with fetch and the stage of development. J. Phys. Oceanogr. 1998, 28, 563–576. [Google Scholar] [CrossRef]
- Björkqvist1, J.V.; Alari, V. Real-time estimates of wind speed and direction from a small spherical wave buoy. In Proceedings of the 4th Workshop on Waves and Wave-Coupled Processes, Uppsala, Sweden, 14–16 February 2023. [Google Scholar]
- Resio, D.T.; Long, C.E.; Vincent, C.L. Equilibrium-range constant in wind-generated wave spectra. J. Geophys. Res. 2004, 109, C1. [Google Scholar] [CrossRef]
- Long, C.; Resio, D. Wind wave spectral observations in Currituck Sound, North Carolina. J. Geophys. Res. 2007, 112, C5. [Google Scholar] [CrossRef]
- Golitsyn, G.S. The Energy Cycle of Wind Waves on the Sea Surface. Izv. Atmos. Ocean. Phys. 2010, 46, 10–18. [Google Scholar] [CrossRef]
- Benilov, A.Y.; Kouznetsov, O.A.; Panin, G.N. On the analysis of wind wave-induced disturbances in the atmospheric turbulent surface layer. Bound.-Layer Meteorol. 1974, 6, 269–285. [Google Scholar] [CrossRef]
- Kahma, K.K. On prediction of the fetch-limited wave spectrum in a steady wind. Finn. Mar. Res. 1986, 253, 52–78. [Google Scholar]
- Babanin, A.V.; Soloviev, Y.P. Variability of directional spectra of wind-generated waves, studied by means of wave staff arrays. Mar. Freshwater Res. 1998, 49, 89–101. [Google Scholar] [CrossRef]



| Stage | Coord. | Depth, m | Fetch, m | Dates | Data Type | Number of Records |
|---|---|---|---|---|---|---|
| 1 | 44.7191 N, 37.4343 E | 18 | 600 | 31 January 2020–21 February 2020; 17 July 2020–2 October 2020; 27 October 2020–18 February 2021 | wave height, zero-crossing period, spectra | 11,143 |
| 2 | 44.716 N, 37.428 E | 42 | 1500 | 15 March 2021–17 June 2021 | wave height, zero-crossing period, spectra | 4569 |
| Wave Motion Sensor | Precision | 1–2 cm, all directions (1) |
| Periods | 1.6–20 s | |
| Wave data | Resolution | 1 cm (north 2 cm, LSB “north” is GPS data gap indicator) |
| Range | −20 ± 20 m | |
| Rate | 1.28 Hz | |
| Reference | WGS84 | |
| Spectral data | Frequency resolution | 0.005 Hz below 0.10 Hz and 0.010 Hz above frequency range 0.025–0.60 Hz |
| Direction resolution | ||
| Direction range | 0–360° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rybalko, A.; Myslenkov, S.; Badulin, S. Wave Buoy Measurements at Short Fetches in the Black Sea Nearshore: Mixed Sea and Energy Fluxes. Water 2023, 15, 1834. https://doi.org/10.3390/w15101834
Rybalko A, Myslenkov S, Badulin S. Wave Buoy Measurements at Short Fetches in the Black Sea Nearshore: Mixed Sea and Energy Fluxes. Water. 2023; 15(10):1834. https://doi.org/10.3390/w15101834
Chicago/Turabian StyleRybalko, Aleksandra, Stanislav Myslenkov, and Sergei Badulin. 2023. "Wave Buoy Measurements at Short Fetches in the Black Sea Nearshore: Mixed Sea and Energy Fluxes" Water 15, no. 10: 1834. https://doi.org/10.3390/w15101834







