A Preliminary Study of the Seepage Hammer Effect and Its Impacts on the Stability of Layered Infinite Slope
Abstract
:1. Introduction
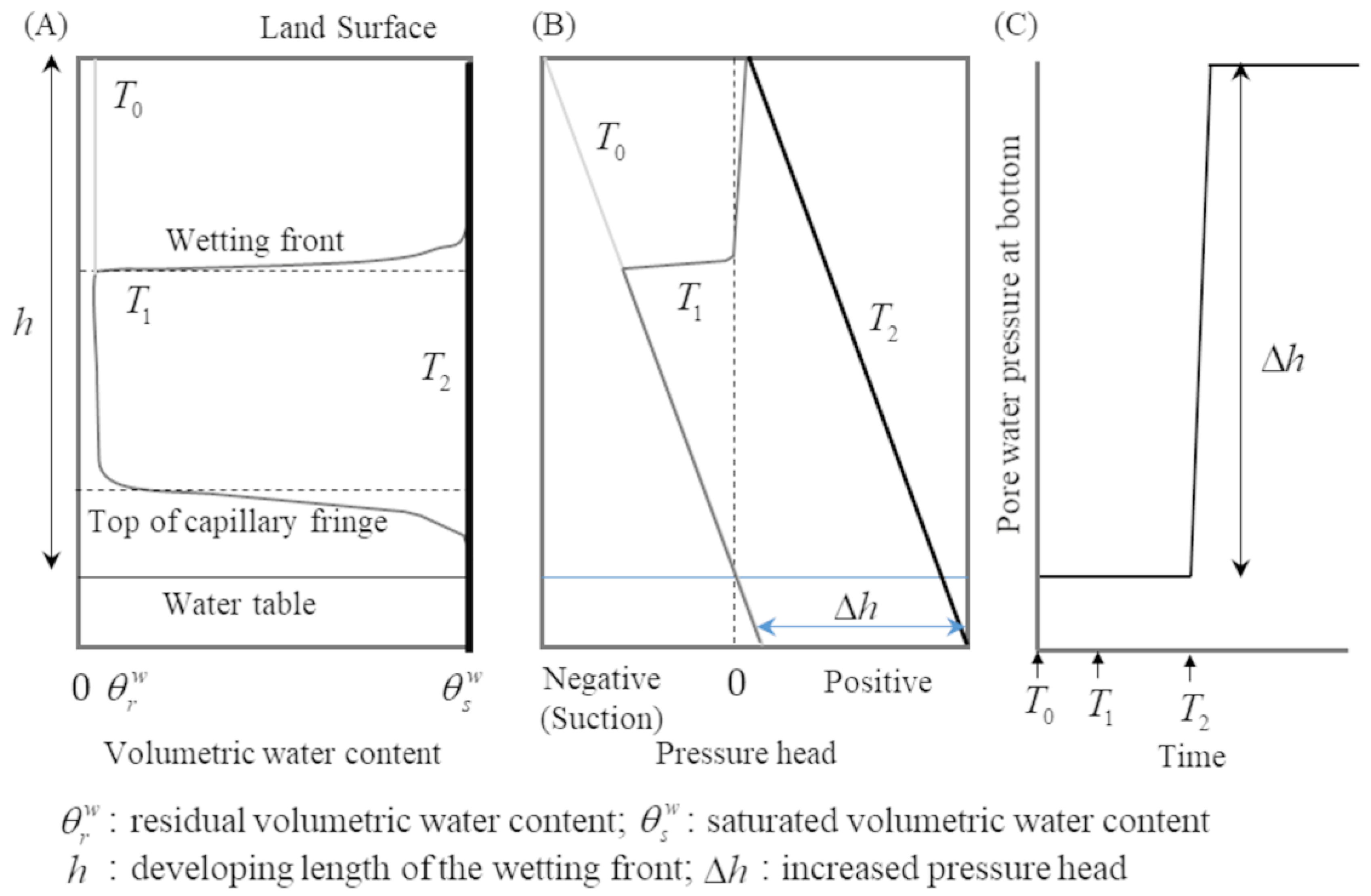
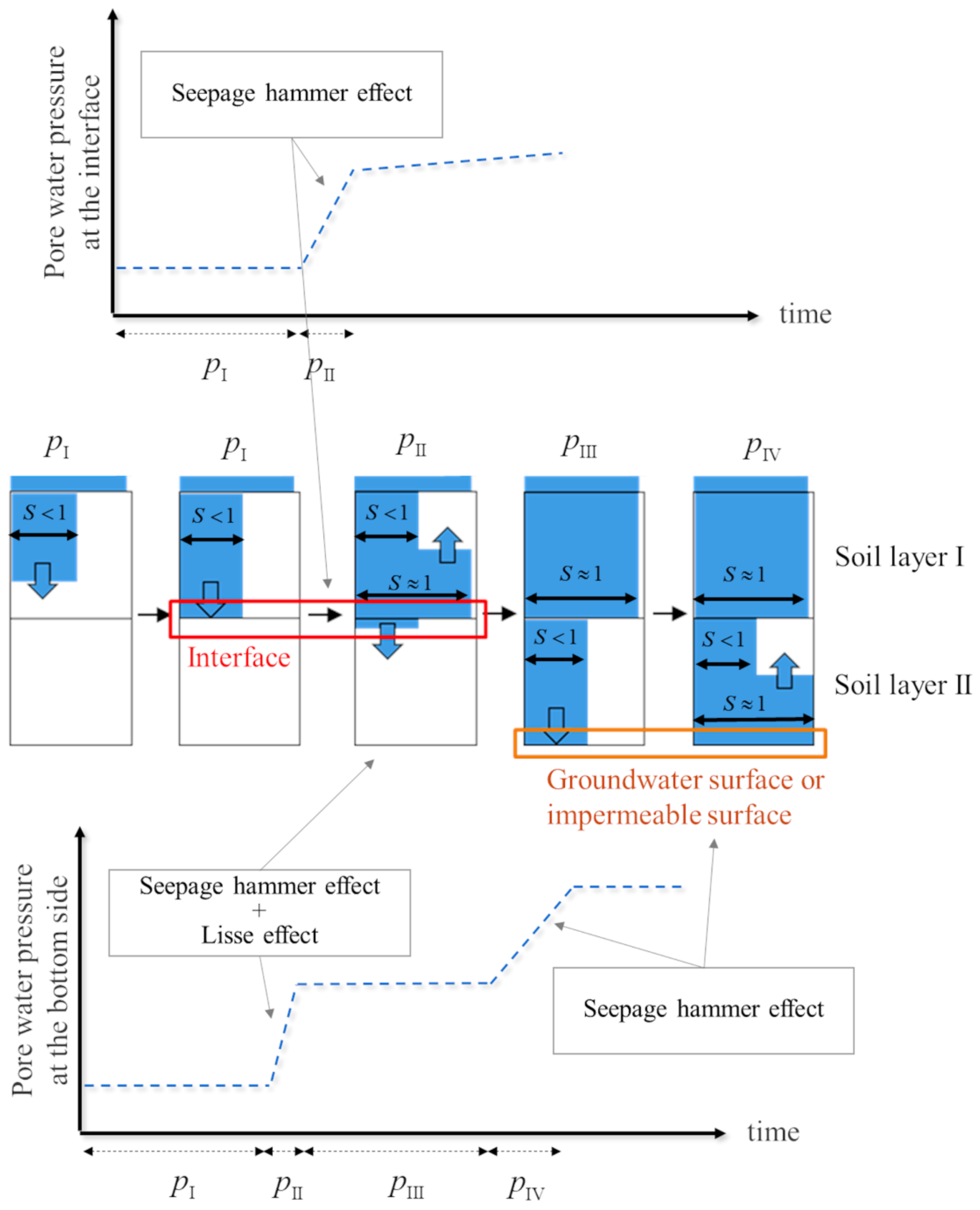
2. Concept of Seepage Hammer Effect
3. Column Test
3.1. Column Test and Experimental Installation
3.2. Experimental Results and Discussion
4. 1D Numerical Model
4.1. 1D Numerical Model and Numerical Implementation
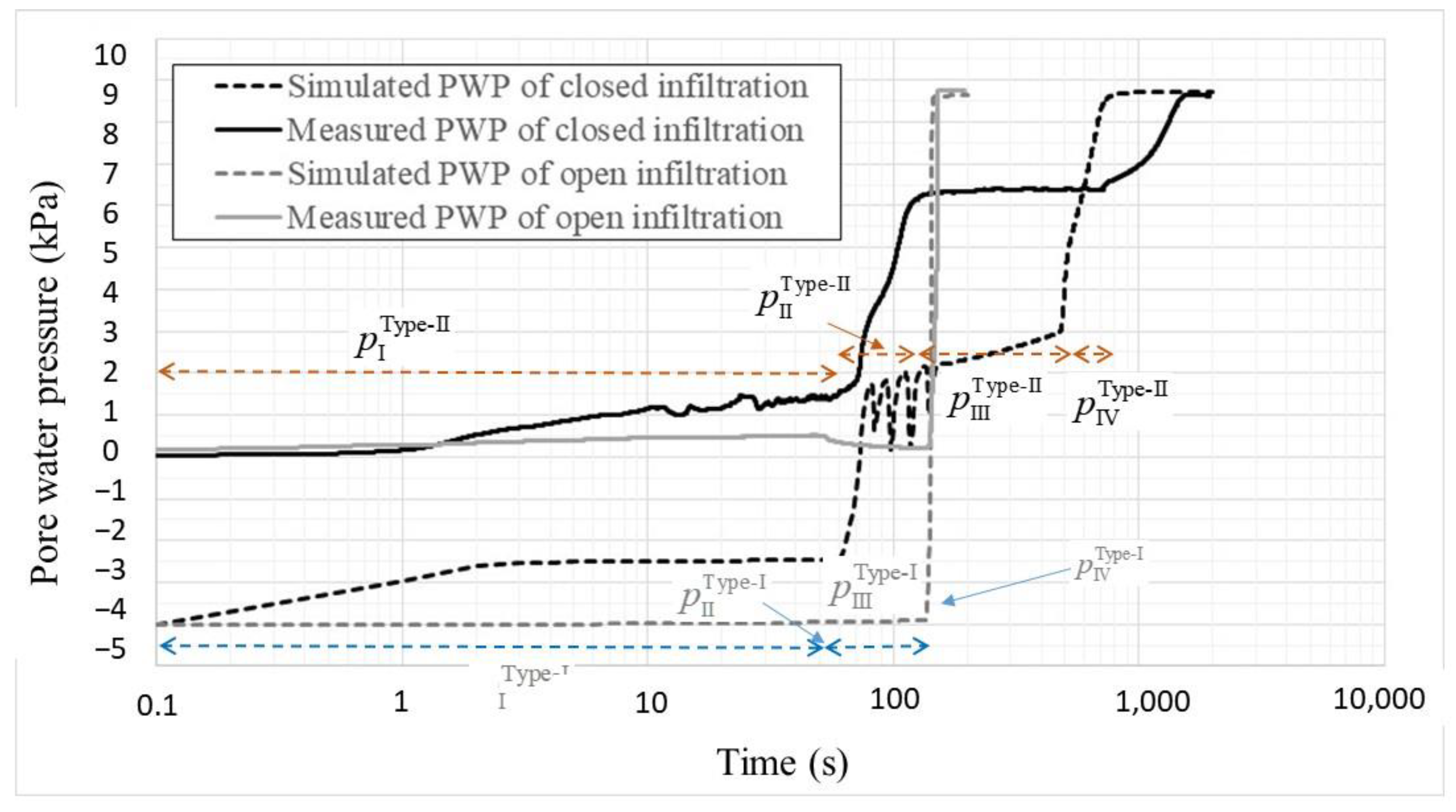
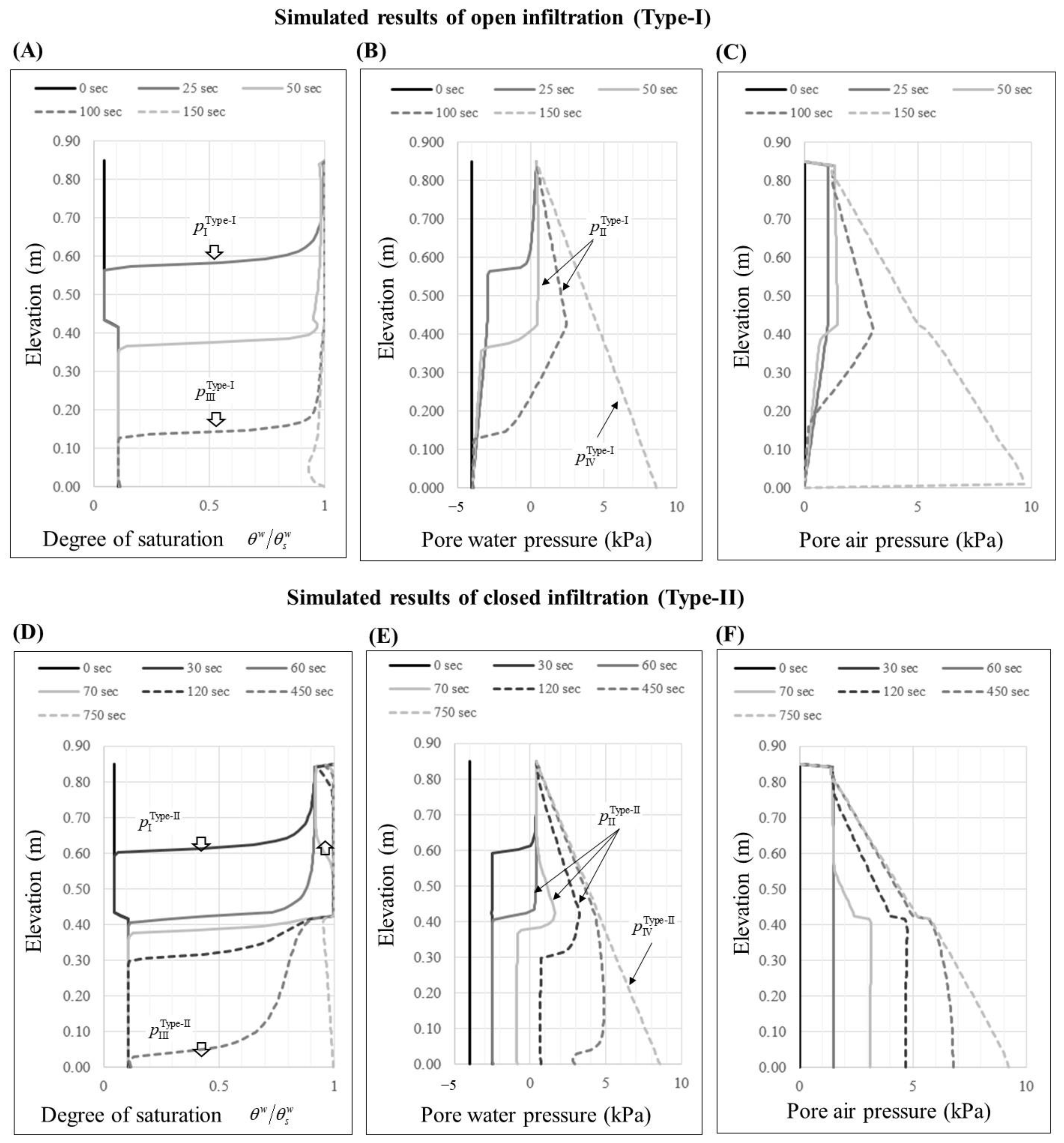
4.2. Simulated Results and Discussion
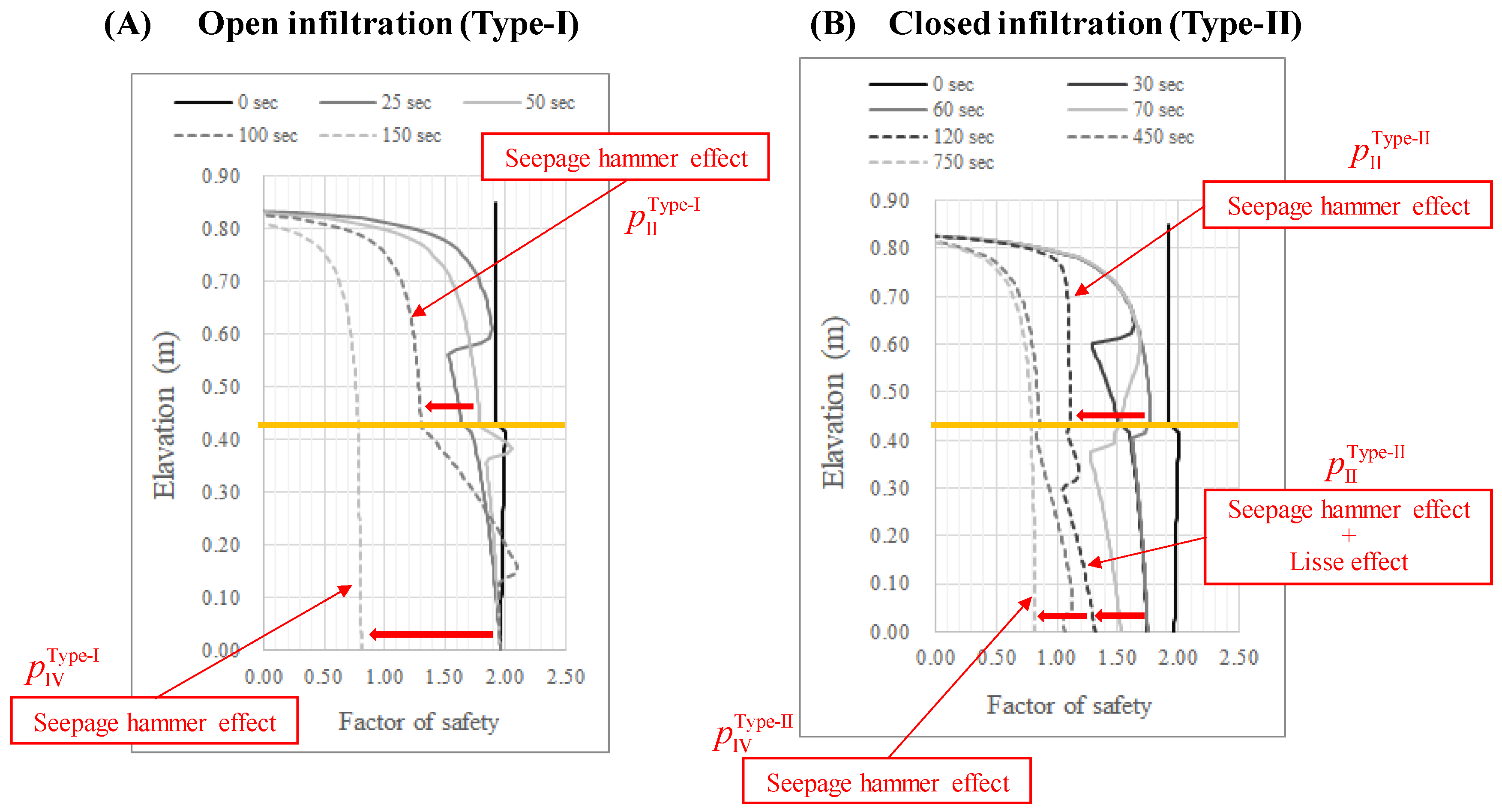
5. Impact of the Seepage Hammer Effect on Infinite Slope Stability
6. Conclusions
- This study proposed a new concept of the seepage hammer effect, which is a mechanism of rainfall-induced abnormal rising pore water pressure. It is triggered when the wetting front reaches the interface of multiple layers or impermeable layers. The increase in pore water pressure is proportional to the developing length of the wetting front. It is different from the Lisse effect and the reverse Wieringermeer effect;
- The intensity of the seepage hammer effect is affected by the soil properties and geological structure. The effect of the mechanical properties of soil is related to permeability. When the soil layer is highly permeable for water/air and the interstitial air can vent freely, the seepage hammer effect is intense and can trigger a sudden jump in pore water pressure. In the case of open infiltration, the pore water pressure jumped to the total water head of the soil column (0.89 m) in approximately 10 s. In contrast, if the pore air is trapped by infiltrated water and the air venting rate is small, then the seepage hammer effect becomes small and causes a gently rising pore water pressure. In the case of closed infiltration, the pore water pressure took more than 1000 s to reach the total water head of the soil column (0.89 m). In a geological structure that has two layers, an interesting finding is that the seepage hammer effect of the upper layer can be transmitted to the bottom of the lower layer with the help of the Lisse effect;
- The seepage hammer effect can weaken the slope stability significantly. The decrease in the safety factor is proportional to the intensity of the seepage hammer effect. In the case of open infiltration, the FS can be reduced from ca. 1.97 to ca. 0.81 in approximately 10 s. In contrast, in the case of closed infiltration, the same change of FS took more than 1000 s, and with two stages of decay. The relation between the change in the safety factor and the sliding velocity is positive, thus implying that an intense seepage hammer effect could possibly trigger a fast-moving landslide. Thus, the detection of geological structure and soil properties (i.e., interface layer, impermeable layer, hydraulic conductivity, etc.) could be a potential application in the investigation of potential fast-moving landslides;
- This paper presents preliminary research on the investigation of the seepage hammer effect and its impacts. Some limitations in this study should be improved in future work. For the column test, more sensors should be installed during the experiment to enhance the spatial resolution and measure other physical factors, i.e., volumetric water content and pore air pressure. These data are expected to improve the accuracy of the simulation. For the stability analysis, in reality, different types of slopes (convex slope, concave slope … etc.) require individual approaches, so 2D and 3D numerical modeling should be implemented to investigate general slope problems. Then, the potential application of the seepage hammer effect in landslide studies can be promoted.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lan, H.; Tian, N.; Li, L.; Wu, Y.; Macciotta, R.; Clague, J.J. Kinematic-based landslide risk management for the Sichuan-Tibet Grid Interconnection Project (STGIP) in China. Eng. Geol. 2022, 308, 106823. [Google Scholar] [CrossRef]
- Lan, H.; Zhang, Y.; Macciotta, R.; Li, L.; Wu, Y.; Bao, H.; Peng, J. The role of discontinuities in the susceptibility, development, and runout of rock avalanches: A review. Landslides 2022, 19, 1391–1404. [Google Scholar] [CrossRef]
- Miao, F.; Zhao, F.; Wu, Y.; Li, L.; Török, Á. Landslide susceptibility mapping in Three Gorges Reservoir area based on GIS and boosting decision tree model. Stoch. Environ. Res. Risk Assess. 2023, 1–21. [Google Scholar] [CrossRef]
- Miao, F.; Zhao, F.; Wu, Y.; Li, L.; Xue, Y.; Meng, J. A novel seepage device and ring-shear test on slip zone soils of landslide in the Three Gorges Reservoir area. Eng. Geol. 2022, 307, 106779. [Google Scholar] [CrossRef]
- Rahardjo, H.; Santoso, V.A.; Leong, E.C.; Ng, Y.S.; Hua, C.J. Numerical analyses and monitoring performance of residual soil slopes. Soils Found. 2011, 51, 471–482. [Google Scholar] [CrossRef]
- Touma, J.; Vauclin, M. Experimental and numerical analysis of two-phase infiltration in a partially saturated soil. Transp. Porous Med. 1986, 1, 27–55. [Google Scholar] [CrossRef]
- Weeks, E.P. The Lisse effect revisited. Groundwater 2002, 40, 652–656. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Infinite slope stability under steady unsaturated seepage conditions. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Kuang, X.; Jiao, J.J.; Li, H. Review on airflow in unsaturated zones induced by natural forcings. Water Resour. Res. 2013, 49, 6137–6165. [Google Scholar] [CrossRef]
- Duncan, J.M.; Wright, S.G.; Brandon, T.L. Soil Strength and Slope Stability; John Wiley & Sons: Hoboken, NJ, USA, 2014; Available online: http://refhub.elsevier.com/S2214-3912(22)00008-3/h0105 (accessed on 26 March 2020).
- Siemens, G.A.; Take, W.A.; Peters, S.B. Physical and numerical modeling of infiltration including consideration of the poreair phase. Can. Geotech. J. 2014, 51, 1475–1487. [Google Scholar] [CrossRef]
- Appels, W.M.; Bogaart, P.W.; van der Zee, S.E. Feedbacks between shallow ground-water dynamics and surface topography on runoff generation in flat fields. Water Resour. Res. 2017, 53, 10336–10353. [Google Scholar] [CrossRef]
- Lee, W.L.; Tai, Y.C.; Shieh, C.L.; Miyamoto, K.; Lin, Y.F. Hydro-mechanical response with respect to the air ventilation for water filtration in homogeneous soil. J. Mt. Sci. 2019, 16, 2562–2576. [Google Scholar] [CrossRef]
- Horton, R.E. An approach toward a physical interpretation of infiltration-capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Hu, R.; Chen, Y.; Zhou, C. Modeling of coupled deformation, water flow and gas transport in soil slopes subjected to rain infiltration. Sci. China Technol. Sci. 2011, 54, 2561–2575. [Google Scholar] [CrossRef]
- Cho, S.E. Stability analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration. Eng. Geol. 2016, 211, 184–197. [Google Scholar] [CrossRef]
- Kang, S.; Kim, B. Effects of coupled hydro-mechanical model considering dual-phase fluid flow on potential for shallow landslides at a regional scale. Nat. Hazards 2021, 1–29. [Google Scholar] [CrossRef]
- Rahardjo, H.; Lee, T.T.; Leong, E.C.; Rezaur, R.B. Response of a residual soil slope to rainfall. Can. Geotech. J. 2005, 42, 340–351. [Google Scholar] [CrossRef]
- Hooghoudt, S.B. Waarnemingen van grondwaterstanden voor de landbouw. In Verslagen Technische Bijeenkomsten; Scientific Report; Commissie voor hydrologisch onderzoek T.N.O.: Groningen, The Netherlands, 1952; Volume 1–6, pp. 94–110. Available online: https://library.wur.nl/WebQuery/hydrotheek/791175 (accessed on 26 March 2020). (In Dutch)
- Moriwaki, H.; Inokuchi, T.; Hattanji, T.; Sassa, K.; Ochiai, H.; Wang, G. Failure processes in a full-scale landslide experiment using a rainfall simulator. Landslides 2004, 1, 277–288. [Google Scholar] [CrossRef]
- Waswa, G.W.; Clulow, A.D.; Freese, C.; Le Roux, P.A.L.; Lorentz, S.A. Transient pressure waves in the vadose zone and the rapid water table response. Vadose Zone J. 2013, 12, 1–18. [Google Scholar] [CrossRef]
- Nachabe, M.H.; Sabeh, D. Infiltration in shallow water table environments: Simple two-phase model accounting for air compression and counter flow. J. Hydrol. Eng. 2015, 20, 04015013–04015016. [Google Scholar] [CrossRef]
- Lee, W.L.; Martinelli, M.; Shieh, C.L. An Investigation of Rainfall-Induced Landslides from the Pre-Failure Stage to the Post-Failure Stage Using the Material Point Method. Front. Earth Sci. 2021, 9, 764393. [Google Scholar] [CrossRef]
- Wang, Z.; Feyen, J.; Ritsema, C.J. Susceptibility and predictability of conditions for preferential flow. Water Resour. Res. 1998, 34, 2169–2182. [Google Scholar] [CrossRef]
- Wang, G.; Sassa, K. Pore-pressure generation and movement of rainfall-induced landslides: Effects of grain size and fine-particle content. Eng. Geol. 2003, 69, 109–125. [Google Scholar] [CrossRef]
- Lourenço, S.D.; Sassa, K.; Fukuoka, H. Failure process and hydrologic response of a two layer physical model: Implications for rainfall-induced landslides. Geomorphology 2006, 73, 115–130. [Google Scholar] [CrossRef]
- Gallage, C.; Abeykoon, T.; Uchimura, T. Instrumented model slopes to investigate the effects of slope inclination on rainfall-induced landslides. Soils Found. 2021, 61, 160–174. [Google Scholar] [CrossRef]
- Kitamura, R.; Sako, K. Contribution of “Soils and Foundations” to studies on rain-fall-induced slope failure. Soils Found. 2010, 50, 955–964. [Google Scholar] [CrossRef]
- Srivastava, A.; Babu, G.S.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Saada, Z.; Maghous, S.; Garnier, D. Stability analysis of rock slopes subjected to seepage forces using the modified Hoek–Brown criterion. Int. J. Rock Mech. Min. Sci. 2012, 55, 45–54. [Google Scholar] [CrossRef]
- SOCIETE NOUVELLE DU LITTORAL. Available online: https://www.standard-sand.com/en/category/products/ (accessed on 26 March 2020).
- Wyckoff, R.D.; Botset, H.G. The flow of gas-liquid mixtures through unconsolidated sands. Physics 1936, 7, 325–345. [Google Scholar] [CrossRef]
- Goetz, R.O. Investigation into Using Air in the Permeability Testing of Granular Soils; Technical Report; The University of Michigan: Ann Arbor, MI, USA, 1971; Available online: https://deepblue.lib.umich.edu/bitstream/handle/2027.42/5147/bac3009.0001.001.pdf?sequence=5 (accessed on 26 March 2020).
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Sweijen, T.; Aslannejad, H.; Hassanizadeh, S.M. Capillary pressure–saturation relationships for porous granular materials: Pore morphology method vs. pore unit assembly method. Adv. Water Resour. 2017, 107, 22–31. [Google Scholar] [CrossRef]
- Amankwah, S.K.; Ireson, A.M.; Maulé, C.; Brannen, R.; Mathias, S.A. A Model for the Soil Freezing Characteristic Curve That Represents the Dominant Role of Salt Exclusion. Water Resour. Res. 2021, 57, e2021WR030070. [Google Scholar] [CrossRef]
- Siemens, G.A. Thirty-Ninth Canadian Geotechnical Colloquium: Unsaturated soil mechanics—Bridging the gap between research and practice. Can. Geotech. J. 2018, 55, 909–927. [Google Scholar] [CrossRef]
- Vulliet, L.; Hutter, K. Viscous-type sliding laws for landslides. Can. Geotech. J. 1988, 25, 467–477. [Google Scholar] [CrossRef]
- Take, W.A.; Bolton, M.D.; Wong, P.C.P.; Yeung, F.J. Evaluation of landslide triggering mechanisms in model fill slopes. Landslides 2004, 1, 173–184. [Google Scholar] [CrossRef]
- Padilla, C.; Onda, Y.; Iida, T.; Takahashi, S.; Uchida, T. Characterization of the groundwater response to rainfall on a hillslope with fractured bedrock by creep deformation and its implication for the generation of deep-seated landslides on Mt. Wanitsuka, Kyushu Island. Geomorphology 2014, 204, 444–458. [Google Scholar] [CrossRef]
- Wu, J.H.; Chen, J.H.; Lu, C.W. Investigation of the Hsien-du-Shan rock avalanche caused by typhoon Morakot in 2009 at Kaohsiung county, Taiwan. Int. J. Rock Mech. Min. Sci. 2013, 60, 148–159. [Google Scholar] [CrossRef]
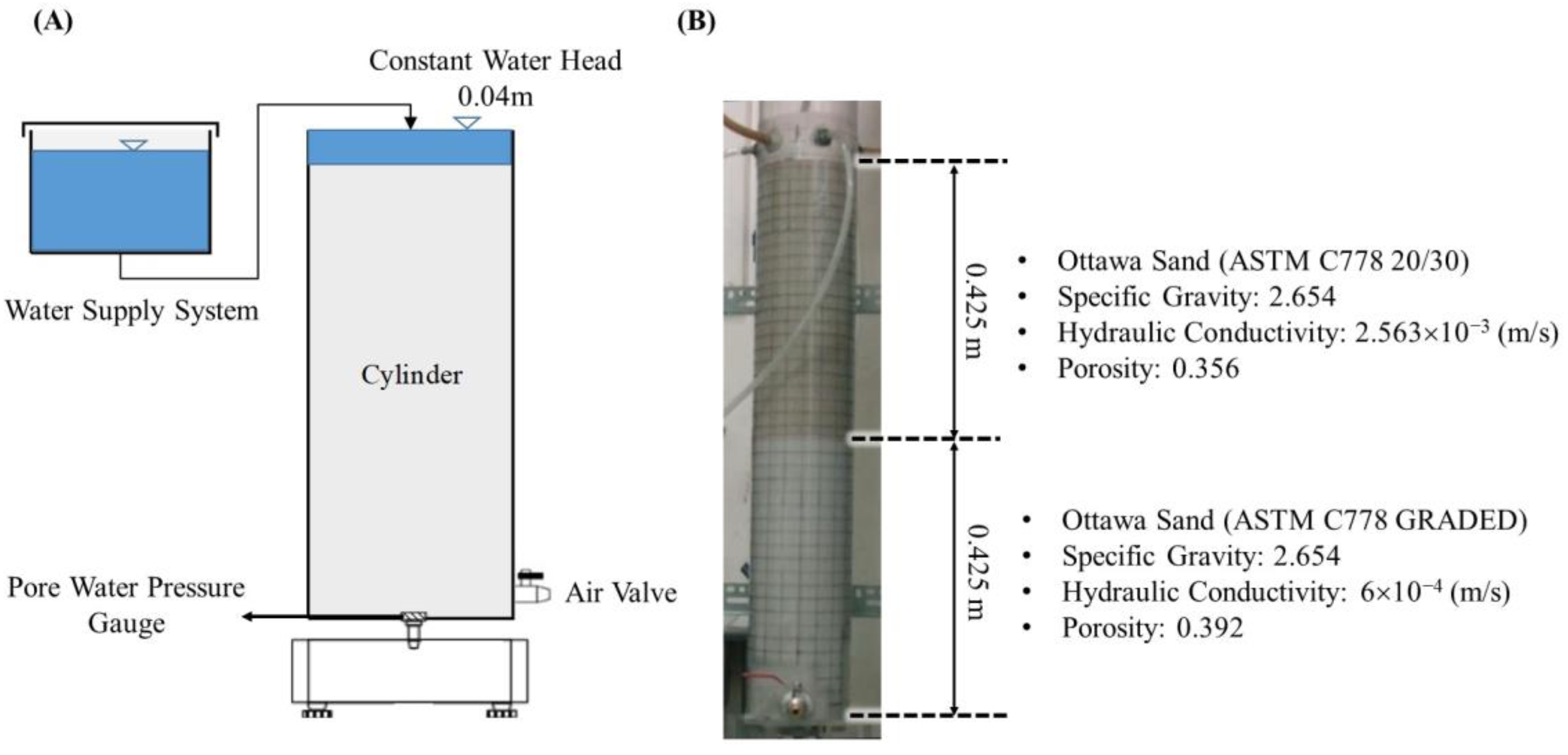



| Material Parameters | Upper Layer (ASTM C778 20/30) | Lower Layer (ASTM C778 GRADED) |
|---|---|---|
| Residual volumetric water content (m3/m3) | 0.016 | 0.018 |
| Saturated volumetric water content (m3/m3) | 0.356 | 0.392 |
| Fitting parameter (kPa) | 1.364 | 2.045 |
| Fitting parameter | 8.9 | 5 |
| Fitting parameter | 0.89 | 0.8 |
| Saturated hydraulic conductivity (m/s) | 2.563 × 10−3 | 6 × 10−4 |
| Air conductivity in the dry condition (m/s) | 7 × 10−2 | 1.5 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.-L.; Tai, Y.-C.; Shieh, C.-L.; Lu, C.-W. A Preliminary Study of the Seepage Hammer Effect and Its Impacts on the Stability of Layered Infinite Slope. Water 2023, 15, 1832. https://doi.org/10.3390/w15101832
Lee W-L, Tai Y-C, Shieh C-L, Lu C-W. A Preliminary Study of the Seepage Hammer Effect and Its Impacts on the Stability of Layered Infinite Slope. Water. 2023; 15(10):1832. https://doi.org/10.3390/w15101832
Chicago/Turabian StyleLee, Wei-Lin, Yih-Chin Tai, Chjeng-Lun Shieh, and Chih-Wei Lu. 2023. "A Preliminary Study of the Seepage Hammer Effect and Its Impacts on the Stability of Layered Infinite Slope" Water 15, no. 10: 1832. https://doi.org/10.3390/w15101832






