Monte Carlo Simulation Approach to Shipping Accidents Consequences Assessment
Abstract
1. Introduction
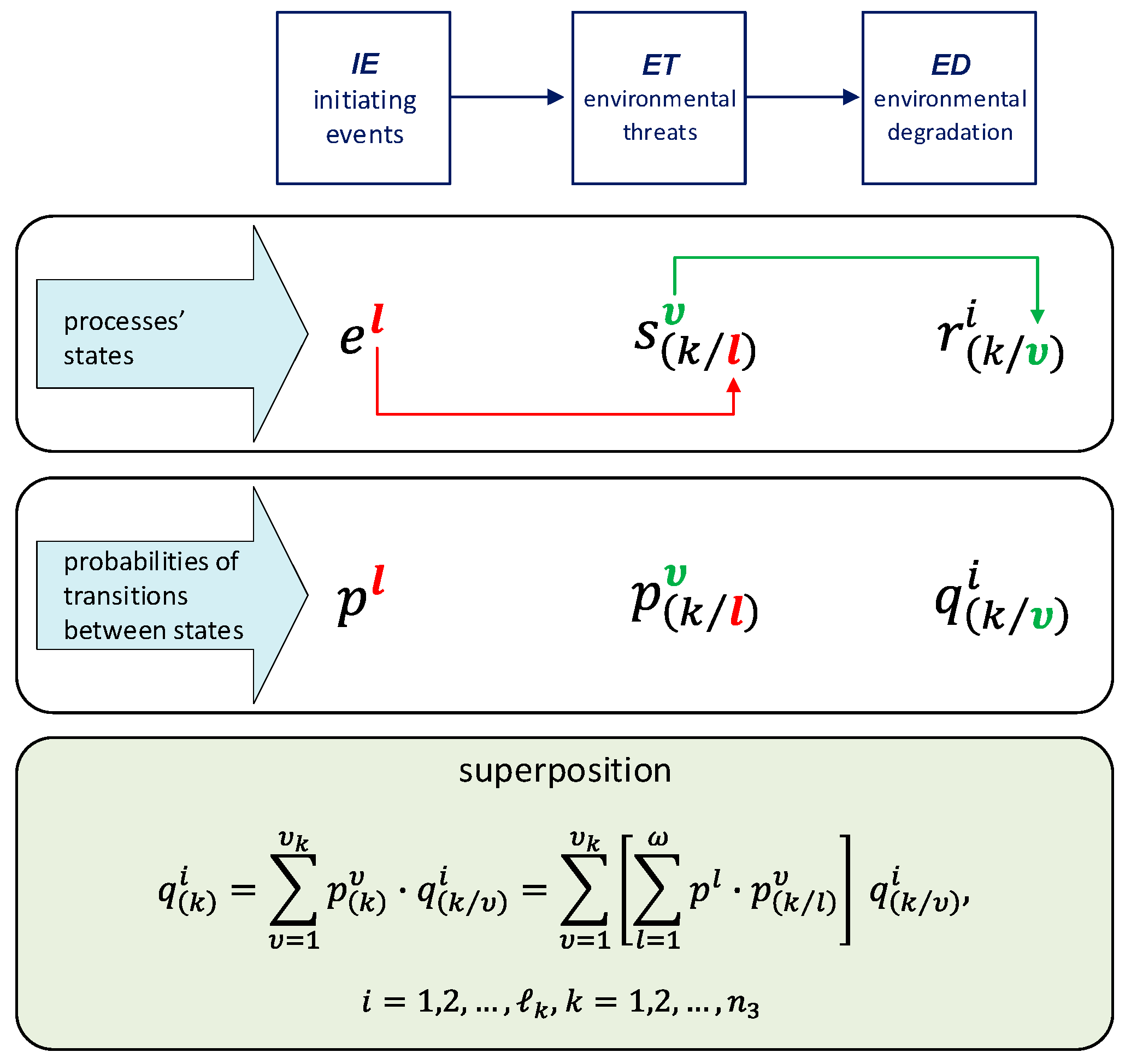
2. Materials and Methods
- the process of initiating events (IE) generated by a critical infrastructure accident;
- the process of environmental threats (ET) coming from dangerous situations in the critical infrastructure operating area that are a result of IE;
- the process of environmental degradation (ED) as a result of environmental threats (ET).
2.1. General Model of Shipping Accident and Chemical Release Consequences
- the process of IE generated by a shipping critical infrastructure accident;
- the ET process stemming from released chemicals that are a result of IE;
- the ED process as a result of ET.
2.1.1. Process of Initiating Events (IE)
- the number where , of events initiating a dangerous situation for the ship operating in the specific environment;
- kinds of IE:
- the number of IE states
- IE states where ,
- the process of IE: with states from the set
- the probabilities of transitions between the different states and
- random conditional sojourn times at the state while the next transition will be performed for the different state
- the conditional distribution functions of at the state while the next transition will be performed for the state
- the limit transient probabilities of the probabilities remaining at the states ;
- the mean values of the sojourn total times in the time interval at particular states .
2.1.2. Process of Environmental Threats (ET)
- the number where , of kinds of threats that may cause environmental degradation;
- kinds of environmental threats: ;
- factors characterising the environmental threats;
- the number , where , , of factors’ values ranges;
- ranges of factors’ values;
- the number where of environment sub-areas;
- environment sub-areas of the ship operating within the environment area that may be degraded by the environmental threats;
- the conditional process of ET in the subarea , while the process of IE is at the state ;
- the process of ET in the sub-area ;
- the number of ET states of the sub-area;
- ET states where , , , for ;
- the probabilities of transitions between the different states and ;
- random conditional sojourn times at the state while the next transition will be performed for the different state ;
- the conditional distribution functions of at the state while the next transition will be performed for the state
- the limit transient probabilities of the probabilities remaining at the states ;
- the mean values of the sojourn total times in the time interval at particular states .
- the limit transient probabilities of the probabilities remaining at the states are given bywhere and are mentioned earlier.
2.1.3. Process of Environmental Degradation (ED)
- the number where , of dangerous degradation effects for the environment subarea ;
- degradation effects ;
- states of the degradation effect , which are the levels , ;
- the number , , of degradation effect levels;
- the number of ED states of the sub-area;
- ED states in the sub-area, where , ;
- ED states in the sub-area, when some of the states cannot occur, where , , for ;
- the conditional process of ED in the sub-area , , while the process of environmental threats is at the state and having values in the environmental degradation states set;
- the process of ED in the sub-area , involved with the process of environmental threats ;
- the probabilities of transitions between the different states and ;
- random conditional sojourn times at the state while the next transition will be performed for the different state ;
- the conditional distribution functions of at the state while the next transition will be performed for the state
- the limit transient probabilities of the probabilities remaining at the states ;
- the mean values of the sojourn total times in the time interval at particular states .
- the limit transient probabilities of the probabilities remaining at the states , given bywhere and are mentioned earlier.
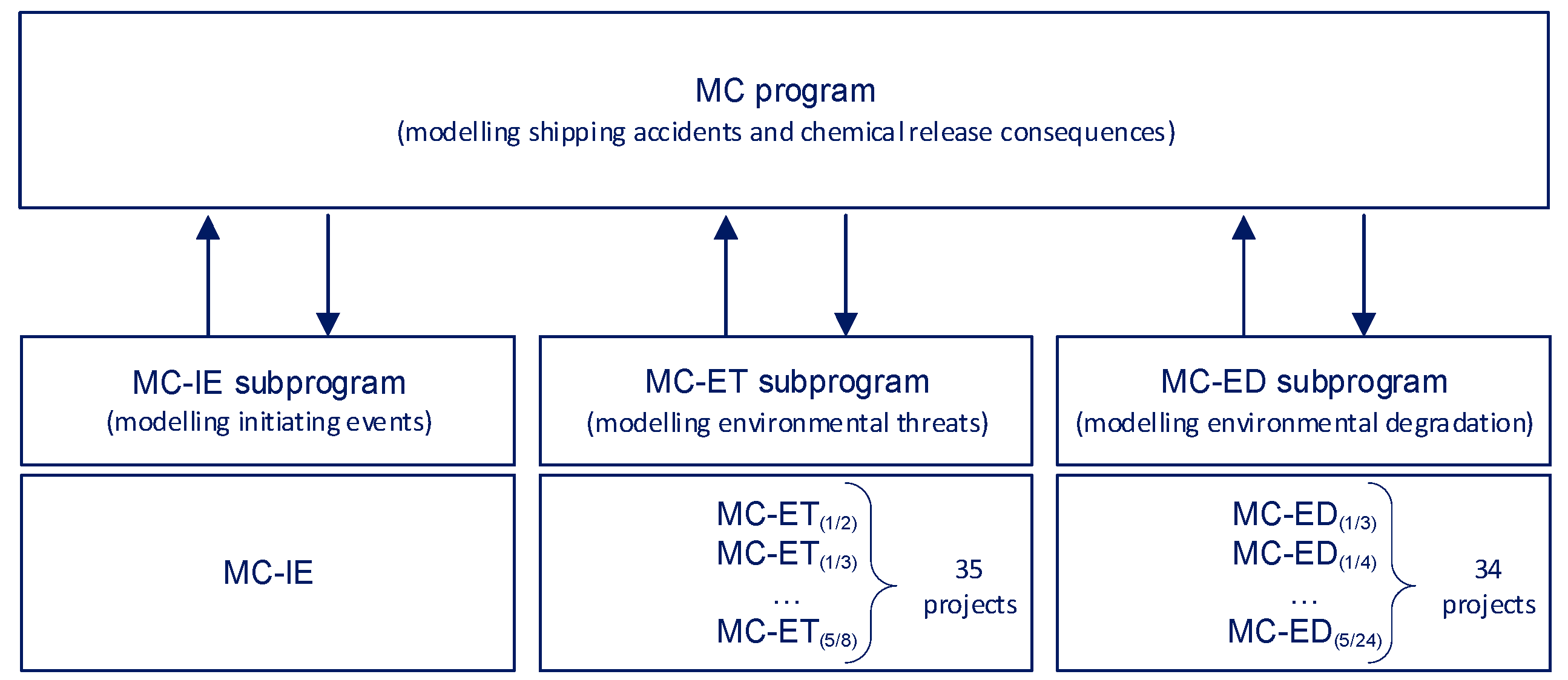
2.2. Monte Carlo Simulation-Based General Model of Shipping Accident and Chemical Release Consequences
2.2.1. Generating Processes’ Basic Parameters
2.2.2. Monte Carlo Simulation Procedure for Processes’ Characteristics Determination
- Draw a randomly generated number from the uniform distribution on the interval (0,1〉;
- Select the initial state , , according to (3);
- Draw another randomly generated number from the uniform distribution on the interval (0,1〉;
- For the fixed , select the next state , , , according to (4);
- Draw a randomly generated number from the uniform distribution on the interval (0,1〉;
- For the fixed and , generate a realization , of the conditional sojourn time , from a given probability distribution, according to (5);
- Substitute and repeat 3.–6., until the sum of all generated realizations reaches a fixed experiment time ;
- Calculate total sojourn times at the states , according to (7);
- Calculate limit transient probabilities at the particular states , according to (8);
- Calculate unconditional mean sojourn times at the states , according to (10);
- Calculate mean values of the total sojourn times at the states , during the fixed time , according to (11).
2.3. Sources of Real Data
3. Results
3.1. Modelling Shipping Accident Consequences
3.1.1. Modelling the Process of IE
- —collision;
- —grounding;
- —contact with an external object;
- —fire or explosion on a board;
- —shipping without control (drifting, or missing ship);
- —capsizing or listing of a ship;
- —movement of cargo in a ship.
3.1.2. Modelling the Conditional ET Process
- —explosion of a chemical substance;
- —fire due to a chemical substance;
- —toxic substance presence;
- —corrosive substance presence;
- —bio-accumulative substance presence;
- —other dangerous chemical substances presence.
- —explosiveness of the chemical substance causing the explosion (based on the classification of the International Maritime Dangerous Goods Code—IMDG [55]; explosives belong to class 1 of IMDG), 6;
- —flashpoint (the lowest temperature creating a sufficient amount of vapour to lead to the fire) of the chemical substance causing the fire, 4;
- —toxicity (defined by the average lethal concentration—LC50—the concentration that is lethal for 50% of the exposed organisms) of the chemical substance, 6;
- —time of causing skin necrosis by the corrosive substance, 3;
- —ability of the chemical substance to bioaccumulate in living organisms (defined by logP that points the substance’s ability to dissolve in water and nonpolar solvents), 5;
- —ability of the chemical substance to cause other threats, specially long-term, such as carcinogenic, reprotoxic, teratogenic, 1.
- —air;
- —water surface;
- —water column;
- —sea floor;
- —coast.
3.1.3. Modelling the Conditional ED Process
- —increase of temperature;
- —decrease in oxygen concentration;
- —disturbance of pH regime;
- —aesthetic nuisance;
- —pollution.
3.2. Statistical Identification of Processes
3.3. Sensitivity Analysis and Potential Limitations of the Methodology
3.3.1. A Step-by-Step Guide to Sensitivity Analysis in Simulation-Based Methods
- Identification of the input variables: The first step is to identify the input variables that are used in the simulation-based method. These are the variables that are randomly sampled during the simulation, as well as those which are fixed.
- Definition of the ranges for input variables: for each input variable, a range of values is defined over which it can vary.
- Run of the simulation: the Monte Carlo simulation is run multiple times, each time using a different set of randomly sampled input variables within their defined ranges [56].
- Analyzing the results: after running the simulation multiple times, the analysis of the results was performed to identify which input variables had the greatest impact on the output.
- Performing additional analyses (optional): Depending on the results of the sensitivity analysis (point 4), additional analyses may be necessary to further investigate the relationships between input variables and output. For example, regression analysis can be performed to identify nonlinear relationships, or the results can be plotted to identify any trends or patterns.
- Adjusting the model: based on the results of the sensitivity analysis, the model may need to be adjusted to better reflect the real-world situation being modeled. This could involve changing the input ranges, adding or removing input variables, or adjusting the weighting of input variables in the model.
3.3.2. Identifying Input Variables and Analysing Simulation Results for the IE Process
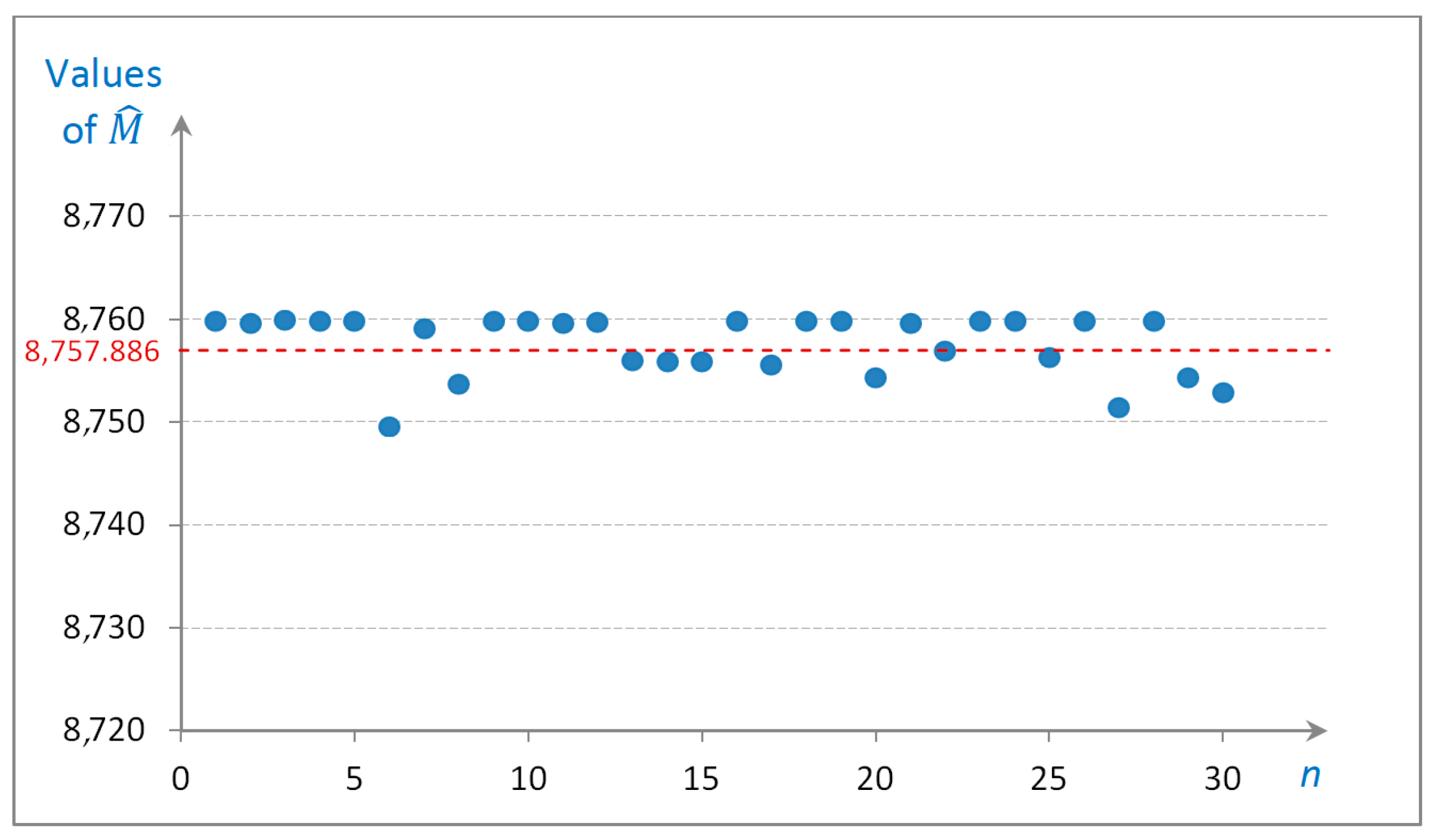
- The input variables identification.After consultation with experts from the Maritime Search and Rescue Service, Gdynia, Poland, selected key variables were assumed that can affect the outcome of the simulation: fixed experiment time (affecting the number of simulation iterations), initial probabilities (assumed), probabilities of transitions between the states (calculated from the historical numbers of transitions) and distribution functions (verified statistically). The experiment time is the same for all program projects and was designated on the basis of the simulation convergence. An exemplary illustration is shown in Figure 3.There is only one simplification in the model, i.e., the initial probabilities are assumed in a way in which no initiating events happen at t = 0 (all probabilities are equal to 0 at a starting point). This assumption cannot be changed. Table A5 in Appendix C determines the probabilities of transitions. These input parameters should be randomly sampled from the same matrix that was used to generate the original input parameters, as they are calculated from the historical data. Moreover, the hypotheses on the distribution functions of the realizations of the conditional sojourn times were verified on the basis of the sufficiently large number of realizations, and the empirical distribution functions were determined for numbers of realizations less than 30. This assumption is necessary from the statistical point of view.
- The ranges for input variables statement.The generating functions for input parameters remain the same for the input variables and, for this simulation method, they sufficiently reflect the expected variability of the real-world situation being modeled.
- The simulation run.The Monte Carlo simulation is run 30 times, each time using a different set of randomly sampled input variables, for a large number of iterations in order to ensure that the results are statistically significant. The simulation time is equal to 25 years and, therefore, the number of iterations is different for each simulation run, depending on the sojourn times.
- The results analysis.The statistical measures of interest for the outputs, such as the means and standard deviations, are calculated. These measures can provide an overall understanding of the behavior of the output variables.
- Additional analysis.The relationships between the input and output variables have been sufficiently investigated and no further investigation is needed.
- The model adjustments.The model can be adjusted using the results of the sensitivity analysis. However, it is also possible to evaluate the significance of the remaining two (simulating successively 35 and then 34 projects). That is why, it is still possible to analyse the sensitivity of the overall output globally to variations in each sub-program.
3.3.3. Limitations and Weaknesses of the Monte Carlo Method
- Accuracy depends on the quality of the model: the accuracy of the results obtained depends on the quality of the model used to represent the problem regarding ship accident consequences being analyzed. If the model is oversimplified or does not capture all the important features, the results may not be accurate. Mostly, the accuracy of the model is limited by the accuracy of the input data used. Inaccurate or incomplete data can lead to inaccurate results.
- Computationally intensive: Monte Carlo simulations can be computationally intensive and require a large number of random samples to obtain accurate results. This is a limitation when dealing with a complex problem that requires a significant amount of computational resources. It can lead to long simulation times and high computing costs.
- Uncertainty: simulation-based models are inherently probabilistic, meaning that there is always a degree of uncertainty in the results. This uncertainty can be difficult to quantify and communicate to stakeholders.
- Difficulty in modelling human factors: the method is less effective at modelling the impact of human factors, such as operator error, which can play a significant role in the occurrence and severity of accidents.
- Convergence issues: the convergence of a Monte Carlo simulation can be slow, especially when dealing with systems that exhibit rare events. This can make it difficult to obtain accurate results in a reasonable amount of time. The model is less effective for dealing with rare events, such as major chemical spills or catastrophic accidents, when the degradation effects listed in Table 2 reach high levels of their parameters, or accidents lead to the release of less frequently transported substances, especially those other than oil, due to the low probability of these events occurring (see results given in Section 3.5).
- Requires distributional assumptions: Monte Carlo simulations rely on the assumption that the input variables have statistically verified distributions. This can be a limitation when dealing with a problem in which distribution functions do not fit to any of the known functions.
3.3.4. Additional Limitations of the Model
3.3.5. Justification of the Programming Language Used
3.4. Prediction of Shipping Accident Consequences
3.4.1. Prediction of the IE Process
3.4.2. Prediction of the Conditional ET Process
3.4.3. Prediction of the Conditional ED Process
3.5. Joint IE Process, ET Process and ED Process—Superposition
4. Discussion
- within the air subarea: reaches the value of the transient probability equals to 0.00033, which means that this state lasts 2.9 h per a year (Figure 5);
- within the water surface subarea: reaches the value of the transient probability equals to 0.00024, which means that this state lasts 2.1 h per a year (Figure 6);
- within the water column subarea: and reach the value of the transient probabilities equal to 0.00024 and 0.00006 respectively, which means that these states lasts 2.1 and 0.5 h per a year (Figure 7);
- within the sea floor subarea: and reach the value of the transient probabilities equal to 0.00004 and 0.00023 respectively, which means that these states last 0.4 and 2.0 h per a year (Figure 8);
- within the coast subarea: and reach the value of the transient probabilities equal to 0.00019, 0.00007 and 0.00008 respectively, which means that these states last 1.7, 0.6 and 0.7 h per year (Figure 9).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Description |
|---|---|
| IE | process of initiating events generated by a shipping critical infrastructure accident |
| ET | process of environmental threats coming from released chemicals that are a result of IE |
| ED | process of environmental degradation as a result of ET |
| realization of the process’ initial state at the moment t = 0 | |
| w | number of process’ states |
| random conditional sojourn times of a process at state when its next state is | |
| realization of the conditional sojourn time of a process | |
| experiment time | |
| number of sojourn time realizations during the time | |
| conditional distribution function of conditional sojourn time | |
| inverse function of distribution function | |
| g, h | randomly generated numbers from the interval 〈0,1) |
| vector of initial probabilities of a process at initial state | |
| matrix of probabilities of transitions of a process between states and | |
| transient probability of a process at state at the moment t | |
| limit value of a transient probability | |
| unconditional sojourn time of a process at state | |
| mean value of unconditional sojourn time at state | |
| fixed time, e.g., 1 year to illustrate the results | |
| total sojourn time at state , during the fixed time | |
| mean value of total sojourn time at state during the fixed time | |
| number of simulation iterations | |
| relative error between simulation and analytical expected values |
Appendix B
| IE State | Type of IE * | ||||||
|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | E4 | E5 | E6 | E7 | |
| e1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| e2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| e3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| e4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| e5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| e6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| e7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| e8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| e9 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| e10 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| e11 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| e12 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| e13 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| e14 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| e15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| e16 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Subarea | ||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Air | Water Surface | Water Column | Sea Floor | Coast | ||||||||||||||||||||||||||||||
| ET State | Type of ET * | ET State | Type of ET* | ET State | Type of ET * | ET State | Type of ET * | ET State | Type of ET * | |||||||||||||||||||||||||
| H1 | H2 | H3 | H4 | H5 | H6 | H1 | H2 | H3 | H4 | H5 | H6 | H1 | H2 | H3 | H4 | H5 | H6 | H1 | H2 | H3 | H4 | H5 | H6 | H1 | H2 | H3 | H4 | H5 | H6 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |||||
| 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | |||||
| 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | |||||
| 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | |||||
| 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | |||||
| 0 | 0 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |||||
| 0 | 0 | 4 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | |||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 0 | |||||
| 0 | 0 | 0 | 2 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 1 | |||||
| 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | |||||
| 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | |||||
| 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | |||||
| 0 | 0 | 1 | 3 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | |||||
| 0 | 0 | 2 | 3 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | 3 | 0 | 0 | 1 | |||||
| 0 | 2 | 3 | 0 | 0 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | |||||
| 0 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 3 | 0 | |||||
| 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 | 3 | 1 | 0 | 0 | |||||
| 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 | 3 | 0 | 2 | 1 | 0 | 0 | 4 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 0 | 1 | |||||
| 0 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | |||||
| 0 | 0 | 3 | 2 | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 1 | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 0 | 2 | 0 | 1 | 1 | |||||
| 0 | 0 | 4 | 0 | 1 | 0 | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 | |||||
| 0 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 3 | 2 | 2 | 0 | 0 | 0 | 2 | 0 | 3 | 1 | 0 | 0 | 2 | 0 | 3 | 1 | 0 | 0 | 2 | 0 | 3 | 1 | |||||
| 0 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 0 | 0 | 0 | 3 | 0 | 2 | 1 | 0 | 0 | 3 | 0 | 2 | 1 | 0 | 0 | 3 | 0 | 2 | 1 | |||||
| 0 | 0 | 2 | 0 | 1 | 1 | 0 | 0 | 4 | 2 | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 1 | 0 | 0 | 3 | 0 | 3 | 1 | 0 | 0 | 3 | 0 | 3 | 1 | |||||
| 0 | 0 | 2 | 0 | 3 | 1 | 0 | 0 | 5 | 0 | 5 | 1 | 0 | 0 | 3 | 2 | 2 | 0 | 0 | 0 | 3 | 2 | 2 | 0 | 0 | 0 | 3 | 2 | 2 | 0 | |||||
| 0 | 0 | 3 | 1 | 0 | 1 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 0 | 0 | 0 | 3 | 2 | 3 | 0 | 0 | 0 | 3 | 2 | 3 | 0 | |||||
| 0 | 0 | 3 | 2 | 3 | 0 | 0 | 0 | 1 | 3 | 0 | 0 | 0 | 0 | 5 | 0 | 5 | 1 | 0 | 0 | 5 | 0 | 5 | 1 | 0 | 0 | 5 | 0 | 5 | 1 | |||||
| 0 | 0 | 4 | 3 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 1 | |||||||||||||||||||||||
| 0 | 0 | 4 | 0 | 1 | 1 | 0 | 0 | 2 | 0 | 1 | 1 | |||||||||||||||||||||||
| 0 | 0 | 4 | 0 | 5 | 1 | 0 | 0 | 2 | 3 | 0 | 0 | |||||||||||||||||||||||
| 0 | 0 | 4 | 2 | 2 | 0 | 0 | 0 | 2 | 0 | 3 | 1 | |||||||||||||||||||||||
| 3 | 3 | 0 | 0 | 0 | 0 | |||||||||||||||||||||||||||||
| 3 | 4 | 0 | 0 | 0 | 0 | |||||||||||||||||||||||||||||
| Subarea | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Air | Water Surface | Water Column | Sea Floor | Coast | |||||||||||||||||||||||||
| ED State | Type of Degradation Effect * | ED State | Type of Degradation Effect * | ED State | Type of Degradation Effect * | ED State | Type of Degradation Effect * | ED State | Type of Degradation Effect * | ||||||||||||||||||||
| R1 | R2 | R3 | R4 | R5 | R1 | R2 | R3 | R4 | R5 | R1 | R2 | R3 | R4 | R5 | R1 | R2 | R3 | R4 | R5 | R1 | R2 | R3 | R4 | R5 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |||||
| 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | |||||
| 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 3 | |||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | |||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | |||||
| 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 2 | |||||
| 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | |||||
| 0 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 2 | 2 | |||||
| 0 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 2 | 3 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 3 | 3 | |||||
| 0 | 0 | 1 | 0 | 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |||||
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |||||
| 0 | 0 | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2 | 0 | 0 | 1 | 1 | 2 | 0 | 0 | 1 | 1 | 2 | 0 | 0 | 1 | 1 | 2 | |||||
| 0 | 0 | 2 | 2 | 3 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 2 | 0 | 1 | |||||
| 0 | 0 | 2 | 3 | 3 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 2 | 0 | 2 | |||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 2 | 0 | 0 | 2 | 1 | 2 | 0 | 0 | 2 | 1 | 2 | 0 | 0 | 2 | 1 | 2 | |||||
| 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 3 | 0 | 0 | 2 | 2 | 3 | 0 | 0 | 2 | 2 | 3 | 0 | 0 | 2 | 2 | 3 | |||||
| 0 | 3 | 0 | 0 | 0 | 0 | 0 | 2 | 3 | 3 | 0 | 0 | 2 | 3 | 3 | 0 | 0 | 2 | 3 | 3 | 0 | 0 | 2 | 3 | 3 | |||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 3 | 0 | 2 | |||||
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 3 | 0 | 3 | 0 | 0 | 3 | 0 | 3 | |||||
| 1 | 1 | 0 | 2 | 2 | 0 | 0 | 3 | 1 | 2 | 0 | 0 | 3 | 1 | 2 | 0 | 0 | 3 | 1 | 2 | 0 | 0 | 3 | 1 | 2 | |||||
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 2 | 3 | 0 | 0 | 3 | 2 | 3 | 0 | 0 | 3 | 2 | 3 | 0 | 0 | 3 | 2 | 3 | |||||
| 2 | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | ||||||||||
| 2 | 2 | 0 | 3 | 3 | 1 | 0 | 3 | 0 | 3 | 1 | 0 | 3 | 0 | 3 | 0 | 1 | 0 | 2 | 2 | ||||||||||
| 3 | 2 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 2 | 1 | 1 | 0 | 2 | 2 | 0 | 1 | 0 | 3 | 3 | ||||||||||
| 3 | 3 | 0 | 3 | 0 | 2 | 0 | 3 | 0 | 3 | 2 | 0 | 3 | 0 | 3 | 1 | 0 | 0 | 0 | 0 | ||||||||||
| 3 | 3 | 0 | 3 | 3 | 2 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 3 | ||||||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 2 | ||||||||||||||||||||
| 3 | 1 | 0 | 0 | 0 | 2 | 0 | 3 | 0 | 3 | ||||||||||||||||||||
| 2 | 1 | 0 | 0 | 0 | |||||||||||||||||||||||||
Appendix C
- Initial probabilities: ;
- Probabilities of transitions between particular states are given in Table A5.
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | |||||||||||||||||
| 1 | – | 0.2460 | 0.2264 | 0.0754 | 0.1644 | 0.1436 | 0.1258 | 0.0184 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0.5461 | – | 0.2880 | 0.0069 | 0.0092 | 0.0507 | 0.0922 | 0 | 0 | 0.0046 | 0.0023 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0.9908 | 0.0026 | – | 0 | 0 | 0.0053 | 0 | 0 | 0.0013 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 0.7450 | 0.0201 | 0.0872 | – | 0 | 0.0604 | 0.0873 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 0.7692 | 0 | 0 | 0 | – | 0 | 0 | 0 | 0.0659 | 0.1429 | 0 | 0.0037 | 0 | 0 | 0 | 0.0183 | |
| 6 | 0.4488 | 0.0989 | 0.3110 | 0.0777 | 0 | – | 0 | 0 | 0 | 0.0141 | 0.0495 | 0 | 0 | 0 | 0 | 0 | |
| 7 | 0.4115 | 0 | 0.5423 | 0.0038 | 0 | 0 | – | 0.0116 | 0 | 0 | 0.0116 | 0 | 0.0192 | 0 | 0 | 0 | |
| 8 | 0.8750 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0 | 0 | 0 | 0.1250 | 0 | 0 | 0 | |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0.5790 | 0 | 0 | 0 | 0 | 0.3947 | 0 | 0 | 0 | – | 0 | 0 | 0 | 0.0263 | 0 | 0 | |
| 11 | 4444 | 0 | 5556 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0 | 0 | 0 | 0 | |
| 12 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0 | 0 | 0 | |
| 13 | 0.4445 | 0 | 0.3333 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0.2222 | 0 | |
| 14 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0 | |
| 15 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | |
| 16 | 0.4000 | 0 | 0.4000 | 0 | 0 | 0 | 0.2000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | |
- Initial probabilities: for
- Probabilities of transitions between particular states are given in Table A6.
| Subarea | Probabilities of Transitions between Particular States |
|---|---|
| air |
; ; 1; ; ; ; , |
| water surface |
; ; ; ; ; ; |
| water column |
; ; ; ; ; ; |
| sea floor |
; ; ; ; ; ; |
| coast | ; ; ; ; ; ; . |
- Initial probabilities: for:
- and
- and
- and
- and
- and
- Probabilities of transitions between particular states are given in Table A7.
| Subarea | Probabilities of Transitions between Particular States |
|---|---|
| air | ; ; ; ; ; ; ; ; ; ; ; ; ; |
| water surface | ; ; ; ; ; ; , |
| water column | ; ; ; ; ; , |
| sea floor | ; ; ; ; , , |
| coast | ; ; , |
References
- National Research Council. Vessel Navigation and Traffic Services for Safe and Efficient Ports and Waterways: Interim Report; The National Academies Press: Washington, DC, USA, 1996. [Google Scholar] [CrossRef]
- Bekir, E. Introduction to Modern Navigation Systems; World Scientific: Singapore, 2007. [Google Scholar] [CrossRef]
- Rivkin, B.S. The tenth anniversary of e-navigation. Gyroscopy Navig. 2016, 7, 90–99. [Google Scholar] [CrossRef]
- Størkersen, K.V. Safety management in remotely controlled vessel operations. Mar. Policy 2021, 130, 104349. [Google Scholar] [CrossRef]
- Fingas, M. Oil Spill Science and Technology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Bogalecka, M. Consequences of maritime critical infrastructure accidents with chemical releases. TransNav 2019, 13, 771–779. [Google Scholar] [CrossRef]
- ITOPF. Oil Tanker Spill Statistics 2021; ITOPF Ltd.: London, UK, 2022. [Google Scholar]
- “Shipping: Indispensable to the World” Selected as World Maritime Day Theme for 2016. Available online: https://www.imo.org/en/MediaCentre/PressBriefings/Pages/47-WMD-theme-2016-.aspx (accessed on 13 March 2023).
- Dominguez-Péry, C.; Vuddaraju, L.N.R.; Corbett-Etchevers, I.; Tassabehji, R. Reducing maritime accidents in ships by tackling human error: A bibliometric review and research agenda. J. Shipp. Trd. 2021, 6, 20. [Google Scholar] [CrossRef]
- Dobrzycka-Krahel, A.; Bogalecka, M. The Baltic Sea under anthropopressure—The sea of paradoxes. Water 2022, 14, 3772. [Google Scholar] [CrossRef]
- Weng, J.; Yang, D. Investigation of shipping accident injury severity and mortality. Accid. Anal. Prev. 2015, 76, 92–101. [Google Scholar] [CrossRef]
- Yender, R.; Michel, J.; Lord, C. Managing Seafood Safety after an Oil Spill. Seattle: Hazardous Materials Response Division, Office of Response and Restoration, National Oceanic and Atmospheric Administration, 2002. Available online: https://response.restoration.noaa.gov/sites/default/files/managing-seafood-safety-oil-spill.pdf (accessed on 13 March 2023).
- IMO. Casualty-Related Matters Reports on Marine Casualties and Incidents; MSC-MEPC.3/Circ.4/Rev.1; IMO: London, UK, 2014; Available online: https://www.imo.org/en/OurWork/MSAS/Pages/Casualties.aspx (accessed on 13 March 2023).
- Bogalecka, M. Analysis of sea accidents initial events. Pol. J. Environ. Stud. 2010, 19, 5–8. [Google Scholar]
- Goldstein, M.; Ritterling, J. A Practical Guide to Estimating Cleanup Costs; U.S. EPA Pap.: Washington, DC, USA, 2001; p. 30. [Google Scholar]
- Kontovas, C.A.; Ventikos, N.P.; Psaraftis, H.N. Estimating the consequences costs of oil spills from tankers. In Proceedings of the SNAME 2011 Annual Meeting, Houston, TX, USA, 16–18 November 2011. [Google Scholar]
- Liu, X.; Wirtz, K.W. Total oil spill costs and compensations. Mar. Pol. Manag. 2006, 33, 49–60. [Google Scholar] [CrossRef]
- Psaraftis, H.N. Environmental risk evaluation criteria. In Proceedings of the Second International Workshop of Risk-Based Approaches to the Maritime Industry, Ship Stability Research Centre, University of Glasgow and Strathclyde, Glasgow, UK, 5–6 May 2008. [Google Scholar]
- Ventikos, N.P.; Louzis, K.; Sotiralis, P. Oil pollution: Sustainable ships and shipping. In Sustainable Shipping. A Cross-Disciplinary View; Psaraftis, H., Ed.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Allianz Global Corporate & Specialty SE. Safety and Shipping Review 2022. In An Annual Review of Trends and Developments in Shipping Losses and Safety; Allianz Global Corporate & Specialty SE: Munich, Germany, 2022; Available online: https://www.agcs.allianz.com/news-and-insights/reports/shipping-safety.html#download (accessed on 13 March 2023).
- Lloyd’s List Intelligence and DNV Whitepaper. Maritime Safety 2012–2021—A Decade of Progress. Available online: https://www.dnv.com/Publications/whitepaper-maritime-safety-2012-2021-a-decade-of-progress--213588 (accessed on 13 March 2023).
- Marine Traffic. Available online: https://marinetraffic.com (accessed on 13 March 2023).
- Aalberg, A.L.; Bye, R.J.; Ellevseth, P.R. Risk factors and navigation accidents: A historical analysis comparing accident-free and accident-prone vessels using indicators from AIS data and vessel databases. Marit. Transp. Res. 2022, 3, 100062. [Google Scholar] [CrossRef]
- Bogalecka, M. Modelling consequences of maritime critical infrastructure accidents. J. Konbin 2019, 49, 477–495. [Google Scholar] [CrossRef]
- Faghih-Roohi, S.; Xie, M.; Ng, K.M. Accident risk assessment in marine transportation via Markov modelling and Markov chain Monte Carlo simulation. Ocean Eng. 2014, 91, 363–370. [Google Scholar] [CrossRef]
- European Maritime Safety Agency. European Maritime Safety Report 2022. Available online: https://safety4sea.com/wp-content/uploads/2022/11/EMSA-Annual-Overview-of-Marine-Casualties-and-Incidents-2022-2022_11.pdf (accessed on 13 March 2023).
- Fowler, T.G.; Sørgård, E. Modeling ship transportation Risk. Risk Anal. 2002, 20, 225–244. [Google Scholar] [CrossRef]
- Goerlandt, F.; Montewka, J. Maritime transportation risk analysis: Review and analysis in light of some foundational issues. Reliab. Eng. Syst. 2015, 138, 225–244. [Google Scholar] [CrossRef]
- Kulkarni, K.; Goerlandt, F.; Li, J.; Valdez Banda, O.; Kujala, P. Preventing shipping accidents: Past, present, and future of waterway risk management with Baltic Sea focus. Saf. Sci. 2020, 129, 104798. [Google Scholar] [CrossRef]
- Ma, X.-F.; Shi, G.-Y.; Liu, Z.-J. TAR-based domino effect model for maritime accidents. J. Mar. Sci. Eng. 2022, 10, 788. [Google Scholar] [CrossRef]
- Yang, Z.L.; Wang, J.; Li, K.X. Maritime safety analysis in retrospect. Marit. Policy Manag. 2013, 40, 261–277. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, X.; Lin, C. Fusing XGBoost and SHAP models for maritime accident prediction and causality interpretability analysis. J. Mar. Sci. Eng. 2022, 10, 1154. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Meng, Q.; Xie, H. Ship accident consequences and contributing factors analyses using ship accident investigation reports. Proc. Inst. Mech. Eng. O J. Risk Reliab. 2019, 233, 35–47. [Google Scholar] [CrossRef]
- Luo, M.; Shin, S.-H. Half-century research developments in maritime accidents: Future directions. Accid. Anal. Prev. 2019, 123, 448–460. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Pedersen, P.T.; Villavicencio, R. Probability and Mechanics of Ship Collision and Grounding; Butterworth-Heinemann: Portsmouth, NH, USA; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Vukša, S.; Vidan, P.; Bukljaš, M.; Pavić, S. Research on ship collision probability model based on Monte Carlo simulation and Bi-LSTM. J. Mar. Sci. Eng. 2022, 10, 1124. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Q.; Ma, G.; Zhang, T. Analysis of ship collision damage by combining Monte Carlo simulation and the artificial neural network approach. Ships Offshore Struc. 2017, 12 (Suppl. 1), 21–30. [Google Scholar] [CrossRef]
- Taimuri, G.; Ruponen, P.; Hirdaris, S. A novel method for the probabilistic assessment of ship grounding damages and their impact on damage stability. Struct. Saf. 2023, 100, 102281. [Google Scholar] [CrossRef]
- Poulter, S.R. Monte Carlo simulation in environmental risk assessment–science, policy and legal. Risk Health Saf. Environ. 1998, 9, 7–26. [Google Scholar]
- Harris, G.; Van Horn, R. Use of Monte Carlo Methods in Environmental Risk Assessment at the INEL: Application and Issues; Idaho National Engineering Laboratory Environmental Restoration Department Lockheed Martin Idaho Technologies Company: Idaho Falls, Idaho, 1996.
- Bogalecka, M. Consequences of Maritime Critical Infrastructure Accidents. Environmental Impacts. Modeling–Identification–Prediction–Optimization–Mitigation; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Grabski, F. Semi-Markov Processes: Applications in System Reliability and Maintenance; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Kołowrocki, K. Reliability of Large and Complex Systems; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kołowrocki, K.; Soszyńska-Budny, J. Reliability and Safety of Complex Technical Systems and Processes: Modeling–Identification–Prediction–Optimization; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Limnios, N.; Oprişan, G. Semi-Markov Processes and Reliability; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Macci, C. Large deviations for empirical estimators of the stationary distribution of a semi-Markov process with finite state space. Commun. Stat. Theory Meth. 2008, 37, 3077–3089. [Google Scholar] [CrossRef]
- Mercier, S. Numerical bounds for semi-Markovian quantities and application to reliability. Method. Comput. Appl. Probab. 2008, 10, 179–198. [Google Scholar] [CrossRef]
- Bogalecka, M.; Kołowrocki, K. Statistical identification of critical infrastructure accident consequences process, Part 1, Process of initiating events. In Proceedings of the 17th Applied Stochastic Models and Data Analysis International Conference with Demographics Workshop–ASMDA 2017, London, UK, 6–9 June 2017; Skiadac, C.H., Ed.; ISAST: International Society for the Advancement of Science and Technology: San Diego, CA, USA, 2017; pp. 153–166. [Google Scholar]
- Bogalecka, M.; Kołowrocki, K. Statistical identification of critical infrastructure accident consequences process, Part 2, Process of environment threats. In Proceedings of the 17th Applied Stochastic Models and Data Analysis International Conference with Demographics Workshop–ASMDA 2017, London, UK, 6–9 June 2017; Skiadac, C.H., Ed.; ISAST: International Society for the Advancement of Science and Technology: San Diego, CA, USA, 2017; pp. 167–178. [Google Scholar]
- Bogalecka, M.; Kołowrocki, K. Statistical identification of critical infrastructure accident consequences process, Part 3, Process of environment degradations. In Proceedings of the 17th Applied Stochastic Models and Data Analysis International Conference with Demographics Workshop–ASMDA 2017, London, UK, 6–9 June 2017; Skiadac, C.H., Ed.; ISAST: International Society for the Advancement of Science and Technology: San Diego, CA, USA, 2017; pp. 179–189. [Google Scholar]
- Dąbrowska, E. Conception of oil spill trajectory modelling: Karlskrona seaport area as an investigative example. In Proceedings of the 2021 5th International Conference on System Reliability and Safety (ICSRS), Palermo, Italy, 24–26 November 2021; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2021; pp. 307–311. [Google Scholar]
- Dąbrowska, E.; Kołowrocki, K. Monte Carlo simulation approach to determination of oil spill domains at port and sea waters areas. TransNav 2020, 14, 59–64. [Google Scholar] [CrossRef]
- Dąbrowska, E.; Soszyńska-Budny, J. Monte Carlo simulation forecasting of maritime ferry safety and resilience. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management–IEEM 2018, Bangkok, Thailand, 16–19 December 2018; pp. 376–380. [Google Scholar] [CrossRef]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; John Willey & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- IMO. International Maritime Dangerous Goods Code; IMO Publishing: London, UK, 2022. [Google Scholar]
- Drews, T.O.; Braatz, R.D.; Alkire, R.C. Parameter sensitivity analysis of Monte Carlo simulations of copper electrodeposition with multiple additives. J. Electrochem. Soc. 2003, 150, C807–C812. [Google Scholar] [CrossRef]
- National Research Council (US) Committee on Oil in the Sea: Inputs, Fates, and Effects. Oil in the Sea III: Inputs, Fates, and Effects; The National Academies Press: Washington, DC, USA, 2003. [Google Scholar]
- Galieriková, A.; Dávid, A.; Materna, M.; Mako, P. Study of maritime accidents with hazardous substances involved: Comparison of HNS and oil behaviours in marine environment. Transp. Res. Procedia 2021, 55, 1050–1064. [Google Scholar] [CrossRef]
- Liu, X.; Wirtz, K.W. The economy of oil spills: Direct and indirect costs as a function of spill size. J. Hazard. Mater. 2009, 171, 471–477. [Google Scholar] [CrossRef]
- Chang, S.E.; Stone, J.; Demes, K.; Piscitelli, M. Consequences of oil spills: A review and framework for informing planning. Ecol. Soc. 2014, 19, 1–25. Available online: http://www.jstor.org/stable/26269587 (accessed on 13 March 2023). [CrossRef]
- Gill, D.A.; Picou, J.S.; Ritchie, L.A. The Exxon Valdez and BP oil spills: A comparison of initial social and psychological impacts. Am. Behav. Sci. 2012, 56, 3–23. [Google Scholar] [CrossRef]
- Bogalecka, M.; Popek, M. Proaktywne i reaktywne strategie zapobiegania zagrożeniom środowiska morskiego. In Europejski Kontekst Bezpiecznego i Efektywnego Gospodarowania na Morzu; Piocha, S., Ed.; Środkowopomorska Rada Naczelnej Organizacji Technicznej w Koszalinie, Politechnika Koszalińska, Morska Służba Poszukiwania i Ratownictwa w Gdyni: Koszalin/Kołobrzeg, Poland, 2008; pp. 235–240. [Google Scholar]
- Mojtahedi, M.; Oo, B.L. Critical attributes for proactive engagement of stakeholders in disaster risk management. Int. J. Disaster Risk Reduct. 2017, 21, 35–43. [Google Scholar] [CrossRef]
- Dąbrowska, E. Oil discharge trajectory simulation at selected Baltic Sea waterway under variability of hydro-meteorological conditions: Preliminary approach. Water, 2023; submitted. [Google Scholar]
- Dąbrowska, E.; Kołowrocki, K. Probabilistic approach to determination of oil spill domains at port and sea water areas. TransNav 2020, 14, 51–58. [Google Scholar] [CrossRef]
- Torbicki, M. Longtime prediction of climate-weather change influence on critical infrastructure safety and resilience. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management–IEEM 2018, Bangkok, Thailand, 16–19 December 2018; pp. 996–1000. [Google Scholar] [CrossRef]
- Bogalecka, M.; Kołowrocki, K. Chemical spill due to extreme sea surges critical infrastructure chemical accident (spill) consequences related to climate-weather change. J. Pol. Saf. Reliab. Assoc. Summer Saf. Reliab. Semin. 2018, 9, 65–77. [Google Scholar]






| Parameter of Environmental Threat | (# of IMDG Division) | (°C) | (% in Air) or (g/m3 in Water) | (min) | (logP) | ||
|---|---|---|---|---|---|---|---|
| Level | |||||||
| 1 | 1.6 | (61,+∞) | (10,+∞) in air (100,+∞) in water | (60,+∞) | (1,2〉 | yes | |
| 2 | 1.5 | (23,61〉 | (2,10〉 in air (10,100〉 in water | (3,60〉 | (2,3〉 | — | |
| 3 | 1.4 | (−18,23〉 | (0.5,2〉 in air (1,10〉 in water | (0,3〉 | (3,4〉 | — | |
| 4 | 1.3 | (−∞,−18〉 | (0,0.5〉 in air (0.1,1〉 in water | — | (4,5〉 | — | |
| 5 | 1.2 | — | (0.01,0.1〉 in water | — | (5,+∞) | — | |
| 6 | 1.1 | — | (0,0.01〉 in water | — | — | — | |
| Degradation Effect | (°C) | (% in Air) or (g/m3 in Water) | (pH Unit) | (g/m3) | ||
|---|---|---|---|---|---|---|
| Level | ||||||
| 1 | (0,10〉 | (0,2〉 | ±(0,1〉 | closure of accident area is not required | (0,0.5LC50〉 | |
| 2 | (10,20〉 | (2,5〉 | ±(1,2〉 | closure of accident area is required up to 2 days | (0.5LC50,LC50〉 | |
| 3 | (20,+∞) | (5,+∞) | ±(2,14) | closure of accident area is required for more than 2 days | (LC50,+∞) | |
| Limit Transient Probabilities | Mean Values of Sojourn Total Times per 1 Year (h) |
|---|---|
| 0.999648485390849 ≈ 0.99965 | 8756.920732 ≅ 8756.9 |
| 0.000000030155895567252 ≅ 0 | 0.000264166 ≅ 0 |
| 0.000350730555866569 ≅ 0.00035 | 3.072399669 ≅ 3.1 |
| 0 | 0 |
| 0.00000015077947783626 ≅ 0 | 0.001320828 ≅ 0 |
| 0 | 0 |
| 0.000000603117911345039 ≅ 0 | 0.005283313 ≅ 0 |
| 0 | 0 |
| Limit Transient Probabilities | Mean Values of Sojourn Total Times per 1 Year (hrs) |
|---|---|
| 0.999436013641732 ≅ 0.99944 | 8755.05948 ≅ 8755.1 |
| 0.000000479582845682385 ≅ 0 | 0.004201146 ≅ 0 |
| 0.000518379728488059 ≅ 0.00052 | 4.541006422 ≅ 4.5 |
| 0.0000000693390426800051 ≅ 0 | 0.00060741 ≅ 0 |
| 0.0000119479841108746 ≅ 0.00001 | 0.104664341 ≅ 0.1 |
| 0.000018036005559835 ≅ 0.00002 | 0.157995409 ≅ 0.2 |
| 0.0000120960096478568 ≅ 0.00001 | 0.105961045 ≅ 0.1 |
| 0.000000489089788167662 ≅ 0 | 0.004284427 ≅ 0 |
| 0.000000228175065272163 ≅ 0 | 0.001998814 ≅ 0 |
| 0.00000205072197232601 ≅ 0 | 0.017964324 ≅ 0 |
| 0.000000132864320148473 ≅ 0 | 0.001163891 ≅ 0 |
| 0.00000000159802446913971 ≅ 0 | 0.0000139987 ≅ 0 |
| 0.0000000263293555391591 ≅ 0 | 0.000230645 ≅ 0 |
| 0.0000000127841957531177 ≅ 0 | 0.00011199 ≅ 0 |
| 0.0000000158280518848124 ≅ 0 | 0.000138654 ≅ 0 |
| 0.0000000203177396790621 ≅ 0 | 0.000177983 ≅ 0 |
| Subarea | Limit Transient Probabilities | Mean Values of Sojourn Total Times per 1 Year (hrs) |
|---|---|---|
| air | ; 0.00297, 0.98664, 0.00302; 0.00080, 0.00008, 0.37520, 0.00040, 0.02418 0.87936; | 7703.2; |
| water surface | 0.94369; | 8266.7; |
| water column | 0.94102; | 8243.3; |
| sea floor | 0.92868; | 8135.2; |
| coast | 0.99999. | 8759.9. |
| Subarea | Limit Transient Probabilities | Mean Values of Sojourn Total Times per 1 Year (hrs) |
|---|---|---|
| air | 0.09091 0.90909; 0.79823 | 6992.5 |
| water surface | 0.00055 | 4.8 |
| water column | 0.00044 | 3.9 |
| sea floor | 0.00114 | 10.0 |
| coast | 0.20371 | 1784.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogalecka, M.; Dąbrowska, E. Monte Carlo Simulation Approach to Shipping Accidents Consequences Assessment. Water 2023, 15, 1824. https://doi.org/10.3390/w15101824
Bogalecka M, Dąbrowska E. Monte Carlo Simulation Approach to Shipping Accidents Consequences Assessment. Water. 2023; 15(10):1824. https://doi.org/10.3390/w15101824
Chicago/Turabian StyleBogalecka, Magdalena, and Ewa Dąbrowska. 2023. "Monte Carlo Simulation Approach to Shipping Accidents Consequences Assessment" Water 15, no. 10: 1824. https://doi.org/10.3390/w15101824
APA StyleBogalecka, M., & Dąbrowska, E. (2023). Monte Carlo Simulation Approach to Shipping Accidents Consequences Assessment. Water, 15(10), 1824. https://doi.org/10.3390/w15101824








