Parameter Optimization of Centrifugal Pump Splitter Blades with Artificial Fish Swarm Algorithm
Abstract
:1. Introduction
2. Numerical Method
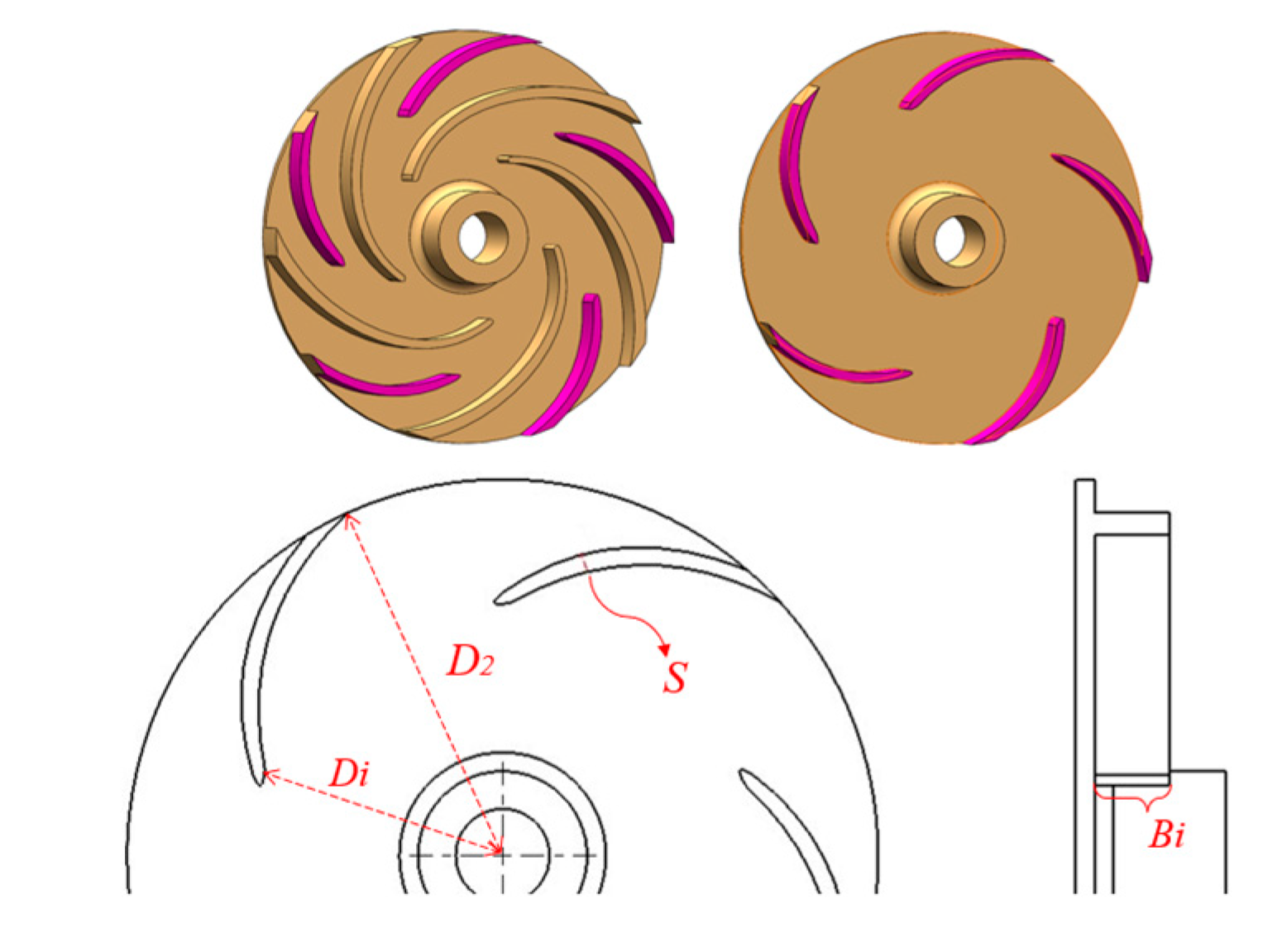
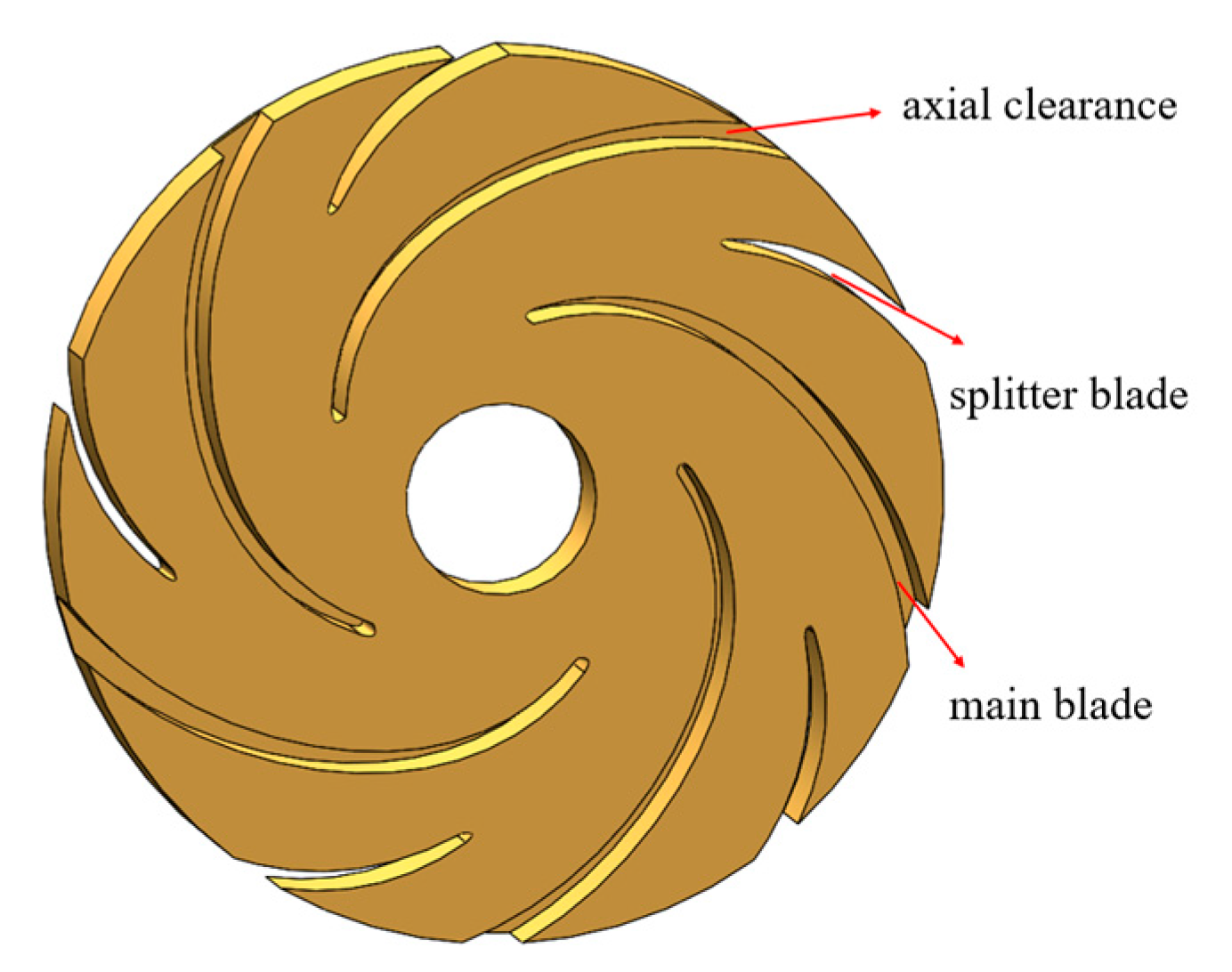
2.1. Research Model
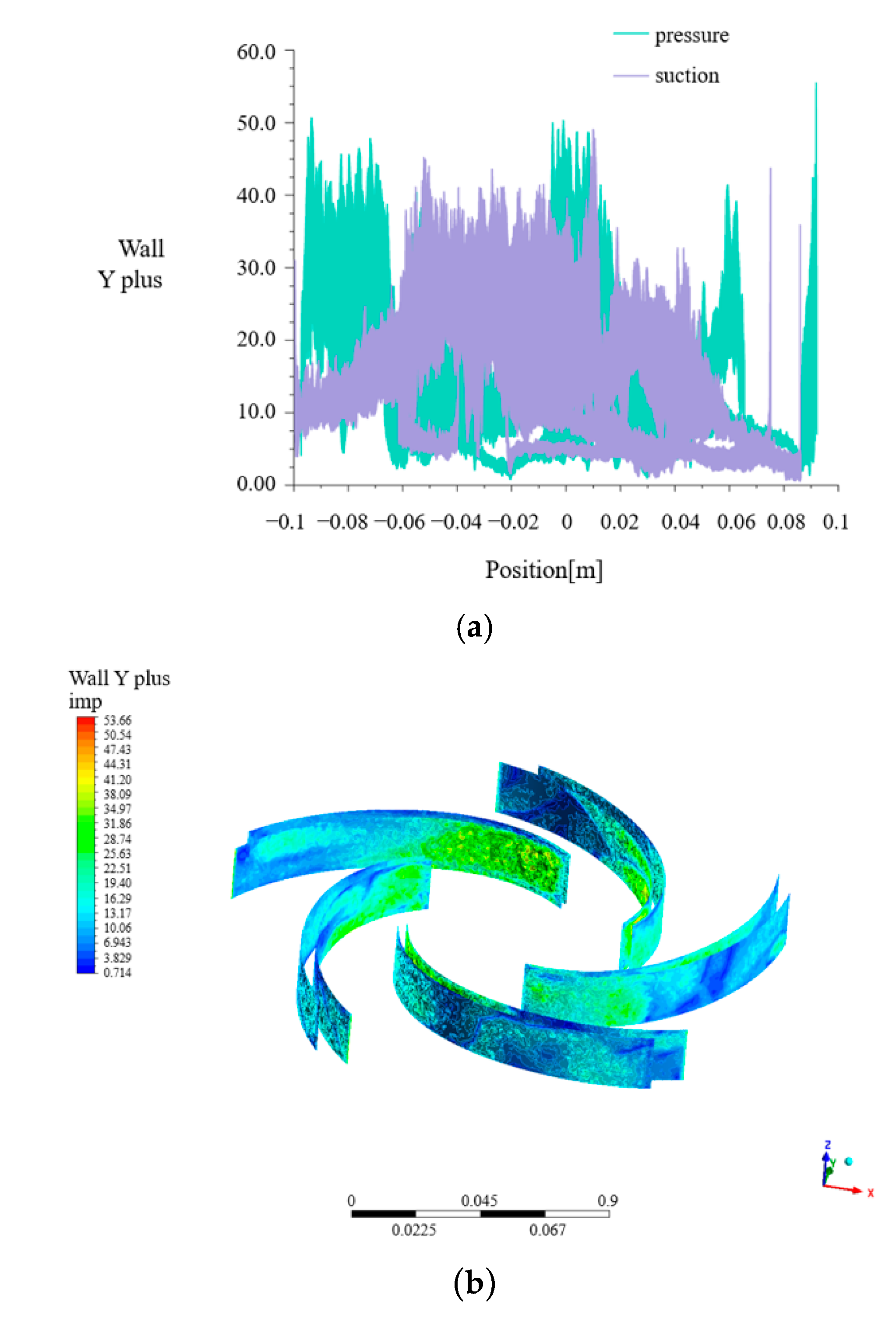
2.2. Turbulence Model and Boundary Conditions
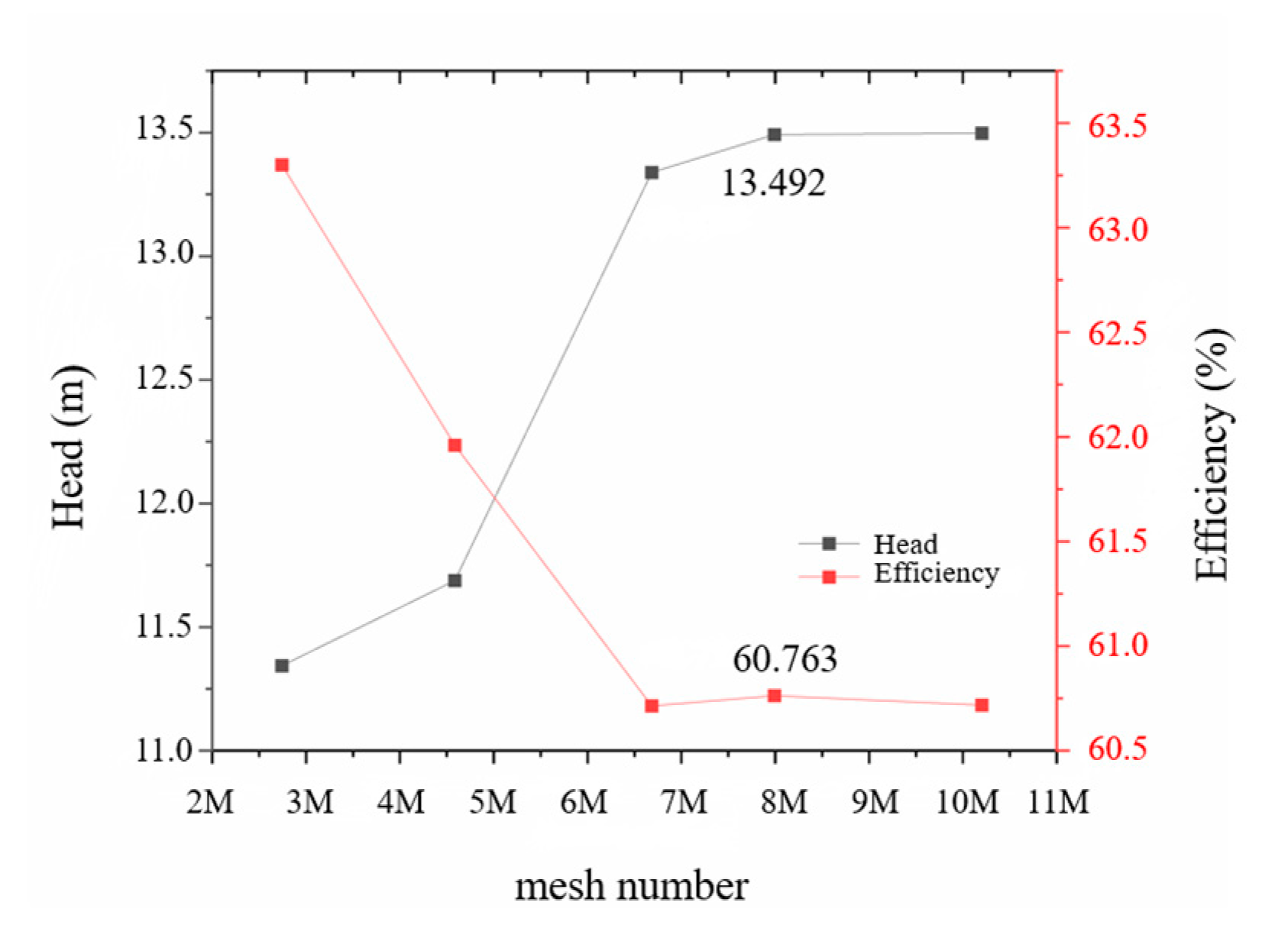
2.3. Mesh
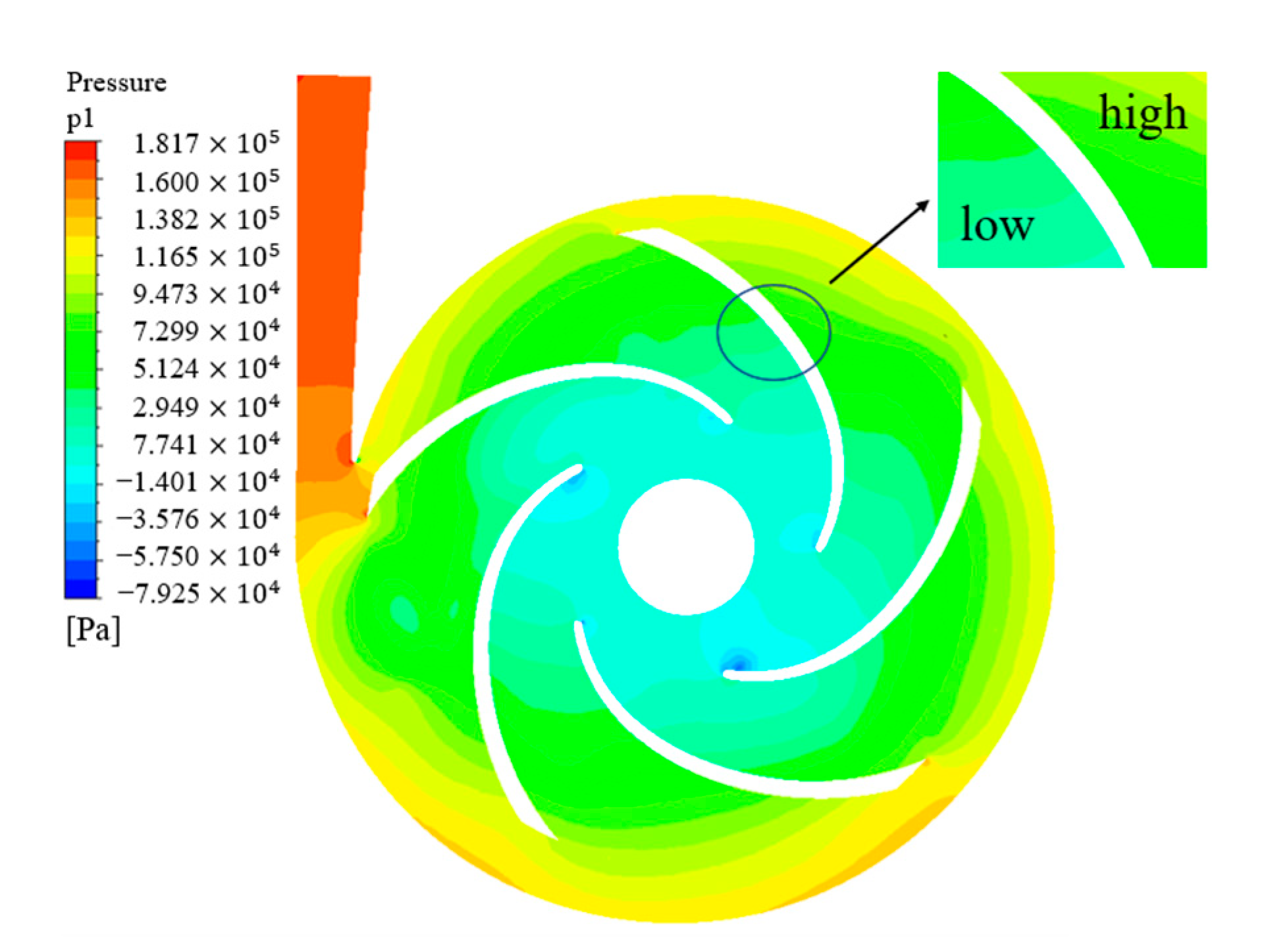
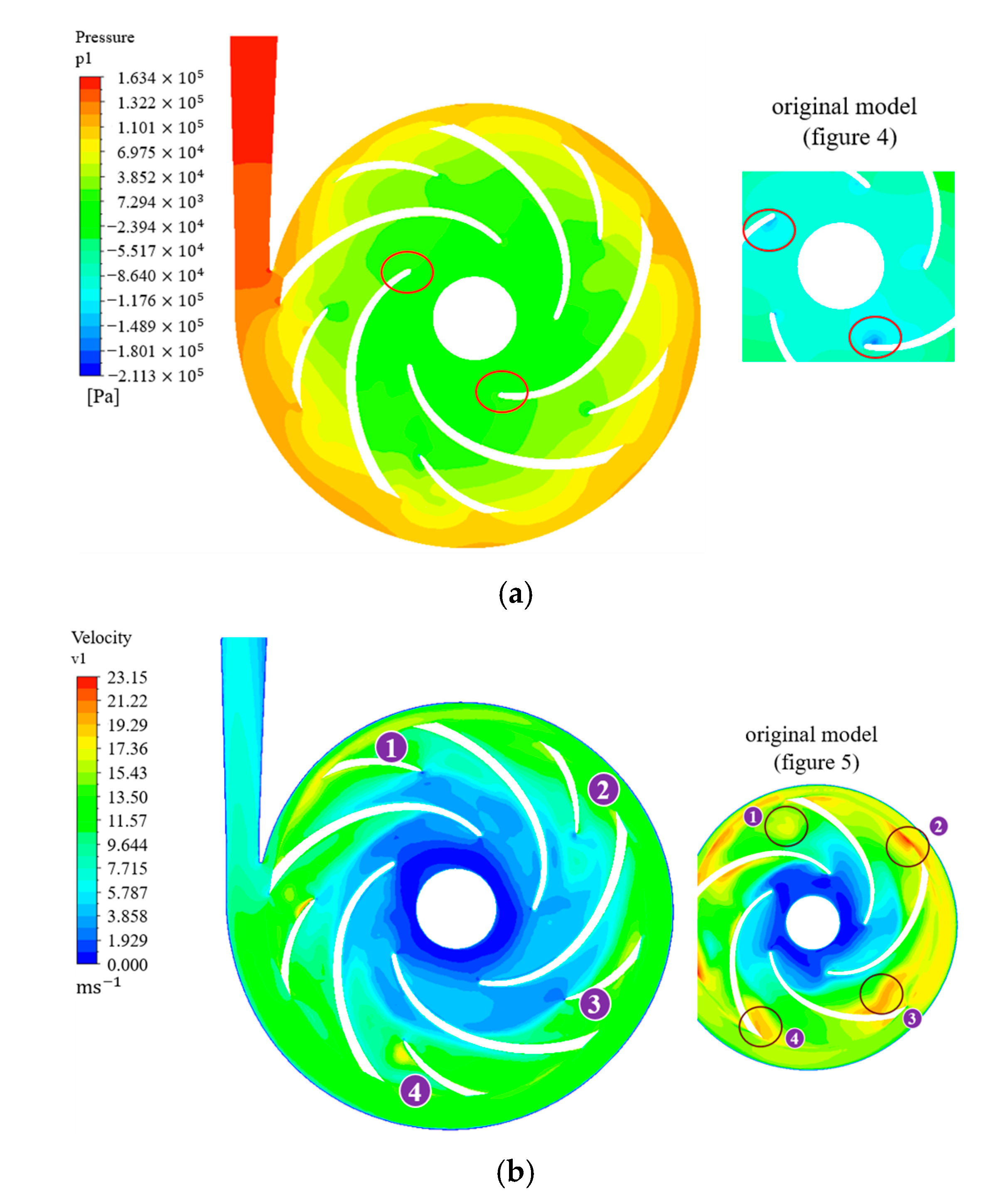
2.4. Flow Field Analysis
3. Orthogonal Test
3.1. Experimental Design
3.2. Data Analysis
4. Artificial Fish Swarm Algorithm Optimization
4.1. Parameter Preparation
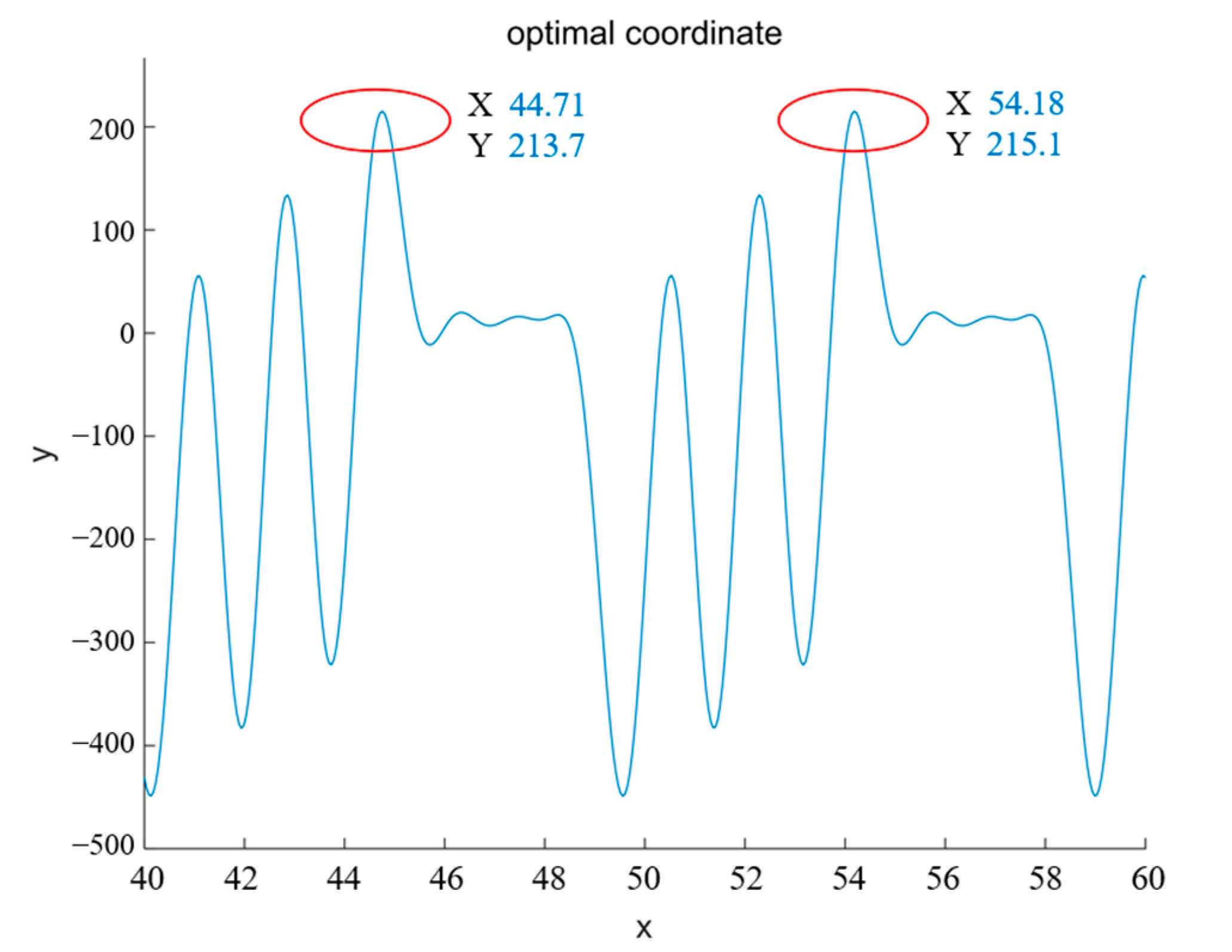
4.2. Parameter Optimization
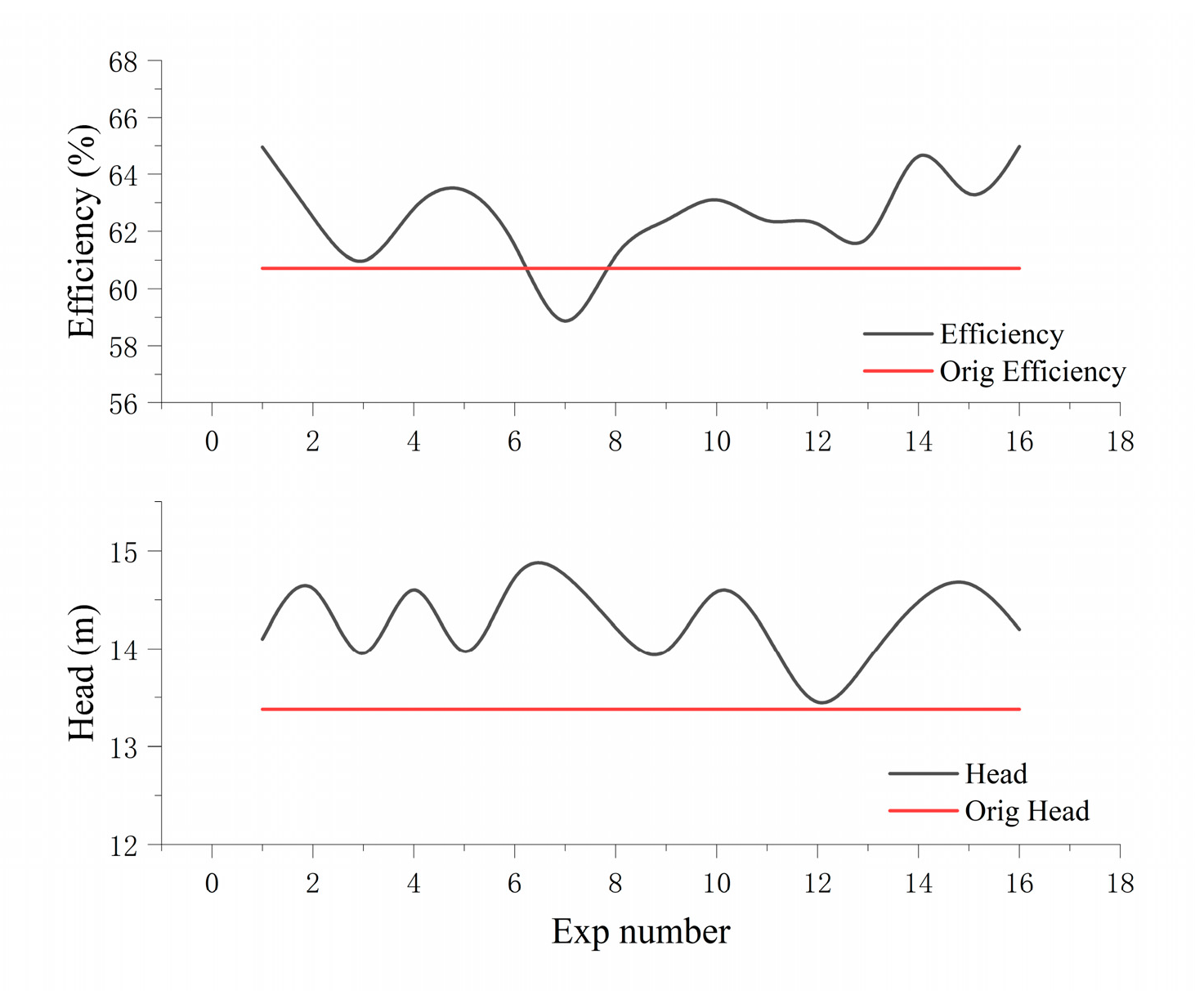
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sorguven, E.; Incir, S.; Highgate, J. Understanding loss generation mechanisms in a centrifugal pump using large eddy simulation. Int. J. Heat Fluid Flow 2022, 96, 108994. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Performance Prediction and Geometry Optimization for Application of Pump as Turbine: A Review. Front. Energy Res. 2022, 9, 818118. [Google Scholar] [CrossRef]
- Gonçalves, L.d.S.; Medeiros, K.A.R.; Barbosa, C.R.H. Hydrometer Design Based on Thin-Film Resistive Sensor for Water Measurement in Residential Buildings. Water 2023, 15, 1045. [Google Scholar] [CrossRef]
- Hu, J.; Li, K.; Su, W.; Zhao, X. Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps. Water 2023, 15, 992. [Google Scholar] [CrossRef]
- Pokharel, N.; Ghimire, A.; Thapa, B.; Thapa, B.S. Wear in centrifugal pumps with causes, effects and remedies: A Review. IOP Conf. Ser. Earth Environ. Sci. 2022, 1037, 012042. [Google Scholar] [CrossRef]
- Kang, C.; Teng, S.; Hu, J.; Ding, K.; Zhang, W. Mitigation of pressure fluctuation through an impeller with splitter blades for a double-volute centrifugal pump. J. Chin. Inst. Eng. 2023, 46, 293–303. [Google Scholar] [CrossRef]
- Namazizadeh, M.; Gevari, M.T.; Mojaddam, M.; Vajdi, M. Optimization of the Splitter Blade Configuration and Geometry of a Centrifugal Pump Impeller using Design of Experiment. J. Appl. Fluid Mech. 2020, 13, 89–101. [Google Scholar] [CrossRef]
- Ke, Q.; Tang, L. Performance Optimization of Slotted Blades for Low-Specific Speed Centrifugal Pumps. Adv. Civ. Eng. 2023, 2023, 9612947. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Xu, H.; Shi, W.; Yang, Y.; Wang, W.; Zhou, L. Experimental and Numerical Investigation of Pressure Fluctuation in a Low-Specific-Speed Centrifugal Pump with a Gap Drainage Impeller. Shock. Vib. 2021, 2021, 5571178. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, L.; Zhou, H.; Lv, W.; Wang, J.; Shi, W.; He, Z. Optimal Design of Slit Impeller for Low Specific Speed Centrifugal Pump Based on Orthogonal Test. J. Mar. Sci. Eng. 2021, 9, 121. [Google Scholar] [CrossRef]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the Impeller Blade with a Slot Structure on the Centrifugal Pump Performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Zhang, Z.-C.; Chen, H.-X.; Ma, Z.; He, J.-W.; Liu, H.; Liu, C. Research on Improving the Dynamic Performance of Centrifugal Pumps With Twisted Gap Drainage Blades. J. Fluids Eng. 2019, 141, 091101. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, L.-C.; Li, J.J.; Jo, H. Investigation on the effect of impeller slot jet on centrifugal pump performance. J. Hydrodyn. 2018, 31, 733–739. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, Y.; Zhou, L.; Jiang, L.; Shi, W.; Huang, G. Influence of Impeller Gap Drainage Width on the Performance of Low Specific Speed Centrifugal Pump. J. Mar. Sci. Eng. 2021, 9, 106. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, L.; Zhao, Y. Influence of Blade Profiles on Plastic Centrifugal Pump Performance. Adv. Mater. Sci. Eng. 2020, 2020, 6665520. [Google Scholar] [CrossRef]
- Xu, Z.; Kong, F.; Tang, L.; Liu, M.; Wang, J.; Qiu, N. Effect of Blade Thickness on Internal Flow and Performance of a Plastic Centrifugal Pump. Machines 2022, 10, 61. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, X.; Gao, B.; Xia, B. DDES analysis of the unsteady wake flow and its evolution of a centrifugal pump. Renew. Energy 2019, 141, 570–582. [Google Scholar] [CrossRef]
- Kye, B.; Park, K.; Choi, H.; Lee, M.; Kim, J.-H. Flow characteristics in a volute-type centrifugal pump using large eddy simulation. Int. J. Heat Fluid Flow 2018, 72, 52–60. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A.; Balaras, E. Investigation of separation phenomena in a radial pump at reduced flow rate by large-eddy simulation. J. Fluids Eng. 2016, 138, 121101. [Google Scholar] [CrossRef]
- Stel, H.; Ofuchi, E.M.; Sabino, R.H.G.; Ancajima, F.C.; Bertoldi, D.; Neto, M.A.M.; Morales, R.E.M. Investigation of the Motion of Bubbles in a Centrifugal Pump Impeller. J. Fluids Eng. 2018, 141, 031203. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Ge, M.; Sun, C.; Zhang, G.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef] [PubMed]
- Ge, M.; Manikkam, P.; Ghossein, J.; Kumar Subramanian, R.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Ge, M.; Petkovšek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Babayigit, O.; Ozgoren, M.; Aksoy, M.H.; Kocaaslan, O.J.D.W.T. Experimental and CFD investigation of a multistage centrifugal pump including leakages and balance holes. Water Treat. 2017, 67, 28–40. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Jiang, X.; Pang, Q.; Ye, D. Vibration. Vibration in a Multistage Centrifugal Pump under Varied Conditions. Shock. Vib. 2019, 2019, 2057031. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Detection of Cavitation Phenomenon within a Centrifugal Pump Based on Vibration Analysis Technique in both Time and Frequency Domains. Exp. Tech. 2020, 44, 329–347. [Google Scholar] [CrossRef]
- Xiao, W.; Tan, L. Design method of controllable velocity moment and optimization of pressure fluctuation suppression for a multiphase pump. Ocean. Eng. 2021, 220, 108402. [Google Scholar] [CrossRef]
- Si, Q.; Ali, A.; Liao, M.; Yuan, J.; Gu, Y.; Yuan, S.; Bois, G. Assessment of cavitation noise in a centrifugal pump using acoustic finite element method and spherical cavity radiation theory. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2173302. [Google Scholar] [CrossRef]
- Lu, Y.; Tan, L.; Han, Y.; Liu, M. Cavitation-vibration correlation of a mixed flow pump under steady state and fast start-up conditions by experiment. Ocean Eng. 2022, 251, 111158. [Google Scholar] [CrossRef]
- De Donno, R.; Ghidoni, A.; Noventa, G.; Rebay, S. Engineering. Shape optimization of the ERCOFTAC centrifugal pump impeller using open-source software. Optim. Eng. 2019, 20, 929–953. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD analysis and optimum design for a centrifugal pump using an effectively artificial intelligent algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Thakkar, S.; Vala, H.; Patel, V.K.; Patel, R. Engineering. Performance improvement of the sanitary centrifugal pump through an integrated approach based on response surface methodology, multi-objective optimization and CFD. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 24. [Google Scholar] [CrossRef]
- Kim, B.; Siddique, M.H.; Samad, A.; Hu, G.; Lee, D.-E. Optimization of Centrifugal Pump Impeller for Pumping Viscous Fluids Using Direct Design Optimization Technique. Machines 2022, 10, 774. [Google Scholar] [CrossRef]
- Chen, X.B.; Zhang, R.H.; Yang, W.F. Inverse Design and Optimization of Low Specific Speed Centrifugal Pump Blade Based on Adaptive POD Hybrid Model. J. Appl. Fluid Mech. 2022, 15, 453–464. [Google Scholar] [CrossRef]
- Pourpanah, F.; Wang, R.; Lim, C.P.; Wang, X.-Z.; Yazdani, D. A review of artificial fish swarm algorithms: Recent advances and applications. Artif. Intell. Rev. 2023, 56, 1867–1903. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Liu, D.; Yuan, S.; Wang, J. Technology. Assessment of a turbulence model for numerical predictions of sheet-cavitating flows in centrifugal pumps? J. Mech. Sci. Technol. 2013, 27, 2743–2750. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Effects of Different Turbulence Models on Three-Dimensional Unsteady Cavitating Flows in the Centrifugal Pump and Performance Prediction. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 487–509. [Google Scholar] [CrossRef]
- Shadab, M.; Karimipour, M.; Najafi, A.F.; Paydar, R.; Nourbakhsh, S.A. Effect of impeller shroud trimming on the hydraulic performance of centrifugal pumps with low and medium specific speeds. Eng. Appl. Comput. Fluid Mech. 2022, 16, 514–535. [Google Scholar] [CrossRef]
- Gu, Y.; Li, J.; Wang, P.; Cheng, L.; Qiu, Y.; Wang, C.; Si, Q. An Improved One-Dimensional Flow Model for Side Chambers of Centrifugal Pumps Considering the Blade Slip Factor. J. Fluids Eng. 2022, 144, 091207. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, W.; Xiao, R. Pressure fluctuation and flow characteristics in a two-stage double-suction centrifugal pump. Symmetry 2019, 11, 65. [Google Scholar] [CrossRef]
- Xu, C.; Fan, C.; Zhang, Z.; Mao, Y. Numerical study of wake and potential interactions in a two-stage centrifugal refrigeration compressor. Eng. Appl. Comput. Fluid Mech. 2021, 15, 313–327. [Google Scholar] [CrossRef]





| Parameters | Flow | Head | Speed |
|---|---|---|---|
| value | 10 | 12.5 | 1440 |
| Factor | A Thickness S | B Diameter Di (Di/D2) | C Width Bi | |
|---|---|---|---|---|
| Level | ||||
| 1 | 4.5 | 0.625 | 17 | |
| 2 | 6 | 0.65 | 19 | |
| 3 | 7.5 | 0.675 | 21 | |
| 4 | 9 | 0.7 | 23 | |
| SN | A (S) | B (Di) | C (Bi) | Head (m) | EFF (%) |
|---|---|---|---|---|---|
| 1 | 6 | 0.65 | 23 | 14.25 | 64.95 |
| 2 | 6 | 0.625 | 19 | 15.21 | 62.50 |
| 3 | 9 | 0.625 | 23 | 13.52 | 60.03 |
| 4 | 7.5 | 0.65 | 17 | 15.35 | 63.20 |
| 5 | 7.5 | 0.625 | 21 | 13.56 | 63.87 |
| 6 | 4.5 | 0.675 | 23 | 15.17 | 61.96 |
| 7 | 4.5 | 0.625 | 17 | 14.98 | 57.36 |
| 8 | 4.5 | 0.7 | 19 | 14.35 | 61.80 |
| 9 | 7.5 | 0.7 | 23 | 13.88 | 62.23 |
| 10 | 4.5 | 0.65 | 21 | 15.02 | 63.60 |
| 11 | 9 | 0.65 | 19 | 14.36 | 61.96 |
| 12 | 9 | 0.7 | 21 | 13.31 | 62.79 |
| 13 | 6 | 0.7 | 17 | 14.04 | 60.40 |
| 14 | 7.5 | 0.675 | 19 | 14.69 | 66.30 |
| 15 | 9 | 0.675 | 17 | 14.96 | 62.15 |
| 16 | 6 | 0.675 | 21 | 14.35 | 64.97 |
| Index | Factor | ||
|---|---|---|---|
| A | B | C | |
| 14.8825 | 14.165 | 14.85 | |
| 14.45 | 14.775 | 14.625 | |
| 14.35 | 14.7825 | 14.05 | |
| 13.89 | 13.85 | 14.0475 | |
| 0.9925 | 0.9325 | 0.8025 | |
| rank | 1 | 2 | 3 |
| Index | Factor | ||
|---|---|---|---|
| A | B | C | |
| 61.18 | 60.94 | 60.7775 | |
| 63.205 | 63.4275 | 63.14 | |
| 63.9 | 63.845 | 63.8075 | |
| 61.7325 | 61.805 | 62.2925 | |
| 2.72 | 2.905 | 3.03 | |
| rank | 3 | 2 | 1 |
| Parameter | Population Size | Maximum Iterations | Maximum Trials | Cognitive Distance | Degrees of Crowding |
|---|---|---|---|---|---|
| value | 50 | 200 | 150 | 0.5 | 0.518 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, Q.; Tang, L.; Luo, W.; Cao, J. Parameter Optimization of Centrifugal Pump Splitter Blades with Artificial Fish Swarm Algorithm. Water 2023, 15, 1806. https://doi.org/10.3390/w15101806
Ke Q, Tang L, Luo W, Cao J. Parameter Optimization of Centrifugal Pump Splitter Blades with Artificial Fish Swarm Algorithm. Water. 2023; 15(10):1806. https://doi.org/10.3390/w15101806
Chicago/Turabian StyleKe, Qidi, Lingfeng Tang, Wenbin Luo, and Jingzhe Cao. 2023. "Parameter Optimization of Centrifugal Pump Splitter Blades with Artificial Fish Swarm Algorithm" Water 15, no. 10: 1806. https://doi.org/10.3390/w15101806
APA StyleKe, Q., Tang, L., Luo, W., & Cao, J. (2023). Parameter Optimization of Centrifugal Pump Splitter Blades with Artificial Fish Swarm Algorithm. Water, 15(10), 1806. https://doi.org/10.3390/w15101806








