Simulating the Flood Limits of Urban Rivers Embedded in the Populated City of Santa Clara, Cuba
Abstract
:1. Introduction
2. Material and Method
2.1. Study Area
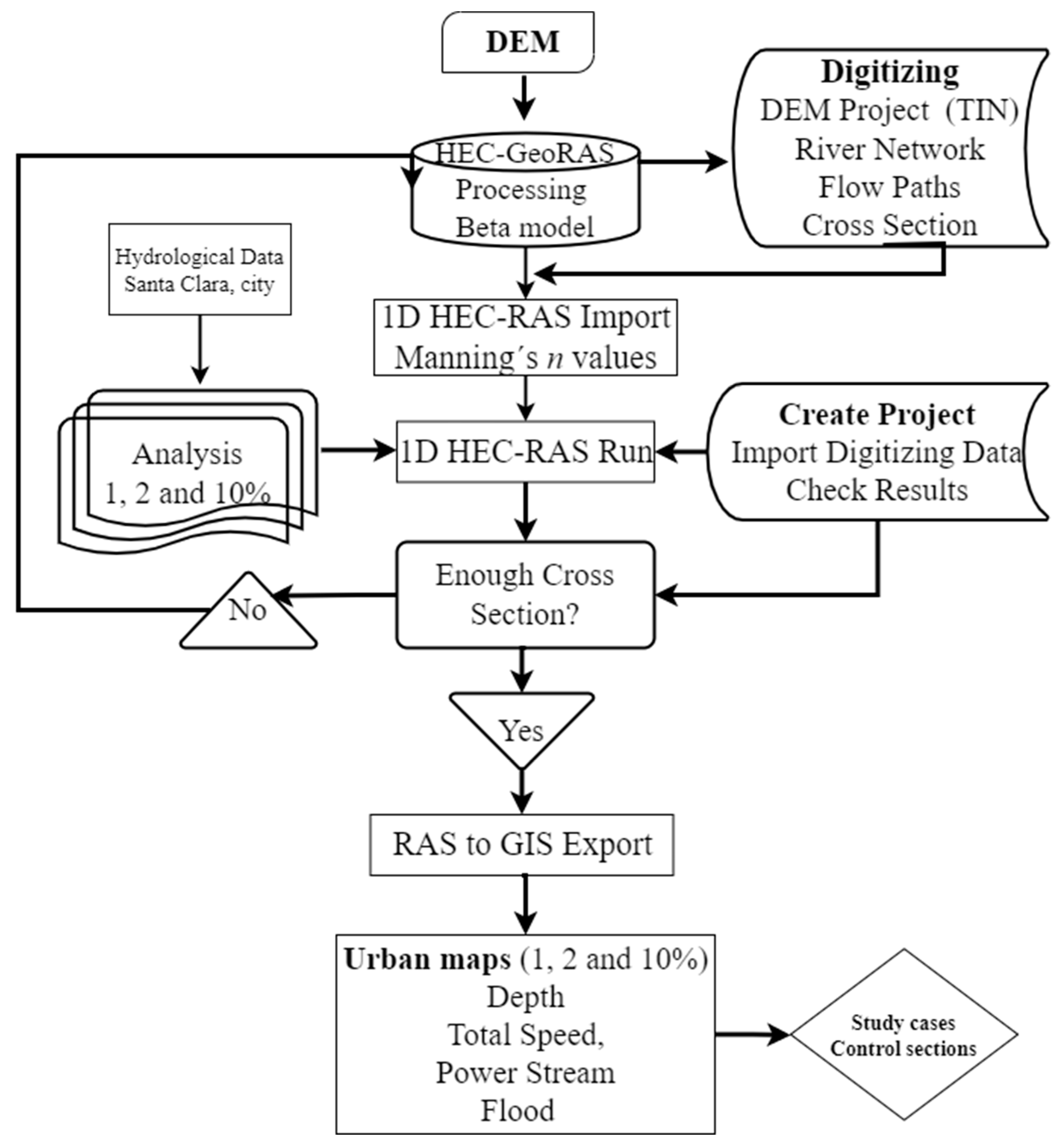
2.2. Methodological Framework
2.3. HEC-RAS One-Dimensional (1D) Model
3. Results and Discussion
3.1. Digital Elevation Model and Manning’s Coefficient
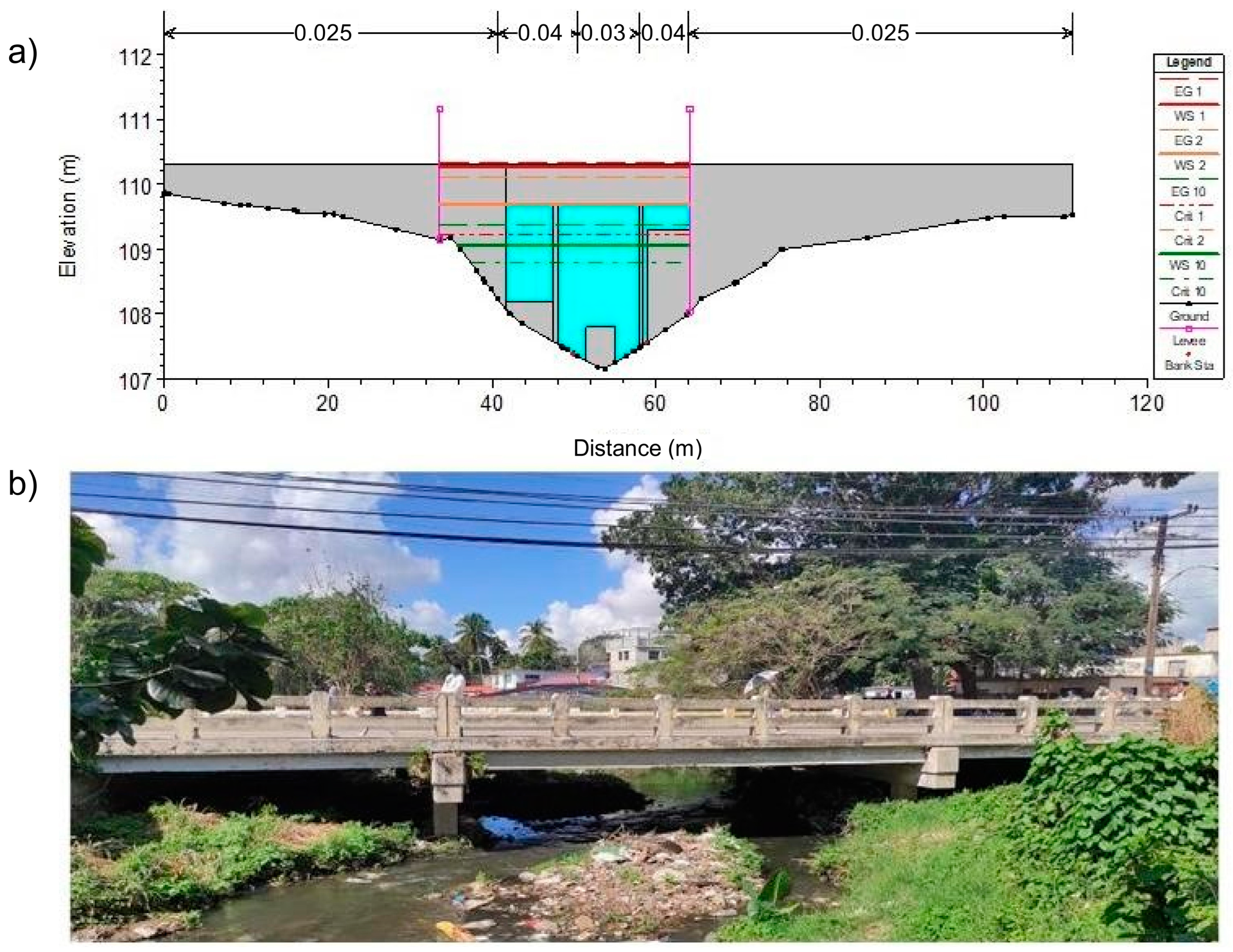
3.2. Channel Cross Section
3.3. Simulation Beta Model
3.3.1. Water Footprint
3.3.2. Urban Flood Maps
3.3.3. Final Remarks and Future Recommendations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, L.; Wei, W.; Yu, Y.; Xiao, J.; Chen, L. Rainfall-runoff risk characteristics of urban function zones in Beijing using the SCS-CN model. J. Geogr. Sci. 2018, 28, 656–668. [Google Scholar] [CrossRef]
- Cui, P.; Peng, J.; Shi, P.; Tang, H.; Ouyang, C.; Zou, Q.; Liu, L.; Li, C.; Lei, Y. Scientific challenges of research on natural hazards and disaster risk. Geogr. Sustain. 2021, 2, 216–223. [Google Scholar] [CrossRef]
- Lechowska, E. What determines flood risk perception? A review of factors of flood risk perception and relations between its basic elements. Nat. Hazards 2018, 94, 1341–1366. [Google Scholar] [CrossRef]
- Membele, G.M.; Naidu, M.; Mutanga, O. Examining flood vulnerability mapping approaches in developing countries: A scoping review. Int. J. Disaster Risk Reduct. 2022, 69, 102766. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: United Kingdom; New York, NY, USA, 2013. [Google Scholar]
- Quesada-Román, A.; Fallas-López, B.; Hernández-Espinoza, K.; Stoffel, M.; Ballesteros-Cánovas, J.A. Relationships between earthquakes, hurricanes, and landslides in Costa Rica. Landslides 2019, 16, 1539–1550. [Google Scholar] [CrossRef]
- Ramos-Scharrón, C.E.; Arima, E.Y.; Hughes, K.S. An assessment of the spatial distribution of shallow landslides induced by Hurricane María in Puerto Rico. Phys. Geogr. 2022, 43, 163–191. [Google Scholar] [CrossRef]
- de Beurs, K.M.; McThompson, N.S.; Owsley, B.C.; Henebry, G.M. Hurricane damage detection on four major Caribbean islands. Remote Sens. Environ. 2019, 229, 1–13. [Google Scholar] [CrossRef]
- Zakrison, T.L.; Valdés, D.M.; Shultz, J.M. The Medical, Public Health, and Emergency Response to the Impact of 2017 Hurricane Irma in Cuba. Disaster Med. Public Health Prep. 2020, 14, 10–17. [Google Scholar] [CrossRef]
- Messina, W.A.; Royce, F.S.; Spreen, T.H. Cuban Agriculture and the Impacts of Tropical Storm Fay and Hurricanes Gustav and Ike 1. 2008. Available online: https://ufdcimages.uflib.ufl.edu/ir/00/00/09/45/00001/fe75500.pdf (accessed on 6 April 2023).
- IFRCRCS. DREF Final Report Cuba: Floods. 2021. Available online: https://reliefweb.int/report/cuba/cuba-floods-dref-final-report-mdrcu006 (accessed on 6 April 2023).
- Iturralde-Vinent, M.A. Peligro De Inundaciones Por Intensas Lluvias En Cuba: Comportamientos. An. Acad. Cienc. Cuba 2018, 11, 16–28. [Google Scholar]
- Castillo García, C.L.; Pérez, T.D.; Gil, L.Á.; Gonzáles, M.Á. Estrategias para el diseño de sistemas de drenaje urbano en la ciudad de Santa Clara. Ing. Hidráulica Ambient. 2022, XLIII, 44–57. [Google Scholar]
- Putri, I.H.S.; Buchori, I.; Handayani, W. Hydrometeorological Disaster Assessment: Study of Risk and Loss Assessment of Disaster Events in Central Java. Sustain. Clim. Chang. 2022, 15, 446–460. [Google Scholar] [CrossRef]
- Sen, S.; Nayak, N.C.; Mohanty, W.K.; Keshri, C.K. Vulnerability and risk perceptions of hydrometeorological disasters: A study of a coastal district of Odisha, India. GeoJournal 2023, 88, 711–731. [Google Scholar] [CrossRef]
- Nkwunonwo, U.C.; Whitworth, M.; Baily, B. A review of the current status of flood modelling for urban flood risk management in the developing countries. Sci. Afr. 2020, 7, e00269. [Google Scholar] [CrossRef]
- Ikirri, M.; Faik, F.; Echogdali, F.Z.; Antunes, I.M.H.R.; Abioui, M.; Abdelrahman, K.; Fnais, M.S.; Wanaim, A.; Id-Belqas, M.; Boutaleb, S.; et al. Flood Hazard Index Application in Arid Catchments: Case of the Taguenit Wadi Watershed, Lakhssas, Morocco. Land 2022, 11, 1178. [Google Scholar] [CrossRef]
- Müller, A.; Reiter, J.; Weiland, U. Assessment of urban vulnerability towards floods using an indicator-based approach-a case study for Santiago de Chile. Nat. Hazards Earth Syst. Sci. 2011, 11, 2107–2123. [Google Scholar] [CrossRef]
- Mokhtar, E.S.; Pradhan, B.; Ghazali, A.H.; Shafri, H.Z.M. Assessing flood inundation mapping through estimated discharge using GIS and HEC-RAS model. Arab. J. Geosci. 2018, 11, 2107–2123. [Google Scholar] [CrossRef]
- Popescu, C.; Bărbulescu, A. Floods Simulation on the Vedea River (Romania) Using Hydraulic Modeling and GIS Software: A Case Study. Water 2023, 15, 483. [Google Scholar] [CrossRef]
- Pinos, J.; Timbe, L.; Timbe, E. Evaluation of 1D hydraulic models for the simulation of mountain fluvial floods: A case study of the santa bárbara river in Ecuador. Water Pract. Technol. 2019, 14, 341–354. [Google Scholar] [CrossRef]
- Ghimire, E.; Sharma, S.; Lamichhane, N. Evaluation of one-dimensional and two-dimensional HEC-RAS models to predict flood travel time and inundation area for flood warning system. ISH J. Hydraul. Eng. 2022, 28, 110–126. [Google Scholar] [CrossRef]
- Imanudin, M.S.; Priatna, S.J.; Armanto, M.E.; Prayitno, M.B. Integrated Duflow-Drainmod model for planning of water management operation in tidal lowland reclamation areas. IOP Conf. Ser. Earth Environ. Sci. 2021, 871, 12035. [Google Scholar] [CrossRef]
- Samanta, R.K.; Bhunia, G.S.; Shit, P.K.; Pourghasemi, H.R. Flood susceptibility mapping using geospatial frequency ratio technique: A case study of Subarnarekha River Basin, India. Model. Earth Syst. Environ. 2018, 4, 395–408. [Google Scholar] [CrossRef]
- Ibacache, V.; Vergara, V.M. Análisis Comparativo De Áreas De Inundación Mediante Diferentes Modelos Digitales De Terreno; Universidad del Bio Bio: Concepción, Chile, 2016. [Google Scholar]
- Gary, W. Brunner HEC-RAS River Analysis System Hydraulic Reference Manual. Hydrol. Eng. Cent. 2016, 547. [Google Scholar]
- Tikul, N.; Shinawanno, S.; Yamyuean, P. PTAD: A web-based climate service for building design adaptation. Clim. Serv. 2022, 25, 100279. [Google Scholar] [CrossRef]
- Syarifudin, A.; Satyanaga, A.; Destania, H.R. Application of the HEC-RAS Program in the Simulation of the Streamflow Hydrograph for Air Lakitan Watershed. Water 2022, 14, 4094. [Google Scholar] [CrossRef]
- Dhungel, S.; Barber, M.E.; Mahler, R.L. Comparison of one-and two-dimensional flood modeling in urban environments. Int. J. Sustain. Dev. Plan. 2019, 14, 356–366. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H. Scenario-based urban flood forecast with flood inundation map. Trop. Cyclone Res. Rev. 2019, 8, 27–34. [Google Scholar] [CrossRef]
- Stoleriu, C.C.; Urzica, A.; Mihu-Pintilie, A. Improving flood risk map accuracy using high-density LiDAR data and the HEC-RAS. J. Flood Risk Manag. 2019, 13, e12572. [Google Scholar]
- Her, Y.G.; Lusher, W.R.; Migliaccio, K.W. How Likely Is a 100-Year Rainfall Event During the Next Ten Years? Agric. Biol. Eng. Trop. REC 2018, 2018, 1–4. [Google Scholar] [CrossRef]
- Stucchi, L.; Bignami, D.F.; Bocchiola, D.; Del Curto, D.; Garzulino, A.; Rosso, R. Assessment of climate-driven flood risk and adaptation supporting the conservation management plan of a heritage site. the national art schools of Cuba. Climate 2021, 9, 23. [Google Scholar] [CrossRef]
- Alvarez González, M. Croquis Tecnológico para la Creación de Modelos Digitales de Elevación del terreno. 2014. [Google Scholar]
- Chen, L.; Xu, J. Optimal delaunay triangulations. J. Comput. Math. 2004, 22, 299–308. [Google Scholar]
- Castillo García, C.L.; Abreu Franco, D.E.; Álvarez González, M. Evaluación de distintas fórmulas empíricas para el cálculo del tiempo de concentración en la cuenca urbana del río Bélico y Cubanicay, ciudad de Santa Clara. Enfoque UTE 2021, 12, 51–64. [Google Scholar] [CrossRef]
- Castillo-García, C. Curvas de Intensidad-Duración-Frecuencia para la ciudad de Santa Clara, Cuba Intensity-Duration-Frequency Curves for Santa Clara. Tecnolgías Cienc. Agua 2022. [Google Scholar] [CrossRef]
- Castillo García, C.L.; Carvajal González, V.M. Modelación hidrológica de la cuenca urbana del río Bélico en la ciudad de Santa Clara, Cuba. Enfoque UTE 2023, 77–93. [Google Scholar] [CrossRef]
- Kastridis, A.; Stathis, D. Evaluation of Hydrological and Hydraulic Models Applied in Typical Mediterranean Ungauged Watersheds Using Post-Flash-Flood Measurements. Hydrology 2020, 7, 12. [Google Scholar] [CrossRef]
- Chow, V.; Maidment, D.; Mays, L. Hidrología Aplicada; McGraw-Hill Science/Engineering/Math: Bogotá, Colombia, 1994; ISBN 958-600-171-7. [Google Scholar]
- USGS. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; USGS Water Supply Paper 2339; USGS: Dallas, TX, USA, 1989; Volume 2339.
- Dyhouse, G.; Hatchett, J.; Benn, J. Floodplain Modeling Using HEC-RAS; (U.S.), H.E.C.; Haestad Press: Waterbury, CT, USA, 2003; ISBN 0971414106. [Google Scholar]
- Castillo-García, C. Parametric models of rainfall temporal distribution at the Yabú meteorological station in Villa Clara province, Cuba. Tecnolgías Cienc. Agua 2022. [Google Scholar] [CrossRef]
- Singh, V.P.; Eng, D. Handbook of Applied Hydrology.; McGraw-Hill Education: New York, NY, USA, 2017; ISBN 9780071835091. [Google Scholar]
- Ibrahim, H.; Elsebaie, A.Q.K.; Alnahit, A.O. Mapping and Assessment of Flood Risk in the Wadi Al-Lith Basin, Saudi Arabia Ibrahim. Water 2023, 15, 902. [Google Scholar]


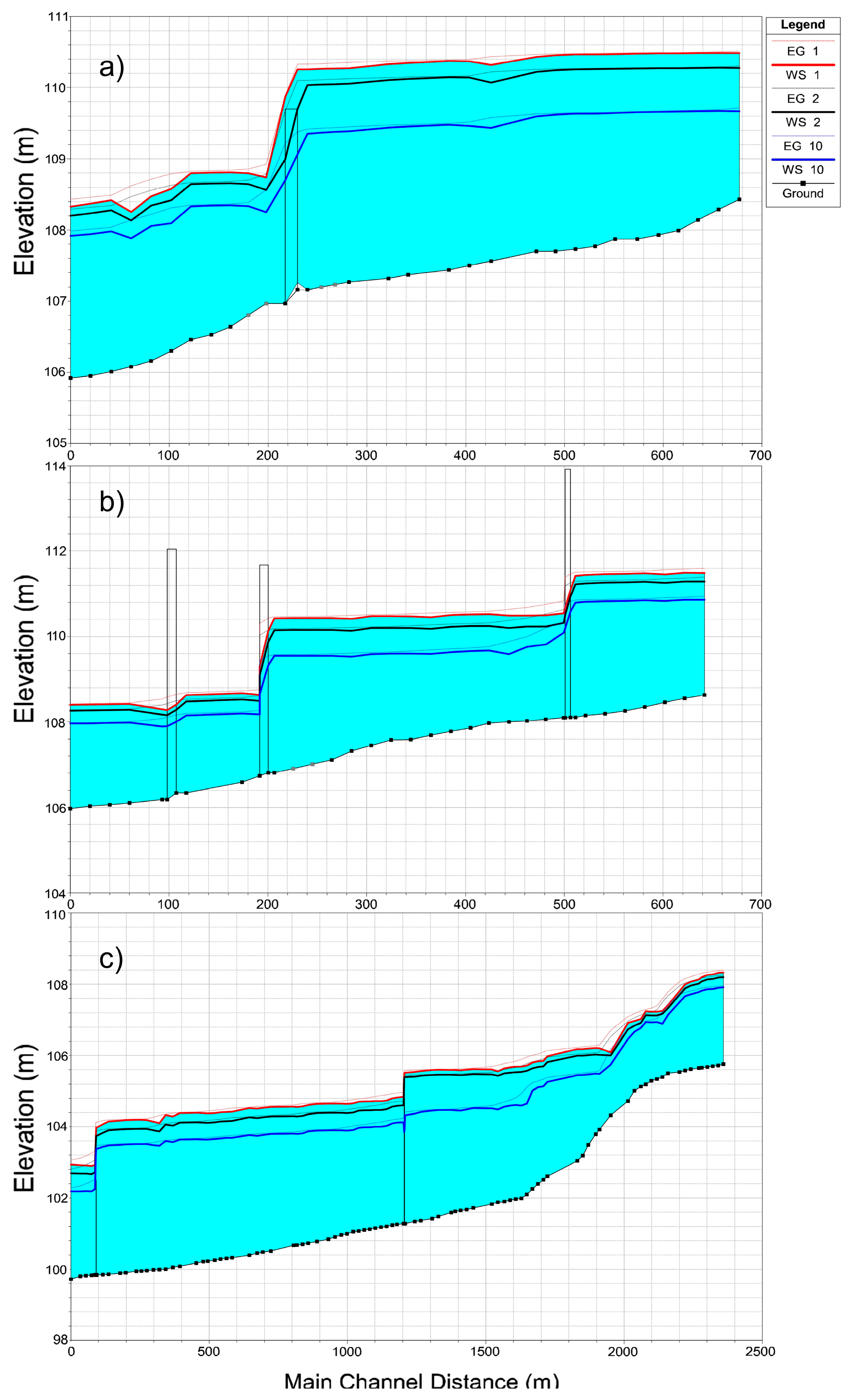


| Beta | |||||||
|---|---|---|---|---|---|---|---|
| River | Section | Control Section | Scenario | Total Flow | Depth | Total Speed | Energy |
| % | (m3/s) | (m) | (m/s) | (m) | |||
| Bélico | T1 | 27 + 14 | 1 | 85.69 | 3.09 | 1.20 | 110.50 |
| T1 | 27 + 14 | 2 | 74.32 | 2.81 | 1.17 | 110.22 | |
| T1 | 27 + 14 | 10 | 52.60 | 2.20 | 1.16 | 109.61 | |
| Cubanicay | T1 | 2 + 87 | 1 | 84.23 | 3.74 | 1.65 | 110.33 |
| T1 | 2 + 87 | 2 | 71.98 | 1.27 | 2.16 | 111.10 | |
| T1 | 2 + 87 | 10 | 49.98 | 1.80 | 2.36 | 109.38 | |
| T2 | 16 + 38.46 | 1 | 170.04 | 3.71 | 1.51 | 105.90 | |
| T2 | 16 + 38.46 | 2 | 146.48 | 3.55 | 1.42 | 105.72 | |
| T2 | 16 + 38.46 | 10 | 101.96 | 2.62 | 1.88 | 104.94 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Socas, R.A.M.; González, M.A.; Marín, Y.R.; Castillo-García, C.L.; Jiménez, J.; da Silva, L.d.D.d.J.; González-Rodríguez, L. Simulating the Flood Limits of Urban Rivers Embedded in the Populated City of Santa Clara, Cuba. Water 2023, 15, 1805. https://doi.org/10.3390/w15101805
Socas RAM, González MA, Marín YR, Castillo-García CL, Jiménez J, da Silva LdDdJ, González-Rodríguez L. Simulating the Flood Limits of Urban Rivers Embedded in the Populated City of Santa Clara, Cuba. Water. 2023; 15(10):1805. https://doi.org/10.3390/w15101805
Chicago/Turabian StyleSocas, Rolando Ariel Martínez, Michael Alvarez González, Yoandy Rodríguez Marín, Carlos Lázaro Castillo-García, Jorge Jiménez, Luciana das Dores de Jesus da Silva, and Lisdelys González-Rodríguez. 2023. "Simulating the Flood Limits of Urban Rivers Embedded in the Populated City of Santa Clara, Cuba" Water 15, no. 10: 1805. https://doi.org/10.3390/w15101805






