Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions
Abstract
:1. Introduction
- Assess the accuracy of PERSIANN-CDR, CMORPH, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Final Run to capture the precipitation characteristics versus rain gauges’ measurements at different temporal resolutions in arid zones.
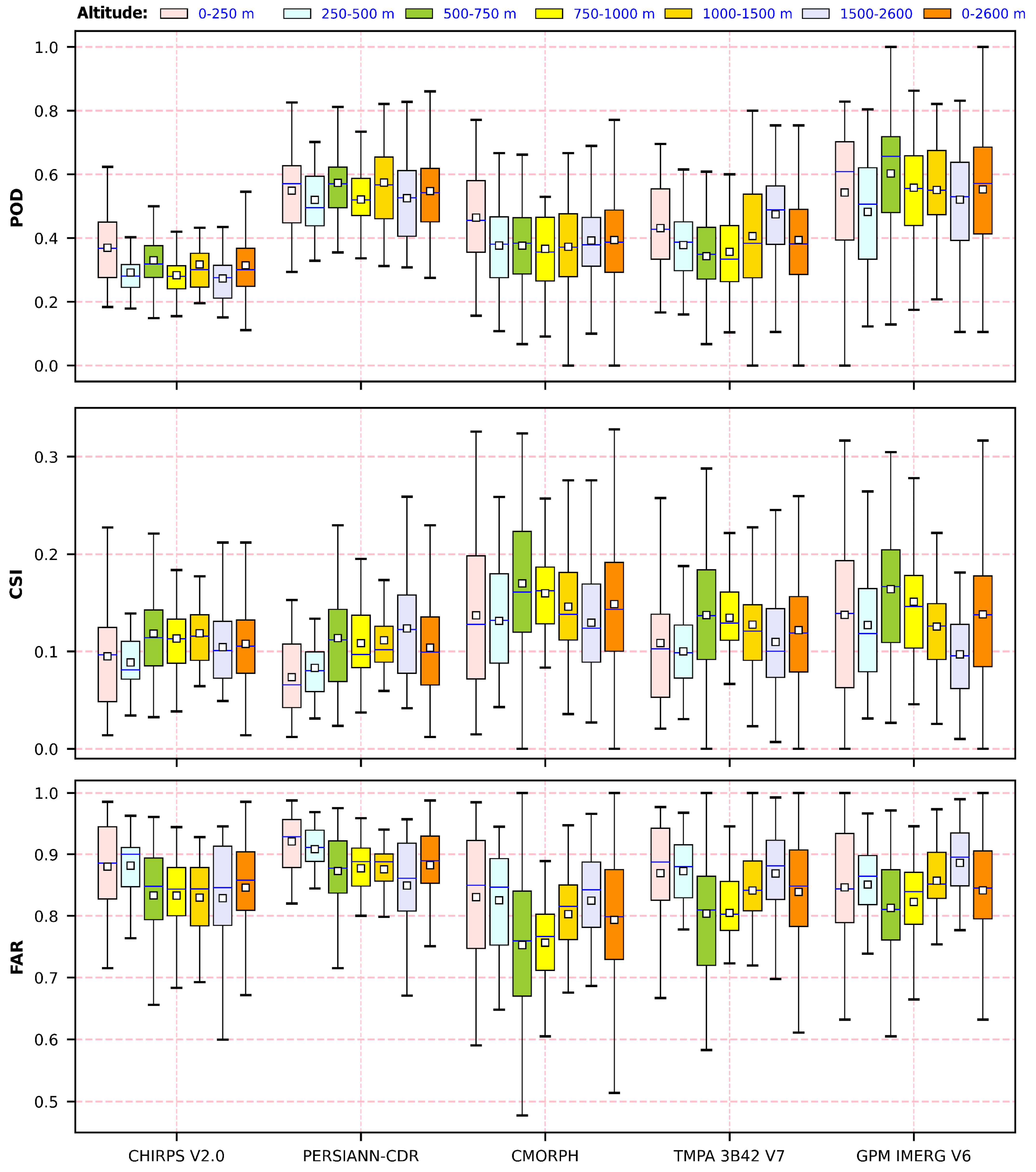
- Evaluate the SPDSs performance at different altitudes.
2. Materials and Methods
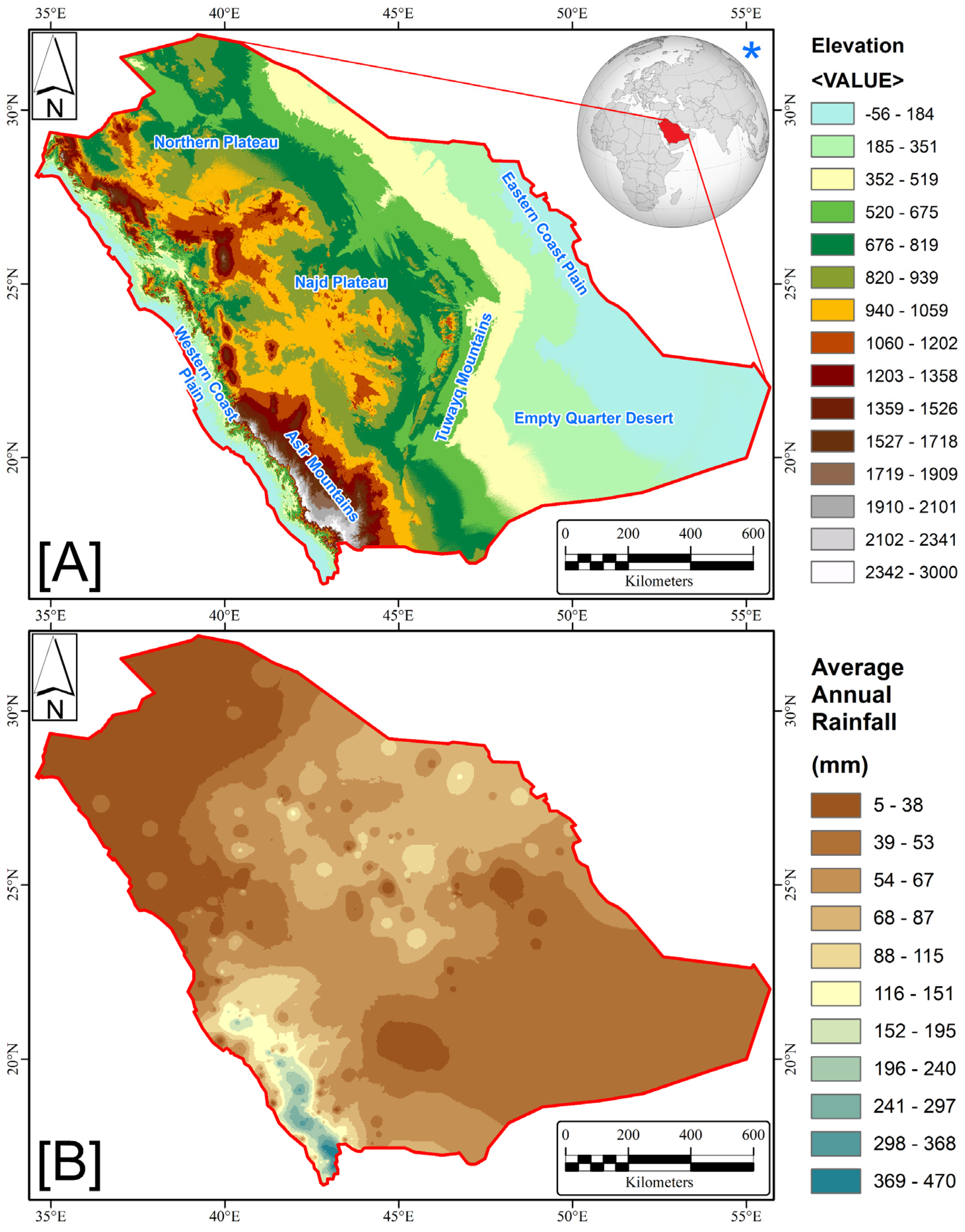
2.1. The Study Area
2.2. Satellite Data
2.3. Rain Gauges
2.4. Evaluation of SPDSs
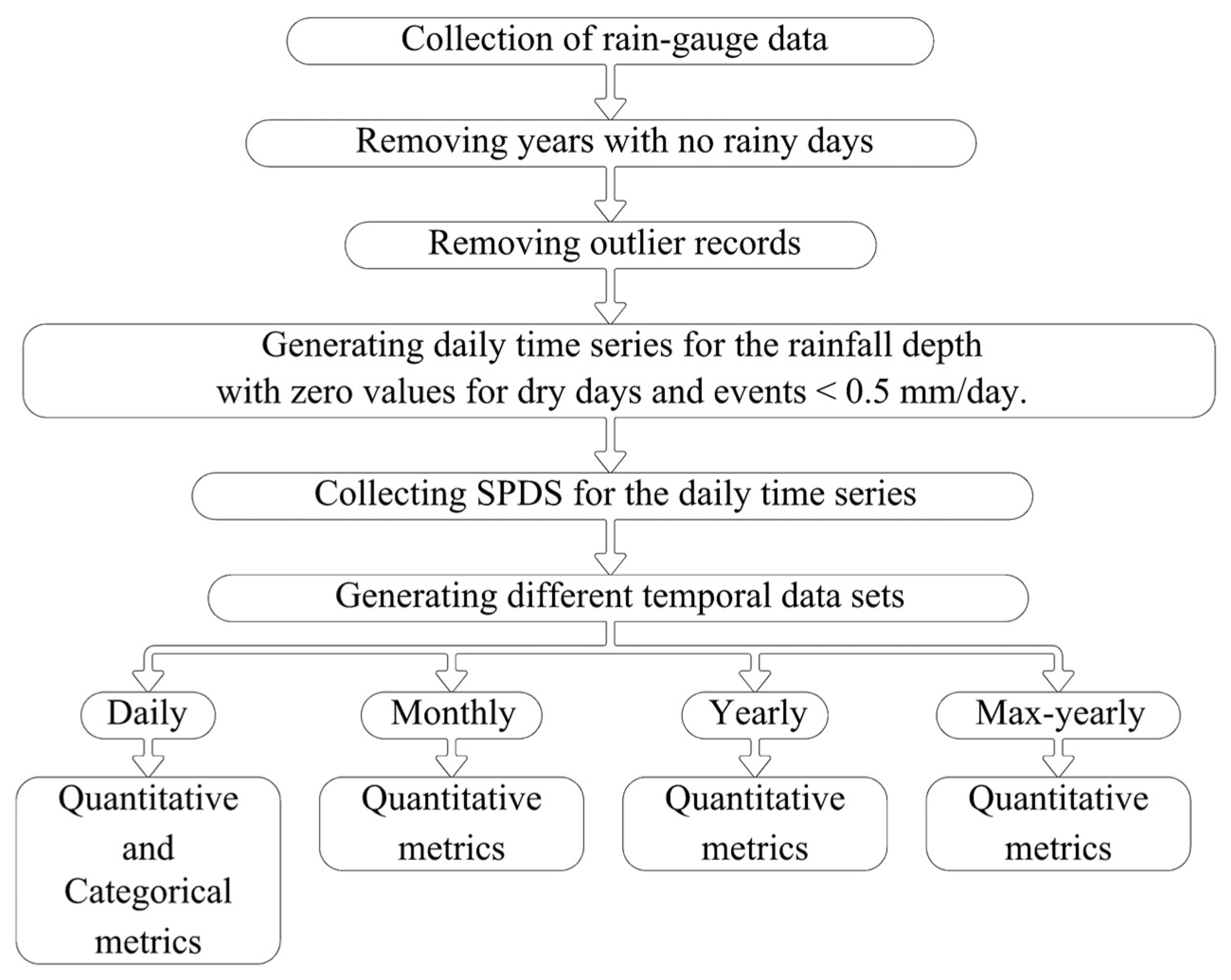
2.4.1. Rain-Gauge Data Screening
2.4.2. Quantitative Statistical Metrics
2.4.3. Categorical Metrics
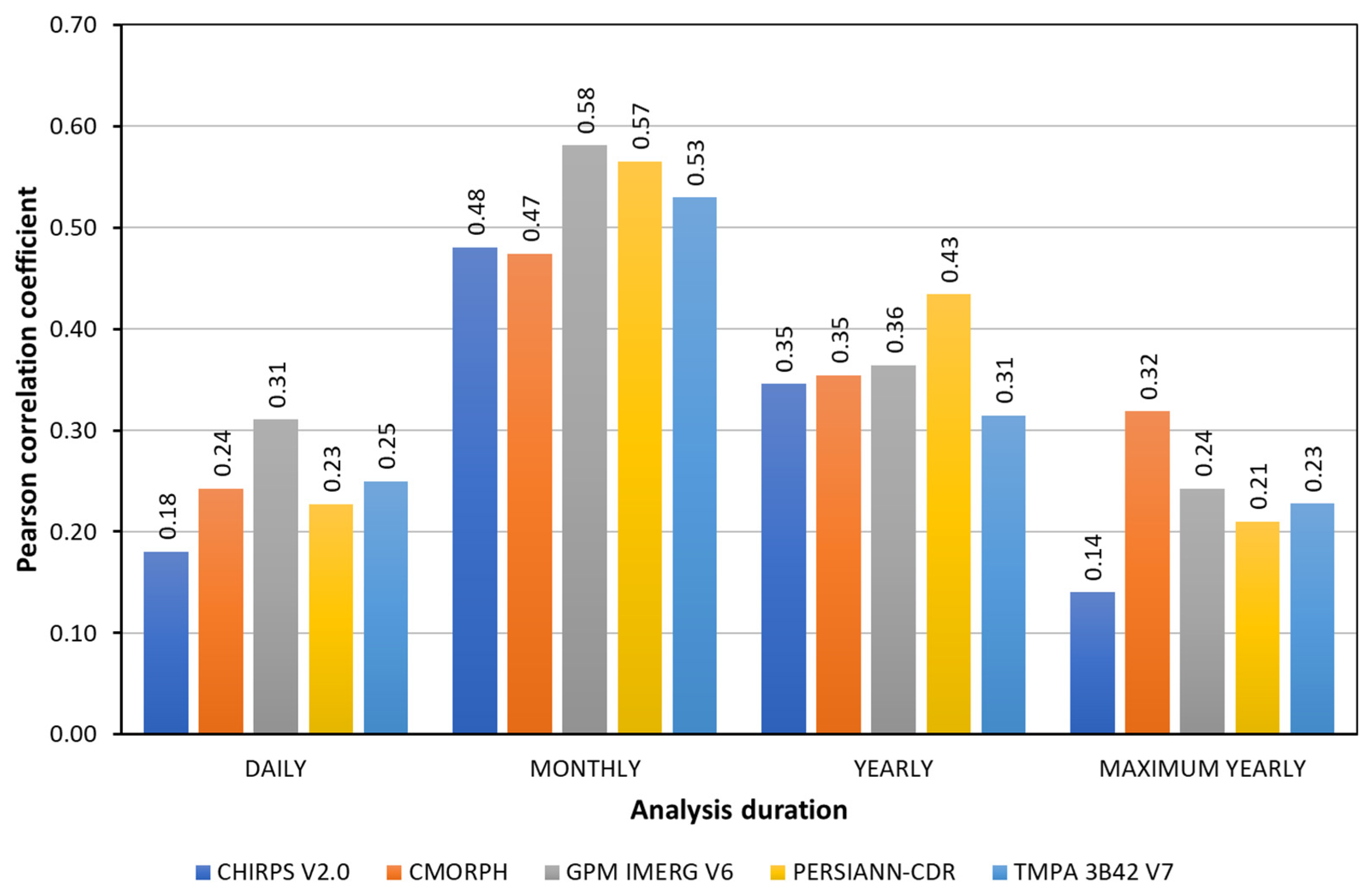
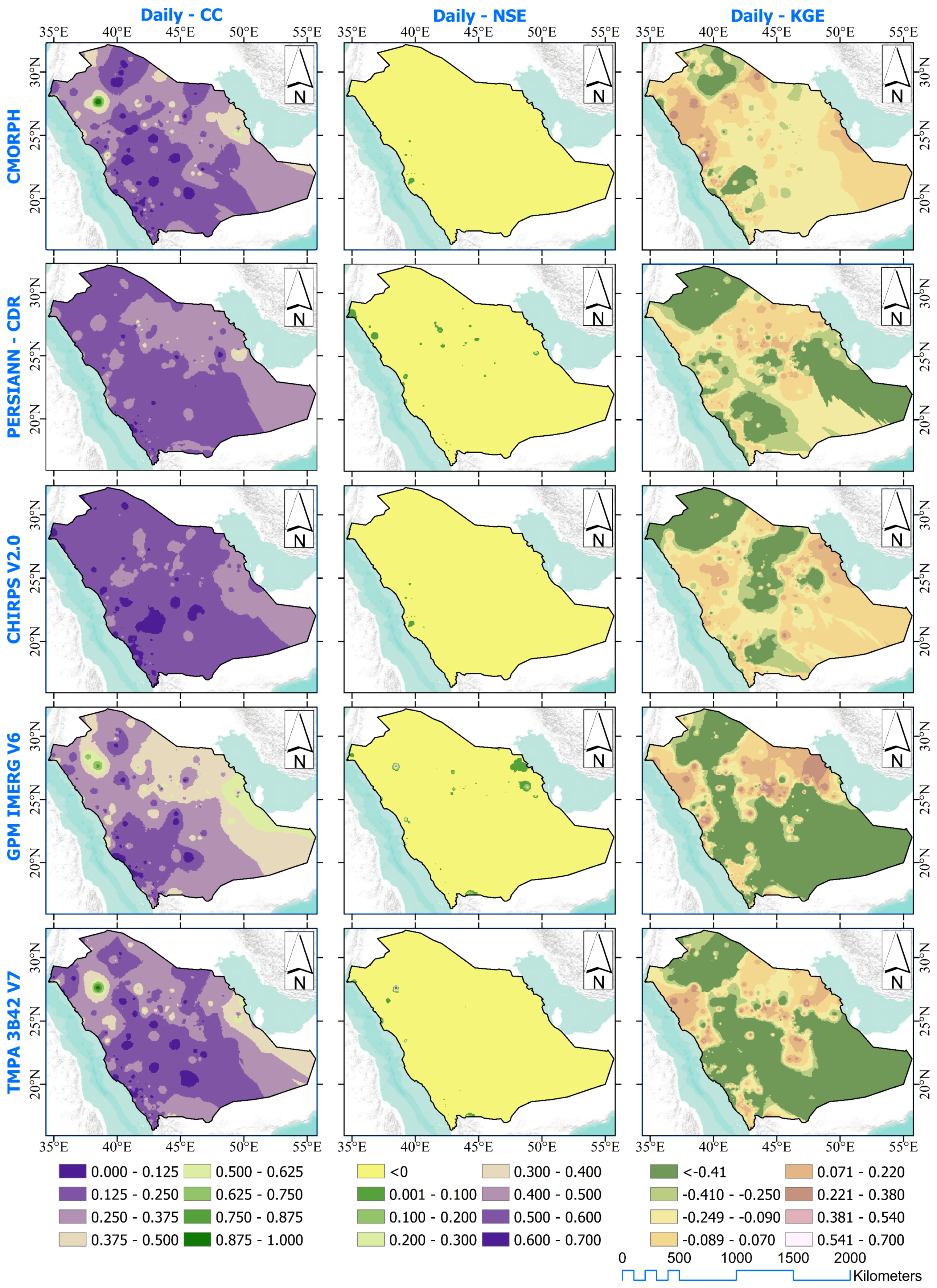
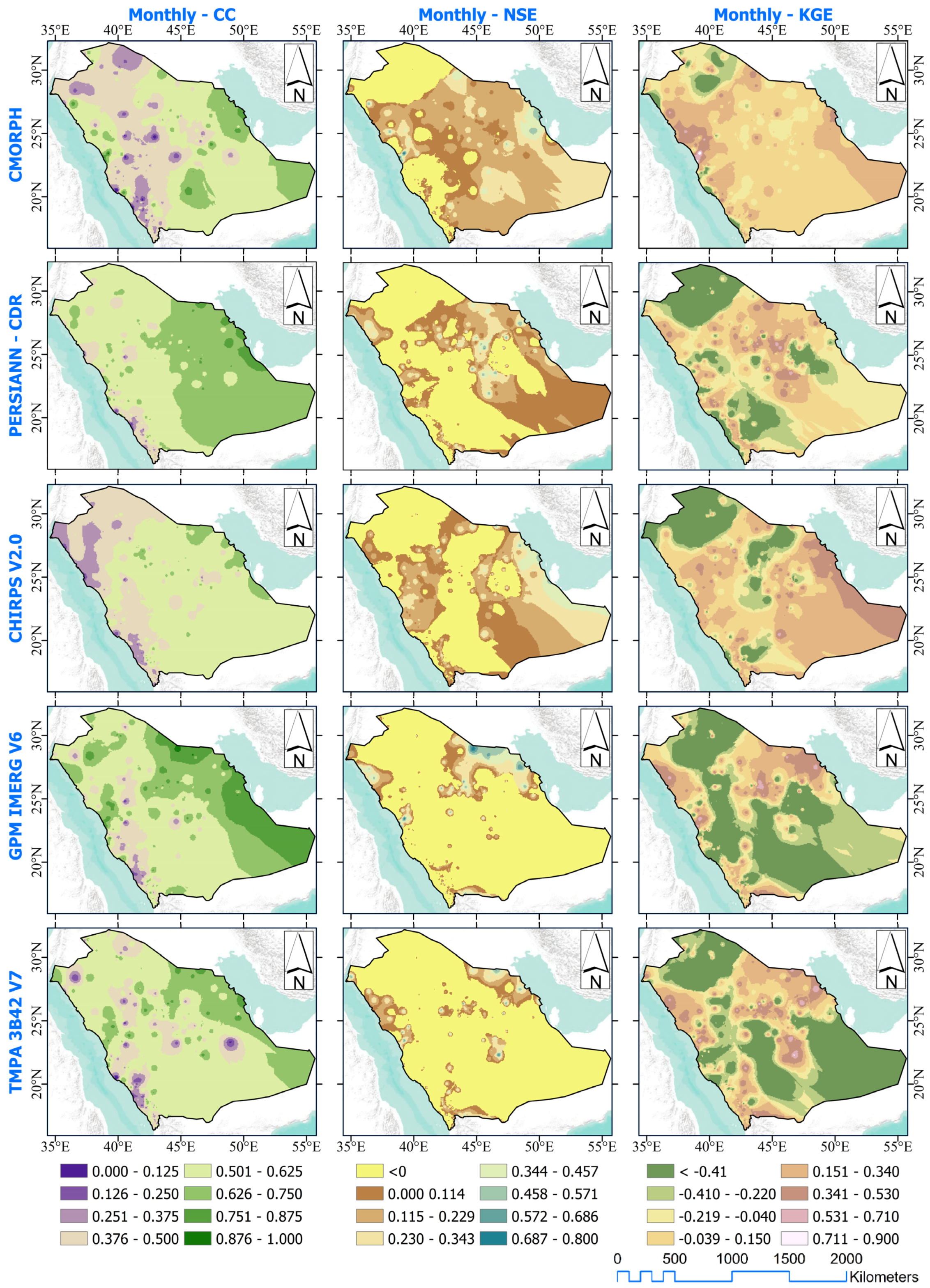
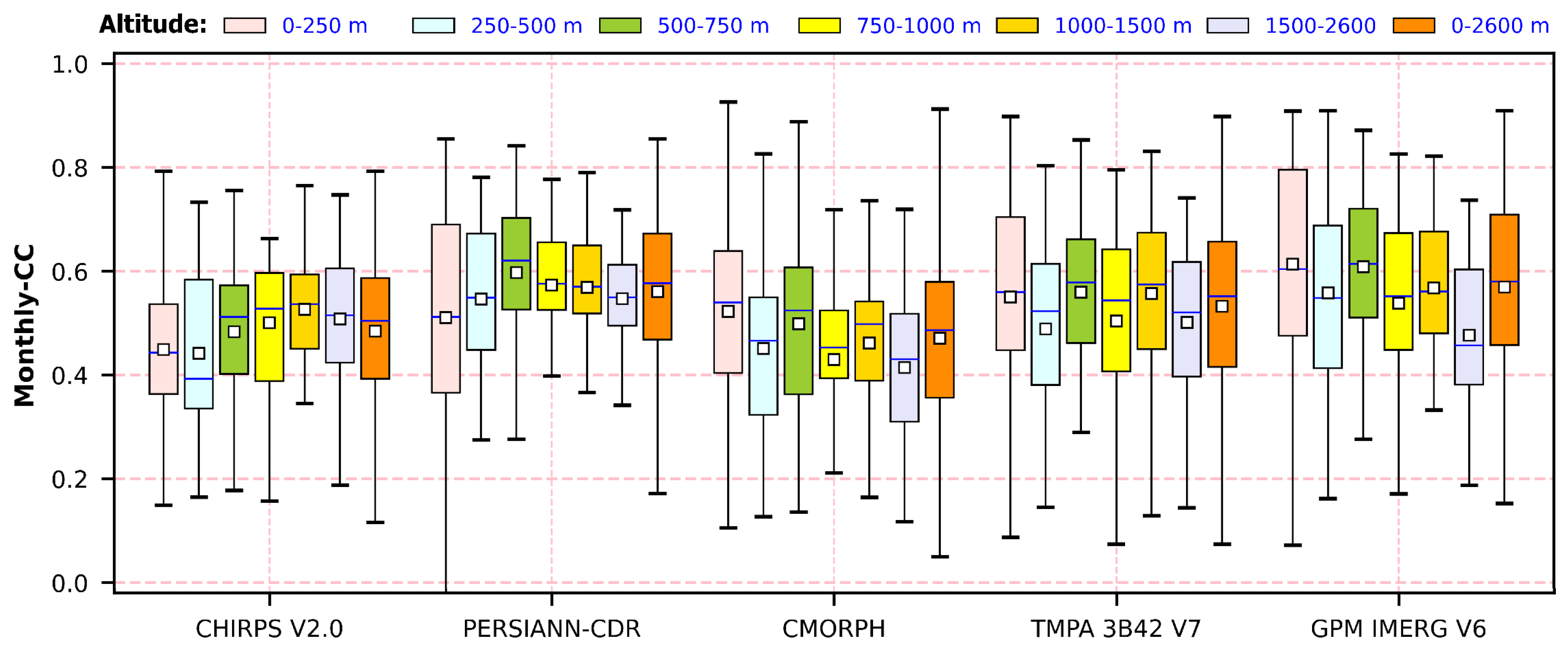
3. Results and Discussion
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, F.; Zhang, L.; Wah Win, K.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data sparse mountainous watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Petersen, W.A.; Christian, H.J.; Rutledge, S.A. TRMM observations of the global relationship between ice water content and lightning. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Dewan, A.; Hu, K.; Kamruzzaman, M.; Uddin, M.R. Evaluating the spatiotemporal pattern of concentration, aggressiveness and seasonality of precipitation over Bangladesh with time–series Tropical Rainfall Measuring Mission data. In Extreme Hydroclimatic Events and Multivariate Hazards in a Changing Environment; Elsevier: Amsterdam, The Netherlands, 2019; pp. 191–219. ISBN 9780128148990. [Google Scholar]
- Nashwan, M.S.; Shahid, S.; Dewan, A.; Ismail, T.; Alias, N. Performance of five high resolution satellite-based precipitation products in arid region of Egypt: An evaluation. Atmos. Res. 2019, 236, 104809. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.J. Selection of climate models for projection of spatiotemporal changes in temperature of Iraq with uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Wang, X. Uncertainty in estimated trends using gridded rainfall data: A case study of Bangladesh. Water 2019, 11, 349. [Google Scholar] [CrossRef] [Green Version]
- Abdul Razzaq, Z.T. The feasibility of using TRMM satellite data for missing terrestrial stations in Iraq for mapping the rainfall contour lines. Civ. Eng. Beyond Limits 2020, 3, 15–19. [Google Scholar] [CrossRef]
- Himanshu, S.K.; Pandey, A.; Patil, A. Hydrologic Evaluation of the TMPA-3B42V7 Precipitation Data Set over an Agricultural Watershed Using the SWAT Model. J. Hydrol. Eng. 2018, 23, 05018003. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef] [Green Version]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Huffman, G.J.; Behrangi, A.; Bolvin, D.T.; Nelkin, E.J. GPCP Version 3.2 Daily Precipitation Data Set; Huffman, G.J., Behrangi, A., Bolvin, D.T., Nelkin, E.J., Eds.; EarthData: Greenbelt, MD, USA, 2022. [Google Scholar]
- Xie, P.; Chen, M.; Shi, W. CPC unified gauge-based analysis of global daily precipitation. In Proceedings of the Preprints, 24th Conference on Hydrology, Atlanta, GA, USA, 17–21 January 2010; American Meteorogical Society: New York, NY, USA; Volume 2. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. TRMM (TMPA) Precipitation L3 1 Day 0.25 Degree × 0.25 Degree V7; Savtchenko, A., Ed.; EarthData: Greenbelt, MD, USA, 2010. [Google Scholar]
- Pingping, X.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1; National Centers for Environmental Information: Asheville, NC, USA, 2019. [Google Scholar]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.; Braithwaite, D.; Ashouri, H. NOAA Climate Data Record (CDR) of Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN-CDR), Version 1 Revision 1; National Centers for Environmental Information: Asheville, NC, USA, 2017. [Google Scholar]
- Hong, Y.; Gochis, D.; Cheng, J.T.; Hsu, K.L.; Sorooshian, S. Evaluation of PERSIANN-CCS rainfall measurement using the NAME event rain gauge network. J. Hydrometeorol. 2007, 8, 469–482. [Google Scholar] [CrossRef] [Green Version]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, K.; Kong, L.; Yang, Z.; Singh, P.; Guo, F.; Xu, Y.; Tang, X.; Hao, J. GPM Annual and Daily Precipitation Data for Real-Time Short-Term Nowcasting: A Pilot Study for a Way Forward in Data Assimilation. Water 2021, 13, 1422. [Google Scholar] [CrossRef]
- Dembélé, M.; Schaefli, B.; van de Giesen, N.; Mariéthoz, G. Suitability of 17 gridded rainfall and temperature datasets for large-scale hydrological modelling in West Africa. Hydrol. Earth Syst. Sci. 2020, 24, 5379–5406. [Google Scholar] [CrossRef]
- Kumar, B.; Lakshmi, V. Accessing the capability of TRMM 3B42 V7 to simulate streamflow during extreme rain events: Case study for a Himalayan River Basin. J. Earth Syst. Sci. 2018, 127, 27. [Google Scholar] [CrossRef] [Green Version]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of satellite rainfall products through hydrologic simulation in a fully distributed hydrologic model. Water Resour. Res. 2011, 47, 1–11. [Google Scholar] [CrossRef]
- Musie, M.; Sen, S.; Srivastava, P. Comparison and evaluation of gridded precipitation datasets for streamflow simulation in data scarce watersheds of Ethiopia. J. Hydrol. 2019, 579, 124168. [Google Scholar] [CrossRef]
- Wang, Q.; Xia, J.; She, D.; Zhang, X.; Liu, J.; Zhang, Y. Assessment of four latest long-term satellite-based precipitation products in capturing the extreme precipitation and streamflow across a humid region of southern China. Atmos. Res. 2021, 257, 105554. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Aryal, A.; Kawaike, K.; Yamanoi, K.; Nakagawa, H.; Bhatta, B.; Karki, S.; Thapa, B.R. Evaluation of precipitation elasticity using precipitation data from ground and satellite-based estimates and watershed modeling in Western Nepal. J. Hydrol. Reg. Stud. 2021, 33, 100768. [Google Scholar] [CrossRef]
- Abdelmoneim, H.; Soliman, M.R.; Moghazy, H.M. Evaluation of TRMM 3B42V7 and CHIRPS Satellite Precipitation Products as an Input for Hydrological Model over Eastern Nile Basin. Earth Syst. Environ. 2020, 4, 685–698. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, C.; Yeh, P.J.F.; Li, J.; Hu, B.X.; Feng, P.; Jun, C. Evaluation and comparison of precipitation estimates and hydrologic utility of CHIRPS, TRMM 3B42 V7 and PERSIANN-CDR products in various climate regimes. Atmos. Res. 2022, 265, 105881. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borga, M.; Boudevillain, B.; Buytaert, W.; Chang, C.H.; Delrieu, G.; Hong, Y.; Hsu, Y.C.; et al. Multiregional satellite precipitation products evaluation over complex terrain. J. Hydrometeorol. 2016, 17, 1817–1836. [Google Scholar] [CrossRef]
- Liu, C.Y.; Aryastana, P.; Liu, G.R.; Huang, W.R. Assessment of satellite precipitation product estimates over Bali Island. Atmos. Res. 2020, 244, 105032. [Google Scholar] [CrossRef]
- Helmi, A.M.; Zohny, O. Flash Flood Risk Assessment in Egypt BT. In Flash Floods in Egypt; Negm, A.M., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 253–312. ISBN 978-3-030-29635-3. [Google Scholar]
- Youssif, M.M.A. Hydrological Study of Large Wadies in Arid and Semi Arid Areas Case Study: Wadi El-Arish, Northern Sinai, Egypt. Master’s Thesis, Cairo University, Cairo, Egypt, 2008. [Google Scholar]
- Hamdi, E.Y. Precipitation Analysis and Hydrological Modeling in Arid Regions. Master’s Thesis, Cairo University, Cairo, Egypt, 2005. [Google Scholar]
- Javanmard, S.; Yatagai, A.; Nodzu, M.I.; Bodaghjamali, J.; Kawamoto, H. Comparing high-resolution gridded precipitation data with satellite rainfall estimates of TRMM-3B42 over Iran. Adv. Geosci. 2010, 25, 119–125. [Google Scholar] [CrossRef] [Green Version]
- Miao, C.; Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Duan, Q. Evaluation of the PERSIANN-CDR daily rainfall estimates in capturing the behavior of extreme precipitation events over China. J. Hydrometeorol. 2015, 16, 1387–1396. [Google Scholar] [CrossRef] [Green Version]
- Abdulrida, M.A.; Al-Jumaily, K.J. Comparisons of Monthly Rainfall Data with Satellite Estimates of TRMM 3B42 over Iraq. Int. J. Sci. Res. Publ. 2016, 6, 494–501. [Google Scholar]
- Moazami, S.; Golian, S.; Hong, Y.; Sheng, C.; Kavianpour, M.R. Comprehensive evaluation of four high-resolution satellite precipitation products under diverse climate conditions in Iran. Hydrol. Sci. J. 2016, 61, 420–440. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS Satellite-Rainfall Products over Mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Wei, G.; Lü, H.; Crow, W.T.; Zhu, Y.; Wang, J.; Su, J. Comprehensive Evaluation of GPM-IMERG, CMORPH, and TMPA Precipitation Products with Gauged Rainfall over Mainland China. Adv. Meteorol. 2018, 2018, 3024190. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Tang, G.; Han, Z.; Guo, X.; Hong, Y. Global intercomparison and regional evaluation of GPM IMERG Version-03, Version-04 and its latest Version-05 precipitation products: Similarity, difference and improvements. J. Hydrol. 2018, 564, 342–356. [Google Scholar] [CrossRef]
- Sultana, R.; Nasrollahi, N. Evaluation of remote sensing precipitation estimates over Saudi Arabia. J. Arid Environ. 2018, 151, 90–103. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Wang, X. Assessment of satellite-based precipitation measurement products over the hot desert climate of Egypt. Remote Sens. 2019, 101, 555. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Shukla, A.K.; Ojha, C.S.P.; Singh, R.P.; Pal, L.; Fu, D. Evaluation of TRMM precipitation dataset over Himalayan Catchment: The upper Ganga Basin, India. Water 2019, 11, 613. [Google Scholar] [CrossRef] [Green Version]
- Bruster-Flores, J.L.; Ortiz-Gómez, R.; Ferriño-Fierro, A.L.; Guerra-Cobián, V.H.; Burgos-Flores, D.; Lizárraga-Mendiola, L.G. Evaluation of precipitation estimates CMORPH-CRT on regions of Mexico with different climates. Water 2019, 11, 1722. [Google Scholar] [CrossRef] [Green Version]
- Gumindoga, W.; Rientjes, T.H.M.; Haile, A.T.; Makurira, H.; Reggiani, P. Performance evaluation of CMORPH satellite precipitation product in the Zambezi Basin. Int. J. Remote Sens. 2019, 40, 7730–7749. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Tan, M.L.; Li, X.; Wang, G.; He, R. Nine-year systematic evaluation of the GPM and TRMM precipitation products in the shuaishui river basin in east-central China. Remote Sens. 2020, 12, 1042. [Google Scholar] [CrossRef]
- Cavalcante, R.B.L.; da Ferreira, D.B.S.; Pontes, P.R.M.; Tedeschi, R.G.; da Costa, C.P.W.; de Souza, E.B. Evaluation of extreme rainfall indices from CHIRPS precipitation estimates over the Brazilian Amazonia. Atmos. Res. 2020, 238, 104879. [Google Scholar] [CrossRef]
- Nwachukwu, P.N.; Satge, F.; El Yacoubi, S.; Pinel, S.; Bonnet, M.P. From trmm to GPM: How reliable are satellite-based precipitation data across Nigeria? Remote Sens. 2020, 12, 3964. [Google Scholar] [CrossRef]
- Kim, J.; Han, H. Evaluation of the CMORPH high-resolution precipitation product for hydrological applications over South Korea. Atmos. Res. 2021, 258, 105650. [Google Scholar] [CrossRef]
- Geleta, C.D.; Deressa, T.A. Evaluation of Climate Hazards Group InfraRed Precipitation Station (CHIRPS) satellite-based rainfall estimates over Finchaa and Neshe Watersheds, Ethiopia. Eng. Rep. 2021, 3, e12338. [Google Scholar] [CrossRef]
- Yang, W.T.; Fu, S.M.; Sun, J.H.; Zheng, F.; Wei, J.; Ma, Z. Comparative Evaluation of the Performances of TRMM-3B42 and Climate Prediction Centre Morphing Technique (CMORPH) Precipitation Estimates over Thailand. J. Meteorol. Soc. Jpn. 2021, 99, 1525–1546. [Google Scholar] [CrossRef]
- Yu, S.; Lu, F.; Zhou, Y.; Wang, X.; Wang, K.; Song, X.; Zhang, M. Evaluation of Three High-Resolution Remote Sensing Precipitation Products on the Tibetan Plateau. Water 2022, 14, 2169. [Google Scholar] [CrossRef]
- Anjum, M.N.; Irfan, M.; Waseem, M.; Leta, M.K.; Niazi, U.M.; Rahman, S.U.; Ghanim, A.; Mukhtar, M.A.; Nadeem, M.U. Assessment of PERSIANN-CCS, PERSIANN-CDR, SM2RAIN-ASCAT, and CHIRPS-2.0 Rainfall Products over a Semi-Arid Subtropical Climatic Region. Water 2022, 14, 147. [Google Scholar] [CrossRef]
- Pai, D.S.; Rajeevan, M.; Sreejith, O.P.; Mukhopadhyay, B.; Satbha, N.S. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. MAUSAM 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of topography and rainfall intensity on the accuracy of imerg precipitation estimates in an arid region. Remote Sens. 2021, 13, 13. [Google Scholar] [CrossRef]
- Al-Ahmadi, K.; Al-Ahmadi, S. Rainfall-altitude relationship in Saudi Arabia. Adv. Meteorol. 2013, 2013, 363029. [Google Scholar] [CrossRef]
- Al-Zahrani, M.; Husain, T. An algorithm for designing a precipitation network in the south-western region of Saudi Arabia. J. Hydrol. 1998, 205, 205–216. [Google Scholar] [CrossRef]
- Hag-Elsafi, S.; El-Tayib, M. Spatial and statistical analysis of rainfall in the Kingdom of Saudi Arabia from 1979 to 2008. Weather 2016, 71, 262–266. [Google Scholar] [CrossRef]
- Almazroui, M. Calibration of TRMM rainfall climatology over Saudi Arabia during 1998–2009. Atmos. Res. 2011, 99, 400–414. [Google Scholar] [CrossRef]
- Hasanean, H.; Almazroui, M. Rainfall: Features and variations over Saudi Arabia, a review. Climate 2015, 3, 578–626. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, M.A.; Almazroui, M. Climatological study of the southwestern region of Saudi Arabia. I. Rainfall analysis. Clim. Res. 1998, 9, 213–223. [Google Scholar] [CrossRef]
- Subyani, A.M. Geostatistical study of annual and seasonal mean rainfall patterns in southwest Saudi Arabia/Distribution géostatistique de la pluie moyenne annuelle et saisonnière dans le Sud-Ouest de l’Arabie Saoudite. Hydrol. Sci. J. 2004, 49, 803–816. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef] [Green Version]
- Hsu, K.; Ashouri, H.; Braithwaite, D.; Sorooshian, S. Climate Algorithm Theoretical Basis Document (C-ATBD)—Precipitation—PERSIANN-CDR; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2014. [Google Scholar]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Koutsouris, A.J.; Chen, D.; Lyon, S.W. Comparing global precipitation data sets in eastern Africa: A case study of Kilombero Valley, Tanzania. Int. J. Climatol. 2016, 36, 2000–2014. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M. Climatologically aided interpolation (CAI) of terrestrial air temperature. Int. J. Climatol. 1995, 15, 221–229. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef] [Green Version]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef] [Green Version]
- Paredes-Trejo, F.; Barbosa, H.A.; Kumar, T.V.L.; Thakur, M.K.; de Oliveira Buriti, C. Assessment of the CHIRPS-Based Satellite Precipitation Estimates. In Inland Waters; Devlin, A., Pan, J., Shah, M.M., Eds.; IntechOpen: Rijeka, Croatia, 2020. [Google Scholar]
- NASA. Global Precipitation Measurement. Available online: https://gpm.nasa.gov/missions/TRMM/satellite/PR (accessed on 7 April 2022).
- Liu, Z. Comparison of versions 6 and 7 3-hourly TRMM multi-satellite precipitation analysis (TMPA) research products. Atmos. Res. 2015, 163, 91–101. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; et al. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. Atmos. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic ext. J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Momin, I.M.; Pai, D.S.; Rajagopal, E.N.; Basu, S. Comparison of TMPA-3B42 versions 6 and 7 precipitation products with gauge-based data over India for the southwest monsoon period. J. Hydrometeorol. 2015, 16, 346–362. [Google Scholar] [CrossRef]
- Qiao, L.; Hong, Y.; Chen, S.; Zou, C.B.; Gourley, J.J.; Yong, B. Performance assessment of the successive Version 6 and Version 7 TMPA products over the climate-transitional zone in the southern Great Plains, USA. J. Hydrol. 2014, 513, 446–456. [Google Scholar] [CrossRef]
- Xu, F.; Guo, B.; Ye, B.; Ye, Q.; Chen, H.; Ju, X.; Guo, J.; Wang, Z. Systematical Evaluation of GPM IMERG and TRMM 3B42V7 Precipitation Products in the Huang-Huai-Hai Plain, China. Remote Sens. 2019, 11, 697. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The global precipitation measurement (GPM) mission for science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Tan, J.; Xie, P. NASA GPM Integrated Multi-SatellitE Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document (ATBD) Version 06; National Aeronautics and Space Administration: Washington, DC, USA, 2020. [Google Scholar]
- Haan, C.T. Statistical Methods in Hydrology, 2nd ed.; Iowa State Press: Ames, IA, USA, 2002; ISBN 0813815037. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash--Sutcliffe and Kling--Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef] [Green Version]
- Schaefer, J.T. The Critical Success Index as an Indicator of Warning Skill. Weather Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Lin, Z.; Yao, X.; Du, J.; Zhou, Z. Refined Evaluation of Satellite Precipitation Products against Rain Gauge Observations along the Sichuan—Tibet Railway. J. Meteorol. Res. 2022, 36, 779–797. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation ofsatellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]




| Precipitation Product | Spatial Coverage | Temporal Coverage | Maximum Spatial Resolution | Maximum Temporal Resolution | Reference | ||||
|---|---|---|---|---|---|---|---|---|---|
| West | East | South | North | From | To | ||||
| The African rainfall climatology–V2 (ARC) | 20° | 55° | 40° | 40° | 1983 | Near Present | 0.1° × 0.1° | 10 Days | [10] |
| Tropical applications of meteorology using satellite data and ground-based observations (TAMSAT) | 20° | 55° | 40° | 40° | 1983 | Near Present | 0.0375° × 0.0375° | Daily | [11] |
| Global precipitation climatology center (GPCP) | 180° | 180° | 90° | 90° | 2000 | 2020 | 0.5° × 0.5° | Daily | [12] |
| Climate prediction center (CPC) | 180° | 180° | 89.5° | 89.5° | 1979 | Near Present | 0.5° × 0.5° | Daily | [13] |
| Tropical rainfall measuring mission–3B43 V7 (TRMM) | 180° | 180° | 50° | 50° | 1998 | 2019 | 0.25° × 0.25° | 3 h | [14] |
| Climate prediction center morphing method (CMORPH) | 180° | 180° | 60° | 60° | 1998 | Near Present | 8 × 8 km | 30 min | [15] |
| Precipitation estimation from remotely sensed information using artificial neural networks (PERSIANN) | 180° | 180° | 60° | 60° | 2000 | Near Present | 0.25° × 0.25° | 1 h | [16] |
| PERSIANN-climate data record (PERSIANN-CDR) | 180° | 180° | 60° | 60° | 1983 | Near Present | 0.25° × 0.25° | Daily | [17] |
| PERSIANN–cloud classification system (PERSIANN-CCS) | 180° | 180° | 60° | 60° | 2003 | Near Present | 0.04° × 0.04° | 1 h | [18] |
| Climate hazards group infrared Precipitation combined with terrestrial stations observations (CHIRPS) | 180° | 180° | 50° | 50° | 1981 | Near Present | 0.05° × 0.05° | Daily | [19] |
| The global precipitation measurement mission (GPM) | 180° | 180° | 90° | 90° | 2000 | Near Present | 0.1° × 0.1° | 30 min | [20] |
| SPDSs | Region | Duration | Main Conclusions | Reference |
|---|---|---|---|---|
| TMPA-3B42V6 | Tapajos river, 500,000 km2, Brazil. | 2000–2003 | The generated modeled hydrographs had acceptable accuracy based on the comparison with 23 flow gauges along the river and its tributaries. | [23] |
| CMORPH TMPA-3B42RT TMPA 3B42 PERSIANN | Gilgel Abay, 1656 km2, a mountainous watershed in northwest Ethiopia | 2006–2007 | The microwave-based SPSDs (CMORPH and TMPA 3B42RT) had a better performance than the infrared-based dataset (PERSIANN). The merged rain gauges and satellite data (TMPA 3B42) gave to lowest performance and inconsistencies | [24] |
| TMPA-3B42V7 CHIRPS, CFSR PERSIANN-CDR | Lake Ziway basin, 7311 km2, Ethiopia | 1985–2004 | All SPDSs have a low correlation on daily temporal scale runoff simulations. CHIRPS, PERSIANN-CDR, and TRMM had good performance on the monthly temporal scale. | [25] |
| CHIRPS, CMORPH TMPA-3B42 V7 PERSIANN | Ganjiang River Basin, 80,948 km2, China | 2000–2014 | TMPA outperformed other SPDSs. CMORPH PDS significantly underestimated streamflow. | [26] |
| CHIRPS, PERSIANN-CCS, IMERG | West Rapti River basin, 5082 km2, Western Nepal | 1986–2015 | The IMERG SPSD had the best accuracy among the used SPDSs. | [27] |
| TMPA-3B42V7 CHIRPS | Eastern Nile Basin, 325,000 km2, East Africa | 1998–2007 | TMPA 3B42V7 slightly had a better performance than CHIRPS in calculating the modeled monthly stream flow. | [28] |
| CHIRPS, PERSIANN-CDR TMPA 3B42 V7 | Three different climate basins in China | 2002–2015 | The three SPDSs performed better in humid regions than in arid ones. TMPA 3B42 V7 showed the best performance over CHIRPS and PERSIANN-CDR, respectively. PERSIANN-CDR had the best performance in the arid basin. Low accuracy included for the three SPDSs on a daily scale | [29] |
| SPDSs | Region | Ground Stations | Temporal Resolution | Duration | Main Conclusions | Reference |
|---|---|---|---|---|---|---|
| TMPA-3B42 | IRAN | Grid * | Annual | 1998–2006 | The TRMM precipitation dataset underestimated the average annual precipitation. | [35] |
| PERSIANN-CDR | China | 1400 | Daily Extreme Events | 1983–2006 | PERSIANN-CDR efficiently captured the precipitation behavior, especially in humid areas. The efficiency was significantly reduced in arid and mountainous areas. | [36] |
| TMPA-3B42 | Iraq | 4 | Monthly | 2000–2010 | Acceptable agreement between TMPA3B42 and ground stations for monthly temporal scale. | [37] |
| TMPA-3B42V7, PERSIANN, CMORPH | Iran | 1000 | Daily | 2003–2008 | 3B42V7 had a better performance than the SPDSs. | [38] |
| IMERG V6, TMPA-3B42 V7 GSMap | India | Grid ** | Daily | Single monsoon 2014 | The IMERG and GSMap SPDSs showed better performance than TMPA SPDS, especially for low precipitation rates. | [39] |
| CHIRPS | China | 2480 | Daily | 1981–2014 | CHIRPS performed better for large rainfall depths than it does in arid and semi-arid land. The variation of CHIRPS performance is strongly affected by monsoon movement. | [40] |
| GPM-IMERG (early, late, final) | KSA | 189 | Daily | October 2015 April 2016 | IMERG’s final run showed significant improvement over the early and late run over 80% of the KSA area. | [41] |
| TMPA-3B42V7, CMORPH GPM-IMERGV05 | China | 542 | Daily Seasonal Annual | 2014–2017 | IMERG results had better performance than TMPA 3B42 and CMORPH SPDSs. The quality of precipitation estimates reduced over the Tibetan plateau. | [42] |
| GPM IMERG (03,04, 05) | CHINA | 30,000 | Daily | June 2014 May 2015 | V04 and V05 Final run show significant differences and improvements from V03 except for mountainous and arid zones. | [43] |
| PERSIANN-CDR PERSIANN TMPA-3B42 CMORPH | KSA | 29 | Daily Monthly | 2003–2011 | All satellites performed better in the wet season. | [44] |
| GSMap GPM-IMERG CHIRPS | Egypt | 29 | Daily | March 2014 May 2018 | None of the SPDSs showed consistent performance to be evaluated as the best quality or lowest quality among them. | [45] |
| TMPA-3B42 GPM-IMERG | CHINA | 830 | Daily | 2000–2017 | The GPM dataset outperformed the TRMM dataset over the same. The performance is better in humid areas and reduced in arid and mountainous areas. | [46] |
| TMPA 3B43V7 | India | Grid ** | Monthly | 1998–2013 | The correlation is higher during post-monsoon and winter seasons than pre-monsoon and monsoon seasons. | [47] |
| CMORPH-CRT | Mexico | 14 | 30 min and Daily | 2000–2018 | Weak to moderate correlation with ground stations. CMORPH-CRT overestimates the number of rainy days. | [48] |
| CMORPH | South Africa | 60 | Daily, Weekly, Seasonal | 1998–2013 | CMORPH predicts 60% of rainfall events. The performance in lower temporal resolution (weeks or months) is better than in high temporal resolution (days). | [49] |
| GPM IMERG V6 TMPA 3B42V7 | CHINA | 13 | Daily | 2009–2017 | The GPM dataset performed better than the TRMM dataset. The correlation coefficient for both falls below 0.6. | [50] |
| CHIRPS | BRAZIL | 45 | Monthly, Annual | 1981–2017 | CHIRPS dataset has a good correlation with mean monthly data with underestimation for the rainiest months and extreme rainfall events. It was concluded that the CHIRPS data could not provide a proper presentation of the trends in rainfall indices. | [51] |
| 16 SPDSs | Nigeria | 11 | Monthly | 2000–2012 | The IMERG SPDS is consistent with its predecessor TMPA, and the best performance was concluded for IMERG-V6 and Multi-Source Weighted-Ensemble Precipitation MSWEP v. 2.2. | [52] |
| CMORPH | South Korea | 48 | Hourly, Daily, Monthly, Annual | 1998–2015 | CMORPH underestimates precipitation over South Korea. Annual-to-daily resolution can be used adequately in hydrological modeling. The hourly resolution requires corrections. | [53] |
| CHIRPS | Ethiopia | 6 | Monthly | 1991–2015 | CHIRPS overestimates the mean monthly data but with a strong positive linear correlation. | [54] |
| TMPA 3B42V7 CMORPH | Thailand | 120 | Daily, Monthly, and Annual | 1998–2012 | Both TRMM and CMORPH had limited ability for producing the characteristics of extreme events. Generally, the TRMM outperformed the CMOPRH in representing precipitation. | [55] |
| TMPA-3B42V7, CMORPH IMERGV05 | Tibetan Plateau China | 87 | Monthly Annual | 2001–2016 | GPM outperformed the TRMM and CMORPH. Underestimation of the annual precipitation was recorded for the three satellites. | [56] |
| PERSIANN-CCS, PERSIANN-CDR SM2RAIN-ASCAT CHIRPS-2.0 | Punjab Province—Pakistan | 26 | Daily, Monthly, Seasonal Annual | 2010–2018 | CHIRPS-2.0 and SM2RAIN-ASCAT outperformed PERSIANN products. | [57] |
| Zone Name | Zone Code | Total Rain Gauges | Rain Gauges Daily Analysis | Rain Gauges Monthly Analysis | Rain Gauges Yearly Analysis |
|---|---|---|---|---|---|
| Holy Makkah | MQ | 45 | 45 | 45 | 39 |
| Asir | AS | 51 | 50 | 50 | 48 |
| Tabouk | TB | 9 | 9 | 9 | 9 |
| Jazan | GA | 24 | 24 | 24 | 21 |
| Al-Baha | BA | 15 | 15 | 15 | 12 |
| Al-Jouf | GO | 17 | 17 | 16 | 14 |
| Madinah | MN | 37 | 25 | 24 | 27 |
| Qaseem | QA | 23 | 22 | 22 | 19 |
| Al-Sharqiyah | SQ | 19 | 17 | 16 | 13 |
| Hail | HA | 21 | 21 | 21 | 15 |
| North Region | SH | 4 | 4 | 4 | 4 |
| Riyadh | RD | 52 | 52 | 48 | 37 |
| Najran | NG | 7 | 3 | 3 | 1 |
| Gauge Data | |||
|---|---|---|---|
| Rain (≥0.5 mm/Day) | No Rain (<0.5 mm/Day) | ||
| Satellite Data | Rain (≥0.5 mm/day) | Hits (H) | False alarm (F) |
| No rain (<0.5 mm/day) | Miss (M) | Correct negative | |
| Region | Daily | Monthly | Yearly | Max. Yearly | Region | Daily | Monthly | Yearly | Max. Yearly | Satellite |
|---|---|---|---|---|---|---|---|---|---|---|
| Al-Baha | 3.65 | 23.81 | 92.57 | 27.37 | Madinah | 1.83 | 11.20 | 36.77 | 14.27 | CHIRPS |
| 3.22 | 22.56 | 99.86 | 28.74 | 1.63 | 10.50 | 40.26 | 14.89 | CMORPH | ||
| 3.22 | 21.08 | 97.68 | 28.56 | 1.95 | 12.04 | 47.70 | 15.25 | GPM | ||
| 3.46 | 24.48 | 93.67 | 27.52 | 1.75 | 11.15 | 39.83 | 14.46 | PERSIANN | ||
| 3.45 | 26.99 | 111.02 | 28.23 | 1.93 | 11.43 | 43.99 | 15.22 | TRMM | ||
| Al-Jouf | 1.46 | 7.61 | 25.88 | 9.08 | Najran | 2.38 | 14.54 | 60.52 | 13.75 | CHIRPS |
| 1.51 | 7.93 | 28.98 | 12.23 | 1.94 | 13.49 | 58.90 | 12.43 | CMORPH | ||
| 1.49 | 7.32 | 23.95 | 11.10 | 2.09 | 14.06 | 74.31 | 16.00 | GPM | ||
| 1.27 | 8.04 | 25.17 | 8.45 | 2.11 | 13.55 | 61.37 | 16.71 | PERSIANN | ||
| 1.84 | 9.42 | 29.11 | 12.74 | 2.20 | 14.43 | 63.67 | 20.73 | TRMM | ||
| Al- Sharqiyah | 1.91 | 10.69 | 41.94 | 13.49 | North Region | 1.80 | 9.74 | 34.80 | 11.50 | CHIRPS |
| 1.37 | 8.57 | 33.28 | 11.88 | 1.42 | 8.89 | 30.65 | 11.38 | CMORPH | ||
| 1.76 | 10.55 | 38.90 | 16.37 | 1.53 | 7.93 | 29.16 | 11.45 | GPM | ||
| 1.81 | 10.93 | 43.41 | 14.61 | 1.61 | 10.11 | 35.32 | 11.86 | PERSIANN | ||
| 2.14 | 12.92 | 47.05 | 18.46 | 1.84 | 9.80 | 34.27 | 14.22 | TRMM | ||
| Asir | 3.09 | 20.42 | 76.54 | 20.08 | Qaseem | 2.61 | 13.77 | 47.85 | 18.70 | CHIRPS |
| 2.65 | 21.25 | 78.53 | 18.80 | 1.64 | 11.89 | 36.40 | 13.94 | CMORPH | ||
| 2.76 | 20.18 | 87.62 | 17.76 | 1.97 | 11.19 | 39.80 | 16.53 | GPM | ||
| 2.81 | 20.86 | 81.38 | 18.67 | 1.87 | 12.01 | 49.48 | 15.07 | PERSIANN | ||
| 2.98 | 21.26 | 88.48 | 22.74 | 2.45 | 13.11 | 43.82 | 16.49 | TRMM | ||
| Hail | 2.15 | 11.79 | 38.15 | 14.12 | Riyadh | 2.14 | 12.73 | 44.46 | 14.39 | CHIRPS |
| 1.44 | 9.33 | 28.23 | 11.98 | 1.45 | 10.03 | 36.53 | 11.82 | CMORPH | ||
| 1.69 | 9.73 | 34.21 | 14.65 | 2.00 | 12.96 | 49.52 | 16.91 | GPM | ||
| 1.81 | 11.77 | 41.80 | 13.46 | 1.84 | 12.03 | 44.67 | 13.55 | PERSIANN | ||
| 2.09 | 11.44 | 37.85 | 16.55 | 2.13 | 12.28 | 43.79 | 16.92 | TRMM | ||
| Holy Makkah | 2.63 | 16.07 | 56.73 | 19.67 | Tabouk | 1.55 | 8.34 | 26.53 | 15.32 | CHIRPS |
| 2.52 | 16.44 | 63.75 | 21.76 | 1.47 | 7.60 | 30.99 | 16.16 | CMORPH | ||
| 2.58 | 16.12 | 62.51 | 19.68 | 1.59 | 7.56 | 28.87 | 12.85 | GPM | ||
| 2.55 | 16.87 | 60.28 | 20.14 | 1.43 | 8.04 | 27.63 | 13.64 | PERSIANN | ||
| 2.78 | 17.45 | 64.69 | 19.60 | 1.67 | 8.37 | 31.82 | 14.16 | TRMM | ||
| Jazan | 4.14 | 29.79 | 128.55 | 20.97 | CHIRPS | |||||
| 4.32 | 31.67 | 126.43 | 25.26 | CMORPH | ||||||
| 4.28 | 28.37 | 118.75 | 21.51 | GPM | ||||||
| 4.10 | 32.68 | 134.32 | 19.98 | PERSIANN | ||||||
| 4.38 | 29.70 | 127.99 | 23.89 | TRMM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helmi, A.M.; Abdelhamed, M.S. Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions. Water 2023, 15, 92. https://doi.org/10.3390/w15010092
Helmi AM, Abdelhamed MS. Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions. Water. 2023; 15(1):92. https://doi.org/10.3390/w15010092
Chicago/Turabian StyleHelmi, Ahmed M., and Mohamed S. Abdelhamed. 2023. "Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions" Water 15, no. 1: 92. https://doi.org/10.3390/w15010092
APA StyleHelmi, A. M., & Abdelhamed, M. S. (2023). Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions. Water, 15(1), 92. https://doi.org/10.3390/w15010092









