Study on the Evolution of a Flooded Tailings Pond and Its Post-Failure Effects
Abstract
:1. Introduction
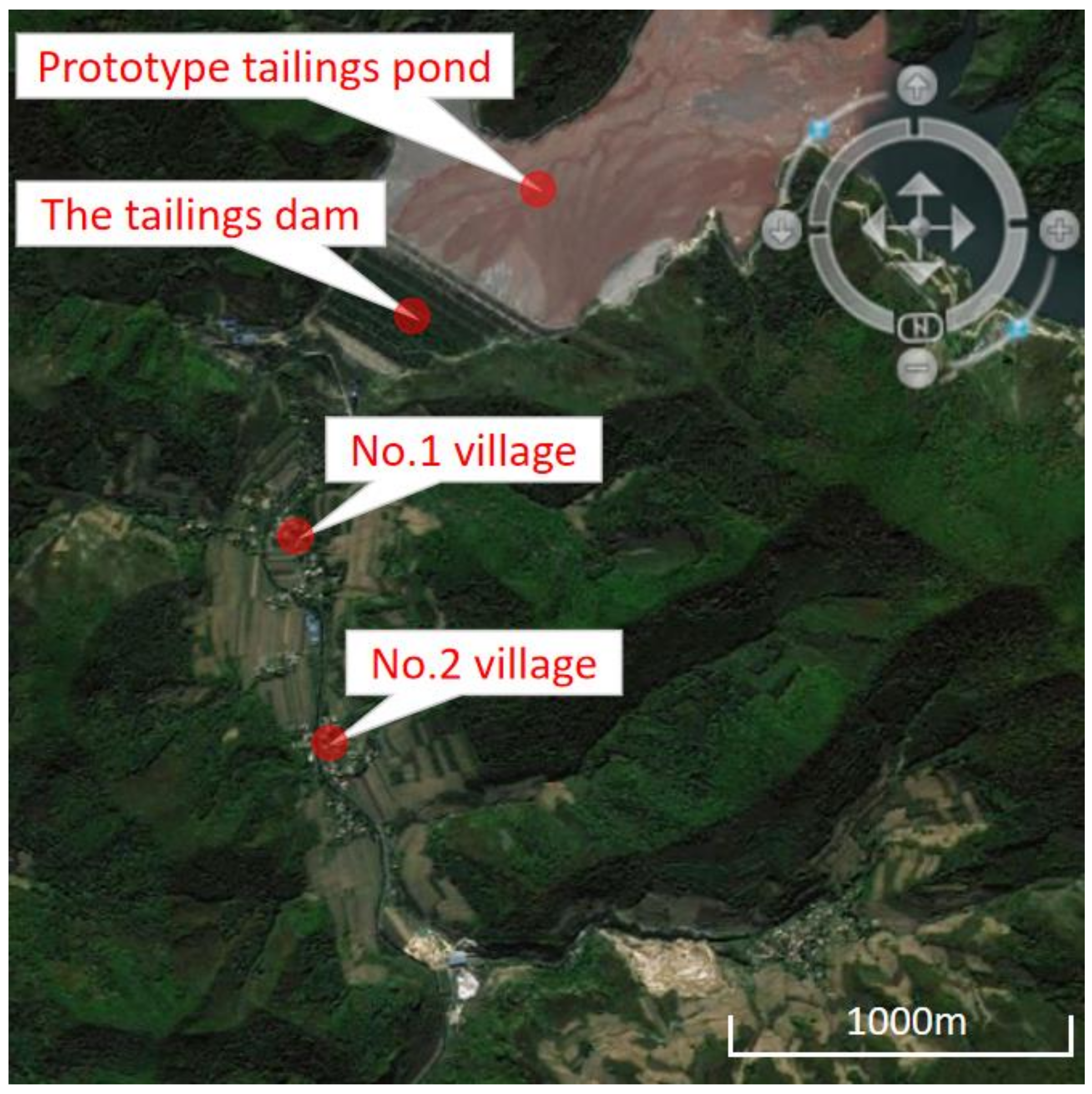
2. Overview of the Tailings Pond
3. Results Dam Failure Physical Model Test
3.1. Test Model
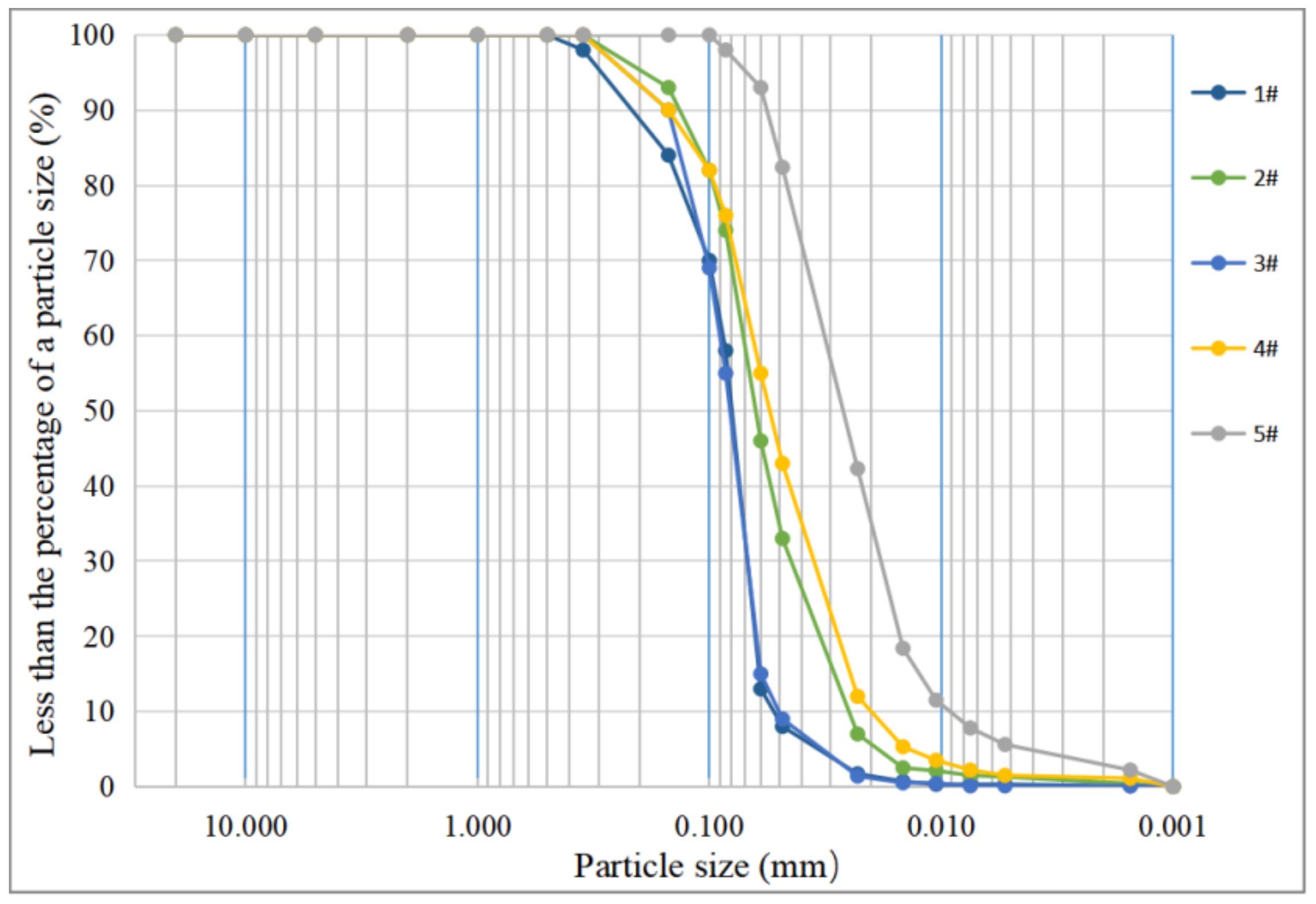
3.2. Test Materials
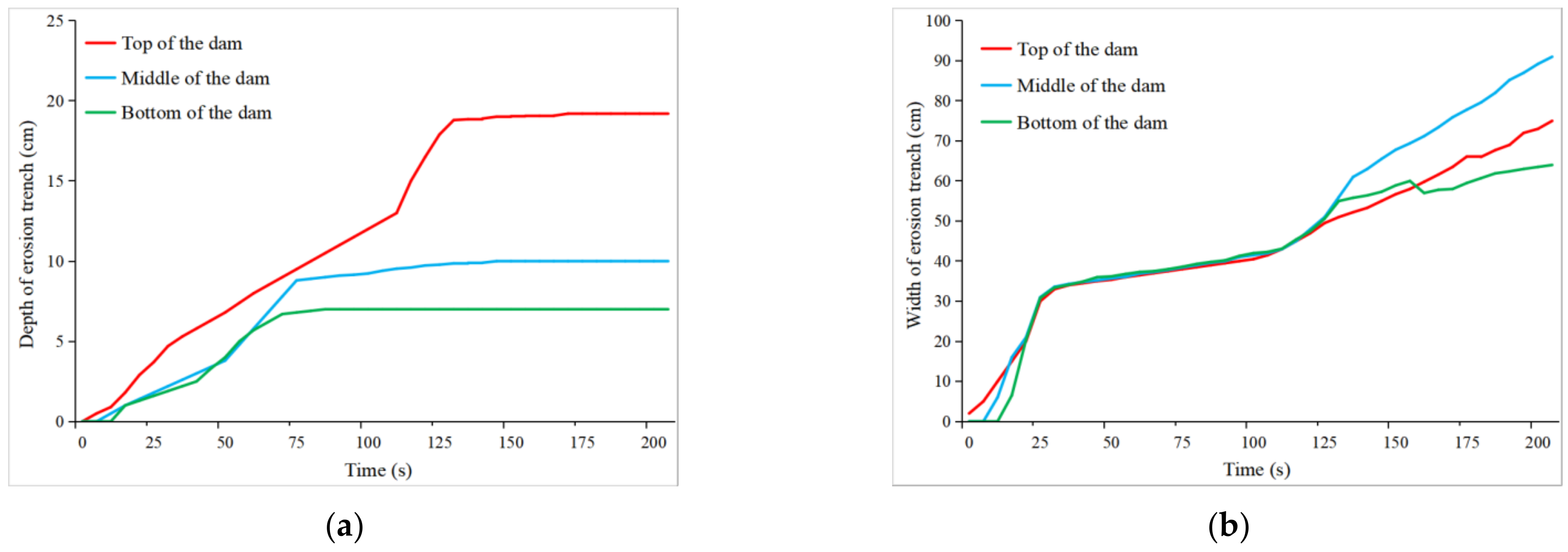
3.3. Dam Failure Process
- With the slow rise of the water level in the reservoir, a small breach began to appear at the weak part of the dam top under the effect of water infiltration, as shown in Figure 5b;
- The water in the reservoir flowed from the breach to the bottom of the dam, and under the action of water erosion, the tail sand was carried away from the outer slope of the dam, forming an erosion trench, as shown in Figure 5c;
- With the development of the erosion trench, the discharged tail sand gradually transformed from the initial single movement to a group movement, and the tail sand in the erosion trench at the bottom of the dam first started to slip, forming a critical surface after slipping, and then forming a multi-level small steep bump in the lower part of the erosion trench. Subsequently, the multi-level steep cans gradually fused into one large steep can, which continuously expanded upstream until extending into the reservoir. During the migration process, a large amount of tail sand was carried away from the dam, and the depth of the erosion trench further increased, as shown in Figure 5d;
- While the steep moved upwards, the flood erosion rate increased, and when the dam body on both sides of the erosion trench was completely saturated, cracks appeared. When the bond force is weaker than gravity, the dam body collapses along the cracks into the trench, and the width of the erosion trench increases at a faster rate, as shown in Figure 5e;
- When the amount of flood water in the reservoir gradually decreased, the rate of increase in the width and depth of the erosion trench slowed down. When the flood water in the reservoir was fully discharged, the erosion trench stopped developing and the dam tended to a stable state, as shown in Figure 5f.
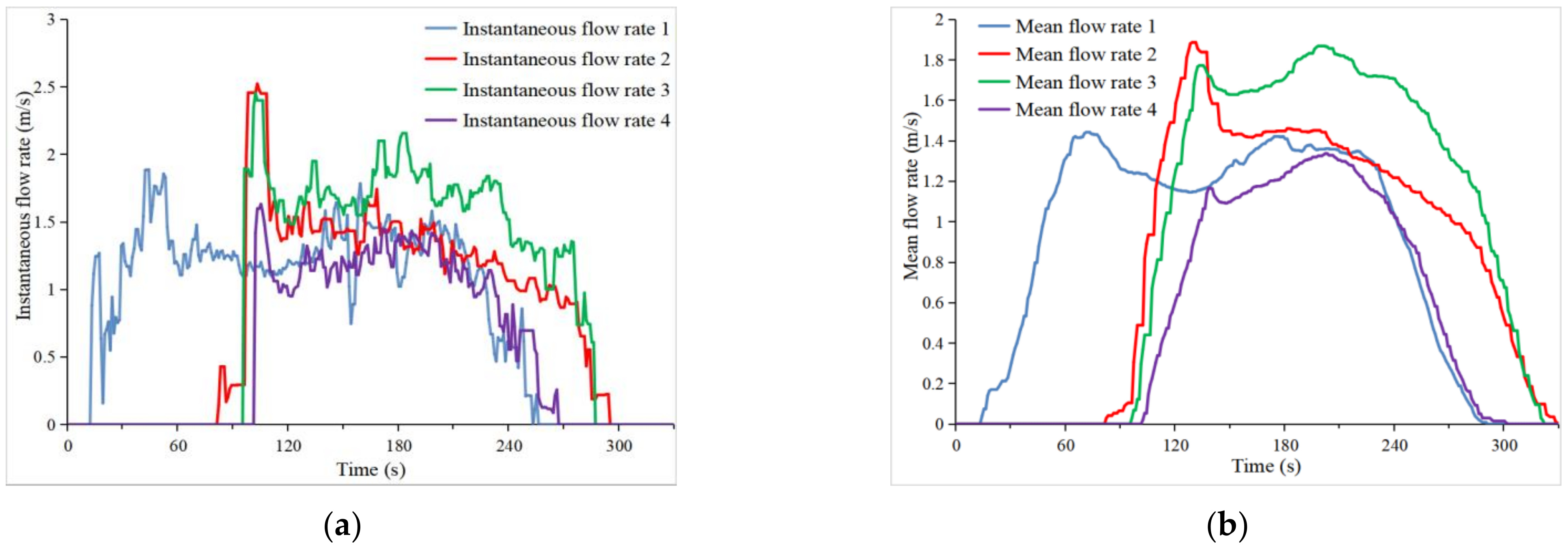
3.4. Evolution of Dam-Break Full-Field Velocity
3.5. Post-Dam Failure Impacts
4. Numerical Simulation
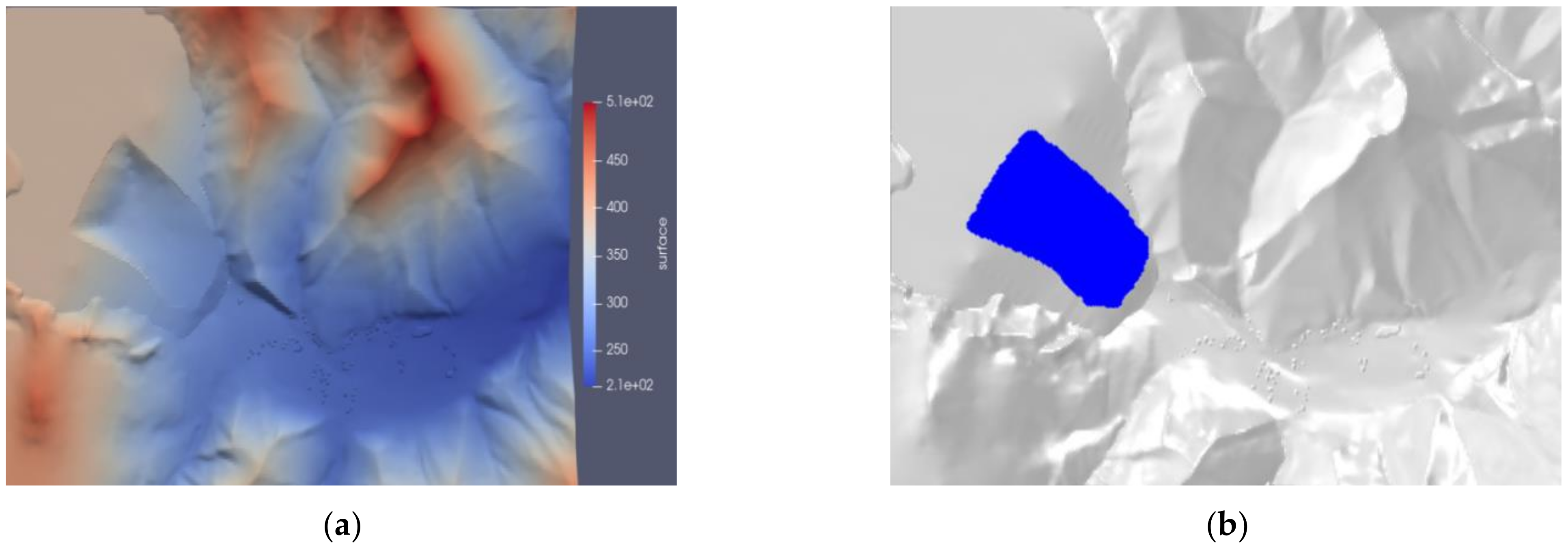
4.1. Numerical Model
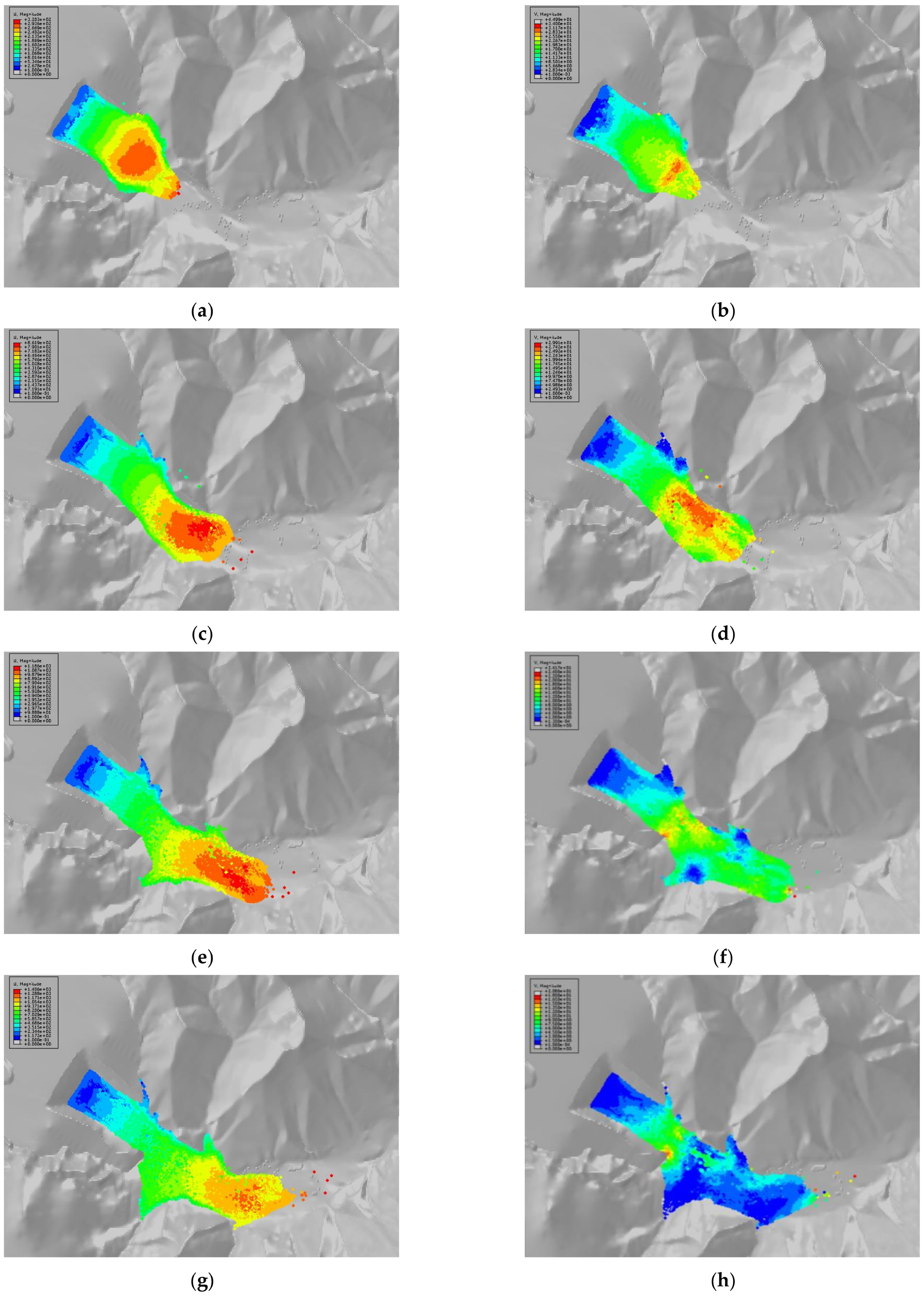
4.2. Analysis of Massflow Calculation Results
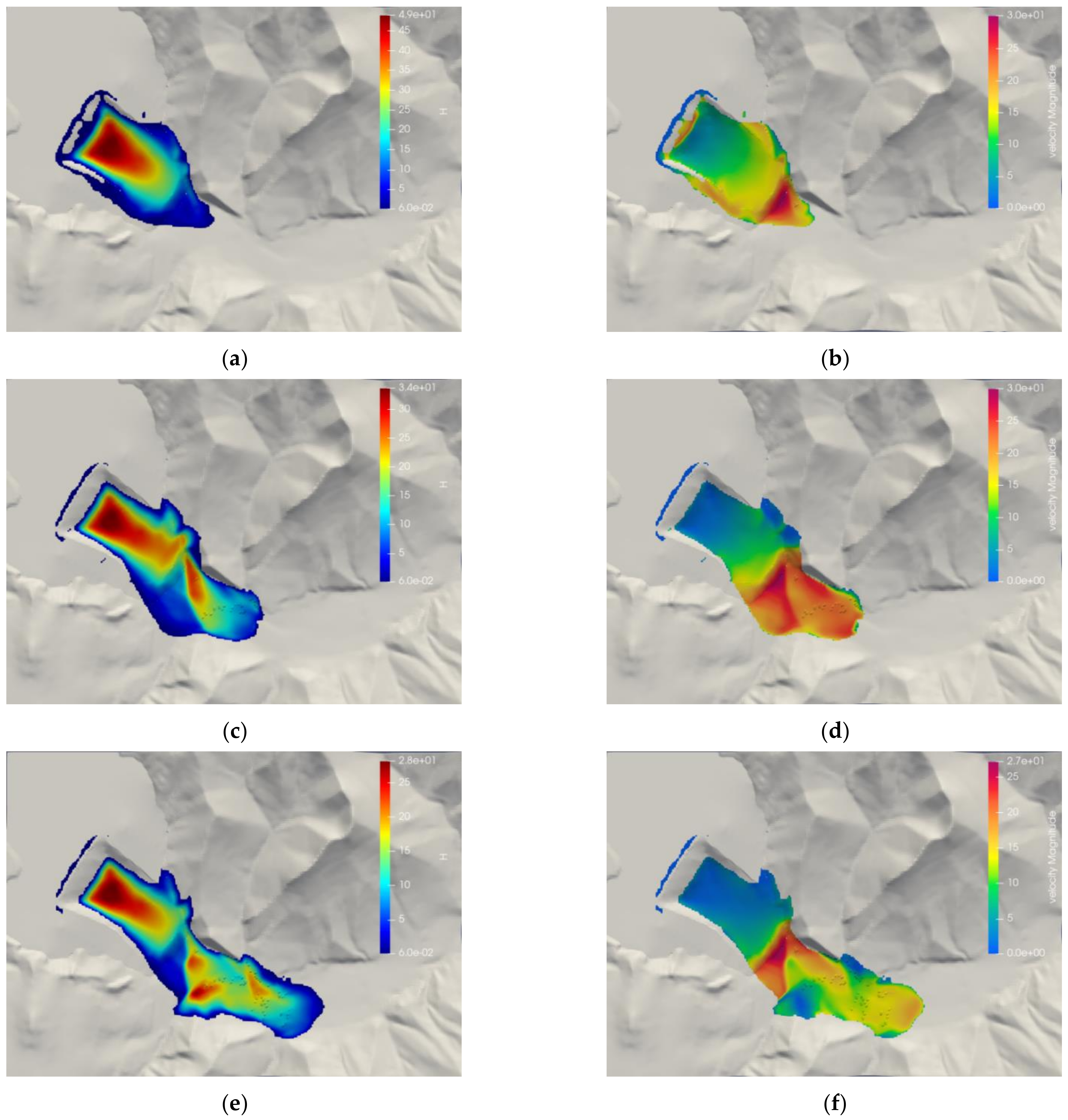
- At 20 s, the maximum accumulation height of the tail sand was about 48.8 m, mainly located in the reservoir area, and part of the sand flow advanced to 350 m downstream. The overall speed of the sand flow ahead of the breach was fast—the maximum was 30.2 m/s, and the direction was northeast;
- At 40 s, the maximum accumulation height of the sand flow was about 33.6 m, located in the reservoir area, and the farthest reach of the sand flow was 670 m downstream. The overall speed of sand flow in front of the breach was still fast, with a maximum of 30.0 m/s, and the direction began to shift northward due to the influence of the mountain;
- At 60 s, the maximum accumulation height of the sand flow was about 31.5 m, mainly located in the reservoir area and 250 m in front of the right side of the dam, and the sand flow reached as far as 1060 m downstream. The maximum travel speed of the sand flow was 27.1 m/s, located directly in front of the breach, and the travel speed of the front edge of the sand flow was reduced by ground friction and the blocking effect of the right side of the mountain to about 16.0 m/s. The direction had turned due north at this point;
- At 80 s, the maximum accumulation height of the sand flow was about 26.2 m, mainly located in the reservoir area and 340 m in front of the left side of the dam, and the sand flow reached as far as 1290 m downstream. The maximum travel speed of sand flow was 25.7 m/s, and the travel speed of sand flow within 150 m of the breach exceeded 20.0 m/s. The travel speed of the front edge of the sand flow decreased to 7.0 m/s, while the flow speed in other areas decreased to 1.0 m/s or less;
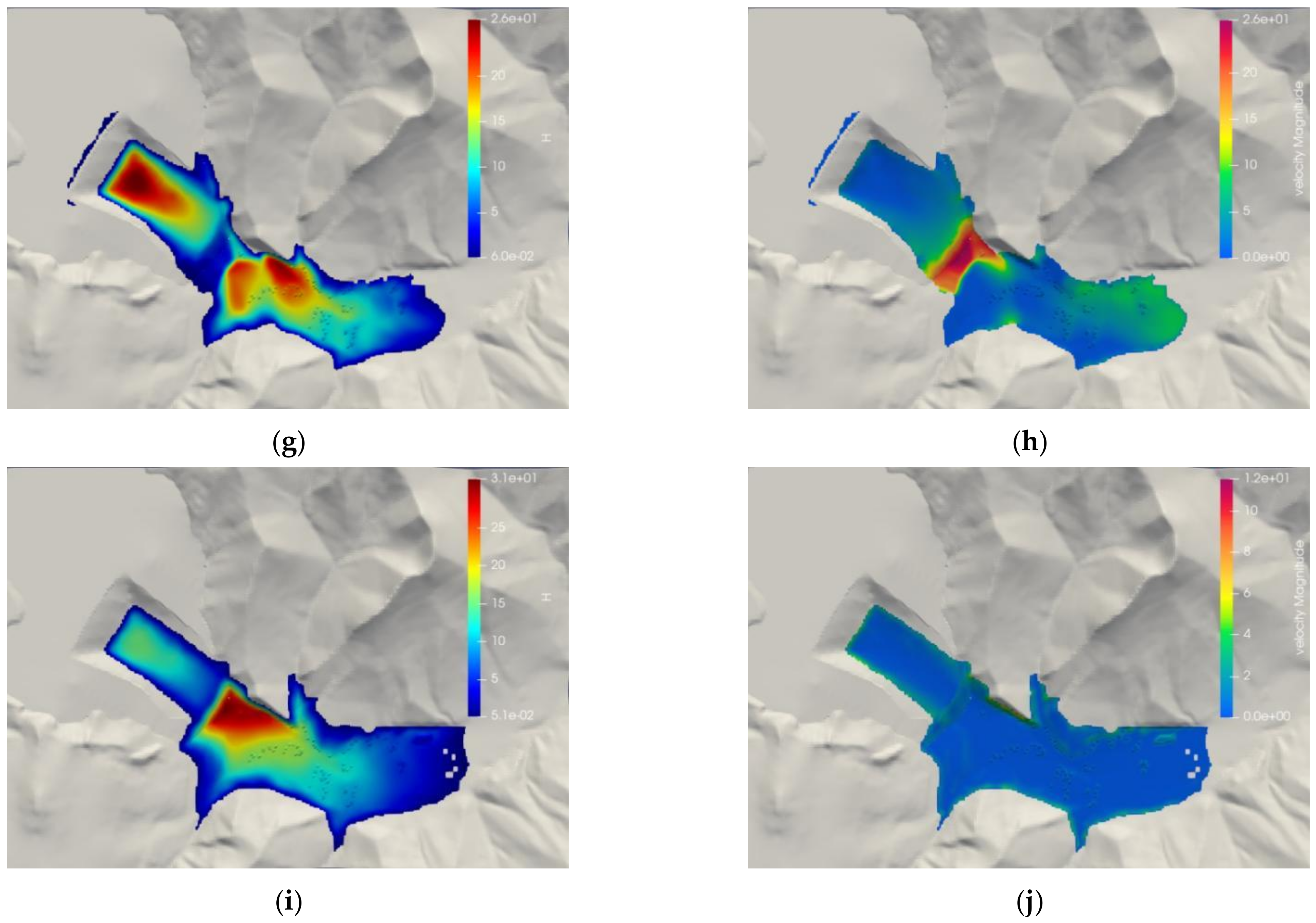
- At 300 s, the sand flow movement basically stopped. The final evolution distance was about 1.43 km, the tail sand accumulation range reached 603,000 m2, and the whole was distributed in strips along the downstream gully, with part of the sand flow entering the gully on both sides. The buildings of the village within 1 km downstream of the dam body were completely submerged—only in the area where the accumulation height of the sand flow front edge was less than 3 m were a small number of village buildings partially submerged. The accumulation height along the evolution path was generally decreasing, and the maximum accumulation area was at the left side of the mountain in front of the dam, with a maximum accumulation height of about 31.5 m.
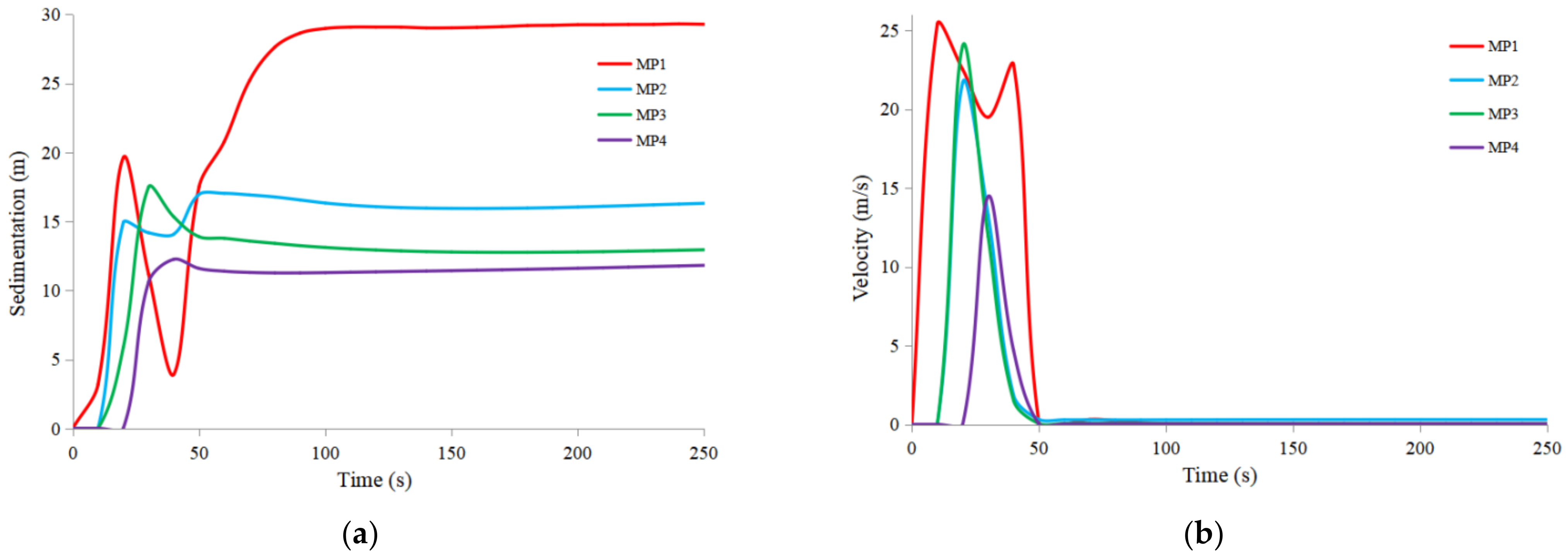
- The tailing sand accumulation on the left side of sections MS1 and MS2 is significantly higher than on the right side, the accumulation at MS3 is low in the middle and high on both sides, and the accumulation on the right side of MS4 is higher than on the left side due to the sand flow being diverted by the mountain. The presence of village buildings will increase the accumulation height in the area;
- The tailing sand accumulates rapidly in the downstream channel after the breach. Before 50 s, a large amount of tailing sand is discharged per unit of time, the potential energy is large, the tailing sand accumulation distance is great, and the tailing sand accumulation height at each measurement point increases rapidly. After 50 s, a small amount of tailing sand is discharged within a unit of time, the potential energy is small, the tailing sand accumulation distance is small, and the tailing sand accumulation height at locations far from the initial dam no longer increases, while the accumulation height near to the dam body continues to increase. The tailing sand accumulation height curve at monitoring points near the dam is bimodal, and can be divided into four stages, i.e., sharp rise–significant decline–continuing to rise–gradually stabilizing, and the tailing sand accumulation height curve at monitoring points farther away from the dam is largely unimodal, and can be divided into three stages, i.e., sharp rise–small decline–gradually stabilizing;
- The change in the velocity curve at the monitoring points near the breach is more complicated—the sand flow is faster and the movement lasts longer. The velocity curve at other monitoring points essentially shows a steep rising and steep falling triangular shape—the sand flow velocity is reduced and the movement lasts for less time.
4.3. Analysis of SPH Calculation Results
- At 20 s, the maximum displacement of the breached tailing sand was about 320 m, and the tailing sand movement speed was fast, with a maximum of about 33.0 m/s;
- At 40 s, the maximum displacement of the breached tailing sand was about 820 m, and the sand flow movement speed was more evenly distributed, with a maximum of about 29.9 m/s;
- At 60 s, the maximum displacement of the breached tailing sand was about 1120 m, and the sand flow front and the tailing sand movement speed in front of the breached opening were at their maximum;
- At 80 s, the maximum displacement of the tail sand of the breached dam was about 1250 m, and the maximum velocity of the tail sand movement was about 18.0 m/s in front of the breached mouth and the front edge of the sand flow, while the velocity of the tail sand movement in other areas had dropped to less than 6.0 m/s;
- At 300 s, the maximum displacement of the tail sand of the breached dam was about 1350 m, and the tail sand movement had basically stopped. The sand accumulated in strips along the gully, with some of the tail sand flowing downstream. At both sides of the ditch, the accumulation range reached 527,000 m2, and village buildings within this range were completely submerged.
5. Results and Discussion
- There is a lag in the physical model test when the maximum flow velocity of the discharged tailings sand appears during the dam breach process, reaching the peak flow velocity of 120 s after the breach appears at the top of the dam, after which it remains relatively stable for a period of time and then starts to decrease rapidly. On the other hand, the numerical simulation reaches the peak flow velocity of the discharged tailings sand at the beginning of the dam breach and then rapidly decreases to close to 0 m/s, creeping for a longer period of time before the end of the dam breach;
- The tailing sand flow velocity, evolution distance and depth obtained from the numerical simulation are large. This is because (i) the breach pattern in the numerical simulation is set with reference to the physical test, but in order to consider more unfavorable conditions, the breach is set larger and deeper, and the total volume of the breached tail sand is slightly higher, and further, (ii) the numerical simulation does not truly reflect the model test conditions and processes. In the test, rainfall continues to wash the breach, carrying the tail sand continuously downstream, and there is obvious mud–water stratification in the tail sand flow, while the numerical simulation is instantaneous. In the full-break mode, the potential energy of the tailing sand body is released instantaneously, while the tailing sand and water are completely mixed, and the flowability is good in all directions.
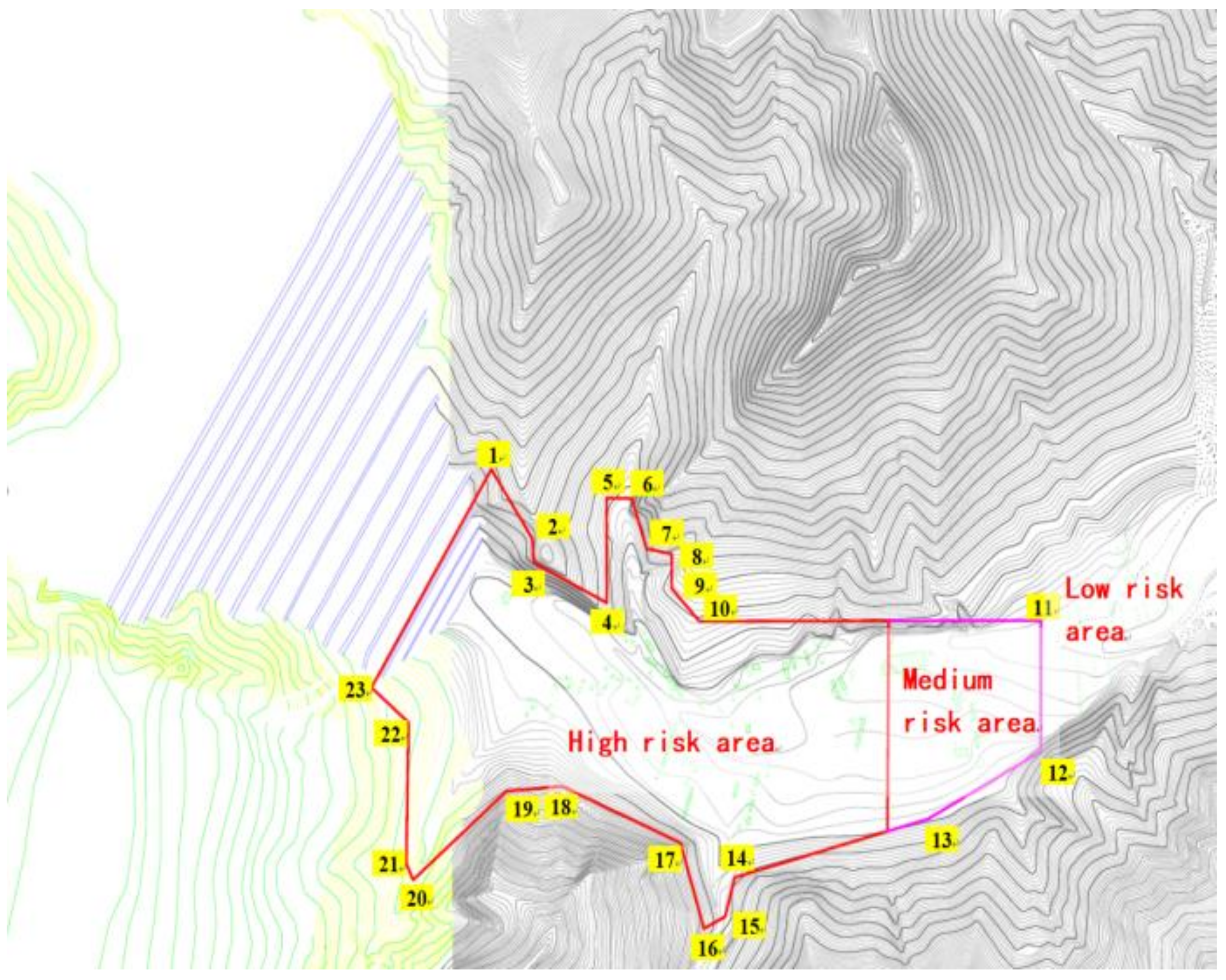
6. Risk Assessment and Recommendations
7. Conclusions
- During the breaching process, after the tailings dam forms an erosion trench, the lower part of the erosion trench is the first to slip, and after the formation of a steep can, the upper part of it causes slippage in the tailings, such that the erosion trench first develops vertically and then laterally. The final evolution of the breach is determined by the amount of water stored in the reservoir;
- When the top of the tailings dam is breached, the downstream tailings sand flow rate will quickly reach a peak value of 33.00 m/s in a short period of time, after which the downstream tailings sand flow rate reduces to a creeping state. After creeping for a long period of time, the front edge of the sand flow is the first to stop moving, while the trailing edge of the tailings sand accumulation depth continues moving until the end of the breach, at which point the tailings sand flow rate of the initial downstream dam bottom area is the largest. The impact force is the most significant factor use to form prevention and control measures;
- The discharged tailings eventually accumulate in the downstream channel, showing a pattern whereby at points further away from the initial dam, the accumulation depth will be smaller and the particle size will be larger, while the larger the elevation of the foundation in the same section, the smaller the accumulation depth and the larger the particle size. The maximum accumulation depth is 31.50 m, at which point the presence of shade will cause the local tailings accumulation depth to increase;
- There are small differences between the results of the numerical simulation and physical model tests, and the bias value should be used as the basis when carrying out engineering prevention and control measures. The final evolution distance of tailing sand after the collapse can reach 1.43 km, and the maximum accumulation depth can reach 31.50 m. Based on the flow velocity, downstream tailing sand accumulation distance and depth, the risk area of the river downstream of the tailing pond can be categorized, such that relocation measures can be formulated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rico, M.; Benito, G.; Salgueiro, A.; Díez-Herrero, A.; Pereira, H. Reported tailings dam failures: A review of the European incidents in the worldwide context. J. Hazard. Mater. 2008, 152, 846–852. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Q.; Fan, X.-M.; Huang, R.-Q.; Van Westen, C. Landslide dams triggered by the Wenchuan Earthquake, Sichuan Province, south west China. Bull. Eng. Geol. Environ. 2009, 68, 373–386. [Google Scholar] [CrossRef]
- Cui, P.; Zhu, Y.-Y.; Han, Y.-S.; Chen, X.-Q.; Zhuang, J.-Q. The 12 May Wenchuan earthquake-induced landslide lakes: Distribution and preliminary risk evaluation. Landslides 2009, 6, 209–223. [Google Scholar] [CrossRef]
- Li, Y.; Gong, J.H.; Zhu, J.; Ye, L.; Song, Y.Q.; Yue, Y.J. Efficient dam break flood simulation methods for developing a preliminary evacuation plan after the Wenchuan Earthquake. Nat. Hazards Earth Syst. Sci. 2012, 12, 97–106. [Google Scholar] [CrossRef]
- Xu, F.; Zhou, H.; Zhou, J.; Yang, X. A Mathematical Model for Forecasting the Dam-Break Flood Routing Process of a Landslide Dam. Math. Probl. Eng. 2012, 2012, 139642. [Google Scholar] [CrossRef] [Green Version]
- Sammarco, O. A Tragic Disaster Caused by the Failure of Tailings Dams Leads to the Formation of the Stava 1985 Foundation. Mine Water Environ. 2004, 23, 91–95. [Google Scholar] [CrossRef]
- Zhang, C.; Chai, J.; Cao, J.; Xu, Z.; Qin, Y.; Lv, Z. Numerical Simulation of Seepage and Stability of Tailings Dams: A Case Study in Lixi, China. Water 2020, 12, 742. [Google Scholar] [CrossRef] [Green Version]
- von der Heyden, C.; New, M. Groundwater pollution on the Zambian Copperbelt: Deciphering the source and the risk. Sci. Total Environ. 2004, 327, 17–30. [Google Scholar] [CrossRef]
- Yin, G.; Li, G.; Wei, Z.; Wan, L.; Shui, G.; Jing, X. Stability analysis of a copper tailings dam via laboratory model tests: A Chinese case study. Miner. Eng. 2011, 24, 122–130. [Google Scholar] [CrossRef]
- Ihle, C.F.; Tamburrino, A. Analytical solutions for the flow depth of steady laminar, Bingham plastic tailings down wide channels. Miner. Eng. 2018, 128, 284–287. [Google Scholar] [CrossRef]
- Shakesby, R.A.; Whitlow, J.R. Failure of a mine waste dump in Zimbabwe: Causes and consequences. Environ. Earth Sci. 1991, 18, 143–153. [Google Scholar] [CrossRef]
- de Lima, R.E.; Picanço, J.D.L.; da Silva, A.F.; Acordes, F.A. An anthropogenic flow type gravitational mass movement: The Córrego do Feijão tailings dam disaster, Brumadinho, Brazil. Landslides 2020, 17, 2895–2906. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Petaccia, G. Review of Historical Dam-Break Events and Laboratory Tests on Real Topography for the Validation of Numerical Models. Water 2021, 13, 1968. [Google Scholar] [CrossRef]
- Della Vecchia, G.; Cremonesi, M.; Pisanò, F. On the rheological characterisation of liquefied sands through the dam-breaking test. Int. J. Numer. Anal. Methods Géoméch. 2019, 43, 1410–1425. [Google Scholar] [CrossRef] [Green Version]
- Schmocker, L. The failure of embankment dams due to overtopping. J. Hydraul. Res. 2009, 47, 288. [Google Scholar] [CrossRef]
- Kho, F.W.L.; Law, P.L.; Lai, S.H.; Oon, Y.W.; Ngu, L.H.; Ting, H.S. Quantitative dam break analysis on a reservoir earth dam. Int. J. Environ. Sci. Technol. 2009, 6, 203–210. [Google Scholar] [CrossRef]
- Zardari, M.A.; Mattsson, H.; Knutsson, S.; Khalid, M.S.; Ask, M.V.S.; Lund, B. Numerical Analyses of Earthquake Induced Liquefaction and Deformation Behaviour of an Upstream Tailings Dam. Adv. Mater. Sci. Eng. 2017, 2017, 5389308. [Google Scholar] [CrossRef] [Green Version]
- Dat, T.T.; Tri, D.Q.; Truong, D.D.; Hoa, N.N. Application of mike flood model in inundation simulation with the Dam-break Scenarios: A case study of Dak-Drinh Reservoir in Vietnam. Int. J. Earth Sci. Eng. 2019, 12, 60–70. [Google Scholar] [CrossRef]
- Dedring, T.; Graw, V.; Thygesen, K.; Rienow, A. Validation of an Empirical Model with Risk Assessment Functionalities to Simulate and Evaluate the Tailings Dam Failure in Brumadinho. Sustainability 2022, 14, 6681. [Google Scholar] [CrossRef]
- Henriquez, J.; Simms, P. Dynamic imaging and modelling of multilayer deposition of gold paste tailings. Miner. Eng. 2009, 22, 128–139. [Google Scholar] [CrossRef]
- Agapito, L.A.; Bareither, C.A. Application of a one-dimensional large-strain consolidation model to a full-scale tailings storage facility. Miner. Eng. 2018, 119, 38–48. [Google Scholar] [CrossRef]
- Voisin, D.; Grillaud, G.; Solliec, C.; Beley-Sayettat, A.; Berlaud, J.-L.; Miton, A. Wind tunnel test method to study out-of-service tower crane behaviour in storm winds. J. Wind. Eng. Ind. Aerodyn. 2004, 92, 687–697. [Google Scholar] [CrossRef]
- Tabri, K.; Määttänen, J.; Ranta, J. Model-scale experiments of symmetric ship collisions. J. Mar. Sci. Technol. 2008, 13, 71–84. [Google Scholar] [CrossRef]
- Börzsönyi, T.; Ecke, R.E.; McElwaine, J.N. Patterns in Flowing Sand: Understanding the Physics of Granular Flow. Phys. Rev. Lett. 2009, 103, 178302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, G.; Tian, S.; Hu, B.; Kong, X.; Chen, J. An experimental study on tailings deposition characteristics and variation of tailings dam saturation line. Geomech. Eng. 2020, 23, 85–92. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, H.; Zhong, D. Properties of the Eulerian–Lagrangian method using linear interpolators in a three-dimensional shallow water model using z-level coordinates. Int. J. Comput. Fluid Dyn. 2009, 23, 271–284. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. Professional Standards Compilation Group of People’s Republic of China: Beijing, China, 2019.
- Ouyang, C.; He, S.; Xu, Q.; Luo, Y.; Zhang, W. A MacCormack-TVD finite difference method to simulate the mass flow in mountainous terrain with variable computational domain. Comput. Geosci. 2012, 52, 1–10. [Google Scholar] [CrossRef]
- Horton, A.J.; Hales, T.C.; Ouyang, C.; Fan, X. Identifying post-earthquake debris flow hazard using Massflow. Eng. Geol. 2019, 258, 105134. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, Y.; Pei, X.; Ouyang, C.; Du, J.; Scaringi, G. Dam-break dynamics at Huohua Lake following the 2017 Mw 6.5 Jiuzhaigou earthquake in Sichuan, China. Eng. Geol. 2021, 289, 106145. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.; Xu, Q.; Xie, P.; Hao, L. Run-out analysis of flow-like landslides triggered by the Ms 8.0 2008 Wenchuan earthquake using smoothed particle hydrodynamics. Landslides 2011, 9, 275–283. [Google Scholar] [CrossRef]
- Vacondio, R.; Mignosa, P.; Pagani, S. 3D SPH numerical simulation of the wave generated by the Vajont rockslide. Adv. Water Resour. 2013, 59, 146–156. [Google Scholar] [CrossRef]
- Rodriguez-Paz, M.X.; Bonet, J. A corrected smooth particle hydrodynamics method for the simulation of debris flows. Numer. Methods Part. Differ. Equ. 2003, 20, 140–163. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. SPH model for fluid–structure interaction and its application to debris flow impact estimation. Landslides 2016, 14, 917–928. [Google Scholar] [CrossRef]
- Roubtsova, V.; Kahawita, R. The SPH technique applied to free surface flows. Comput. Fluids 2006, 35, 1359–1371. [Google Scholar] [CrossRef]
- Prakash, M.; Rothauge, K.; Cleary, P.W. Modelling the impact of dam failure scenarios on flood inundation using SPH. Appl. Math. Model. 2014, 38, 5515–5534. [Google Scholar] [CrossRef]
- Moreira, A.; Leroy, A.; Violeau, D.; Taveira-Pinto, F. Dam spillways and the SPH method: Two case studies in Portugal. J. Appl. Water Eng. Res. 2018, 7, 228–245. [Google Scholar] [CrossRef]
- Hu, K.; Wei, F.; Li, Y. Real-time measurement and preliminary analysis of debris-flow impact force at Jiangjia Ravine, China. Earth Surf. Process. Landf. 2011, 36, 1268–1278. [Google Scholar] [CrossRef]
- Alam, M.; Islam, T.; Rahman, M. Unsteady Hydromagnetic Forced Convective Heat Transfer Flow of a Micropolar Fluid along a Porous Wedge with Convective Surface Boundary Condition. Int. J. Heat Technol. 2015, 33, 115–122. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.-Y.; Pan, J.-P.; Sun, H.-Z. SPH Simulation of Structures Impacted by Tailing Debris Flow and Its Application to the Buffering Effect Analysis of Debris Checking Dams. Math. Probl. Eng. 2020, 2020, 060803. [Google Scholar] [CrossRef]











| Ratios Name | Geometric Ratios | Flow Rate Ratios | Flow Ratios | Time Ratios | Roughness Ratios | Area Ratios | Volumetric Ratios |
|---|---|---|---|---|---|---|---|
| Formula | |||||||
| Numerical Values | 200 | 14.14 | 565,685.4249 | 14.14 | 2.42 | 40,000 | 8,000,000 |
| Specific Gravity | Water Content | Gravity | Porosity Ratio | Saturation | Peak Strength of Ring Shear Test | Residual Strength of Ring Shear Test | ||
|---|---|---|---|---|---|---|---|---|
| Gs | ω(%) | γ/(kN/m3) | e0 | Sr | c/kPa | tan φ | c/kPa | tan φ |
| 2.9 | 16.2 | 16.86 | 0.958 | 49 | 15.9 | 0.2643 | 8.6 | 0.2622 |
| Parameters | ρ kg/m3 | Basic Parameters | USUP Status Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| η0 MPa/s | τ0 MPa | n | k MPa/sn | C0 | s | γ0 | Friction Coefficient | ||
| Takes values | 1950 | 0.2 | 2 | 0.4 | 2.2 | 1480 | 2.0 | 0.9 | 0.26 |
| Simulation Method | Maximum Travel Speed/m∙s−1 | Final Evolution Distance/km | Stacking Range /10,000 m2 | Maximum Accumulation Depth/m | |
|---|---|---|---|---|---|
| Model test | 26.68 | 1.19 | 47.60 | 29.00 | |
| Numerical simulations | Massflow | 30.20 | 1.43 | 60.30 | 31.50 |
| SPH | 33.00 | 1.35 | 48.70 | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.; Qin, W.; Wang, H.; Wang, H.; Wang, C.; Zhang, X. Study on the Evolution of a Flooded Tailings Pond and Its Post-Failure Effects. Water 2023, 15, 173. https://doi.org/10.3390/w15010173
Chang M, Qin W, Wang H, Wang H, Wang C, Zhang X. Study on the Evolution of a Flooded Tailings Pond and Its Post-Failure Effects. Water. 2023; 15(1):173. https://doi.org/10.3390/w15010173
Chicago/Turabian StyleChang, Mengchao, Weimin Qin, Hao Wang, Haibin Wang, Chengtang Wang, and Xiuli Zhang. 2023. "Study on the Evolution of a Flooded Tailings Pond and Its Post-Failure Effects" Water 15, no. 1: 173. https://doi.org/10.3390/w15010173
APA StyleChang, M., Qin, W., Wang, H., Wang, H., Wang, C., & Zhang, X. (2023). Study on the Evolution of a Flooded Tailings Pond and Its Post-Failure Effects. Water, 15(1), 173. https://doi.org/10.3390/w15010173









