Study on the Influence of Water Level on Earth Dam Reinforced by Cut-Off Wall: A Case Study in Wujing Reservoir
Abstract
:1. Introduction
2. Project Overview
3. Study on the Influence of Sudden Drawdown on Dam Slope Stability
3.1. Seepage and Slope Stability Analysis Method
3.2. Numerical Model and Parameters
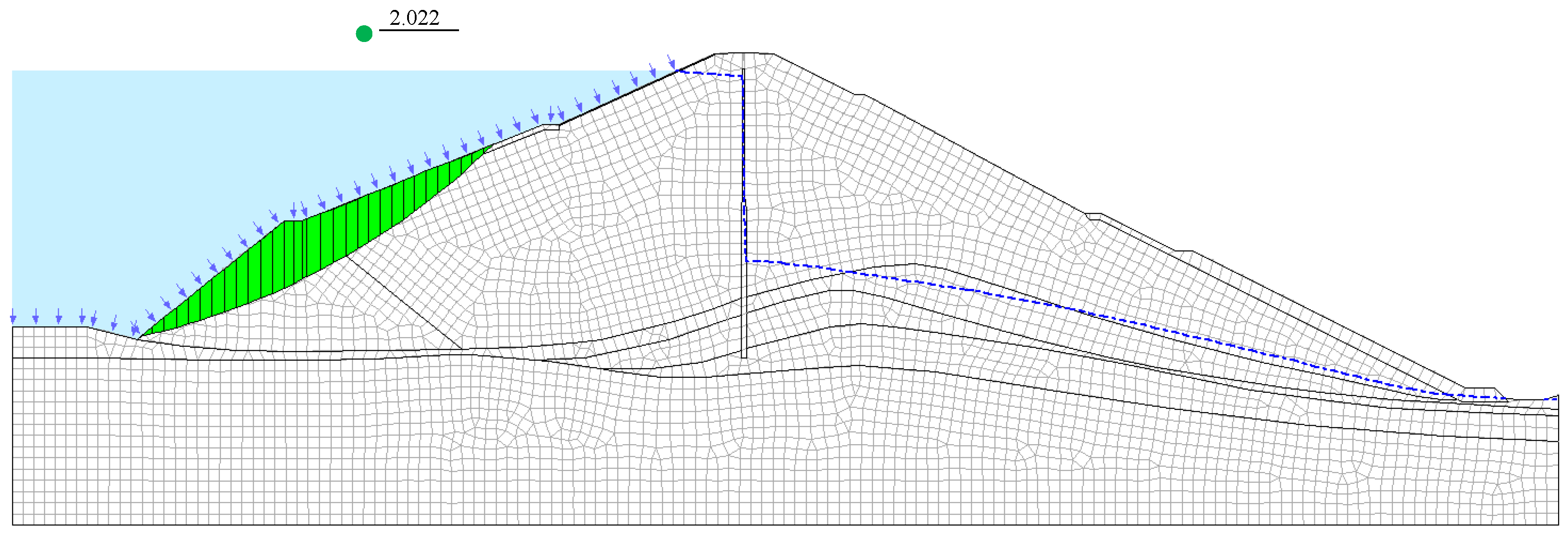
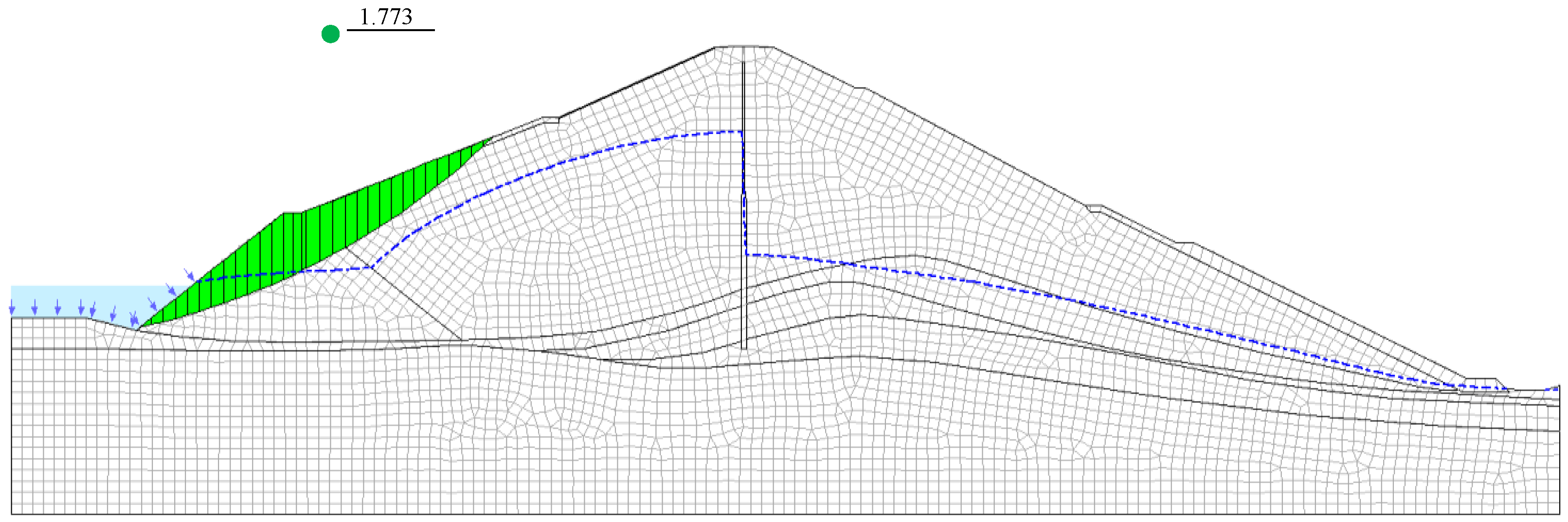
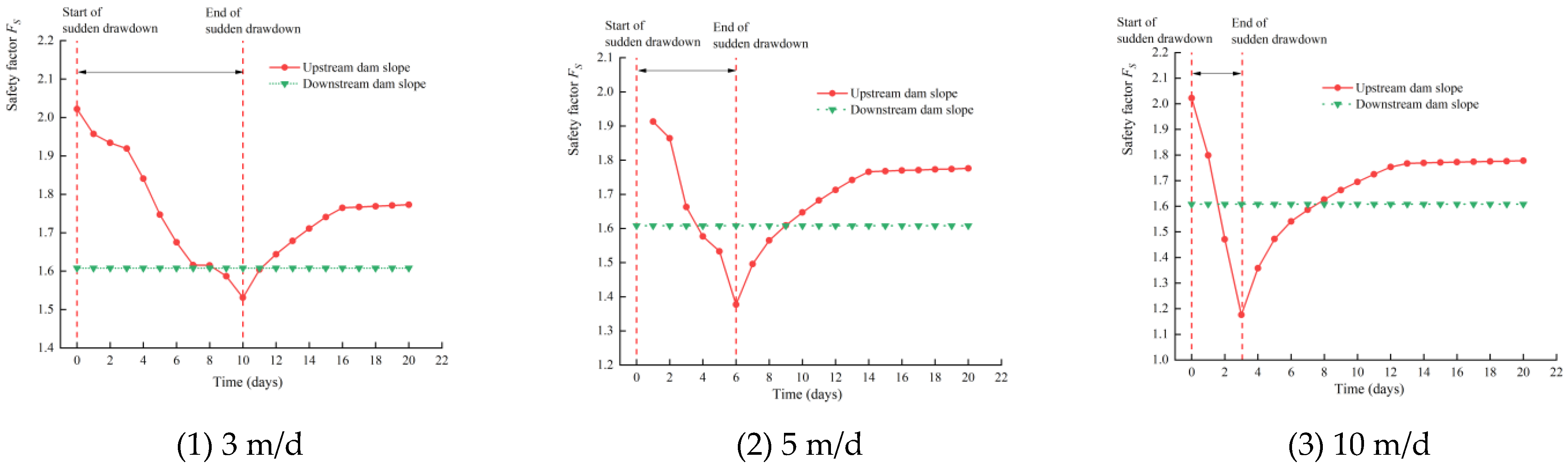
3.3. Stability Analysis of Dam Slope under Sudden Drawdown
4. Measuring and Analysis of Dam Deformation under Water Level Rise and Fall
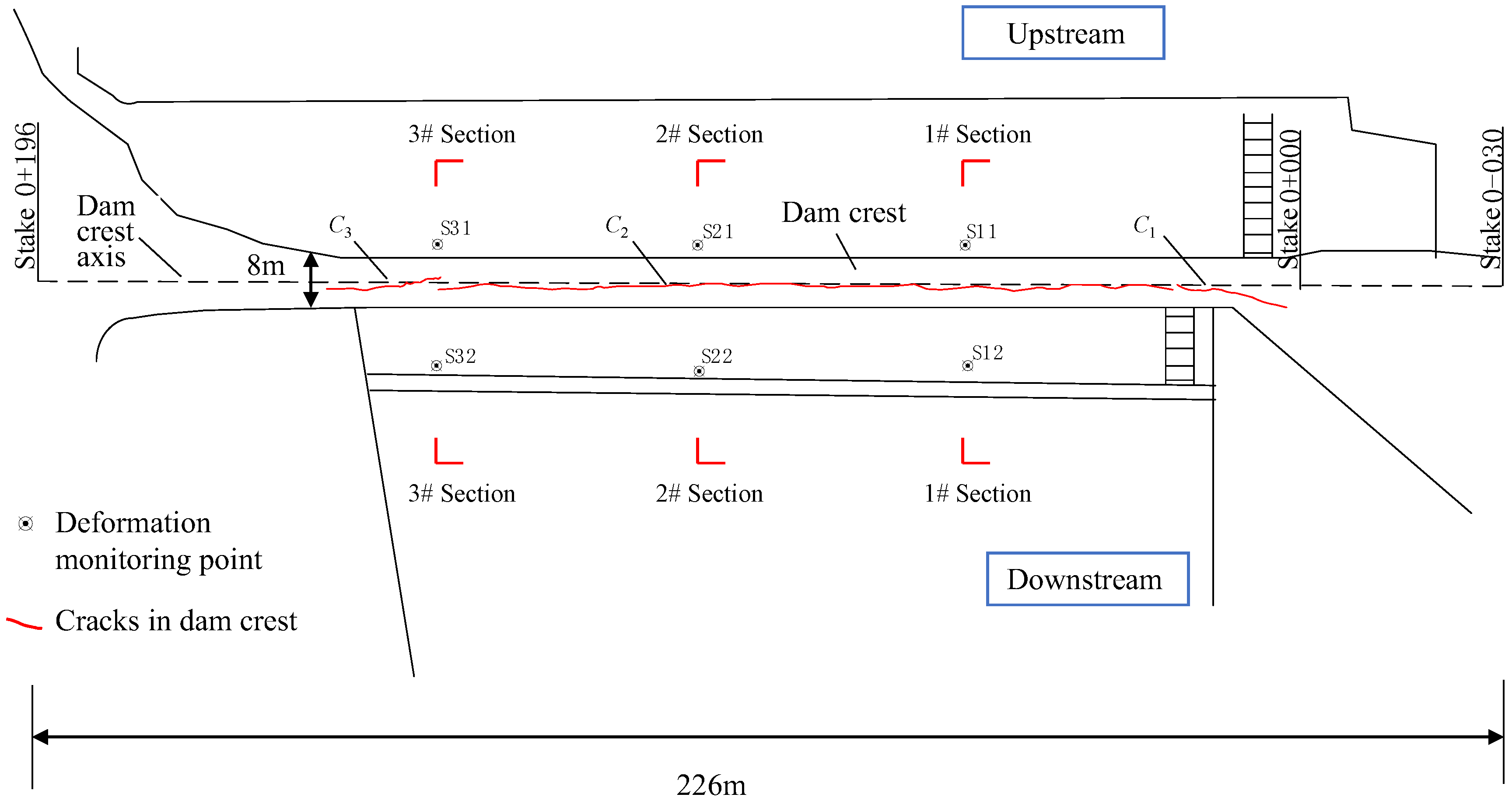
4.1. Arrangement of Measuring Points
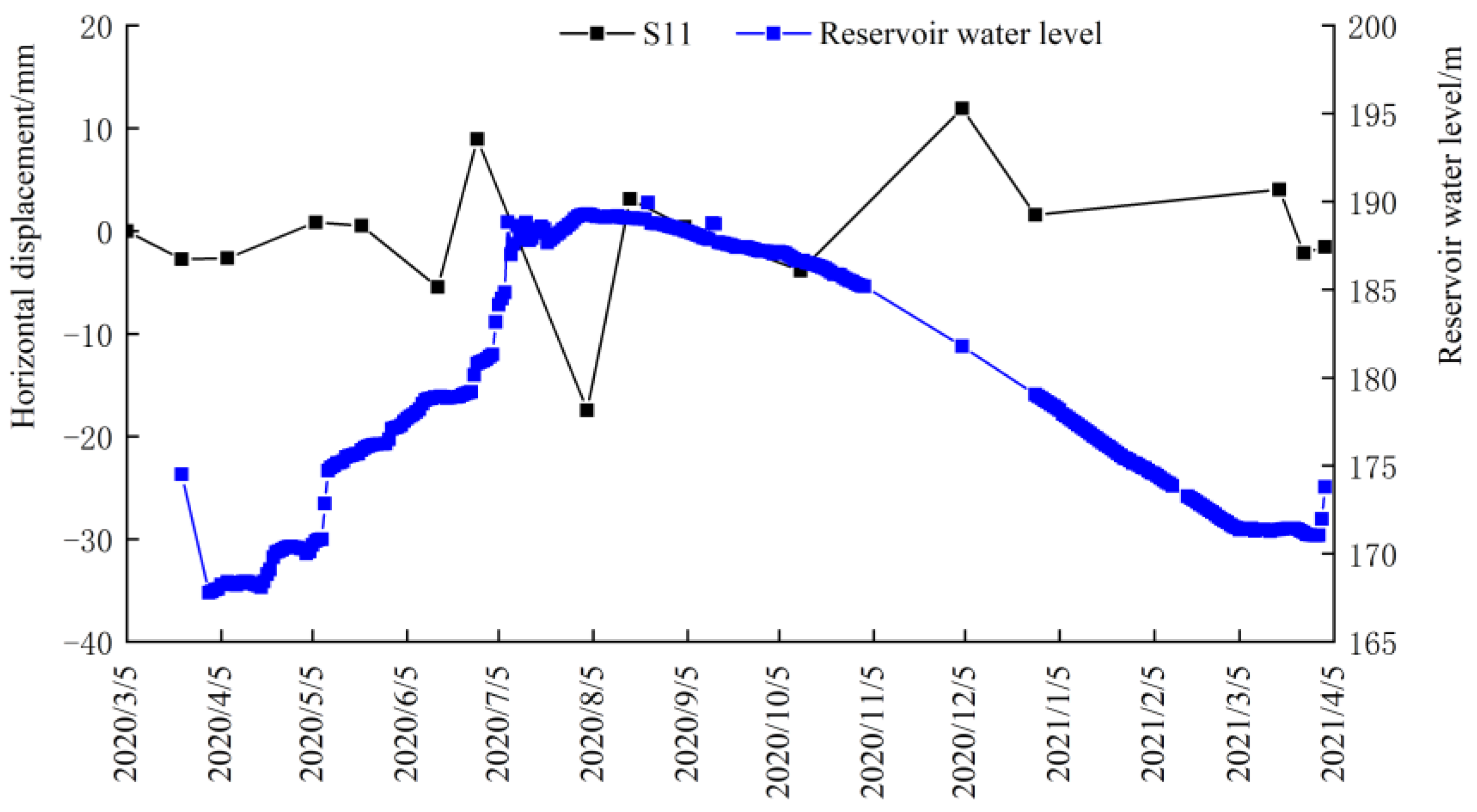
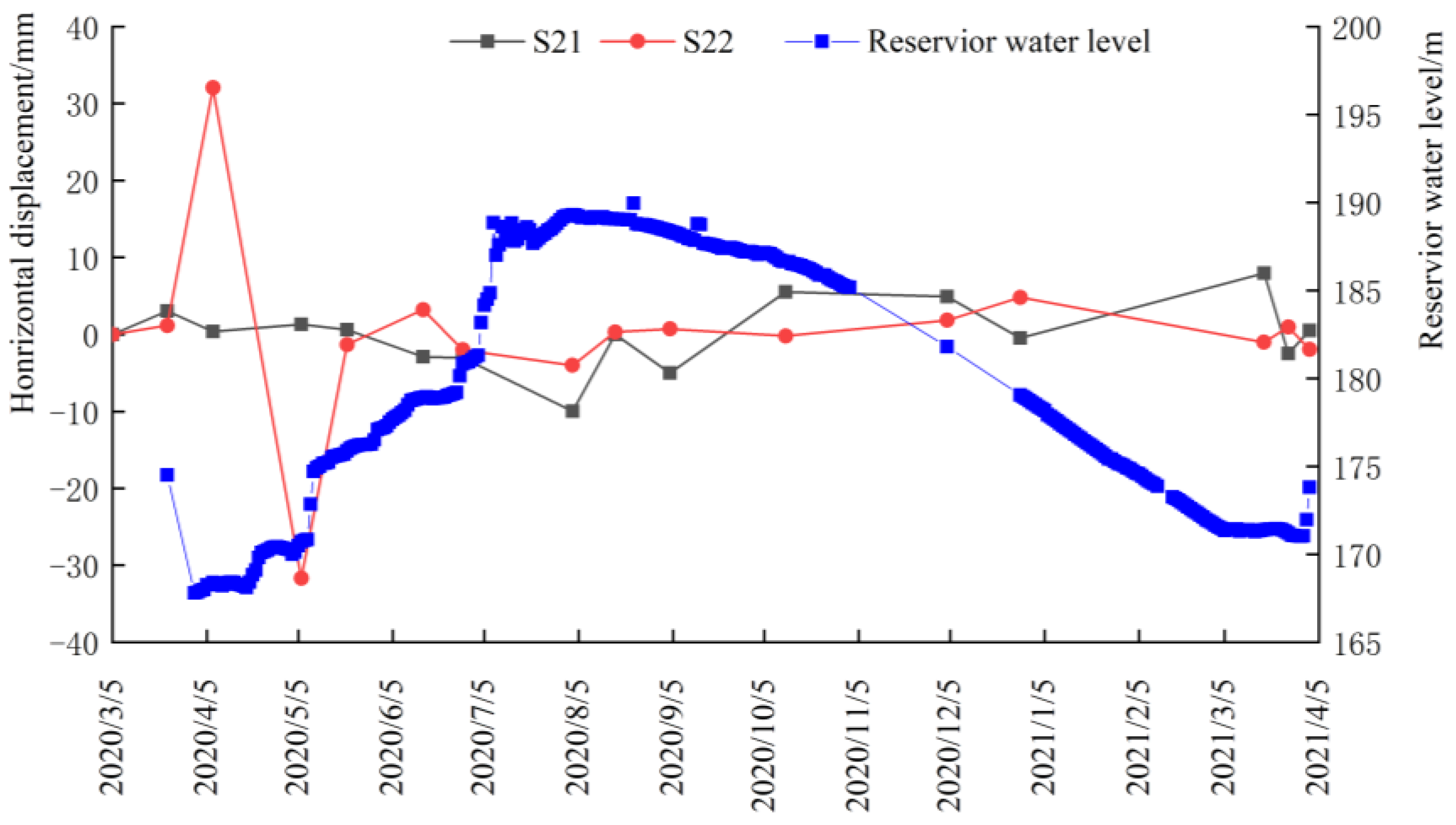
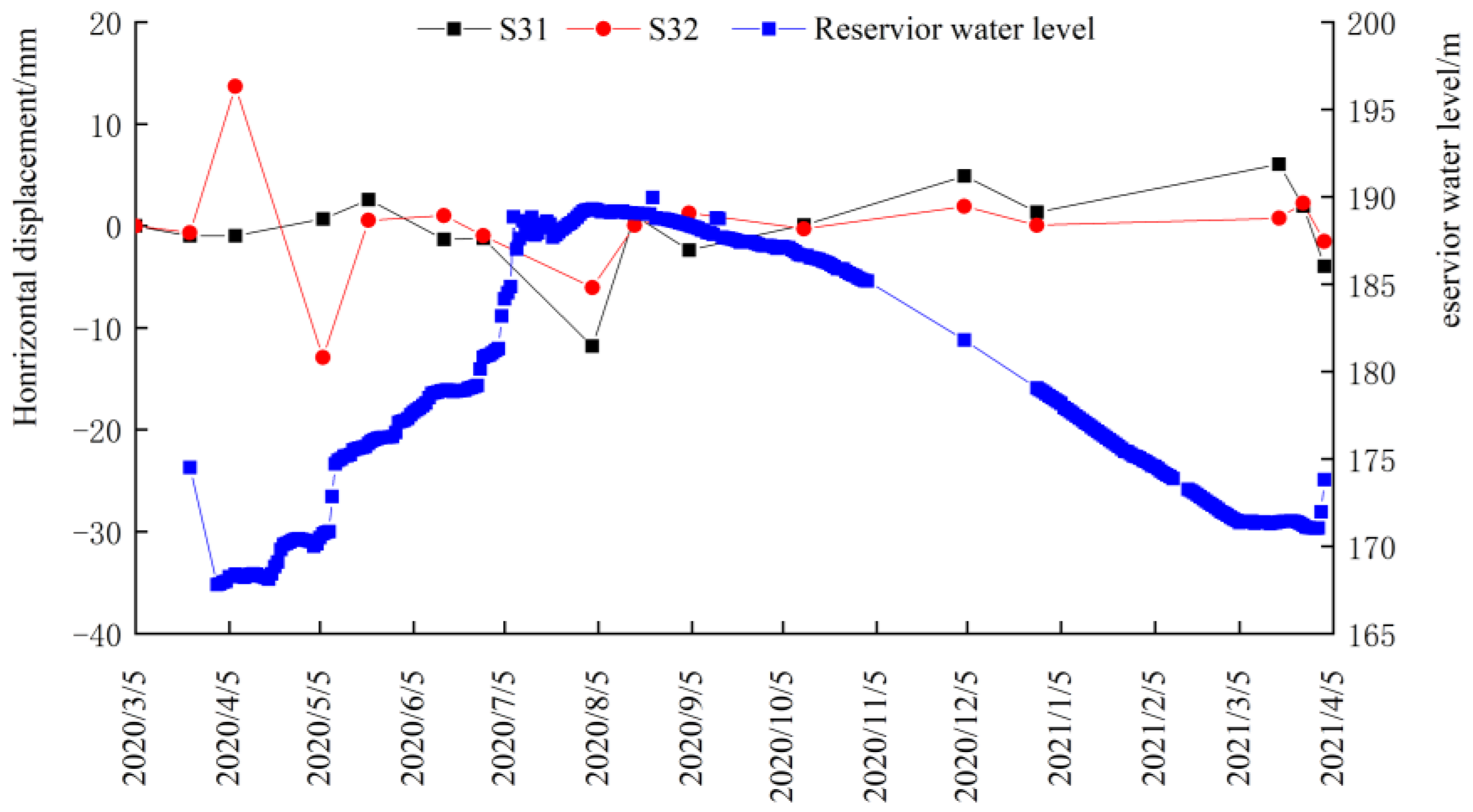
4.2. Horizontal Displacement
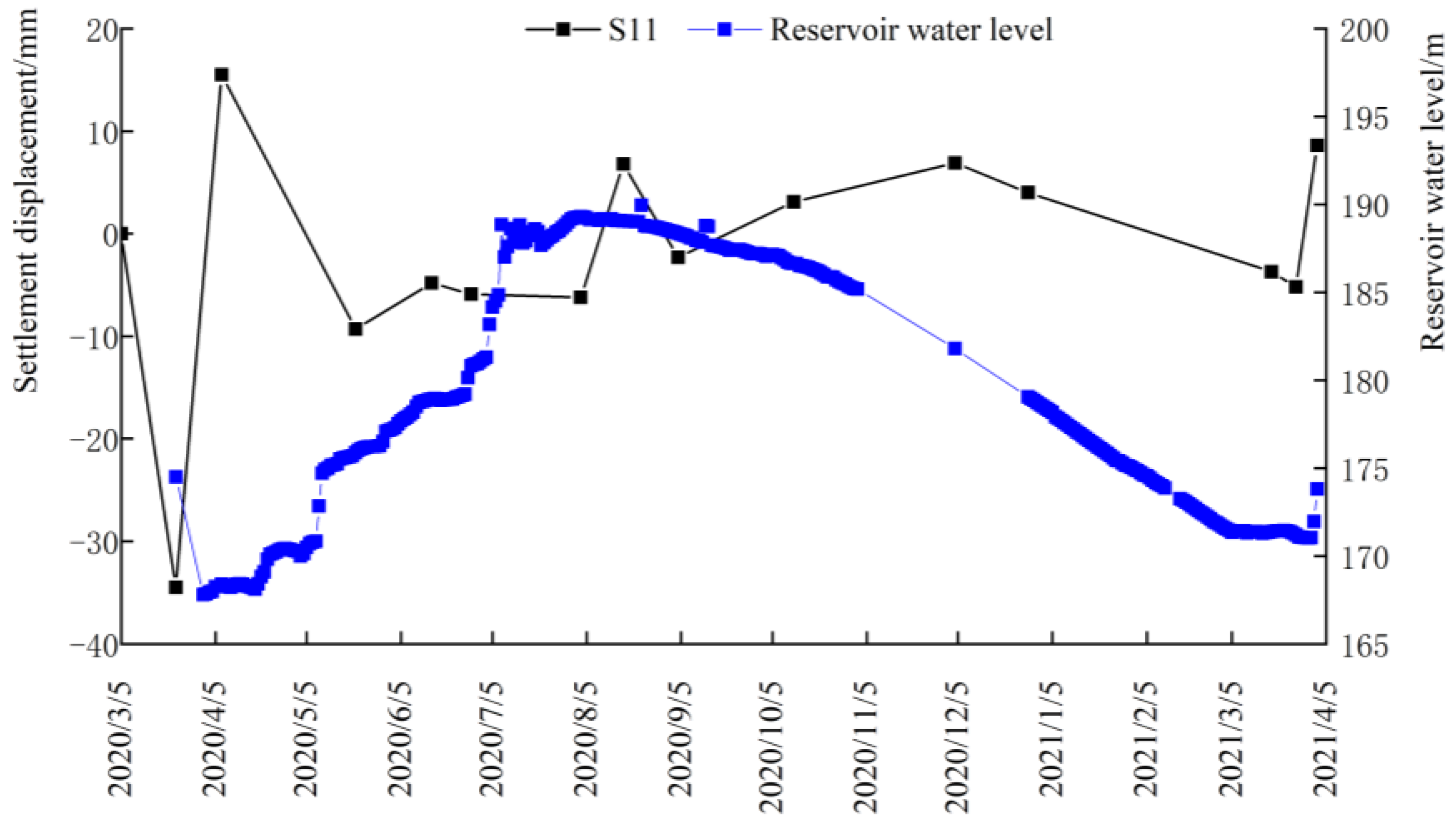
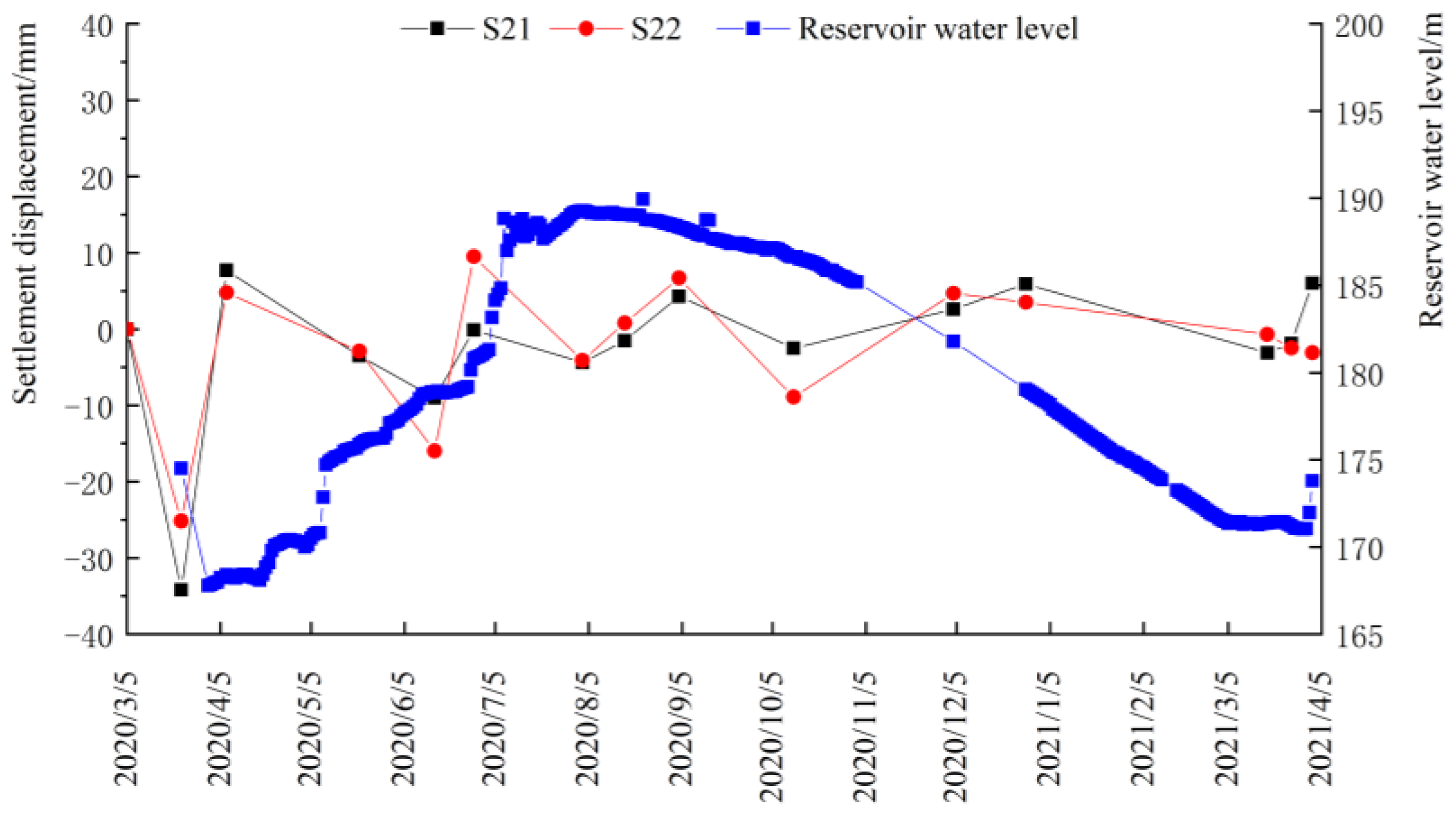
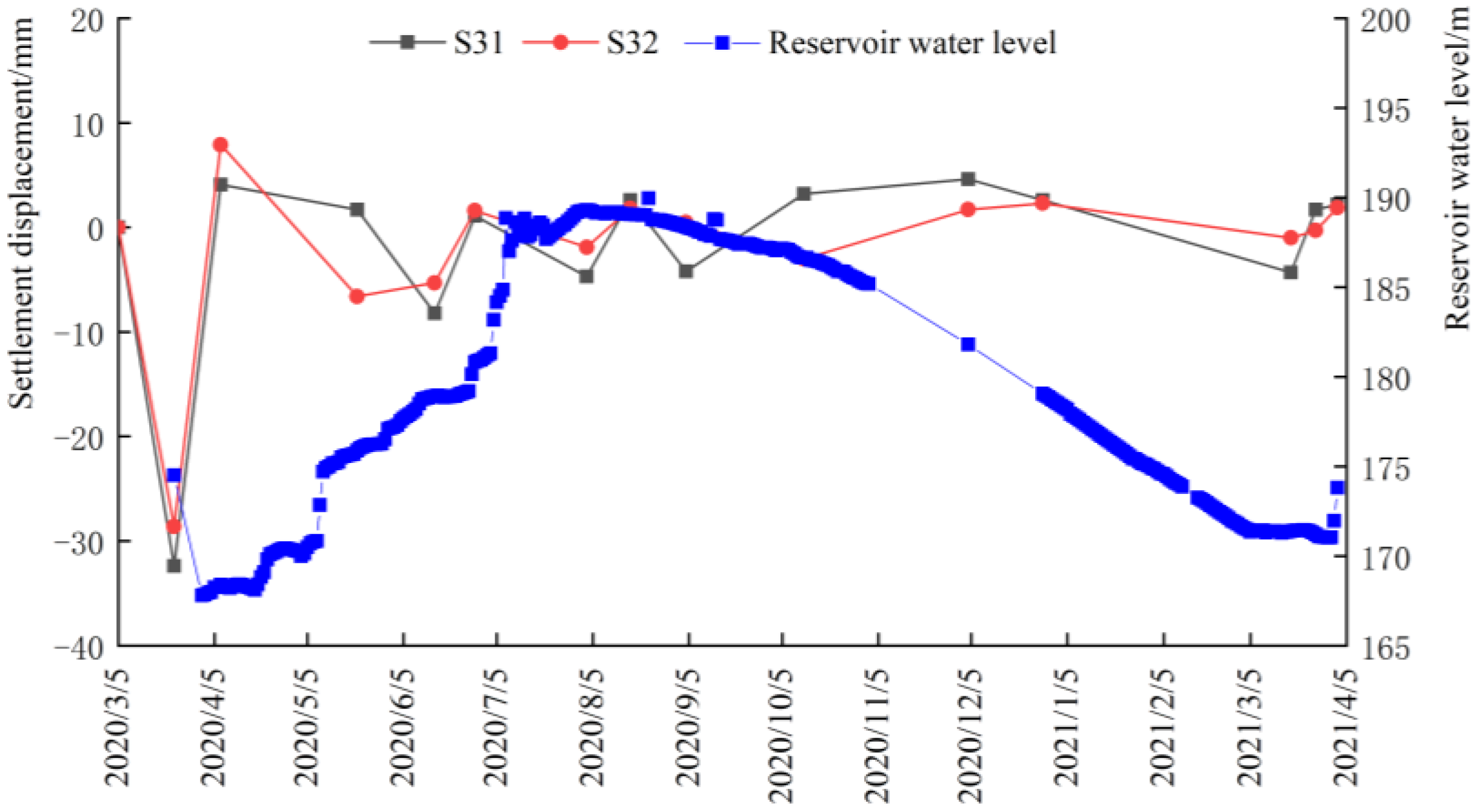
4.3. Settlements
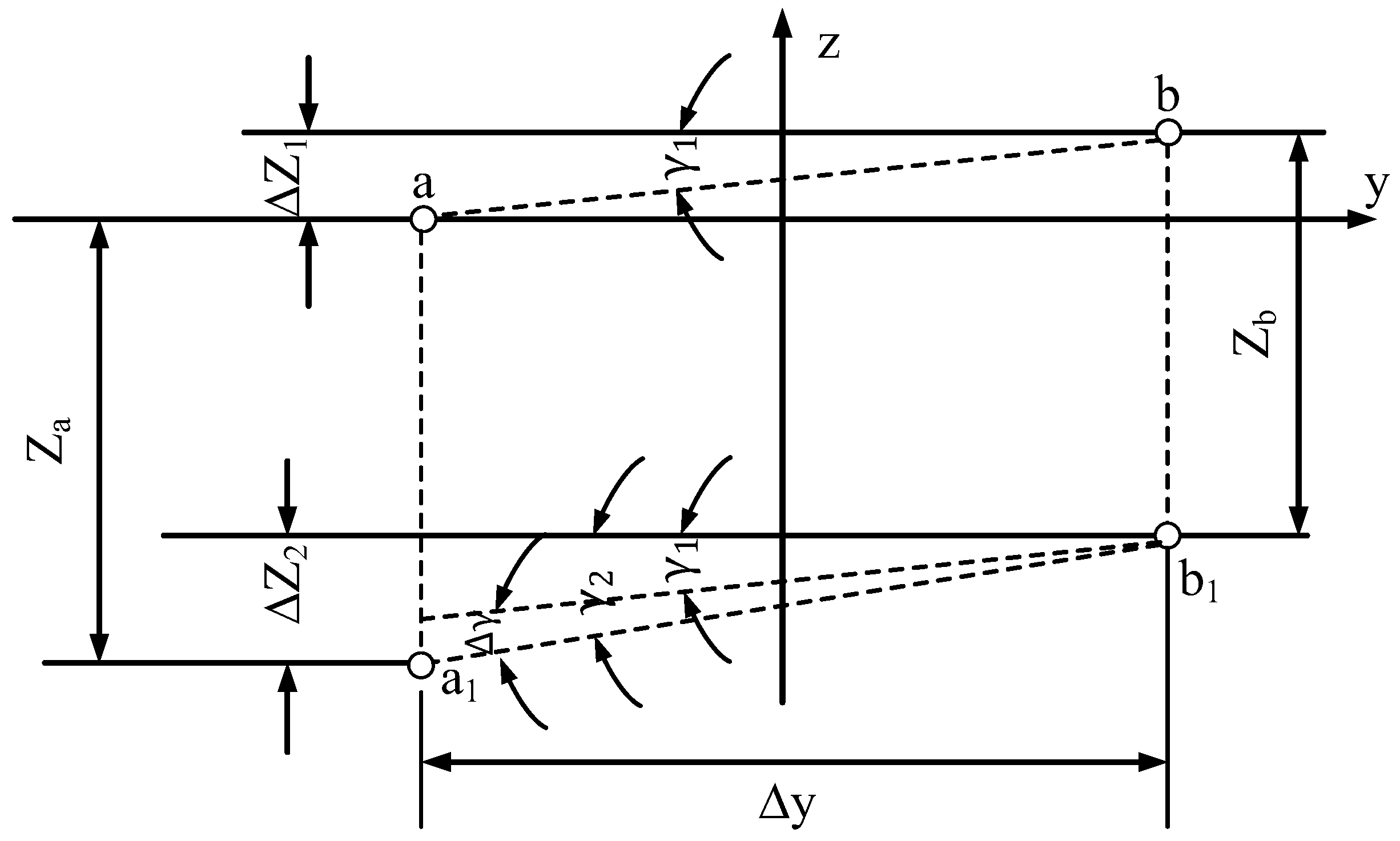
5. Crack Propagation Law Based on Deformation Gradient Method
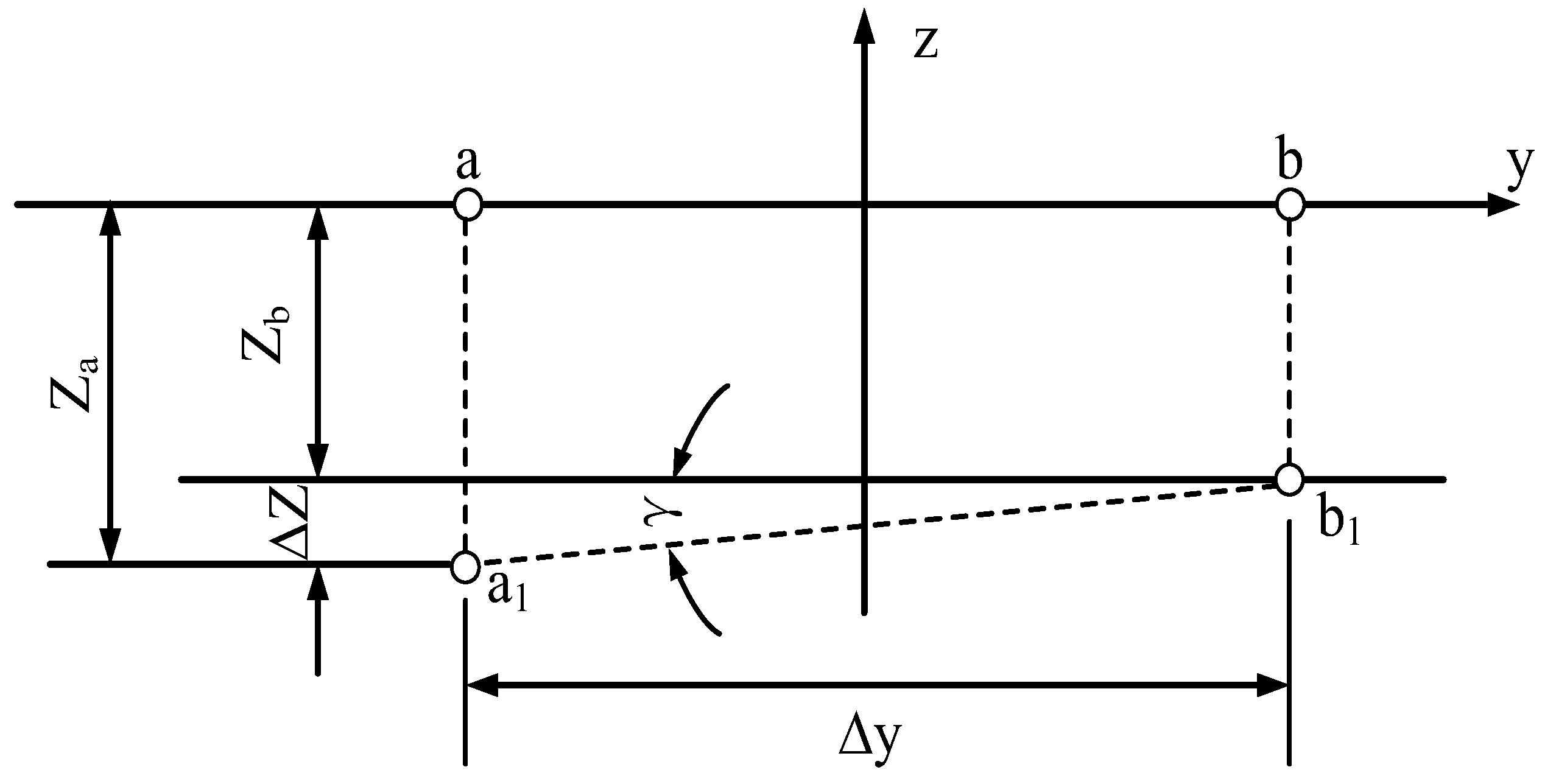
5.1. Deformation Gradient Method
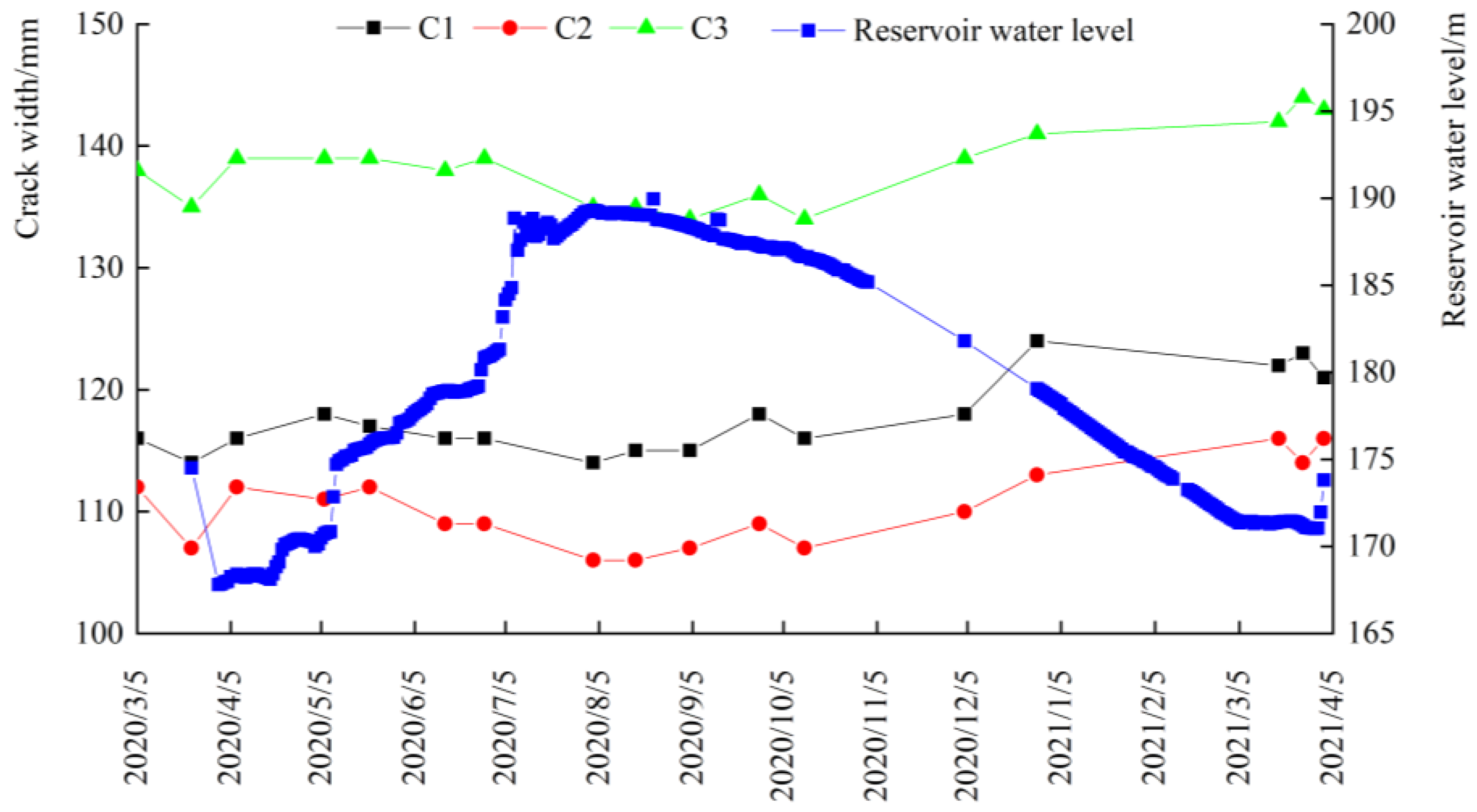
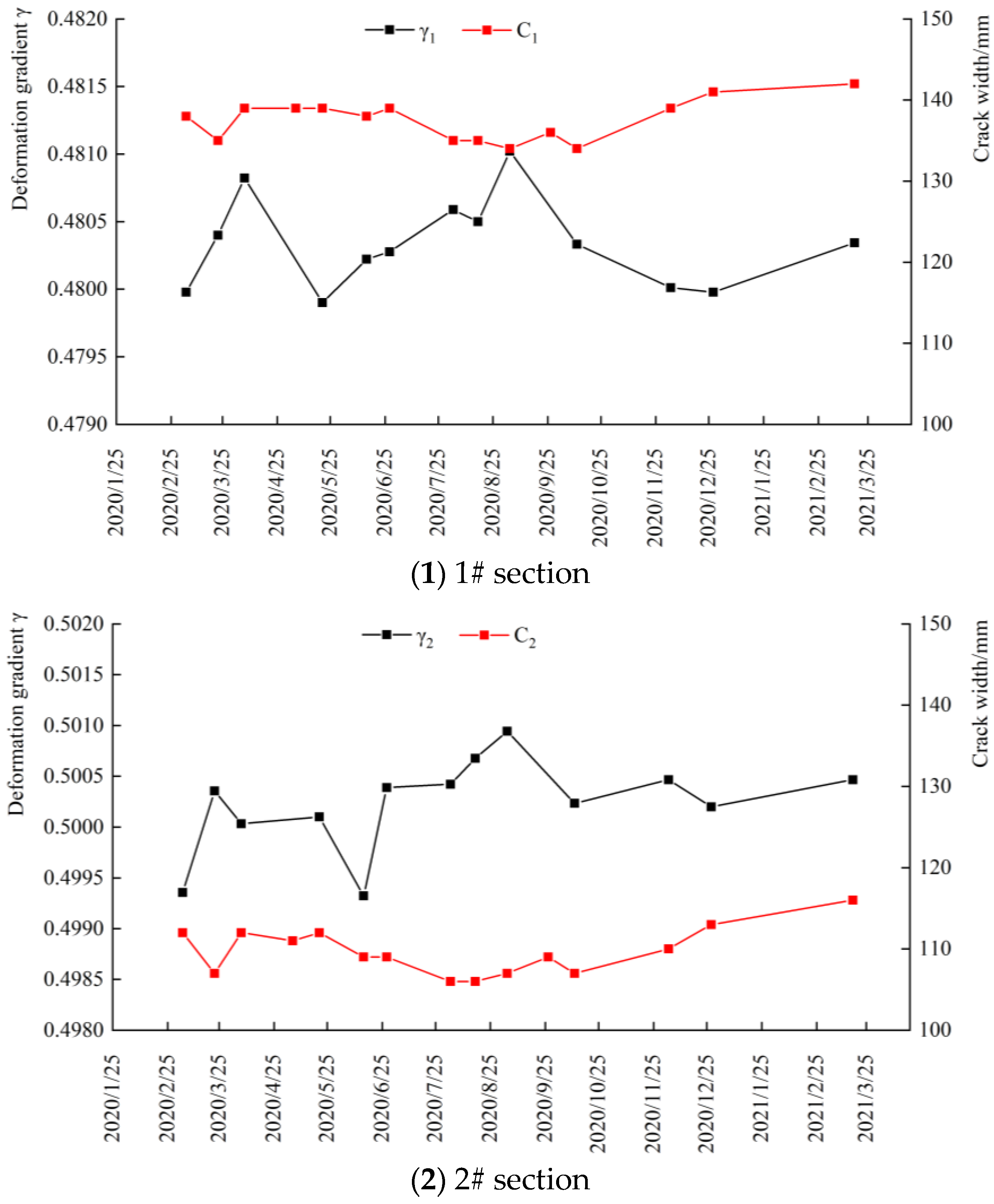
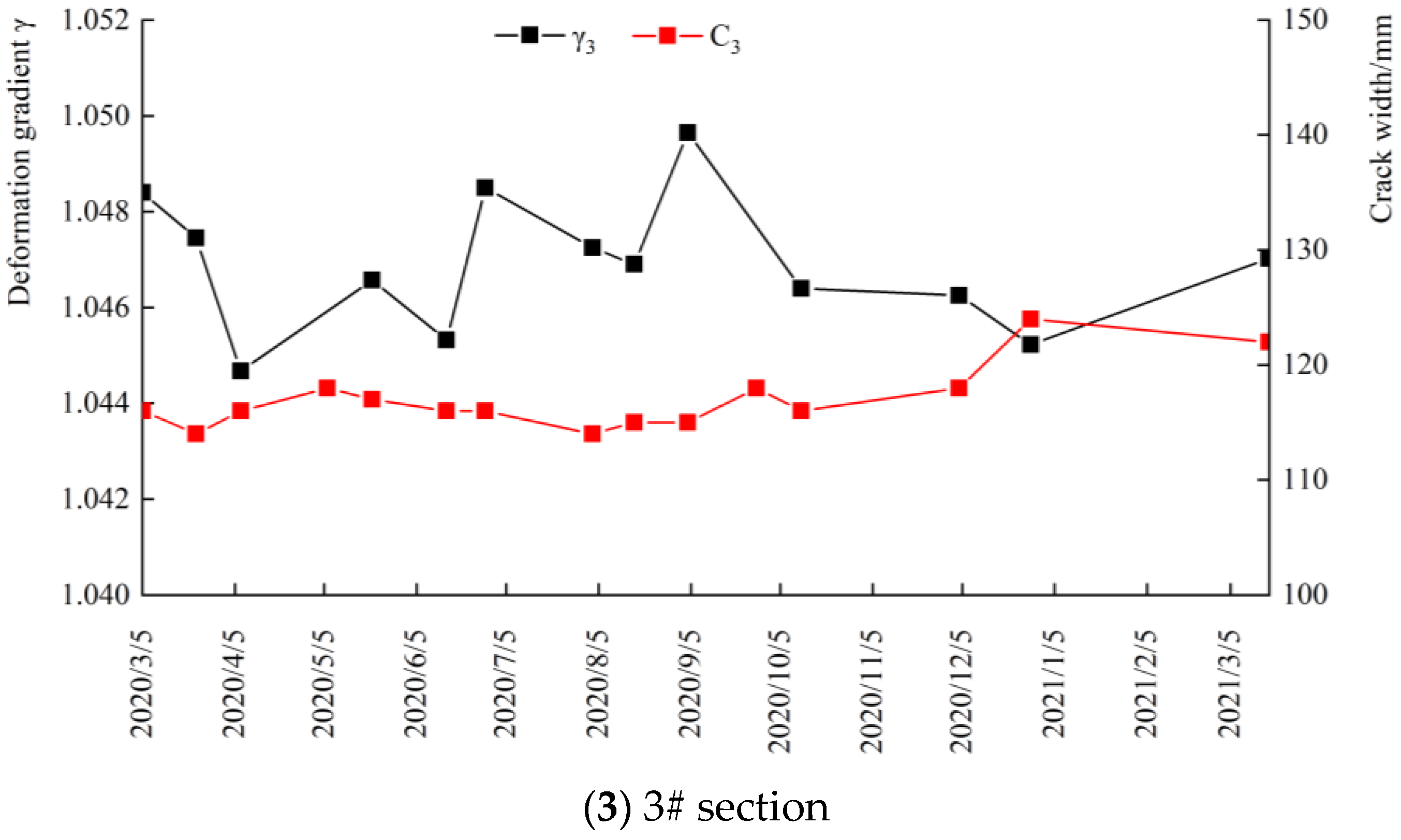
5.2. Analysis of Crack Width Propagation Law
6. Discussion and Conclusions
- Based on the established numerical calculation model of Wujing reservoir, and the geological report parameters, the safety factor of dam slope stability was obtained by the limit equilibrium method, which was about 2.0. When the reservoir encountered a sudden drawdown, the safety factor also decreased sharply. The faster the sudden drawdown was, the faster the safety factor decreased, and the more unfavorable it was to dam slope stability. With the end of the sudden drawdown, the pore water pressure of the dam body soil gradually dissipated, so that the safety factor of stability increased again and finally tended to be stable;
- The horizontal displacement of the dam was affected by the change in the upstream reservoir water level. It was found that the upstream reservoir water level rose and the horizontal displacement of dam shifted to the upstream direction. The upstream reservoir water level dropped, the horizontal displacement of the dam shifted to downstream, and the change of horizontal displacement of downstream slope was significantly larger than that at measuring point of upstream slope;
- The settlement deformation of the dam body was related to the fluctuation of the reservoir water level, in which the water level of upstream reservoir rose, and as surface of the dam body rose, conversely, it tended to sink. The fluctuation of the settlement deformation shows that the upstream side was larger than the downstream side, especially during the period of abrupt change in reservoir water level;
- With the rise in the reservoir water level, the longitudinal cracks on the dam crest showed a tendency of shrinkage, while the cracks showed a tendency of opening when the reservoir water level dropped. The change in the deformation gradient increment was basically consistent with the change in the crack opening, that is, the crack opening decreased with the decrease in the deformation gradient increment and increased with the increase in the gradient increment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, T.; Chen, J.; Li, P.; Yin, Y.; Shen, C. Natural tracing for concentrated leakage detection in a rockfill dam. Eng. Geol. 2019, 249, 1–12. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Wang, Y.; Hariri-Ardebili, M.A. Prediction, monitoring, and interpretation of dam leakage flow via adaptative kernel extreme learning machine. Measurement 2020, 166, 108161. [Google Scholar] [CrossRef]
- Mozafari, M.; Milanović, P.; Jamei, J. Water leakage problems at the Tangab Dam Reservoir (SW Iran), case study of the complexities of dams on karst. Bull. Eng. Geol. Environ. 2021, 80, 7989–8007. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, Y.; Chen, E.J. Probabilistic investigation on defective jet-grouted cut-off wall with random geometric imperfections. Géotechnique 2019, 69, 420–433. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; Zheng, H.; Xu, X.; He, H. A theoretical model for estimating the water-tightness of jet-grouted cut-off walls with geometric imperfections. Comput. Geotech. 2021, 138, 104316. [Google Scholar] [CrossRef]
- Shepherd, D.A.; Kotan, E.; Dehn, F. Plastic concrete for cut-off walls: A review. Constr. Build. Mater. 2020, 255, 119248. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Q.; Li, L.; Xiang, W. Monitoring and characterizing the deformation of an earth dam in Guangxi Province, China. Eng. Geol. 2019, 248, 50–60. [Google Scholar] [CrossRef]
- Yavaşoğlu, H.H.; Kalkan, Y.; Tiryakioğlu, I.; Yigit, C.; Özbey, V.; Alkan, M.N.; Bilgi, S.; Alkan, R.M. Monitoring the deformation and strain analysis on the Ataturk Dam, Turkey. Geomat. Nat. Hazards Risk 2018, 9, 94–107. [Google Scholar] [CrossRef] [Green Version]
- Bestuzheva, A.S.; Anakhaev, K.K. Seepage Through a Homogeneous Earth-Fill Dam with a Cut-Off Wall on a Permeable Foundation. Power Technol. Eng. 2020, 54, 147–153. [Google Scholar] [CrossRef]
- Barzaghi, R.; Cazzaniga, N.E.; De Gaetani, C.I.; Pinto, L.; Tornatore, V. Estimating and Comparing Dam Deformation Using Classical and GNSS Techniques. Sensors 2018, 18, 756. [Google Scholar] [CrossRef]
- Lai, J.; Liu, H.; Qiu, J.; Chen, J. Settlement Analysis of Saturated Tailings Dam Treated by CFG Pile Composite Foundation. Adv. Mater. Sci. Eng. 2016, 2016, 7383762. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Li, Q.; Zhou, Z.; Luo, Z.; Liu, M.; Liu, L. Research on a Seepage Monitoring Model of a High Core Rockfill Dam Based on Machine Learning. Sensors 2018, 18, 2749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ri, Y.N.; Han, U.C.; Jang, U.J.; Jong, D.Y.; Kim, C.U. Study on Stability Reduction Characteristics of Earth and Rockfill Dams under Rapid Drawdown Using Fully Coupled Seepage-Stress Analysis. Adv. Civ. Eng. 2022, 2022, 7954991. [Google Scholar] [CrossRef]
- Azadi, A.; Irani, A.E.; Azarafza, M.; Bonab, M.H.; Sarand, F.B.; Derakhshani, R. Coupled Numerical and Analytical Stability Analysis Charts for an Earth-Fill Dam under Rapid Drawdown Conditions. Appl. Sci. 2022, 12, 4550. [Google Scholar] [CrossRef]
- Sun, G.; Lin, S.; Jiang, W.; Yang, Y. A Simplified Solution for Calculating the Phreatic Line and Slope Stability during a Sudden Drawdown of the Reservoir Water Level. Geofluids 2018, 2018, 1859285. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, Z.; Xue, S.; Wang, R. Stability analysis of a typical landslide mass in the Three Gorges Reservoir under varying reservoir water levels. Environ. Earth Sci. 2020, 79, 42. [Google Scholar] [CrossRef]
- Meng, Q.; Qian, K.; Zhong, L.; Gu, J.; Li, Y.; Fan, K.; Yan, L. Numerical Analysis of Slope Stability under Reservoir Water Level Fluctuations Using a FEM-LEM-Combined Method. Geofluids 2020, 2020, 6683311. [Google Scholar] [CrossRef]
- Zhang, H.; Jing, Y.; Chen, J.; Gao, Z.; Xu, Y. Characteristics and causes of crest cracking on a high core-wall rockfill dam: A case study. Eng. Geol. 2022, 297, 106488. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Wu, Z.; Chen, J.; Yin, C.; Bian, K. Dynamic Risk Evaluation and Early Warning of Crest Cracking for High Earth-Rockfill Dams through Bayesian Parameter Updating. Appl. Sci. 2020, 10, 7627. [Google Scholar] [CrossRef]
- Kaur, A.; Sharma, R. Slope stability analysis techniques: A review. Int. J. Eng. Appl. Sci. Technol. 2016, 1, 52–57. [Google Scholar]
- Firincioglu, B.S.; Ercanoglu, M. Insights and perspectives into the limit equilibrium method from 2D and 3D analyses. Eng. Geol. 2021, 281, 105968. [Google Scholar] [CrossRef]
- Arvin, M.R.; Zakeri, A.; Shoorijeh, M.B. Using Finite Element Strength Reduction Method for Stability Analysis of Geocell-Reinforced Slopes. Geotech. Geol. Eng. 2019, 37, 1453–1467. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, P.; Meng, J.; Li, K.; Fan, W. Modeling the Progressive Failure of Jointed Rock Slope Using Fracture Mechanics and the Strength Reduction Method. Rock Mech. Rock Eng. 2015, 48, 771–785. [Google Scholar] [CrossRef]
- Dong-Ping, D.; Liang, L.; Jian-Feng, W.; Lian-Heng, Z. Limit equilibrium method for rock slope stability analysis by using the Generalized Hoek–Brown criterion. Int. J. Rock Mech. Min. Sci. 2016, 89, 176–184. [Google Scholar] [CrossRef]
- Liu, S.; Su, Z.; Li, M.; Shao, L. Slope stability analysis using elastic finite element stress fields. Eng. Geol. 2020, 273, 105673. [Google Scholar] [CrossRef]
- Siacara, A.; Beck, A.; Futai, M. Reliability analysis of rapid drawdown of an earth dam using direct coupling. Comput. Geotech. 2020, 118, 103336. [Google Scholar] [CrossRef]
- Duncan, J.; Wright, S. The accuracy of equilibrium methods of slope stability analysis. Eng. Geol. 1980, 16, 5–17. [Google Scholar] [CrossRef]
- Kong, X.; Cai, G.; Cheng, Y.; Zhao, C. Numerical Implementation of Three-Dimensional Nonlinear Strength Model of Soil and Its Application in Slope Stability Analysis. Sustainability 2022, 14, 5127. [Google Scholar] [CrossRef]
- Bayrak, T. Modelling the relationship between water level and vertical displacements on the Yamula Dam, Turkey. Nat. Hazards Earth Syst. Sci. 2007, 7, 289–297. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zheng, D.; Georgakis, C.; Kabel, T.; Cao, E.; Wu, X.; Ma, J. Deformation Analysis of an Ultra-High Arch Dam under Different Water Level Conditions Based on Optimized Dynamic Panel Clustering. Appl. Sci. 2022, 12, 481. [Google Scholar] [CrossRef]
- Wu, F.; Qi, S.; Lan, H. Mechanism of uplift deformation of the dam foundation of Jiangya Water Power Station, Hunan Province, P.R. China. Hydrogeol. J. 2005, 13, 451–466. [Google Scholar] [CrossRef]
- Khalilzad, M.; Gabr, M.A.; Hynes, M.E. Deformation-Based Limit State Analysis of Embankment Dams Including Geometry and Water Level Effects. Int. J. Géoméch. 2015, 15, 04014086. [Google Scholar] [CrossRef]
- Jadid, R.; Montoya, B.; Bennett, V.; Gabr, M. Effect of repeated rise and fall of water level on seepage-induced deformation and related stability analysis of Princeville levee. Eng. Geol. 2020, 266, 105458. [Google Scholar] [CrossRef]

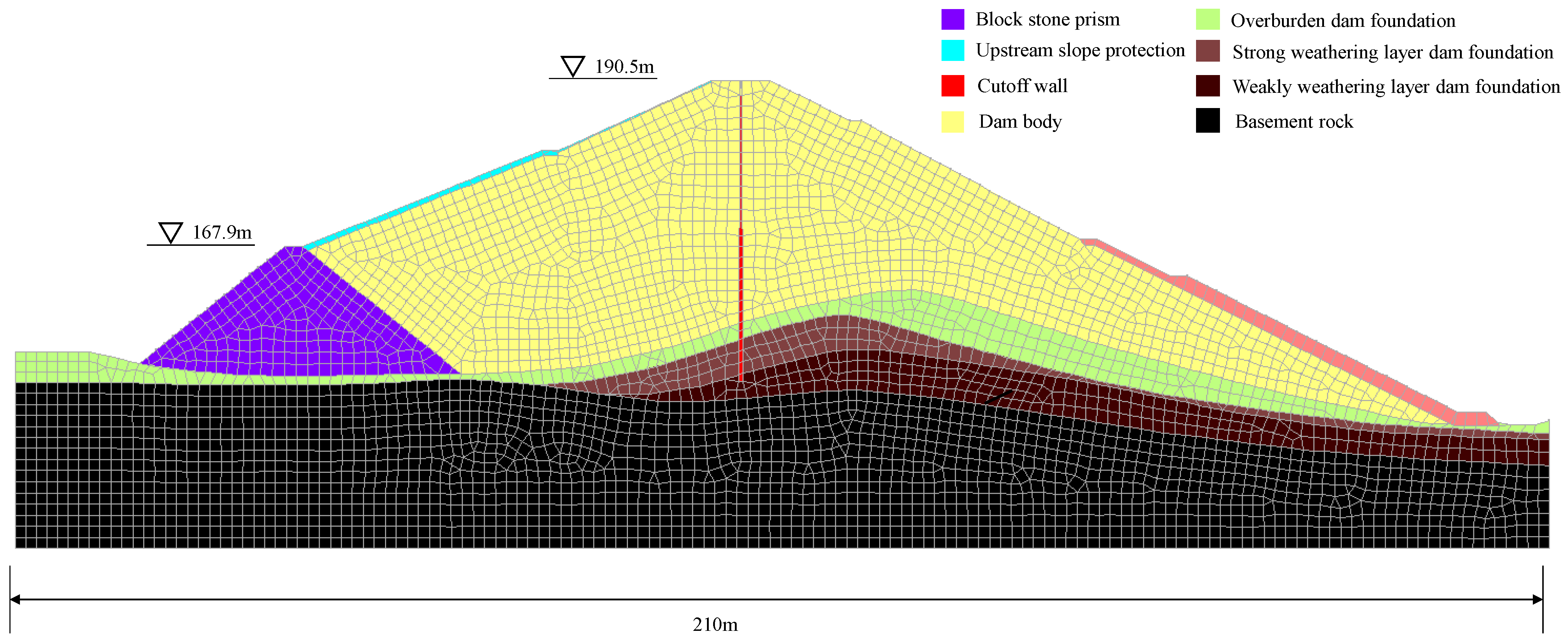
| Material | Permeability Coefficient/cm/s | Density/kg/m3 | Cohesion/kPa | Friction Angle |
|---|---|---|---|---|
| Silty sand of dam body | 5.0 × 10−5 | 1700 | 20 | 20 |
| Dam foundation overburden | 5.0 × 10−4 | 1800 | 15 | 28 |
| Strongly weathered rock mass of dam foundation | 1.0 × 10−4 | 2400 | 15 | 30 |
| Weakly weathered rock mass of dam foundation | 1.0 × 10−5 | 2600 | 20 | 33 |
| Basement rock | 1.0 × 10−6 | 2700 | 30 | 35 |
| Monitoring Time | 1# Section | 2# Section | 3# Section | |||
|---|---|---|---|---|---|---|
| S11 | S12 | S21 | S22 | S31 | S32 | |
| 5 March 2020 | 0.00 | / | 0.00 | 0.00 | 0.00 | 0.00 |
| 23 March 2020 | −2.75 | 3.07 | 1.17 | −0.99 | −0.67 | |
| 7 April 2020 | −2.66 | 0.38 | 32.05 | −0.97 | 13.70 | |
| 6 May 2020 | 0.84 | 1.31 | −31.72 | 0.69 | −12.90 | |
| 21 May 2020 | 0.53 | 0.62 | −1.33 | 2.58 | 0.55 | |
| 15 June 2020 | −5.46 | −2.93 | 3.22 | −1.31 | 1.03 | |
| 28 June 2020 | 8.95 | −3.04 | −2.01 | −1.23 | −0.96 | |
| 3 August 2020 | −17.46 | −9.96 | −4.01 | −11.80 | −6.05 | |
| 17 August 2020 | 3.13 | −0.02 | 0.32 | 0.99 | 0.06 | |
| 4 September 2020 | 0.41 | −5.00 | 0.71 | −2.37 | 1.26 | |
| 12 October 2020 | −3.88 | 5.52 | −0.21 | 0.10 | −0.28 | |
| 4 December 2020 | 11.93 | 4.90 | 1.83 | 4.90 | 1.91 | |
| 28 December 2020 | 1.57 | −0.46 | 4.81 | 1.36 | 0.07 | |
| 18 March 2021 | 4.04 | 7.98 | −1.01 | 6.04 | 0.76 | |
| 26 March 2021 | −2.17 | −2.50 | 0.98 | 1.94 | 2.25 | |
| 2 April 2021 | −1.54 | 0.54 | −1.95 | −3.96 | −1.54 | |
| Monitoring Time | 1# Section | 2# Section | 3# Section | |||
|---|---|---|---|---|---|---|
| S11 | S12 | S21 | S22 | S31 | S32 | |
| 5 March 2020 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 23 March 2020 | −34.50 | −38.30 | −34.20 | −25.19 | −32.40 | −28.60 |
| 7 April 2020 | 15.50 | 4.40 | 7.70 | 4.79 | 4.10 | 7.90 |
| 21 May 2020 | −9.30 | −1.70 | −3.50 | −2.90 | 1.70 | −6.60 |
| 15 June 2020 | −4.80 | −9.80 | −9.00 | −16.00 | −8.20 | −5.30 |
| 28 June 2020 | −5.90 | 6.80 | −0.10 | 9.50 | 1.10 | 1.60 |
| 3 August 2020 | −6.20 | −11.20 | −4.40 | −4.10 | −4.70 | −1.90 |
| 17 August 2020 | 6.80 | 5.40 | −1.50 | 0.80 | 2.60 | 1.80 |
| 4 September 2020 | −2.30 | 8.70 | 4.30 | 6.70 | −4.20 | 0.50 |
| 12 October 2020 | 3.10 | −9.90 | −2.50 | −8.90 | 3.20 | −3.00 |
| 4 December 2020 | 6.90 | 6.30 | 2.60 | 4.70 | 4.60 | 1.70 |
| 28 December 2020 | 4.00 | −0.10 | 5.90 | 3.50 | 2.60 | 2.30 |
| 18 March 2021 | −3.70 | 3.50 | −3.10 | −0.70 | −4.30 | −1.00 |
| 26 March 2021 | −5.20 | −1.60 | −1.90 | −2.50 | 1.70 | −0.30 |
| 2 April 2021 | 8.60 | −1.00 | 6.00 | −3.10 | 2.20 | 1.90 |
| Monitoring Time | Settlement Z/mm | Horizontal Distance of Observation Points on the Same Section/m | Deformation Gradient/% | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1# Section | 2# Section | 3# Section | γ1 | γ2 | γ3 | |||||
| S31 | S32 | S21 | S22 | S11 | S12 | |||||
| 5 March 2020 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 9.00 | 0 | 0 | 0 |
| 23 March 2020 | −32.4 | −28.6 | −34.2 | −25.19 | −34.5 | −38.3 | 0.0422 | 0.1001 | 0.0422 | |
| 7 April 2020 | 4.1 | 7.9 | 7.7 | 4.79 | 15.5 | 4.4 | 0.0422 | 0.0323 | 0.1233 | |
| 21 May 2020 | 1.7 | −6.6 | −3.5 | −2.9 | −9.3 | −1.7 | 0.0922 | 0.0067 | 0.0844 | |
| 15 June 2020 | −8.2 | −5.3 | −9 | −16 | −4.8 | −9.8 | 0.0322 | 0.0778 | 0.0556 | |
| 28 June 2020 | 1.1 | 1.6 | −0.1 | 9.5 | −5.9 | 6.8 | 0.0056 | 0.1067 | 0.1411 | |
| 3 August 2020 | −4.7 | −1.9 | −4.4 | −4.1 | −6.2 | −11.2 | 0.0311 | 0.0033 | 0.0556 | |
| 17 August 2020 | 2.6 | 1.8 | −1.5 | 0.8 | 6.8 | 5.4 | 0.0089 | 0.0256 | 0.0156 | |
| 4 September 2020 | −4.2 | 0.5 | 4.3 | 6.7 | −2.3 | 8.7 | 0.0522 | 0.0267 | 0.1222 | |
| 12 October 2020 | 3.2 | −3 | −2.5 | −8.9 | 3.1 | −9.9 | 0.0689 | 0.0711 | 0.1444 | |
| 4 December 2020 | 4.6 | 1.7 | 2.6 | 4.7 | 6.9 | 6.3 | 0.0322 | 0.0233 | 0.0067 | |
| 28 December 2020 | 2.6 | 2.3 | 5.9 | 3.5 | 4.0 | −0.1 | 0.0033 | 0.0267 | 0.0456 | |
| 18 March 2021 | −4.3 | −1.0 | −3.1 | −0.7 | −3.7 | 3.5 | 0.0367 | 0.0267 | 0.0800 | |
| Dam | Dam Type | Research Method | Whether the Water Level Fluctuation Affects the Dam Deformation | How Water Level Fluctuation Affects Dam Deformation |
|---|---|---|---|---|
| Chengbihe [7] | Earth dam | In situ measurements | Yes | Settlement on the dam’s upstream side |
| Yamula [29] | Earth dam | In situ measurements | Yes | Vertical deformation. The rising water level increases the subsidence velocity |
| An ultra-high arch dam [30] | Concrete arch dam | In situ measurements | Yes, but the influence of water level on dam deformation is hysteretic. | With the rise of the water level, the cluster center area also rises, indicating that the trend of the expansion and upward movement of the maximum deformation area of the dam body |
| Jiangya [31] | Gravity dam | In situ measurements | Yes | The reservoir impoundment is the predominant cause of the uplift of dam foundation. |
| An earth embankments of dams [32] | Earth dam. | Numerical simulation | Yes | The horizontal deformation of the dam toe is higher for a higher rising rate |
| Princeville [33] | Earth levee | Numerical simulation | Yes | The Factor of safety is affected by rate of rise/drawdown of the water level |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Lin, T.; Gao, J.; Xue, B.; Yang, J.; Chen, C.; Zhang, W.; Sun, W. Study on the Influence of Water Level on Earth Dam Reinforced by Cut-Off Wall: A Case Study in Wujing Reservoir. Water 2023, 15, 140. https://doi.org/10.3390/w15010140
Liu D, Lin T, Gao J, Xue B, Yang J, Chen C, Zhang W, Sun W. Study on the Influence of Water Level on Earth Dam Reinforced by Cut-Off Wall: A Case Study in Wujing Reservoir. Water. 2023; 15(1):140. https://doi.org/10.3390/w15010140
Chicago/Turabian StyleLiu, Da, Taiqing Lin, Jianglin Gao, Binghan Xue, Jianhua Yang, Congxin Chen, Weipeng Zhang, and Wenbin Sun. 2023. "Study on the Influence of Water Level on Earth Dam Reinforced by Cut-Off Wall: A Case Study in Wujing Reservoir" Water 15, no. 1: 140. https://doi.org/10.3390/w15010140







