Flood Vulnerability Study of a Roadway Bridge Subjected to Hydrodynamic Actions, Local Scour and Wood Debris Accumulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Properties and Input Data
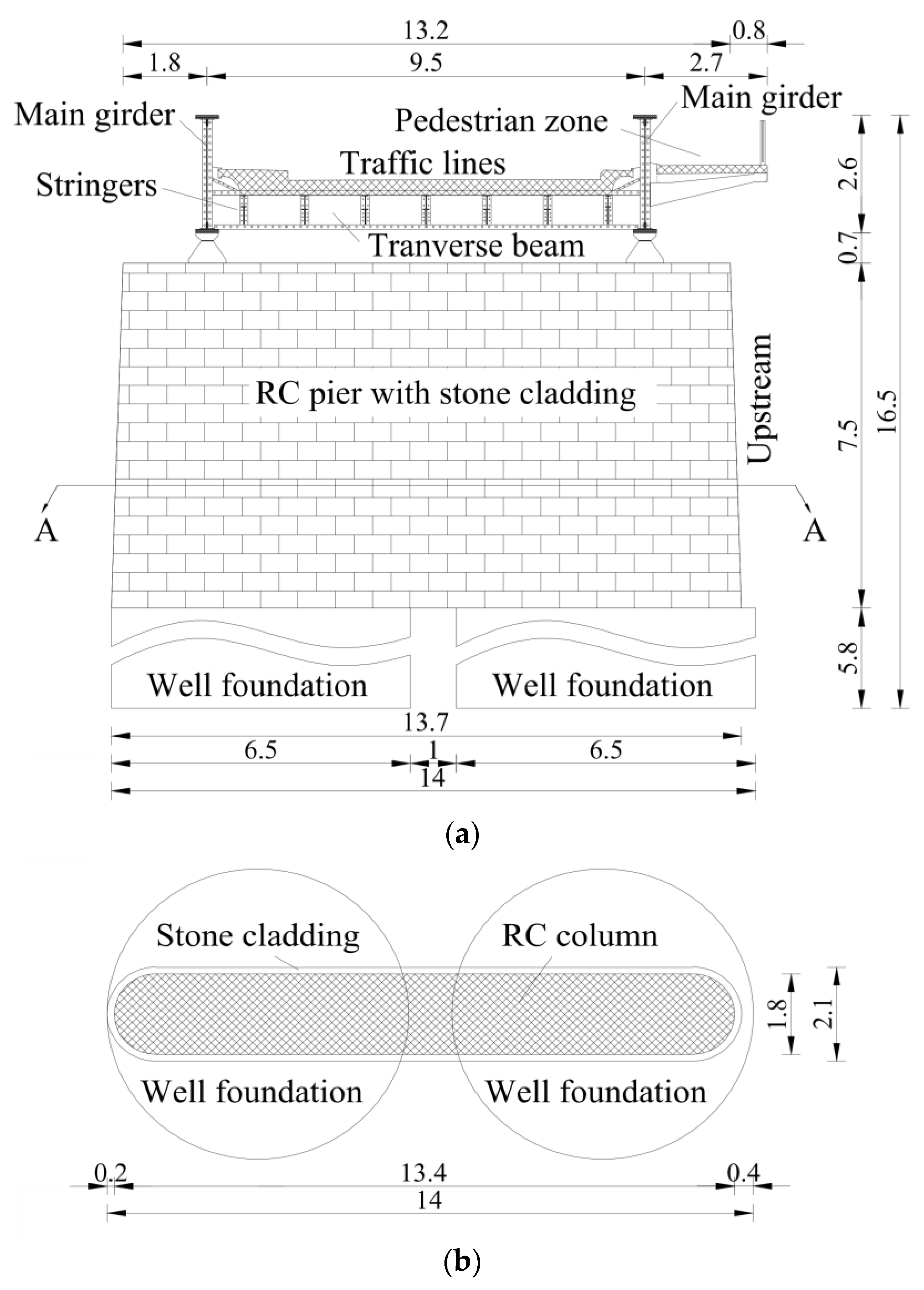
2.1.1. Geometry and Materials
2.1.2. Geotechnical Data
2.1.3. Hydraulic Data
2.2. Methodology and Modelling Approach
2.2.1. Overview
2.2.2. Structural Finite-Element Modelling
2.2.3. Soil–Structure Interaction Modelling
2.2.4. Loads Modelling
Hydrodynamic Forces
Wood Debris Forces
2.2.5. Local Scour Modelling
Effect of Local Scour on SSI and Flood Loading
2.2.6. Parameters’ Uncertainty
2.2.7. Latin Hypercube Sampling
3. Results
3.1. Model Validation
3.2. Vulnerability Analysis
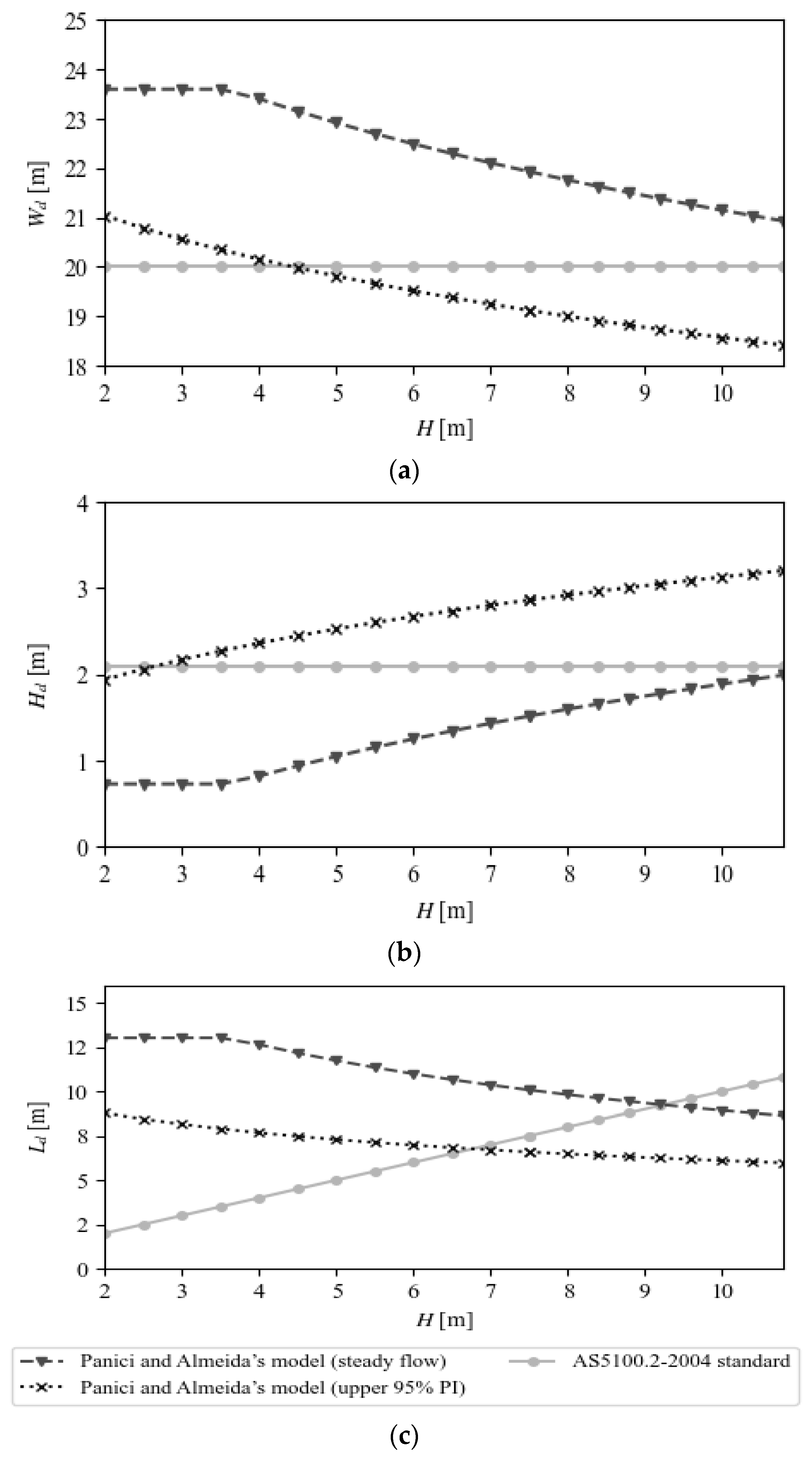
3.2.1. Debris Accumulation Sizes
3.2.2. Limit State Definition
- Bending and shear failure at the base of the piers;
- Shear failure of the bearing above the pier and the abutments;
- Bending failure of the deck around the weak axis at the section above the piers and the midspan of the bridge;
- Bearing failure of the foundation (vertical and bending capacity at the base);
- Failure due to local scour reaching the base of the foundation.
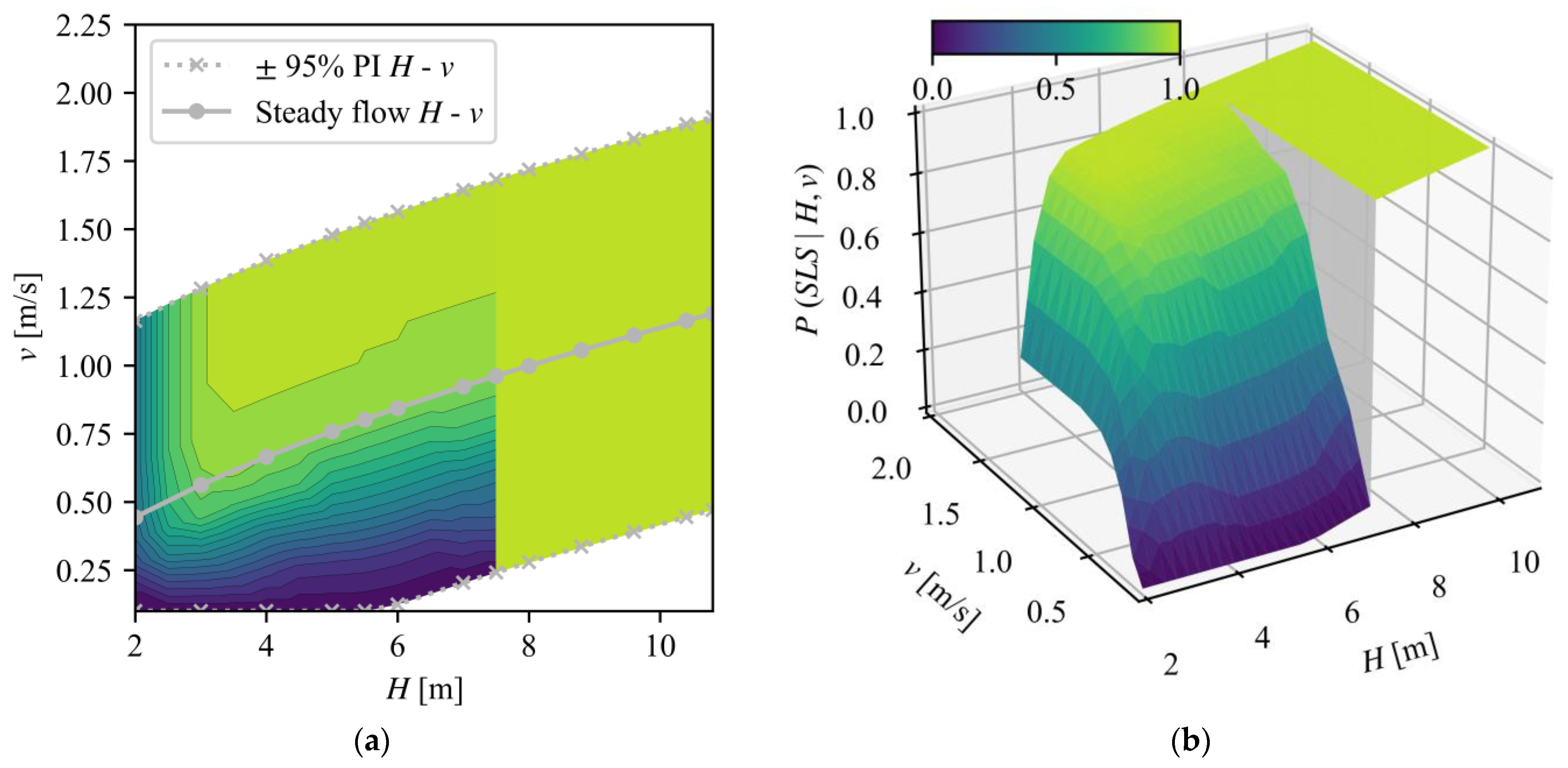
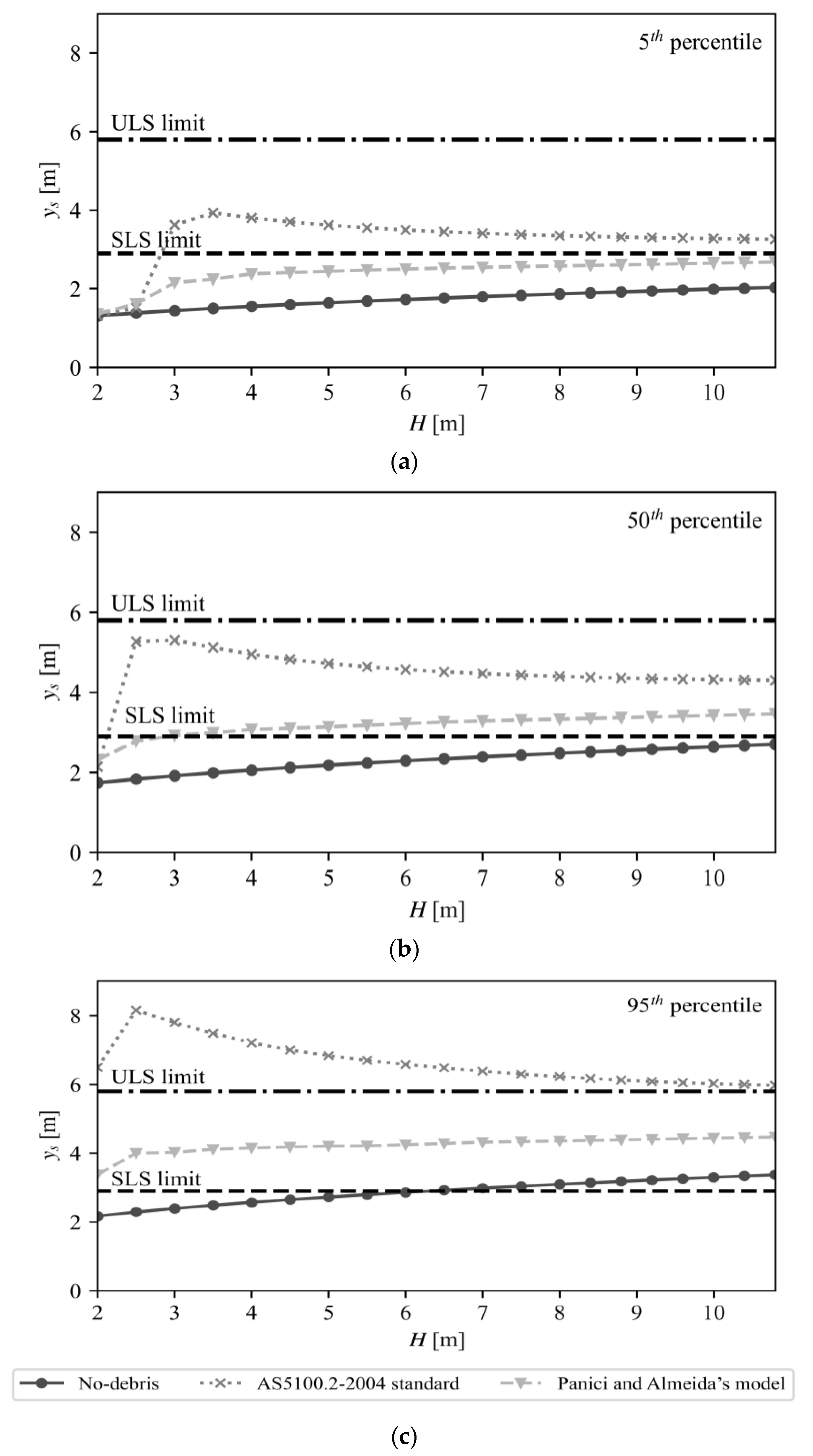
3.2.3. Results for Serviceability Limit State
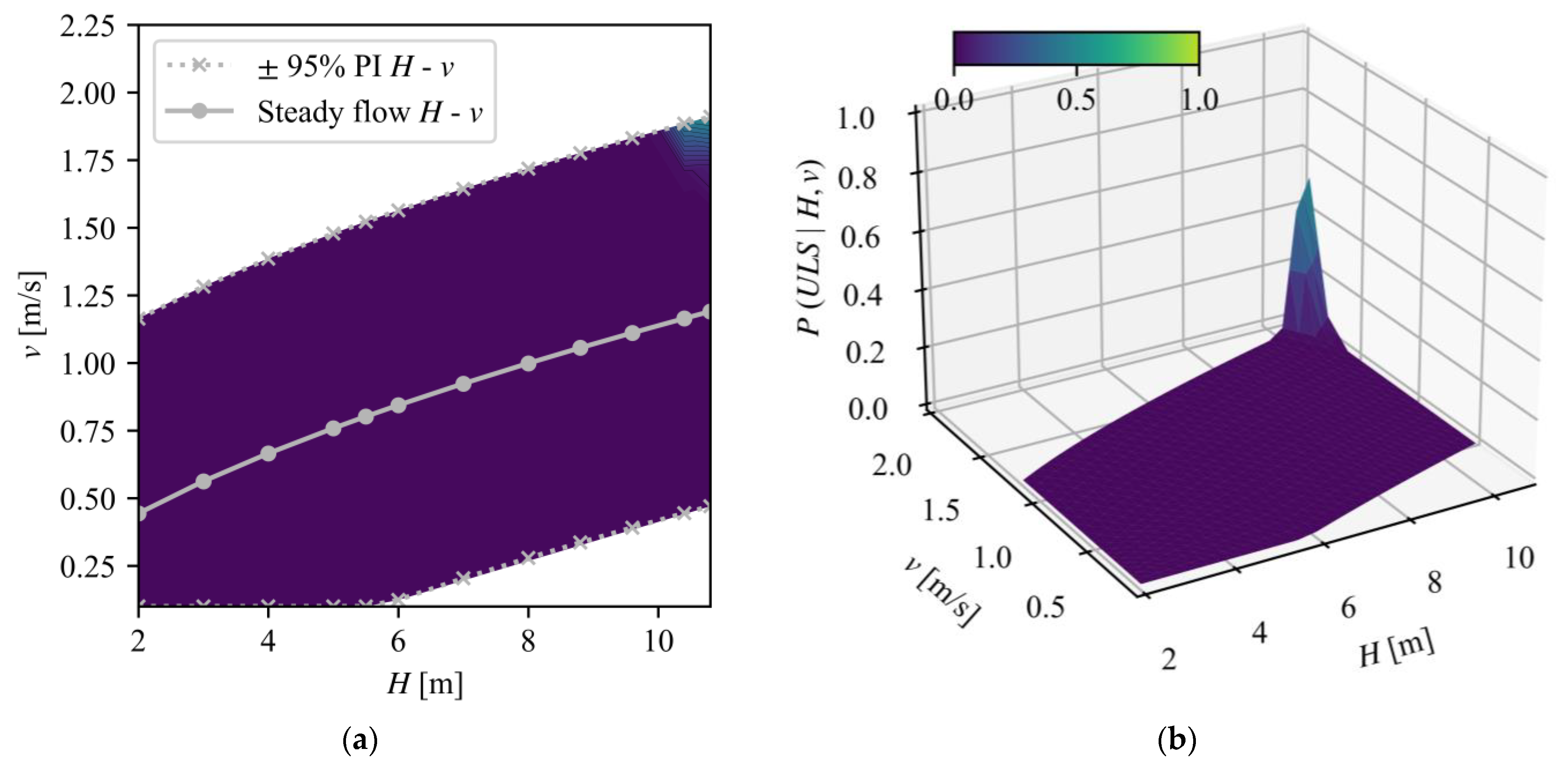
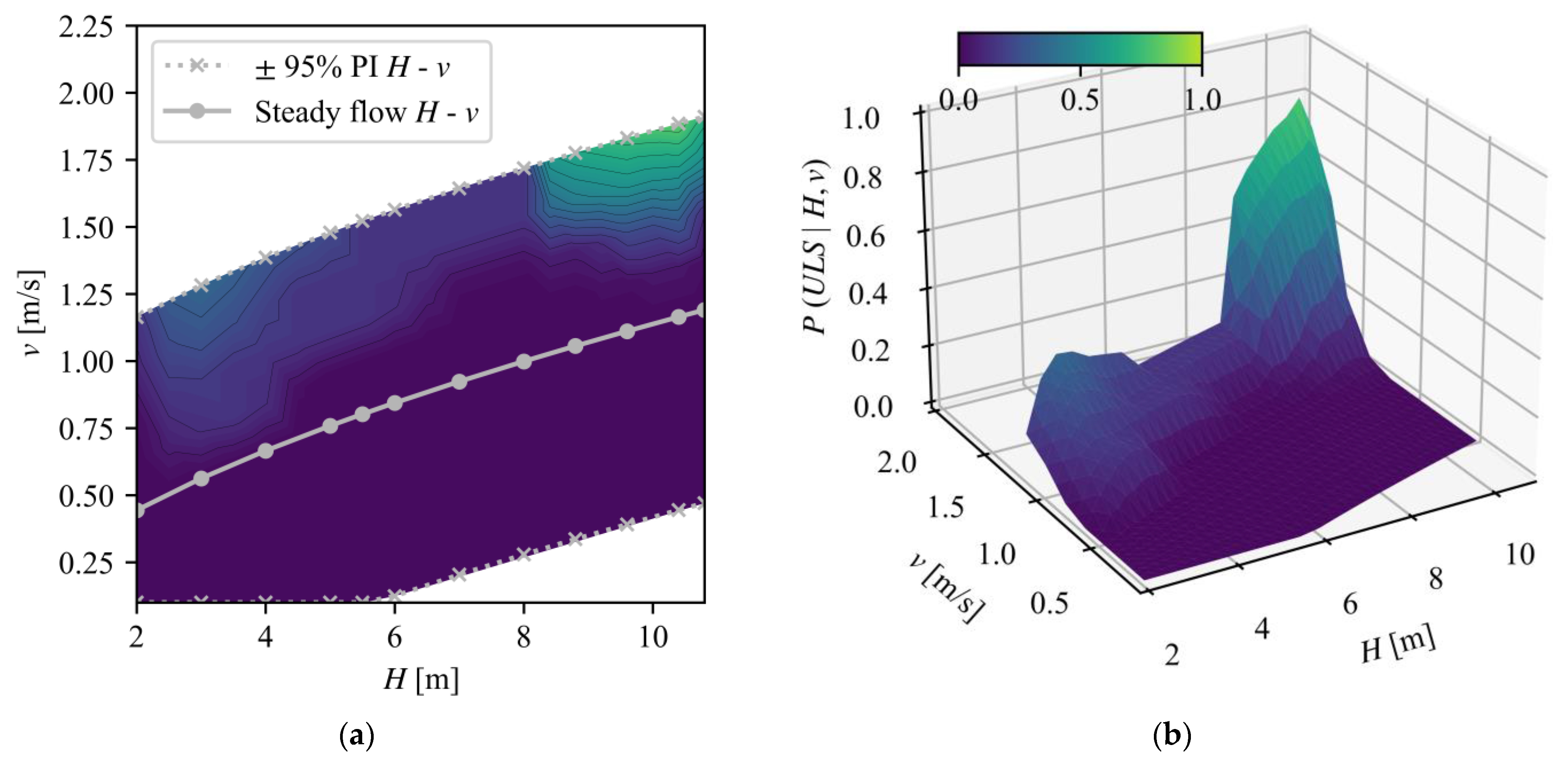
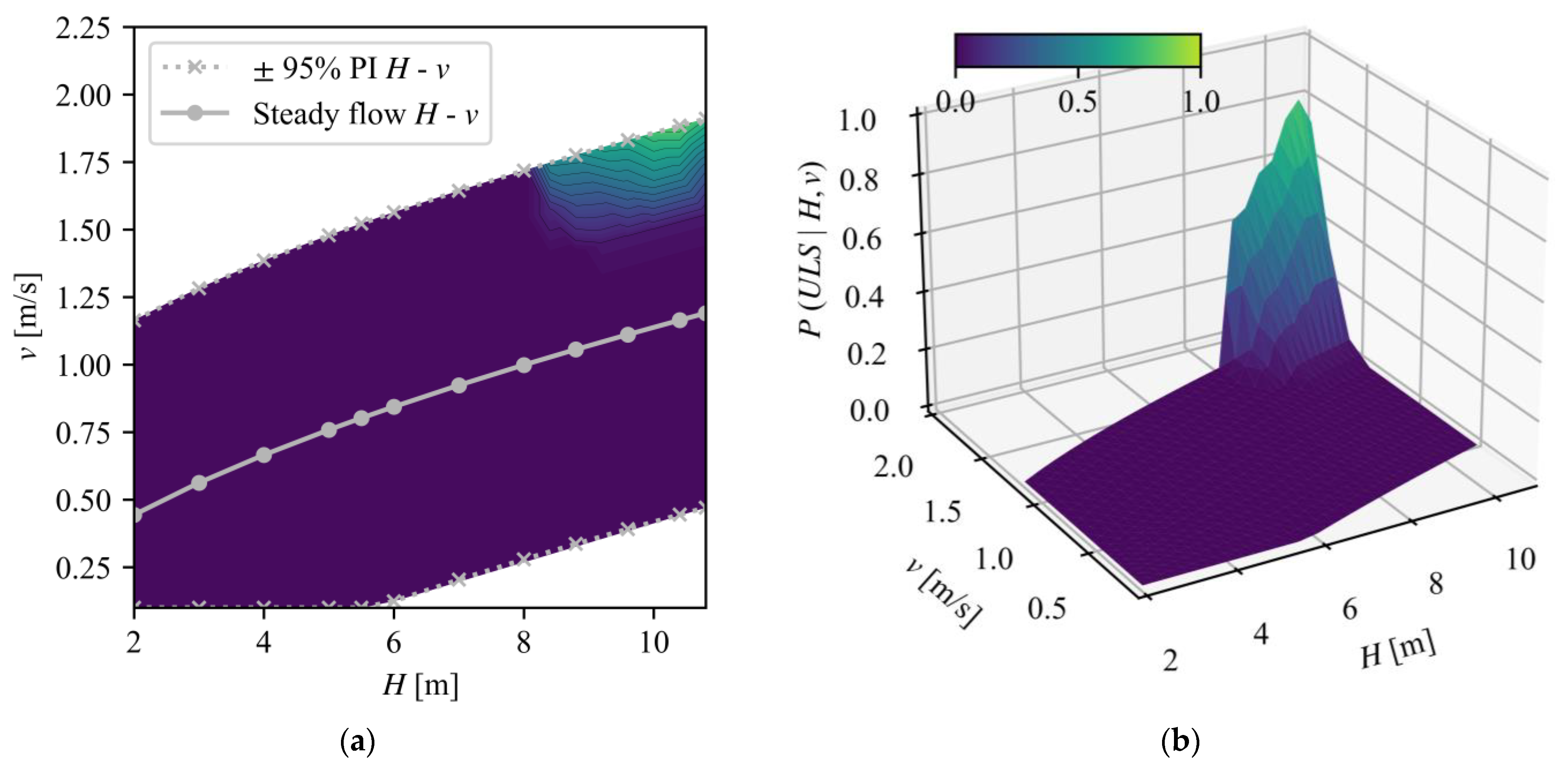
3.2.4. Results for Ultimate Limit State
3.3. Sensitivity Analysis
3.3.1. Scour Depths
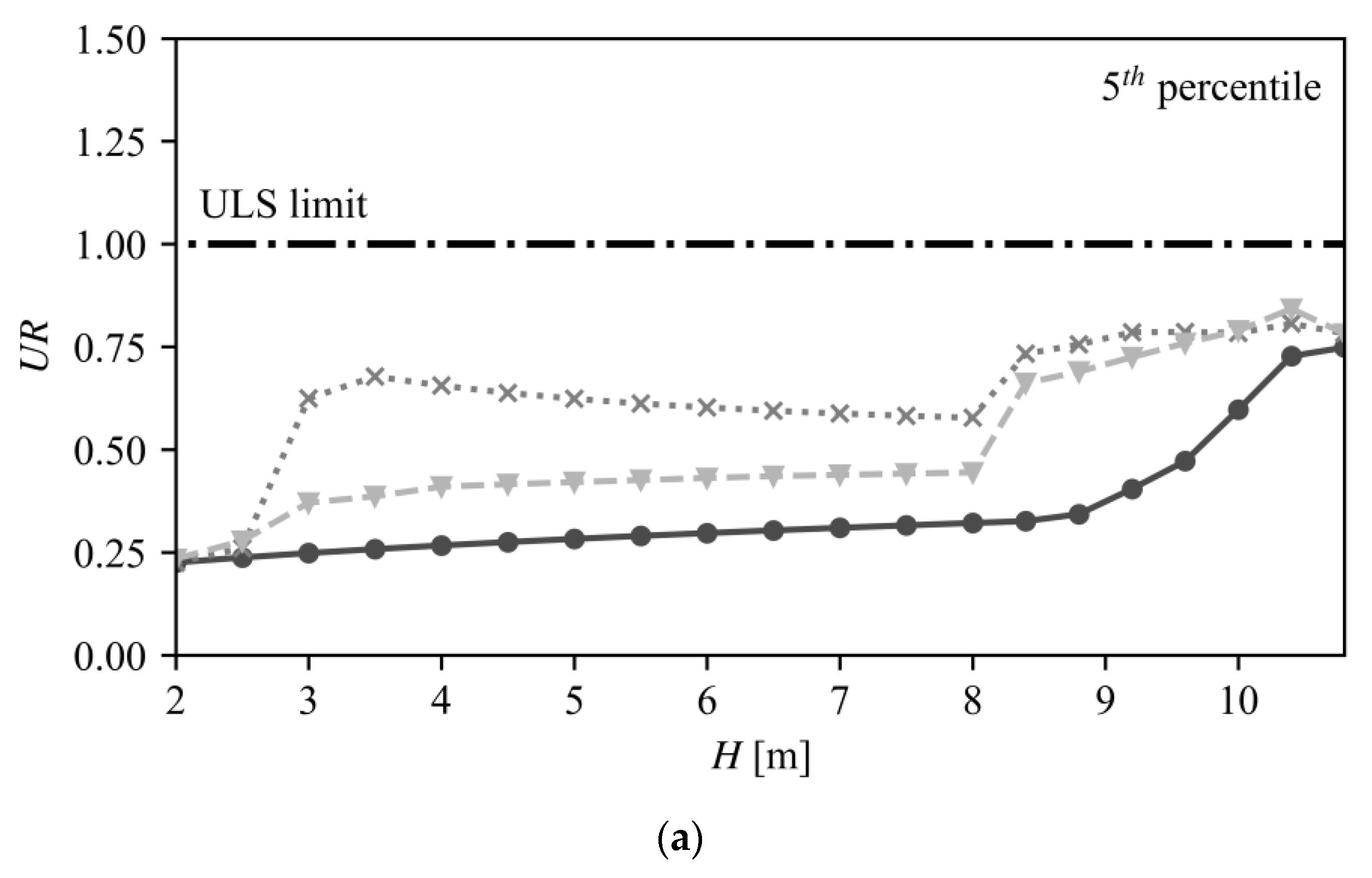
3.3.2. Utilization Ratios for ULS
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols and Notations
| Pier width | |
| Equivalent pier width | |
| Projected wetted area in the direction of the flow | |
| Wetted area perpendicular to the flow | |
| Effective cohesion of the soil | |
| Drag coefficient | |
| Lift coefficient | |
| CPT | Cone Penetration Test |
| Diameter of a well foundation | |
| Embedment depth of the foundation | |
| Length of the deck | |
| Wetted depth of the deck | |
| Wetted depth of the solid superstructure | |
| Distance from the girder soffit to the flood water surface | |
| Soil elastic modulus | |
| Steel elastic modulus | |
| Concrete compressive strength | |
| Steel yield strength | |
| Hydrodynamic drag force | |
| Hydrodynamic lift force | |
| Debris Froude number | |
| Froude number | |
| Gravitational acceleration | |
| Shear modulus of the soil | |
| Water height | |
| Height of wood debris accumulation | |
| IM | Intensity measure |
| Index vector for each LS and each H-v | |
| Index of j-th LHS simulation | |
| Correction factor for the pier nose shape | |
| Correction factor for the angle of attack flow | |
| Correction factor for the riverbed condition | |
| Correction factors used in the calculation of the equivalent pier width depending on the shape of the debris raft | |
| Horizontal embedded stiffness of the well foundation | |
| Rocking embedded stiffness of the well foundation | |
| Vertical embedded stiffness of the well foundation | |
| Torsional embedded stiffness of the well foundation | |
| Depth of the foundation | |
| Length of wood debris accumulation in the flow direction | |
| Key log length | |
| LHS | Latin Hypercube Sampling |
| LS | Limit state |
| Equivalent number of Standard Penetration Test (SPT) blows of the soil | |
| Number of simulations that leads to the exceedance of LS for a given H-v | |
| Number of LHS simulations | |
| Number of random input variables | |
| Probability of exceeding the designated LS for a given H-v | |
| PI | Prediction Intervals |
| Proximity ratio | |
| Water discharge | |
| RC | Reinforced Concrete |
| Foundation radius | |
| Span length of the bridge | |
| Relative submergence of the deck | |
| SLS | Serviceability Limit State |
| SSI | Soil–Structure Interaction |
| ULS | Ultimate Limit State |
| Utilization ratio | |
| Mean flow velocity | |
| Width of wood debris accumulation | |
| Average vertical distance from the girder soffit to the riverbed | |
| Local scour depth | |
| Effective shear angle of the soil | |
| Soil unit weight | |
| Poisson’s ratio | |
| Angle of flow attack |
References
- Jean-Louis, J.B.; Paolo, G.; Congpu, Y. Statistical, Risk, and Reliability Analyses of Bridge Scour. J. Geotech. Geoenviron. Eng. 2014, 140, 4013011. [Google Scholar] [CrossRef]
- Benn, J. Railway bridge failure during flooding in the UK and Ireland. Proc. Inst. Civ. Eng. Forensic Eng. 2013, 166, 163–170. [Google Scholar] [CrossRef]
- Kumalasari, W.; Hadipriono, F.C. Analysis of Recent Bridge Failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Zampieri, P.; Zanini, M.A.; Faleschini, F.; Hofer, L.; Pellegrino, C. Failure analysis of masonry arch bridges subject to local pier scour. Eng. Fail. Anal. 2017, 79, 371–384. [Google Scholar] [CrossRef]
- Stefanidis, S.; Alexandridis, V.; Theodoridou, T. Flood exposure of residential areas and infrastructure in Greece. Hydrology 2022, 9, 145. [Google Scholar] [CrossRef]
- Karatzetzou, A.; Stefanidis, S.; Stefanidou, S.; Tsinidis, G.; Pitilakis, D. Unified hazard models for risk assessment of transportation networks in a multi-hazard environment. Int. J. Disaster Risk Reduct. 2022, 75, 102960. [Google Scholar] [CrossRef]
- Banerjee, S.; Shinozuka, M. Nonlinear Static Procedure for Seismic Vulnerability Assessment of Bridges. Comput. Civ. Infrastruct. Eng. 2007, 22, 293–305. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, W. Dynamic amplification responses of short span bridges considering scour and debris impacts. Eng. Struct. 2022, 252, 113644. [Google Scholar] [CrossRef]
- Pagliara, S.; Carnacina, I. Influence of wood debris accumulation on bridge pier scour. J. Hydraul. Eng. 2011, 137, 254–261. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Gavin, K. A review of bridge scour monitoring techniques. J. Rock Mech. Geotech. Eng. 2014, 6, 138–149. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Djordjević, S.; Panici, D.; Tabor, G.; Kripakaran, P. A method for evaluating local scour depth at bridge piers due to debris accumulation. In Proceedings of the Institution of Civil Engineers—Bridge Engineering; Thomas Telford Ltd.: London, UK, 2020; Volume 173, pp. 86–99. [Google Scholar]
- Shen, H.W.; Schneider, V.R.; Karaki, S. Local scour around bridge piers. J. Hydraul. Div. 1969, 95, 1919–1940. [Google Scholar] [CrossRef]
- Lagasse, P.F. Countermeasures to Protect Bridge Piers from Scour; Transportation Research Board: Washington, DC, USA, 2007; Volume 593. [Google Scholar]
- Lin, C.; Han, J.; Bennett, C.; Parsons, R.L. Case history analysis of bridge failures due to scour. In Climatic Effects on Pavement and Geotechnical Infrastructure; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 204–216. [Google Scholar]
- Zhang, Y. Economic Impact of Bridge Damage in a Flood Event. Master‘s Thesis, RMIT University, Melbourne, Australia, 2016. [Google Scholar]
- Stewart, M.G. Reliability-based assessment of ageing bridges using risk ranking and life cycle cost decision analyses. Reliab. Eng. Syst. Saf. 2001, 74, 263–273. [Google Scholar] [CrossRef]
- Billah, A.; Alam, M.S. Seismic fragility assessment of highway bridges: A state-ofthe-art review. Struct. Infrastruct. Eng. 2015, 11, 804–832. [Google Scholar] [CrossRef]
- Karamlou, A.; Bocchini, P. Computation of bridge seismic fragility by large-scale simulation for probabilistic resilience analysis. Earthq. Eng. Struct. Dyn. 2015, 44, 1959–1978. [Google Scholar] [CrossRef]
- Mosleh, A.; Jara, J.; Razzaghi, M.S.; Varum, H. Probabilistic seismic performance analysis of RC bridges. J. Earthq. Eng. 2020, 24, 1704–1728. [Google Scholar] [CrossRef]
- Turmo, J.; Ramos, G.; Aparicio, A.C. Shear truss analogy for concrete members of solid and hollow circular cross section. Eng. Struct. 2009, 31, 455–465. Available online: http://www.sciencedirect.com/science/article/B6V2Y-4TMYJYT-1/2/8f69b9f83b0bb052df05ff98d8a38d13 (accessed on 20 December 2022). [CrossRef]
- Kappos, A.J.; Saiid, S.M.; Nuray, A.M.; Isaković, I. (Eds.) Seismic Design and Assessment of Bridges; Spinger: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Deco, A.; Frangopol, D.M. Risk assessment of highway bridges under multiple hazards. J. Risk Res. 2011, 14, 1057–1089. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M.; Saydam, D. Time-variant sustainability assessment of seismically vulnerable bridges subjected to multiple hazards. Earthq. Eng. Struct. Dyn. 2013, 42, 1451–1467. [Google Scholar] [CrossRef]
- Kim, H.; Sim, S.-H.; Lee, J.; Lee, Y.-J.; Kim, J.-M. Flood fragility analysis for bridges with multiple failure modes. Adv. Mech. Eng. 2017, 9, 1687814017696415. [Google Scholar] [CrossRef] [Green Version]
- Ahamed, T.; Duan, J.G.; Jo, H. Flood-fragility analysis of instream bridges—Consideration of flow hydraulics, geotechnical uncertainties, and variable scour depth. Struct. Infrastruct. Eng. 2021, 17, 1494–1507. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Mitoulis, S.A. Vulnerability of bridges to individual and multiple hazards—Floods and earthquakes. Reliab. Eng. Syst. Saf. 2021, 210, 107564. [Google Scholar] [CrossRef]
- Tanasić, N.; Ilić, V.; Hajdin, R. Vulnerability assessment of bridges exposed to scour. Transp. Res. Rec. 2013, 2360, 36–44. [Google Scholar] [CrossRef]
- Anisha, A.; Jacob, A.; Davis, R.; Mangalathu, S. Fragility functions for highway RC bridge under various flood scenarios. Eng. Struct. 2022, 260, 114244. [Google Scholar] [CrossRef]
- George, J.; Menon, A. Analytical fragility curves for displacement-based scour assessment of masonry arch bridges. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 46, pp. 172–185. [Google Scholar]
- Homaei, F.; Najafzadeh, M. Failure analysis of scouring at pile groups exposed to steady-state flow: On the assessment of reliability-based probabilistic methodology. Ocean Eng. 2022, 266, 112707. [Google Scholar] [CrossRef]
- Homaei, F.; Najafzadeh, M. A reliability-based probabilistic evaluation of the wave-induced scour depth around marine structure piles. Ocean Eng. 2020, 196, 106818. [Google Scholar] [CrossRef]
- Kwon, O.-S.; Elnashai, A. The effect of material and ground motion uncertainty on the seismic vulnerability curves of RC structure. Eng. Struct. 2006, 28, 289–303. [Google Scholar] [CrossRef]
- Bartlett, F.M.; MacGregor, J.G. Statistical analysis of the compressive strength of concrete in structures. Mater. J. 1996, 93, 158–168. [Google Scholar]
- Kolisko, J.; Hunka, P.; Jung, K. A statistical analysis of the modulus of elasticity and compressive strength of concrete C45/55 for pre-stressed precast beams. J. Civ. Eng. Archit. 2012, 6, 1571. [Google Scholar]
- Yáñez-Godoy, H.; Mokeddem, A.; Elachachi, S.M. Influence of spatial variability of soil friction angle on sheet pile walls’ structural behaviour. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2017, 11, 299–314. [Google Scholar] [CrossRef]
- Breysse, D.; Niandou, H.; Elachachi, S.; Houy, L. A generic approach to soil–structure interaction considering the effects of soil heterogeneity. Geotechnique 2005, 55, 143–150. [Google Scholar] [CrossRef]
- Tubaldi, E.; White, C.J.; Patelli, E.; Mitoulis, S.A.; de Almeida, G.; Brown, J.; Cranston, M.; Hardman, M.; Koursari, E.; Lamb, R.; et al. Invited perspectives: Challenges and future directions in improving bridge flood resilience. Nat. Hazards Earth Syst. Sci. 2021, 22, 795–812. [Google Scholar] [CrossRef]
- Diehl, T.H. Potential Drift Accumulation at Bridges; US Department of Transportation, Federal Highway Administration, Research and Development, Turner-Fairbank Highway Research Center: McLean, VA, USA, 1997.
- European Standard EN 1993-1-1:2005; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Switzerland, 2005.
- European standard EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Switzerland, 2004.
- Herschy, R.W. Streamflow Measurement; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Zhu, M. The OpenSeesPy Library, Version 3.2.2—2020. 2020. Available online: https://openseespydoc.readthedocs.io/en/latest/ (accessed on 1 November 2022).
- McKenna, F.; Fenves, G.L.; Scott, M.H. Open System for Earthquake Engineering Simulation (OpenSees); Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2020. [Google Scholar]
- Pais, A.; Kausel, E. Approximate formulas for dynamic stiffnesses of rigid foundations. Soil Dyn. Earthq. Eng. 1988, 7, 213–227. [Google Scholar] [CrossRef]
- Australian Standard AS-5100.2-2004; Bridge Desing—Part 2: Design Loads. Standards Australia: Sydney, Australia, 2004.
- Yung-Yen, K.; Jiunn-Shyang, C.; Yu-Ching, T.; Cheng-Hsing, C.; Helsin, W.; Chung-Yue, W. Evaluation of Flood-Resistant Capacity of Scoured Bridges. J. Perform. Constr. Facil. 2014, 28, 61–75. [Google Scholar] [CrossRef]
- Hung, C.-C.; Yau, W.-G. Vulnerability evaluation of scoured bridges under floods. Eng. Struct. 2017, 132, 288–299. [Google Scholar] [CrossRef]
- Panici, D.; de Almeida, G.A.M. Formation, growth, and failure of debris jams at bridge piers. Water Resour. Res. 2018, 54, 6226–6241. [Google Scholar] [CrossRef]
- Hess, J.M. Distribution and Residence Times of Large Woody Debris along South River, Shenandoah Valley, Virginia; University of Delaware: Newark, DE, USA, 2007. [Google Scholar]
- Gurnell, A.; Bertoldi, W. Wood in fluvial systems. In Treatise on Geomorphology; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Schwarz, U. Sava white book. In River Sava: Threats and Restoration Potential; EuroNatur/Riverwatch: Radolfzell/Wien, Germany/Austria, 2016. [Google Scholar]
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating Scour at Bridges. HEC-18, 5th ed.; Hydraulic Engineering Circular No. 18.; National Highway Institute: Wahington, DC, USA, 2012.
- Lagasse, P.F.; Zevenbergen, L.W.; Clopper, P.E. Effects of debris on bridge pier scour. In Proceedings of the 5th International Conference on Scour and Erosion (ICSE-5), San Francisco, CA, USA, 7–11 November 2010; pp. 854–863. [Google Scholar]
- Zhang, Y. Probabilistic Structural Seismic Performance Assessment Methodology and Application to an Actual Bridge-Foundation-Ground System. Ph. D. Thesis, University of California, San Diego, CA, USA, 2006. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Prediction; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- JCSS. Probabilistic Model Code; Part 3, Resistance models, Section 3.0, Static Properties of Structural Steel; JCSS: 2001. Available online: https://www.jcss-lc.org/publications/jcsspmc/part_iii.pdf (accessed on 5 December 2022).
- Aygün, B.; Dueñas-Osorio, L.; Padgett, J.E.; DesRoches, R. Efficient Longitudinal Seismic Fragility Assessment of a Multispan Continuous Steel Bridge on Liquefiable Soils. J. Bridg. Eng. 2011, 16, 93–107. [Google Scholar] [CrossRef] [Green Version]
- Johnson, P.A.; Clopper, P.; Zevenbergen, L.; Lagasse, P.F. Quantifying Uncertainty and Reliability in Bridge Scour Estimations. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Vořechovský, M.; Novák, D. Correlation control in small-sample Monte Carlo type simulations I: A simulated annealing approach. Probabilistic Eng. Mech. 2009, 24, 452–462. [Google Scholar] [CrossRef]
- Dolsek, M. Incremental dynamic analysis with consideration of modeling uncertainties. Earthq. Eng. Struct. Dyn. 2009, 38, 805–825. [Google Scholar] [CrossRef]
- Dolšek, M. Simplified method for seismic risk assessment of buildings with consideration of aleatory and epistemic uncertainty. Struct. Infrastruct. Eng. 2012, 8, 939–953. [Google Scholar] [CrossRef]
- Kosič, M.; Dolšek, M.; Fajfar, P. Dispersions for the pushover-based risk assessment of reinforced concrete frames and cantilever walls. Earthq. Eng. Struct. Dyn. 2016, 45, 2163–2183. [Google Scholar] [CrossRef]
- Meyerhof, G.G. Some Recent Research on the Bearing Capacity of Foundations. Can. Geotech. J. 1963, 1, 16–26. [Google Scholar] [CrossRef]
- Ligthart, F. Failure Mechanisms of Bridge Structures under Natural Hazards; RMIT University: Melbourne, Australia, 2015. [Google Scholar]
- Tanasic, N.; Hajdin, R. Performance indicators for bridges exposed to a flooding hazard. In Proceedings of the Joint COST TU 1402—COST TU 1406-IABSE WC1 Workshop, Zagreb, Croatia, 2–3 March 2017. [Google Scholar]









| Parameters | Value |
|---|---|
| ) | 40° |
| ) | 0 kPa |
| ) | 19.8 kN/m3 |
| ) | 0.30 |
| ) | 50 Mpa |
| ) | 19 Mpa |
| ) | 19 |
| Wood Debris Accumulation Properties | ||||
|---|---|---|---|---|
| shape | ||||
| AS5100.2-2004 | rectangular | 1.2–3 m | Pier: | not specified |
| Panici and Almeida’s model [48] | half conical | |||
| Parameters | Probabilistic Distributions | References |
|---|---|---|
| ) | [55] | |
| ) | ) | [56] |
| ) | ) | [56] |
| ) | ) | [54,57] |
| ) | [54,57] | |
| Soil unit weight (γ) | [54] | |
| ) | [24] | |
| ) | ) | [58] |
| ) | [48] | |
| ) | [48] | |
| ) | [48] |
| 1.0 | 0.35 | 0.45 | |
| 0.35 | 1.0 | 0.30 | |
| 0.45 | 0.30 | 1.0 |
| No. | Description | Period (s)—Calculated | Period (s)—Measured |
|---|---|---|---|
| 1 | 1st vertical mode of the deck | 0.67 | 0.68 |
| 2 | Global longitudinal mode | 0.58 | ND |
| 3 | 2nd vertical mode of the deck | 0.41 | 0.43 |
| 4 | Global transverse mode | 0.36 | ND |
| 5 | Global vertical mode | 0.21 | ND |
| 6 | 1st transverse mode of the deck | 0.21 | 0.21 |
| 7 | 3rd vertical mode of the deck | 0.18 | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosič, M.; Anžlin, A.; Bau’, V. Flood Vulnerability Study of a Roadway Bridge Subjected to Hydrodynamic Actions, Local Scour and Wood Debris Accumulation. Water 2023, 15, 129. https://doi.org/10.3390/w15010129
Kosič M, Anžlin A, Bau’ V. Flood Vulnerability Study of a Roadway Bridge Subjected to Hydrodynamic Actions, Local Scour and Wood Debris Accumulation. Water. 2023; 15(1):129. https://doi.org/10.3390/w15010129
Chicago/Turabian StyleKosič, Mirko, Andrej Anžlin, and Valentina Bau’. 2023. "Flood Vulnerability Study of a Roadway Bridge Subjected to Hydrodynamic Actions, Local Scour and Wood Debris Accumulation" Water 15, no. 1: 129. https://doi.org/10.3390/w15010129
APA StyleKosič, M., Anžlin, A., & Bau’, V. (2023). Flood Vulnerability Study of a Roadway Bridge Subjected to Hydrodynamic Actions, Local Scour and Wood Debris Accumulation. Water, 15(1), 129. https://doi.org/10.3390/w15010129






