A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dam Displacement Prediction Process
- (1)
- Data preprocessing: elimination of outliers and missing value interpolation.
- (2)
- The decomposition and reconstruction of multi-factor time series data through the EMD method.
- (3)
- Determining the input sequence by the lag autocorrelation coefficient method.
- (4)
- Parameter adjustment of lagging LSTM network based on attention mechanism.
- (5)
- Results prediction and accuracy evaluation.
2.1.1. Principle of EMD Method
2.1.2. Lagged Autocorrelation Coefficient
2.1.3. LSTM Network
2.1.4. Attention Mechanism
2.1.5. Prediction Model Structure
2.2. A Tailing Dam Study
2.2.1. Introduction of Background
2.2.2. The Outlier Data Processing
2.2.3. Missing Value Date Processing
2.2.4. Data Normalization
3. Results
3.1. Data Analysis and Processing
3.2. EMD Reorganization of Absolute Deformation of the Tailings Dam
3.2.1. Stationarity Test
3.2.2. Component Identification
3.3. Input Sequence
3.4. Model Parameter Setting
4. Discussion
4.1. Factor Analysis
4.2. Model Application
5. Conclusions
- (1)
- In this study, the EMD-attention-LSTM neural network model is proposed. Compared with the control models, this model achieves higher accuracy in the prediction of tailings dam deformation under the influence of rainfall and phreatic line, and also has good performance in multiple directions. The prediction effect reflects the universality of this model in the prediction of tailings dam deformation. This method is suitable for dam deformation prediction under the influence of rainfall and phreatic line and has engineering significance.
- (2)
- The LSTM model used in this study effectively avoids the problem of gradient disappearance and gradient explosion, while the model considers the lag to better reflect the delayed impact of external factors on the dam deformation in real situations.
- (3)
- Compared with a single LSTM model, the addition of the attention mechanism takes into account the characteristics of the input variables and the long-term dependence of the time series, which improves the prediction accuracy of the dam displacement.
- (4)
- The significance test reveals that atmospheric rainfall and the change of phreatic line in the tailings dam will accelerate the tailings dam deformation process, and the change of phreatic line has a more significant effect on tailings dam deformation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burritt, R.L.; Christ, K.L. Water risk in mining: Analysis of the Samarco dam failure. J. Clean. Prod. 2018, 178, 196–205. [Google Scholar] [CrossRef]
- Kossoff, D.; Dubbin, W.E.; Alfredsson, M.; Edwards, S.J.; Macklin, M.G.; Hudson-Edwards, K.A. Mine tailings dams: Characteristics, failure, environmental impacts, and remediation. Appl. Geochem. 2014, 51, 229–245. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z. Mineral processing technology (5th edition): B.A. Wills Pergamon Press, Oxford, UK, 1992, 855 pps. Price £29.95 (flexicover); £75 (hardback) ISBN 0 08041872 4 F (flexicover); 0 08041885 6 (hardback). Miner. Eng. 1994, 7, 427–428. [Google Scholar] [CrossRef]
- Barrie, S.; Baker, E.; Howchin, J.; Matthews, A. Chapter XVI Investor Mining And Tailings Safety Initiative. In Towards Zero Harm: A Compendium of Papers Prepared for the Global Tailings; GRID-Arendal: Arendal, Norway, 2020; p. 216. [Google Scholar]
- Hancock, G.R.; Loch, R.J.; Willgoose, G.R. The design of post-mining landscapes using geomorphic principles. Earth Surf. Process. Landf. 2003, 28, 1097–1110. [Google Scholar] [CrossRef]
- Beauchemin, S.; Langley, S.; MacKinnon, T. Geochemical properties of 40-year old forested pyrrhotite tailings and impact of organic acids on metal cycling. Appl. Geochem. 2019, 110, 104437. [Google Scholar] [CrossRef]
- Xuecheng, S.; Jianxu, W.; Xinbin, F. Distribution and Potential Environmental Risk of Mercury and Arsenic in Slag, Soil and Water of Danzhai Mercury Mining Area, Guizhou Province, China. Asian J. Ecotoxicol. 2014, 6, 1173–1180. [Google Scholar] [CrossRef]
- Dong, L.; Deng, S.; Wang, F. Some developments and new insights for environmental sustainability and disaster control of tailings dam. J. Clean. Prod. 2020, 269, 122270. [Google Scholar] [CrossRef]
- Lang, X.Z.; Xu, T.L.; Huang, X.J.; Du, H.C.; Song, H.Y. PCA and neural network are used to predict underground water level of tailings dam. Hydrogeol. Eng. Geol. 2014, 2, 13–17. [Google Scholar]
- Li, Z.W.; Hu, Z.Q. Stability analysis of tailings dam based on seepage theory. J. Hydraul. Archit. Eng. 2010, 8, 56–59. [Google Scholar]
- Godt, J.W.; Baum, R.L.; Lu, N. Landsliding in partially saturated materials. Geophys. Res. Lett. 2009, 36, L02403. [Google Scholar] [CrossRef]
- Sun, H.; Pan, P.; Lu, Q.; Zhenlei, W.; Xie, W.; Zhan, W. A case study of a rainfall-induced landslide involving weak interlayer and its treatment using the siphon drainage method. Bull. Eng. Geol. Environ. 2018, 78, 4063–4074. [Google Scholar] [CrossRef]
- Wei, Z.; Lü, Q.; Sun, H.; Shang, Y. Estimating the rainfall threshold of a deep-seated landslide by integrating models for predicting the groundwater level and stability analysis of the slope. Eng. Geol. 2019, 253, 14–26. [Google Scholar] [CrossRef]
- Rosone, M.; Ziccarelli, M.; Ferrari, A.; Farulla, C. On the reactivation of a large landslide induced by rainfall in highly fissured clays. Eng. Geol. 2018, 235, 20–38. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillan, D. Seepage and dam deformation analyses with statistical models: Support vector regression machine and random forest. In Proceedings of the 3rd International Conference on Structural Integrity, ICSI 2019, Funchal, Portugal, 2–5 September 2019; Volume 17, pp. 698–703. [Google Scholar] [CrossRef]
- Zhao, E.; Wu, C. Centroid deformation-based nonlinear safety monitoring model for arch dam performance evaluation. Eng. Struct. 2021, 243, 112652. [Google Scholar] [CrossRef]
- Xu, C.; Yue, D.; Deng, C. Hybrid GA/SIMPLS as alternative regression model in dam deformation analysis. Eng. Appl. Artif. Intell. 2012, 25, 468–475. [Google Scholar] [CrossRef]
- Jung, I.-S.; Berges, M.; Garrett, J.H.; Poczos, B. Exploration and evaluation of AR, MPCA and KL anomaly detection techniques to embankment dam piezometer data. Adv. Eng. Inform. 2015, 29, 902–917. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Tang, H.; Tannant, D.D.; Lin, C.; Xia, D.; Liu, X.; Zhang, Y.; Ma, J. Combined forecasting model with CEEMD-LCSS reconstruction and the ABC-SVR method for landslide displacement prediction. J. Clean. Prod. 2021, 293, 126205. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, X. Prediction of dam horizontal displacement based on CNN-LSTM and attention mechanism. Acad. J. Archit. Geotech. Eng. 2021, 3, 6. [Google Scholar]
- Le, X.-H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Zhou, R.; Geng, Z.; Chen, K.; Wang, Y.; Wei, Q. Production prediction modeling of industrial processes based on Bi-LSTM. In Proceedings of the 2019 34rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Jinzhou, China, 6–8 June 2019; pp. 285–289. [Google Scholar] [CrossRef]
- Huo, Y.; Yan, Y.; Du, D.; Wang, Z.; Zhang, Y.; Yang, Y. Long-Term Span Traffic Prediction Model Based on STL Decomposition and LSTM. In Proceedings of the 2019 20th Asia-Pacific Network Operations and Management Symposium (APNOMS), Matsue, Japan, 18–20 September 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Lin, H.-M.; Chang, S.-K.; Wu, J.-H.; Juang, C.H. Neural network-based model for assessing failure potential of highway slopes in the Alishan, Taiwan Area: Pre- and post-earthquake investigation. Eng. Geol. 2009, 104, 280–289. [Google Scholar] [CrossRef]
- Chang, S.-K.; Lee, D.-H.; Wu, J.-H.; Juang, C.H. Rainfall-based criteria for assessing slump rate of mountainous highway slopes: A case study of slopes along Highway 18 in Alishan, Taiwan. Eng. Geol. 2011, 118, 63–74. [Google Scholar] [CrossRef]
- Li, Q.; Geng, J.; Song, D.; Nie, W.; Saffari, P.; Liu, J. Automatic Recognition of Erosion Area on the Slope of Tailings Dam Using Region Growing Segmentation Algorithm. Arab. J. Geosci. 2022, 15, 438. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C.; Hsu, M.-H. Comparison of ANN approach with 2D and 3D hydrodynamic models for simulating estuary water stage. Adv. Eng. Softw. 2012, 45, 69–79. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C. Artificial neural network modeling of dissolved oxygen in reservoir. Environ. Monit. Assess. 2013, 186, 1203–1217. [Google Scholar] [CrossRef]
- Chiang, S.; Chang, C.-H.; Chen, W.-B. Comparison of Rainfall-Runoff Simulation between Support Vector Regression and HEC-HMS for a Rural Watershed in Taiwan. Water 2022, 14, 191. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Li, H.; Shen, Y. A novel deep learning prediction model for concrete dam displacements using interpretable mixed attention mechanism. Adv. Eng. Inform. 2021, 50, 101407. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Zhu, Y.; Dai, B.; Zhang, K.; Zhang, Z.; Li, B. A Concrete Dam Deformation Prediction Method Based on LSTM With Attention Mechanism. IEEE Access 2020, 8, 185177–185186. [Google Scholar] [CrossRef]
- Guo, H.Q.; Wu, Z.R.; Yang, J. Grey nonlinear time series combination model for rockfill dam deformation monitoring. J. Hohai Univ. 2001, 29, 51–55. [Google Scholar]
- Yuan, R.; Su, C.; Cao, E.; Hu, S.; Zhang, H. Exploration of Multi-Scale Reconstruction Framework in Dam Deformation Prediction. Appl. Sci. 2021, 11, 7334. [Google Scholar] [CrossRef]
- Xing, Y.; Yue, J.; Chen, C.; Cong, K.; Zhu, S.; Bian, Y. Dynamic Displacement Forecasting of Dashuitian Landslide in China Using Variational Mode Decomposition and Stack Long Short-Term Memory Network. Appl. Sci. 2019, 9, 2951. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Zhang, P.; Jiang, J. Dam Deformation Prediction Based on EMD-GAELM-ARIMA Algorithm. Comput. Mod. 2020, 0, 1–5. [Google Scholar] [CrossRef]
- Li, M.; Wang, J. An Empirical Comparison of Multiple Linear Regression and Artificial Neural Network for Concrete Dam Deformation Modelling. Math. Probl. Eng. 2019, 2019, 7620948. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Huang, N. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yan, T.; Chen, B.; Cao, E.H.; Liu, Y.T. Prediction of Dam Deformation Using EEMD-ELM Model. J. Yangtze River Sci. Res. Inst. 2020, 37, 70. [Google Scholar] [CrossRef]
- Nie, W.; Luo, M.; Wang, Y.; Li, R. 3D Visualization Monitoring and Early Warning System of a Tailings Dam—Gold Copper Mine Tailings Dam in Zijinshan, Fujian, China. Front. Earth Sci. 2022, 10, 800924. [Google Scholar] [CrossRef]
- Nie, W.; Krautblatter, M.; Leith, K.; Thuro, K.; Festl, J. A modified tank model including snowmelt and infiltration time lags for deep-seated landslides in Alpine Environments (Aggenalm, Germany). Nat. Hazards Earth Syst. Sci. Discuss. 2016, 2016, 1. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks, Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Weng, K.; Lin, C.; Chen, Z. Dam Deformation Interpretation and Prediction Based on a Long Short-Term Memory Model Coupled with an Attention Mechanism. Appl. Sci. 2021, 11, 6625. [Google Scholar] [CrossRef]
- Xue, K.; Ruan, S.K. Geological characteristics and genesis of the Luoboling copper (Molybdenum) deposit in Zijinshan orefield, Fujian. Resour. Environ. Eng. 2008, 22, 491–496. [Google Scholar]
- Earl, T.A. A Hydrogeologic Study of an Unstable Open-Pit Slope, Miami, Gila County, Arizona; The University of Arizona: Tucson, AZ, USA, 2022. [Google Scholar]
- Wu, P.; Liang, B.; Jin, J.; Zhou, K.; Guo, B.; Yang, Z. Solution and Stability Analysis of Sliding Surface of Tailings Pond under Rainstorm. Sustainability 2022, 14, 3081. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, H.; Ran, J.; Li, W.; Sun, X. Field monitoring of groundwater responses to heavy rainfalls and the early warning of the Kualiangzi landslide in Sichuan Basin, southwestern China. Landslides 2016, 13, 1555–1570. [Google Scholar] [CrossRef]
- Chen, M.; Qi, S.; Lv, P.; Yang, X.; Zhou, J. Hydraulic response and stability of a reservoir slope with landslide potential under the combined effect of rainfall and water level fluctuation. Environ. Earth Sci. 2021, 80, 25. [Google Scholar] [CrossRef]
- Probabilistic Stability Analysis of Bazimen Landslide with Monitored Rainfall Data and Water Level Fluctuations in Three Gorges Reservoir, China|SpringerLink [WWW Document]. Available online: https://link.springer.com/article/10.1007/s11709-020-0655-y (accessed on 31 March 2022).
- Yang, H.; Jian, W.; Wang, F.; Meng, F.; Okeke, A.C. Numerical Simulation of Failure Process of the Qianjiangping Landslide Triggered by Water Level Rise and Rainfall in the Three Gorges Reservoir, China. In Progress of Geo-Disaster Mitigation Technology in Asia; Wang, F., Miyajima, M., Li, T., Shan, W., Fathani, T.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 503–523. [Google Scholar] [CrossRef]
- Zou, Z.; Yang, Y.; Fan, Z.; Tang, H.; Zou, M.; Hu, X.; Xiong, C.; Ma, J. Suitability of data preprocessing methods for landslide displacement forecasting. Stoch. Environ. Res. Risk Assess. 2020, 34, 1105–1119. [Google Scholar] [CrossRef]
- Yu, Y.; Workman, A.; Grasmick, J.G.; Mooney, M.A.; Hering, A.S. Space-time outlier identification in a large ground deformation data set. J. Qual. Technol. 2018, 50, 431–445. [Google Scholar] [CrossRef]
- Mahapatra, A.P.K.; Nanda, A.; Mohapatra, B.B.; Padhy, A.K.; Padhy, I. Concept of Outlier Study: The Management of Outlier Handling with Significance in Inclusive Education Setting. Asian Res. J. Math. 2020, 16, 7–25. [Google Scholar] [CrossRef]
- Dastorani, M.T.; Moghadamnia, A.; Piri, J.; Rico-Ramirez, M. Application of ANN and ANFIS models for reconstructing missing flow data. Environ. Monit. Assess. 2010, 166, 421–434. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.Á.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Computat. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Shu, X.; Bao, T.; Li, Y.; Gong, J.; Zhang, K. VAE-TALSTM: A temporal attention and variational autoencoder-based long short-term memory framework for dam displacement prediction. Eng. Comput. 2021, 37, 1–16. [Google Scholar] [CrossRef]
- Büyükşahin, Ü.; Ertekin, Ş. Improving forecasting accuracy of time series data using a new ARIMA-ANN hybrid method and empirical mode decomposition. Neurocomputing 2019, 361, 151–163. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.J.; Liao, X.P. Tourist volume Prediction based on EMD-BP neural Network. Stat. Decis. 2019, 0, 85–89. [Google Scholar]
- Wang, Z.Y. Analysis of groundwater recharge lag time by precipitation infiltration. Hydrological 2011, 31, 42–45. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2017, arXiv:1609.04747. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Park, H.; Stefanski, L.A. Relative-error prediction. Stat. Probab. Lett. 1998, 40, 227–236. [Google Scholar] [CrossRef]











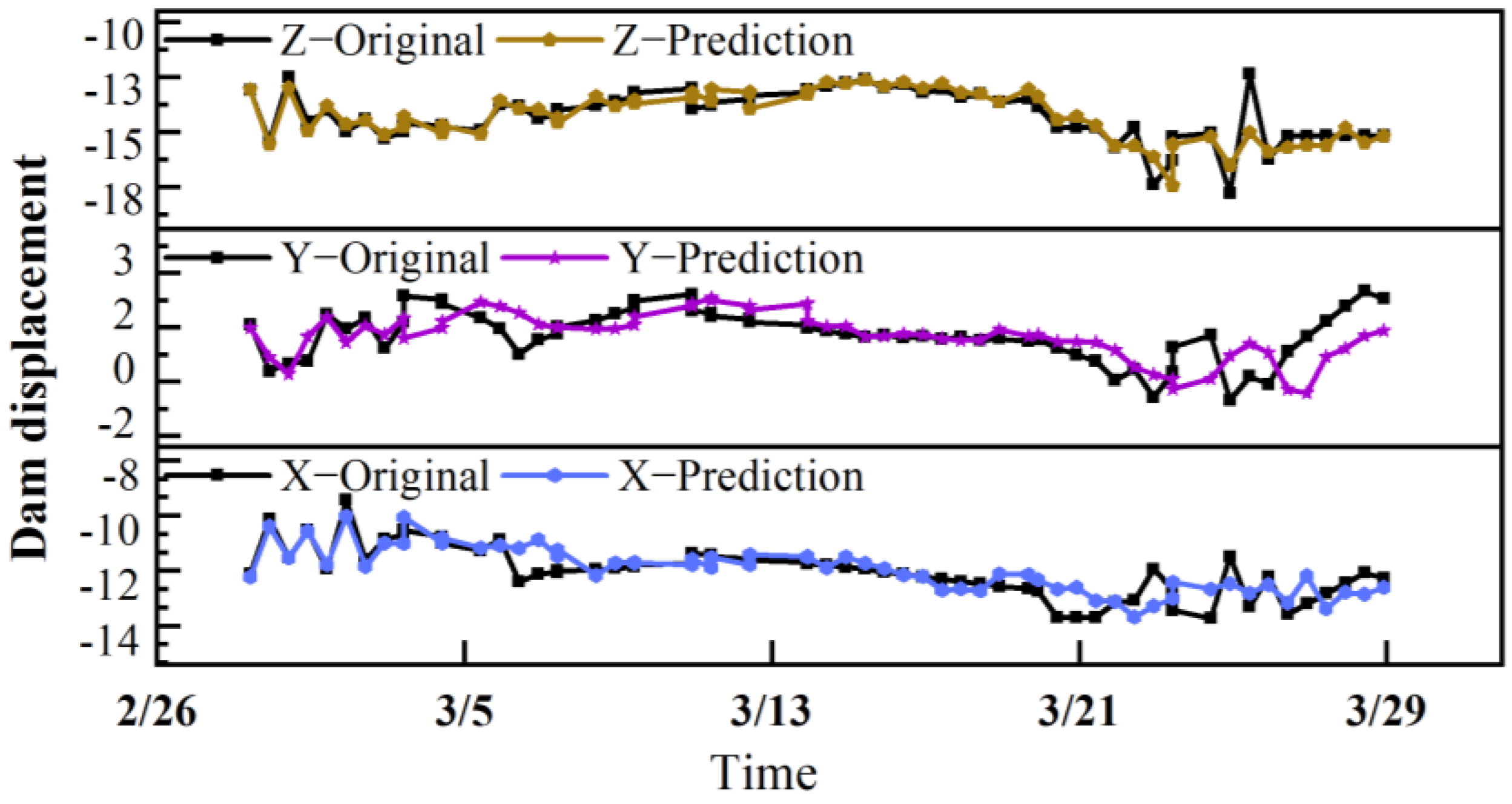
| Original Data | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | Residual Term | |
|---|---|---|---|---|---|---|---|
| Test Statistic | 0.900 | −8.065 | −7.577 | −7.348 | −4.637 | −4.225 | −0.641 |
| p-value | 0.788 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.861 |
| Stationarity | N | Y | Y | Y | Y | Y | N |
| IMFs and Residual Term | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | Residual Term |
|---|---|---|---|---|---|---|
| Pearson Correlation Coefficient | 0.2077 | 0.1264 | 0.1453 | 0.1470 | 0.4599 | 0.9122 |
| Day | EMD-Attention-LSTM | EMD-LSTM | EMD-ARIMA | Multiple Regression | LSTM | SVM | |
|---|---|---|---|---|---|---|---|
| RMSE | 1 | 0.144 | 0.371 | 0.529 | 4.760 | 0.470 | 0.296 |
| 5 | 0.183 | 0.351 | 0.410 | 4.398 | 0.411 | 0.496 | |
| 10 | 0.549 | 0.934 | 1.049 | 4.673 | 0.945 | 1.167 | |
| 15 | 0.553 | 0.835 | 0.992 | 4.675 | 0.907 | 1.129 | |
| 20 | 0.607 | 0.865 | 1.010 | 4.844 | 0.893 | 1.222 | |
| 25 | 0.625 | 0.898 | 1.053 | 5.237 | 0.908 | 1.208 | |
| 30 | 0.729 | 0.955 | 1.120 | 4.937 | 0.970 | 1.285 | |
| MAE | 1 | 0.157 | 0.524 | 0.676 | 6.731 | 0.642 | 0.384 |
| 5 | 0.215 | 0.439 | 0.536 | 6.080 | 0.462 | 0.573 | |
| 10 | 0.509 | 0.992 | 1.059 | 6.455 | 0.955 | 1.078 | |
| 15 | 0.555 | 0.906 | 1.035 | 6.455 | 0.950 | 1.145 | |
| 20 | 0.636 | 0.945 | 1.054 | 6.668 | 0.934 | 1.274 | |
| 25 | 0.664 | 0.996 | 1.111 | 6.747 | 0.965 | 1.294 | |
| 30 | 0.770 | 1.068 | 1.207 | 6.801 | 1.063 | 1.394 |
| Multiple Regression Model | Unstandardized Coefficient B | Standard Error | t | Significance |
|---|---|---|---|---|
| Constant | −22.890 | 5.631 | −4.065 | 0.000 |
| Phreatic line | 0.524 | 0.263 | 1.991 | 0.047 |
| rainfall | −0.392 | 0.152 | −2.588 | 0.010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Gao, Y.; Wang, Z.; Cao, G.; Wang, R.; Lu, S.; Li, W.; Nie, W.; Zhang, Z. A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism. Water 2022, 14, 1229. https://doi.org/10.3390/w14081229
Zhu Y, Gao Y, Wang Z, Cao G, Wang R, Lu S, Li W, Nie W, Zhang Z. A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism. Water. 2022; 14(8):1229. https://doi.org/10.3390/w14081229
Chicago/Turabian StyleZhu, Yang, Yijun Gao, Zhenhao Wang, Guansen Cao, Renjie Wang, Song Lu, Wei Li, Wen Nie, and Zhongrong Zhang. 2022. "A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism" Water 14, no. 8: 1229. https://doi.org/10.3390/w14081229
APA StyleZhu, Y., Gao, Y., Wang, Z., Cao, G., Wang, R., Lu, S., Li, W., Nie, W., & Zhang, Z. (2022). A Tailings Dam Long-Term Deformation Prediction Method Based on Empirical Mode Decomposition and LSTM Model Combined with Attention Mechanism. Water, 14(8), 1229. https://doi.org/10.3390/w14081229







