A Simple Approach to Account for Stage–Discharge Uncertainty in Hydrological Modelling
Abstract
1. Introduction
2. Materials and Methods
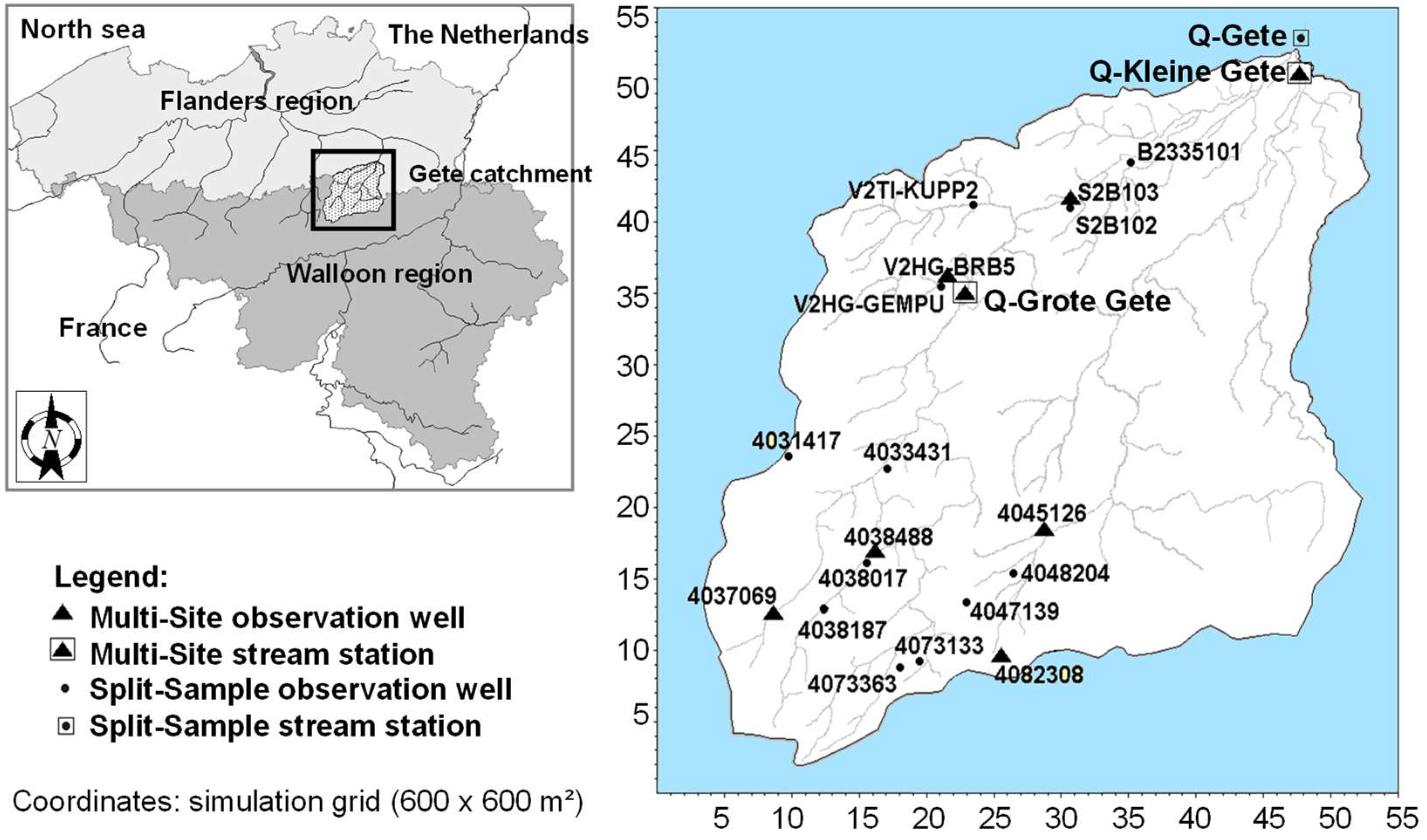
2.1. The Study Site
2.2. Hydrometeorological Data
2.3. The Hydrologic Code
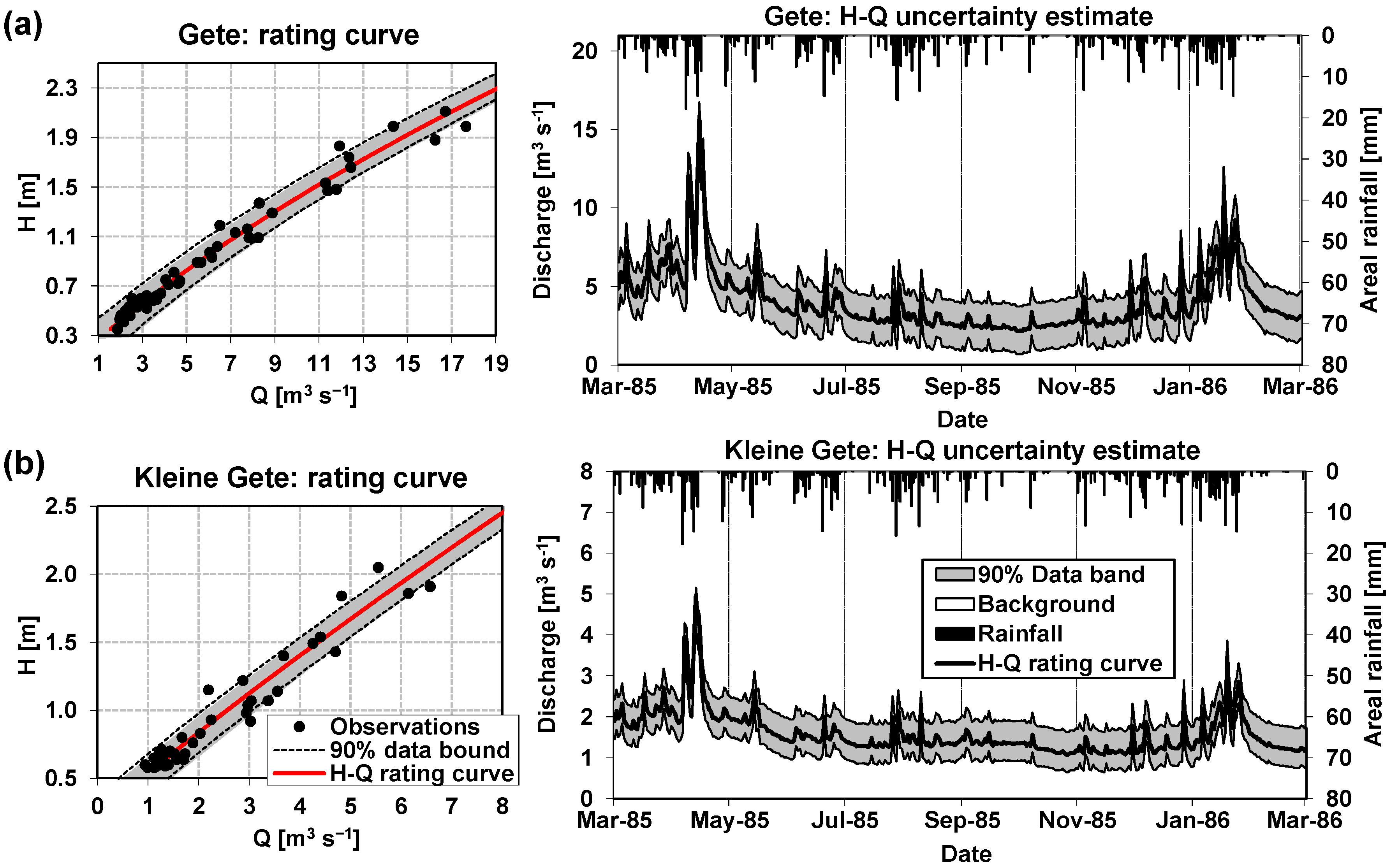
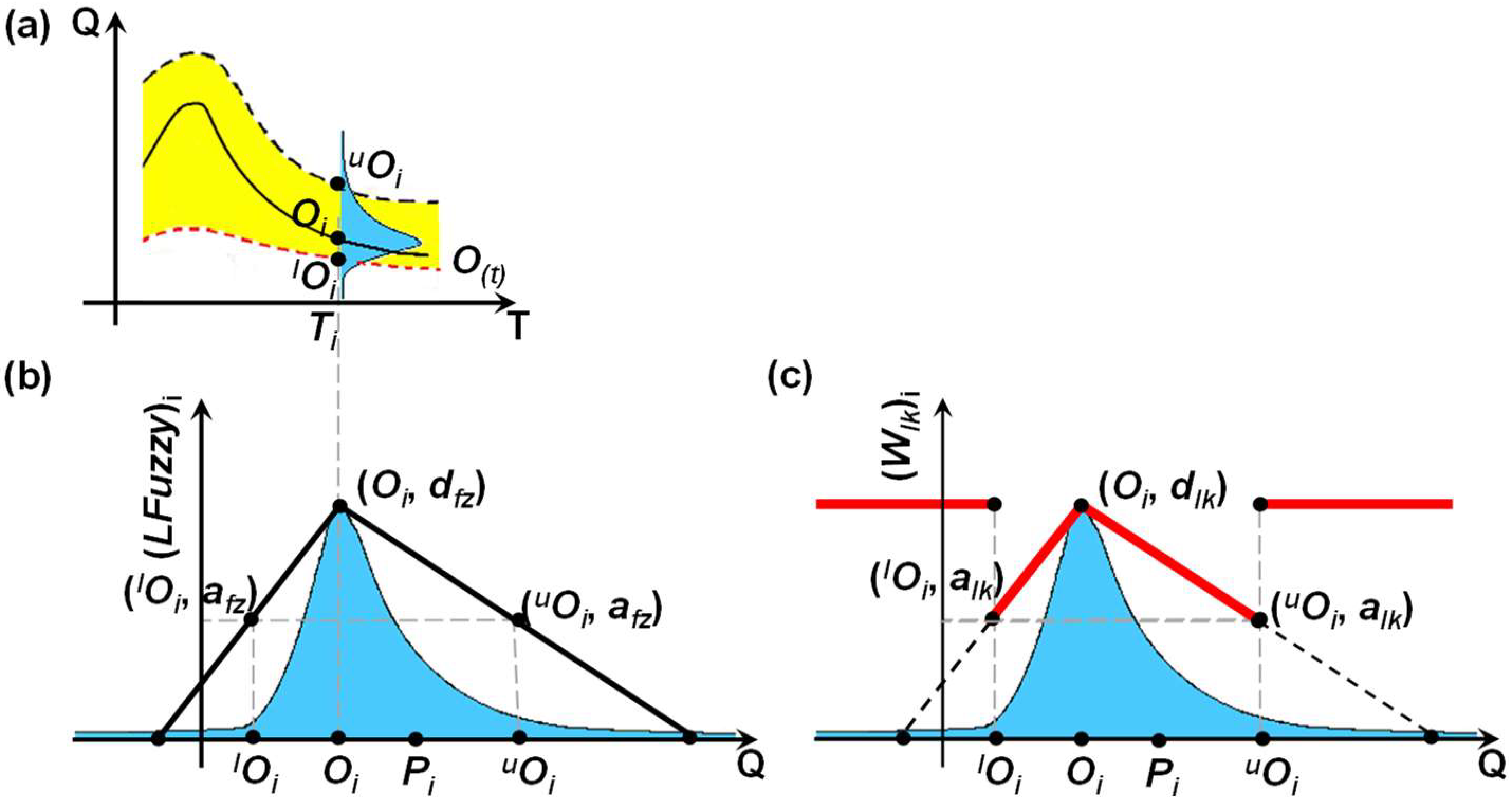
2.4. Estimating the Uncertainty Attached to Stage–Discharge Data
2.5. Initial Parameterisation of the Hydrological Model
2.6. Model Calibration, Validation and Sensitivity Analysis
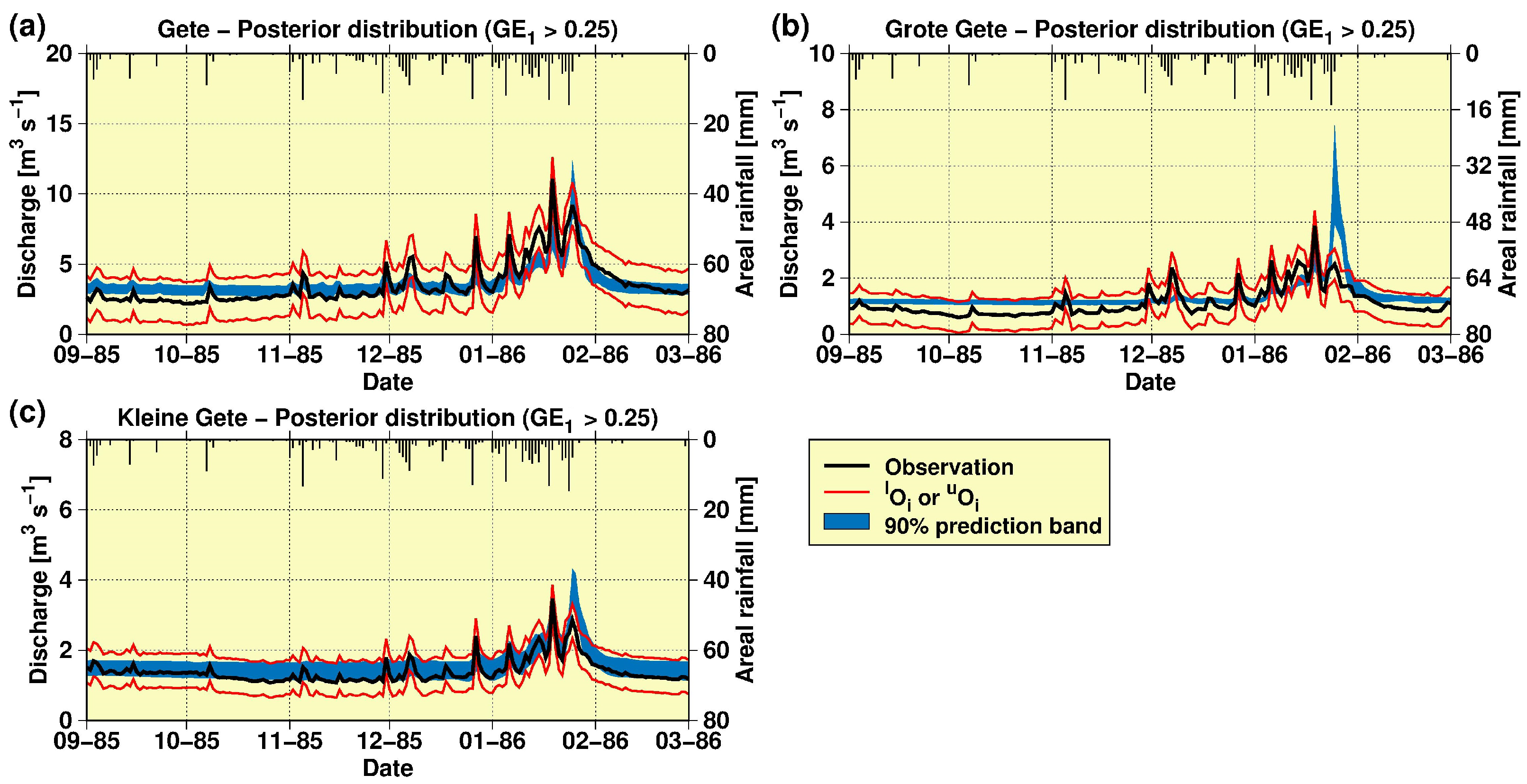
3. Results
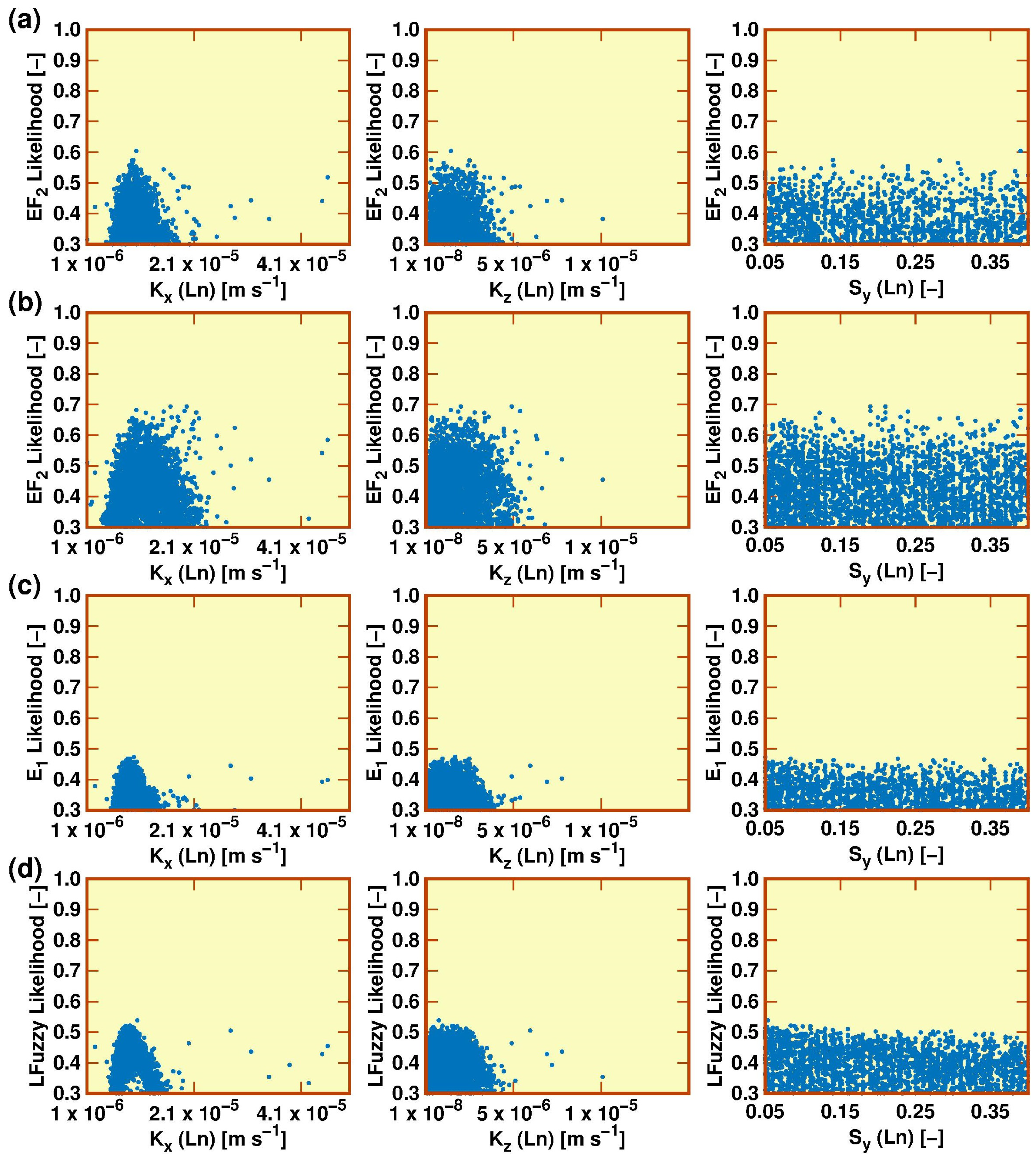
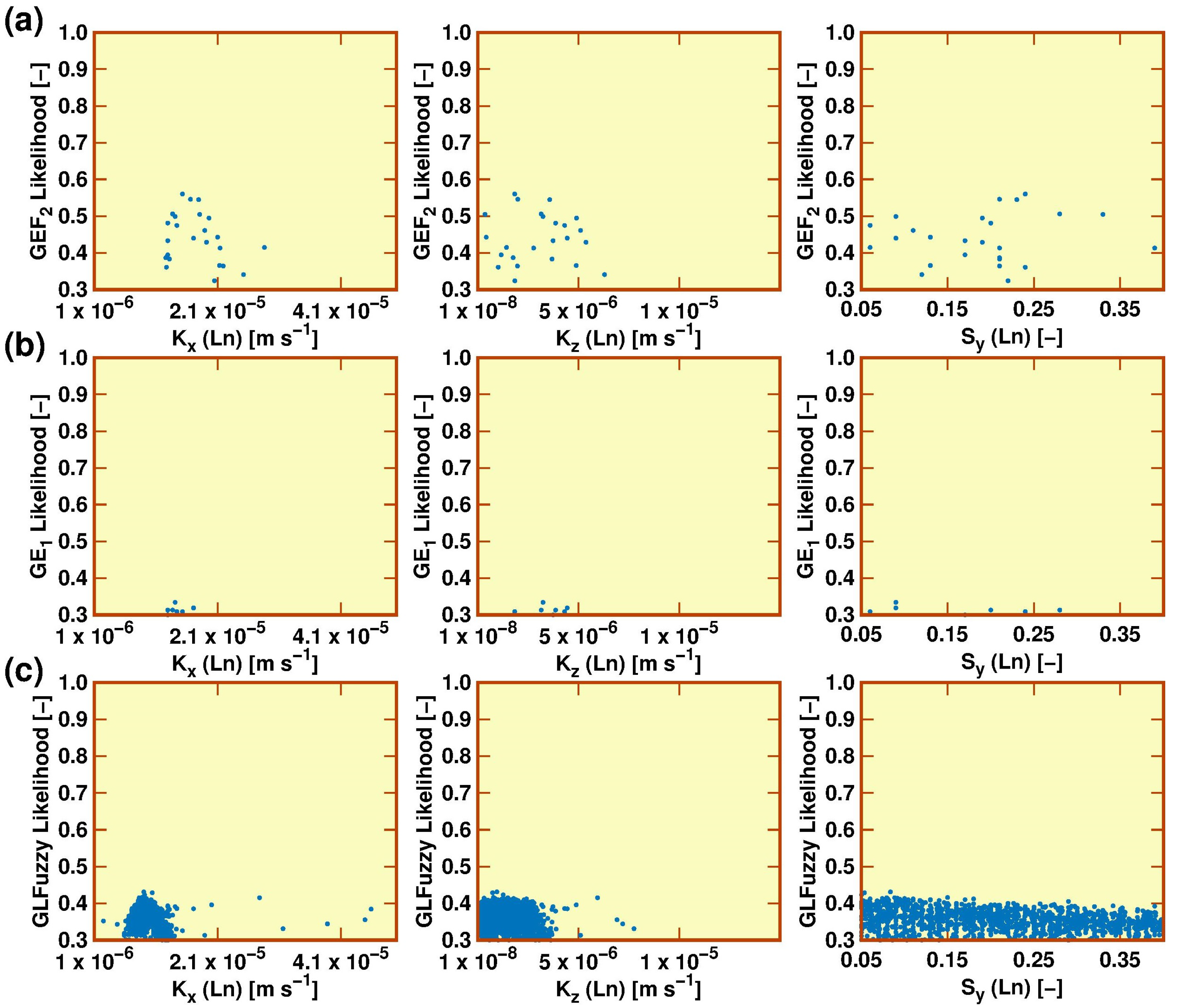
3.1. Uncertainty Attached to the Stage–Discharge Data
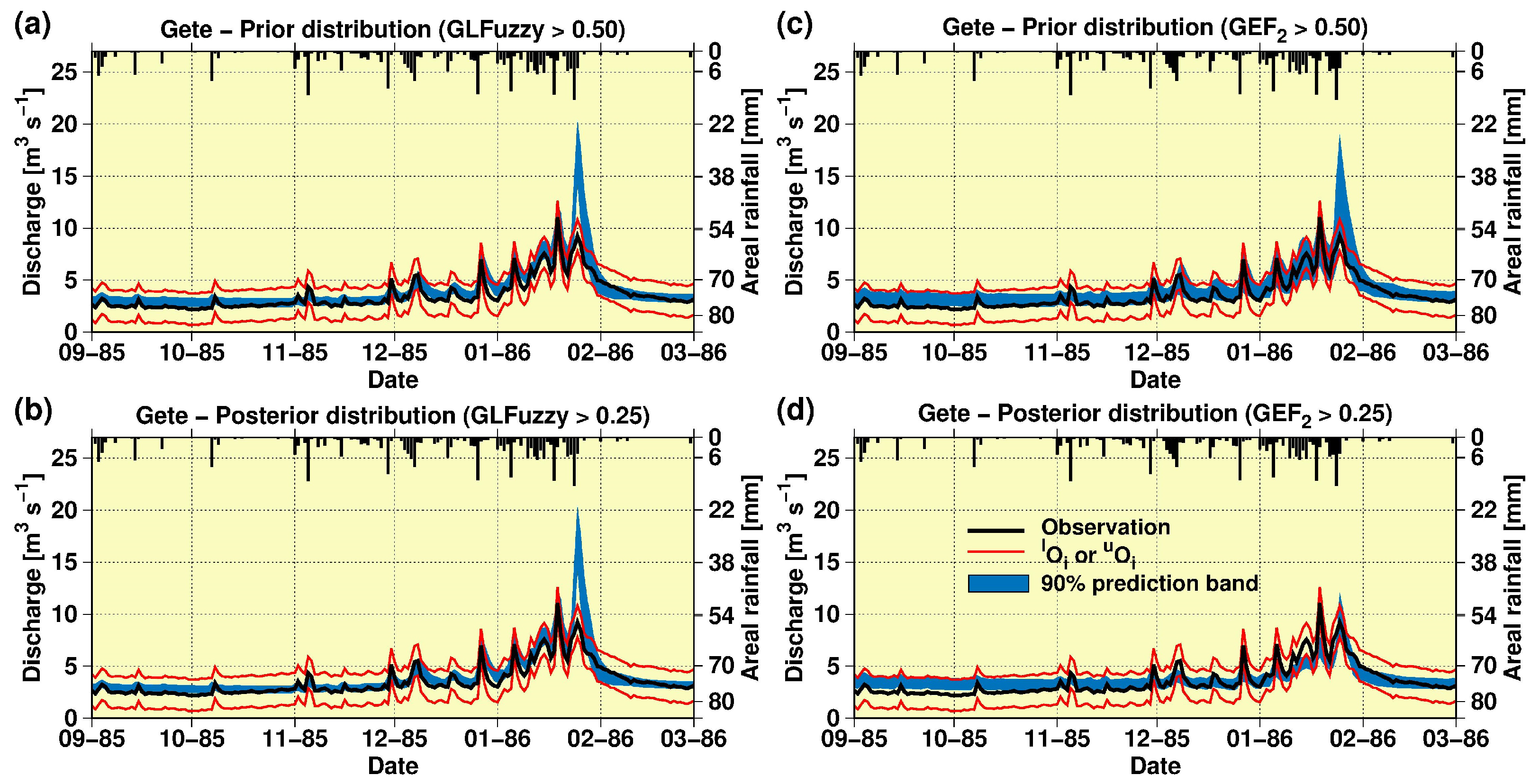
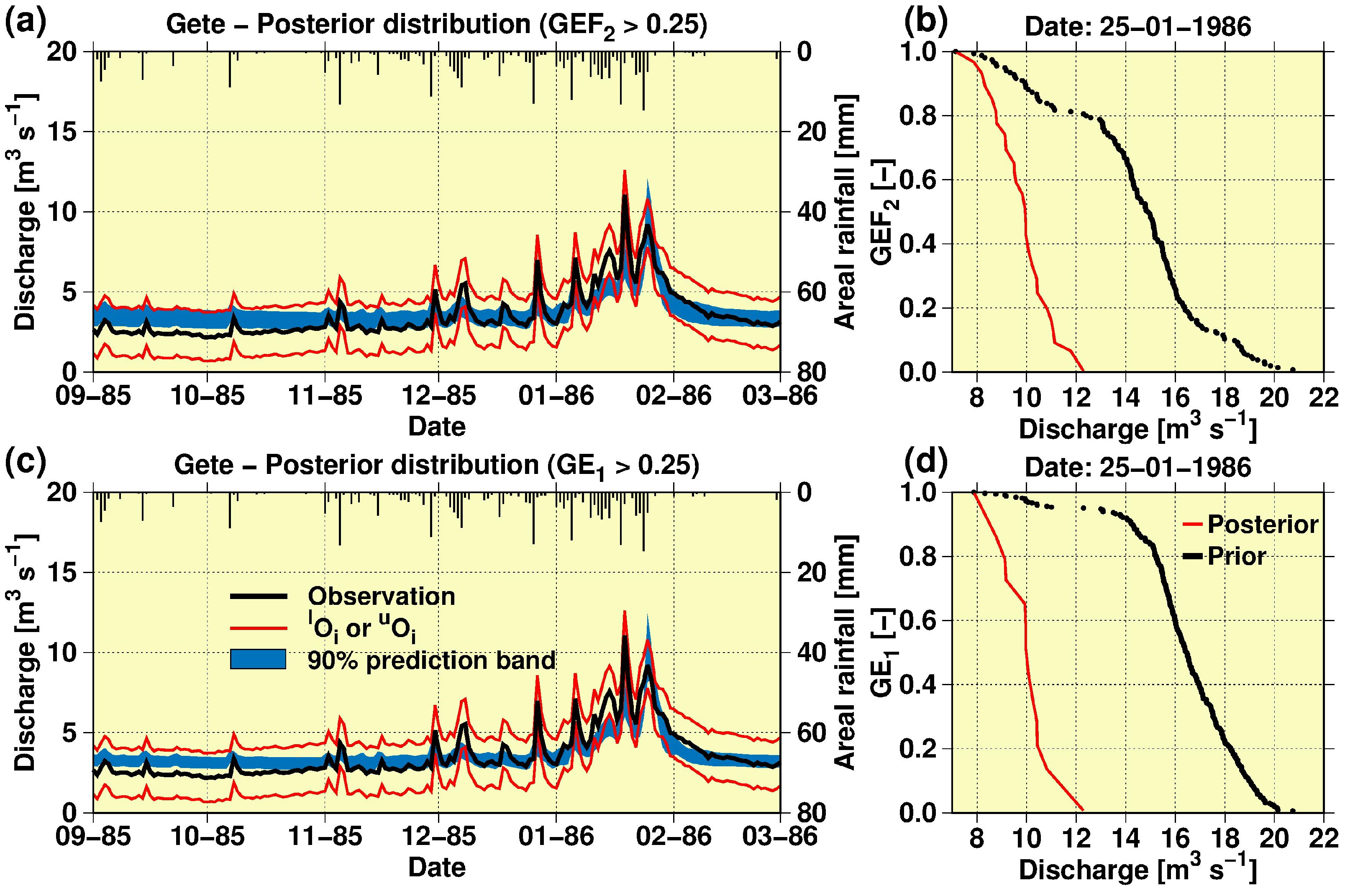
3.2. Model Calibration, Validation and Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sikorska, A.E.; Renard, B. Calibrating a hydrological model in stage space to account for rating curve uncertainties: General framework and key challenges. Adv. Water Resour. 2017, 105, 51–66. [Google Scholar] [CrossRef]
- Ocio, D.; Le Vine, N.; Westerberg, I.; Pappenberger, F.; Buytaert, W. The role of rating curve uncertainty in real-time flood forecasting. Water Resour. Res. 2017, 53, 4197–4213. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Kuo, J.-J.; Yu, S.-R.; Liao, Y.-J.; Yang, H.-C. Discharge Estimation in a Lined Canal Using Information Entropy. Entropy 2014, 16, 1728–1742. [Google Scholar] [CrossRef]
- McMillan, H.; Seibert, J.; Petersen-Overleir, A.; Lang, M.; White, P.; Snelder, T.; Rutherford, K.; Krueger, T.; Mason, R.; Kiang, J. How uncertainty analysis of streamflow data can reduce costs and promote robust decisions in water management applications. Water Resour. Res. 2017, 53, 5220–5228. [Google Scholar] [CrossRef]
- Shah, M.A.A.; Anwar, A.A.; Bell, A.R.; ul Haq, Z. Equity in a tertiary canal of the Indus Basin Irrigation System (IBIS). Agric. Water Manag. 2016, 178, 201–214. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Muttil, N. Discharge Rating Curve Extension—A New Approach. Water Resour. Manag. 2005, 19, 505–520. [Google Scholar] [CrossRef]
- Lang, M.; Pobanz, K.; Renard, B.; Renouf1, E.; Sauquet, E. Extrapolation of rating curves by hydraulic modelling, with application to flood frequency analysis. Hydrol. Sci. J. 2010, 55, 883–898. [Google Scholar] [CrossRef]
- Westerberg, I.K.; McMillan, H.K. Uncertainty in hydrological signatures. Hydrol. Earth Syst. Sci. 2015, 19, 3951–3968. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Stisen, S.; Koch, J. Hydrological process knowledge in catchment modelling—Lessons and perspectives from 60 years development. Hydrol. Processes 2022, 36, e14463. [Google Scholar] [CrossRef]
- Gravelle, R. Discharge Estimation: Techniques and Equipment. In Geomorphological Techniques; Cook, S.J., Clarke, L.E., Nield, J.M., Eds.; British Society for Geomorphology: London, UK, 2015; Volume 3, pp. 1–8. [Google Scholar]
- Muste, M.; Hoitink, T. Measuring Flood Discharge; Oxford Research Encyclopedia of Natural Hazar: Oxford, UK, 2017. [Google Scholar]
- Pedersen, Ø.; Rüther, N. Hybrid modelling of a gauging station rating curve. Procedia Eng. 2016, 154, 433–440. [Google Scholar] [CrossRef]
- Tsubaki, R.; Fujita, I.; Tsutsumi, S. Measurement of the flood discharge of a small-sized river using an existing digital video recording system. J. Hydro-Environ. Res. 2011, 5, 313–321. [Google Scholar] [CrossRef]
- Habib, E.H.; Meselhe, E.A. Stage–Discharge Relations for Low-Gradient Tidal Streams Using Data-Driven Models. J. Hydraul. Eng. 2006, 132, 482–492. [Google Scholar] [CrossRef]
- Petersen-Øverleir, A. Modelling stage–discharge relationships affected by hysteresis using the Jones formula and nonlinear regression. Hydrol. Sci. J. 2006, 51, 365–388. [Google Scholar] [CrossRef]
- Garcia, R.; Costa, V.; Silva, F. Bayesian Rating Curve Modeling: Alternative Error Model to Improve Low-Flow Uncertainty Estimation. J. Hydrol. Eng. 2020, 25, 04020012. [Google Scholar] [CrossRef]
- Pedersen, Ø.; Aberle, J.; Rüther, N. Hydraulic scale modelling of the rating curve for a gauging station with challenging geometry. Hydrol. Res. 2019, 50, 825–836. [Google Scholar] [CrossRef]
- Coxon, G.; Freer, J.; Westerberg, I.K.; Wagener, T.; Woods, R.; Smith, P.J. A novel framework for discharge uncertainty quantification applied to 500 UK gauging stations. Water Resour. Res. 2015, 51, 5531–5546. [Google Scholar] [CrossRef] [PubMed]
- Westerberg, I.; Guerrero, J.-L.; Seibert, J.; Beven, K.J.; Halldin, S. Stage-discharge uncertainty derived with a non-stationary rating curve in the Choluteca River, Honduras. Hydrol. Processes 2011, 25, 603–613. [Google Scholar] [CrossRef]
- Qiu, J.; Liu, B.; Yu, X.; Yang, Z. Combining a segmentation procedure and the BaRatin stationary model to estimate nonstationary rating curves and the associated uncertainties. J. Hydrol. 2021, 597, 126168. [Google Scholar] [CrossRef]
- Morlot, T.; Perret, C.; Favre, A.-C.; Jalbert, J. Dynamic rating curve assessment for hydrometric stations and computation of the associated uncertainties: Quality and station management indicators. J. Hydrol. 2014, 517, 173–186. [Google Scholar] [CrossRef]
- Shao, Q.; Dutta, D.; Karim, F.; Petheram, C. A method for extending stage-discharge relationships using a hydrodynamic model and quantifying the associated uncertainty. J. Hydrol. 2018, 556, 154–172. [Google Scholar] [CrossRef]
- van der Keur, P.; Henriksen, H.J.; Refsgaard, J.C.; Brugnach, M.; Pahl-Wostl, C.; Dewulf, A.; Buiteveld, H. Identification of Major Sources of Uncertainty in Current IWRM Practice. Illustrated for the Rhine Basin. Water Resour. Manag. 2008, 22, 1677–1708. [Google Scholar] [CrossRef]
- Baldassarre, G.; Montanari, A. Uncertainty in river discharge observations: A quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913–921. [Google Scholar] [CrossRef]
- Bales, J.D.; Wagner, C.R. Sources of uncertainty in flood inundation maps. J. Flood Risk Manag. 2009, 2, 139–147. [Google Scholar] [CrossRef]
- Le Coz, J.; Renard, B.; Bonnifait, L.; Branger, F.; Le Boursicaud, R. Combining hydraulic knowledge and uncertain gaugings in the estimation of hydrometric rating curves: A Bayesian approach. J. Hydrol. 2014, 509, 573–587. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Larsen, L.; Yassin, F. Review: Sources of Hydrological Model Uncertainties and Advances in Their Analysis. Water 2021, 13, 28. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D.; Montanari, A. Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: A large-sample experiment at monthly timescale. Adv. Water Resour. 2020, 136, 103470. [Google Scholar] [CrossRef]
- Petersen-Øverleir, A.; Soot, A.; Reitan, T. Bayesian Rating Curve Inference as a Streamflow Data Quality Assessment Tool. Water Resour. Manag. 2009, 23, 1835–1842. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H.; Byrd, A.R. Derivation of rating curve by the Tsallis entropy. J. Hydrol. 2014, 513, 342–352. [Google Scholar] [CrossRef]
- Barbetta, S.; Moramarco, T.; Perumal, M. A Muskingum-based methodology for river discharge estimation and rating curve development under significant lateral inflow conditions. J. Hydrol. 2017, 554, 216–232. [Google Scholar] [CrossRef]
- Horner, I.; Renard, B.; Le Coz, J.; Branger, F.; McMillan, H.K.; Pierrefeu, G. Impact of Stage Measurement Errors on Streamflow Uncertainty. Water Resour. Res. 2018, 54, 1952–1976. [Google Scholar] [CrossRef]
- Westerberg, I.K.; Sikorska-Senoner, A.E.; Viviroli, D.; Vis, M.; Seibert, J. Hydrological model calibration with uncertain discharge data. Hydrol. Sci. J. 2020. [Google Scholar] [CrossRef]
- Kiang, J.E.; Gazoorian, C.; McMillan, H.; Coxon, G.; Le Coz, J.; Westerberg, I.K.; Belleville, A.; Sevrez, D.; Sikorska, A.E.; Petersen-Øverleir, A.; et al. A Comparison of Methods for Streamflow Uncertainty Estimation. Water Resour. Res. 2018, 54, 7149–7176. [Google Scholar] [CrossRef]
- Muñoz, P.; Orellana-Alvear, J.; Bendix, J.; Feyen, J.; Célleri, R. Flood Early Warning Systems Using Machine Learning Techniques: The Case of the Tomebamba Catchment at the Southern Andes of Ecuador. Hydrology 2021, 8, 183. [Google Scholar] [CrossRef]
- Nanding, N.; Rico-Ramirez, M.A.; Han, D.; Wu, H.; Dai, Q.; Zhang, J. Uncertainty assessment of radar-raingauge merged rainfall estimates in river discharge simulations. J. Hydrol. 2021, 603, 127093. [Google Scholar] [CrossRef]
- Aronica, G.T.; Candela, A.; Viola, F.; Cannarozzo, M. Influence of rating curve uncertainty on daily rainfall–runoff model predictions. In Proceedings of the Seventh IAHS Scientific Assembly, Foz do Iguacu, Brazil, 3–9 April 2005; pp. 116–124. [Google Scholar]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.-B.; Pfister, L.; de Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Huard, D.; Mailhot, A. Calibration of hydrological model GR2M using Bayesian uncertainty analysis. Water Resour. Res. 2008, 44, W02424. [Google Scholar] [CrossRef]
- Liu, Y.L.; Freer, J.; Beven, K.; Matgen, P. Towards a limits of acceptability approach to the calibration of hydrological models: Extending observation error. J. Hydrol. 2009, 367, 93–103. [Google Scholar] [CrossRef]
- Krueger, T.; Freer, J.; Quinton, J.N.; Macleod, C.J.A.; Bilotta, G.S.; Brazier, R.; Butler, P.; Haygarth, P. Ensemble evaluation of hydrological model hypotheses. Water Resour. Res. 2010, 46, W07516. [Google Scholar] [CrossRef]
- McMillan, H.; Freer, J.; Pappenberger, F.; Krueger, T.; Clark, M. Impacts of uncertain river flow data on rainfall-runoff model calibration and discharge predictions. Hydrol. Processes 2010, 24, 1270–1284. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Assessing rating-curve uncertainty and its effects on hydraulic model calibration. Hydrol. Earth Syst. Sci. 2012, 16, 1191–1202. [Google Scholar] [CrossRef]
- Bermudez, M.; Neal, J.C.; Bates, P.D.; Coxon, G.; Freer, J.E.; Cea, L.; Puertas, J. Quantifying local rainfall dynamics and uncertain boundary conditions into a nested regional-local flood modeling system. Water Resour. Res. 2017, 53, 2770–2785. [Google Scholar] [CrossRef]
- Kastali, A.; Zeroual, A.; Zeroual, S.; Hamitouche, Y. Auto-calibration of HEC-HMS Model for Historic Flood Event under Rating Curve Uncertainty. Case Study: Allala Watershed, Algeria. KSCE J. Civ. Eng. 2022, 26, 482–493. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Feyen, L.; Feyen, J.; Refsgaard, J.C. Effect of grid-size on effective parameters and model performance of the MIKE SHE code applied to a medium sized catchment. Hydrol. Processes 2002, 16, 355–372. [Google Scholar] [CrossRef]
- Van Poucke, L.; Verhoeven, R. Onderzoek Naar de Relatie Debiet—Waterpeil, Het Schatten van Ontbrekende Gegevens en Verwerking van de Gegevens van de Hydrometrische Stations van de Afdeling Water, Administratie Milieu-, Natuur-, Land- en Waterbeheer, Ministerie van de Vlaamse Gemeenschap (Dienstjaar 1995); Universiteit Gent, Laboratorium voor Hydraulica: Gent, Belgium, 1996. [Google Scholar]
- Vázquez, R.F.; Feyen, J. Effect of potential evapotranspiration estimates on effective parameters and performance of the MIKE SHE-code applied to a medium-size catchment. J. Hydrol. 2003, 270, 309–327. [Google Scholar] [CrossRef]
- DHI. MIKE-SHE v. 5.30 User Guide and Technical Reference Manual; Danish Hydraulic Institute: Horsholm, Denmark, 1998; p. 50. [Google Scholar]
- Christiaens, K.; Feyen, J. Constraining soil hydraulic parameter and output uncertainty of the distributed hydrological MIKE SHE model using the GLUE framework. Hydrol. Processes 2002, 16, 373–391. [Google Scholar] [CrossRef]
- Daneshmand, H.; Alaghmand, S.; Camporese, M.; Talei, A.; Daly, E. Water and salt balance modelling of intermittent catchments using a physically-based integrated model. J. Hydrol. 2019, 568, 1017–1030. [Google Scholar] [CrossRef]
- Vázquez, R.F.; Hampel, H. Prediction limits of a catchment hydrological model using different estimates of ETp. J. Hydrol. 2014, 513, 216–228. [Google Scholar] [CrossRef]
- Janert, P.K. Gnuplot in Action, 2nd ed.; Manning Publications Co.: New York, NY, USA, 2016; p. 372. [Google Scholar]
- Vázquez, R.F.; Beven, K.; Feyen, J. GLUE based assessment on the overall predictions of a MIKE SHE application. Water Resour. Manag. 2009, 23, 1325–1349. [Google Scholar] [CrossRef]
- Haan, C.T.; Barfield, B.J.; Hayes, J.C. (Eds.) Design Hydrology and Sedimentology for Small Catchments; Harcourt Brace & Company: San Diego, CA, USA, 1994; p. 587. [Google Scholar]
- Beven, K.J.; Binley, A. GLUE: 20 years on. Hydrol. Processes 2014, 28, 5897–5918. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrological and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Douinot, A.; Roux, H.; Dartus, D. Modelling errors calculation adapted to rainfall—Runoff model user expectations and discharge data uncertainties. Environ. Model. Softw. 2017, 90, 157–166. [Google Scholar] [CrossRef][Green Version]
- Sellami, H.; La Jeunesse, I.; Benabdallah, S.; Vanclooster, M. Parameter and rating curve uncertainty propagation analysis of the SWAT model for two small Mediterranean catchments. Hydrol. Sci. J. 2013, 58, 1635–1657. [Google Scholar] [CrossRef]
- Beven, K.; Smith, P.; Freer, J. Comment on ‘‘Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology’’ by Pietro Mantovan and Ezio Todini. J. Hydrol. 2007, 338, 315–318. [Google Scholar] [CrossRef]
- Mantovan, P.; Todini, E. Hydrological forecasting uncertainty assessment: Incoherence of the GLUE methodology. J. Hydrol. 2006, 330, 368–381. [Google Scholar] [CrossRef]
- Jian, J.; Ryu, D.; Costelloe, J.F.; Su, C.-H. Towards hydrological model calibration using river level measurements. J. Hydrol. 2017, 10, 95–109. [Google Scholar] [CrossRef]
- Piet, M.M. Dropping the Rating Curve: Calibrating a Rainfall-Runoff Model on Stage to Reduce Discharge Uncertainty. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez, R.F.; Hampel, H. A Simple Approach to Account for Stage–Discharge Uncertainty in Hydrological Modelling. Water 2022, 14, 1045. https://doi.org/10.3390/w14071045
Vázquez RF, Hampel H. A Simple Approach to Account for Stage–Discharge Uncertainty in Hydrological Modelling. Water. 2022; 14(7):1045. https://doi.org/10.3390/w14071045
Chicago/Turabian StyleVázquez, Raúl F., and Henrietta Hampel. 2022. "A Simple Approach to Account for Stage–Discharge Uncertainty in Hydrological Modelling" Water 14, no. 7: 1045. https://doi.org/10.3390/w14071045
APA StyleVázquez, R. F., & Hampel, H. (2022). A Simple Approach to Account for Stage–Discharge Uncertainty in Hydrological Modelling. Water, 14(7), 1045. https://doi.org/10.3390/w14071045






