A Novel Radial Basis Function Approach for Infiltration-Induced Landslides in Unsaturated Soils
Abstract
:1. Introduction
2. The Richards Equation
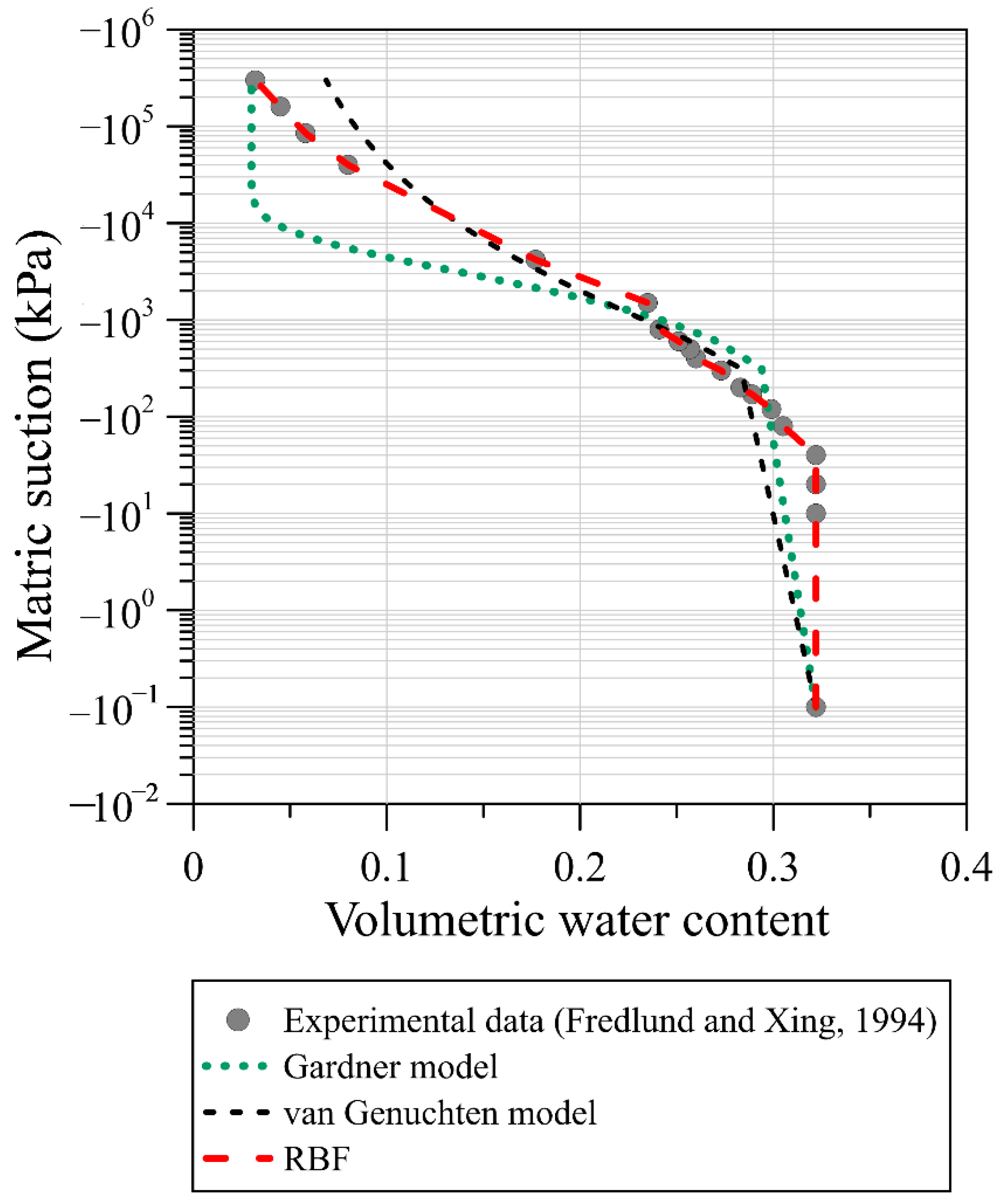
3. The SWCC Model
4. Numerical Methods for Richards Equation
4.1. The RBF Methods for the Richards Equation
4.2. The Fictitious Time Integration Method
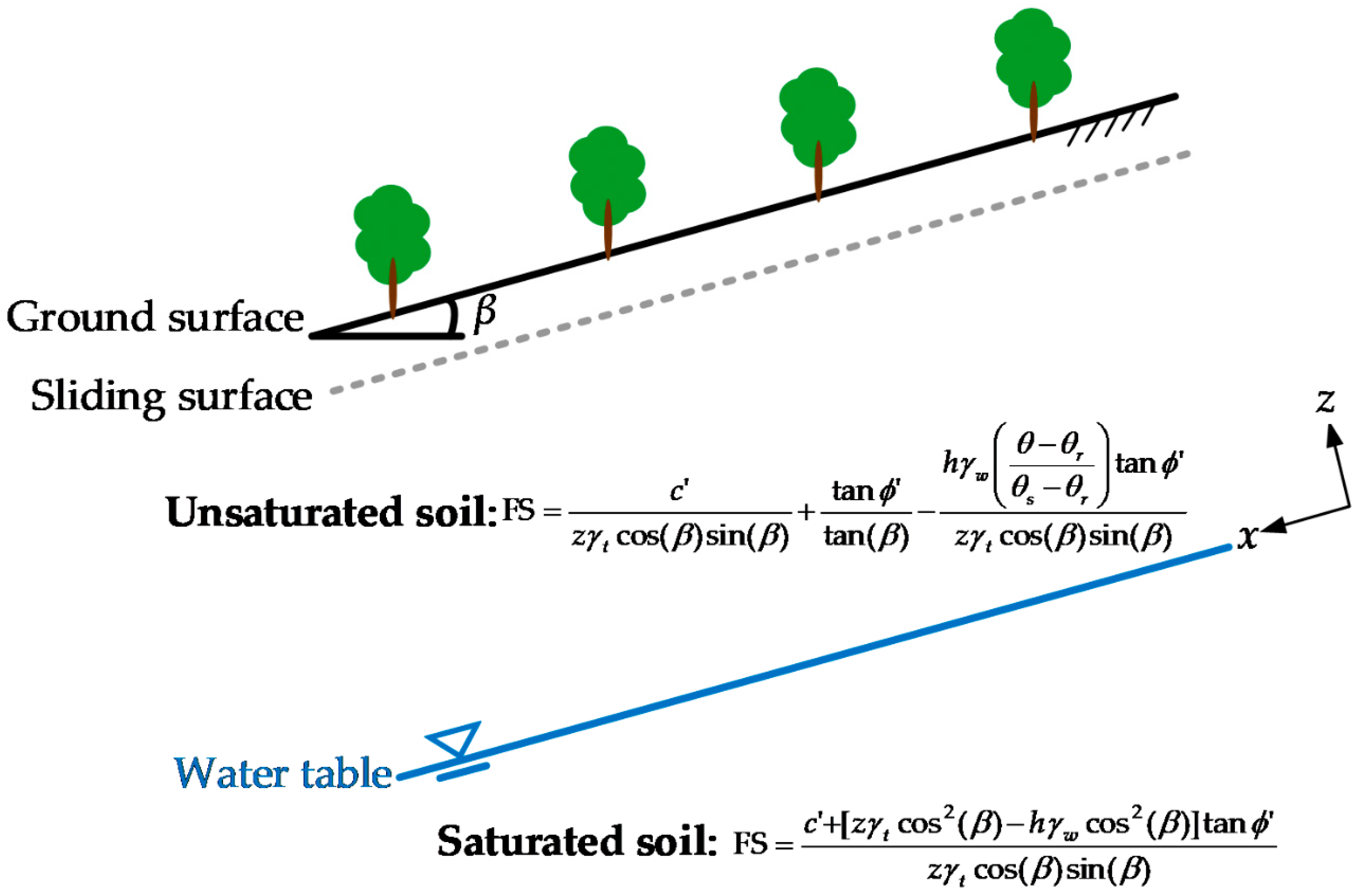
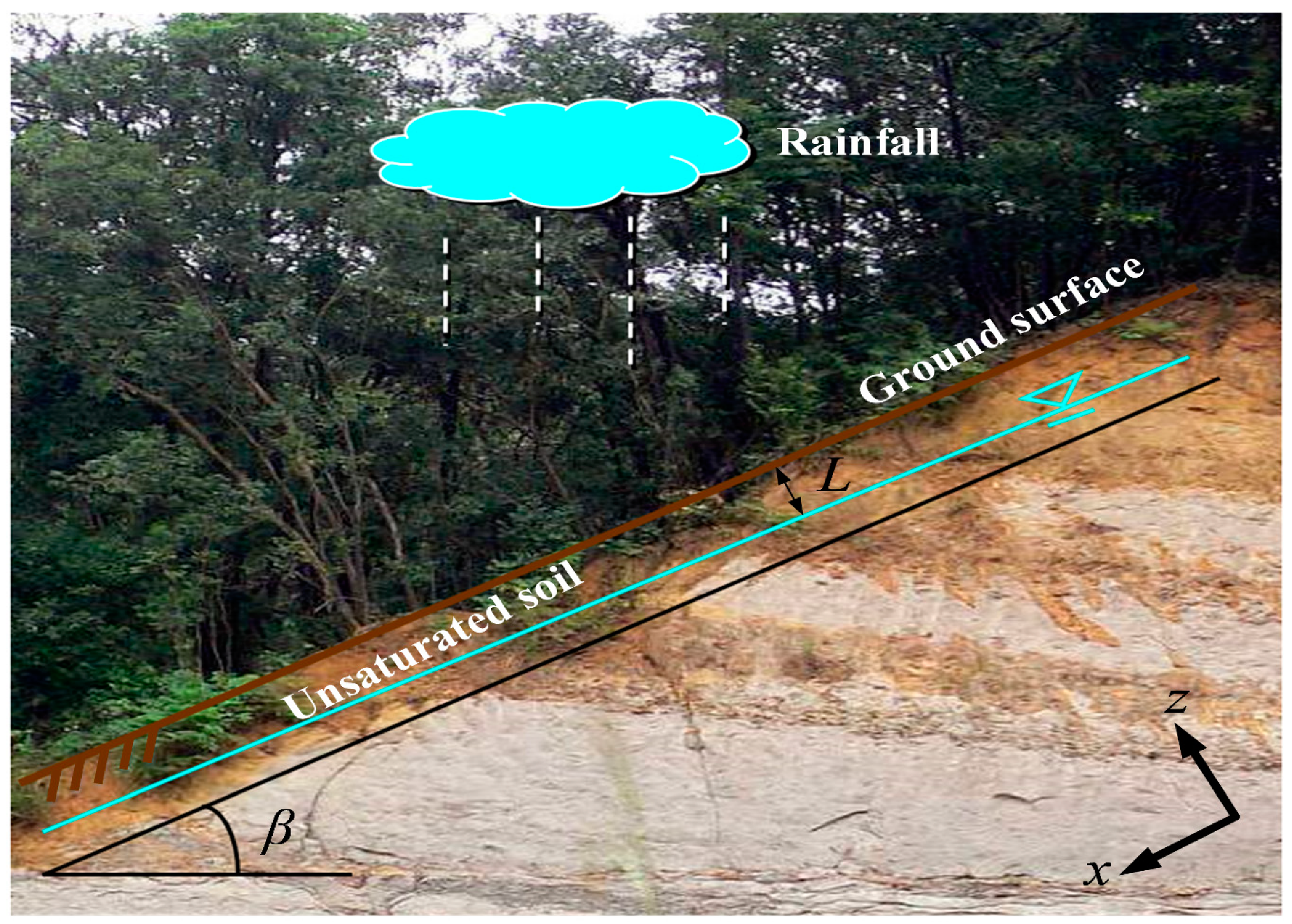
5. Landslide Stability for Unsaturated Soils
6. Numerical Examples
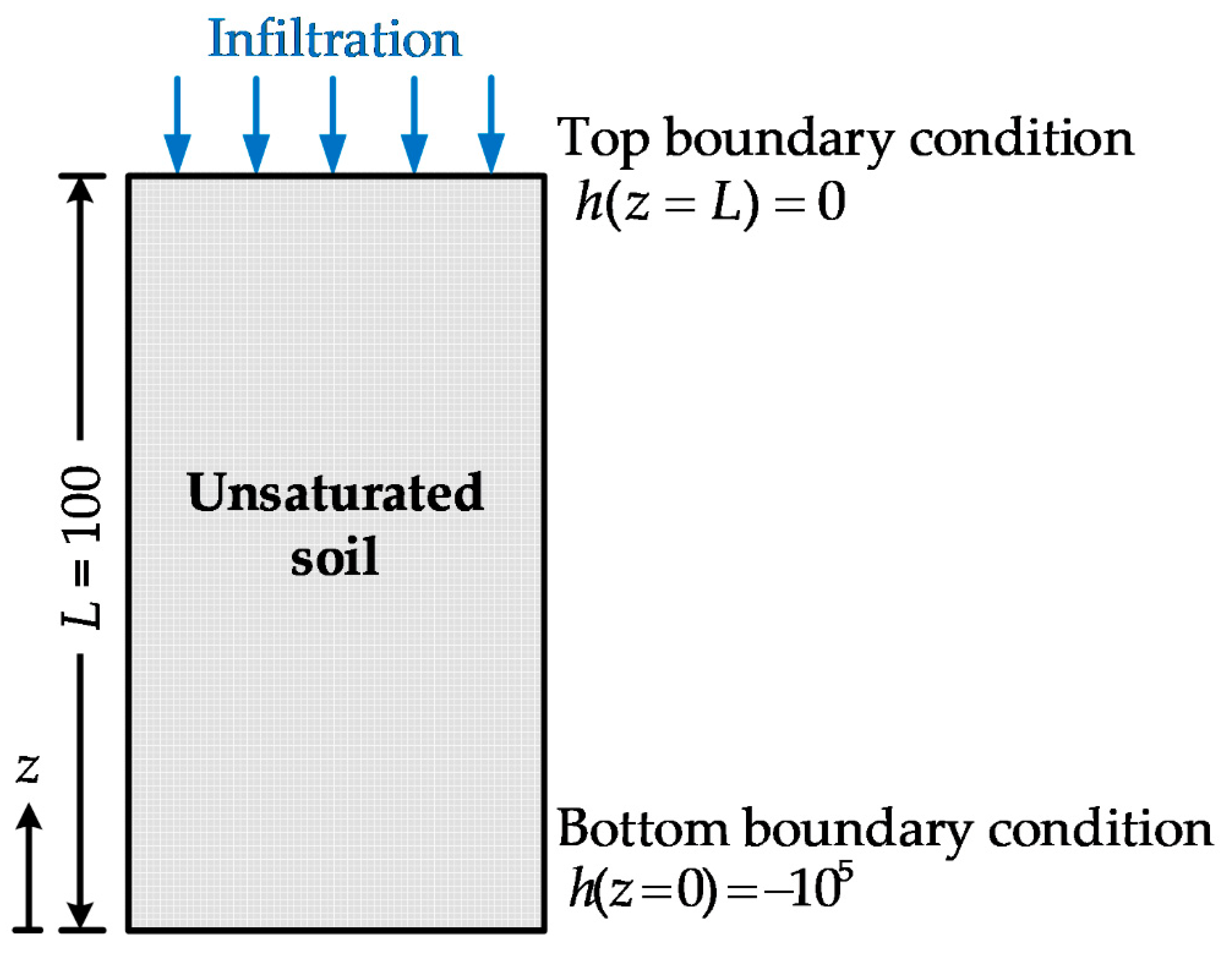
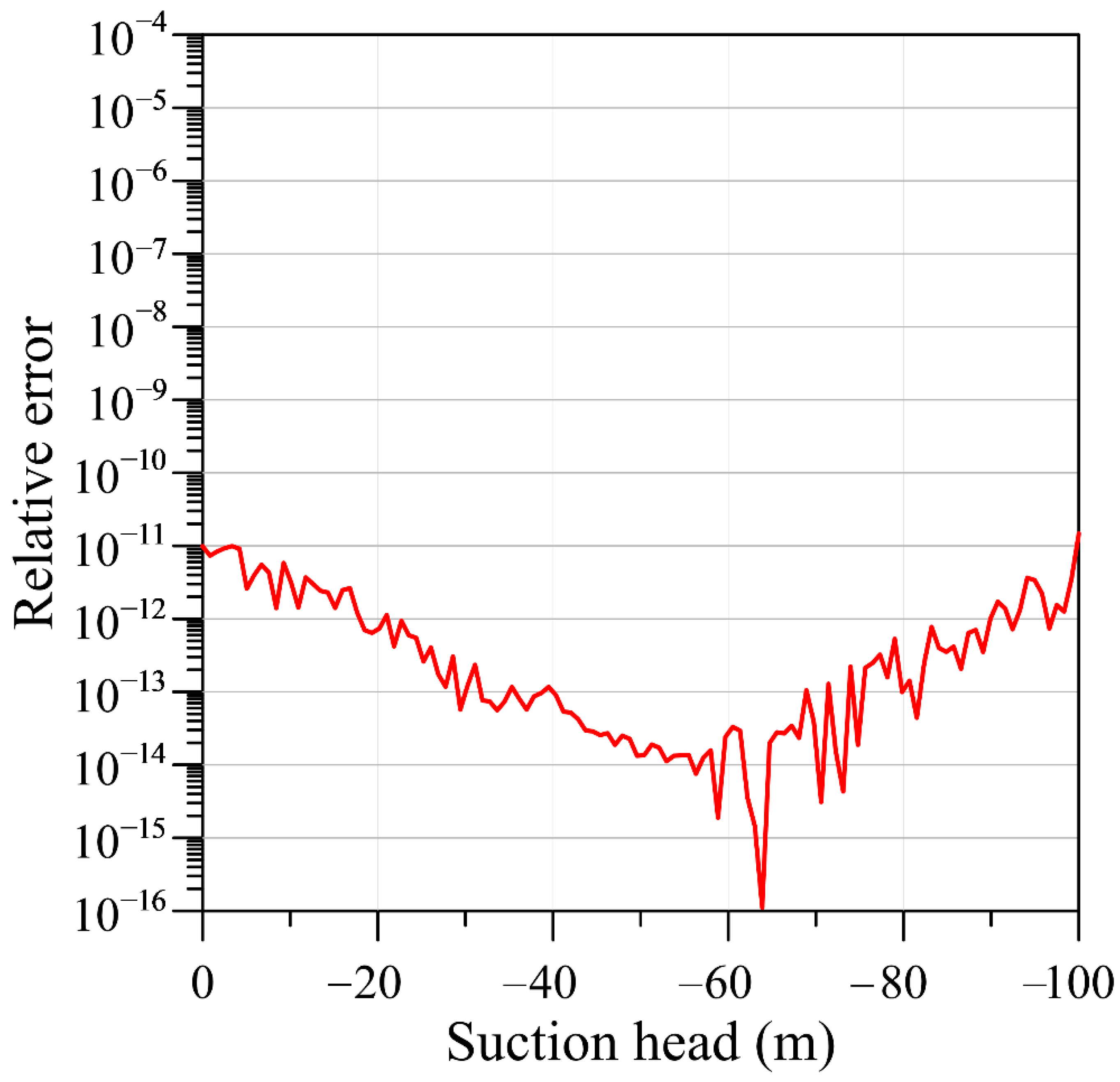
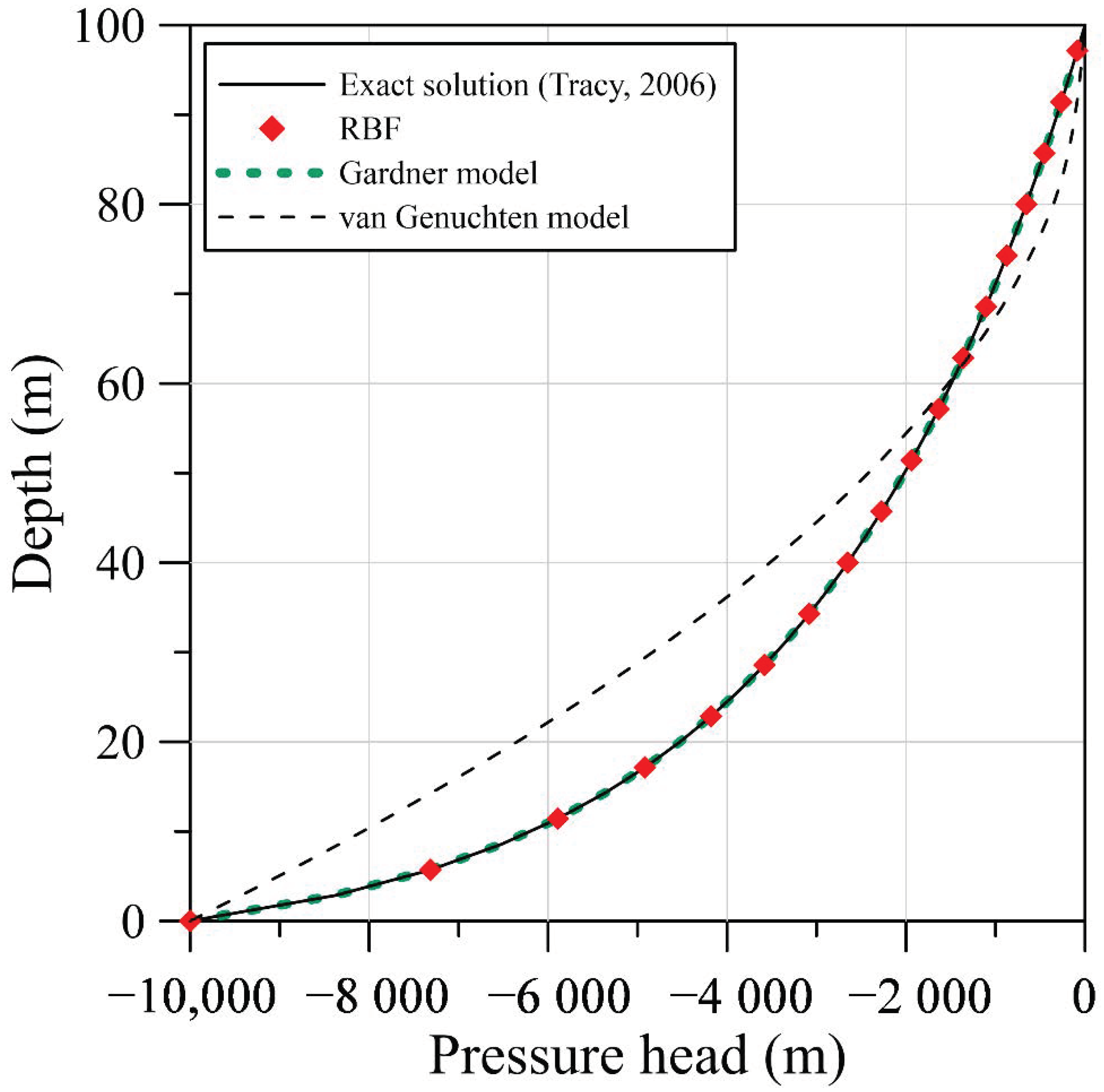
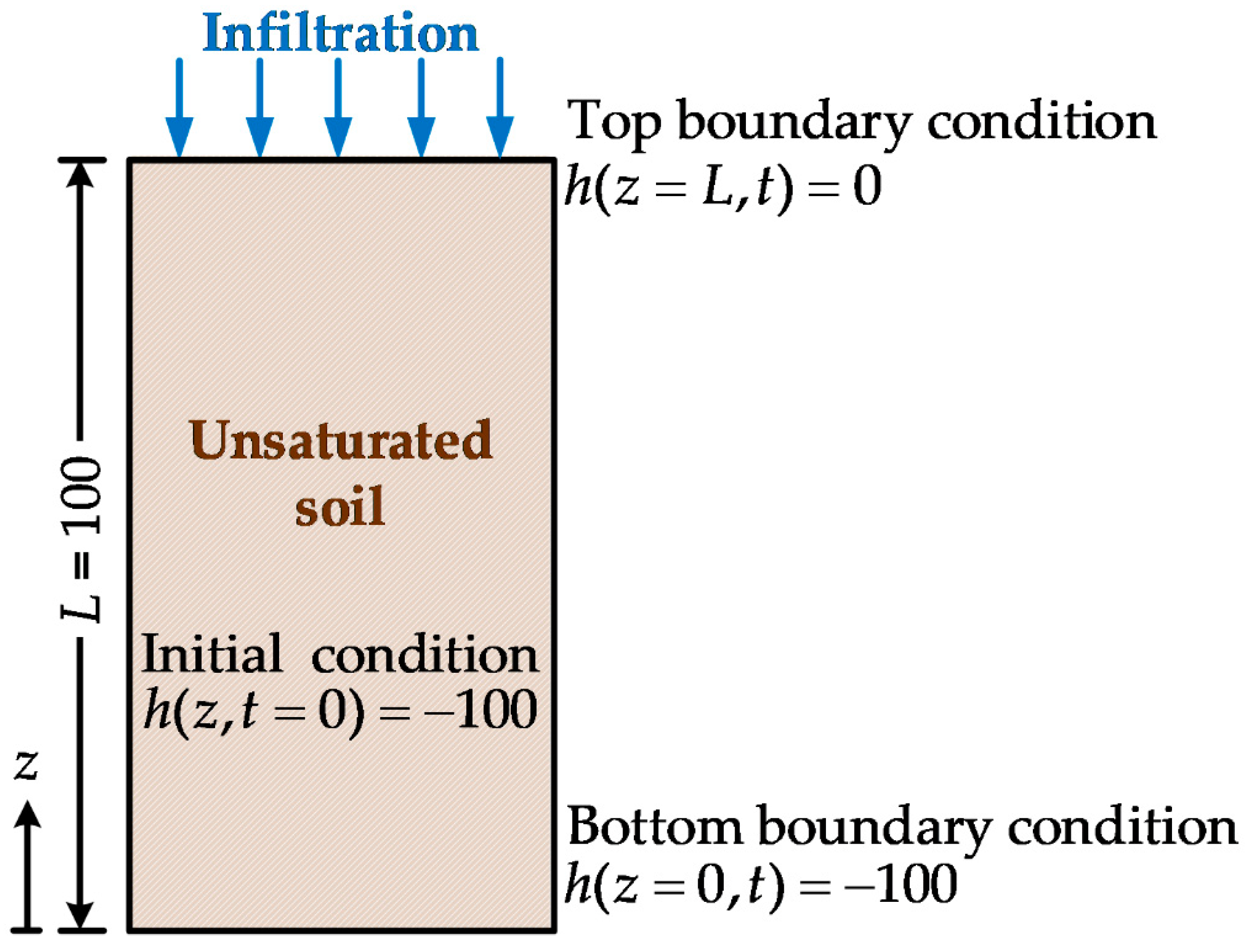
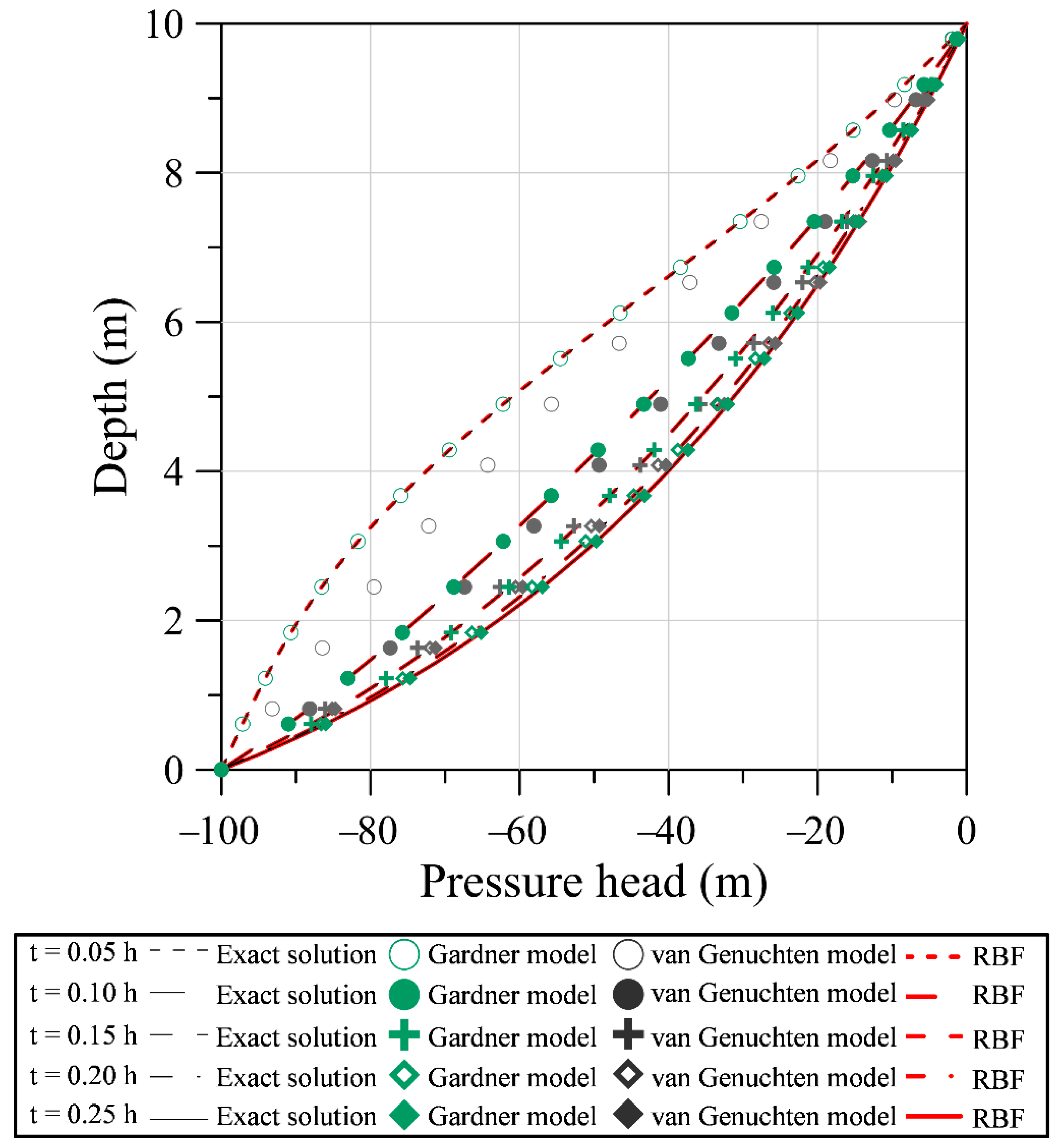
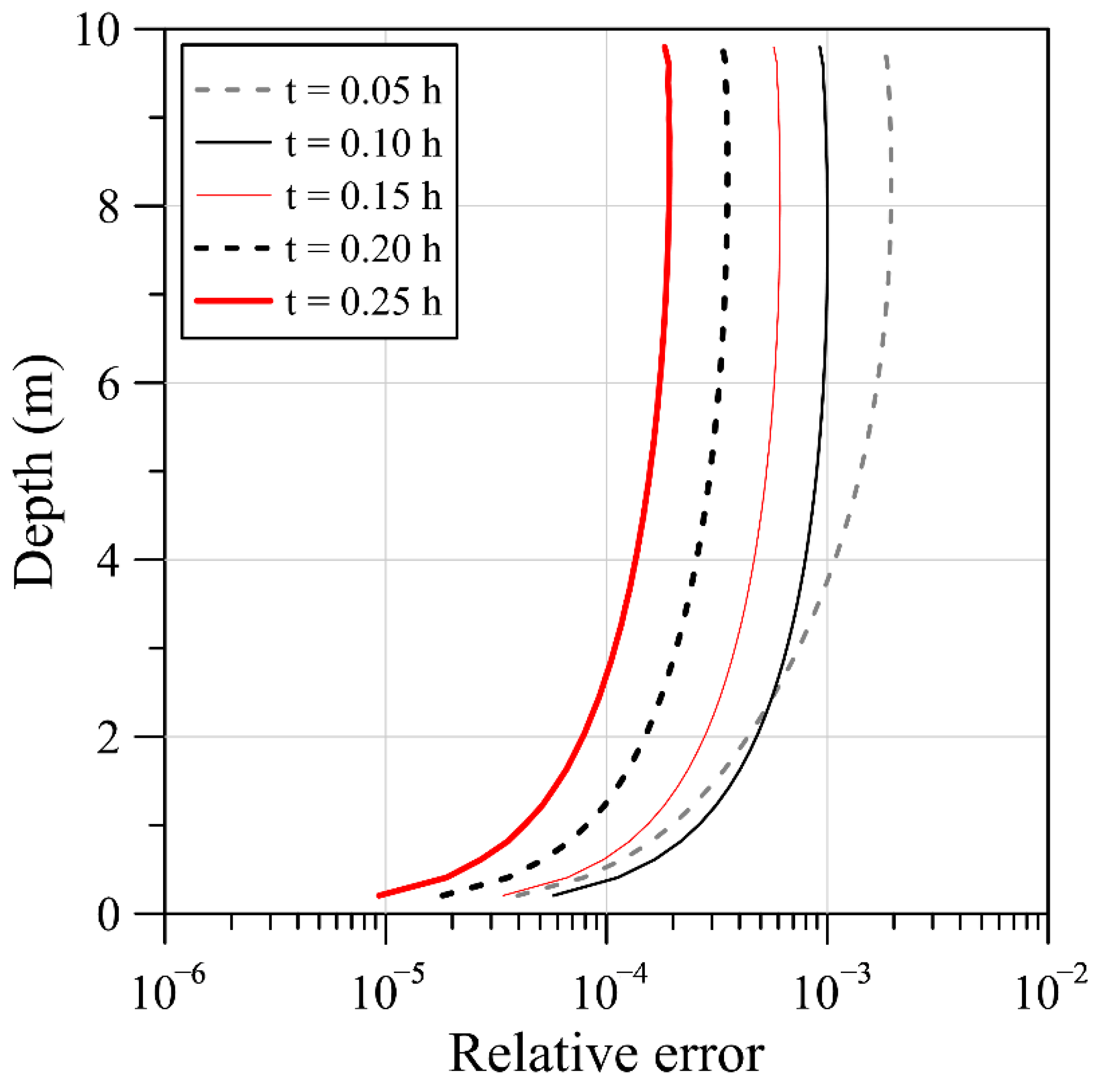
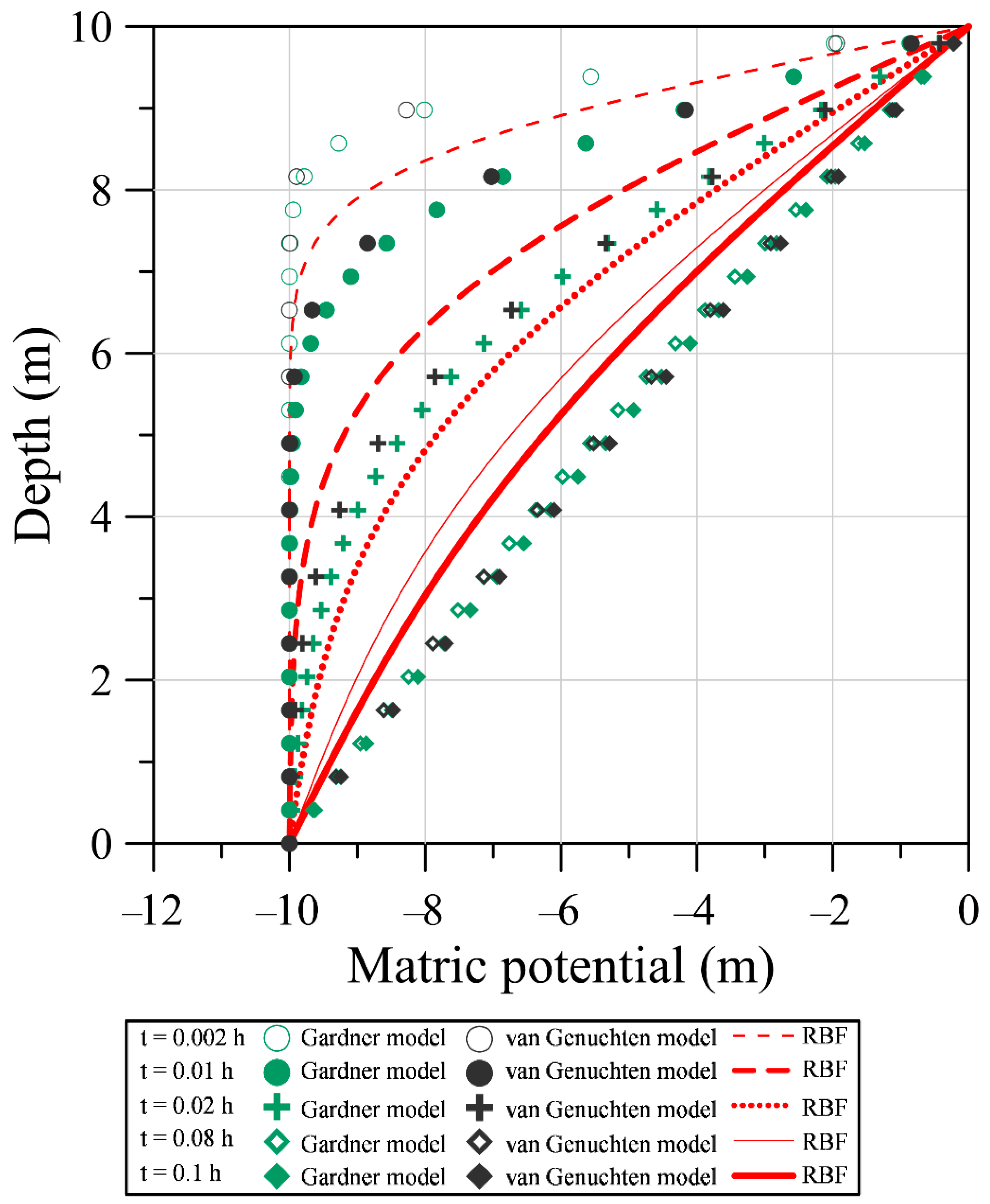
6.1. One-Dimensional Steady-State Infiltration Problem
6.2. The Green–Ampt Problem
6.3. Infiltration-Induced Landslide Problem
7. Conclusions
- (1)
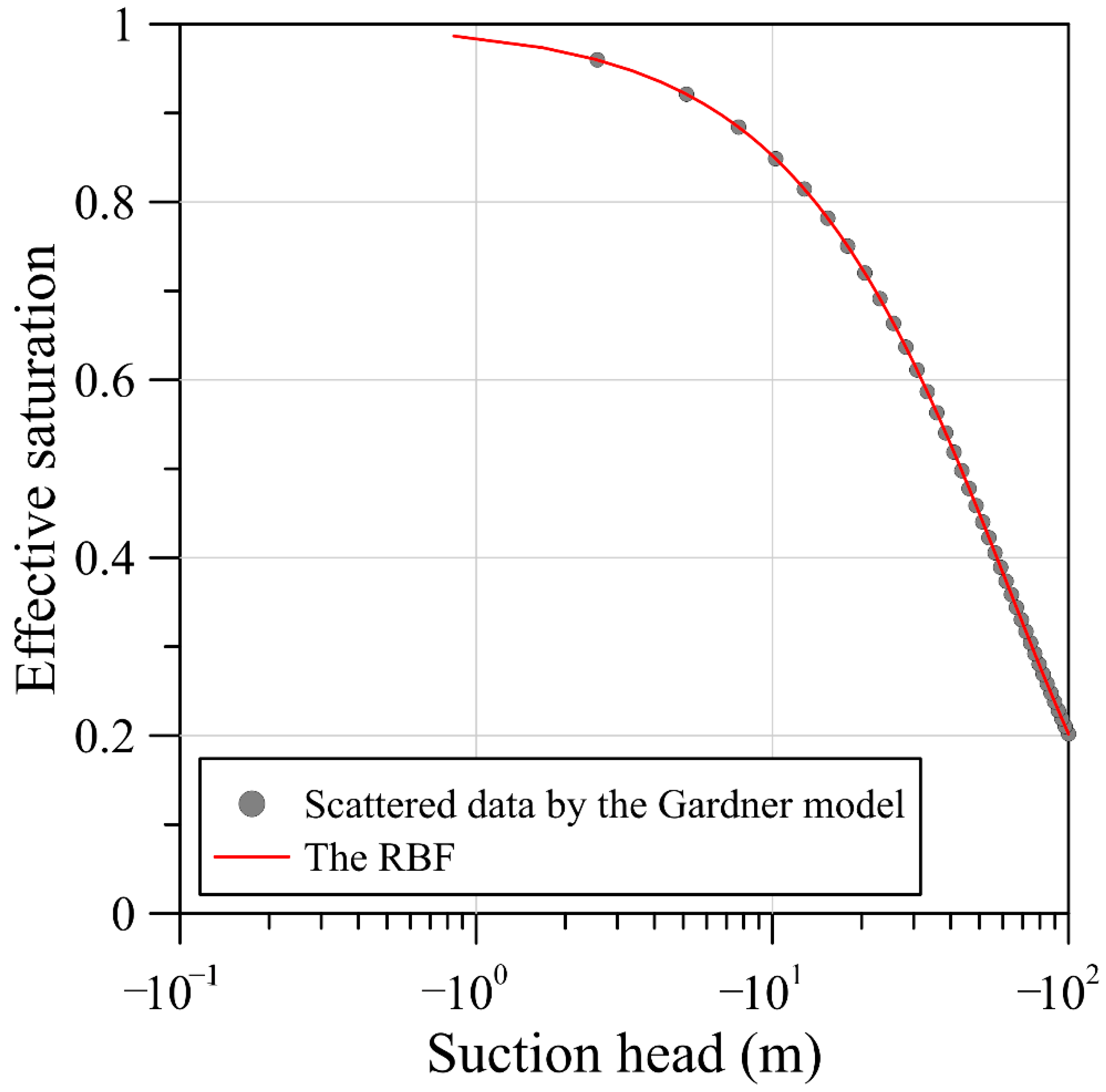
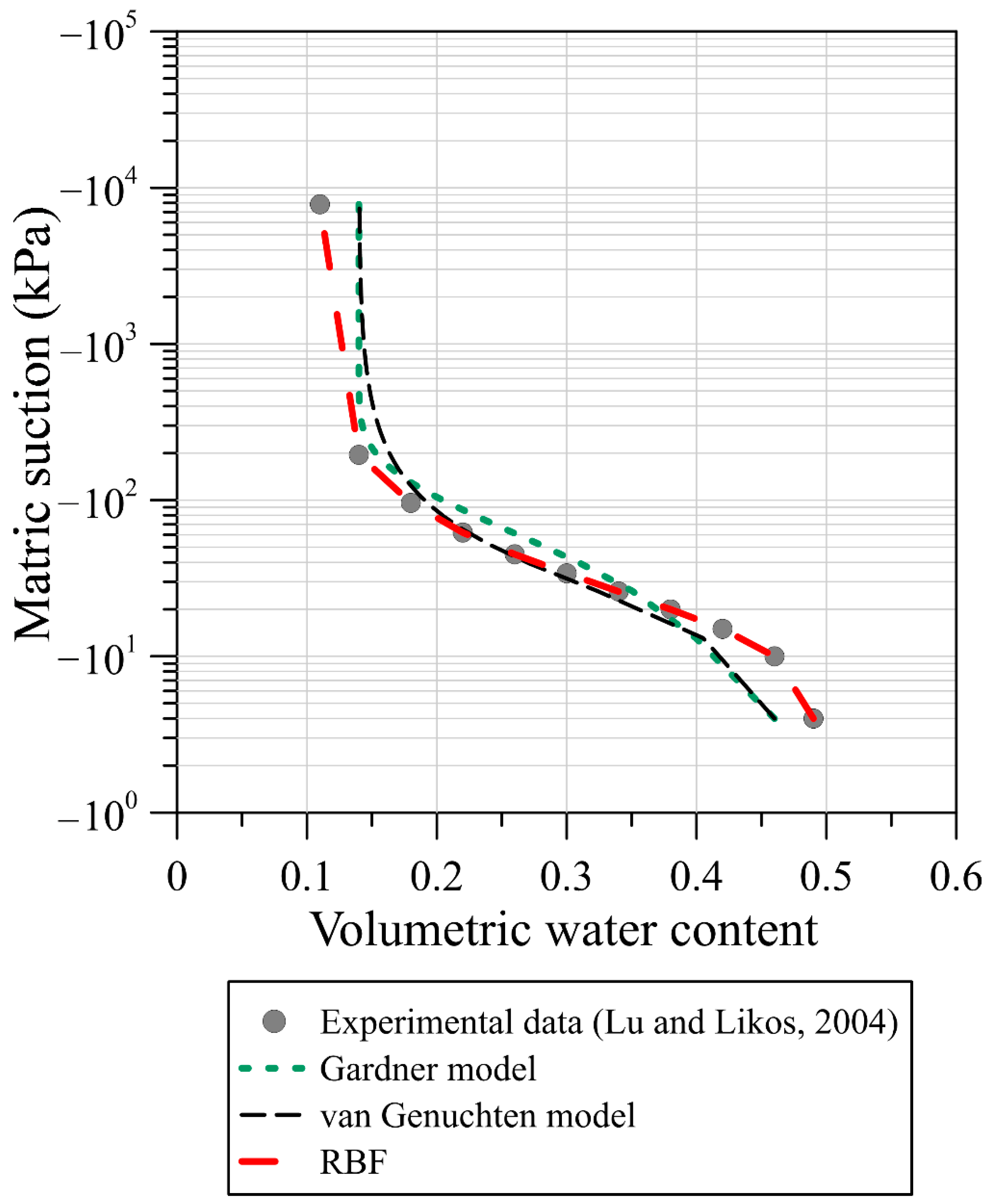
- This article is a leading attempt to model infiltration-induced landslides in unsaturated soils utilizing the RBF method. Since the soil water characteristic curve is a primary factor defining the nonlinearity of unsaturated soils, we first utilize the RBF for curve fitting to build the representation of the SWCC. Results demonstrate that the RBF seems to be advantageous for reconstructing the SWCC of glacial till and sand soil with better estimation of the relationship than conventional parametric Gardner and van Genuchten models.
- (2)
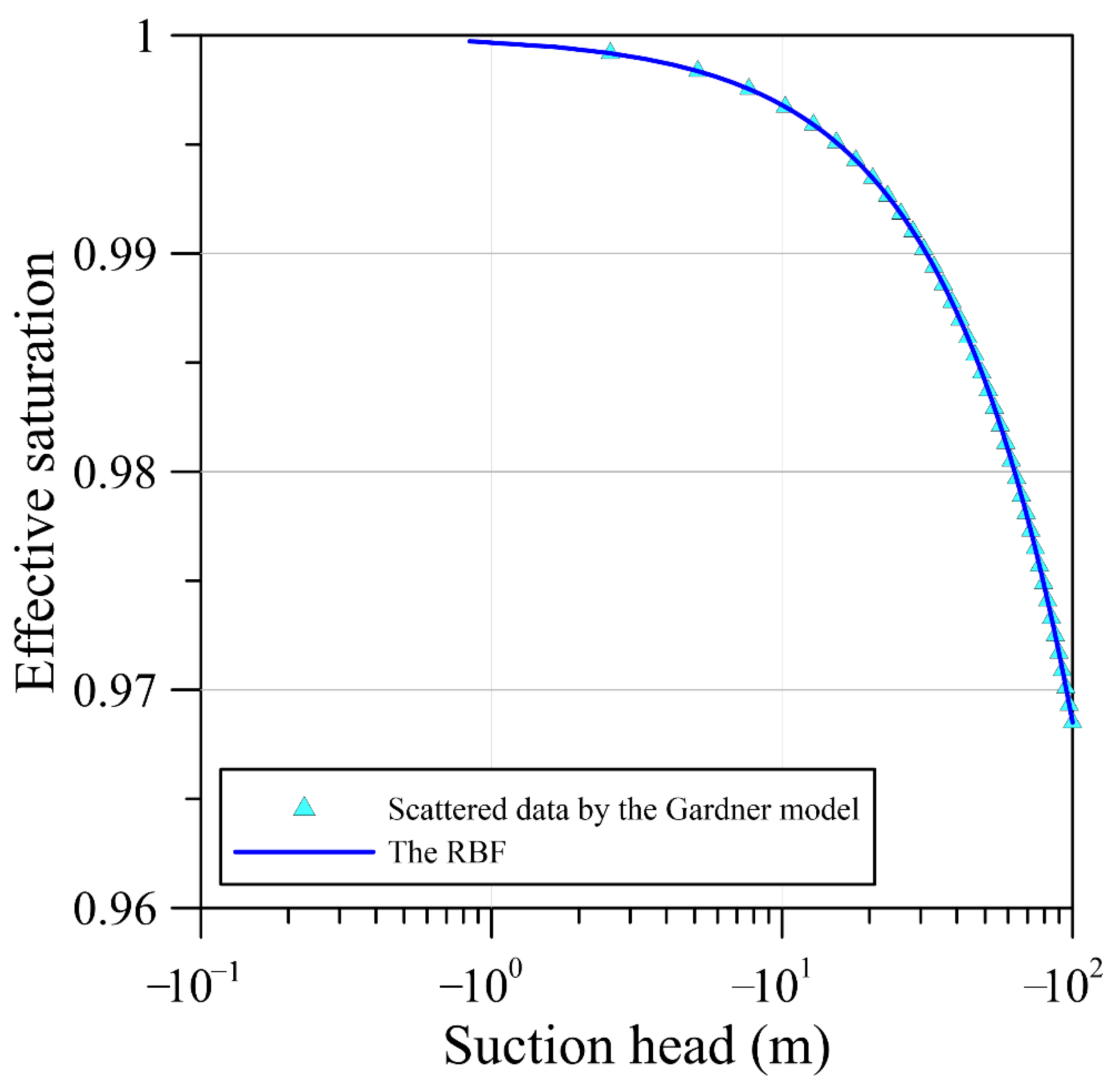
- For solving the nonlinear Richards equation, we developed a novel work using the RBF approach with the infiltration boundary conditions. The fictitious time integration method is adopted in the RBF approach for tackling the nonlinearity of the Richards equation. We propose the novel RBF approach for reconstructing the SWCC to directly solving the nonlinear Richards equation such that the conventional parametric Gardner model and van Genuchten model are not required in the proposed approach.
- (3)
- The hydrological model considering the stability analysis of infinite slope is conducted to analyze the infiltration-induced landslides with emphasis on the behavior of unsaturated soils. Additionally, the proposed RBF method for the nonlinear Richards equation in an inclined slope can be widely applied for disparate types of unsaturated soils. We also found that the stability of landslides is highly related to the variation of matric potential in unsaturated soils during the infiltration process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chiang, S.H.; Chang, K.T. The potential impact of climate change on typhoon-triggered landslides in Taiwan, 2010–2099. Geomorphology 2011, 133, 143–151. [Google Scholar] [CrossRef]
- Mani, A.; Tsai, F.; Kao, S.C.; Naz, B.S.; Ashfaq, M.; Rastogi, D. Conjunctive management of surface and groundwater resources under projected future climate change scenarios. J. Hydrol. 2016, 540, 397–411. [Google Scholar] [CrossRef] [Green Version]
- Bordoni, M.; Galanti, Y.; Bartelletti, C.; Persichillo, M.G.; Barsanti, M.; Giannecchini, R.; D’Amato Avanzi, G.; Cevasco, A.; Brandolini, P.; Galve, J.P.; et al. The influence of the inventory on the determination of the rainfall-induced shallow landslides susceptibility using generalized additive models. Catena 2020, 193, 104630. [Google Scholar] [CrossRef]
- Wu, L.Z.; Selvadurai, A.P.S.; Zhang, L.M.; Huang, R.Q.; Huang, J. Poro-mechanical coupling influences on potential for rainfall-induced shallow landslides in unsaturated soils. Adv. Water Resour. 2016, 98, 114–121. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Mirus, B.B.; Baum, R.L.; Allocca, V.; Tufano, R.; Calcaterra, D. Physically based estimation of rainfall thresholds triggering shallow landslides in volcanic slopes of Southern Italy. Water 2019, 11, 1915. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.L.; Fredlund, M.D.; Fredlund, D.G.; Lu, H.; Wilson, G.W. The influence of the unsaturated soil zone on 2-D and 3-D slope stability analyses. Eng. Geol. 2015, 193, 374–383. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Infinite slope stability under steady unsaturated seepage conditions. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Keles, F.; Nefeslioglu, H.A. Infinite slope stability model and steady-state hydrology-based shallow landslide susceptibility evaluations: The Guneysu catchment area (Rize, Turkey). Catena 2021, 200, 105161. [Google Scholar] [CrossRef]
- Urciuoli, G.; Pirone, M.; Picarelli, L. Considerations on the mechanics of failure of the infinite slope. Comput. Geotech. 2019, 107, 68–79. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis. US Geol. Surv. Open-File Rep. 2002, 424, 38. [Google Scholar]
- Ciurleo, M.; Mandaglio, M.C.; Moraci, N. Landslide susceptibility assessment by TRIGRS in a frequently affected shallow instability area. Landslides 2019, 16, 175–188. [Google Scholar] [CrossRef]
- Liu, W.; Luo, X.; Huang, F.; Fu, M. Uncertainty of the soil–water characteristic curve and its effects on slope seepage and stability analysis under conditions of rainfall using the markov chain monte carlo method. Water 2017, 9, 758. [Google Scholar] [CrossRef] [Green Version]
- Rajesh, S.; Roy, S.; Madhav, S. Study of measured and fitted SWCC accounting the irregularity in the measured dataset. Int. J. Geotech. Eng. 2017, 11, 321–331. [Google Scholar] [CrossRef]
- Chiu, C.F.; Yan, W.M.; Yuen, K.V. Reliability analysis of soil–water characteristics curve and its application to slope stability analysis. Eng. Geol. 2012, 135, 83–91. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; Van Genuchten, M.T.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Liu, C.Y.; Ku, C.Y.; Huang, C.C.; Lin, D.G.; Yeih, W.C. Numerical solutions for groundwater flow in unsaturated layered soil with extreme physical property contrasts. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 325–335. [Google Scholar] [CrossRef]
- List, F.; Radu, F.A. A study on iterative methods for solving Richards’ equation. Comput. Geosci. 2016, 20, 341–353. [Google Scholar] [CrossRef] [Green Version]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Liu, C.S.; El-Zahar, E.R.; Chang, C.W. A boundary shape function iterative method for solving nonlinear singular boundary value problems. Math. Comput. Simul. 2021, 187, 614–629. [Google Scholar] [CrossRef]
- Qi, S.; Vanapalli, S.K. Influence of swelling behavior on the stability of an infinite unsaturated expansive soil slope. Comput. Geotech. 2016, 76, 154–169. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R. Stress state variables for unsaturated soils. J. Geotech. Eng.-Asce 1977, 103, 447–466. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Baiamonte, G. Analytical solution of the Richards equation under gravity-driven infiltration and constant rainfall intensity. J. Hydrol. Eng. 2020, 25, 04020031. [Google Scholar] [CrossRef]
- Ku, C.Y.; Hong, L.D.; Liu, C.Y.; Xiao, J.E. Space–time polyharmonic radial polynomial basis functions for modeling saturated and unsaturated flows. Eng. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Rate of capillary rise in soil. J. Geotech. Geoenviron. Eng. 2004, 130, 646–650. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef] [Green Version]
- Sarra, S.A. Adaptive radial basis function methods for time dependent partial differential equations. Appl. Numer. Math. 2005, 54, 79–94. [Google Scholar] [CrossRef] [Green Version]
- Ku, C.Y.; Liu, C.Y.; Su, Y.; Xiao, J.E. Modeling of transient flow in unsaturated geomaterials for rainfall-induced landslides using a novel spacetime collocation method. Geofluids 2018, 2018, 7892789. [Google Scholar] [CrossRef] [Green Version]
- Tracy, F.T. Clean two- and three-dimensional analytical solutions of Richards’ equation for testing numerical solvers. Water Resour. Res. 2006, 42, 8. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics I. The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]


| Type of RBF | RBF |
|---|---|
| Gaussian | |
| Multiquadric | |
| Inverse quadratic | |
| Inverse multiquadric | |
| Polyharmonic spline | |
| Thin plate spline | |
| Radial polynomials |
| SWCC Model | Fitted Parameters | RMSE |
|---|---|---|
| Gardner model | ||
| van Genuchten model | ||
| RBF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Liu, C.-Y.; Tsai, F.T.-C. A Novel Radial Basis Function Approach for Infiltration-Induced Landslides in Unsaturated Soils. Water 2022, 14, 1036. https://doi.org/10.3390/w14071036
Ku C-Y, Liu C-Y, Tsai FT-C. A Novel Radial Basis Function Approach for Infiltration-Induced Landslides in Unsaturated Soils. Water. 2022; 14(7):1036. https://doi.org/10.3390/w14071036
Chicago/Turabian StyleKu, Cheng-Yu, Chih-Yu Liu, and Frank T.-C. Tsai. 2022. "A Novel Radial Basis Function Approach for Infiltration-Induced Landslides in Unsaturated Soils" Water 14, no. 7: 1036. https://doi.org/10.3390/w14071036
APA StyleKu, C.-Y., Liu, C.-Y., & Tsai, F. T.-C. (2022). A Novel Radial Basis Function Approach for Infiltration-Induced Landslides in Unsaturated Soils. Water, 14(7), 1036. https://doi.org/10.3390/w14071036








