Aosta Valley Mountain Springs: A Preliminary Analysis for Understanding Variations in Water Resource Availability under Climate Change
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Studies
2.1.1. Promise Spring
2.1.2. Alpe Perrot Spring
2.1.3. Promiod Spring
2.1.4. Cheserod Spring
2.2. Data
2.3. Hydro-Meteorological Data Analysis
2.4. Rainfall Time Series Analysis
2.5. Trend Analysis of Flow Rate Long-Term Series
3. Results
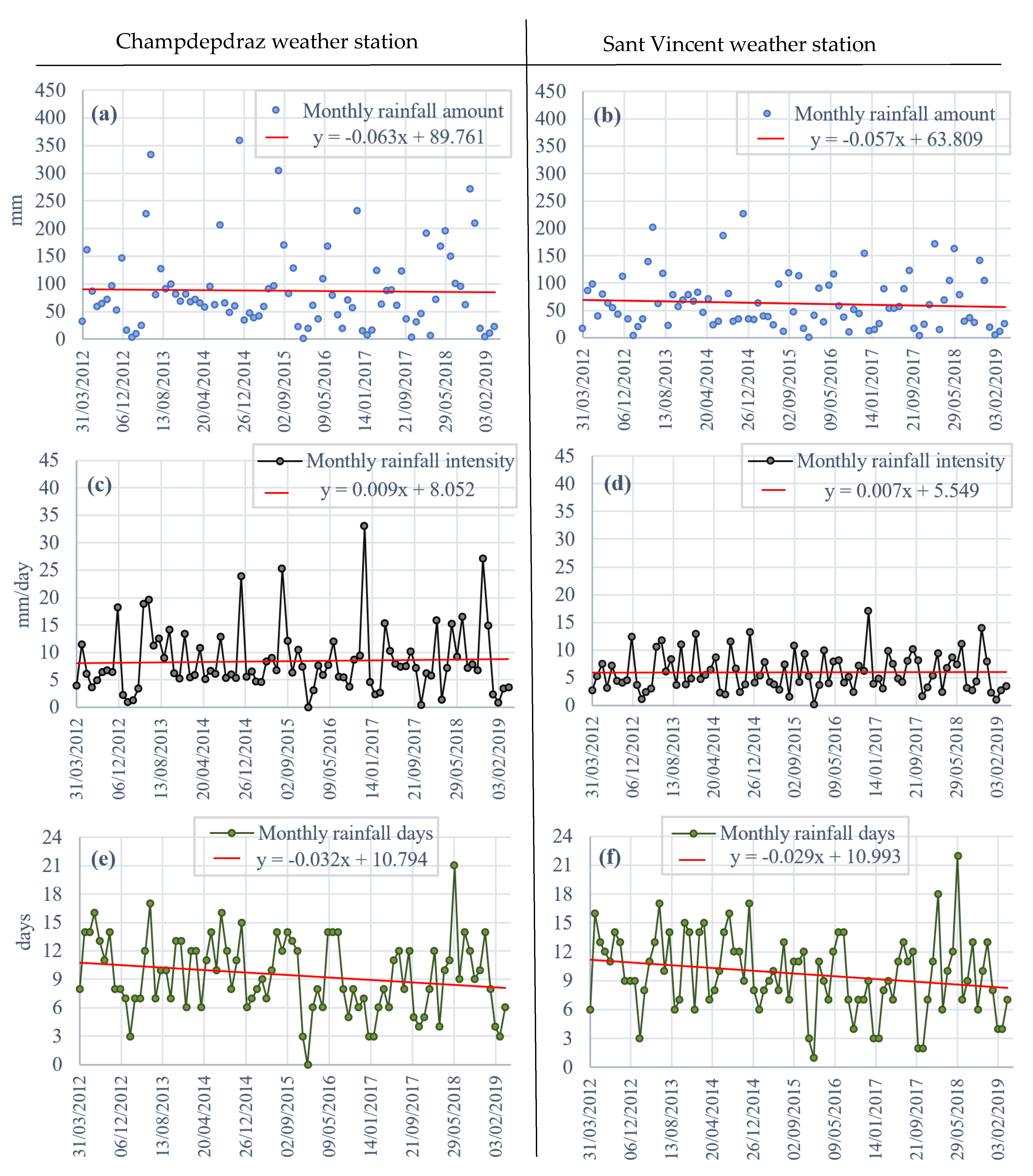
3.1. Hydro-Meteorological Data Analysis Results
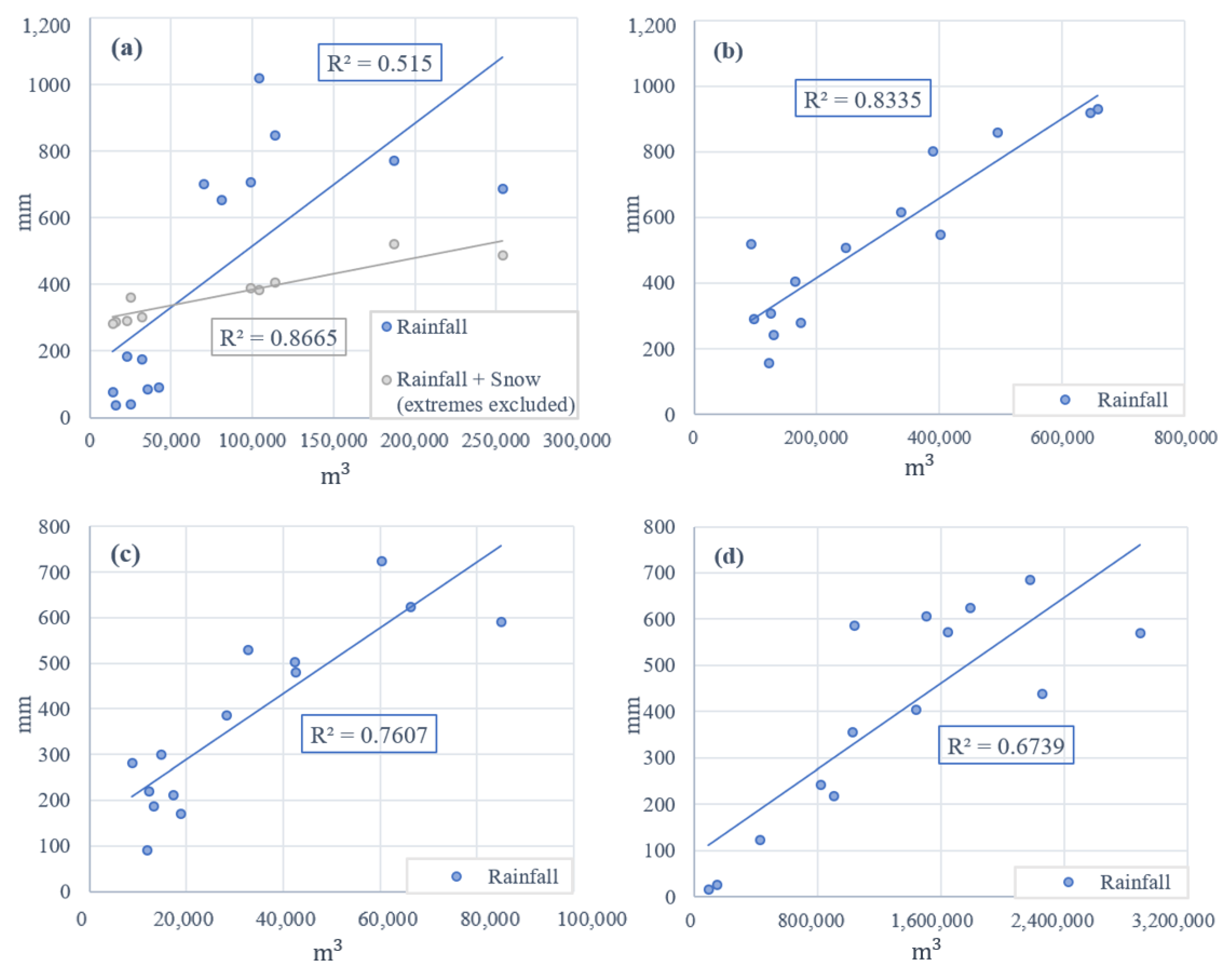
3.2. Rainfall Time Series Analysis Results
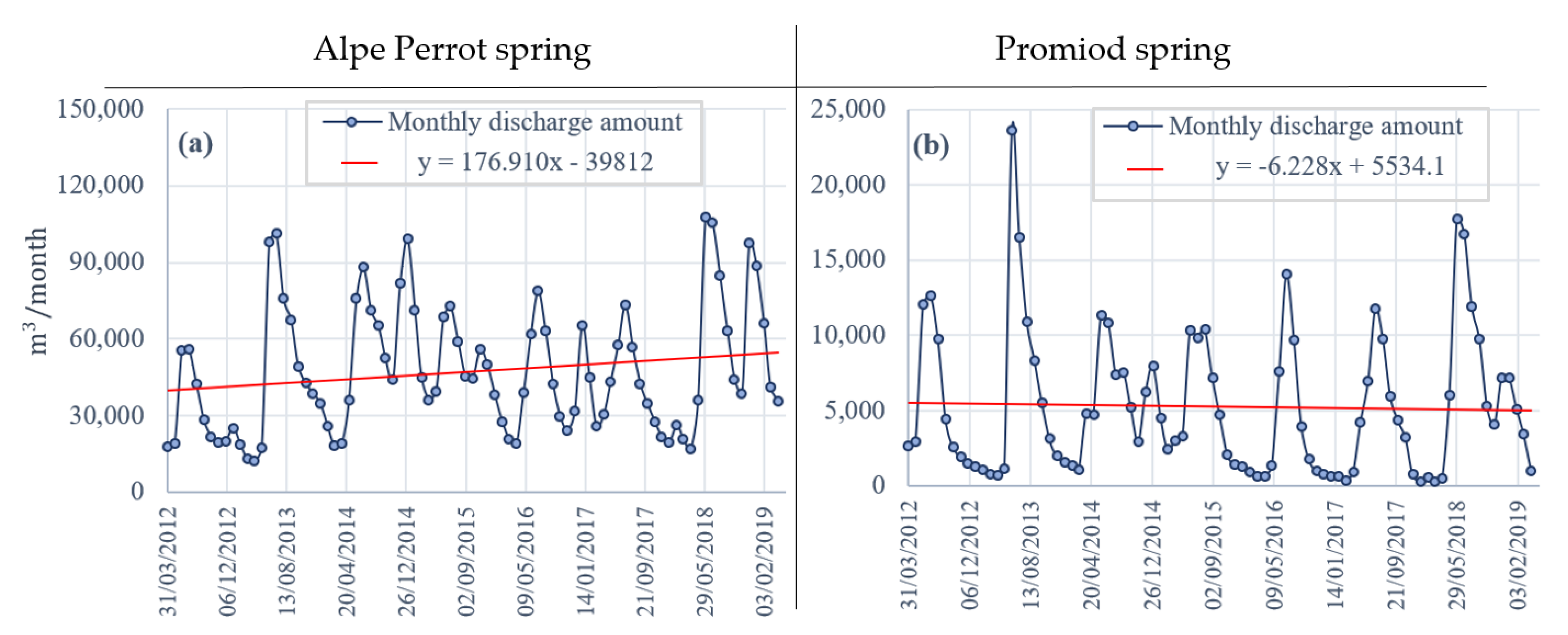
3.3. Trend Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Unesco, Leaving No One Behind, The United Nations World Water Development Report; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2019.
- Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.F.; Ducharne, A.; Yang, Z.L. Divergent Effects of Climate Change on Future Groundwater Availability in Key Mid-Latitude Aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.-P.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate Change and Interconnected Risks to Sustainable Development in the Mediterranean. Nat. Clim. Chang. 2018, 8, 972–980. [Google Scholar] [CrossRef] [Green Version]
- Saadi, S.; Todorovic, M.; Tanasijevic, L.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Climate Change and Mediterranean Agriculture: Impacts on Winter Wheat and Tomato Crop Evapotranspiration, Irrigation Requirements and Yield. Agric. Water Manag. 2015, 147, 103–115. [Google Scholar] [CrossRef]
- De Biase, M.; Chidichimo, F.; Maiolo, M.; Micallef, A. The Impact of Predicted Climate Change on Groundwater Resources in a Mediterranean Archipelago: A Modelling Study of the Maltese Islands. Water 2021, 13, 3046. [Google Scholar] [CrossRef]
- Van Engelenburg, J.; Hueting, R.; Rijpkema, S.; Teuling, A.J.; Uijlenhoet, R.; Ludwig, F. Impact of Changes in Groundwater Extractions and Climate Change on Groundwater-Dependent Ecosystems in a Complex Hydrogeological Setting. Water Resour. Manag. 2018, 32, 259–272. [Google Scholar] [CrossRef] [Green Version]
- Green, T.R. Linking Climate Change and Groundwater. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Jakeman, A.J., Barreteau, O., Hunt, R.J., Rinaudo, J.-D., Ross, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 97–141. [Google Scholar] [CrossRef] [Green Version]
- Riedel, T.; Weber, T.K.D. Review: The Influence of Global Change on Europe’s Water Cycle and Groundwater Recharge. Hydrogeol. J. 2020, 28, 1939–1959. [Google Scholar] [CrossRef]
- Szwed, M. Variability of Precipitation in Poland under Climate Change. Theor. Appl. Climatol. 2019, 135, 1003–1015. [Google Scholar] [CrossRef] [Green Version]
- Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater System and Climate Change: Present Status and Future Considerations. J. Hydrol. 2020, 589, 125163. [Google Scholar] [CrossRef]
- Madakumbura, G.D.; Kim, H.; Utsumi, N.; Shiogama, H.; Fischer, E.M.; Seland, Ø.; Scinocca, J.F.; Mitchell, D.M.; Hirabayashi, Y.; Oki, T. Event-to-Event Intensification of the Hydrologic Cycle from 1.5 °C to a 2 °C Warmer World. Sci. Rep. 2019, 9, 3483. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Revisiting the Global Hydrological Cycle: Is It Intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Rottler, E.; Francke, T.; Bürger, G.; Bronstert, A. Long-Term Changes in Central European River Discharge for 1869-2016: Impact of Changing Snow Covers, Reservoir Constructions and an Intensified Hydrological Cycle. Hydrol. Earth Syst. Sci. 2020, 24, 1721–1740. [Google Scholar] [CrossRef] [Green Version]
- Todzo, S.; Bichet, A.; Diedhiou, A. Intensification of the Hydrological Cycle Expected in West Africa over the 21st Century. Earth Syst. Dyn. 2020, 11, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Carvalho-Santos, C.; Monteiro, A.T.; Azevedo, J.C.; Honrado, J.P.; Nunes, J.P. Climate Change Impacts on Water Resources and Reservoir Management: Uncertainty and Adaptation for a Mountain Catchment in Northeast Portugal. Water Resour. Manag. 2017, 31, 3355–3370. [Google Scholar] [CrossRef] [Green Version]
- Duratorre, T.; Bombelli, G.M.; Menduni, G.; Bocchiola, D. Hydropower Potential in the Alps under Climate Change Scenarios. The Chavonne Plant, Val D’Aosta. Water 2020, 12, 2011. [Google Scholar] [CrossRef]
- Polemio, M.; Casarano, D. Climate Change, Drought and Groundwater Availability in Southern Italy. Geol. Soc. Spec. Publ. 2008, 288, 39–51. [Google Scholar] [CrossRef] [Green Version]
- Bocchiola, D.; Diolaiuti, G. Evidence of Climate Change within the Adamello Glacier of Italy. Theor. Appl. Climatol. 2010, 100, 351–369. [Google Scholar] [CrossRef]
- Forestieri, A.; Arnone, E.; Blenkinsop, S.; Candela, A.; Fowler, H.; Noto, L.V. The Impact of Climate Change on Extreme Precipitation in Sicily, Italy. Hydrol. Process. 2018, 32, 332–348. [Google Scholar] [CrossRef] [Green Version]
- Padulano, R.; Reder, A.; Rianna, G. An Ensemble Approach for the Analysis of Extreme Rainfall under Climate Change in Naples (Italy). Hydrol. Process. 2019, 33, 2020–2036. [Google Scholar] [CrossRef]
- Leone, G.; Pagnozzi, M.; Catani, V.; Ventafridda, G.; Esposito, L.; Fiorillo, F. A Hundred Years of Caposele Spring Discharge Measurements: Trends and Statistics for Understanding Water Resource Availability under Climate Change. Stoch. Environ. Res. Risk Assess. 2020, 35, 345–370. [Google Scholar] [CrossRef]
- Atlante Climatico Della Valle d’Aosta/Coord; Societá Meteorologica Subalpina: Torino, Italy, 2003.
- Amanzio, G.; Bertolo, D.; De Maio, M.; Lodi, L.P.; Pitet, L.; Suozzi, E. Global Warming in the Alps: Vulnerability and Climatic Dependency of Alpine Springs in Italy, Regione Valle d’aosta and Switzerland, Canton Valais. In Engineering Geology for Society and Territory; Springer: Cham, Switzerland, 2015; Volume 5, pp. 1375–1378. [Google Scholar] [CrossRef]
- Lo Russo, S.; Amanzio, G.; Ghione, R.; De Maio, M. Recession Hydrographs and Time Series Analysis of Springs Monitoring Data: Application on Porous and Shallow Aquifers in Mountain Areas (Aosta Valley). Environ. Earth Sci. 2015, 73, 7415–7434. [Google Scholar] [CrossRef]
- ISTAT. Available online: https://demo.istat.it/bilmens/index.php?anno=2021&lingua=ita (accessed on 1 March 2022).
- Martin, S.; Godard, G.; Rebay, G. 32nd International Geological Congress. The Subducted Tethys in the Aosta Valley (Italian Western Alps). Volume 2. APAT Roma. 2004. Available online: https://www.researchgate.net/publication/236944206_The_subducted_Tethys_in_the_Aosta_Valley_Italian_Western_Alps (accessed on 27 February 2022).
- Bistacchi, A.; Dal Piaz, G.; Massironi, M.; Zattin, M.; Balestrieri, M. The Aosta-Ranzola Extensional Fault System and Oligocene-Present Evolution of the Austroalpine-Penninic Wedge in the Northwestern Alps. Int. J. Earth Sci. 2001, 90, 654–667. [Google Scholar] [CrossRef]
- Cremonese, E.; Carlson, B.; Filippa, G.; Pogliotti, P.; Alvarez, I.; Fosson, J.P.; Ravanel, L.; Delestrade, A. AdaPT Mont-Blanc: Rapport Climat: Changements climatiques dans le massif du Mont-Blanc et impacts sur les activités humaines. In Rédigé dans le Cadre du Projet AdaPT Mont-Blanc Financé par le Programme Européen de Coopération Territoriale Alcotra Italie-France 2014–2020; 2019; 101p, Available online: https://www.preventionweb.net/publication/climate-report-climate-change-mont-blanc-massif-and-its-impacts-human-activity (accessed on 27 February 2022).
- Cerino Abdin, E.; Taddia, G.; Gizzi, M.; Lo Russo, S. Reliability of spring recession curve analysis as a function of the temporal resolution of the monitoring dataset. Environ. Earth Sci. 2021, 80, 249. [Google Scholar] [CrossRef]
- Tiao, G.C.; Draper, N.R.; Smith, H. Applied Regression Analysis. Rev. l’Institut Int. Stat./Rev. Int. Stat. Inst. 1968, 36, 104. [Google Scholar] [CrossRef]
- Attah, D.A.; Bankkole, G.M. Time Series Analysis Model for Annual Rainfall Data in Lower Kaduna Catchment Kaduna, Nigeria. Glob. J. Res. Eng. 2012, 2, 82–87. [Google Scholar]
- Olatayo, T.O.; Taiwo, A.I. Statistical Modelling and Prediction of Rainfall Time Series Data. Glob. J. Comuter Sci. Technol. 2014, 14, 1–10. [Google Scholar]
- Machiwal, D.; Jha, M.K. Time Series Analysis of Hydrologic Data for Water Resources Planning and Management: A Review. J. Hydrol. Hydromech. 2006, 54, 237–257. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
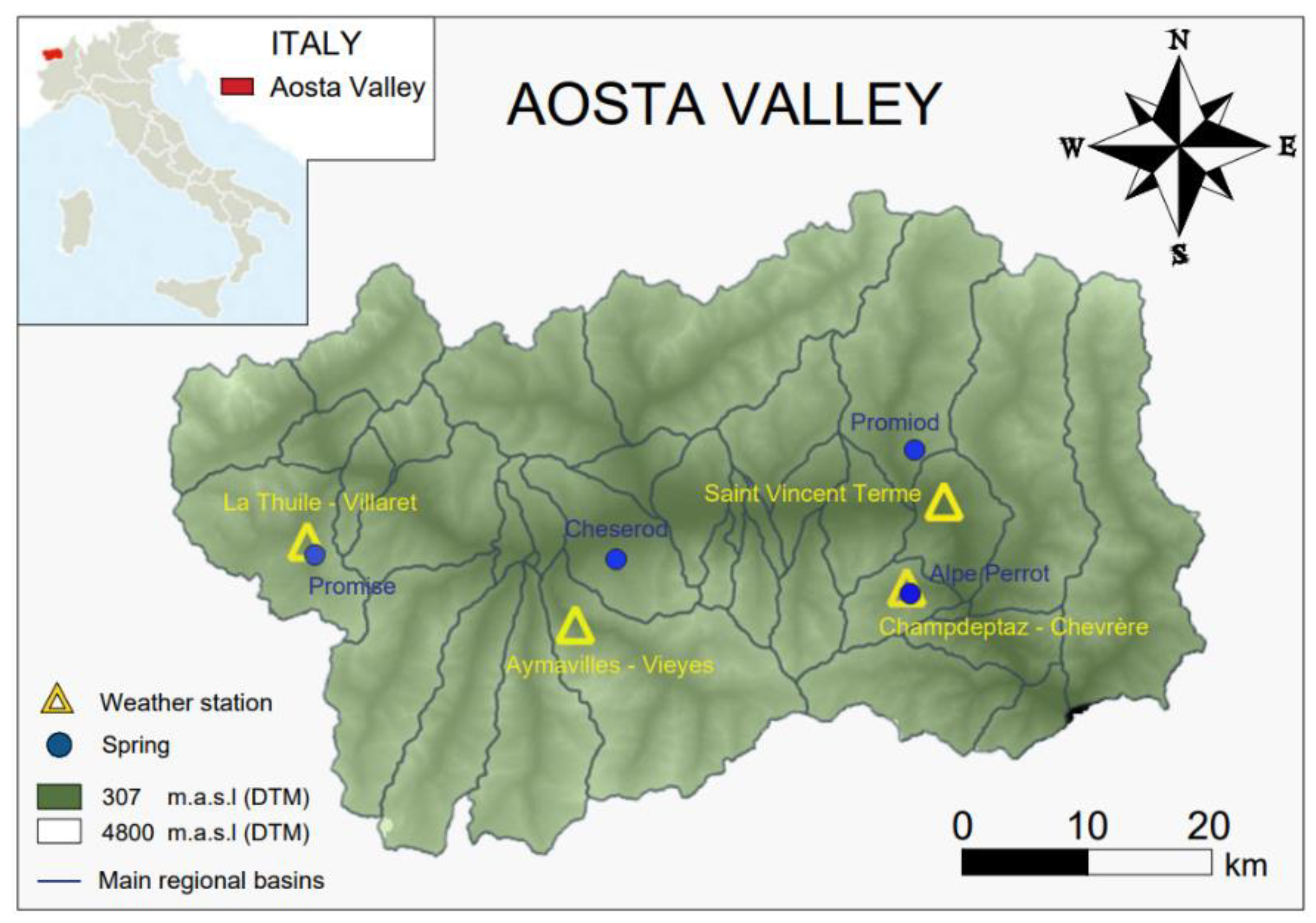
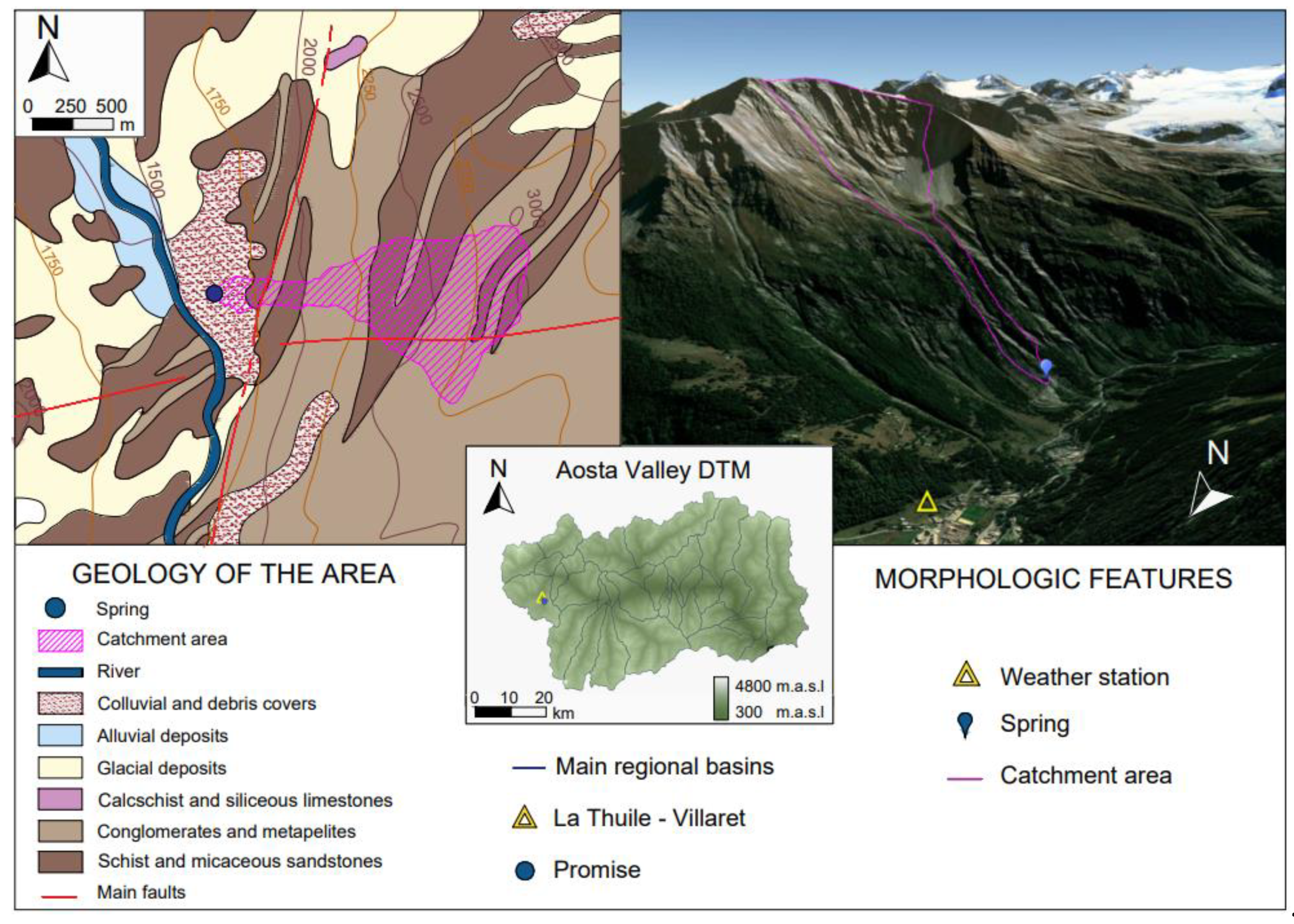
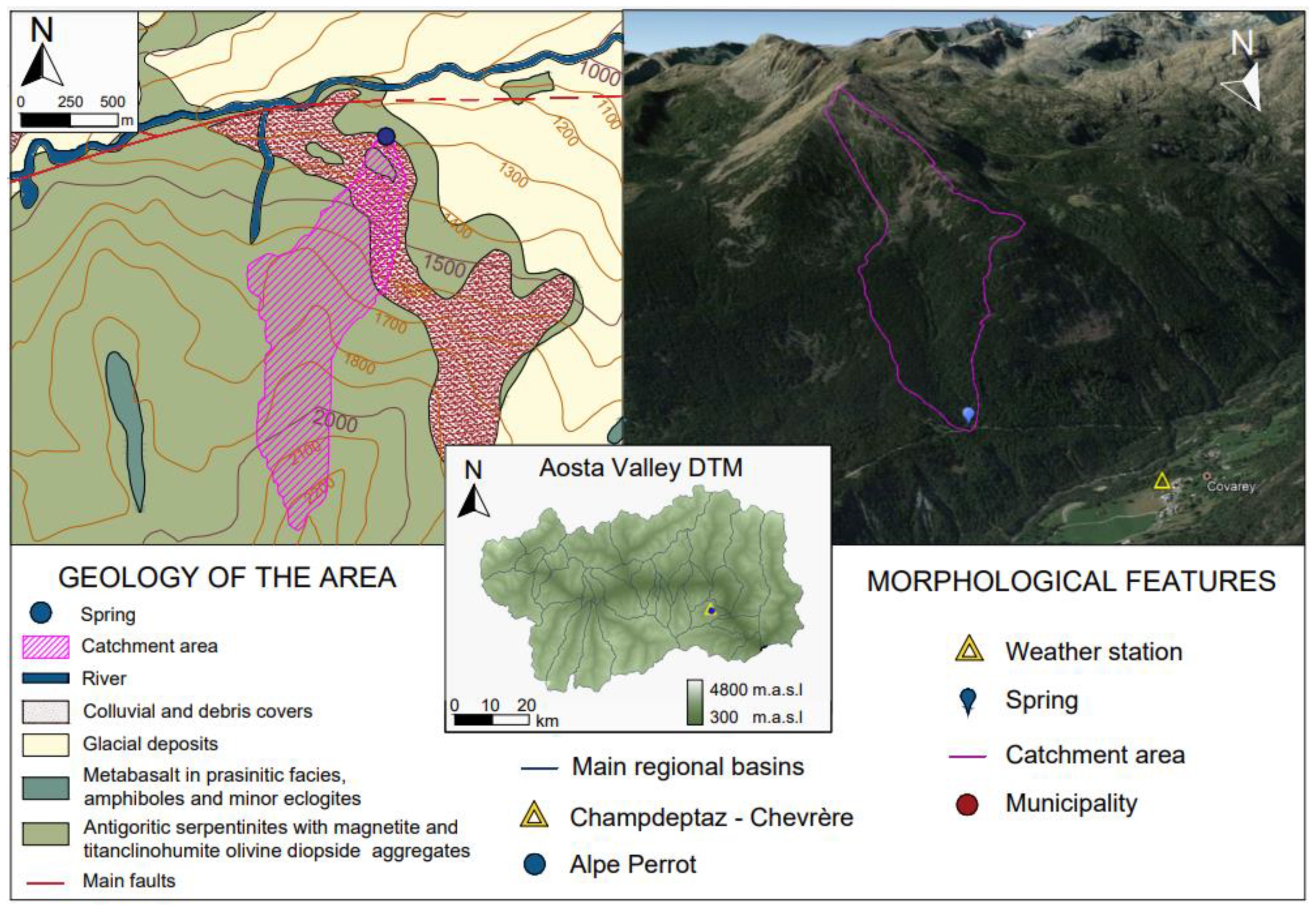
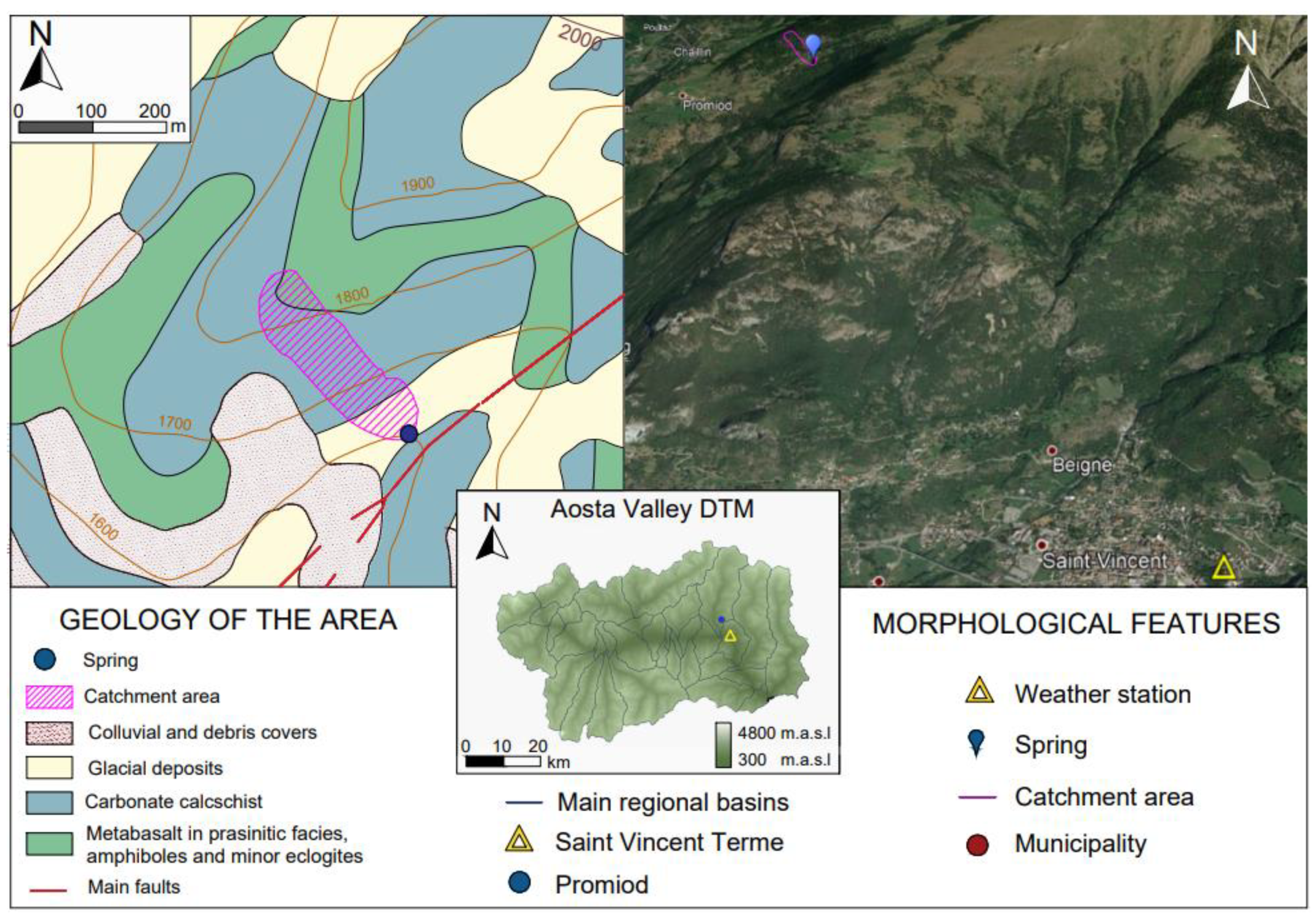
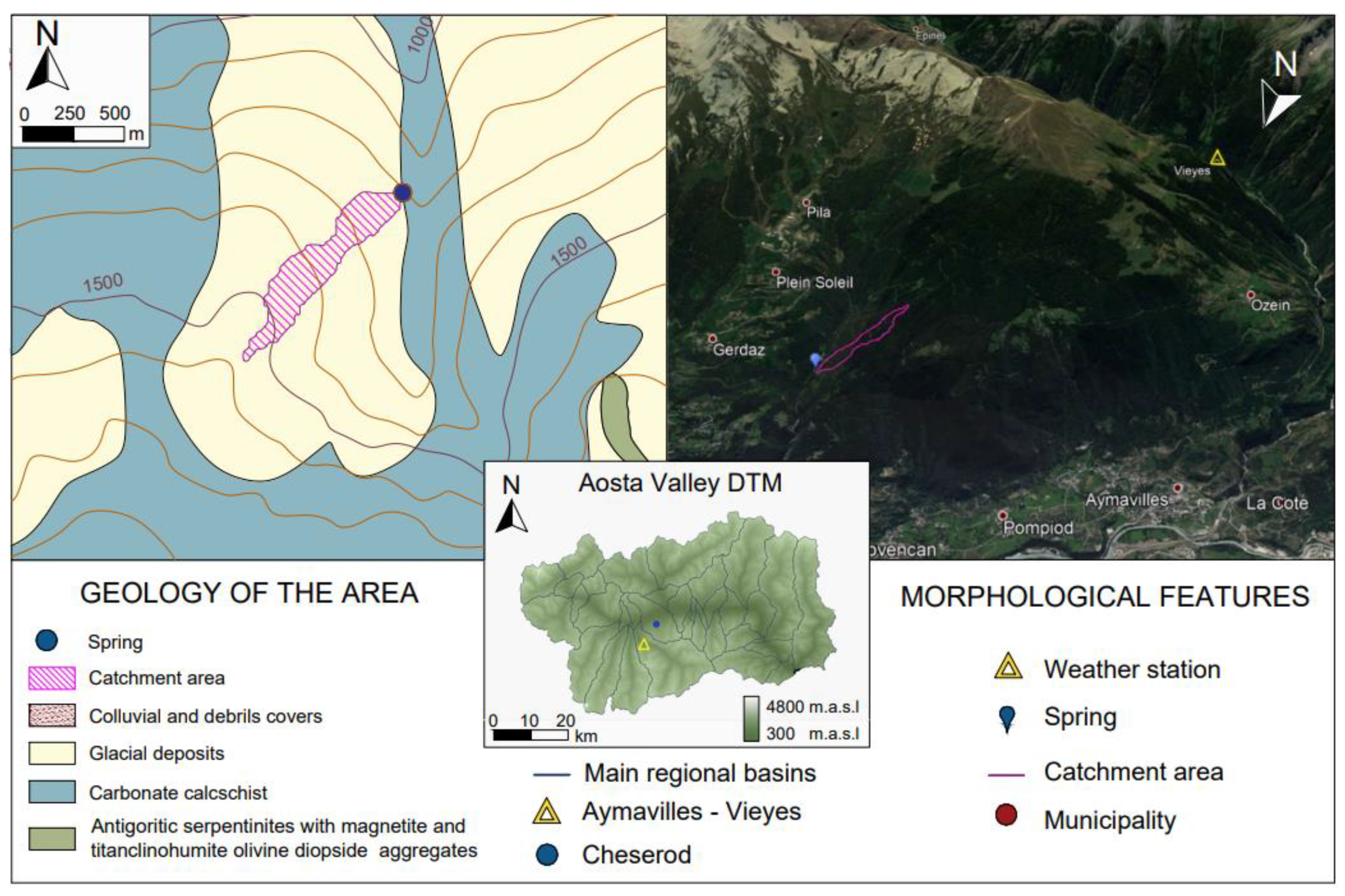
| Weather Stations: | Aymavilles—Vieyes | Saint Vincent—Terme | La Thuile—Villaret | Champdepraz—Chevrère | |||
|---|---|---|---|---|---|---|---|
| Place: | Vieyes | Terme | Villaret | Chevrère | |||
| Municipality: | Aymavilles | Saint Vincent | La Thuile | Champdepraz | |||
| Basin: | s. Grand’Eyvia | Dora Baltea | s. Ruitor | s. Chalamy | |||
| Spring: | Cheserod spring | Promiod spring | Promise spring | Alpe Perrot spring | |||
| Elevation (m a.s.l.): | 1139 | 626 | 1488 | 1260 | |||
| Latitude (WGS84) | 45.6497° | 45.7495° | 45.7095° | 45.6835° | |||
| Longitude (WGS84) | 7.2508° | 7.6526° | 6.95609° | 7.61357° | |||
| Weather Station–Spring distance | 6650 m | 5147 m | 1342 m | 612 m | |||
 |  |  |  | ||||
| Aymavilles—Vieyes | Saint Vincent—Terme | La Thuile—Villaret | Champdepraz—Chevrère | ||||
| Promise | Alpe Perrot | Promiod | Cheserod | |
|---|---|---|---|---|
| 1° h.y. | 09/03/2012–12/04/2013 | 12/03/2012–25/03/2013 | 29/02/2012–19/04/2013 | 17/12/2011–26/03/2013 |
| (recharge season; discharge season) | (09/03/2012–08/05/2012; 09/05/2012–12/04/2013) | (12/03/2012–05/06/2012; 06/06/2012–25/03/2013) | (29/02/2012–21/05/2012; 22/05/2012–19/04/2013) | (17/12/2011–06/07/2012; 07/07/2012–26/03/2013) |
| 2° h.y. | 13/04/2013–09/03/2014 | 26/03/2013–14/03/2014 | 20/04/2013–08/02/2014 | 27/03/2013–23/05/2014 |
| (recharge season; discharge season) | (13/04/2013–06/05/2013; 07/05/2013–09/03/2014) | (26/03/2013–24/05/2013; 25/05/2013–14/03/2014 | (20/04/2013–18/05/2013; 19/05/2013–08/02/2014) | (27/03/2013–25/08/2013; 26/08/2013–23/05/2014) |
| 3° h.y. | 10/03/2014–15/03/2015 | 15/03/2014–13/03/2015 | 09/02/2014–13/03/2015 | 24/05/2014–02/05/2015 |
| (recharge season; discharge season) | (10/03/2014–21/04/2014; 22/04/2014–15/03/2015) | (15/03/2014–30/05/2014; 31/05/2014–13/03/2015) | (09/02/2014–23/05/2014; 24/05/2014–13/03/2015) | (24/05/2014–05/06/2014; 06/06/2014–02/05/2015) |
| 4° h.y. | 16/03/2015–26/02/2016 | 14/03/2015–20/03/2016 | 14/03/2015–17/02/2016 | 03/05/2015–09/04/2016 |
| (recharge season; discharge season) | (16/03/2015–08/05/2015; 09/05/2015–26/02/2016) | (14/03/2015 -17/06/2015; 18/06/2015–20/03/2016) | (14/03/2015–21/05/2015; 22/05/2015–17/02/2016) | (03/05/2015–11/07/2015; 12/07/2015–09/04/2016) |
| 5° h.y. | 27/02/2016–10/03/2017 | 21/03/2016–09/03/2017 | 18/02/2016–11/02/2017 | 10/04/2016–13/05/2017 |
| (recharge season; discharge season) | (27/02/2016–27/04/2016; 28/04/2016–10/03/2017) | (21/03/2016–06/06/2016; 07/06/2016–09/03/2017) | (18/02/2016 -10/06/2016; 11/06/2016–11/02/2017) | (10/04/2016–07/09/2016; 08/09/2016–13/05/2017) |
| 6° h.y. | 11/03/2017–05/04/2018 | 10/03/2017–24/03/2018 | 12/02/2017–17/02/2018 | 14/05/2017–12/04/2018 |
| (recharge season; discharge season) | (11/03/2017–20/04/2017; 21/04/2017–05/04/2018) | (10/03/2017–01/06/2017; 02/06/2017–24/03/2018) | (12/02/2017–12/06/2017; 13/06/2017–17/02/2018) | (14/05/2017–07/06/2017; 08/06/2017–12/04/2018) |
| 7° h.y. | 06/04/2018–02/04/2019 | 25/03/2018–31/03/2019 | 18/02/2018–31/03/2019 | 13/04/2018–06/06/2019 |
| (recharge season; discharge season) | (06/04/2018–02/05/2018; 03/05/2018–02/04/2019) | (25/03/2018–04/06/2018; 05/06/2018–31/03/2019) | (18/02/2018–11/05/2018; 12/05/2018–31/03/2019) | (13/04/2018–23/07/2018; 24/07/2018–06/06/2019) |
| p-Value | |||||
|---|---|---|---|---|---|
| Promise | 87.02 | 3.66 × 10−5 | 0.00 | 25.643 | 130.2 |
| Alpe Perrot | 33.13 | 6.39 × 10−5 | 0.00 | 87.107 | 176.91 |
| Promiod | −23.04 | −5.08 × 10−6 | 0.00 | −0.214 | −6.23 |
| Cheserod | 69.81 | 9.68 × 10−5 | 0.00 | 219.32 | 378.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gizzi, M.; Mondani, M.; Taddia, G.; Suozzi, E.; Lo Russo, S. Aosta Valley Mountain Springs: A Preliminary Analysis for Understanding Variations in Water Resource Availability under Climate Change. Water 2022, 14, 1004. https://doi.org/10.3390/w14071004
Gizzi M, Mondani M, Taddia G, Suozzi E, Lo Russo S. Aosta Valley Mountain Springs: A Preliminary Analysis for Understanding Variations in Water Resource Availability under Climate Change. Water. 2022; 14(7):1004. https://doi.org/10.3390/w14071004
Chicago/Turabian StyleGizzi, Martina, Michele Mondani, Glenda Taddia, Enrico Suozzi, and Stefano Lo Russo. 2022. "Aosta Valley Mountain Springs: A Preliminary Analysis for Understanding Variations in Water Resource Availability under Climate Change" Water 14, no. 7: 1004. https://doi.org/10.3390/w14071004
APA StyleGizzi, M., Mondani, M., Taddia, G., Suozzi, E., & Lo Russo, S. (2022). Aosta Valley Mountain Springs: A Preliminary Analysis for Understanding Variations in Water Resource Availability under Climate Change. Water, 14(7), 1004. https://doi.org/10.3390/w14071004









