Optimal Design of Water Treatment Contact Tanks
Abstract
:1. Introduction
2. Computational and Optimization Models
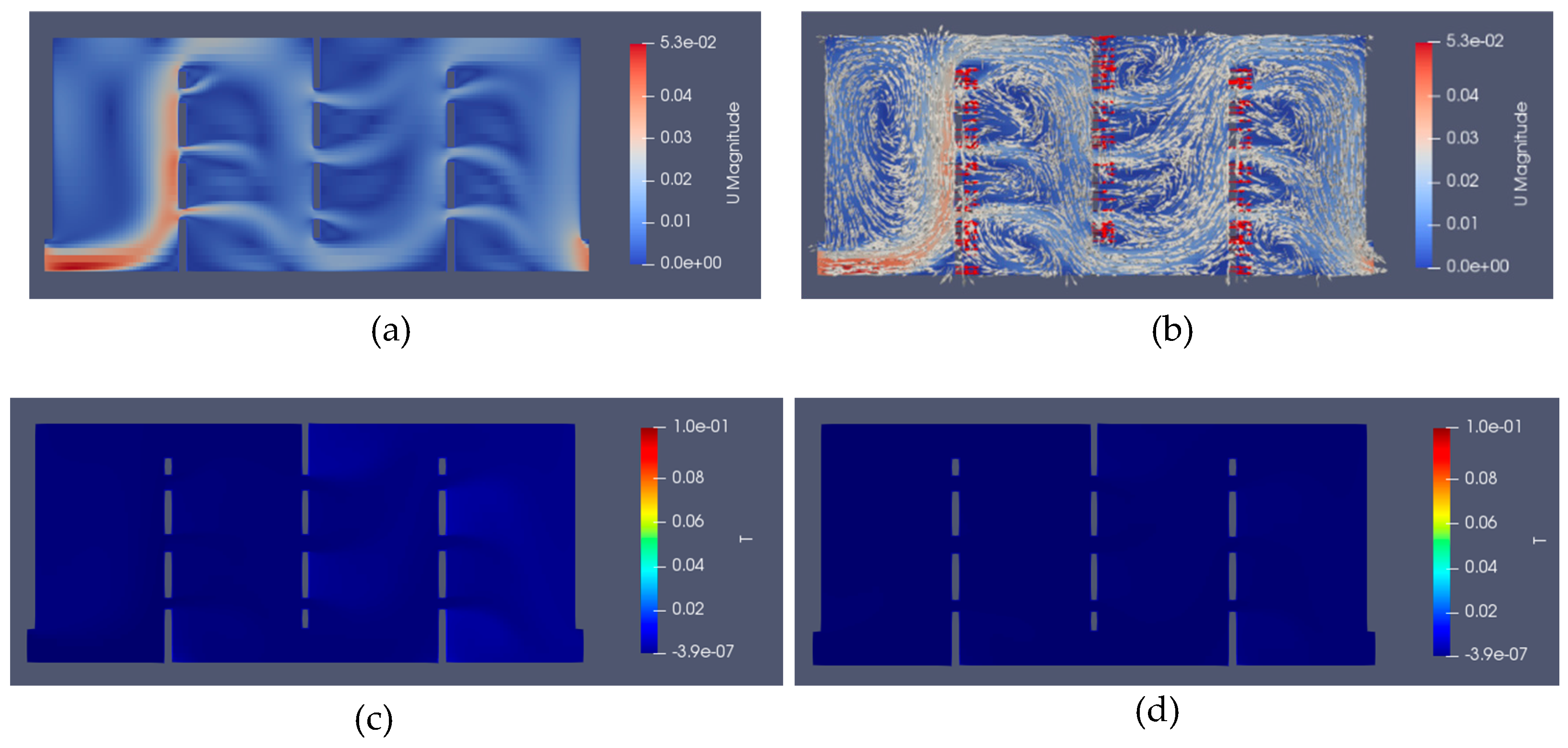
2.1. Flow Model
2.2. Conservative Tracer Model
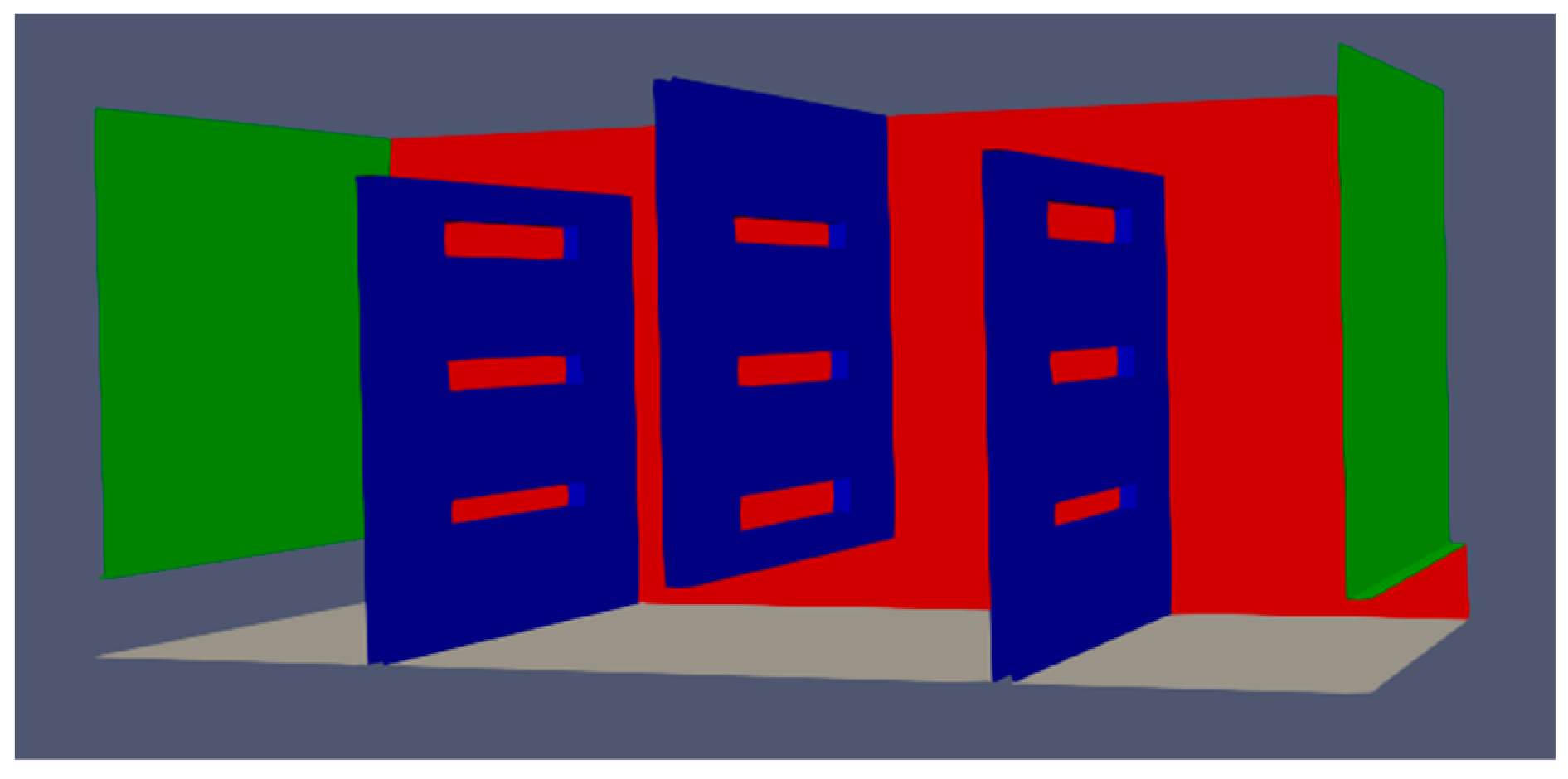
2.3. Computational Domain and Boundary Conditions
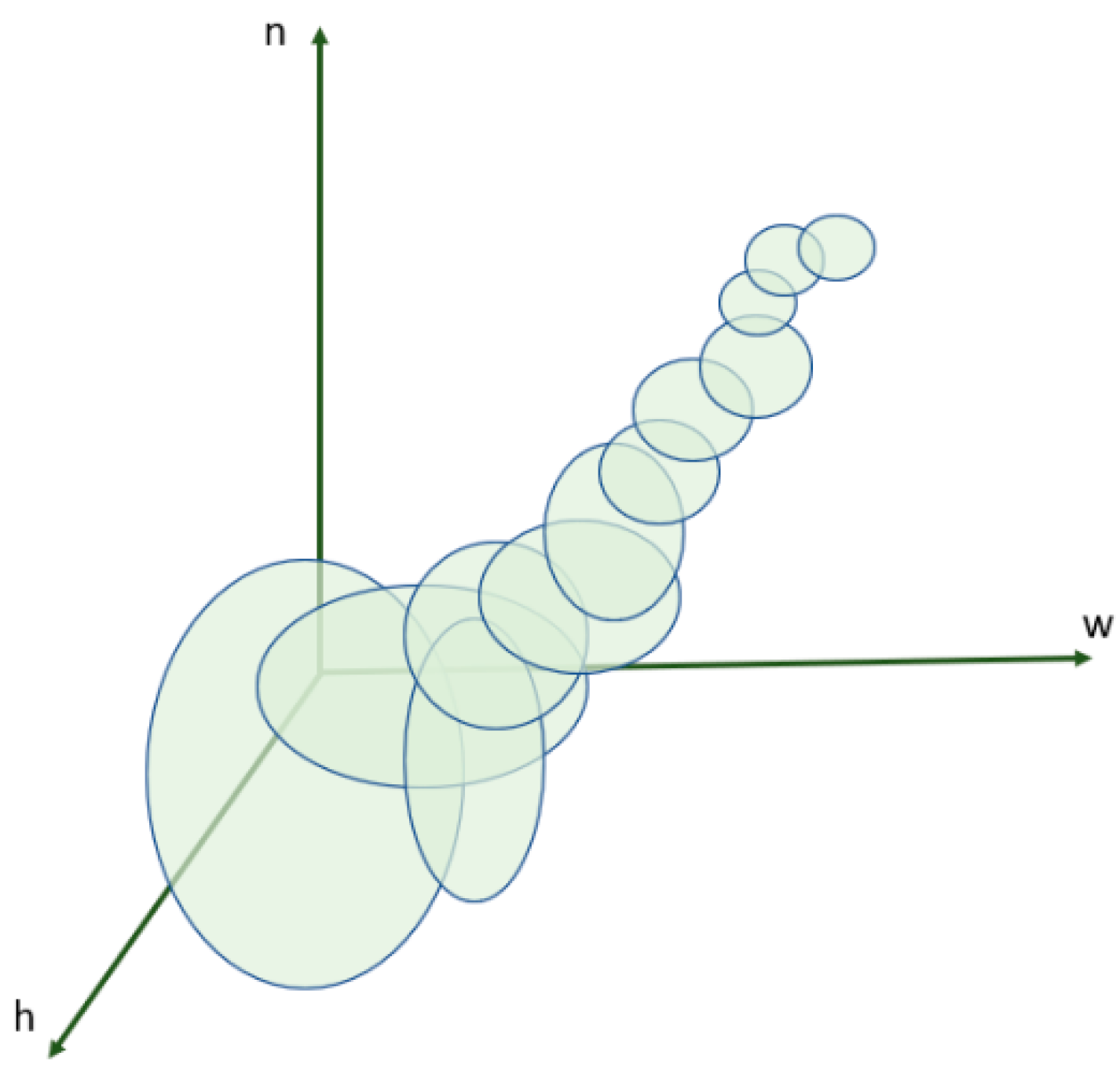
2.4. Optimization Model
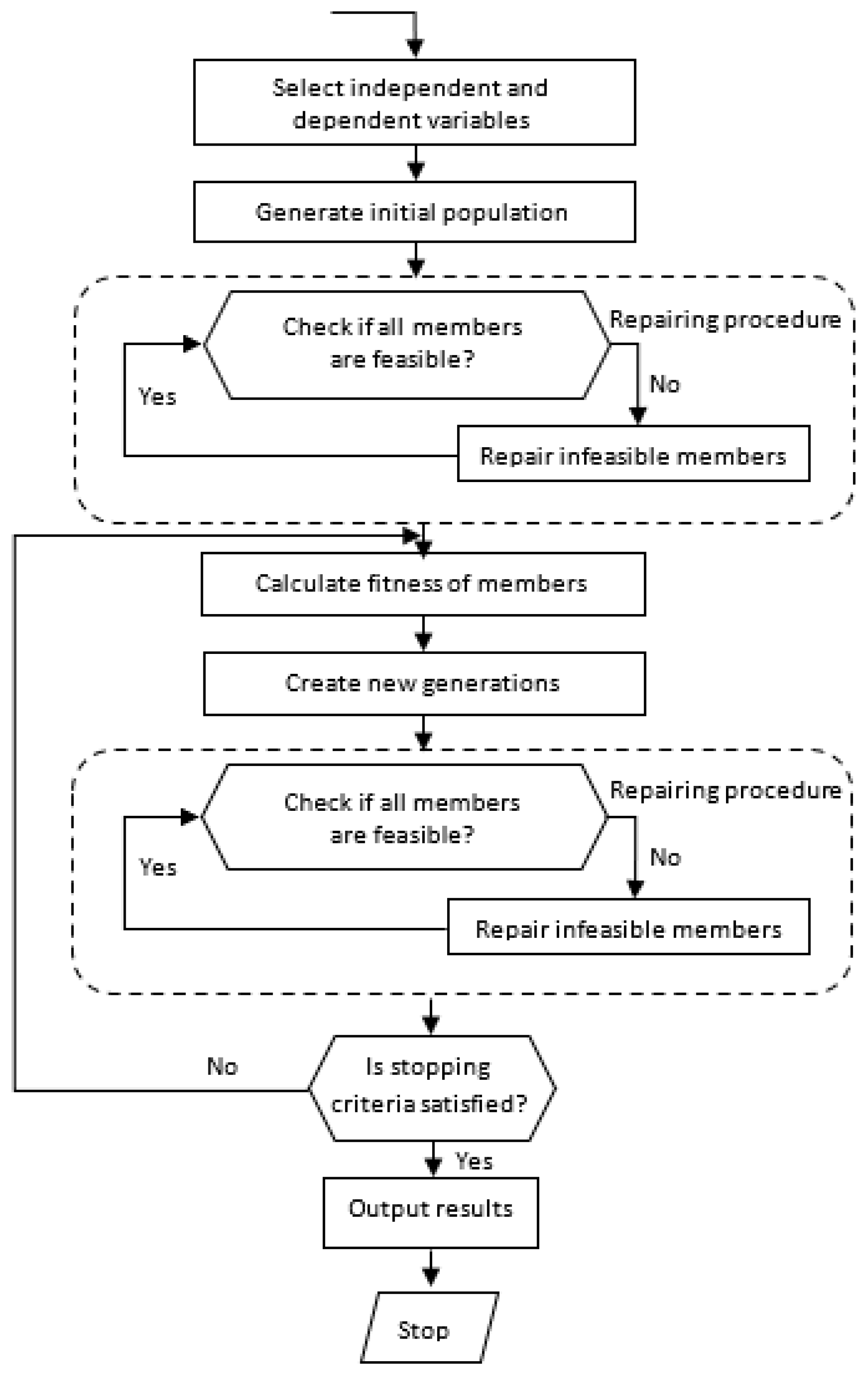
2.5. Simulation-Optimization Procedure
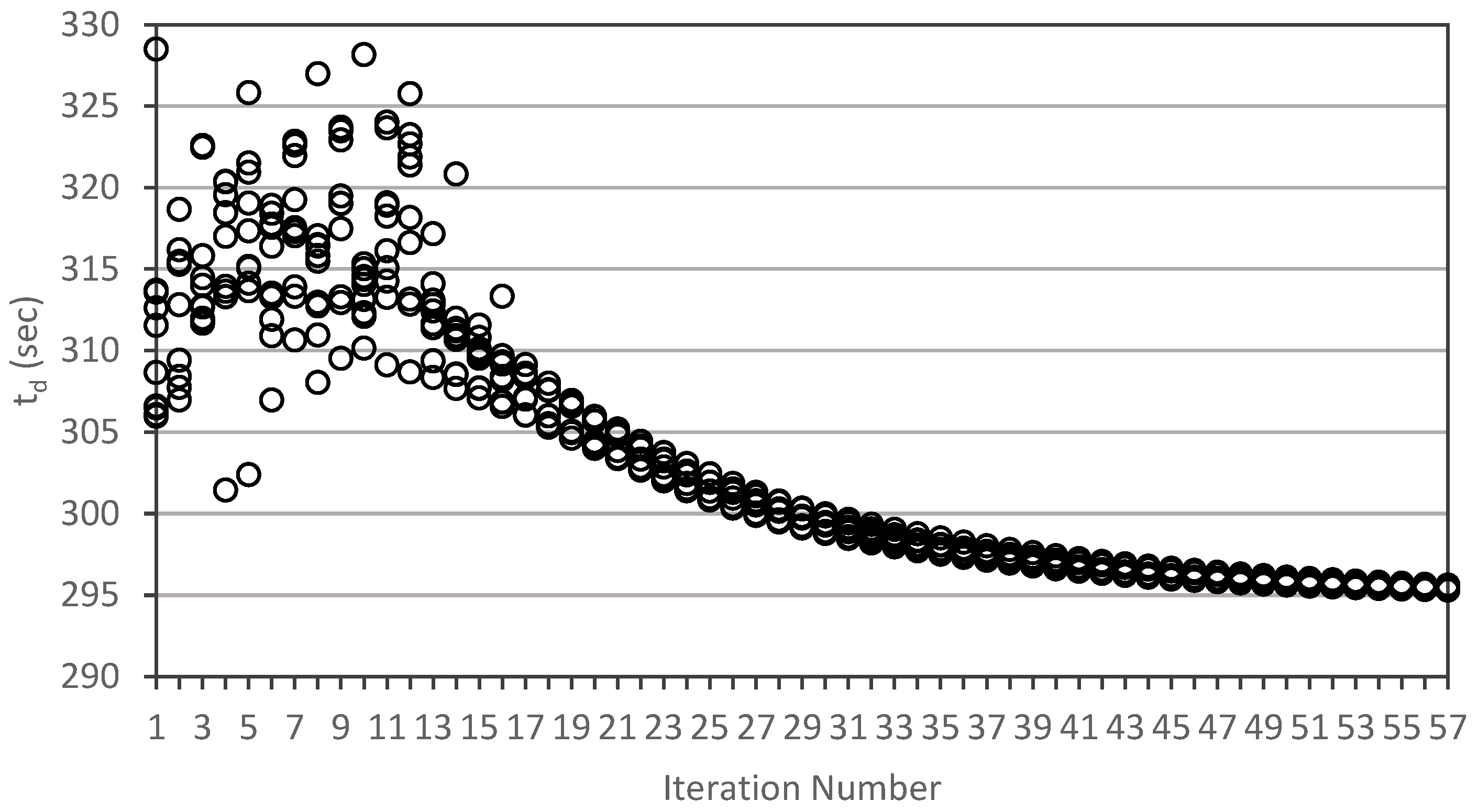
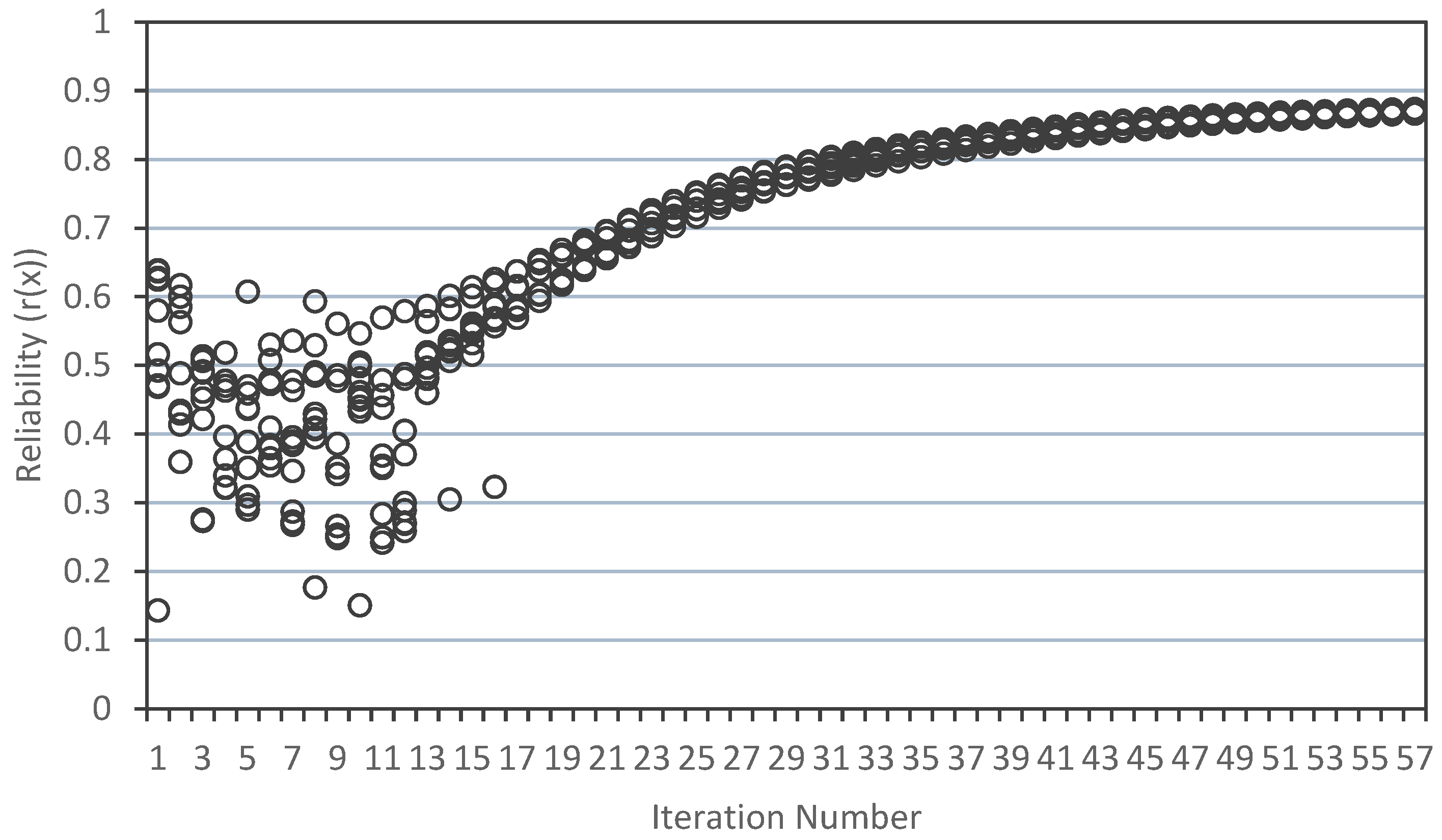
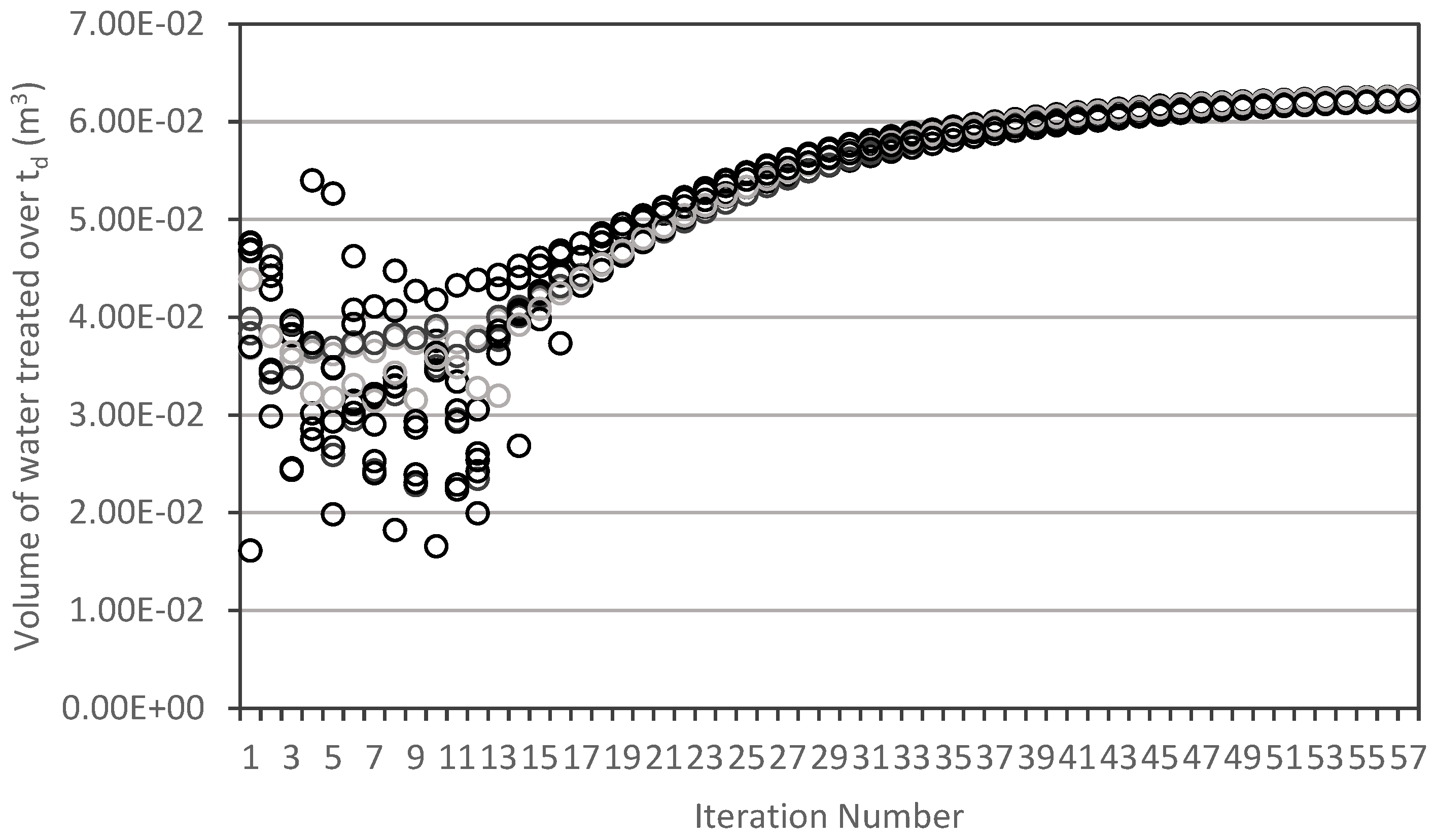
3. Results
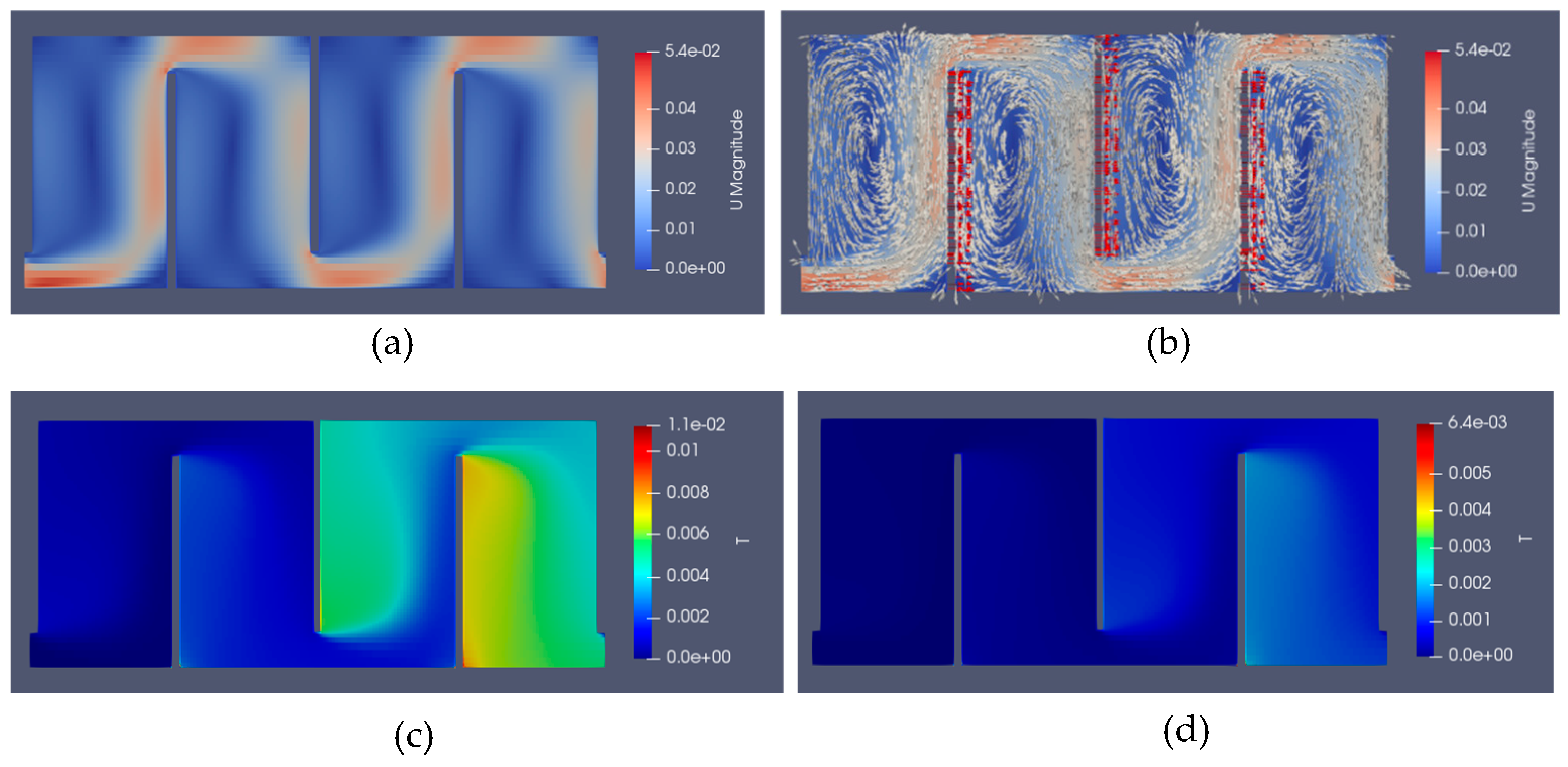
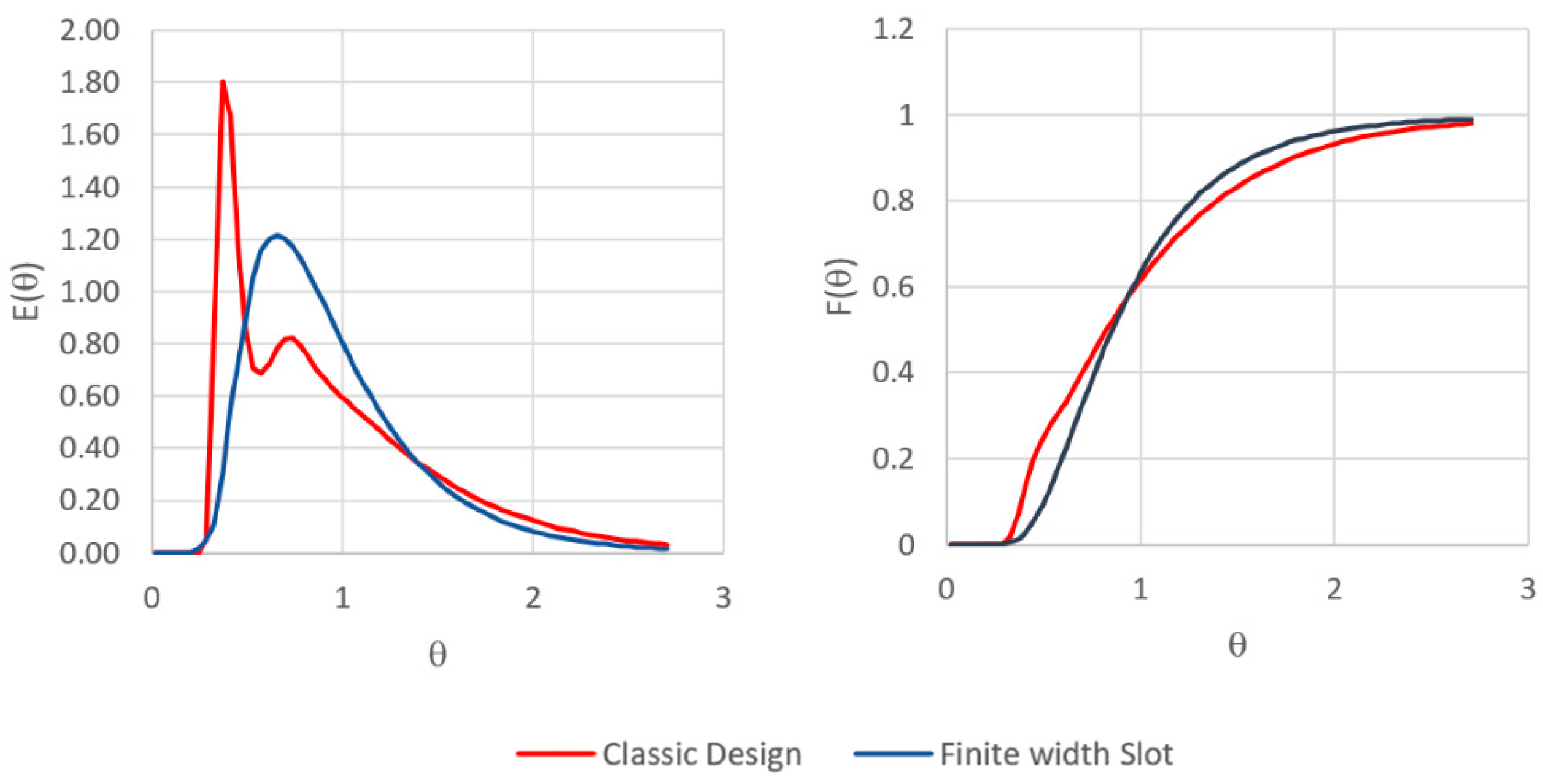
3.1. Baffle without Slots
3.2. Finite Width Slot Baffle Population
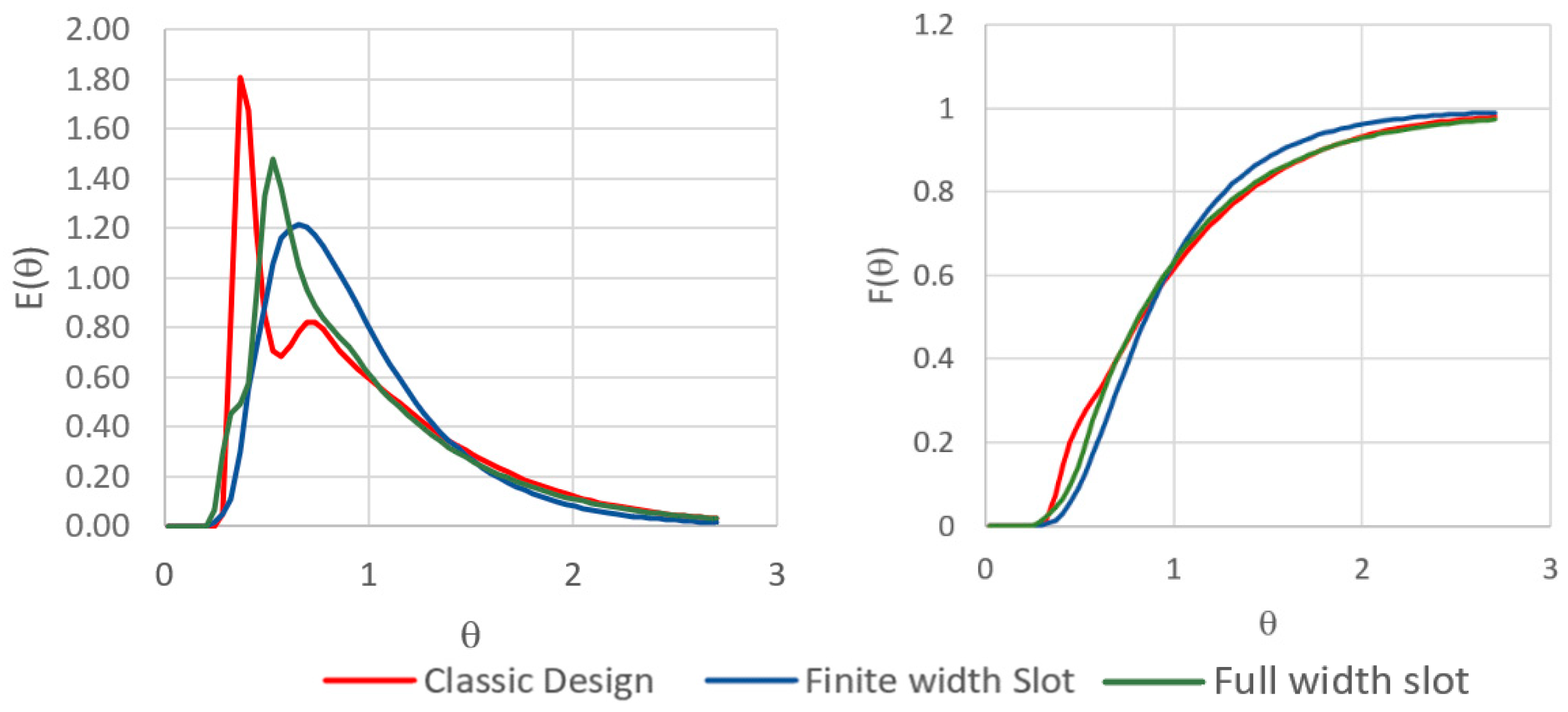
3.3. Full Width Slot Baffle Population
3.4. Optimal Baffle Geometry
4. Discussion
5. Conclusions
- The multidimensional design concept introduced is important in the overall design of the contact tanks since it provides a platform to include multiple design criteria that would contribute to the overall performance of contact tank design beyond a one-dimensional approach of baffle geometry design to improve mixing.
- The appropriate development of the optimization algorithm is important since a multitude of optimization solution strategies exist in the literature for the solution of multi-dimensional optimization problems, such as multi-objective approaches. The strategy recommended in this study, which is the use of a single objective function approach, performed well for the problem considered in this case without artificial controls on the final selection.
- Simulation-optimization techniques have been previously used in the literature. The recommended CFD analysis combined with PGA assisted genetic algorithm approach provided a preferable and efficient computational platform for the application considered in this case and may be adopted in future studies.
- The optimum contact tank design achieved that would satisfy the four design objectives in a smart manner, and using a single objective function, yielded a new contact tank baffle design that was not reported in the earlier literature. This indicates that the multidimensional analysis concept developed in this study is an important concept which may be adopted in future studies.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aral, M.M. Environmental Modeling and Health Risk Analysis; Springer Publishers: Berlin/Heidelberg, Germany, 2011; 487p, ISBN 978-90-481-8607-5. [Google Scholar]
- Langlais, B.; Reckhow, D.A.; Brink, D.R. (Eds.) Ozone in Water Treatment: Application and Engineering; Lewis: Chelsea, MI, USA, 1991. [Google Scholar]
- Zhang, J.; Martinez, A.E.T.; Zhang, Q. Hydraulic efficiency in RANS of the flow in multi-chambered contactors. J. Hydraul. Eng. 2013, 139, 1150–1157. [Google Scholar] [CrossRef]
- Angeloudis, A.; Stoesser, T.; Falconer, R.A. Predicting the disinfection efficiency range in chlorine contact tanks through a CFD-based approach. Water Res. 2014, 60, 118–129. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Elovitz, M.; Roberts, P.J.W.; Kim, J.H. Using 3D LIF to investigate and improve performance of a multi-chamber ozone contactor. J. Am. Water Works Assoc. 2010, 102, 61–70. [Google Scholar] [CrossRef]
- Rauen, W.B.; Lin, B.; Falconer, R.A.; Teixeira, E.C. CFD and experimental model studies for water disinfection tanks with low Reynolds number flows. Chem. Eng. J. 2008, 137, 550–560. [Google Scholar] [CrossRef]
- Taylor, Z.H.; Carlston, J.S.; Venayagamoorthy, S.K. Hydraulic design of baffles in disinfection contact tanks. J. Hydraul. Res. 2015, 53, 400–407. [Google Scholar] [CrossRef]
- Wang, H.; Falconer, R.A. Simulating disinfection processes in chlorine contact tanks using various turbulence models and high order accurate difference schemes. Water Res. 1998, 32, 1529–1543. [Google Scholar] [CrossRef]
- Zhang, J.; Martinez, A.E.T.; Zhang, Q. Reynolds-averaged Navier-Stokes simulation of the flow and tracer transport in a multichambered ozone contactor. J. Environ. Eng. 2013, 139, 450–454. [Google Scholar] [CrossRef]
- Zhang, J.; Martinez, A.E.T.; Zhang, Q.; Lei, H. Evaluating hydraulic and disinfection efficiencies of a full-scale ozone contactor using a RANS-based modeling framework. Water Res. 2014, 52, 155–167. [Google Scholar] [CrossRef]
- Teixeira, E.C.; Rauen, W.B. Hydrodynamic Design and Assessment of Water and Wastewater Treatment Units; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Boca Raton, FL, USA, 2020; 101p, ISBN 9781138495890. [Google Scholar]
- Demirel, E.; Aral, M.M. Unified Analysis of Multi-Chamber Contact Tanks and Mixing Efficiency Based on Vorticity Field. Part I: Hydrodynamic Analysis. Water 2016, 8, 495. [Google Scholar] [CrossRef] [Green Version]
- Demirel, E.; Aral, M.M. Unified Analysis of Multi-Chamber Contact Tanks and Mixing Efficiency Based on Vorticity Field. Part II: Transport Analysis. Water 2016, 8, 537. [Google Scholar] [CrossRef] [Green Version]
- Aral, M.M.; Demirel, E. Novel slot-baffle design to improve mixing efficiency and reduce cost of disinfection in drinking water treatment. ASCE J. Environ. Eng. 2017, 143, 06017006. [Google Scholar] [CrossRef]
- Demirel, E.; Aral, M.M. An Efficient Contact Tank Design for Potable Water Treatment. Tek. Dergi 2018, 29, 8279–8294. [Google Scholar] [CrossRef]
- Demirel, E.; Aral, M.M. Performance Assessment of Efficiency Indexes for Contact Tanks. ASCE J. Environ. Eng. 2018, 144, 04018076. [Google Scholar] [CrossRef]
- Kizilaslan, A.M.; Demirel, E.; Aral, M.M. Effect of Porous Baffles on the Energy Performance of Contact Tanks in Water Treatment. Water 2018, 10, 1084. [Google Scholar] [CrossRef] [Green Version]
- Demirel, E.; Aral, M.M. Liquid Sloshing Damping in an Accelerated Tank using a Novel Slot-Baffle Design. Water 2018, 10, 1565. [Google Scholar] [CrossRef] [Green Version]
- Kizilaslan, M.A.; Demirel, E.; Aral, M.M. Efficiency Enhancement of Chlorine Contact Tanks in Water Treatment Plants: A Full-Scale Application. Processes 2019, 7, 551. [Google Scholar] [CrossRef] [Green Version]
- Demirel, E.; Aral, M.M. A Design for Vortex Suppression Downstream of a Submerged Gate. Water 2020, 12, 750. [Google Scholar] [CrossRef] [Green Version]
- Nasyrlayev, N.; Kizilaslan, M.A.; Kurumus, A.T.; Demirel, E.; Aral, M.M. A Perforated Baffle Design to Improve Mixing in Contact Tanks. Water 2020, 12, 1022. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Pierre, K.C.; Tejada-Martinez, A.E. Impacts of flow and tracer release unsteadiness on tracer analysis of water and wastewater treatment facilities. J. Hydraul. Eng. 2019, 145, 04019004. [Google Scholar] [CrossRef]
- OpenFOAM9. The OpenFOAM Foundation; OpenCFD Ltd.: Bracknell, UK, 2015. [Google Scholar]
- Okuducu, M.B.; Aral, M.M. Performance Analysis and Numerical Evaluation of Mixing in 3-D T-Shape Passive Micromixers. Micromach. J. Spec. Issue Passiv. Micromixers 2018, 9, 210. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989; p. 412. [Google Scholar]
- Aral, M.M.; Guan, J.; Maslia, M.L. Optimal Design of Sensor Placement in Water Distribution Systems. ASCE J. Water Resour. Plan. Manag. 2010, 136, 5–18. [Google Scholar] [CrossRef]
- Guan, J.B.; Aral, M.M. Progressive genetic algorithm for solution of optimization problems with nonlinear equality and inequality constraints. Appl. Math. Model. 1999, 23, 329–343. [Google Scholar] [CrossRef] [Green Version]
- Park, C.H.; Aral, M.M. Multi-objective optimization of pumping rates and well placement in coastal aquifers. J. Hydrol. 2004, 290, 80–99. [Google Scholar] [CrossRef]
- Guan, J.; Aral, M.M.; Maslia, M.L.; Grayman, W.M. Identification of Contaminant Sources in Water-Distribution Systems Using Simulation-Optimization Method: A Case Study. ASCE J. Water Resour. Plan. Manag. 2006, 132, 252–262. [Google Scholar] [CrossRef]
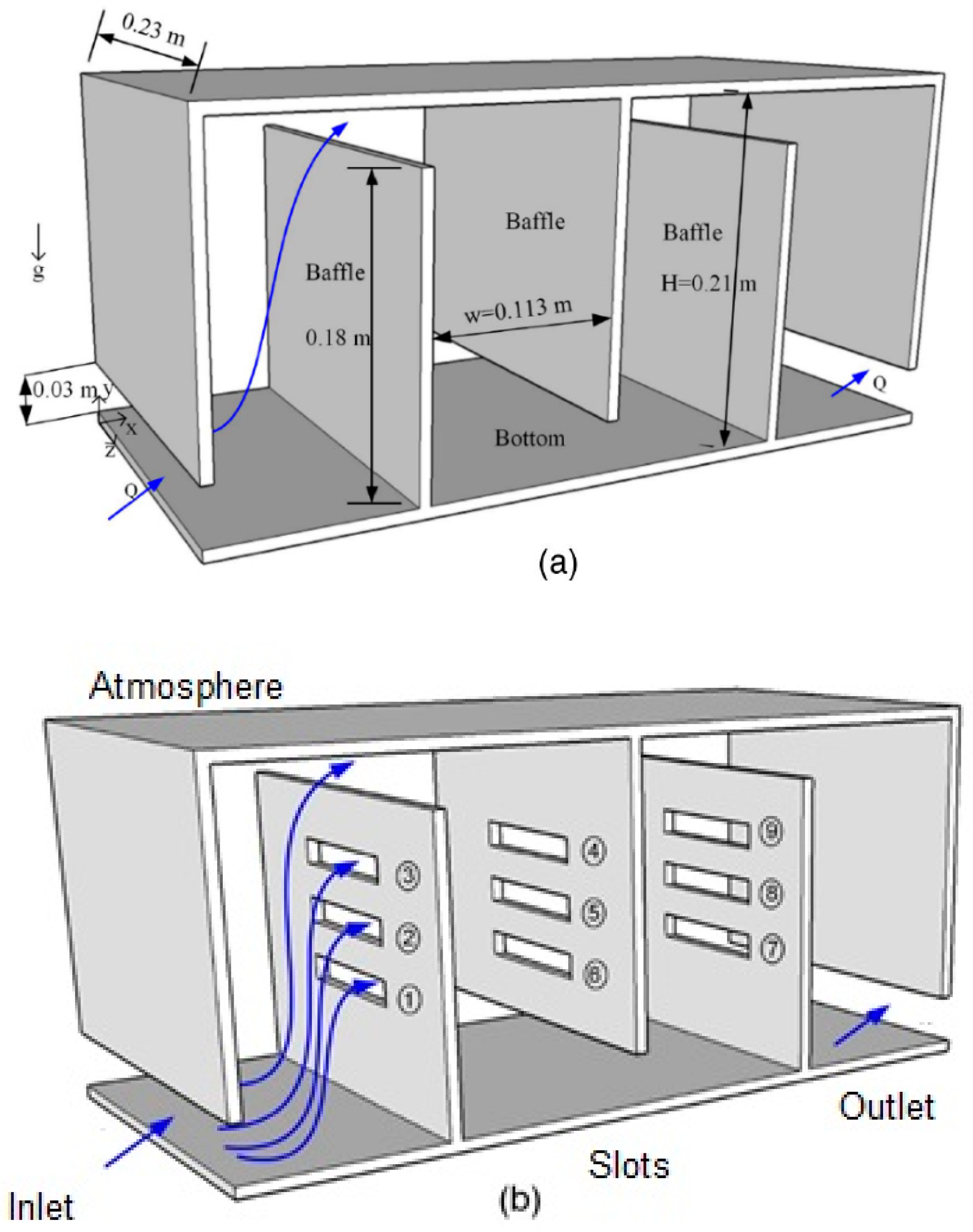






| Variables | Boundary Conditions Used | |||
|---|---|---|---|---|
| Inlet Region | Outlet Region | Atmosphere Boundary | Wall Regions | |
| U | mapped | inletOutlet | symmetryPlane | noSlip |
| p | mapped | inletOutlet | symmetryPlane | zeroGradient |
| k | mapped | inletOutlet | symmetryPlane | kqRWallFunction |
| ε | mapped | inletOutlet | symmetryPlane | epsilonWallFunction |
| nut | mapped | inletOutlet | symmetryPlane | nutkWallFunction |
| Parameters | Cases Considered | |||
|---|---|---|---|---|
| Baffle 1 | Baffle 2 | Baffle 3 | Options | |
| Number of Slots | 1, 2, 3, 4 | 1, 2, 3, 4 | 1, 2, 3, 4 | PGA Elim. 1, 2, 4 |
| Finite Slot (w-mm) | 100, 110, 120, 160 | 100, 110, 120, 160 | 100, 110, 120, 160 | Random |
| Finite Slot (h-mm) | 10, 12, 14, 16 | 10, 12, 14, 16 | 10, 12, 14, 16 | Random |
| Full Slot (h-mm) | 10, 12, 14, 16 | 10, 12, 14, 16 | 10, 12, 14, 16 | Random |
| Space between slots (mm) | 40, 42, 44, 46 | 40, 42, 44, 46 | 40, 42, 44, 46 | Random Sym. |
| Parameters | PGA Parameters |
|---|---|
| Value | |
| Population Size | 60 |
| Crossover Ratio | 0.8 |
| New Member Generation Ratio | 0.3 |
| Elitism Ratio | Best Member |
| Mutation Ratio | 0.2 |
| Maximum generation for each Subdomain | 40 |
| Slot Number | Optimal Slot Geometry |
|---|---|
| (w, h) (mm) | |
| Slot 1 | (230, 12) |
| Slot 2 | (230, 16) |
| Slot 3 | (230, 14) |
| Slot 4 | (230, 14) |
| Slot 5 | (230, 16) |
| Slot 6 | (230, 12) |
| Slot 7 | (230, 12) |
| Slot 8 | (230, 16) |
| Slot 9 | (230, 14) |
| Spacing between slots | (39, 38) |
| Distance from base to first slot | (45) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aral, M.M. Optimal Design of Water Treatment Contact Tanks. Water 2022, 14, 973. https://doi.org/10.3390/w14060973
Aral MM. Optimal Design of Water Treatment Contact Tanks. Water. 2022; 14(6):973. https://doi.org/10.3390/w14060973
Chicago/Turabian StyleAral, Mustafa M. 2022. "Optimal Design of Water Treatment Contact Tanks" Water 14, no. 6: 973. https://doi.org/10.3390/w14060973