A Sink Screening Approach for 1D Surface Network Simplification in Urban Flood Modelling
Abstract
:1. Introduction
- (i)
- The criteria reflecting the “small/big” conception concerning the sinks’ geometry may ignore the sinks’ primary subcatchment behaviour (“strong/poor”) of retaining runoffs in relation to flood inundations, and therefore may lead to the removal of strong runoff retention sinks, while saving poor ones, and vice versa;
- (ii)
- Due to the accumulated effect of the converging networks, negligible small volume losses from excluded sinks may upscale to substantial amounts, leading to massive overestimated flood volumes concentrated at a specific spot;
- (iii)
- The method tends to be case-dependent and thus challenged by identifying an optimal combination of these two criteria, i.e., a balanced result that achieves the maximal number of removed sinks and the minimal volume losses, simultaneously, across various landscapes;
- (iv)
- Treating the sink screening process homogeneously, the use of uniform criteria may overlook the spatial variability in case of large-scale areas (e.g., basins), where the intensified heterogeneity may affect the final screening results significantly.
2. Methodology
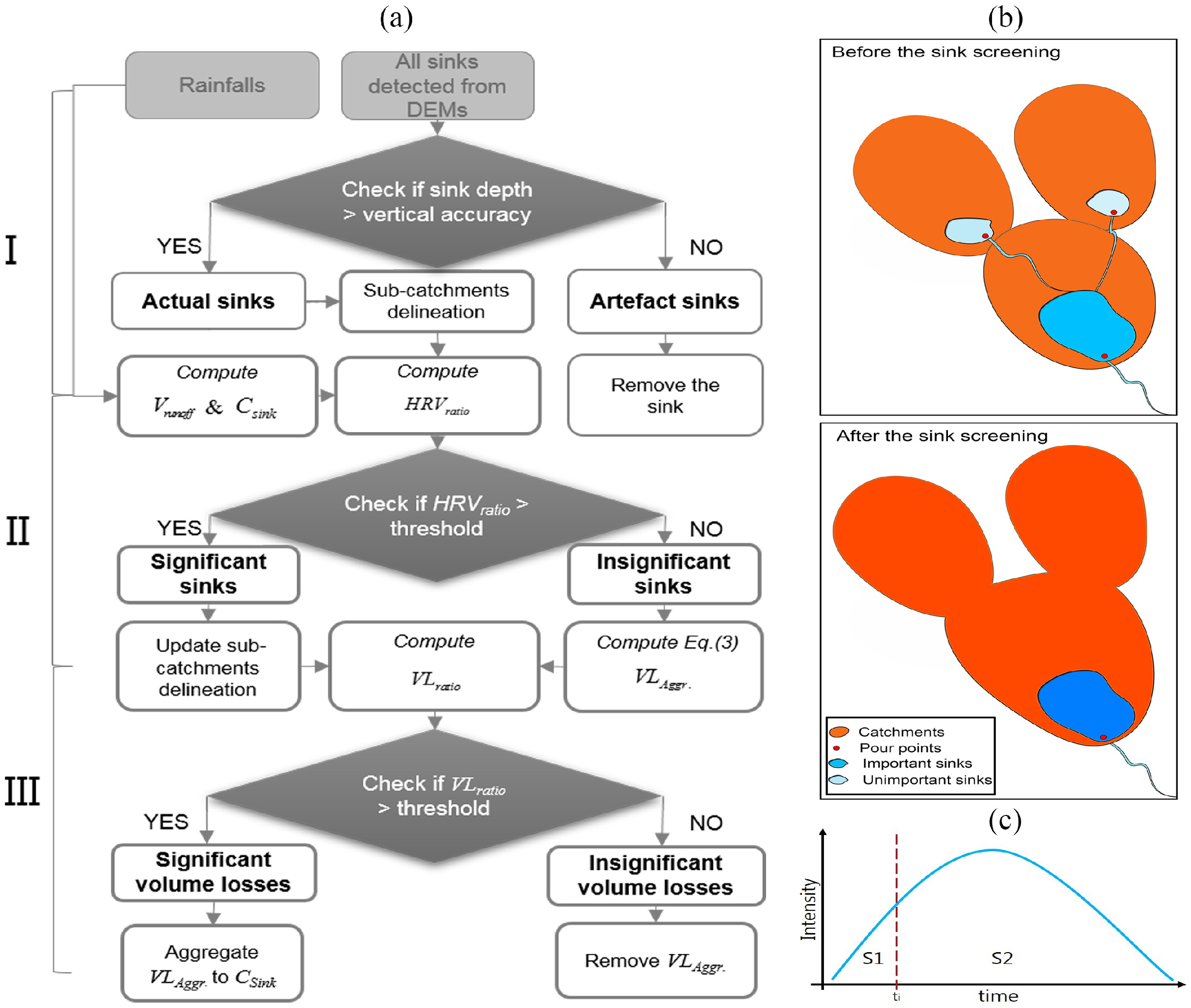
2.1. The Volume Ratio Sink Screening Method
2.2. Sink Screening Experiment Design
2.2.1. Sink Reduction Tests
- (i)
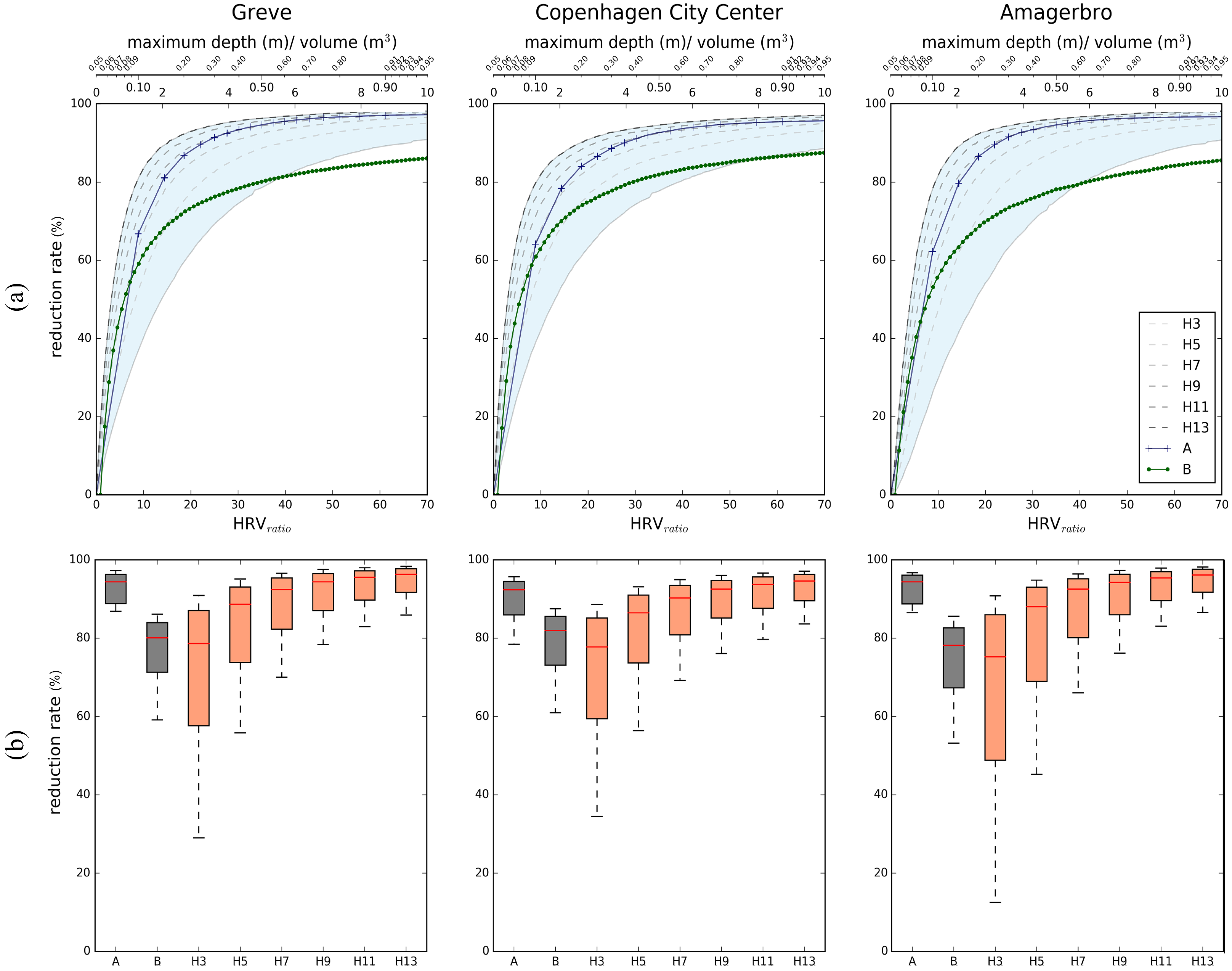
- The total number of sink reductions.To quantify the reduction effect of the two approaches in the total number of sinks, an iteration procedure was programmed to obtain the sensitivity analysis results (the detailed workflow is illustrated in Figure A1a, Appendix A). By adopting stepwise incremental threshold values, this procedure was executed using different criteria (i.e., maximum depth, volume and ) within their predefined iteration ranges. For the geometry-based approach, a concatenation of the maximum depth and volume based on the logic operator “AND” is used. In order to clarify their individual reduction effect, each criterion was investigated in an independent iteration. Next, their combined effect was analysed and discussed to address their mutual interference. The detailed parameter settings for the sensitivity analysis are elaborated in Appendix B. To compare the results derived from different criteria, the obtained results were interpreted and analysed by: (i) the curves for the sink reduction reflecting the total number of the reduced sinks in relation to the change of the threshold values, and (ii) boxplots illustrating the distribution of the results. Here, the reduction rate (reduction rate = reduced number of sinks/origin number of sinks × 100%) was taken as the indicator. Six accumulated rainfalls of 30 mm, 50 mm, 70 mm, 90 mm, 110 mm and 130 mm covering rainfall return periods of 10–100 years were used to explore the ’s responses to various rainfall variations.
- (ii)
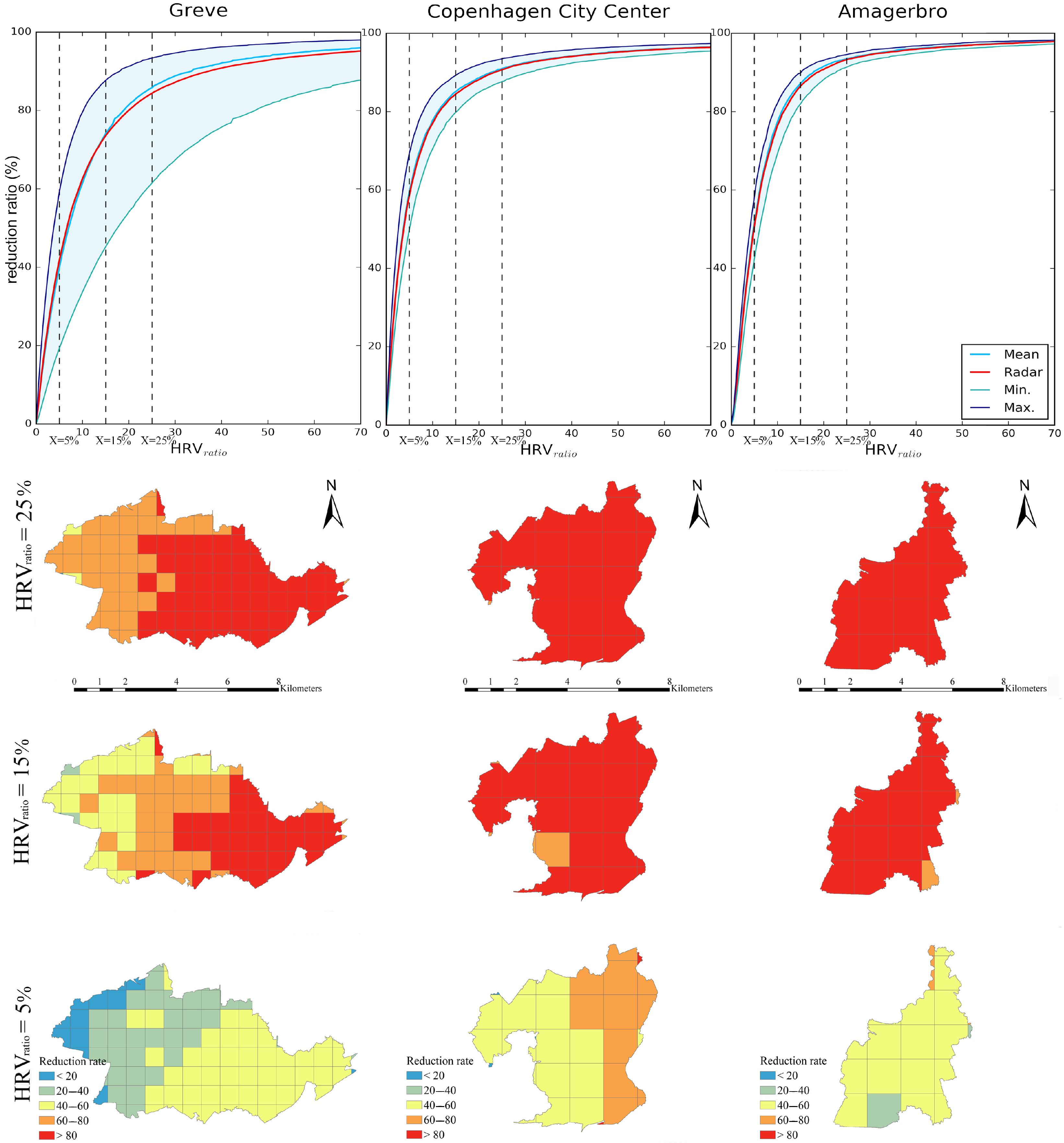
- Spatially varying reduction of sinks.The use of enables adaptive reductions over the variation of rainfalls. To invoke a spatially varying reduction based on rainfall heterogeneity, a rainfall recorded from a radar source (also referred to as “radar rainfall”) was used to compute each sink’s , and the matching -derived curves were produced from the same iteration procedures (Figure A1a, Appendix A). For comparison, other -derived curves, disregarding the rainfall heterogeneity, were generated by assuming statistic values (i.e., maximum, mean and minimum) of associated radar rainfall cells as accumulated rainfalls. In addition, threshold values of 5%, 15% and 25% were selected as representatives of , and the spatial variations of the removed sinks were summarized cell-wise (1000 m resolution) based on the radar rainfall grids of each of the three cases. Finally, the sink reduction rate was used as the indicator to maintain the comparison consistency for all three case areas.
2.2.2. Volume Loss Reduction Tests
- (i)
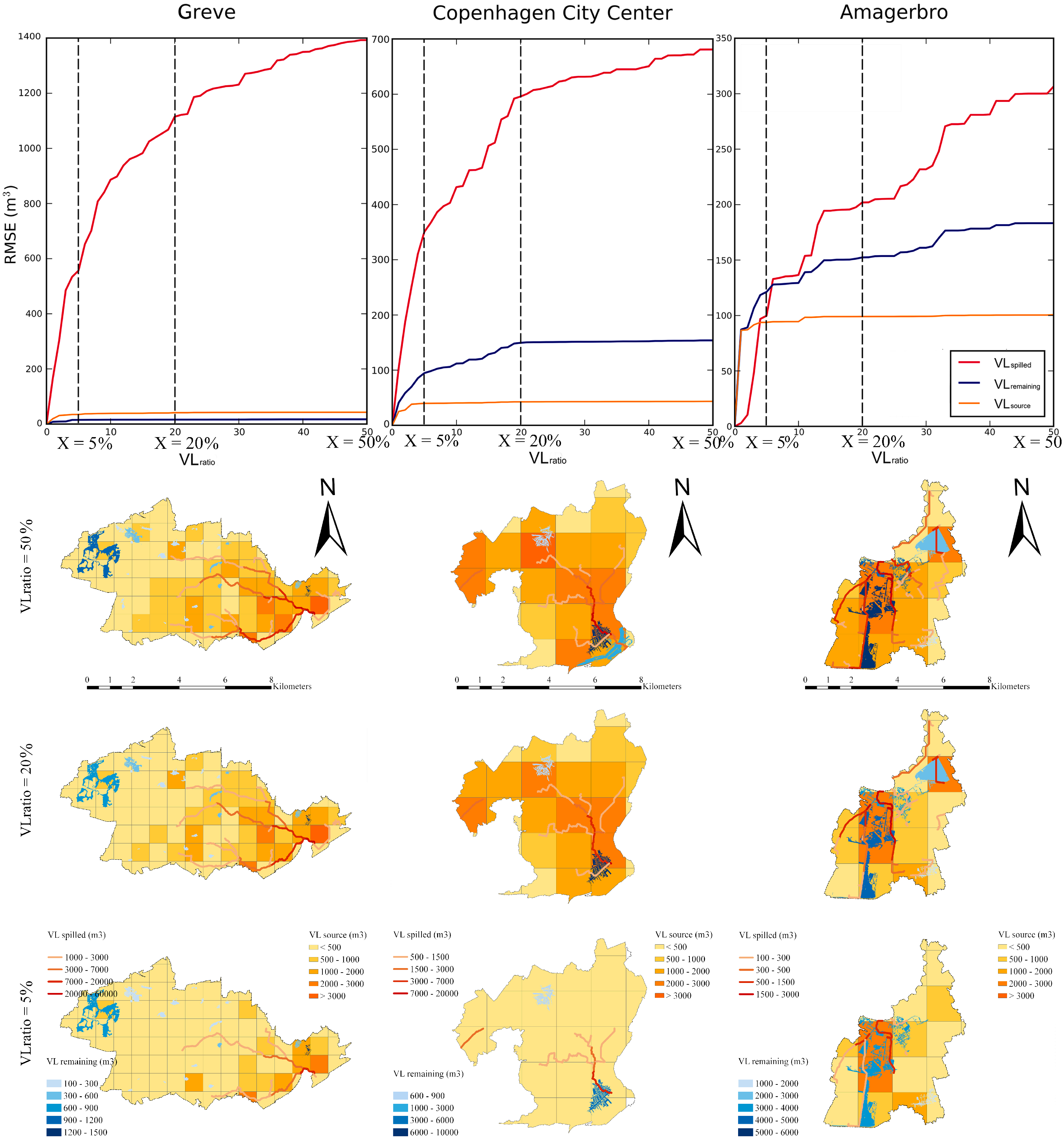
- Quantification of volume losses (the volume loss spreading solver).In order to evaluate the volume loss accumulations over the convergence of stream branches, a volume loss spreading solver was developed to quantify the volume discrepancies in the 1D surface network. As suggested by Figure A1c in Appendix A, the general workflow illustrates two successive computations: (i) flood volume computations (i.e., blue zones, Figure A3c) and (ii) volume loss computations (i.e., red zones, Figure A3c). In order to quantify the flood volumes for each sink (i.e., ), a link-based fast-inundation spreading algorithm, as reported by [26], was used to enable a filling-and-spilling routine that distributes flood volumes to all sinks rapidly from following the sequence of the Shreve stream order [73]. Furthermore, the removed sinks contain volumes for storing of water, so an exclusion hereof may result in identical volumetric overestimations at downstream via the spillover (Figure A3a). Therefore, we modelled the overestimated volumes as the oil liquids following a spilling-and-remaining routine. Detailed computational equations, processes and the computation example are provided in Appendix C.
- (ii)
- The reduction of volume losses.In order to quantify impacts of the volume losses, which in turn proves the sensitivity of , the redistributed volume losses were computed by using the volume loss spreading solver and an iterative procedure was programmed to conduct sensitivity analysis using different threshold values (see Figure A1b). Thus, the stepwise reductions in volume losses were investigated from the curves for the volume loss reduction, and were further discussed from the perspectives of (i) the source volume losses, (ii) the spilled volume losses and (iii) the remaining volume losses, where the is taken as the indicator, and n is the total number of streams (polylines) or sink polygons. The detailed parameter settings for the sensitivity analysis are elaborated in Appendix B. To retrieve the consistent source volume losses for each case, the screening results based on of 15% were used. The spatially varying reductions in volume losses were investigated from maps, and values of 50%, 20% and 5% were considered as representative threshold values. Once again, identical grid meshes (Section 2.2.1-(ii)) were used to sum up the for each cell, while networks (polylines) and sink polygons were applied to explore the redistributed volume losses in and .
3. Case Studies
4. Results
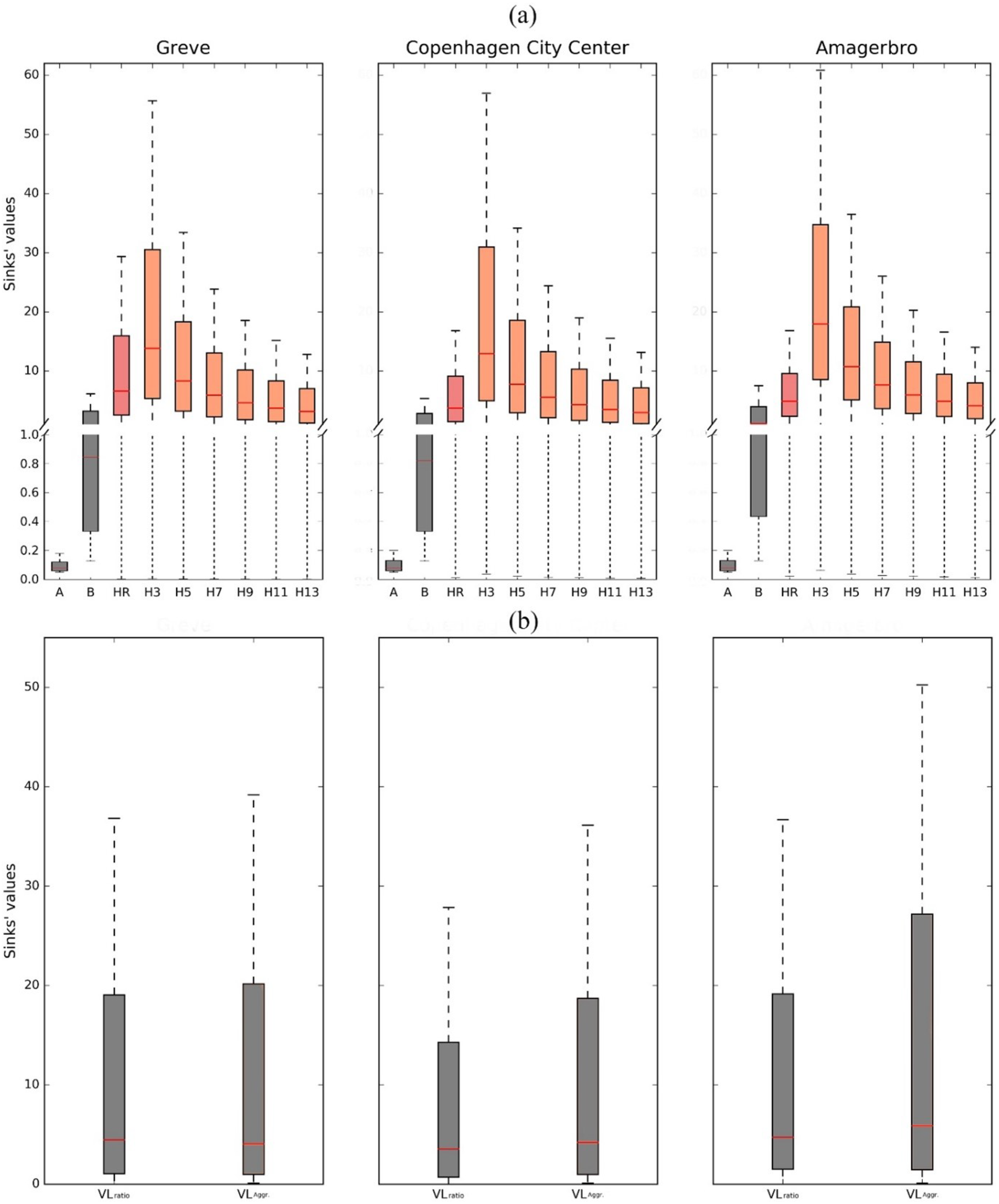
4.1. Total Number of Sink Reductions
4.2. Spatially Varying Sink Reductions
4.3. Distribution and Redistribution of Volume Losses
4.4. The Reduction of Volume Losses
5. Discussion
5.1. Sink Reductions
5.2. Volume Loss Reductions
5.3. Computational Efficiency and Accuracy in 1D Urban Surface Flood Modelling
6. Conclusions
- Considering accumulated rainfalls as the relative reference, performs an adaptive reduction in the total number of sinks, which indicates efficient reductions for extreme rainfalls. Based on the comparison of the three distinct cases, the sink screening performance of is stable, thus proving the general applicability and robustness of this proposed criterion. Furthermore, the inclusion of a radar rainfall for the computation of triggers spatially varying sink reductions. Based on the curve deviation deviations for the three cases, the significance of the rainfall heterogeneity affects the final sink screening result significantly. We therefore recommend the implementation of this method, especially for large-scale studies, in case that the significance of heterogeneity may intensify with the upscaled study area;
- In contrast, the geometry-based sink screening method is less adequate in sink reductions from four aspects: (i) the sink screening process based on the maximum depth is coarse, which reflects an oversensitive response in the total number of sink reductions (i.e., over 60% reduction rates and above 20 percentage points for stepwise changes of reduction rates); (ii) the screening process based on the volume indicates a ceiling effect, which results in incomplete screening results (i.e., covers 85% of sinks only); (iii) the combined reductions triggered by the concatenation of the two criteria are sensitive to distinct topographies, which may hinder its general applicability when dealing with various landscapes; (iv) in the context of urban inundation simulations, sinks’ catchment behaviours (runoff retention performance, strong/poor) are a more suitable criterion than the sinks’ geometries (big/small);
- The volume loss spreading solver reveals a great degree of accumulation and concentration in volume losses over the converging network. The reduction process based on illustrates efficient reductions in volume losses with respect to the RMSE, as well as the specific sinks. However, the redistributed volume losses depend significantly on the computed flows for the individual case; thus, the corresponding controlling process based on may vary from one case to another. Here, we recommend that the modeller consider the computed flows of focused sinks, as well as the tolerance level in relation to the specific modelling objective to determine an optimal . In contrast with the geometry-based sink screening method, the VRSS method shows a significant advantage by conducting sink reductions and the volume loss reduction separately from the two independent criteria.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
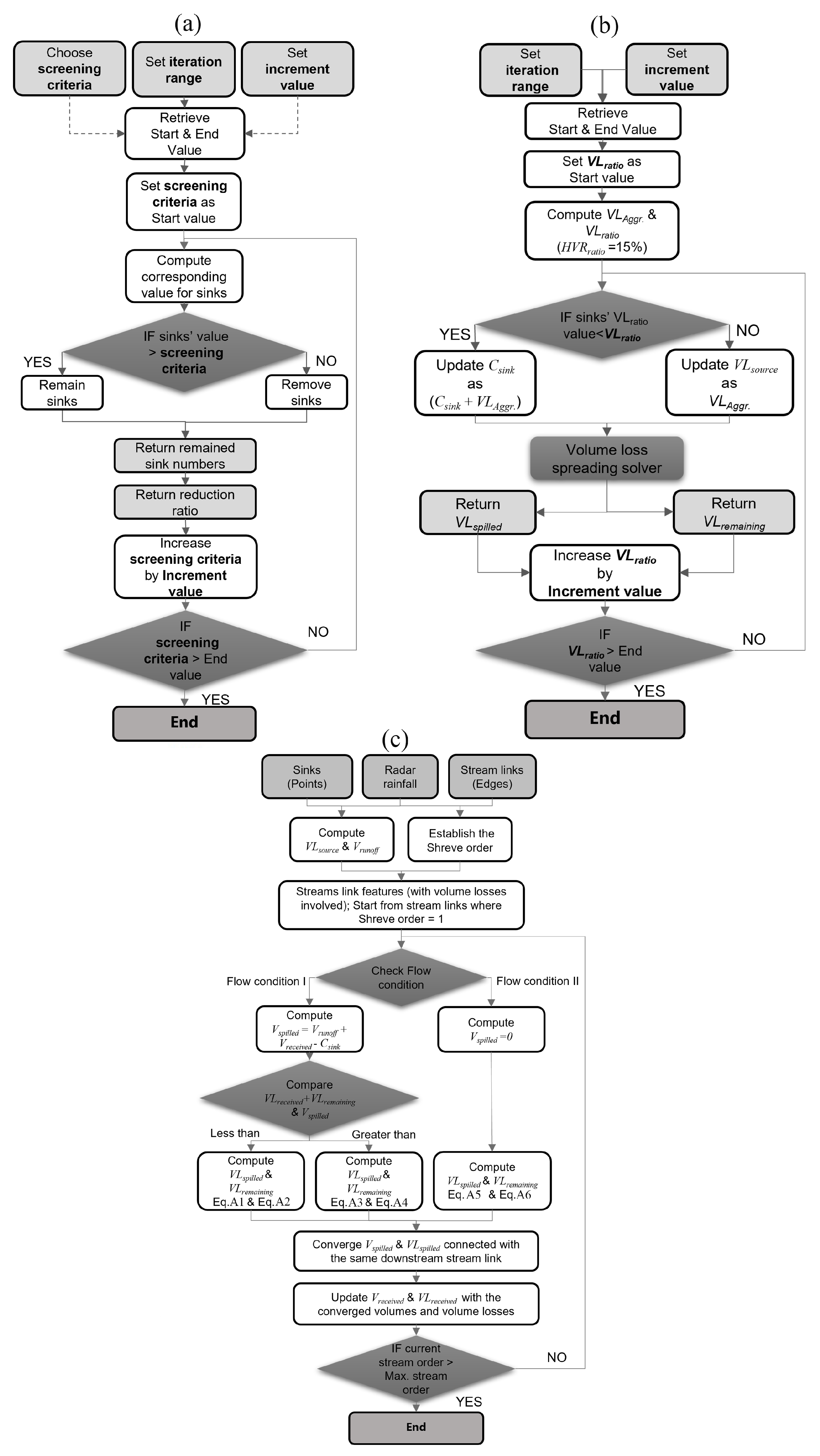
Appendix B
Appendix C

Appendix D
- Stream order I: S1, S2, S4, S5.
- For S1, m3, m3 and m3.
- (i)
- For flood volume computations (blue zones):m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, ;m3;m3.
- For S2, m3, and m3, m3.
- (i)
- For flood volume computations (blue zones):m3 m3;m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, m3;m3;m3.
- For S4, m3, m3 and m3.
- (i)
- For flood volume computations (blue zones):m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, ;m3;m3.
- For S5, m3, m3 and m3.
- (i)
- For flood volume computations (blue zones):m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, ;m3;m3.
- Stream order II: S3, S7.
- For S3, m3, and m3, m3.
- (i)
- For flood volume computations (blue zones):m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, ;m3;m3.
- For S7, m3, and m3, m3.
- (i)
- For flood volume computations (blue zones):m3 m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, m3;m3;m3.
- Stream order III: S6.
- For S6, m3, and m3, m3.
- (i)
- For flood volume computations (blue zones):m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, ;m3;m3.
- Stream order IV: S8.
- For S8, m3, and m3, m3.
- (i)
- For flood volume computations (blue zones):m3;
- (ii)
- For volume loss computations (red zones):m3 and m3;Here, ;m3;m3.
References
- Bernstein, L.; Bosch, P.; Canziani, O.; Chen, Z.; Christ, R.; Riahi, K. Climate Change 2007: Synthesis Report; IPCC: Geneva, Switzerland, 2008. [Google Scholar]
- Yu, D.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling–a state of the art. J. Hyrdoinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Parkinson, J.; Mark, O. Urban Stormwater Management in Developing Countries; IWA Publishing: London, UK, 2005. [Google Scholar]
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and modeling of flooding in urban drainage systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Chang, T.J.; Wang, C.H.; Chen, A.S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas. J. Hydrol. 2015, 524, 662–679. [Google Scholar] [CrossRef] [Green Version]
- Courty, L.G.; Rico-Ramirez, M.Á.; Pedrozo-Acuña, A. The Significance of the Spatial Variability of Rainfall on the Numerical Simulation of Urban Floods. Water 2018, 10, 207. [Google Scholar] [CrossRef] [Green Version]
- Courty, L.G.; Pedrozo-Acuna, A.; Bates, P.D. Itzi (version 17.1): An open-source, distributed GIS model for dynamic flood simulation. Geosci. Model Dev. 2017, 10, 1835–1847. [Google Scholar] [CrossRef] [Green Version]
- Guo, K.; Guan, M.; Yu, D. Urban surface water flood modelling–a comprehensive review of current models and future challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 1: Mesh resolution effects. Hydrol. Process. Int. J. 2006, 20, 1541–1565. [Google Scholar] [CrossRef]
- Fewtrell, T.; Bates, P.D.; Horritt, M.; Hunter, N. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Process. Int. J. 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Ramsauer, S.; Leandro, J.; Lin, Q. Inclusion of Narrow Flow Paths between Buildings in Coarser Grids for Urban Flood Modeling: Virtual Surface Links. Water 2021, 13, 2629. [Google Scholar] [CrossRef]
- Chen, A.S.; Evans, B.; Djordjević, S.; Savić, D.A. A coarse-grid approach to representing building blockage effects in 2D urban flood modelling. J. Hydrol. 2012, 426, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 2: Development of a sub-grid-scale treatment. Hydrol. Process. Int. J. 2006, 20, 1567–1583. [Google Scholar] [CrossRef]
- Chen, A.S.; Evans, B.; Djordjević, S.; Savić, D.A. Multi-layered coarse grid modelling in 2D urban flood simulations. J. Hydrol. 2012, 470, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.; Lane, S.N. Interactions between subgrid-scale resolution, feature representation and grid-scale resolution in flood inundation modelling. Hydrol. Process. 2011, 25, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Henonin, J.; Hongtao, M.; Zheng-Yu, Y.; Hartnack, J.; Havnø, K.; Gourbesville, P.; Mark, O. Citywide multi-grid urban flood modelling: The July 2012 flood in Beijing. Urban Water J. 2015, 12, 52–66. [Google Scholar] [CrossRef]
- Bruwier, M.; Archambeau, P.; Erpicum, S.; Pirotton, M.; Dewals, B. Shallow-water models with anisotropic porosity and merging for flood modelling on Cartesian grids. J. Hydrol. 2017, 554, 693–709. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E.; Gallegos, H.A. Integral formulation of shallow-water equations with anisotropic porosity for urban flood modeling. J. Hydrol. 2008, 362, 19–38. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. Formulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinform. 2013, 15, 676–686. [Google Scholar] [CrossRef] [Green Version]
- Guidolin, M.; Chen, A.S.; Ghimire, B.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Model. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef] [Green Version]
- Gibson, M.J.; Savic, D.A.; Djordjevic, S.; Chen, A.S.; Fraser, S.; Watson, T. Accuracy and computational efficiency of 2D urban surface flood modelling based on cellular automata. Procedia Eng. 2016, 154, 801–810. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Balstrøm, T.; Mark, O.; Jensen, M.B. Multi-Scale Target-Specified Sub-Model Approach for Fast Large-Scale High-Resolution 2D Urban Flood Modelling. Water 2021, 13, 259. [Google Scholar] [CrossRef]
- Yu, D. Parallelization of a two-dimensional flood inundation model based on domain decomposition. Environ. Model. Softw. 2010, 25, 935–945. [Google Scholar] [CrossRef] [Green Version]
- Neal, J.C.; Fewtrell, T.J.; Bates, P.D.; Wright, N.G. A comparison of three parallelisation methods for 2D flood inundation models. Environ. Model. Softw. 2010, 25, 398–411. [Google Scholar] [CrossRef]
- Neal, J.; Fewtrell, T.; Trigg, M. Parallelisation of storage cell flood models using OpenMP. Environ. Model. Softw. 2009, 24, 872–877. [Google Scholar] [CrossRef]
- Lamb, R.; Crossley, M.; Waller, S. A fast two-dimensional floodplain inundation model. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2009; Volume 162, pp. 363–370. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Shankar, S.; Pardyjak, E.R.; Judi, D.R.; Burian, S.J. Assessment of GPU computational enhancement to a 2D flood model. Environ. Model. Softw. 2011, 26, 1009–1016. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Sharif, M.B.; Kalyanapu, A.; Ghafoor, S.K.; Dullo, T.T.; Gangrade, S.; Kao, S.C.; Norman, M.R.; Evans, K.J. TRITON: A Multi-GPU open source 2D hydrodynamic flood model. Environ. Model. Softw. 2021, 141, 105034. [Google Scholar] [CrossRef]
- Glenis, V.; McGough, A.S.; Kutija, V.; Kilsby, C.; Woodman, S. Flood modelling for cities using Cloud computing. J. Cloud Comput. Adv. Syst. Appl. 2013, 2, 7. [Google Scholar] [CrossRef] [Green Version]
- Balstrøm, T.; Crawford, D. Arc-Malstrøm: A 1D hydrologic screening method for stormwater assessments based on geometric networks. Comput. Geosci. 2018, 116, 64–73. [Google Scholar] [CrossRef]
- Jamali, B.; Bach, P.M.; Cunningham, L.; Deletic, A. A Cellular Automata fast flood evaluation (CA-ffé) model. Water Resour. Res. 2019, 55, 4936–4953. [Google Scholar] [CrossRef] [Green Version]
- Samela, C.; Persiano, S.; Bagli, S.; Luzzi, V.; Mazzoli, P.; Humer, G.; Reithofer, A.; Essenfelder, A.; Amadio, M.; Mysiak, J.; et al. Safer_RAIN: A DEM-based hierarchical filling-&-Spilling algorithm for pluvial flood hazard assessment and mapping across large urban areas. Water 2020, 12, 1514. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Zhao, B. Calculation and visualization of flood inundation based on a topographic triangle network. J. Hydrol. 2014, 509, 406–415. [Google Scholar] [CrossRef]
- Jamali, B.; Löwe, R.; Bach, P.M.; Urich, C.; Arnbjerg-Nielsen, K.; Deletic, A. A rapid urban flood inundation and damage assessment model. J. Hydrol. 2018, 564, 1085–1098. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Lin, Q.; Leandro, J.; Wu, W.; Bhola, P.; Disse, M. Prediction of maximum flood inundation extents with resilient backpropagation neural network: Case study of Kulmbach. Front. Earth Sci. 2020, 8, 332. [Google Scholar] [CrossRef]
- Bermúdez, M.; Ntegeka, V.; Wolfs, V.; Willems, P. Development and comparison of two fast surrogate models for urban pluvial flood simulations. Water Resour. Manag. 2018, 32, 2801–2815. [Google Scholar] [CrossRef]
- Guo, Z.; Leitao, J.P.; Simões, N.E.; Moosavi, V. Data-driven flood emulation: Speeding up urban flood predictions by deep convolutional neural networks. J. Flood Risk Manag. 2021, 14, e12684. [Google Scholar] [CrossRef]
- Hofmann, J.; Schüttrumpf, H. floodGAN: Using Deep Adversarial Learning to Predict Pluvial Flooding in Real Time. Water 2021, 13, 2255. [Google Scholar] [CrossRef]
- Liu, Y.; Pender, G. A flood inundation modelling using v-support vector machine regression model. Eng. Appl. Artif. Intell. 2015, 46, 223–231. [Google Scholar] [CrossRef]
- Bermúdez, M.; Cea, L.; Puertas, J. A rapid flood inundation model for hazard mapping based on least squares support vector machine regression. J. Flood Risk Manag. 2019, 12, e12522. [Google Scholar] [CrossRef] [Green Version]
- Jhong, B.C.; Wang, J.H.; Lin, G.F. An integrated two-stage support vector machine approach to forecast inundation maps during typhoons. J. Hydrol. 2017, 547, 236–252. [Google Scholar] [CrossRef]
- Chang, L.C.; Amin, M.Z.M.; Yang, S.N.; Chang, F.J. Building ANN-Based Regional Multi-Step-Ahead Flood Inundation Forecast Models. Water 2018, 10, 1283. [Google Scholar] [CrossRef] [Green Version]
- Chang, L.C.; Shen, H.Y.; Wang, Y.F.; Huang, J.Y.; Lin, Y.T. Clustering-based hybrid inundation model for forecasting flood inundation depths. J. Hydrol. 2010, 385, 257–268. [Google Scholar] [CrossRef]
- Pan, T.Y.; Lai, J.S.; Chang, T.J.; Chang, H.K.; Chang, K.C.; Tan, Y.C. Hybrid neural networks in rainfall-inundation forecasting based on a synthetic potential inundation database. Nat. Hazards Earth Syst. Sci. 2011, 11, 771–787. [Google Scholar] [CrossRef]
- Jamali, B.; Haghighat, E.; Ignjatovic, A.; Leitão, J.P.; Deletic, A. Machine learning for accelerating 2D flood models: Potential and challenges. Hydrol. Process. 2021, 35, e14064. [Google Scholar] [CrossRef]
- Shen, H.Y.; Chang, L.C. Online multistep-ahead inundation depth forecasts by recurrent NARX networks. Hydrol. Earth Syst. Sci. 2013, 17, 935–945. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.J.; Chen, P.A.; Lu, Y.R.; Huang, E.; Chang, K.Y. Real-time multi-step-ahead water level forecasting by recurrent neural networks for urban flood control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of terrestrial laser scanning data to drive decimetric resolution urban inundation models. Adv. Water Resour. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Mark, O. Deterministic Modelling of Urban Stormwater and Sewer Systems; Aalborg Universitetsforlag: Aalborg, Denmark, 2019. [Google Scholar]
- Zhao, G. A Sub-Model Approach for Fast Large-Scale High-Resolution Two-Dimensional Urban Surface Flood Modelling. Ph.D. Thesis, Department of Geosciences and Natural Resource Management, University of Copenhagen, Copenhagen, Denmark, 2020. [Google Scholar]
- Thorndahl, S.; Beven, K.; Jensen, J.; Schaarup-Jensen, K. Event based uncertainty assessment in urban drainage modelling, applying the GLUE methodology. J. Hydrol. 2008, 357, 421–437. [Google Scholar] [CrossRef] [Green Version]
- Allitt, R.; Blanksby, J.; Djordjević, S.; Maksimović, Č.; Stewart, D. Investigations into 1D-1D and 1D-2D Urban Flood Modelling. In Proceedings of the WaPUG Autumn Conference 2009, Blackpool, UK, 11–13 November 2009. [Google Scholar]
- Pina, R.D.; Ochoa-Rodriguez, S.; Simões, N.E.; Mijic, A.; Marques, A.S.; Maksimović, Č. Semi- vs. fully-distributed urban stormwater models: Model set up and comparison with two real case studies. Water 2016, 8, 58. [Google Scholar] [CrossRef] [Green Version]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Leitao, J.P.; Simões, N.; Maksimović, Č.; Ferreira, F.; Prodanović, D.; Matos, J.; Sá Marques, A. Real-time forecasting urban drainage models: Full or simplified networks? Water Sci. Technol. 2010, 62, 2106–2114. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Djordjević, S.; Savić, D.A. Comparison of 1D/1D and 1D/2D coupled (sewer/surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Maksimović, Č.; Prodanović, D.; Boonya-Aroonnet, S.; Leitao, J.P.; Djordjević, S.; Allitt, R. Overland flow and pathway analysis for modelling of urban pluvial flooding. J. Hydraul. Res. 2009, 47, 512–523. [Google Scholar] [CrossRef]
- McCormack, J.; Gahegan, M.; Roberts, S.A.; Hogg, J.; Hoyle, B. Feature-based derivation of drainage networks. Int. J. Geogr. Inf. Syst. 1993, 7, 263–279. [Google Scholar] [CrossRef]
- Hankin, B.; Waller, S.; Astle, G.; Kellagher, R. Mapping space for water: Screening for urban flash flooding. J. Flood Risk Manag. 2008, 1, 13–22. [Google Scholar] [CrossRef]
- Jenson, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, B. An urban storm-inundation simulation method based on GIS. J. Hydrol. 2014, 517, 260–268. [Google Scholar] [CrossRef]
- Leitão, J.P.; Boonya-Aroonnet, S.; Prodanović, D.; Maksimović, Č. The influence of digital elevation model resolution on overland flow networks for modelling urban pluvial flooding. Water Sci. Technol. 2009, 60, 3137–3149. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, J.B.; Creed, I.F. Sensitivity of digital landscapes to artifact depressions in remotely-sensed DEMs. Photogramm. Eng. Remote Sens. 2005, 71, 1029–1036. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Creed, I.F. Distinguishing actual and artefact depressions in digital elevation data. Comput. Geosci. 2006, 32, 1192–1204. [Google Scholar] [CrossRef]
- Adeyemo, O.; Maksimović, Č.; Boonya-Aroonnet, S.; Leitão, J.; Butler, D.; Makropoulos, C. Sensitivity analysis of surface runoff generation for pluvial urban flooding. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, UK, 31 August–5 September 2008. [Google Scholar]
- Shreve, R.L. Statistical law of stream numbers. J. Geol. 1966, 74, 17–37. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop 10.6. 2017. Available online: https://desktop.arcgis.com/en/arcmap/10.6/get-started/introduction/whats-new-in-arcgis.htm (accessed on 6 February 2022).
- Data Supply and Efficiency Board, DHM/Nedbør, Copenhagen. 2013. Available online: https://download.kortforsyningen.dk/ (accessed on 6 February 2022).
- Hartell, W.; Cook, J.J.; Mankowski, R.; Herrin, G.; Wu, Z. Automated Skeletonization Techniques; Haestad Methods, Inc.: Waterbury, CT, USA, 2002. [Google Scholar]
- WaPUG. Code of Practice for the Hydraulic Modelling of Sewer Systems; Wastewater Planning Users Group: London, UK, 2002. [Google Scholar]
- Hartell, W.; Cook, J.J.; Mankowski, R.; Herrin, G.; Wu, Z. Method and System for Reduction of a Network Topology-Based System Having Automated Optimization Features. US Patent 7,054,799 B1, 8 July 2002. [Google Scholar]
- Simões, N.; Leitão, J.; Maksimović, Č.; Sá Marques, A.; Pina, R. Sensitivity analysis of surface runoff generation in urban flood forecasting. Water Sci. Technol. 2010, 61, 2595–2601. [Google Scholar] [CrossRef]
| Greve | Copenhagen City Center | Amagerbro | |||
|---|---|---|---|---|---|
| Topographic overviews | Elevation (m) | Min. | −1.29 | −0.89 | −5.16 |
| Max. | 80.62 | 98.55 | 87.8 | ||
| Mean | 22.37 | 12.87 | 4.26 | ||
| St. dev. | 15.08 | 7.91 | 4.99 | ||
| Slope (%) | Mean | 9 | 30 | 17 | |
| St. dev. | 19 | 49 | 36 | ||
| Sink statistics | Total number | 30,556 | 13,899 | 7356 | |
| Max. depth (m) | Min. | 0.05 | 0.05 | 0.05 | |
| Max. | 20.6 | 22.27 | 26.3 | ||
| Mean | 0.18 | 0.28 | 0.22 | ||
| St. dev. | 0.48 | 1.26 | 0.95 | ||
| Volume (m3) | Min. | 0.13 | 0.13 | 0.13 | |
| Max. | 5,027,476 | 602,870 | 564,441 | ||
| Mean | 485 | 210 | 278 | ||
| St. dev. | 33,930 | 6200 | 9976 | ||
| Sum. | 14,819,660 | 2,918,790 | 2,044,968 | ||
| Radar rainfall statistics | Rain amounts (mm) | Min. | 23.6 | 77.4 | 88.09 |
| Max. | 109.19 | 147.5 | 133 | ||
| Mean | 58.97 | 104.68 | 111.46 | ||
| St. dev. | 26.82 | 12.2 | 14.69 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Mark, O.; Balstrøm, T.; Jensen, M.B. A Sink Screening Approach for 1D Surface Network Simplification in Urban Flood Modelling. Water 2022, 14, 963. https://doi.org/10.3390/w14060963
Zhao G, Mark O, Balstrøm T, Jensen MB. A Sink Screening Approach for 1D Surface Network Simplification in Urban Flood Modelling. Water. 2022; 14(6):963. https://doi.org/10.3390/w14060963
Chicago/Turabian StyleZhao, Guohan, Ole Mark, Thomas Balstrøm, and Marina B. Jensen. 2022. "A Sink Screening Approach for 1D Surface Network Simplification in Urban Flood Modelling" Water 14, no. 6: 963. https://doi.org/10.3390/w14060963







