Pond Energy Dynamics, Evaporation Rate and Ensemble Deep Learning Evaporation Prediction: Case Study of the Thomas Pond—Brenne Natural Regional Park (France)
Abstract
:1. Introduction
2. Materials and Methods
- Study area description
- Materials
- Methods
- Aerodynamic models
- Combined models (Table 1, Equations (10)–(13))
- Penman Model (Table 1, Equations (10) and (11))
- Priestly and Taylor model (Table 1, Equation (12))
- De Bruin model (Table 1, Equation (13))
- Energy balance model (Table 1, Equation (14))
3. Results
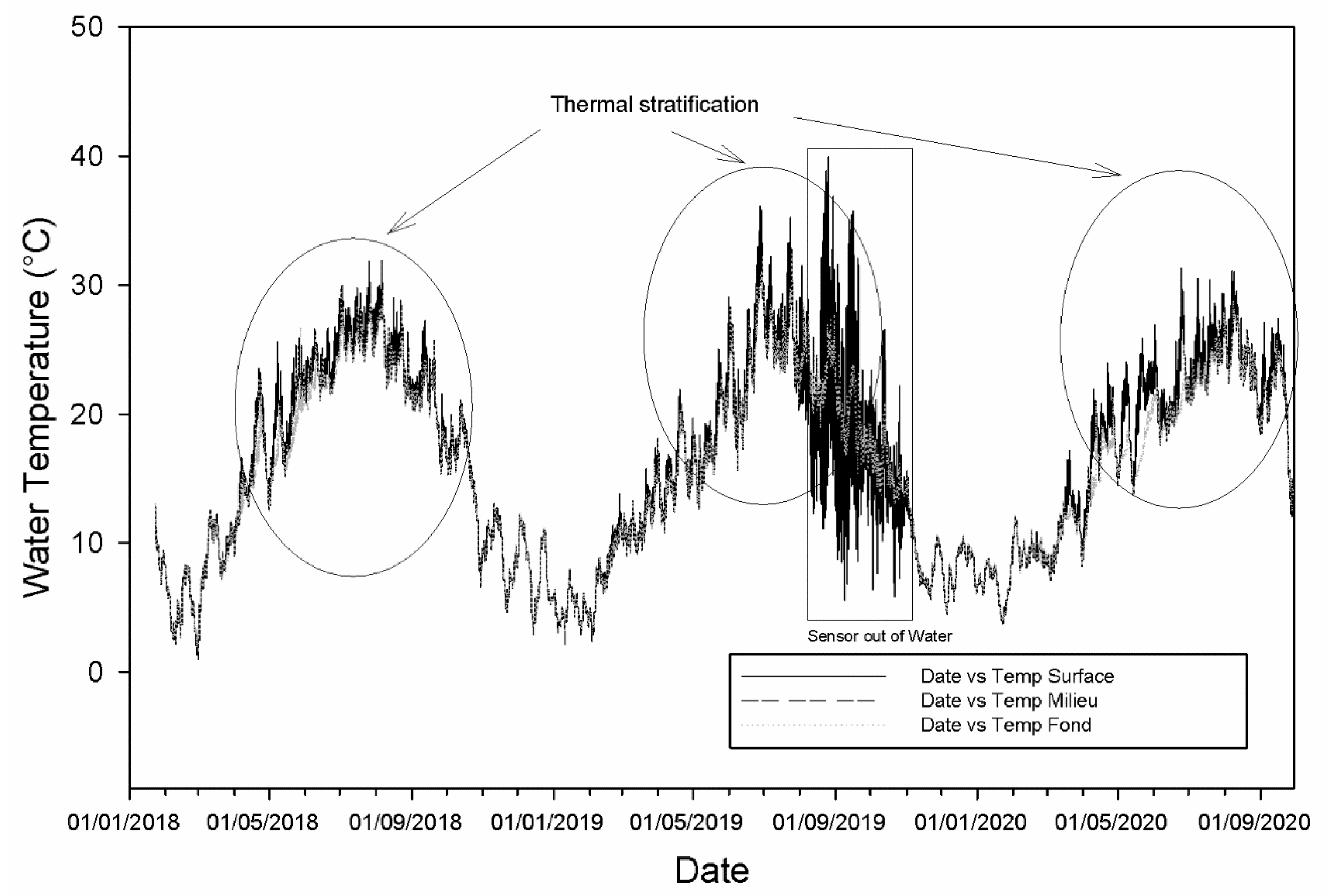
3.1. Thermal Variations of Water Body
3.1.1. Analysis of Thermal Variations of Water Masses over the Measurement Period
3.1.2. Thermal Analysis of the Water Masses of the Thomas Pond
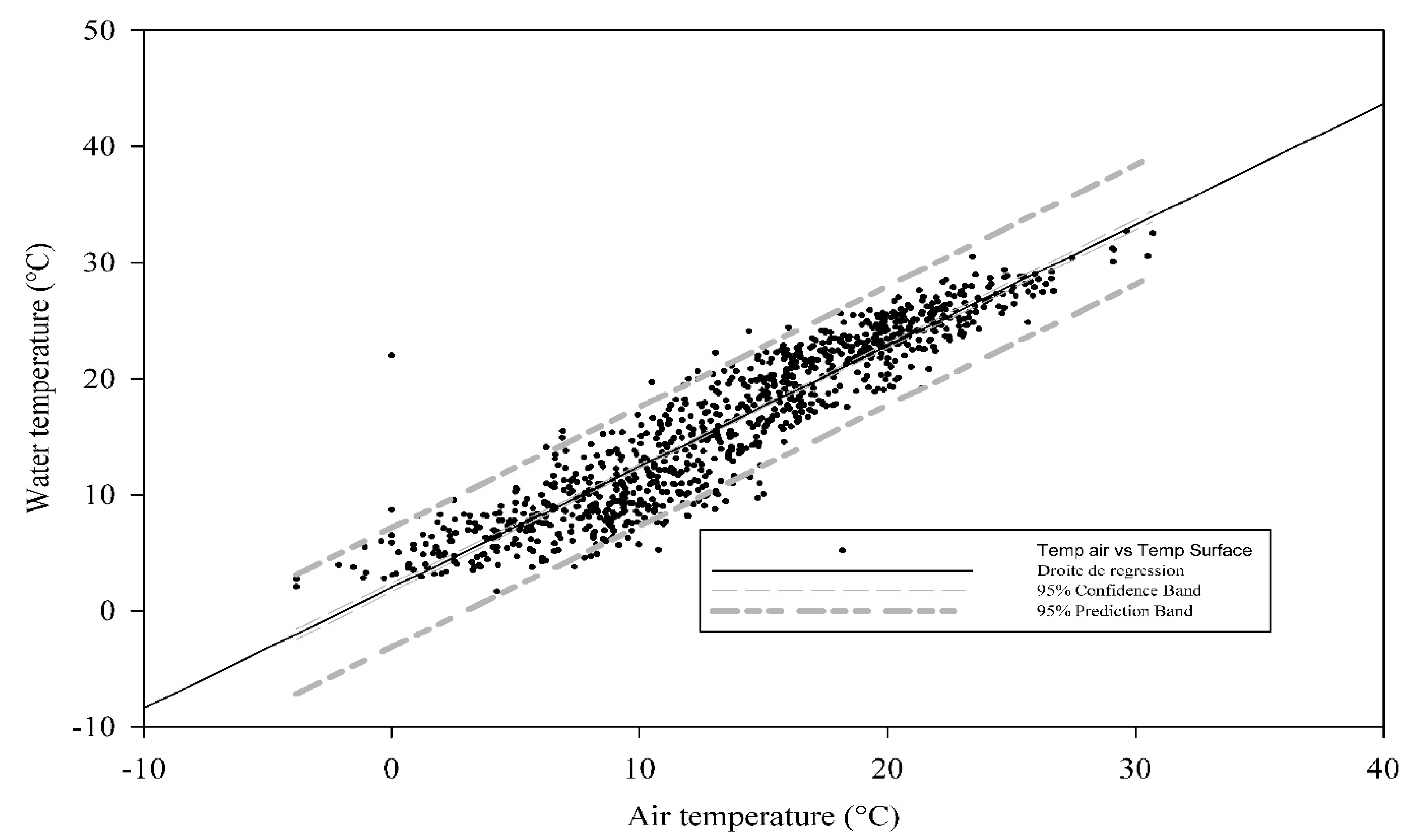
3.1.3. Adjustment of Air and Water Temperatures According to the S-Shaped Function
3.2. Estimation of Evaporation and the Energy Consumption Induced by This Process
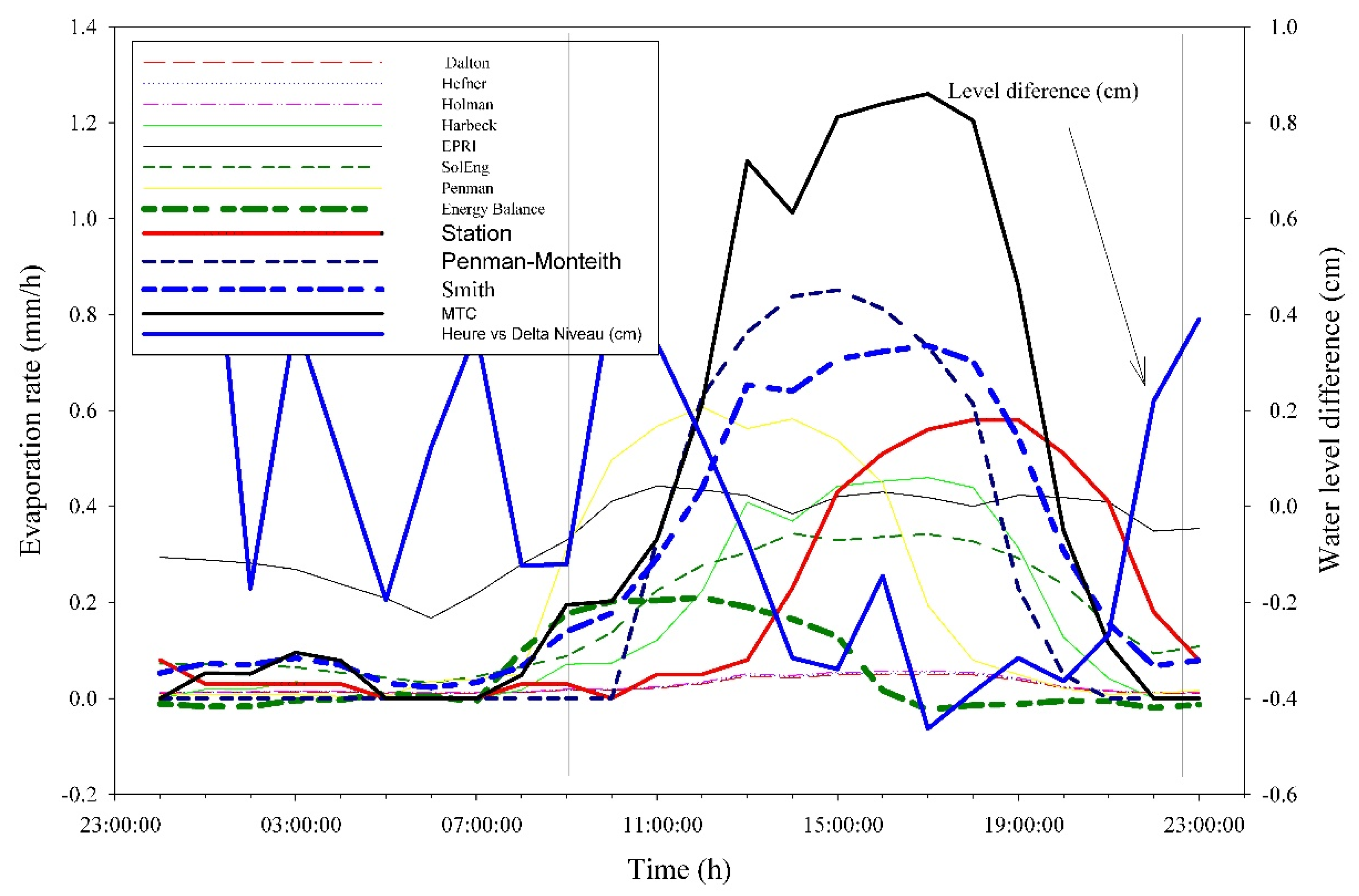
3.3. Appreciation of Daily Exchanges
- -
- We observe a direct relationship between surface water temperature and evaporation. This relationship is much more visible for low water temperatures (winter period) and characterised by low exchanges with the atmosphere. During this phase, the reconstitution of the energetic stock of the water mass takes place. Conversely, it tends to increase with time until summer (water temperature varying between 12 °C and 25 °C). Very high temperatures tend to show relative evaporation stability around 3–5 mm. This stability probably indicates an over-saturation of the air with moisture and the low renewal of the ambient air. The low renewal rates might arise from the absence of winds or a reduction of its speed during most of this season.
- -
- The evaporation rates differ for the same water temperature and depending on the air temperature and, more precisely, the season. Thus, depending on whether the season is cold or warm, the same temperature is experiences different evaporation rates. The thermal energy stored in the mass is directly responsible for this effect giving rise to hysteresis. As shown Figure 12, the graphical representation of air temperatures and ET indicates that for the lowest temperatures and at the beginning of the energy stock reconstitution, the thermal amplitude is high for the same evaporation value. At an average temperature of 17.5 °C, the evaporation gap can vary from 1 to 6 mm.
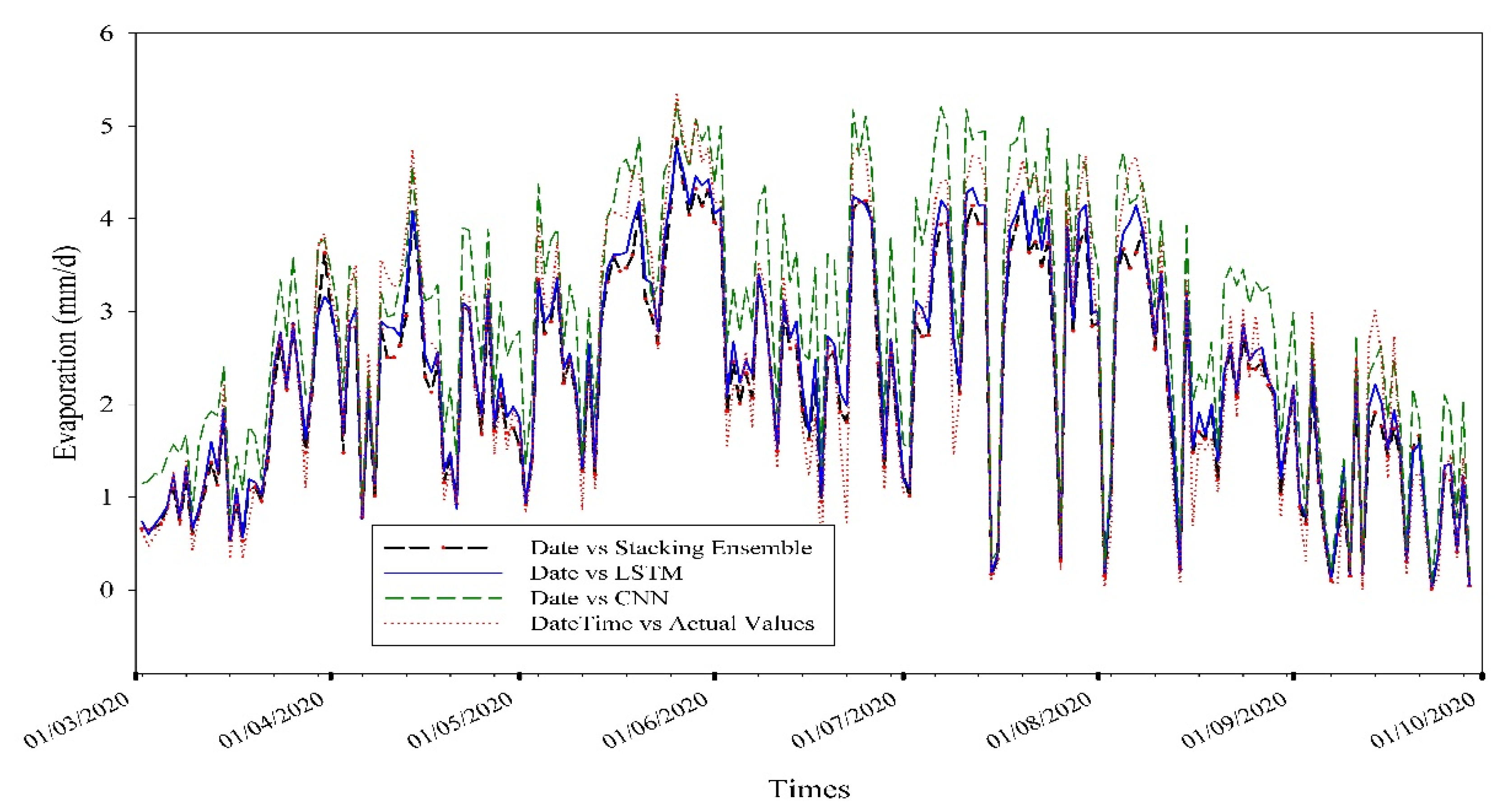
3.4. Prediction Using Deep Learning Methods
3.5. Extended Water Storages Recorded during the Last Two Decades Reflect the Deficit Caused by Direct Abstraction by Evaporation: Prediction of Sustained Shortage under Rising Temperatures
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| E | evaporation (mm) |
| m | evaporated mass [kg] |
| f(u) | wind function |
| es | saturated vapor pressure |
| ea | the actual vapour pressure in the air in mm of mercury |
| u | wind speed measured at 2 m height (m/s), |
| hfg | Latent heat of vaporization |
| W | evaporative energy flux, W/m2 |
| Ep | evaporation rate (mm/d) |
| Rn | daily average of net radiation |
| G | soil heat flux (MJ/m2/d) |
| γ | Psychrometric constant (0.66 KPa/°C) |
| β | Priestly-Taylor coefficient equal to 1.26 in our case |
| ∆ or D | slope of vapour pressure curve |
| U or u | wind speed measured at 2 m height (m/s) |
| ET° | reference evapotranspiration |
| Eap | aerodynamic part of evaporation |
| Ep-T | evaporation rate (mm/d) |
| Ts | Surface temperature (°C) |
| Qevap | Heat evaporation flux (W/m2) |
| ρw | water density (kg/m3) |
| QSolar | incident solar radiation (direct and diffuse) |
| Qsky | radiative energy from the atmosphere (sky) |
| Qcond | energy received by the water mass by conduction |
| Qconv | convective energy from or to the atmosphere |
| Qevap | evaporation of water to the air |
| Qwater | radiative energy emitted by water to the atmosphere |
| Qadvected | energy lost due to air movement |
References
- Downing, J.A.; Prairie, Y.T.; Cole, J.J.; Duarte, C.M.; Tranvik, L.J.; Striegl, R.G.; McDowell, W.H.; Kortelainen, P.; Caraco, N.F.; Melack, J.M.; et al. The global abundance and size distribution of lakes, ponds, and impoundments. Limnol. Oceanogr. 2006, 51, 2388–2397. [Google Scholar] [CrossRef] [Green Version]
- Potts, D.F. Estimation of evaporation from shallow ponds and impoundments in Montana. In Miscellaneous Publication N° 48; U.S. Department of Agriculture: Washington, DC, USA, 1988. [Google Scholar]
- Bastiaanssen, W.G.M.; Cheema, M.J.M.; Immerzeel, W.; Miltenburg, I.J.; Pelgrum, H. Surface energy balance and actual evapotranspiration of the transboundary Indus Basin estimated from satellite measurements and the ETLook model. Water Resour. Res. 2012, 48, W11512. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Q.; Chiew, F.H.S.; Zhang, L.; Leuning, R.; Cleugh, H.A. Estimating catchment evaporation and runoff using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, W10420. [Google Scholar] [CrossRef]
- Enku, T.; Assefa, M.M. A simple temperature method for the estimation of evapotranspiration. Hydrol. Process. 2014, 28, 2945–2960. [Google Scholar] [CrossRef]
- El-Mahdy, M.E.-S.; Abbas, M.S.; Sobhy, H.M. Development of mass-transfer evaporation model for Lake Nasser. Egypt. J. Water Clim. Chang. 2019, 12, 223–237. [Google Scholar] [CrossRef]
- Luki, S.; Takehiko, F.; Yuichi, O.; Shigeru, M.; Takashi, G.; Ken’ichirou, K.; Shinya, H.; Hikaru, K.; Koichiro, K.; Tomomi, T. Analysis of stream water temperature changes during rainfall events in forested watersheds. Limnology 2010, 11, 115–124. [Google Scholar] [CrossRef]
- Eaton, G.J.; Scheller, R.M. Effects of climate warming on fish thermal habitat in stream of the United States. Limnol. Oceanogr. 1996, 41, 1109–1115. [Google Scholar] [CrossRef] [Green Version]
- Fukushima, T.; Ozaki, N.; Kaminishi, H.; Harasawa, H.; Matsushige, K. Forecasting the changes in lake water quality in response to climate changes, using past relationships between meteorological conditions and water quality. Hydrol. Process. 2000, 14, 593–604. [Google Scholar] [CrossRef]
- Herb, W.R.; Stefan, H.G. Temperature Stratification and Mixing Dynamics in a Shallow Lake With Submersed Macrophytes. Lake Reserv. Manag. 2004, 20, 296–308. [Google Scholar] [CrossRef] [Green Version]
- Prats, J.; Danis, P.-A. An epilimnion and hypolimnion temperature model based on air temperature and lake characteristics. Knowl. Manag. Aquat. Ecosyst. 2019, 8, 420. [Google Scholar] [CrossRef]
- Culberson, S.D. Simplified Model for Prediction of Temperature and Dissolved Oxygen in Aquaculture Ponds: Using Reduced Data Inputs. Master’s Thesis, University of California, Davis, CA, USA, 1993; 212p. [Google Scholar]
- Hondzo, M.; Stefan, H.G. Regional water temperature characteristics of lakes subjected to climate change. Clim. Chang. 1993, 24, 187–211. [Google Scholar] [CrossRef]
- Hondzo, M.; Stefan, H.G. Lake water temperature simulation model. J. Hydraul. Eng. 1993, 119, 1251–1273. [Google Scholar] [CrossRef]
- Bogan, T.; Stefan, H.G.; Mohseni, O. Imprints of secondary heat sources on the stream temperature/equilibrium temperature relationship. Water Resour. Res. 2004, 40, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Boyd, C.E. Water Quality in Ponds for Aquaculture; Auburn University Agricultural Experimentation Station: Auburn, AL, USA, 1990; 482p. [Google Scholar]
- Boyd, C.E.; Romaire, R.P.; Johnston, E. Predicting Early Morning Dissolved Oxygen Concentrations in Channel Catfish Ponds. Trans. Am. Fish. Soc. 1978, 107, 484–492. [Google Scholar] [CrossRef]
- Mohseni, O.; Stefan, H. Stream temperature/air temperature relationship: A physical interpretation. J. Hydrol. 1999, 218, 128–141. [Google Scholar] [CrossRef]
- Mohseni, O.; Stefan, H.G.; Erickson, T.R. A non-linear regression model for weekly stream temperatures. Water Res. 1998, 34, 2685–2693. [Google Scholar] [CrossRef]
- Water Resources Engineers, Inc. (WRE). Prediction of Thermal Energy Distribution in Streams and Reservoirs. In Report Prepared for the Department of Fish and Game, State of California; Water Resources Engineers, Inc.: San Francisco, CA, USA, 30 August 1968; 90p. [Google Scholar]
- Robitu, M.; Inard, C.; Musy, M.; Groleau, D. Energy balance study of water ponds and its influence on building energy consumption. In Proceedings of the Eighth International IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003. [Google Scholar]
- Kroger, D.G. Evaporation-from a Water Suylface. Theor. J. Exp. J. 2007, 23, 3. [Google Scholar]
- Sinokrot, B.A.; Gulliver, J.S. In-stream flow impact on river water temperatures. J. Hydraul. Res. 2000, 38, 339–349. [Google Scholar] [CrossRef]
- Harbeck, E.G. For Measuring Reservoir Evaporation Utilizing Mass-Transfer Theory; Geological Survey Professional Paper 272-E; United States Government Printing Office: Washington, DC, USA, 1962.
- Malik, A.; Kumar, A.; Kim, S.; Kashani, M.H.; Karimi, V.; Sharafati, A.; Ghorbani, M.A.; Al-Ansari, N.; Salih, S.Q.; Yaseen, Z.M.; et al. Modeling monthly pan evaporation process over the Indian central Himalayas: Application of multiple learning artificial intelligence model. Eng. Appl. Comput. Fluid Mech. 2020, 14, 323–338. [Google Scholar] [CrossRef] [Green Version]
- Webb, B.W.; Clack, P.D.; Walling, D.E. Water-air temperature relationships in a Devon river system and the role of flow. Hydrol. Process. 2003, 17, 3069–3083. [Google Scholar] [CrossRef]
- Wen, Y.; Yuan, B. Use CNN-LSTM network to analyze secondary market data. In Proceedings of the 2nd International Conference on Innovation in Artificial Intelligence, Shanghai, China, 9–12 March 2018; pp. 54–58. [Google Scholar]
- Liu, S.; Zhang, C.; Ma, J. CNN-LSTM neural network model for quantitative strategy analysis in stock markets. In International Conference on Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 198–206. [Google Scholar]
- Aseen, Z.M.; Al-Juboori, A.M.; Beyaztas, U.; Al-Ansari, N.; Chau, K.-W.; Qi, C.; Ali, M.; Salih, S.Q.; Shahid, S. Prediction of evaporation in arid and semi-arid regions: A comparative study using different machine learning models. Eng. Appl. Comput. Fluid Mech. 2019, 14, 70–89. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://pandas.pydata.org/ (accessed on 15 November 2021).
- Available online: https://numpy.org/ (accessed on 15 November 2021).
- Available online: https://keras.io/ (accessed on 20 November 2021).
- Available online: https://matplotlib.org/ (accessed on 20 November 2021).
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Stewart, R.; Rouse, W. Simple model for calculating evaporation from dry and wet tundra surfaces. Arctic. Alp. Res. 1976, 8, 263–274. [Google Scholar] [CrossRef]
- Mosner, M.S.; Aulenbach, B.T. Comparison of methods used to estimate lake evaporation for a water budget of Lake of estimation methods. Hydrol. Process. 1998, 12, 429–442. [Google Scholar]
- Pallavi, K.; Rajeev, S. Evaluation of evaporation models based on climate factors. Int. J. Civ. Eng. Technol. 2016, 7, 111–120. [Google Scholar]
- Available online: https://scikit-learn.org/stable/ (accessed on 22 November 2021).









| Hydrodynamic Models | |||
| (1) | Hefner | E = 0.26 (1 + 0.54 u) (es − ea) | In/Day |
| (2) | Dalton [9] | E = 0.26 (1 + 0.54 u) (es − ea) | In/Day |
| (3) | Harbeck | E = 2.909 As − 0.05 u (es − ea) 0.88 | In/Day |
| (4) | Holman | E = 0.8 (0.37 + 0.0041 u) (es − ea) 0.88 | In/Day |
| (5) | Smith (1993) | E = (0.76(0.08893 + 0.7835 u) (es − ea))/hfg | |
| (6) | ASHRAE | E = (0.08893 + 0.7835 u) (es − ea))/hfg | |
| (7) | EPRI | E = (9.2 + 0.46 W2) (es − ea) | W/m2. |
| (8) | Sol Engi | Qevap = 9.15 KE (es − ea) | W/m2. |
| (9) | MTC | E = 0.00338 A − 0.05 + u × (es − ea) | |
| Combined Models | |||
| (10) | Penman Model | With:Eap = 0.26 (1 + 0.536 u) (es − ea) | |
| (11) | Penman-Monteith | ||
| (12) | Priestly and Taylor [32] | Ep-T = β[(∆/(∆ + γ)) × (Rn/λ)] | |
| (13) | De Bruin Model | With:F(u): 2.9 + 2.1 u | |
| Energy Balance | |||
| (14) | Energy Balance Model | αsQSolar + εQsky + QCond = Qconv + Qevap + Qwater + Qadvected | |
| Dalton | Hefner | Holman | Harbeck | EPRI | SolEng | DeBruin | |
| Min | 37.70 | 4.59 | 3.06 | 0.00 | 46.42 | 6.57 | 2.08 |
| Max | 126.45 | 971.77 | 392.39 | 1038.78 | 1275.06 | 621.90 | 343.45 |
| Moyenne | 48.67 | 186.80 | 81.09 | 129.76 | 496.81 | 165.24 | 57.73 |
| Penman | Taylor | Energy Balance | Station | Penman-Monteith | Smith | MTC | |
| Min | 5.78 | 0.00 | −11.58 | 0.00 | 0.00 | 10.28 | 0.00 |
| Max | 830.48 | 334.62 | 298.42 | 885.45 | 1105.03 | 3086.85 | 2916.41 |
| Moyenne | 253.30 | 67.76 | 153.27 | 290.92 | 312.73 | 530.92 | 358.24 |
| Dalton | Hefner | Holman | Harbeck | EPRI | SolEng | DeBruin | Penman | Taylor | Energy Balance | Station | Penman-Monteith | Smith | MTC | Delta Niveau (cm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dalton | 1.00 | 0.94 | 0.95 | 1.00 | 0.60 | 0.79 | 0.92 | 0.66 | 0.58 | 0.27 | 0.08 | 0.07 | 0.97 | 0.14 | 0.10 |
| Hefner | 0.94 | 1.00 | 1.00 | 0.95 | 0.77 | 0.95 | 0.91 | 0.74 | 0.68 | 0.30 | 0.16 | 0.15 | 1.00 | 0.18 | 0.13 |
| Holman | 0.95 | 1.00 | 1.00 | 0.95 | 0.78 | 0.94 | 0.92 | 0.74 | 0.67 | 0.31 | 0.15 | 0.15 | 1.00 | 0.18 | 0.13 |
| Harbeck | 1.00 | 0.95 | 0.95 | 1.00 | 0.61 | 0.79 | 0.92 | 0.66 | 0.58 | 0.27 | 0.08 | 0.07 | 0.97 | 0.14 | 0.10 |
| EPRI | 0.60 | 0.77 | 0.78 | 0.61 | 1.00 | 0.85 | 0.59 | 0.71 | 0.62 | 0.31 | 0.26 | 0.25 | 0.74 | 0.23 | 0.18 |
| SolEng | 0.79 | 0.95 | 0.94 | 0.79 | 0.85 | 1.00 | 0.80 | 0.75 | 0.71 | 0.30 | 0.22 | 0.22 | 0.92 | 0.20 | 0.14 |
| DeBruin | 0.92 | 0.91 | 0.92 | 0.92 | 0.59 | 0.80 | 1.00 | 0.61 | 0.53 | 0.29 | 0.09 | 0.08 | 0.92 | 0.12 | 0.13 |
| Penman | 0.66 | 0.74 | 0.74 | 0.66 | 0.71 | 0.75 | 0.61 | 1.00 | 0.88 | 0.64 | 0.03 | 0.03 | 0.73 | 0.06 | 0.20 |
| Taylor | 0.58 | 0.68 | 0.67 | 0.58 | 0.62 | 0.71 | 0.53 | 0.88 | 1.00 | 0.68 | 0.05 | 0.04 | 0.67 | 0.10 | 0.16 |
| Energy Balance | 0.27 | 0.30 | 0.31 | 0.27 | 0.31 | 0.30 | 0.29 | 0.64 | 0.68 | 1.00 | −0.17 | −0.16 | 0.29 | −0.08 | 0.14 |
| Station | 0.08 | 0.16 | 0.15 | 0.08 | 0.26 | 0.22 | 0.09 | 0.03 | 0.05 | −0.17 | 1.00 | 0.98 | 0.14 | 0.76 | 0.18 |
| Penman-Monteith | 0.07 | 0.15 | 0.15 | 0.07 | 0.25 | 0.22 | 0.08 | 0.03 | 0.04 | −0.16 | 0.98 | 1.00 | 0.14 | 0.70 | 0.16 |
| Smith | 0.97 | 1.00 | 1.00 | 0.97 | 0.74 | 0.92 | 0.92 | 0.73 | 0.67 | 0.29 | 0.14 | 0.14 | 1.00 | 0.18 | 0.12 |
| MTC | 0.14 | 0.18 | 0.18 | 0.14 | 0.23 | 0.20 | 0.12 | 0.06 | 0.10 | −0.08 | 0.76 | 0.70 | 0.18 | 1.00 | 0.07 |
| Delta Niveau (cm) | 0.10 | 0.13 | 0.13 | 0.10 | 0.18 | 0.14 | 0.13 | 0.20 | 0.16 | 0.14 | 0.18 | 0.16 | 0.12 | 0.07 | 1.00 |
| Methods\Volume Evaporation at Temp °C | Current | 1 °C | 2 °C | 3 °C | 4 °C |
|---|---|---|---|---|---|
| MTC | 656,996,80.2 | 698,356,98.3 | 741,889,20.5 | 787,780,45.1 | 836,138,17.8 |
| Penman-Monteith | 544,286,00.00 | 558,940,27.5 | 573,514,13.79 | 588,383,72.2 | 603,569,64.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rachid, N.; Issam, N.; Abdelkrim, B.; Abdelhamid, A.; Amina, H. Pond Energy Dynamics, Evaporation Rate and Ensemble Deep Learning Evaporation Prediction: Case Study of the Thomas Pond—Brenne Natural Regional Park (France). Water 2022, 14, 923. https://doi.org/10.3390/w14060923
Rachid N, Issam N, Abdelkrim B, Abdelhamid A, Amina H. Pond Energy Dynamics, Evaporation Rate and Ensemble Deep Learning Evaporation Prediction: Case Study of the Thomas Pond—Brenne Natural Regional Park (France). Water. 2022; 14(6):923. https://doi.org/10.3390/w14060923
Chicago/Turabian StyleRachid, Nedjai, Nedjai Issam, Bensaid Abdelkrim, Azaroual Abdelhamid, and Haouchine Amina. 2022. "Pond Energy Dynamics, Evaporation Rate and Ensemble Deep Learning Evaporation Prediction: Case Study of the Thomas Pond—Brenne Natural Regional Park (France)" Water 14, no. 6: 923. https://doi.org/10.3390/w14060923






