A GPU-Accelerated and LTS-Based Finite Volume Shallow Water Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations and Empirical Relations
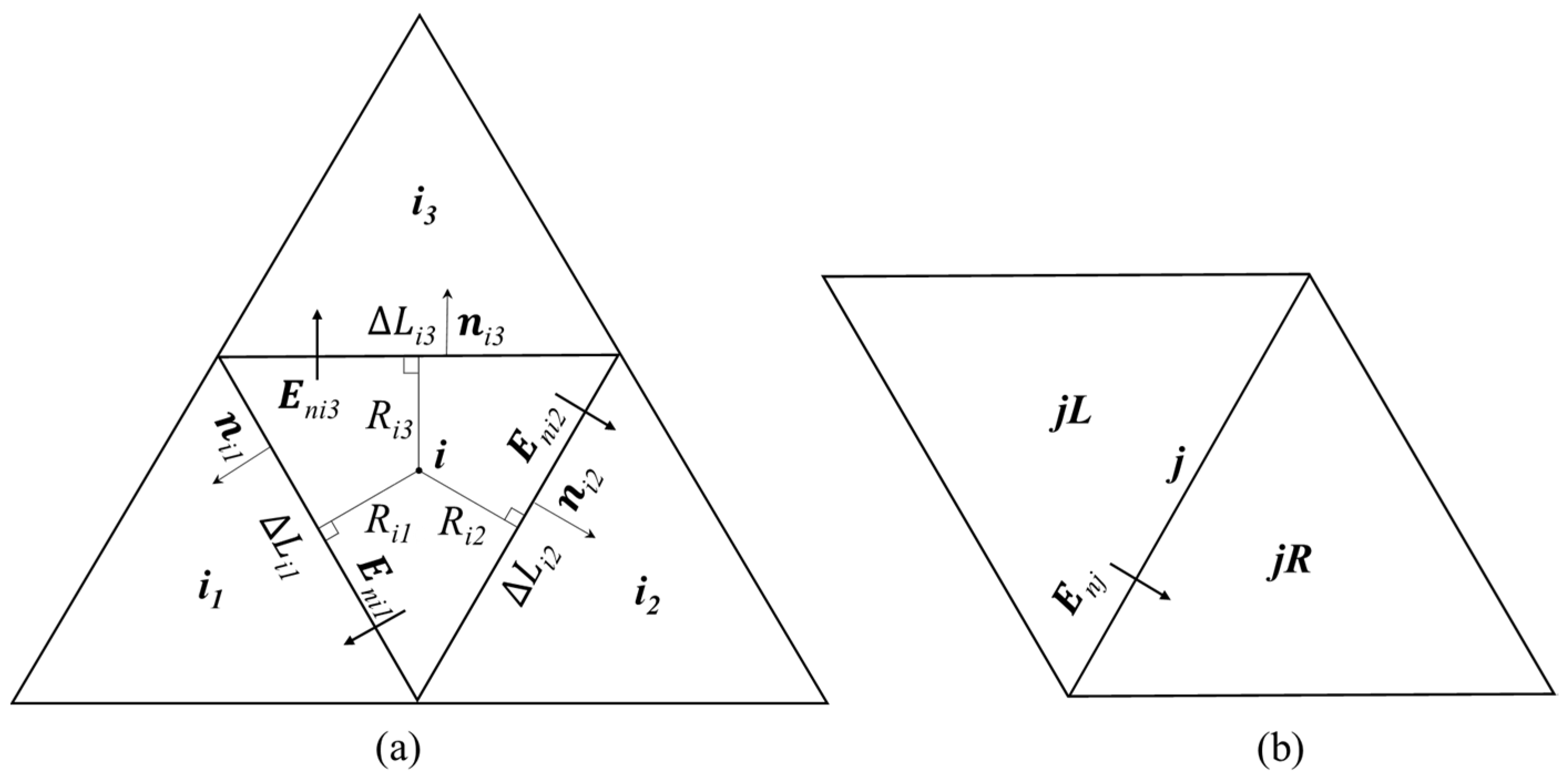
2.2. Finite Volume Discretization on Unstructured Triangular Grids
2.3. The Local Time Step Estimations
2.4. The Six SWM Versions and Their Numerical Structures
- (a)
- The model is initiated on the host by reading data (e.g., mesh information; basic parameters; boundary conditions such as time series of water level or discharge, if any); setting initial conditions; computing basic parameters (e.g., face length, normal direction, cell area). Afterwards, necessary data are transferred from the host (CPU) to the device (GPU). This data transfer occurs once per numerical case, of which the overhead is negligible as compared to the whole computational cost.
- (b)
- The LTS estimation involves twice implementation of the reduction algorithm (RA1, RA2) and five kernels: Kernel ‘Cell_Time_Step (CTS)’ computes the locally allowable maximum time step; the reduction algorithm (RA1) finds the globally minimum time step; Kernel ‘Cell_Potential_Exponent (CPE)’ computes the potential grade exponent. Kernel ‘Cell-Modified_Exponent (CME)’ modifies the potential grade exponents around dynamic/static fronts. Kernel ‘Face_Final_Exponent (FFE)’ computes the grade exponent of each face. Kernel ‘Cell_Final_Exponent (CFE)’ computes the actual grade exponent of cells. The reduction algorithm (RA2) finds .
- (c)
- The parameter and is transferred from the device to the host, such that a full cycle of can be defined in the host. For each sub-cycle, the parameter is firstly transferred from the host to the device (on constant memory); afterwards, two kernels [Face_Flux (FF), Cell_Variable (CV)] are invoked: ‘Face_Flux (FF)’ computes numerical fluxes of faces; Cell_Variable (CV)’ updates the conserved variables of cells at a time interval of by firstly estimating the bed slope and frictions, and secondly implement Equation (3). At the end of each sub-cycle, is increased by unity until it exceeds , and subsequently, the computation goes to the LTS estimation again.
3. Results and Discussion
3.1. Simulation of the Idealized Dam-Break Flows
3.2. Simulation of the Experimental Partial Dam-Break Flow Propagating through Buildings
3.3. Simulation of Tidal Flows in Yangtze Estuary and Hangzhou Bay
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cea, L.; French, J.R.; Vazquez-Cendon, M.E. Numerical modelling of tidal flows in complex estuaries including turbulence: An unstructured finite volume solver and experimental validation. Int. J. Numer. Methods Eng. 2006, 67, 1909–1932. [Google Scholar] [CrossRef]
- Hu, P.; Han, J.J.; Li, W.; Sun, Z.L.; He, Z.G. Numerical investigation of a sandbar formation and evolution in a tide-dominated estuary using a hydro-sediment-morphodynamic model. Coast. Eng. J. 2018, 60, 466–483. [Google Scholar] [CrossRef]
- Luan, H.L.; Ding, P.X.; Wang, Z.B.; Ge, J.Z. Process-based morphodynamic modeling of the Yangtze Estuary at a decadal timescale: Controls on estuarine evolution and future trends. Geomorphology 2017, 290, 347–364. [Google Scholar] [CrossRef]
- Qin, X.; LeVeque, R.J.; Motley, M.R. Accelerating an adaptive mesh refinement code for depth-averaged flows using GPUs. J. Adv. Modeling Earth Syst. 2019, 11, 2606–2628. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.H.; Cho, Y.S.; Yi, Y.K. Propagation and run-up of nearshore tsunamis with HLLC approximate Riemann solver. Ocean Eng. 2007, 34, 1164–1173. [Google Scholar] [CrossRef]
- Kernkamp, H.W.J.; van Dam, A.; Stelling, G.S.; de Goede, E.D. Efficient scheme for the shallow water equations on unstructured grids with application to the Continental Shelf. Ocean Dyn. 2011, 61, 1175–1188. [Google Scholar] [CrossRef]
- Hu, P.; Li, W.; He, Z.G.; Pahtz, T.; Yue, Z.Y. Well-balanced and flexible modelling of swash hydrodynamics and sediment transport. Coast. Eng. 2015, 96, 27–37. [Google Scholar] [CrossRef] [Green Version]
- Hu, P.; Tan, L.; He, Z. Numerical investigation on the adaptation of dam-break flow-induced bed load transport to the capacity regime over a sloping bed. J. Coast. Res. 2020, 36, 1237–1246. [Google Scholar] [CrossRef]
- Yu, H.; Huang, G.; Wu, C. Efficient finite volume model for shallow-water flows using an Implicit Dual Time-Stepping Method. J. Hydraul. Eng. ASCE 2015, 141, 04015004. [Google Scholar] [CrossRef]
- Gaudreault, S.; Pudykiewicz, J.A. An efficient exponential time integration method for the numerical solution of the shallow water equations on the spher. J. Comput. Phys. 2016, 322, 827–848. [Google Scholar] [CrossRef] [Green Version]
- Crossley, A.J.; Wright, N.G. Time accurate local time stepping for the unsteady shallow water equations. Int. J. Numer. Methods Fluids 2005, 48, 775–799. [Google Scholar] [CrossRef]
- Dazzi, S.; Maranzoni, A.; Mignosa, P. Local time stepping applied to mixed flow modeling. J. Hydraul. Res. 2016, 54, 1–13. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Palu, A.D.; Mignosa, P. A local time stepping algorithm for GPU-accelerated 2D shallow water models. Adv. Water Resour. 2018, 111, 274–288. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.L.; Han, J.J.; Cao, Z.X.; Liu, H.H.; Yue, Z.Y.; He, Z.G. An improved local-time-step for 2D shallow water modeling based on unstructured grids. J. Hydraul. Eng. ASCE 2019, 145, 06019017. [Google Scholar] [CrossRef]
- Hu, P.; Lei, Y.L.; Han, J.J.; Cao, Z.X.; Liu, H.H.; He, Z.G. Computationally efficient hydro-morphodynamic modelling using a hybrid local-time-step and the global maximum-time-step. Adv. Water Resour. 2019, 127, 26–38. [Google Scholar] [CrossRef]
- Sanders, B.F. Integration of a shallow water model with a local time step. J. Hydraul. Res. 2008, 46, 466–475. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E.; Detwiler, R.L. ParBreZo: A parallel, unstructured grid, Godunov-type, shallow-water code for high-resolution flood inundation modeling at the regional scale. Adv. Water Resour. 2010, 33, 1456–1467. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E. PRIMo: Parallel raster inundation model. Adv. Water Resour. 2019, 126, 79–95. [Google Scholar] [CrossRef]
- Brodtkorb, A.R.; Sætra, M.L.; Altinakar, M. Efficient shallow water simulations on GPUs: Implementation, visualization, verification, and validation. Comput. Fluids 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Castro, M.J.; Ortega, S.; de la Asuncion, M.; Mantas, J.M.; Gallardo, J.M. GPU computing for shallow water flow simulation based on finite volume schemes. Comptes Rendus Mécanique 2011, 339, 165–184. [Google Scholar] [CrossRef]
- de la Asuncion, M.; Castro, M.J. Simulation of tsunamis generated by landslides using adaptive mesh refinement on GPU. J. Comput. Phys. 2017, 345, 91–110. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernandez, M.; Murillo, J.; Garcia-Navarro, P. An optimized GPU implementation of a 2D free surface simulation model on unstructured meshes. Adv. Eng. Softw. 2014, 78, 1–15. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernandez, M.; Murillo, J.; Garcia-Navarro, P. GPU implementation of the 2D shallow water equations for the simulation of rainfall/runoff events. Environ. Earth Sci. 2015, 74, 7295–7305. [Google Scholar] [CrossRef]
- Vacondio, R.; Palu, A.D.; Ferrari, A.; Mignosa, P.; Aureli, F.; Dazzi, S. A non-uniform efficient grid type for GPU-parallel Shallow Water Equations models. Environ. Model. Softw. 2017, 88, 119–137. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.; Klein, R.; Perthame, B.T. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- He, Z.G.; Wu, T.; Weng, H.X.; Hu, P.; Wu, G.F. Numerical investigation of the vegetation effects on dam-flows and bed morphological changes. Int. J. Sediment Res. 2017, 32, 105–120. [Google Scholar] [CrossRef]
- Toro, E. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley: Chichester, UK, 2001. [Google Scholar]
- Yoon, T.H.; Kang, S. Finite volume model for two-dimensional shallow water flows on unstructured grids. J. Hydraul. Eng. ASCE 2004, 130, 678–688. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Zech, Y. Dam-break flow through an idealised city. J. Hydraul. Res. IAHR 2008, 46, 648–658. [Google Scholar] [CrossRef] [Green Version]










| SWM Version | LTS | Parallel Language | |
|---|---|---|---|
| V1 | single-core CPU | No | NA |
| V2 | (multi-core CPU) | Open MP | |
| V3 | GPU | CUDA Fortran | |
| V4 | single-core CPU + LTS | YES | NA |
| V5 | multi-core CPU + LTS | Open MP | |
| V6 | GPU + LTS | CUDA Fortran | |
| No. | Computational Cost (s) of V1 | Speeding-Up Ratios Compared to Single-Core CPU Version | LTS Benefits | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V6 | V4 vs. V1 | V5 vs. V2 | V6 vs. V3 | |||
| 1 | 1010/0.14/0.7/1.1 | 0.079 | 1 | 1.4 | 2.6 | 2.6 | 2.0 | 2.3 | 2.6 | 1.4 | 0.9 |
| 2 | 4762/0.066/0.7/1.0 | 0.585 | 1 | 2.4 | 12.4 | 2.1 | 3.8 | 9.3 | 2.1 | 1.6 | 0.7 |
| 3 | 18,824/0.033/0.7/1.0 | 6.772 | 1 | 2.9 | 37.4 | 2.8 | 6.6 | 37.2 | 2.8 | 2.3 | 1.0 |
| 4 | 73,508/0.016/0.7/1.0 | 44.56 | 1 | 2.8 | 77.4 | 2.2 | 5.2 | 82.1 | 2.2 | 1.9 | 1.1 |
| No. | Computational Cost (s) of V1 | Speeding-Up Ratios Compared to Single-Core CPU Version | LTS Benefits | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V6 | V4 vs. V1 | V5 vs. V2 | V6 vs. V3 | |||
| 1 | 5000/0.1/1.5/1.5 | 2.9 | 1 | 1.2 | 3.7 | 2.4 | 3.7 | 7.3 | 2.4 | 3.0 | 2.0 |
| 2 | 10,510/0.1/1.6/1.7 | 6.3 | 1 | 1.4 | 6.3 | 2.1 | 3.2 | 7.9 | 2.1 | 2.3 | 1.3 |
| 3 | 20,523/0.07/1.8/2.0 | 26.3 | 1 | 1.9 | 13.8 | 3.8 | 2.3 | 10.1 | 3.8 | 3.4 | 1.4 |
| 4 | 28,694/0.07/1.7/1.9 | 72.1 | 1 | 2.1 | 17.6 | 4.5 | 8.8 | 28.8 | 4.5 | 4.1 | 1.6 |
| 5 | 43,302/0.05/1.6/1.8 | 105.8 | 1 | 2.2 | 25.2 | 4.5 | 9.2 | 39.2 | 4.5 | 4.1 | 1.6 |
| 6 | 68,892/0.04/1.3/1.3 | 196.0 | 1 | 2.1 | 31.3 | 3.4 | 8.0 | 53.0 | 3.4 | 3.8 | 1.7 |
| 7 | 153,218/0.03/1.4/1.5 | 694.1 | 1 | 2.0 | 39.4 | 3.3 | 7.9 | 79.8 | 3.3 | 4.0 | 2.0 |
| 8 | 263,115/0.02/1.8/2.1 | 1628.1 | 1 | 1.8 | 44.2 | 4.0 | 8.4 | 101.8 | 4.0 | 4.6 | 2.3 |
| 9 | 609,916/0.01/1.4/1.5 | 5954.3 | 1 | 1.9 | 51 | 3.6 | 9.1 | 132.9 | 3.6 | 4.9 | 2.6 |
| No. | Computational Cost (min) of V1 | Speeding-Up Ratios Compared to Single-Core CPU Version | LTS Benefits | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V6 | V4 vs. V1 | V5 vs. V2 | V6 vs. V3 | |||
| 1 | 21,629/10.3/1.7/1.7 | 20.3 | 1 | 3.2 | 7.0 | 8.1 | 33.8 | 25.4 | 8.1 | 10.5 | 3.6 |
| 2 | 44,606/9.6/1.9/1.9 | 28.5 | 1 | 2.4 | 10.2 | 5.6 | 20.4 | 35.6 | 5.6 | 8.4 | 3.5 |
| 3 | 61,315/9.6/1.9/2.0 | 35.7 | 1 | 2.9 | 17.9 | 6.0 | 14.3 | 44.6 | 6.0 | 5.0 | 2.5 |
| 4 | 82,717/9.6/1.8/1.8 | 59.3 | 1 | 2.9 | 22.0 | 4.1 | 12.6 | 65.9 | 4.1 | 4.4 | 3.0 |
| 5 | 190,308/2.5/1.7/1.8 | 104.8 | 1 | 2.8 | 18.7 | 4.1 | 11.9 | 61.6 | 4.1 | 4.3 | 3.3 |
| 6 | 269,945/2.4/1.4/1.4 | 442.9 | 1 | 3.1 | 24.2 | 6.4 | 18.1 | 79.1 | 6.4 | 5.9 | 3.3 |
| 7 | 422,853/1.8/1.2/1.2 | 662.7 | 1 | 3.0 | 24.6 | 5.5 | 18.3 | 98.9 | 5.5 | 6.1 | 4.0 |
| 8 | 518,175/1.6/1.2/1.2 | 1024.8 | 1 | 2.5 | 27.0 | 6.0 | 19.9 | 150.7 | 6.0 | 8.1 | 5.6 |
| 9 | 1,756,679/1.3/1.4/1.4 | 5954.8 | 1 | 2.6 | 108.1 | 3.5 | 12.4 | 350.3 | 3.5 | 4.7 | 3.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Zhao, Z.; Ji, A.; Li, W.; He, Z.; Liu, Q.; Li, Y.; Cao, Z. A GPU-Accelerated and LTS-Based Finite Volume Shallow Water Model. Water 2022, 14, 922. https://doi.org/10.3390/w14060922
Hu P, Zhao Z, Ji A, Li W, He Z, Liu Q, Li Y, Cao Z. A GPU-Accelerated and LTS-Based Finite Volume Shallow Water Model. Water. 2022; 14(6):922. https://doi.org/10.3390/w14060922
Chicago/Turabian StyleHu, Peng, Zixiong Zhao, Aofei Ji, Wei Li, Zhiguo He, Qifeng Liu, Youwei Li, and Zhixian Cao. 2022. "A GPU-Accelerated and LTS-Based Finite Volume Shallow Water Model" Water 14, no. 6: 922. https://doi.org/10.3390/w14060922





