Efficiency of Geospatial Technology and Multi-Criteria Decision Analysis for Groundwater Potential Mapping in a Semi-Arid Region
Abstract
:1. Introduction
2. Study Area Description
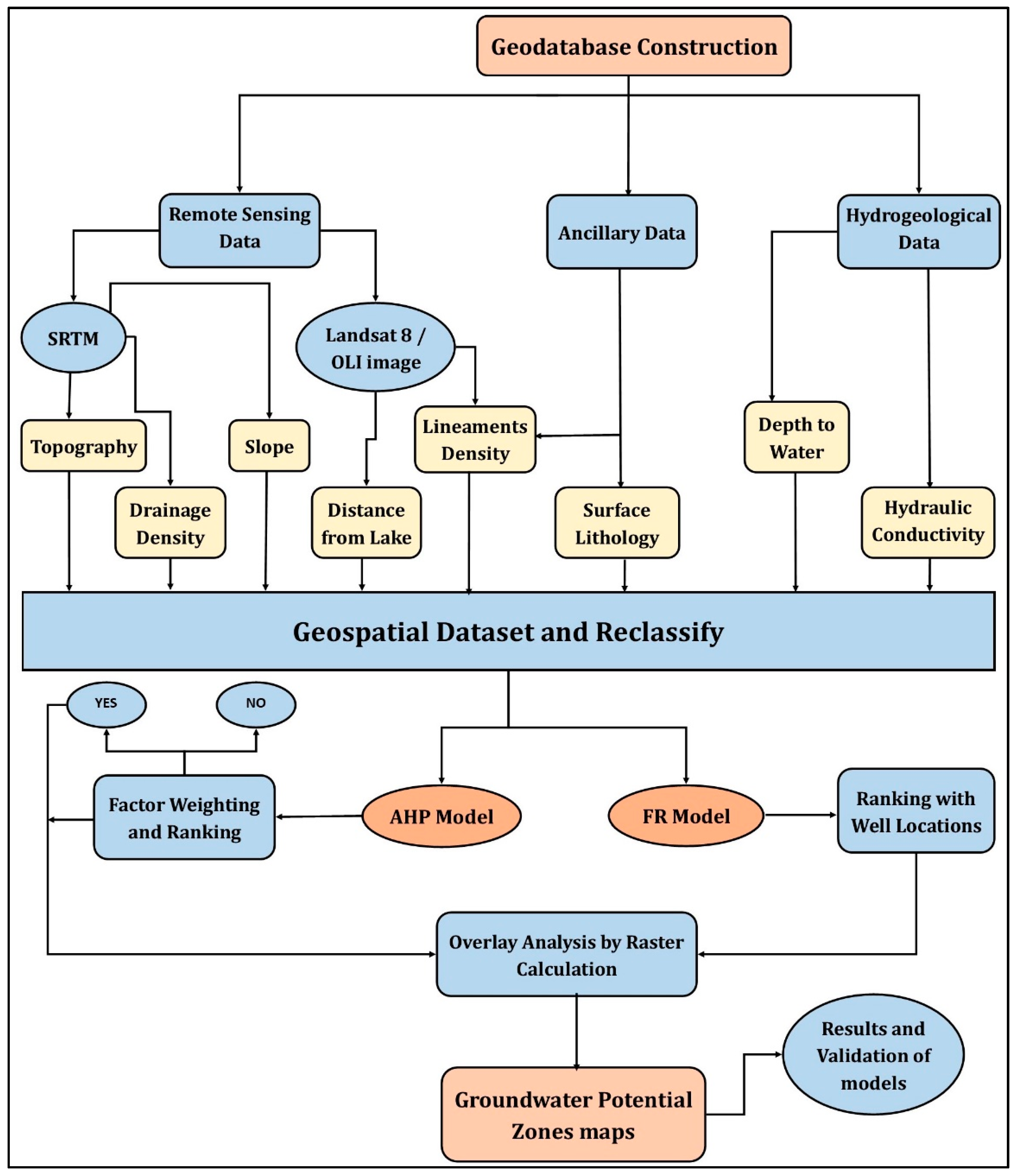
3. Materials and Methods
3.1. Thematic Layer Preparation
3.1.1. Hydraulic Conductivity
3.1.2. Distance from the Lake (Lake Nasser)
3.1.3. Lineaments Density
3.1.4. Surface Lithology
3.1.5. Topography and Slope
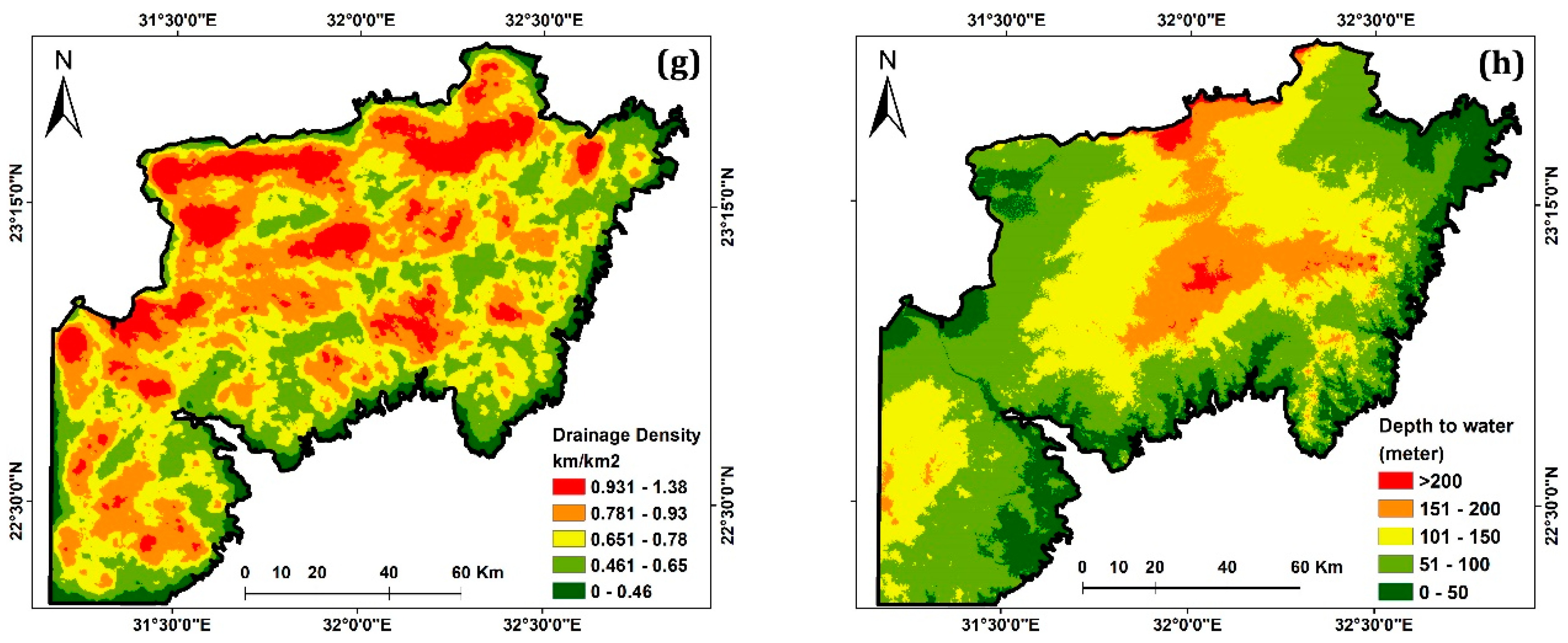
3.1.6. Drainage Density
3.1.7. Depth to Water
3.2. Analytical Hierarchy Process (AHP) Method
3.3. Frequency Ratio (FR) Method
4. Results
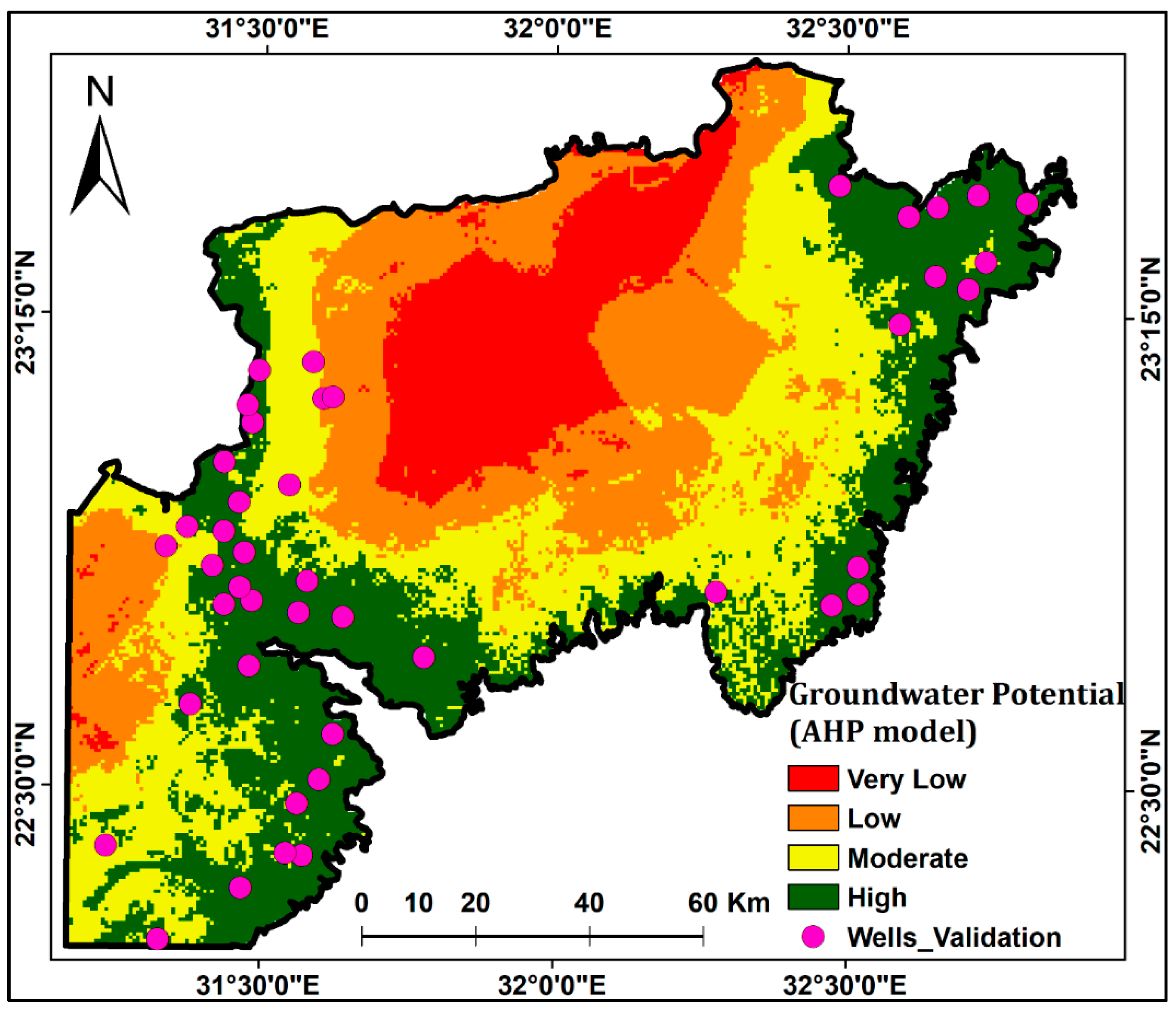
4.1. Results of AHP Model
4.2. Results of FR Model
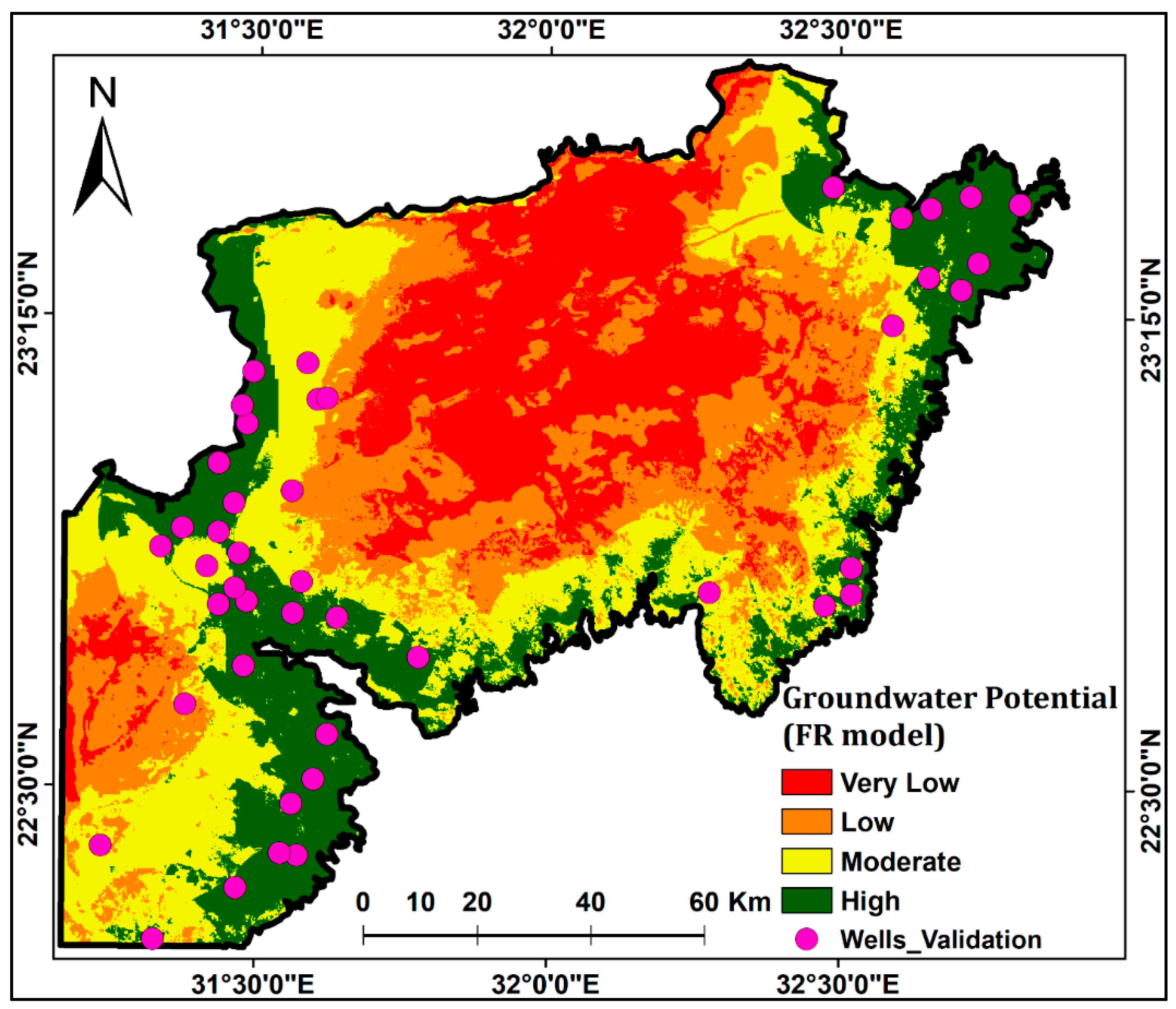
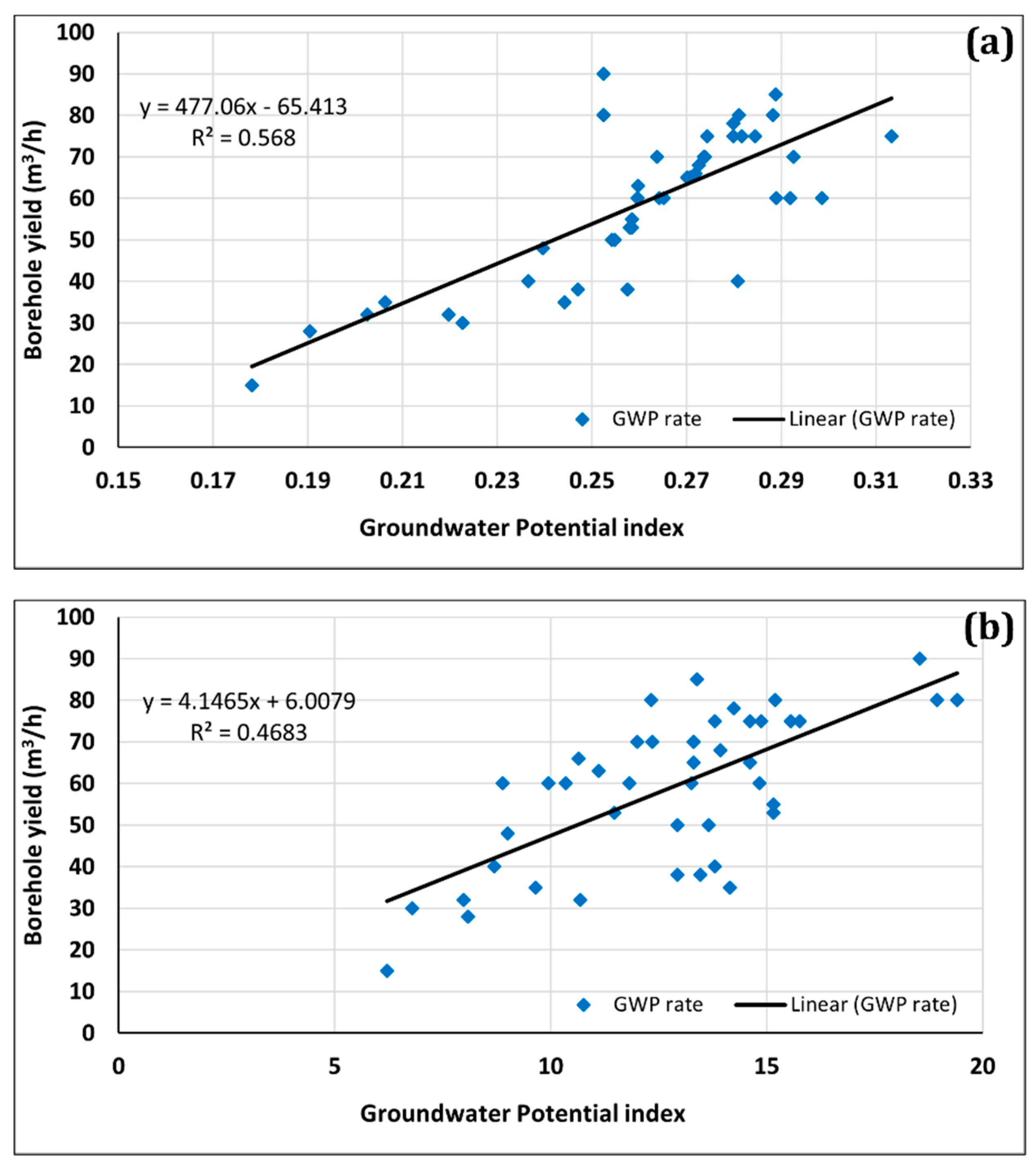
4.3. Validation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pradhan, B. Groundwater potential zonation for basaltic watersheds using satellite remote sensing data and GIS techniques. Cent. Eur. J. Geosci. 2009, 1, 120–129. [Google Scholar] [CrossRef]
- Al-Shabeeb, A.A.R.; Al-Adamat, R.; Al-Fugara, A.; Al-Amoush, H.; AlAyyash, S. Delineating groundwater potential zones within the Azraq Basin of Central Jordan using multi-criteria GIS analysis. Groundw. Sustain. Dev. 2018, 7, 82–90. [Google Scholar] [CrossRef]
- Jasrotia, A.S.; Kumar, R.; Saraf, A.K. Delineation of groundwater recharge sites using integrated remote sensing and GIS in Jammu district, India. Int. J. Remote Sens. 2007, 28, 5019–5036. [Google Scholar] [CrossRef]
- Hammouri, N.; Al-Amoush, H.; Al-Raggad, M.; Harahsheh, S. Groundwater recharge zones mapping using GIS: A case study in Southern part of Jordan Valley, Jordan. Arab. J. Geosci. 2014, 7, 2815–2829. [Google Scholar] [CrossRef]
- Kumar, P.K.D.; Gopinath, G.; Seralathan, P. Application of remote sensing and GIS for the demarcation of groundwater potential zones of a river basin in Kerala, southwest coast of India. Int. J. Remote Sens. 2007, 28, 5583–5601. [Google Scholar] [CrossRef]
- Das, S.; Pardeshi, S.D. Integration of different influencing factors in GIS to delineate groundwater potential areas using IF and FR techniques: A study of Pravara basin, Maharashtra, India. Appl. Water Sci. 2018, 8, 197. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Gupta, A.; Ghosh, S. Exploring groundwater potential zones using MIF technique in semi-arid region: A case study of Hingoli district, Maharashtra. Spat. Inf. Res. 2017, 25, 749–756. [Google Scholar] [CrossRef]
- Magesh, N.S.; Chandrasekar, N.; Soundranayagam, J.P. Delineation of groundwater potential zones in Theni district, Tamil Nadu, using remote sensing, GIS and MIF techniques. Geosci. Front. 2012, 3, 189–196. [Google Scholar] [CrossRef] [Green Version]
- Saaty, T.L. What is the analytic hierarchy process. In Mathematical Models for Decision Support; Springer: Berlin/Heidelberg, Germany, 1988; pp. 109–121. [Google Scholar]
- Agarwal, E.; Agarwal, R.; Garg, R.D.; Garg, P.K. Delineation of groundwater potential zone: An AHP/ANP approach. J. Earth Syst. Sci. 2013, 122, 887–898. [Google Scholar] [CrossRef] [Green Version]
- Jenifer, M.A.; Jha, M.K. Comparison of Analytic Hierarchy Process, Catastrophe and Entropy techniques for evaluating groundwater prospect of hard-rock aquifer systems. J. Hydrol. 2017, 548, 605–624. [Google Scholar] [CrossRef]
- Rahmati, O.; Nazari Samani, A.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2015, 8, 7059–7071. [Google Scholar] [CrossRef]
- Das, S. Comparison among influencing factor, frequency ratio, and analytical hierarchy process techniques for groundwater potential zonation in Vaitarna basin, Maharashtra, India. Groundw. Sustain. Dev. 2019, 8, 617–629. [Google Scholar] [CrossRef]
- Mohammadi-Behzad, H.R.; Charchi, A.; Kalantari, N.; Nejad, A.M.; Vardanjani, H.K. Delineation of groundwater potential zones using remote sensing (RS), geographical information system (GIS) and analytic hierarchy process (AHP) techniques: A case study in the Leylia–Keynow watershed, southwest of Iran. Carbonates Evaporites 2019, 34, 1307–1319. [Google Scholar] [CrossRef]
- Arulbalaji, P.; Padmalal, D.; Sreelash, K. GIS and AHP Techniques Based Delineation of Groundwater Potential Zones: A case study from Southern Western Ghats, India. Sci. Rep. 2019, 9, 2082. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, Y.; Yu, N.; Wan, J. Fuzzy comprehensive approach based on AHP and entropy combination weight for pipeline leak detection system performance evaluation. In Proceedings of the 2012 IEEE International Systems Conference, Vancouver, BC, Canada, 19–22 March 2012; pp. 606–611. [Google Scholar]
- Waris, M.; Panigrahi, S.; Mengal, A.; Soomro, M.I.; Mirjat, N.H.; Ullah, M.; Azlan, Z.S.; Khan, A. An Application of Analytic Hierarchy Process (AHP) for Sustainable Procurement of Construction Equipment: Multicriteria-Based Decision Framework for Malaysia. Math. Probl. Eng. 2019, 2019, 6391431. [Google Scholar] [CrossRef]
- Guru, B.; Seshan, K.; Bera, S. Frequency ratio model for groundwater potential mapping and its sustainable management in cold desert, India. J. King Saud Univ. Sci. 2017, 29, 333–347. [Google Scholar] [CrossRef] [Green Version]
- Trabelsi, F.; Lee, S.; Khlifi, S.; Arfaoui, A. Frequency Ratio Model for Mapping Groundwater Potential Zones Using GIS and Remote Sensing; Medjerda Watershed Tunisia; Springer: Cham, Switzerland, 2019; pp. 341–345. [Google Scholar]
- Ahmadi, H.; Kaya, O.A.; Babadagi, E.; Savas, T.; Pekkan, E. GIS-Based Groundwater Potentiality Mapping Using AHP and FR Models in Central Antalya, Turkey. Environ. Sci. Proc. 2020, 5, 8741. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Abu El-Magd, S.A.; Embaby, A. To investigate groundwater potentiality, a GIS-based model was integrated with remote sensing data in the Northwest Gulf of Suez (Egypt). Arab. J. Geosci. 2021, 14, 2737. [Google Scholar] [CrossRef]
- Lee, S.; Kim, Y.S.; Oh, H.J. Application of a weights-of-evidence method and GIS to regional groundwater productivity potential mapping. J. Environ. Manag. 2012, 96, 91–105. [Google Scholar] [CrossRef]
- Sahoo, S.; Munusamy, S.B.; Dhar, A.; Kar, A.; Ram, P. Appraising the Accuracy of Multi-Class Frequency Ratio and Weights of Evidence Method for Delineation of Regional Groundwater Potential Zones in Canal Command System. Water Resour. Manag. 2017, 31, 4399–4413. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Nobre, A.D.; Melesse, A.M. Development of an automated GIS tool for reproducing the HAND terrain model. Environ. Model. Softw. 2018, 102, 1–12. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Rahmati, O.; Melesse, A.M. Application of Dempster–Shafer theory, spatial analysis and remote sensing for groundwater potentiality and nitrate pollution analysis in the semi-arid region of Khuzestan, Iran. Sci. Total Environ. 2016, 568, 1110–1123. [Google Scholar] [CrossRef]
- Abu El-Magd, S.A.; Eldosouky, A.M. An improved approach for predicting the groundwater potentiality in the low desert lands; El-Marashda area, Northwest Qena City, Egypt. J. Afr. Earth Sci. 2021, 179, 104200. [Google Scholar] [CrossRef]
- Hou, E.; Wang, J.; Chen, W. A comparative study on groundwater spring potential analysis based on statistical index, index of entropy and certainty factors models. Geocarto Int. 2018, 33, 754–769. [Google Scholar] [CrossRef]
- Ozdemir, A. GIS-based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydrol. 2011, 411, 290–308. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef]
- Garcia-Ayllon, S.; Radke, J. Diffuse Anthropization Impacts in Vulnerable Protected Areas: Comparative Analysis of the Spatial Correlation between Land Transformation and Ecological Deterioration of Three Wetlands in Spain. ISPRS Int. J. Geo Inf. 2021, 10, 630. [Google Scholar] [CrossRef]
- Witkowski, W.T.; Hejmanowski, R. Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir. Appl. Sci. 2020, 10, 3287. [Google Scholar] [CrossRef]
- Greenbaum, D. Structural influences on the occurrence of groundwater in SE Zimbabwe. Geol. Soc. Spec. Publ. 1992, 66, 77–85. [Google Scholar] [CrossRef]
- Abdelmohsen, K.; Sultan, M.; Save, H.; Abotalib, A.Z.; Yan, E. What can the GRACE seasonal cycle tell us about lake-aquifer interactions? Earth Sci. Rev. 2020, 211, 103392. [Google Scholar] [CrossRef]
- Aggour, T.A.; Korany, E.A.; Mosaad, S.; Kehew, A.E. Geological conditions and characteristics of the Nubia Sandstone aquifer system and their hydrogeological impacts, Tushka area, south Western Desert, Egypt. Egypt J. Pure Appl. Sci. 2012, 50, 27–37. [Google Scholar] [CrossRef]
- Ghoubachi, S.Y. Impact of Lake Nasser on the groundwater of the Nubia sandstone aquifer system in Tushka area, South Western Desert, Egypt. J. King Saud Univ. Sci. 2012, 24, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Sultan, M. Assessment of the long-term hydrologic impacts of Lake Nasser and related irrigation projects in southwestern Egypt. J. Hydrol. 2002, 262, 68–83. [Google Scholar] [CrossRef]
- Geological Map of Egypt, El Sad El Ali-Sheet, Scale 1:500,000; CONOCO Coral, and Egyptian General Petroleum Company: Cairo, Egypt, 1987.
- Sultan, M.; Chamberlain, K.R.; Bowring, S.A.; Arvidson, R.E.; Abuzied, H.; El Kaliouby, B. Geochronologic and isotopic evidence for involvement of pre-Pan- African crust in the Nubian shield, Egypt. Geology 1990, 18, 761–764. [Google Scholar] [CrossRef]
- Stern, R.J.; Kroner, A. Late Precambrian crustal evolution in NE Sudan: Isotopic and geochronologic constraints. J. Geol. 1993, 101, 555–574. [Google Scholar] [CrossRef]
- Issawi, B. Review of Upper Cretaceous-Lower Tertiary Stratigraphy in Central and Southern Egypt. Am. Assoc. Pet. Geol. Bull. 1972, 56, 1448–1463. [Google Scholar] [CrossRef]
- Issawi, B. Geology of the southwestern desert of Egypt. Ann. Geol. Surv. Egypt 1982, 11, 57–66. [Google Scholar]
- Darwish, M.A.G. Geochemistry of the High Dam Lake sediments, south Egypt: Implications for environmental significance. Int. J. Sediment Res. 2013, 28, 544–559. [Google Scholar] [CrossRef]
- AbdelMoneim, A.A.; Zaki, S.; Diab, M. Groundwater Conditions and the Geoenvironmental Impacts of the Recent Development in the South Eastern Part of the Western Desert of Egypt. J. Water Resour. Prot. 2014, 06, 381–401. [Google Scholar] [CrossRef] [Green Version]
- Sharaky, A.M.; El Abd, E.S.A.; Shanab, E.F. Groundwater Assessment for Agricultural Irrigation in Toshka Area, Western Desert, Egypt. Handb. Environ. Chem. 2019, 74, 347–387. [Google Scholar] [CrossRef]
- Jasrotia, A.S.; Kumar, A.; Singh, R. Integrated remote sensing and GIS approach for delineation of groundwater potential zones using aquifer parameters in Devak and Rui watershed of Jammu and Kashmir, India. Arab. J. Geosci. 2016, 9, 304. [Google Scholar] [CrossRef]
- Sallam, O.M. Aquifers Parameters Estimation Using Well Log and Pumping Test Data, in Arid Regions -Step in Sustainable Development. In Proceedings of the the 2nd International Conference on Water Resources & Arid Environment, Muscat, Oman, 21–24 September 2006; pp. 1–12. [Google Scholar]
- O’leary, D.W.; Friedman, J.D.; Pohn, H.A. Lineament, linear, lineation: Some proposed new standards for old terms. Bull. Geol. Soc. Am. 1976, 87, 1463–1469. [Google Scholar] [CrossRef]
- Sitender, R. Delineation of groundwater potential zones in Mewat District, Haryana, India. Int. J. Geomat. Geosci. 2019, 2, 270–281. [Google Scholar]
- PCI Geomatica-10, Version 10.3.1; PCI Geomatics Enterprises Inc: Markham, ON, Canada, 2010.
- Alikhanov, B.; Juliev, M.; Alikhanova, S.; Mondal, I. Assessment of influencing factor method for delineation of groundwater potential zones with geospatial techniques. Case study of Bostanlik district, Uzbekistan. Groundw. Sustain. Dev. 2021, 12, 100548. [Google Scholar] [CrossRef]
- Etikala, B.; Golla, V.; Li, P.; Renati, S. Deciphering groundwater potential zones using MIF technique and GIS: A study from Tirupati area, Chittoor District, Andhra Pradesh, India. HydroResearch 2019, 1, 1–7. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision-Making with the AHP: Why is the Principal Eigenvector Necessary? Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar] [CrossRef]
- Saaty, T.L. An Exposition of the AHP in Reply to the Paper “Remarks on the Analytic Hierarchy Process". Manag. Sci. 1990, 36, 259–268. [Google Scholar] [CrossRef]
- Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Manap, M.A.; Sulaiman, W.N.A.; Ramli, M.F.; Pradhan, B.; Surip, N. A knowledge-driven GIS modeling technique for groundwater potential mapping at the Upper Langat Basin, Malaysia. Arab. J. Geosci. 2013, 6, 1621–1637. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar]
- Andualem, T.G.; Demeke, G.G. Groundwater potential assessment using GIS and remote sensing: A case study of Guna tana landscape, upper blue Nile Basin, Ethiopia. J. Hydrol. Reg. Stud. 2019, 24, 100610. [Google Scholar] [CrossRef]
- Oikonomidis, D.; Dimogianni, S.; Kazakis, N.; Voudouris, K. A GIS/Remote Sensing-based methodology for groundwater potentiality assessment in Tirnavos area, Greece. J. Hydrol. 2015, 525, 197–208. [Google Scholar] [CrossRef]
- Lentswe, G.B.; Molwalefhe, L. Delineation of potential groundwater recharge zones using analytic hierarchy process-guided GIS in the semi-arid Motloutse watershed, eastern Botswana. J. Hydrol. Reg. Stud. 2020, 28, 100674. [Google Scholar] [CrossRef]


| Hydraulic Conductivity | Distance from Lake | Lineament Density | Surface Lithology | Topography | Slope | Drainage Density | Static Water Level | |
|---|---|---|---|---|---|---|---|---|
| Hydraulic Conductivity | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 |
| Distance from Lake | ½ | 1 | 2 | 3 | 3 | 4 | 4 | 5 |
| Lineament Density | ½ | ½ | 1 | 2 | 2 | 3 | 3 | 4 |
| Surface Lithology | ⅓ | ⅓ | ½ | 1 | 2 | 3 | 3 | 4 |
| Topography | ¼ | ⅓ | ½ | ½ | 1 | 2 | 1 | 2 |
| Slope | ⅕ | ¼ | ⅓ | ⅓ | ½ | 1 | 1 | 2 |
| Drainage Density | ⅕ | ¼ | ⅓ | ⅓ | 1 | 1 | 1 | 2 |
| Static Water Level | ⅙ | ⅕ | ¼ | ¼ | ½ | ½ | ½ | 1 |
| Sum | 3.15 | 4.87 | 6.92 | 10.42 | 14.00 | 19.50 | 18.50 | 26.00 |
| Hydraulic Conductivity | Distance from Lake | Lineament Density | Surface Lithology | Topography | Slope | Drainage Density | Static Water Level | Weights | |
|---|---|---|---|---|---|---|---|---|---|
| Hydraulic Conductivity | 0.317 | 0.411 | 0.289 | 0.288 | 0.286 | 0.256 | 0.270 | 0.231 | 0.294 |
| Distance from Lake | 0.159 | 0.205 | 0.289 | 0.288 | 0.214 | 0.205 | 0.216 | 0.192 | 0.221 |
| Lineament Density | 0.159 | 0.103 | 0.145 | 0.192 | 0.143 | 0.154 | 0.162 | 0.154 | 0.151 |
| Surface Lithology | 0.106 | 0.068 | 0.072 | 0.096 | 0.143 | 0.154 | 0.162 | 0.154 | 0.119 |
| Topography | 0.079 | 0.068 | 0.072 | 0.048 | 0.071 | 0.103 | 0.054 | 0.077 | 0.072 |
| Slope | 0.063 | 0.051 | 0.048 | 0.032 | 0.036 | 0.051 | 0.054 | 0.077 | 0.052 |
| Drainage Density | 0.063 | 0.051 | 0.048 | 0.032 | 0.071 | 0.051 | 0.054 | 0.077 | 0.056 |
| Static Water Level | 0.053 | 0.041 | 0.036 | 0.024 | 0.036 | 0.026 | 0.027 | 0.038 | 0.035 |
| Sum | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Less Importance | More Importance | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 | 1.51 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| No. | Factors | Subclasses | Rating | Weights |
|---|---|---|---|---|
| 1 | Hydraulic conductivity | 0.066–3.5 | 0.053 | 0.294 |
| 3.5–6.567 | 0.158 | |||
| 6.567–9.318 | 0.211 | |||
| 9.318–11.6 | 0.263 | |||
| 11.6–16.00 | 0.316 | |||
| 2 | Distance from Lake | 0–5 | 0.316 | 0.221 |
| 5–10 | 0.263 | |||
| 10–20 | 0.211 | |||
| 20–30 | 0.158 | |||
| >30 | 0.053 | |||
| 3 | Lineament Density | 0–0.1 | 0.067 | 0.151 |
| 0.1–0.2 | 0.133 | |||
| 0.2–0.3 | 0.200 | |||
| 0.3–0.4 | 0.267 | |||
| >0.4 | 0.333 | |||
| 4 | Surface lithology | Igneous and Metamorphic rocks | 0.059 | 0.119 |
| Clay, claystone, fine sandstone, and sand sheets | 0.118 | |||
| Limestone of Kurukur and Garra Fms. | 0.176 | |||
| Wadi and Quaternary deposits | 0.294 | |||
| Nubian Sandstone and Gravels | 0.353 | |||
| 5 | Topography | <200 | 0.353 | 0.072 |
| 200–230 | 0.294 | |||
| 230–260 | 0.176 | |||
| 260–300 | 0.118 | |||
| >300 | 0.059 | |||
| 6 | Slope | 0–1.5 | 0.333 | 0.052 |
| 5–3 | 0.267 | |||
| 3–7.5 | 0.200 | |||
| 7.5–20 | 0.133 | |||
| >20 | 0.067 | |||
| 7 | Drainage Density | <0.46 | 0.333 | 0.056 |
| 0.46–0.65 | 0.267 | |||
| 0.65–0.78 | 0.200 | |||
| 0.78–0.93 | 0.133 | |||
| 0.93–1.38 | 0.067 | |||
| 8 | Static water level | 0–50 | 0.353 | 0.035 |
| 50–100 | 0.294 | |||
| 100–150 | 0.176 | |||
| 150–200 | 0.118 | |||
| >200 | 0.059 |
| No. | Factors | Subclasses | No. of Pixels | Percentage of Subclass | No. of Wells | Percentage of Wells | FR |
|---|---|---|---|---|---|---|---|
| 1 | Hydraulic conductivity | 0.066–3.5 | 210,565 | 14.70 | 0 | 0.00 | 0.000 |
| 3.5–6.567 | 227,811 | 15.91 | 1 | 2.27 | 0.143 | ||
| 6.567–9.318 | 338,147 | 23.61 | 3 | 6.82 | 0.289 | ||
| 9.318–11.6 | 339,749 | 23.72 | 11 | 25.00 | 1.054 | ||
| 11.6–16.00 | 315,848 | 22.05 | 29 | 65.91 | 2.988 | ||
| 2 | Distance from Lake | 0–5 | 281,709 | 19.63 | 20 | 45.45 | 2.316 |
| 5–10 | 227,445 | 15.85 | 17 | 38.64 | 2.438 | ||
| 10–20 | 371,659 | 25.89 | 5 | 11.36 | 0.439 | ||
| 20–30 | 259,197 | 18.06 | 2 | 4.55 | 0.252 | ||
| >30 | 295,346 | 20.58 | 0 | 0.00 | 0.000 | ||
| 3 | Lineament Density | 0–0.1 | 346,082 | 24.11 | 15 | 34.09 | 1.414 |
| 0.1–0.2 | 487,932 | 34.00 | 9 | 20.45 | 0.602 | ||
| 0.2–0.3 | 329,150 | 22.93 | 7 | 15.91 | 0.694 | ||
| 0.3–0.4 | 193,369 | 13.47 | 7 | 15.91 | 1.181 | ||
| >0.4 | 78,730 | 5.49 | 6 | 13.64 | 2.486 | ||
| 4 | Surface lithology | Ign. And Meta. Rocks | 52,600 | 3.66 | 0 | 0.00 | 0.000 |
| Clays, fine s.s, and sand sheets | 697,457 | 48.59 | 17 | 38.64 | 0.795 | ||
| L.S of Kurukur and Garra Fms. | 17,444 | 1.22 | 3 | 6.82 | 5.610 | ||
| Wadi and Qs. Deposits | 13,411 | 0.93 | 0 | 0.00 | 0.000 | ||
| Nubian S.S and Gravels | 654,459 | 45.60 | 24 | 54.55 | 1.196 | ||
| 5 | Topography | <200 | 276,288 | 19.25 | 21 | 47.73 | 2.479 |
| 200–230 | 384,425 | 26.78 | 19 | 43.18 | 1.612 | ||
| 230–260 | 356,523 | 24.84 | 4 | 9.09 | 0.366 | ||
| 260–300 | 307,777 | 21.44 | 0 | 0.00 | 0.000 | ||
| >300 | 110,307 | 7.69 | 0 | 0.00 | 0.000 | ||
| 6 | Slope | 0–1.5 | 729,970 | 51.13 | 24 | 54.55 | 1.067 |
| 5–3 | 545,889 | 38.23 | 18 | 40.91 | 1.070 | ||
| 3–7.5 | 106,144 | 7.43 | 2 | 4.55 | 0.611 | ||
| 7.5–20 | 32,691 | 2.29 | 0 | 0.00 | 0.000 | ||
| >20 | 13,106 | 0.92 | 0 | 0.00 | 0.000 | ||
| 7 | Drainage Density | <0.46 | 927,935 | 6.47 | 0 | 0.00 | 0.000 |
| 0.46–0.65 | 3,121,085 | 21.75 | 19 | 43.18 | 1.986 | ||
| 0.65–0.78 | 4,592,402 | 32.00 | 7 | 15.91 | 0.497 | ||
| 0.78–0.93 | 4,046,225 | 28.19 | 13 | 29.55 | 1.048 | ||
| 0.93–1.38 | 1,664,497 | 11.60 | 5 | 11.36 | 0.980 | ||
| 8 | Static water level | 0–50 | 232,236 | 16.18 | 15 | 34.09 | 2.107 |
| 50–100 | 573,308 | 39.95 | 25 | 56.82 | 1.422 | ||
| 100–150 | 454,686 | 31.68 | 4 | 9.09 | 0.287 | ||
| 150–200 | 156,139 | 10.88 | 0 | 0.00 | 0.000 | ||
| >200 | 18,782 | 1.31 | 0 | 0.00 | 0.000 |
| AHP Model | FR Model | |||||||
|---|---|---|---|---|---|---|---|---|
| Range | Area (km2) | Area% | Pumping Wells | Range | Area (km2) | Area% | Pumping Wells | |
| Very Low | 0.0787–0.142 | 1906.24 | 13.43 | 0 | 0.891–4.701 | 3275.38 | 23.07 | 0 |
| Low | 0.142–0.196 | 3662.00 | 25.80 | 2 | 4.701–7.38 | 3592.61 | 25.31 | 2 |
| Moderate | 0.196–0.242 | 4452.89 | 31.37 | 6 | 7.38–10.65 | 4004.96 | 28.21 | 9 |
| High | 0.242–0.3167 | 4174.97 | 29.41 | 36 | 10.65–20.09 | 3323.26 | 23.41 | 33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masoud, A.M.; Pham, Q.B.; Alezabawy, A.K.; El-Magd, S.A.A. Efficiency of Geospatial Technology and Multi-Criteria Decision Analysis for Groundwater Potential Mapping in a Semi-Arid Region. Water 2022, 14, 882. https://doi.org/10.3390/w14060882
Masoud AM, Pham QB, Alezabawy AK, El-Magd SAA. Efficiency of Geospatial Technology and Multi-Criteria Decision Analysis for Groundwater Potential Mapping in a Semi-Arid Region. Water. 2022; 14(6):882. https://doi.org/10.3390/w14060882
Chicago/Turabian StyleMasoud, Ahmed M., Quoc Bao Pham, Ahmed K. Alezabawy, and Sherif A. Abu El-Magd. 2022. "Efficiency of Geospatial Technology and Multi-Criteria Decision Analysis for Groundwater Potential Mapping in a Semi-Arid Region" Water 14, no. 6: 882. https://doi.org/10.3390/w14060882









