Optimal Location of Water Quality Monitoring Stations Using an Artificial Neural Network Modeling in the Qarah-Chay River Basin, Iran
Abstract
:1. Introduction
2. Materials and Methods
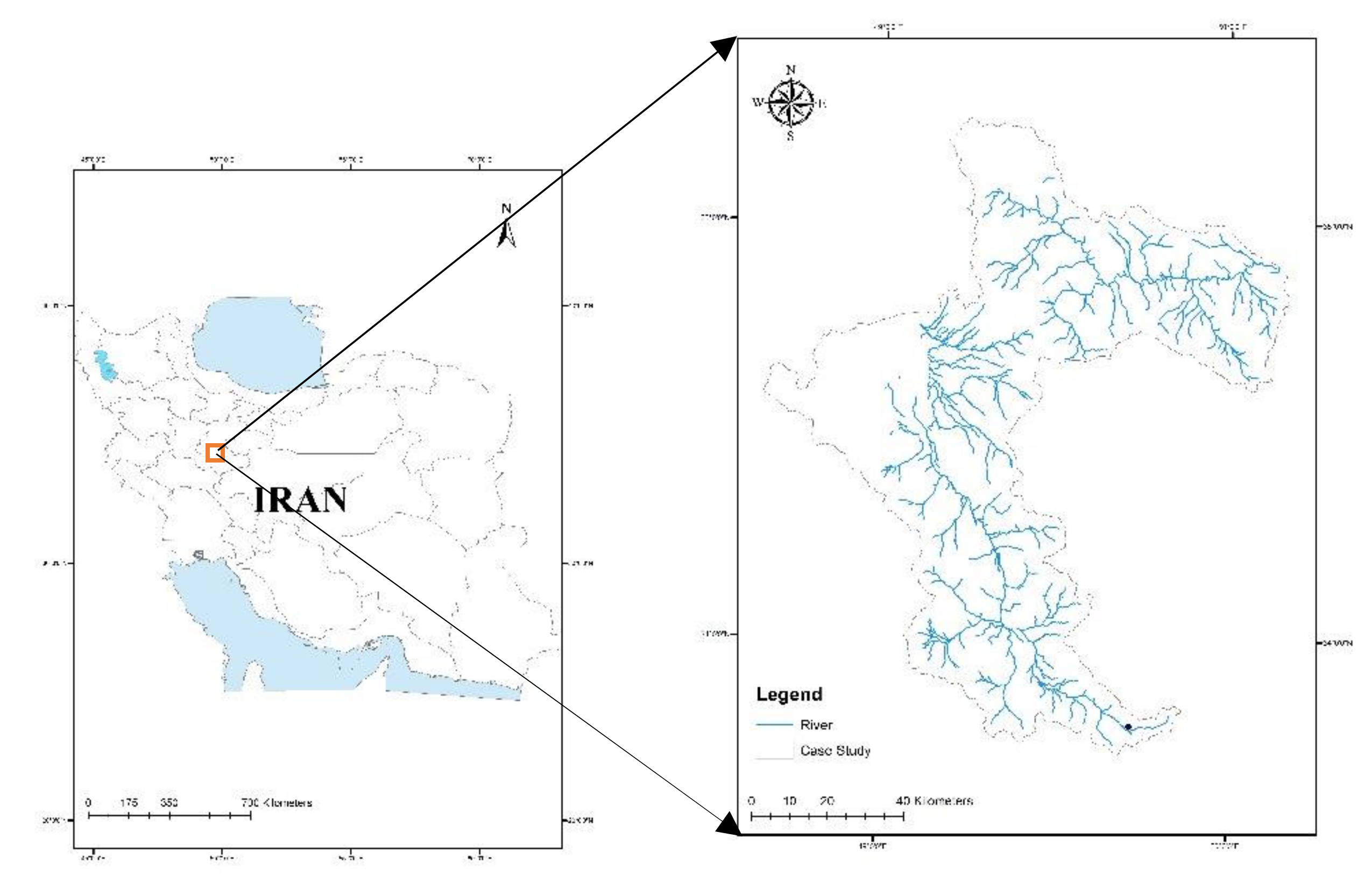
2.1. Study Area
2.2. Data and Methods
2.2.1. Data Base
Model Input Information
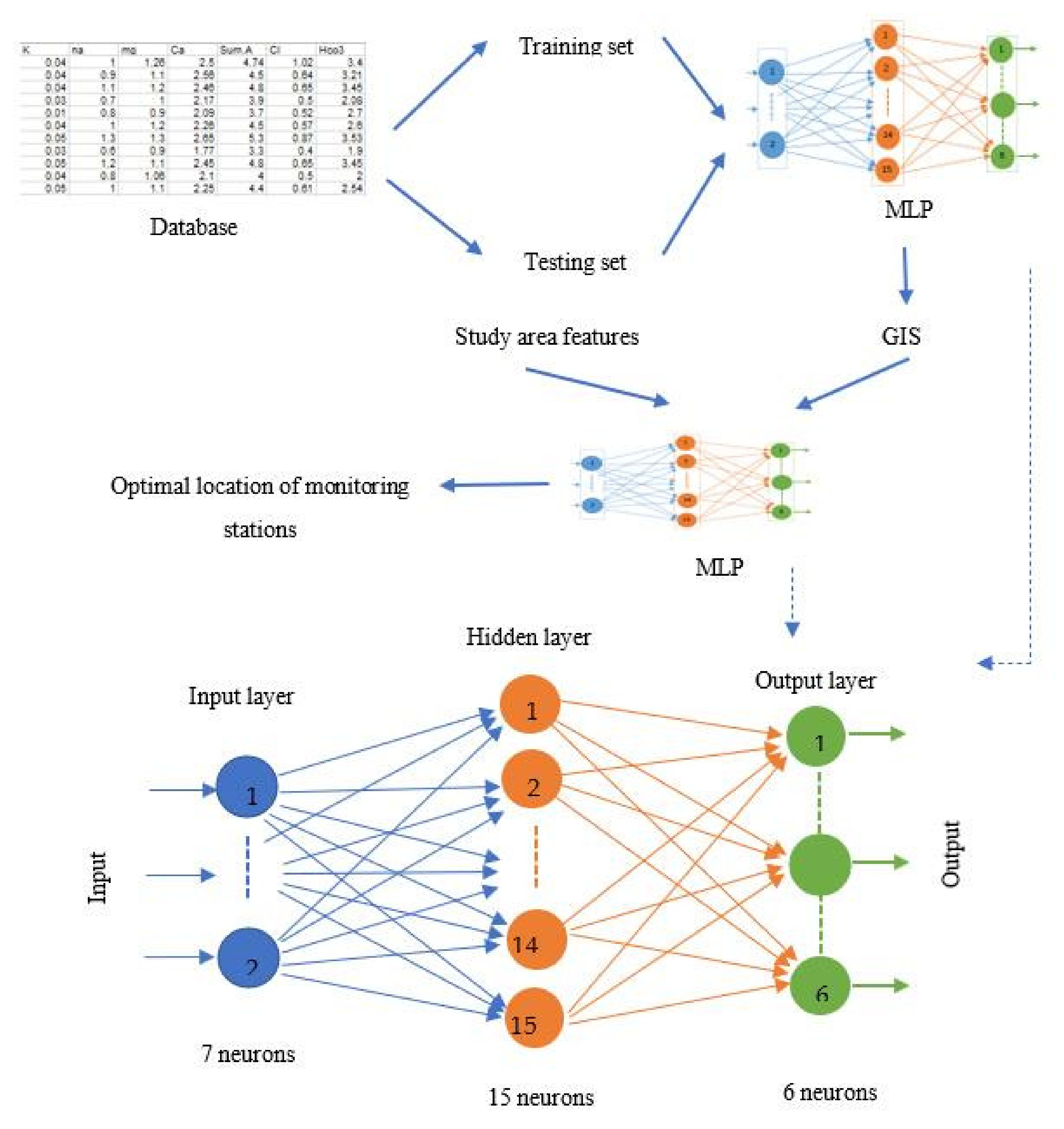
2.2.2. Multilayer Perceptron (MLP) Neural Network
2.2.3. Evaluation Criteria of the Proposed Model
3. Results
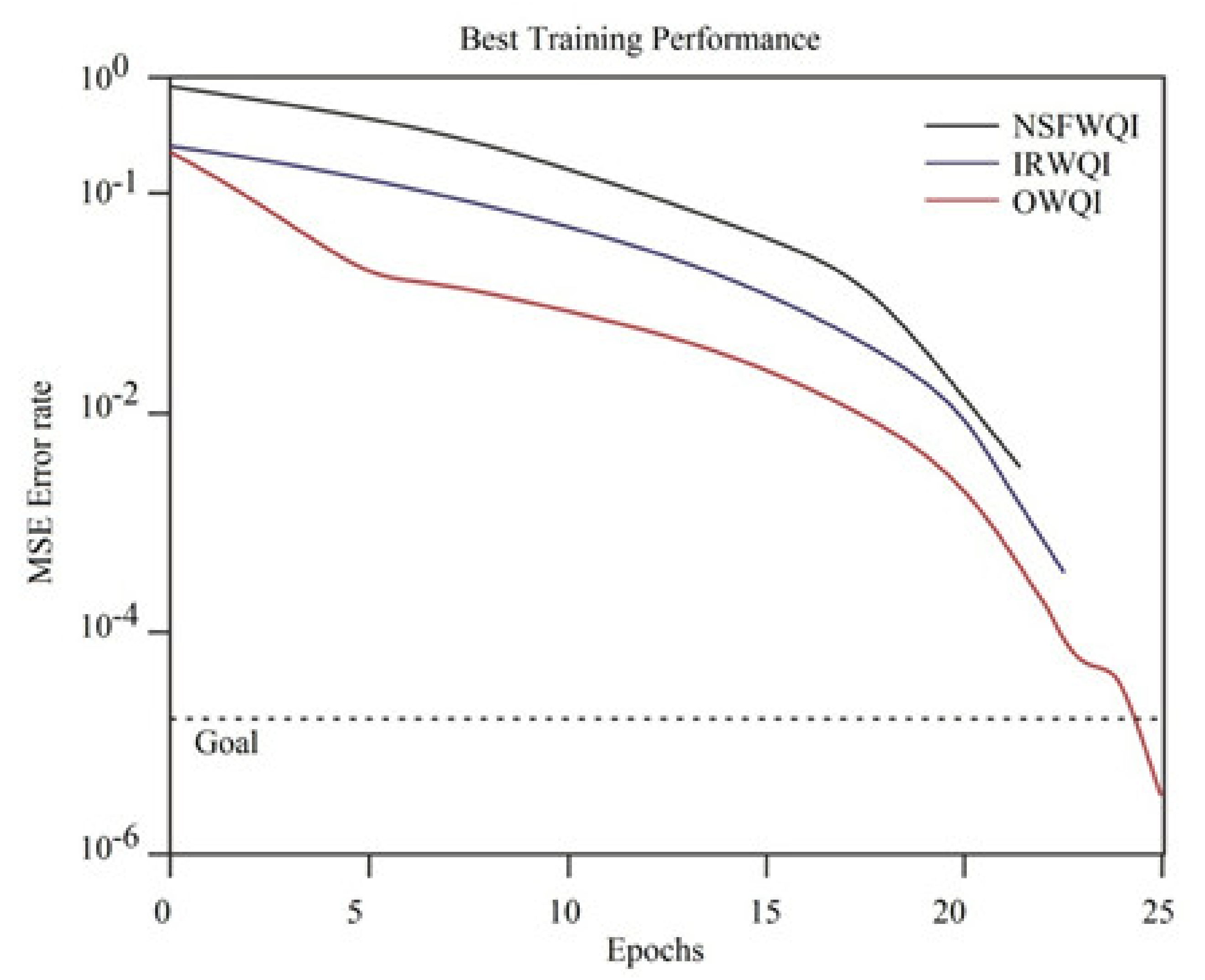
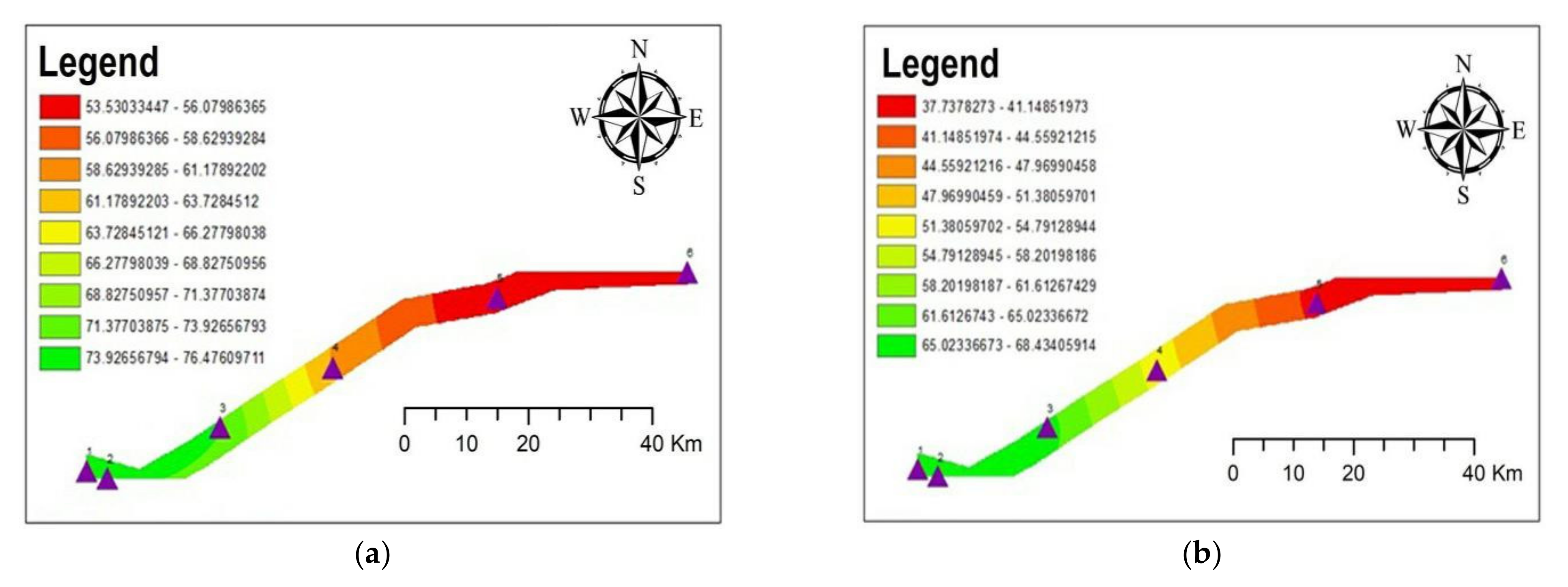
3.1. Quantitative Results
3.2. Data Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dimri, D.; Daverey, A.; Humar, A.; Sharma, A. Monitoring water quality of River Ganga Using Multivariate Techniques and WQI in Upper Ganga Basin of Uttarakhand, India. Environ. Nanotechnol. 2020, 15, 100375. [Google Scholar]
- Salman, R.; Nikoo, M.R.; Shojaeezadeh, S.A.; Bahman Beiglou, P.H.; Sadegh, M.; Adamowski, J.F.; Alamdari, N. A novel Bayesian maximum entropy-based approach for optimal design of water quality monitoring networks in rivers. J. Hydrol. 2021, 603, 126822. [Google Scholar] [CrossRef]
- UNEP. A Snapshot of the World’s Water Quality: Towards a Global Assessment. In Technical Report–United Nations Environment Programme; UNEP: Nairobi, Kenya, 2016. [Google Scholar]
- Kim, H.G.; Hong, S.; Jeong, K.S.; Kim, D.K.; Joo, G.J. Determination of sensitive variables regardless of hydrological alteration in artificial neural network model of chlorophyll a: Case study of Nakdong River. Ecol. Model. 2019, 398, 67–76. [Google Scholar] [CrossRef]
- Vega-Rodríguez, M.A.; Pérez, C.J.; Reder, K.; Flörke, M. A Stage-Based Approach to AllocatingWater Quality Monitoring Stations Based on the World Qual Model: The Jubba River as a Case Study. Sci. Total Environ. 2020, 762, 144162. [Google Scholar] [CrossRef] [PubMed]
- Banik, B.K.; Alfonso, A.; Torres, A.S.; Mynett, A.; Di Cristo, C.; Leopardi, A. Optimal placement of water quality monitoring stations in sewer systems: An information theory approach. Procedia Eng. 2015, 119, 1308–1317. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Paik, K.; Yoo, D.G.; Kim, J.H. Efficient method for optimal placing of water quality monitoring stations for an ungauged basin. J. Environ. Manag. 2014, 132, 24–31. [Google Scholar] [CrossRef]
- Mahjouri, N.; Kerachian, R. Optimal Location of River Water Quality Monitoring Stations using the Discrete Entropy Theory: A Case Study. In Proceedings of the IWA World Water Congress and Exhibition, Vienna, Austria, 7–12 September 2008. [Google Scholar]
- Asadollahfardi, G.; Heidarzadeh, N.; Sekhavati, A.; Asadi, M. Optimization of water quality monitoring stations using dynamic programming approach, a case study of the Mond Basin Rivers. Iran. Environ. Dev. Sustain. 2008, 23, 2867–2881. [Google Scholar] [CrossRef]
- Varekar, V.; Yadav, V.; Karmakar, S. Rationalization of water quality monitoring locations under spatiotemporal heterogeneity of diffuse pollution using seasonal export coefficient. J. Environ. Manag. 2021, 277, 111342. [Google Scholar] [CrossRef]
- Park, S.Y.; Choi, J.H.; Wang, S.; Park, S.S. Design of a water quality monitoring network in a large river system using the genetic algorithm. Ecol. Model 2006, 199, 289–297. [Google Scholar] [CrossRef]
- Telci, I.T.; Nam, K.; Guan, J.; Aral, M.M. Optimal water quality monitoring network design for river systems. J. Environ. Manag. 2009, 90, 2987–2998. [Google Scholar] [CrossRef]
- Ozkul, S.; Harmancioglu, N.B.; Singh, V.P. Entropy-based assessment of water quality monitoring networks. J. Hydrol. Eng. 2000, 5, 90–100. [Google Scholar] [CrossRef] [Green Version]
- Karamouz, M.; Nokhandan, A.K.; Kerachian, R.; Maksimovic, C. Design of online river water quality monitoring systems using the entropy theory: A case study. Environ. Monit. Assess 2009, 155, 63–81. [Google Scholar] [CrossRef] [PubMed]
- Romić, D.; Castrignano, A.; Romić, M.; Buttafuoco, G.; Kovačić, M.B.; Ondrašek, G.; Zovko, M. Modelling spatial and temporal variability of water quality from different monitoring stations using mixed effects model theory. Sci. Total Environ. 2019, 704, 135875. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Niazmardi, S. A Novel Multiple-Kernel Support Vector Regression Algorithm for Estimation of Water Quality Parameters. Nat. Resour. Res. 2021, 30, 3761–3775. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Farhadi, H. Reliability assessment of water quality index based on guidelines of national sanitation foundation in natural streams: Integration of remote sensing and data-driven models. Artif. Intell. Rev. 2021, 54, 4619–4651. [Google Scholar] [CrossRef]
- Krtolica, I.; Cvijanović, D.; Obradović, D.; Novković, M.; Milošević, D.; Savić, D.; Vojinović-Miloradov, M.; Radulović, S. Water quality and macrophytes in the Danube River: Artificial neural network modelling. Ecol. Indic. 2021, 121, 107076. [Google Scholar] [CrossRef]
- Gajendran, C.; Srinivasamoorthy, K.; Thamarai, P. GIS and Geostatistical Techniques for Groundwater Science; Elsevier: Amsterdam, The Netherlands, 2019; pp. 153–164. [Google Scholar] [CrossRef]
- Saber, A.; James, D.E.; Hayes, D.F. Estimation of water quality profiles in deep lakes based on easily measurable constituents at the water surface using artificial neural networks coupled with stationary wavelet transform. Sci. Total Environ. 2019, 694, 133690. [Google Scholar] [CrossRef]
- Zhang, L.; Han, X.; Yuan, B.; Zhang, A.; Feng, J.; Zhang, J. Mechanism of purification of low-pollution river water using a modified biological contact oxidation process and artificial neural network modeling. J. Environ. Chem. Eng. 2021, 9, 104832. [Google Scholar] [CrossRef]
- Kadiyala, P.K.; Chattopadhyay, H. Optimal location of three heat sources on the wall of a square cavity using genetic algorithms integrated with artificial neural networks. Int. Commun. Heat Mass Transf. 2011, 38, 620–624. [Google Scholar] [CrossRef]
- Nayak, J.G.; Patil, L.G.; Patki, V.K. Artificial neural network based water quality index (WQI) for river Godavari (India). Mater. Today Proc. 2021, 52. [Google Scholar] [CrossRef]
- Sarkar, A.; Pandey, O. River water quality modelling using artificial neural network technique. Aquat. Procedia 2015, 4, 1070–1077. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Reineh, S.M.M.; Abolghasemi, M. Spatial predication of flood zonation mapping in Kan River Basin, Iran, using artificial neural network algorithm. Weather Clim. Extrem. 2019, 25, 100215. [Google Scholar] [CrossRef]
- Zhu, H.; Leandro, J.; Lin, Q. Optimization of Artificial Neural Network (ANN) for Maximum Flood Inundation Forecasts. Water 2021, 13, 2252. [Google Scholar] [CrossRef]
- Chang, F.J.; Chiang, Y.M.; Chang, L.C. Multi-step-ahead neural networks for flood forecasting. Hydrol. Sci. J. 2007, 52, 114–130. [Google Scholar] [CrossRef]
- Mitrović, T.; Antanasijević, D.; Lazović, S.; Perić-Grujić, A.; Ristić, M. Virtual water quality monitoring at inactive monitoring sites using Monte Carlo optimized artificial neural networks: A case study of Danube River (Serbia). Sci. Total Environ. 2019, 654, 1000–1009. [Google Scholar] [CrossRef]
- Beck, M.W. NeuralNetTools: Visualization and Analysis Tools for Neural Networks. J. Stat. Softw. 2018, 85, 1–20. [Google Scholar] [CrossRef]
- Mitra, S.; Rashmi, N. An approach to utilize artificial neural network for runoff prediction: River perspective. Mater. Today Proc. 2021, 52. [Google Scholar] [CrossRef]
- Qiu, R.; Wang, Y.; Wang, D.; Qiu, W.; Wu, J.; Tao, Y. Water temperature forecasting based on modified artificial neural network methods: Two cases of the Yangtze River. Sci. Total Environ. 2020, 737, 139729. [Google Scholar] [CrossRef]
- Raid, S.; Mania, J. Rainfall-runoff model using an artificial neural network approach, Math. Comput. Modell 2004, 40, 839–846. [Google Scholar] [CrossRef]
- Chanu, S.N.; Kumar, P. Application of multilayer perceptron based artificial neural network for modeling of rainfall runoff in a Himalayan. In Proceedings of the 8th International Conference on Recent Innovations in Science, Engineering and Management, New Delhi, India, 21 October 2016; p. 15. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Ar-Shad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [Green Version]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applica-tions and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Velasco, L.C.P.; Serquina, R.P.; Abdul Zamad, M.S.A.; Juanico, B.F.; Lomocso, J.C. Week-ahead Rainfall Forecasting Using Multilayer Perceptron Neural Network. Procedia Comput. Sci. 2019, 161, 386–397. [Google Scholar] [CrossRef]
- Markazi Province Department of Environment. Water Quality Study Plan of Qarah-Chay in Markazi Province. Reports and Maps Unit, Executive Deputy 2020; Markazi Province Department of Environment: Arak, Iran, 2020.
- Khosravi, A.; Syri, S. Modeling of geothermal power system equipped with absorption refrigeration and solar energy using multilayer perceptron neural network optimized with imperialist competitive algorithm. J. Clean. Prod. 2020, 276, 124216. [Google Scholar] [CrossRef]
- Ewees, A.A.; Elaziz, M.A.; Alameer, Z.; Ye, H.; Jianhua, Z. Improving multilayer perceptron neural network using chaotic grasshopper optimization algorithm to forecast iron ore price volatility. Resour. Policy 2020, 65, 101555. [Google Scholar] [CrossRef]
- Jin, D.; Lin, S. Advances in Computer Science and Information Engineering; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Shadkani, S.; Abbaspour, A.; Samadianfard, S.; Hashemi, S.; Mosavi, A.; Band, S.B. Comparative study of multilayer perceptron-stochastic gradient descent and gradient boosted trees for predicting daily suspended sediment load: The case study of the Mississippi River, U.S. Int. J. Sedim. Res. 2021, 36, 512–523. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks and Learning Machines; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Yonaba, H.; Anctil, F.; Fortin, V. Comparing Sigmoid Transfer Functions for Neural Network Multistep Ahead Streamflow Forecasting. J. Hydrol. Eng. 2010, 15, 275–283. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer: New York, NY, USA, 2018. [Google Scholar]
- Buduma, N.; Locascio, N. Fundamentals of Deep Learning: Designing Next-Generation Machine Intelligence Algorithms; O’Reilly Media: New York, NY, USA, 2017. [Google Scholar]
- Mudashiru, R.B.; Sabtu, N.; Abustan, I. Quantitative and semi-quantitative methods in flood hazard/susceptibility mapping: A review. Arab. J. Geosci. 2021, 14, 941. [Google Scholar] [CrossRef]
- Niroobakhsh, M. Prediction of water quality parameter in Jajrood River basin: Application of multi layer perceptron (MLP) perceptron and radial basis function networks of artificial neural networks (ANNs). Afr. J. Agric. Res. 2012, 7, 4131–4139. [Google Scholar] [CrossRef]
- Qishlaqi, A.; Kordian, S.; Parsaie, A. Field measurements and neural network modeling of water quality parameters. Appl. Water Sci. 2017, 7, 523. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Seo, D.; Jang, M.; Kim, J. Augmentation of limited input data using an artificial neural network method to improve the accuracy of water quality modeling in a large lake. J. Hydrol. 2021, 602, 126817. [Google Scholar] [CrossRef]



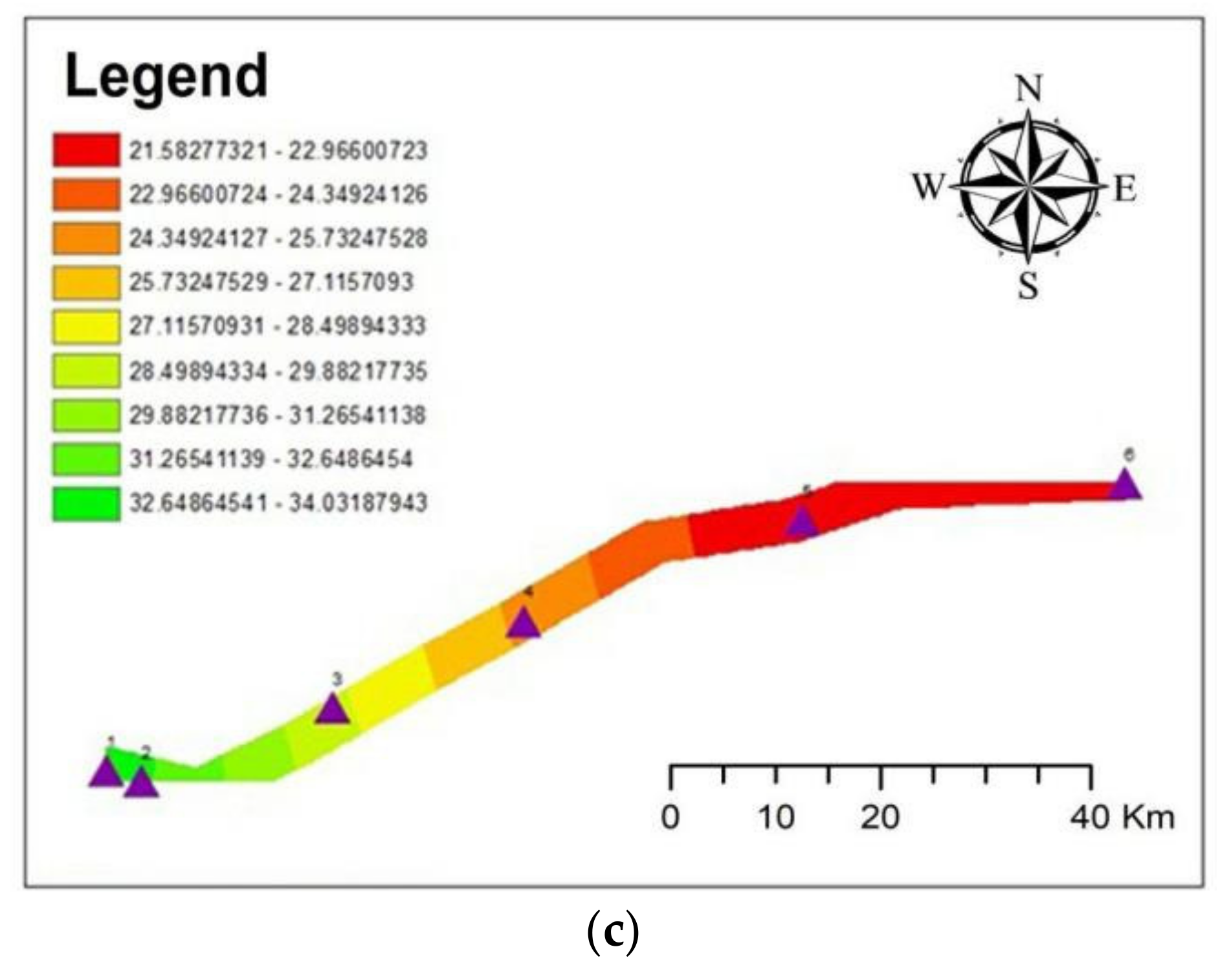
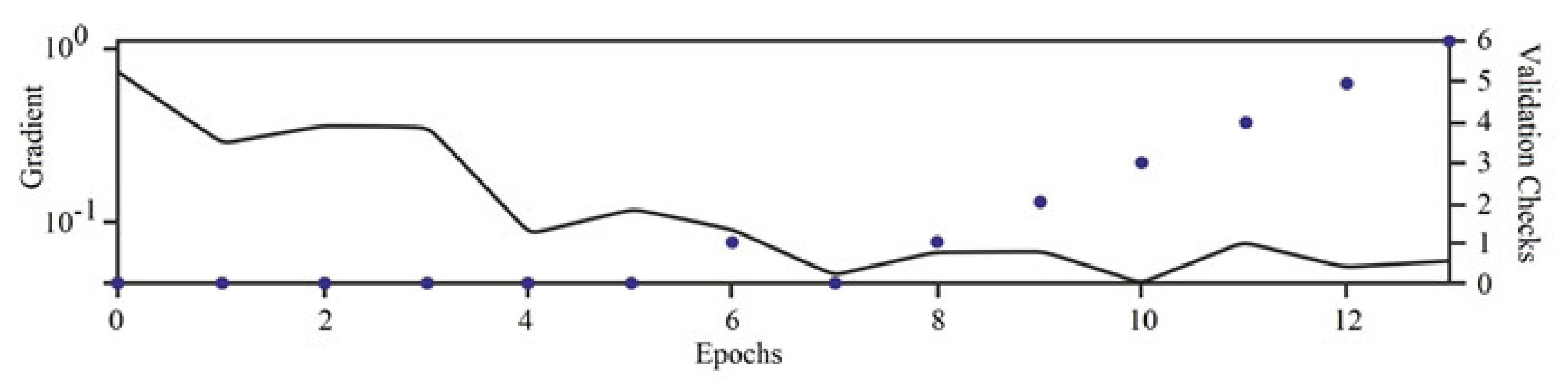
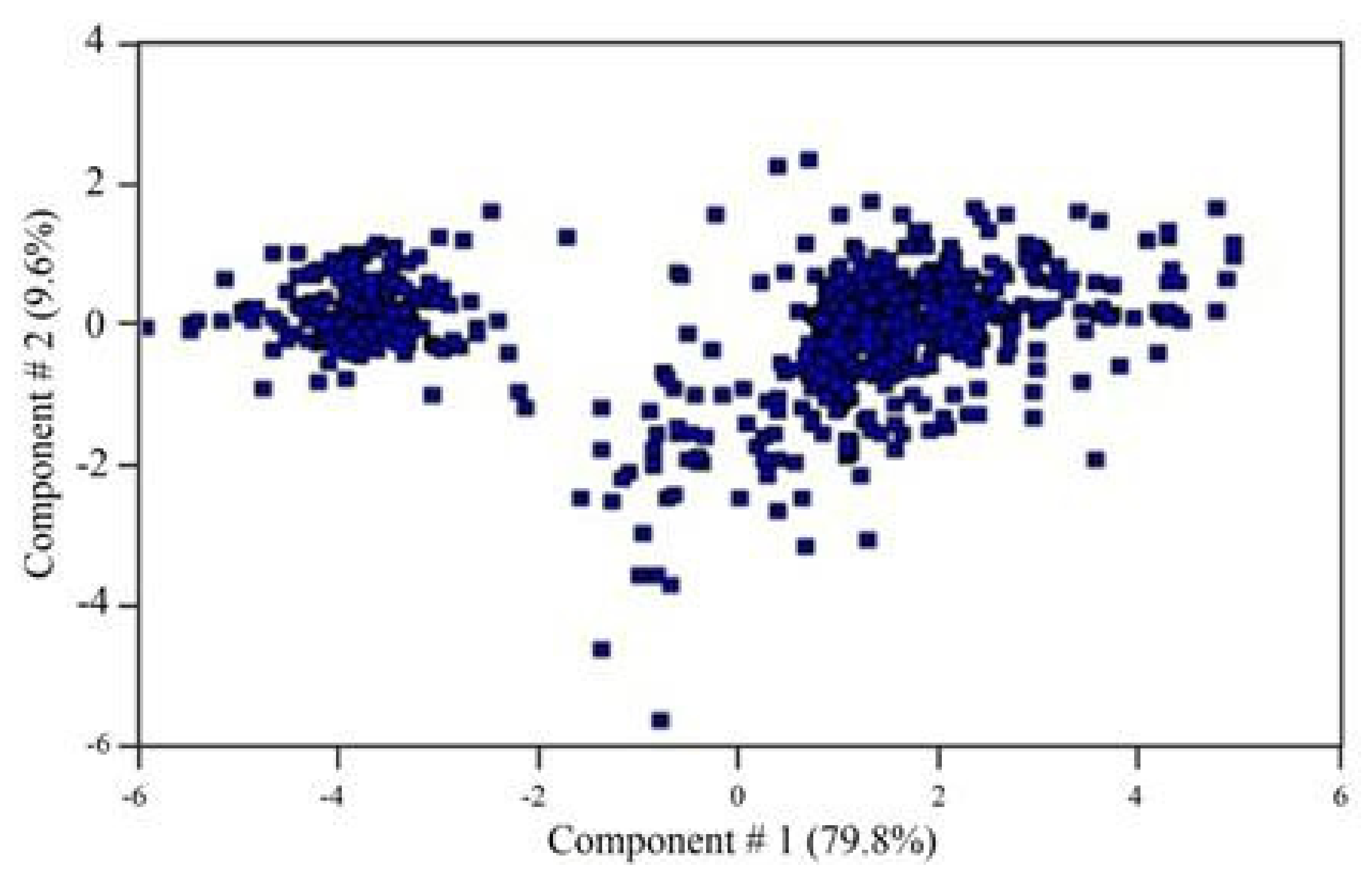
| Index | Parameter | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PH | T | TUR | DO | BOD5 | NO3 | PO4 | FC | TS | COD | TH | EC | NH4 | |
| IRWQI | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| NSFWQI | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| OWQI | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| F1 | Recall | Precision | Accuracy | |
|---|---|---|---|---|
| SVM | 0.56 | 0.60 | 0.55 | 0.60 |
| DT | 0.56 | 0.62 | 0.45 | 0.40 |
| RF | 0.37 | 0.82 | 0.51 | 0.42 |
| Proposed Method | 0.85 | 0.84 | 0.88 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goudarzi, F.; Hedayatiaghmashhadi, A.; Kazemi, A.; Fürst, C. Optimal Location of Water Quality Monitoring Stations Using an Artificial Neural Network Modeling in the Qarah-Chay River Basin, Iran. Water 2022, 14, 870. https://doi.org/10.3390/w14060870
Goudarzi F, Hedayatiaghmashhadi A, Kazemi A, Fürst C. Optimal Location of Water Quality Monitoring Stations Using an Artificial Neural Network Modeling in the Qarah-Chay River Basin, Iran. Water. 2022; 14(6):870. https://doi.org/10.3390/w14060870
Chicago/Turabian StyleGoudarzi, Fatemeh, Amir Hedayatiaghmashhadi, Azadeh Kazemi, and Christine Fürst. 2022. "Optimal Location of Water Quality Monitoring Stations Using an Artificial Neural Network Modeling in the Qarah-Chay River Basin, Iran" Water 14, no. 6: 870. https://doi.org/10.3390/w14060870





