A Novel Calculation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM and Its Application in Nonlinear Cross-Scale CFRD-Reservoir Systems
Abstract
:1. Introduction
2. A Calculation Method of Hydrodynamic Pressure and Polyhedral Fluid Element
2.1. Computation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM
2.2. Polyhedral Scaled Boundary Finite Element of Fluid
2.2.1. Polygon Mean-Value Shape Function
2.2.2. Polyhedral Fluid Elements
3. A Nonlinear Dynamic Coupling Method for Cross-Scale Dam-Reservoir Systems Based on the Polyhedron SBFEM
3.1. Polyhedron SBFEM Procedure for Fluid
3.2. Nonlinear Dynamic Coupling Method for Cross-Scale CFRD-Reservoir Systems
4. Numerical Examples of Rigid Dams and River Valley
4.1. Dams with Polygonal Mesh on Upstream Face
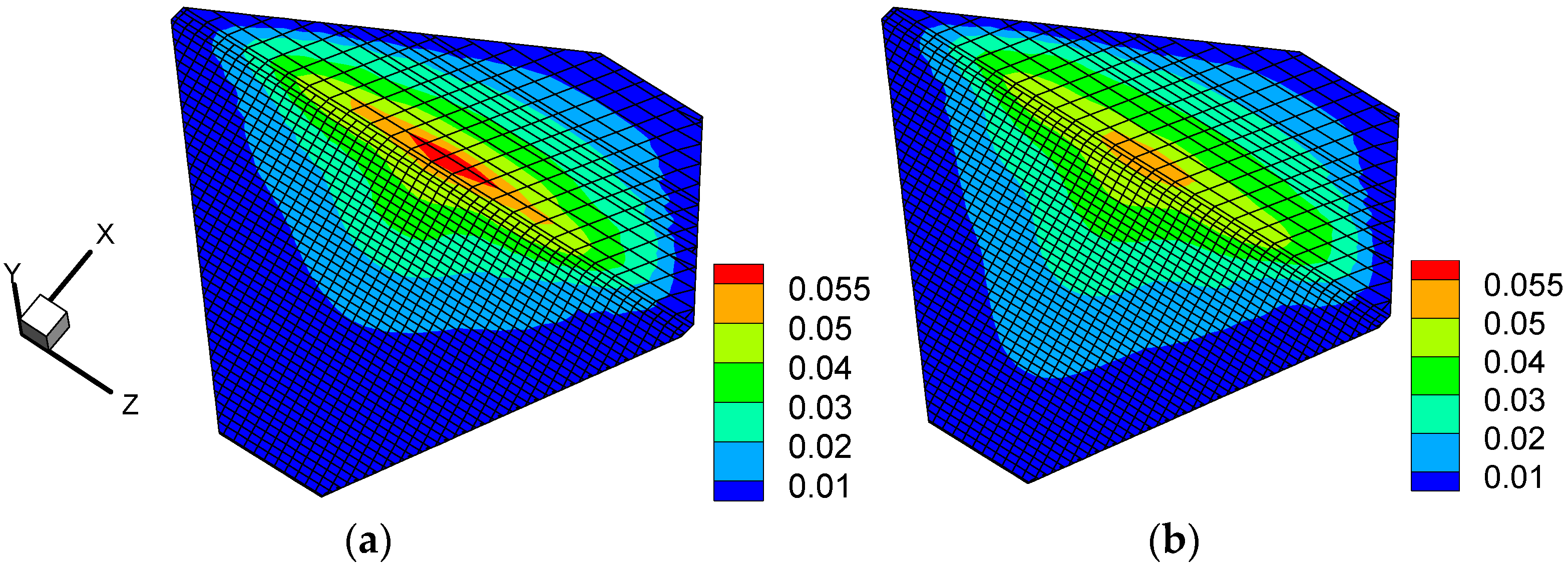
4.2. Results and Discussion
5. Dynamic Coupling Analysis of Nonlinear Cross-Scale CFRD and Reservoir Systems
5.1. Cross-Scale Model of the CFRD and Reservoir
5.2. Material Parameters, Damping Methods, and Ground Motion
5.3. Results and Discussion
5.3.1. Rockfill
5.3.2. Concrete Face Slabs
6. Conclusions
- (1)
- A 3D hydrodynamic pressure calculation method based on the polyhedron SBFEM was proposed, in which the reservoir in front of a dam was simulated with polygonal semi-infinite prismatic fluid elements. The pre-processing of the reservoir model was simplified to a large extent, as the 3D mesh of the reservoir could be generated automatically from the 2D grid of the upstream face of dam. A high efficiency was achieved also by reducing the one-dimensional discretization. The proposed method has a high accuracy and provides a convenient numerical tool for a dynamic coupling analysis of a dam–reservoir system, when the cross-scale dam is modeled by the polyhedron SBFEM.
- (2)
- With an elastic–plastic CFRD being simulated by the polyhedron SBFEM and the hydrodynamic pressure of the reservoir being computed by the proposed polyhedron SBFEM for fluid, respectively, a nonlinear dynamic coupling method for cross-scale CFRD-reservoir systems based on the polyhedron SBFEM was developed. The results of a further numerical analysis showed that neglecting hydrodynamic pressure may produce obvious errors and lead to overestimation of the dynamic acceleration and displacement response of the rockfill, which is not conducive to an accurate and reasonable safety evaluation of a CFRD under an earthquake. Moreover, the hydrodynamic pressure had a big influence on the dynamic face slabs’ stresses, and the hydrodynamic pressure cannot be ignored in the dynamic stress analysis of face slabs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ▽2 | Laplacian operator |
| p | Hydrodynamic pressure |
| ρ | Fluid density |
| ün | Normal accelerations of the dam–reservoir interface |
| ϋn | Normal accelerations of the river –valley interface |
| Polygon mean-value shape function | |
| [J] | Jacobian matrix |
| w | weight function |
| [E0], [E1], [E2], [C0], [M1] | Coefficient matrices |
| Nodal force | |
| [Z] | Hamilton coefficient matrix |
| [Λ] | Eigenvalue matrix |
| [Φ] | Eigenvector matrix |
| [A] | The inverse of eigenvector matrix [Φ] |
| Interpolation function in mean-value coordinate system | |
| Weight function of mean-value coordinate system | |
| Eulerian distance between points | |
| We | Cartesian coordinate system |
| W0 | Local coordinate system |
| [Ms], [Cs], [Ks] | Mass, damping and stiffness matrices |
| {ür(t)}, , {ur(t)} | Relative acceleration, velocity, and displacement |
| {üg(t)} | Input earthquake acceleration |
| [Mp] | Additional mass matrix of hydrodynamic pressure |
| [L1], [L2] | Conversion matrix |
| (x1, x2, x3) | Global coordinates |
| (ξ1, ξ2, ξ3) | Local scaled boundary coordinates |
| E | Elasticity modulus |
| Poisson’s ratios | |
| SBFEM | Scaled boundary finite element method |
| CFRD | Concrete faced rockfill dam |
| 3D | Three-dimensional |
| 2D | Two-dimensional |
| DOF | Degrees of freedom |
| FEM | Finite element method |
| BEM | Boundary element method |
| PSBFEM | Polyhedron SBFEM |
| PGA | Peak ground acceleration |
References
- Song, C.M. The Scaled Boundary Finite Element Method: Introduction to Theory and Implementation; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Wolf, J.P.; Song, C. The scaled boundary finite-element method—A primer: Derivations. Comput. Struct. 2000, 78, 191–210. [Google Scholar] [CrossRef]
- Ooi, E.T.; Song, C.M.; Natarajan, S. A scaled boundary finite element formulation with bubble functions for elasto-static analyses of functionally graded materials. Comput. Mech. 2017, 60, 943–967. [Google Scholar] [CrossRef]
- Xue, B.; Lin, G.; Hu, Z. Scaled boundary isogeometric analysis for electrostatic problems. Eng. Anal. Bound. Elem. 2017, 85, 20–29. [Google Scholar] [CrossRef]
- Zhang, X.; Wegner, J.L.; Haddow, J.B. Three-dimensional dynamic soil-structure interaction analysis in the time domain. Earthq. Eng. Struct. Dyn. 1999, 28, 1501–1524. [Google Scholar] [CrossRef]
- Wegner, J.L.; Zhang, X. Free-vibration analysis of a three-dimensional soil-structure system. Earthq. Eng. Struct. Dyn. 2001, 30, 43–57. [Google Scholar] [CrossRef]
- Genes, M.C.; Aslmand, M.; Kani, M. Efficient Dynamic Analysis of Foundation Via a Coupled Axisymmetric SBFEM-3D FEM. Teknik Dergi 2019, 30, 9327–9352. [Google Scholar] [CrossRef]
- Schauer, M.; Rios Rodriguez, G. A coupled FEM-SBFEM approach for soil-structure-interaction analysis using non-matching meshes at the near-field far-field interface. Soil Dyn. Earthq. Eng. 2019, 121, 466–479. [Google Scholar] [CrossRef]
- Yaseri, A. 2.5D coupled FEM-SBFEM analysis of ground vibrations induced by train movement. Soil Dyn. Earthq. Eng. 2017, 104, 307–318. [Google Scholar] [CrossRef]
- Chen, D.; Dai, S. Dynamic fracture analysis of the soil-structure interaction system using the scaled boundary finite element method. Eng. Anal. Bound. Elem. 2017, 77, 26–35. [Google Scholar] [CrossRef]
- Song, C.; Wolf, J.P. Semi-analytical representation of stress singularities as occurring in cracks in anisotropic multi-materials with the scaled boundary finite-element method. Comput. Struct. 2002, 80, 183–197. [Google Scholar] [CrossRef]
- Zhang, P.; Du, C.; Tian, X.; Jiang, S. A scaled boundary finite element method for modelling crack face contact problems. Comput. Methods Appl. Mech. Eng. 2018, 328, 431–451. [Google Scholar] [CrossRef]
- Yao, F.; Yang, Z.J.; Hu, Y.J. An SBFEM-Based Model for Hydraulic Fracturing in Quasi-Brittle Materials. Acta Mech. Solida Sin. 2018, 31, 416–432. [Google Scholar] [CrossRef]
- Adak, D.; Pramod, A.; Ooi, E.T.; Natarajan, S. A combined virtual element method and the scaled boundary finite element method for linear elastic fracture mechanics. Eng. Anal. Bound. Elem. 2020, 113, 9–16. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Tang, H.; Liu, J.; Zhuo, Y. Scaled boundary polygon formula for Cosserat continuum and its verification. Eng. Anal. Bound. Elem. 2021, 126, 136–150. [Google Scholar] [CrossRef]
- Qu, Y.; Zou, D.; Kong, X.; Yu, X.; Chen, K. Seismic cracking evolution for anti-seepage face slabs in concrete faced rockfill dams based on cohesive zone model in explicit SBFEM-FEM frame. Soil Dyn. Earthq. Eng. 2020, 133, 106106. [Google Scholar] [CrossRef]
- Jiang, S.; Du, C.; Ooi, E.T. Modelling strong and weak discontinuities with the scaled boundary finite element method through enrichment. Eng. Fract. Mech. 2019, 222, 106734. [Google Scholar] [CrossRef]
- Liu, J.; Hao, C.; Ye, W.; Yang, F.; Lin, G. Free vibration and transient dynamic response of functionally graded sandwich plates with power-law nonhomogeneity by the scaled boundary finite element method. Comput. Methods Appl. Mech. Eng. 2021, 376, 113665. [Google Scholar] [CrossRef]
- Zhang, P.; Du, C.; Tian, X.; Jiang, S. Buckling analysis of three-dimensional functionally graded sandwich plates using two-dimensional scaled boundary finite element method. Mech. Adv. Mater. Struct. 2021, 3, 431–451. [Google Scholar]
- He, Y.; Guo, J.; Yang, H. Image-based numerical prediction for effective thermal conductivity of heterogeneous materials: A quadtree based scaled boundary finite element method. Int. J. Heat Mass Transf. 2019, 128, 335–343. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Song, C.; He, K.; Saputra, A.A.; Gao, W. Automatic scaled boundary finite element method for three-dimensional elastoplastic analysis. Int. J. Mech. Sci. 2020, 171, 105374. [Google Scholar] [CrossRef]
- Wijesinghe, D.R.; Dyson, A.; You, G.; Khandelwal, M.; Song, C.; Ooi, E.T. Development of the scaled boundary finite element method for image-based slope stability analysis. Comput. Geotech. 2022, 143, 104586. [Google Scholar] [CrossRef]
- Li, J.; Shi, Z.; Liu, L.; Song, C. An efficient scaled boundary finite element method for transient vibro-acoustic analysis of plates and shells. Comput. Struct. 2020, 231, 106211. [Google Scholar] [CrossRef]
- Lin, G.; Xue, B.; Hu, Z. A mortar contact formulation using scaled boundary isogeometric analysis. Sci. China Phys. Mech. Astron. 2018, 61, 74621. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, P.; Lin, G.; Wang, W.; Lu, S. Solutions for the magneto-electro-elastic plate using the scaled boundary finite element method. Eng. Anal. Bound. Elem. 2016, 68, 103–114. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Kong, X. A nonlinear approach for the three-dimensional polyhedron scaled boundary finite element method and its verification using Koyna gravity dam. Soil Dyn. Earthq. Eng. 2017, 96, 1–12. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Kong, X.; Zhou, Y. Global concurrent cross-scale nonlinear analysis approach of complex CFRD systems considering dynamic impervious panel-rockfill material-foundation interactions. Soil Dyn. Earthq. Eng. 2018, 114, 51–68. [Google Scholar] [CrossRef]
- Chen, K.; Zou, D.; Kong, X.; Yu, X. An efficient nonlinear octree SBFEM and its application to complicated geotechnical structures. Comput. Geotech. 2018, 96, 226–245. [Google Scholar] [CrossRef]
- Zou, D.; Chen, K.; Kong, X.; Liu, J. An enhanced octree polyhedral scaled boundary finite element method and its applications in structure analysis. Eng. Anal. Bound. Elem. 2017, 84, 87–107. [Google Scholar] [CrossRef]
- Vaghefi, M.; Behroozi, A.M. Radial basis function differential quadrature for hydrodynamic pressure on dams with arbitrary reservoir and face shapes affected by earthquake. J. Appl. Fluid Mech. 2020, 13, 1759–1768. [Google Scholar]
- Pasbani Khiavi, M.; Sari, A. Evaluation of hydrodynamic pressure distribution in reservoir of concrete gravity dam under vertical vibration using an analytical solution. Math. Probl. Eng. 2021, 2021, 6669366. [Google Scholar] [CrossRef]
- Gorai, S.; Maity, D. Seismic Performance Evaluation of Concrete Gravity Dams in Finite-Element Framework. Pract. Period. Struct. Des. Constr. 2022, 27, 04021072. [Google Scholar] [CrossRef]
- Babaee, R.; Khaji, N. Decoupled scaled boundary finite element method for analysing dam–reservoir dynamic interaction. Int. J. Comput. Math. 2020, 97, 1725–1743. [Google Scholar] [CrossRef]
- Liu, J.; Lin, G.; Li, J. Short-crested waves interaction with a concentric cylindrical structure with double-layered perforated walls. Ocean Eng. 2012, 40, 76–90. [Google Scholar] [CrossRef]
- Song, H.; Tao, L. An efficient scaled boundary FEM model for wave interaction with a nonuniform porous cylinder. Int. J. Numer. Methods Fluids 2010, 63, 96–118. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.V.; Tornyeviadzi, H.M.; Bui, D.T.; Seidu, R. Predicting Discharges in Sewer Pipes Using an Integrated Long Short-Term Memory and Entropy A-TOPSIS Modeling Framework. Water 2022, 14, 300. [Google Scholar] [CrossRef]
- Teng, B.; Zhao, M.; He, G.H. Scaled boundary finite element analysis of the water sloshing in 2D containers. Int. J. Numer. Methods Fluids 2006, 52, 659–678. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Z.Q.; Guo, W.D. Hydrodynamic pressures on arch dam faces with irregular reservoir geometry. J. Vibrat. Control 2019, 25, 627–638. [Google Scholar] [CrossRef]
- Zeinizadeh, A.; Mirzabozorg, H.; Noorzad, A.; Amirpour, A. Hydrodynamic pressures in contraction joints including waterstops on seismic response of high arch dams. Structures 2018, 14, 1–14. [Google Scholar] [CrossRef]
- Wang, J.T.; Chopra, A.K. Linear analysis of concrete arch dams including dam-water-foundation rock interaction considering spatially varying ground motions. Earthq. Eng. Struct. Dyn. 2010, 39, 731–750. [Google Scholar] [CrossRef]
- Gao, Y.; Jin, F.; Wang, X.; Wang, J. Finite Element Analysis of Dam-Reservoir Interaction Using High-Order Doubly Asymptotic Open Boundary. Math. Probl. Eng. 2011, 2011, 668–680. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Zhang, G.; Jiang, C.; Liao, J.; Zhou, Q. Analysis of seismic damage process of high concrete dam-foundation system. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 042068. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Zhang, H.; Zhang, Y.; Guo, L.; Wang, Y.; Thira Htun, T.T. Influences on the seismic response of a gravity dam with different foundation and reservoir modeling assumptions. Water 2021, 13, 3072. [Google Scholar] [CrossRef]
- Feng, S.J.; Chen, Z.L.; Chen, H.X. Effects of multilayered porous sediment on earthquake-induced hydrodynamic response in reservoir. Soil Dyn. Earthq. Eng. 2017, 94, 47–59. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Hu, Z. Study on the effects of hydrodynamic pressure on the dynamic stresses in slabs of high CFRD based on the scaled boundary finite-element method. Soil Dyn. Earthq. Eng. 2016, 88, 223–236. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Su, X. Error study of Westergaard’s approximation in seismic analysis of high concrete-faced rockfill dams based on SBFEM. Soil Dyn. Earthq. Eng. 2017, 94, 88–91. [Google Scholar] [CrossRef]
- Fu, Z.Z.; Chen, S.S.; Li, G.Y. Hydrodynamic pressure on concrete face rockfill dams subjected to earthquakes. J. Hydrodyn. 2019, 32, 152–168. [Google Scholar] [CrossRef]
- Xu, H.; Zou, D.; Kong, X.; Hu, Z.; Su, X. A nonlinear analysis of dynamic interactions of CFRD-compressible reservoir system based on FEM-SBFEM. Soil Dyn. Earthq. Eng. 2018, 112, 24–34. [Google Scholar] [CrossRef]
- Karalar, M.; Çavuşli, M. Assessing 3D seismic damage performance of a CFR dam considering various reservoir heights. Earthq. Struct. 2019, 16, 221–234. [Google Scholar]
- Lin, G.; Wang, Y.; Hu, Z. An efficient approach for frequency-domain and time-domain hydrodynamic analysis of dam-reservoir systems. Earthq. Eng. Struct. Dyn. 2012, 41, 1725–1749. [Google Scholar] [CrossRef]
- Floater, M.S. Mean value coordinates. Comput. Aided Geom. Des. 2003, 20, 19–27. [Google Scholar] [CrossRef]
- Sukumar, N.; Tabarraei, A. Conforming polygonal finite elements. Int. J. Numer. Methods Eng. 2004, 61, 2045–2066. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Xu, J.; Zheng, H.; Wang, Y.; Sun, G.; Yang, Y. Novel displacement function for discontinuous deformation analysis based on mean value coordinates. Int. J. Numer. Methods Eng. 2020, 121, 4768–4792. [Google Scholar] [CrossRef]
- Degao, Z.; Xianjing, K.; Bin, X. User Manual for Geotechnical Dynamic Nonlinear Analysis; Institute of Earthquake Engineering, Dalian University of Technology: Dalian, China, 2005. [Google Scholar]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Zhang, X.; Wang, X. Fragility analysis of high CFRDs subjected to mainshock-aftershock sequences based on plastic failure. Eng. Struct. 2020, 206, 110152. [Google Scholar] [CrossRef]
- Xu, B.; Pang, R.; Zhou, Y. Verification of stochastic seismic analysis method and seismic performance evaluation based on multi-indices for high CFRDs. Eng. Geol. 2020, 264, 105412. [Google Scholar] [CrossRef]
- Li, Y.; Pang, R.; Xu, B.; Wang, X.; Fan, Q.; Jiang, F. GPDEM-based stochastic seismic response analysis of high concrete-faced rockfill dam with spatial variability of rockfill properties based on plastic deformation. Comput. Geotech. 2021, 139, 104416. [Google Scholar] [CrossRef]
- Qu, Y.; Zou, D.; Kong, X.; Liu, J.; Zhang, Y.; Yu, X. Seismic damage performance of the steel fiber reinforced face slab in the concrete-faced rockfill dam. Soil Dyn. Earthq. Eng. 2019, 119, 320–330. [Google Scholar] [CrossRef]
- Zou, D.; Sui, Y.; Chen, K. Plastic damage analysis of pile foundation of nuclear power plants under beyond-design basis earthquake excitation. Soil Dyn. Earthq. Eng. 2020, 136, 106179. [Google Scholar] [CrossRef]
- Zou, D.; Xu, B.; Kong, X.; Liu, H.; Zhou, Y. Numerical simulation of the seismic response of the Zipingpu concrete face rockfill dam during the Wenchuan earthquake based on a generalized plasticity model. Comput. Geotech. 2013, 49, 111–122. [Google Scholar] [CrossRef]
- Zou, D.; Han, H.; Liu, J.; Yang, D.; Kong, X. Seismic failure analysis for a high concrete face rockfill dam subjected to near-fault pulse-like ground motions. Soil Dyn. Earthq. Eng. 2017, 98, 235–243. [Google Scholar] [CrossRef]
- Chwang, A.T. Hydrodynamic pressures on sloping dams during earthquakes. Part 2. Exact theory. J. Fluid Mech. 1978, 87, 343–348. [Google Scholar] [CrossRef] [Green Version]
- Zhencheng, C. Dynamic water pressure on inclined dam face due to earthquake. Acta Mech. Sin. 1964, 7, 48–62. (In Chinese) [Google Scholar]
- Werner, P.; Sundquist, K. On hydrodynamic earthquake effects. Eos Trans. Am. Geophys. Union 1949, 30, 636–657. [Google Scholar] [CrossRef]
- Siao, T.-T.; Zhou, G.-M. Effects of shapes of valley cross-section on earthquake hydrodynamic pressure. J. Hydraul. Eng. 1965, 1, 1–15. (In Chinese) [Google Scholar]
- Xu, B.; Zou, D.; Liu, H. Three-dimensional simulation of the construction process of the Zipingpu concrete face rockfill dam based on a generalized plasticity model. Comput. Geotech. 2012, 43, 143–154. [Google Scholar] [CrossRef]























| G0 | K0 | Mg | Mf | αf | αg | H0 | HU0 | ms |
| 2400 | 2500 | 1.75 | 1.5 | 0.45 | 0.45 | 2900 | 2900 | 0.2 |
| mv | mt | mu | rd | γDM | γU | β0 | β1 | |
| 0.28 | 0.2 | 0.25 | 105 | 70 | 7 | 50 | 0.023 |
| k1 | k2 | n | φ/° | c/Pa |
| 300 | 1 × 1010 | 0.8 | 41.5 | 0 |
| Hydrodynamic Pressure | Acceleration (m/s2) | Displacement (m) | ||
|---|---|---|---|---|
| ax | ay | dx | dy | |
| Polyhedron SBFEM | 4.61 | 2.72 | 0.062 | 0.055 |
| Neglecting | 5.32 | 2.87 | 0.071 | 0.059 |
| Error | 15.4% | 5.5% | 12.7% | 7.3% |
| Hydrodynamic Pressure | Slope Direction (MPa) | Dam Axial Direction (MPa) | ||
|---|---|---|---|---|
| Tensile | Compressive | Tensile | Compressive | |
| Polyhedron SBFEM | −3.83 | 3.16 | −2.05 | 3.38 |
| Neglecting | −4.69 | 3.48 | −1.88 | 2.54 |
| Error | 22.5% | 9.2% | 8.3% | 24.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Xu, H.; Yan, D.; Chen, K.; Zou, D. A Novel Calculation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM and Its Application in Nonlinear Cross-Scale CFRD-Reservoir Systems. Water 2022, 14, 867. https://doi.org/10.3390/w14060867
Xu J, Xu H, Yan D, Chen K, Zou D. A Novel Calculation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM and Its Application in Nonlinear Cross-Scale CFRD-Reservoir Systems. Water. 2022; 14(6):867. https://doi.org/10.3390/w14060867
Chicago/Turabian StyleXu, Jianjun, He Xu, Dongming Yan, Kai Chen, and Degao Zou. 2022. "A Novel Calculation Method of Hydrodynamic Pressure Based on Polyhedron SBFEM and Its Application in Nonlinear Cross-Scale CFRD-Reservoir Systems" Water 14, no. 6: 867. https://doi.org/10.3390/w14060867







